Task Assignment of UAV Swarm Based on Wolf Pack Algorithm
Abstract
:1. Introduction
2. Task Assignment Model
- There are no obstacles and no-fly zones in the task scenario. A flight trajectory can be described as connections of straight lines.
- It does not take into account the consumption of time spent preparing and firing the weapon. In other words, only the time the UAV swarm takes to reach the target positions is considered.
- The UAV swarm maintains the same constant velocity and hence the flight time can be represented with the flight distance.
- Each target can be attacked only once. There are more targets than UAVs in the swarm, which means each UAV will probably be assigned multiple targets.
- Total range of all UAVsFor all UAVs in the swarm, the average range is
- Time to complete all taskswhere is the time of UAV to finish all of its tasks. With consideration of the same constant velocity for all UAVs, the time of UAV to finish all of its tasks can be expressed as its total range. Therefore, Equation (4) can be represented as Equation (5).
3. The Wolf Pack Algorithm
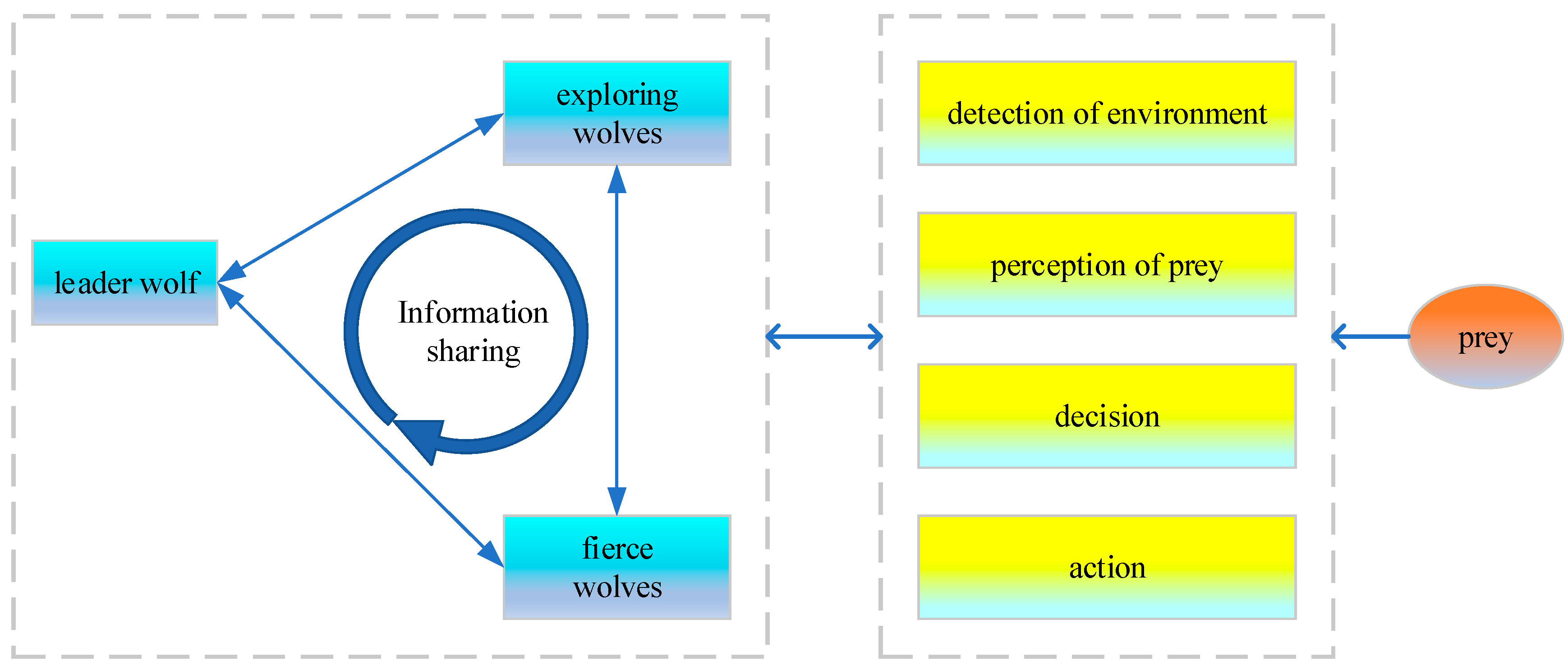
3.1. The Basics of the Wolf Pack Algorithm
- the selection of the leader wolf based on the winner-take-all rule;
- three cooperative behaviors including walking, calling and sieging;
- an update mechanism based on the strongest-survives law.
| Alorithm 1: WPA |
 |
3.1.1. The Selection of Leader Wolf Based on Winner-Take-All Rule
3.1.2. Three Cooperative Behaviors
- Walking behavior. suboptimal wolves are selected as exploring wolves to perform the walking behavior. is a random integer picked from , where is the scale factor of exploring wolves. Starting from the current position, exploring wolf makes one step forward towards directions. On account of individual differences, generally takes a random integer within a limited range. The new position to the direction is obtained bywhere is the length of walking step. Exploring wolf will return to its initial position after detecting each direction, then choose the best one to update its position. All exploring wolves will keep walking until the satisfy one of the following conditions.
- As long as one exploring wolf’s new position is better than that of the leader wolf, this exploring wolf will be the new leader wolf and the wolf pack will move to the calling behavior.
- When walking times reach the maximum , the wolf pack move to the calling behavior.
- 2.
- Calling behavior. The leader wolf calls for nearest wolves as fierce wolves to get close to its position rapidly with a large step. The new position of fierce wolf is obtained bywhere is the length of raid step. Fierce wolves will continue to get close to the leader wolf until one of the following conditions is satisfied.
- As long as one fierce wolf’s new position is better than that of the leader wolf, this fierce wolf will be the new leader and the wolf pack moves to the sieging behavior.
- The Manhattan distance between a fierce wolf and the leader wolf is less than the threshold distance . is estimated according towhere is the factor representing the threshold distance and is the variable’s domain in the dimension.
- 3.
- Sieging behavior. The leader wolf, whose position is treated as the prey’s position, guides all other wolves to siege the prey with a small step. For iteration , the position of the prey is ; then the new position of wolf is updated according towhere is a random real number in , and is the length of the siege step. For any wolf, if its new position is better than the current position, its position will be updated, otherwise its current position will be kept. The wolf whose position is the best will be chosen as the leader wolf.
3.1.3. Update Mechanism Based on Strong-Survive Law
3.2. The Proposed PSO-GA-DWPA
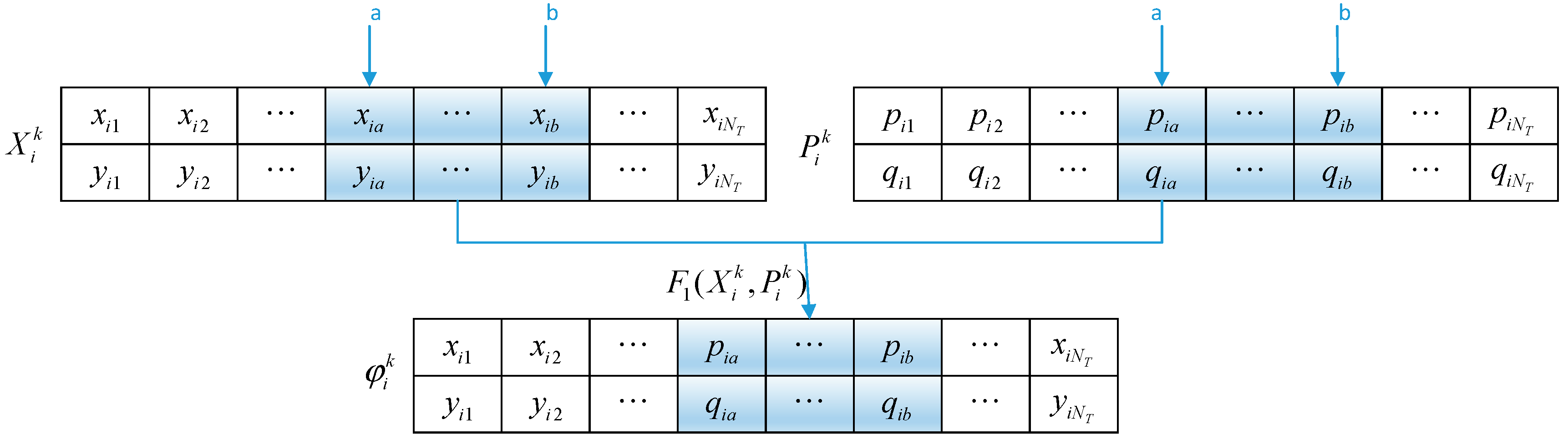
3.2.1. Integer Matrix Coding
3.2.2. Improvement on Walking Behavior
- Tracking individual extremum
- 2.
- Tracking global extremum
- 3.
- Individual variation
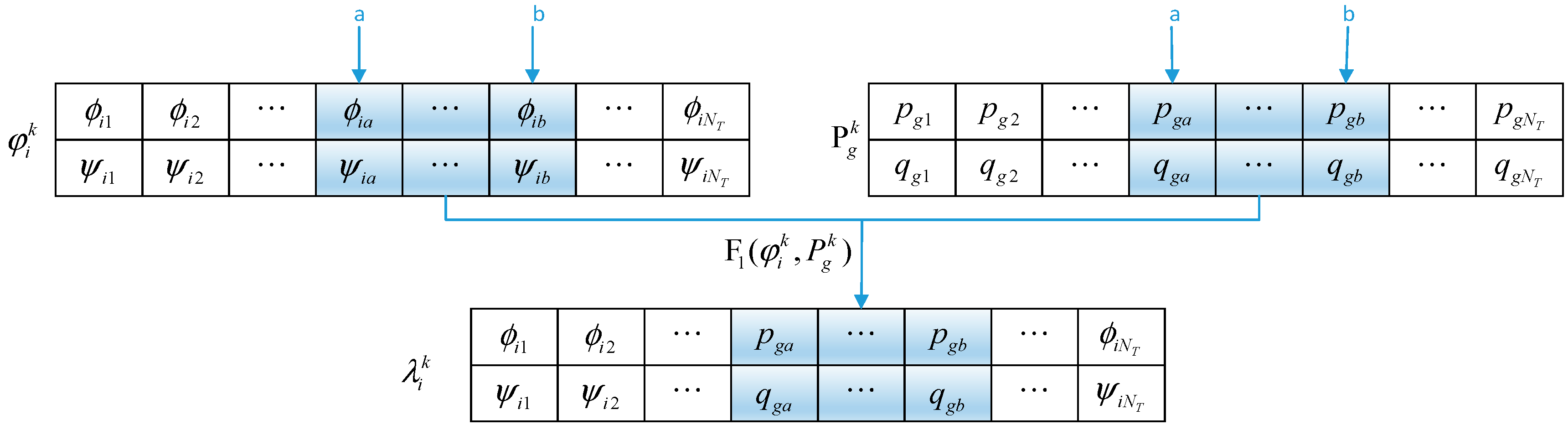
3.2.3. Improvement on Calling Behavior
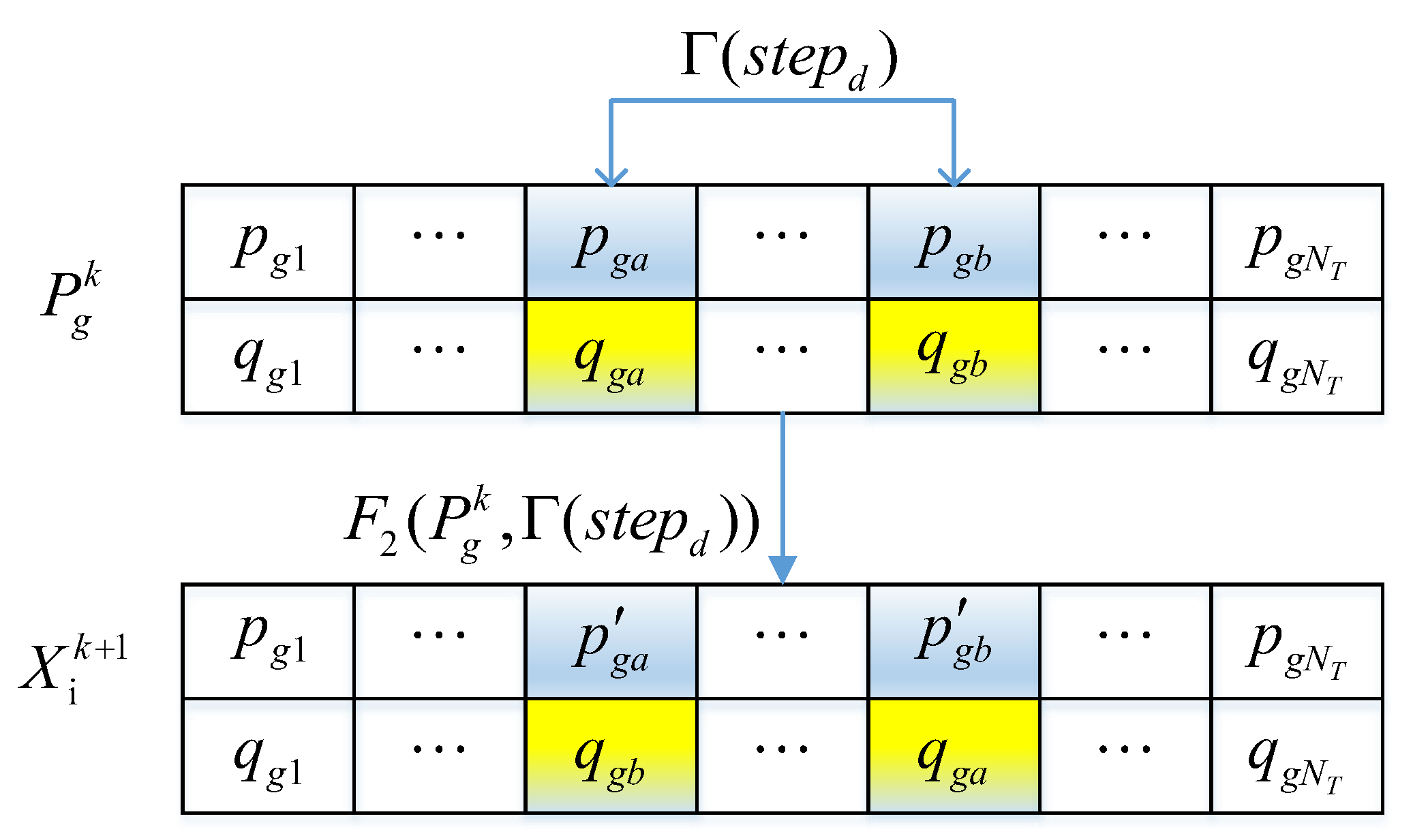
3.2.4. Improvement on Sieging Behavior
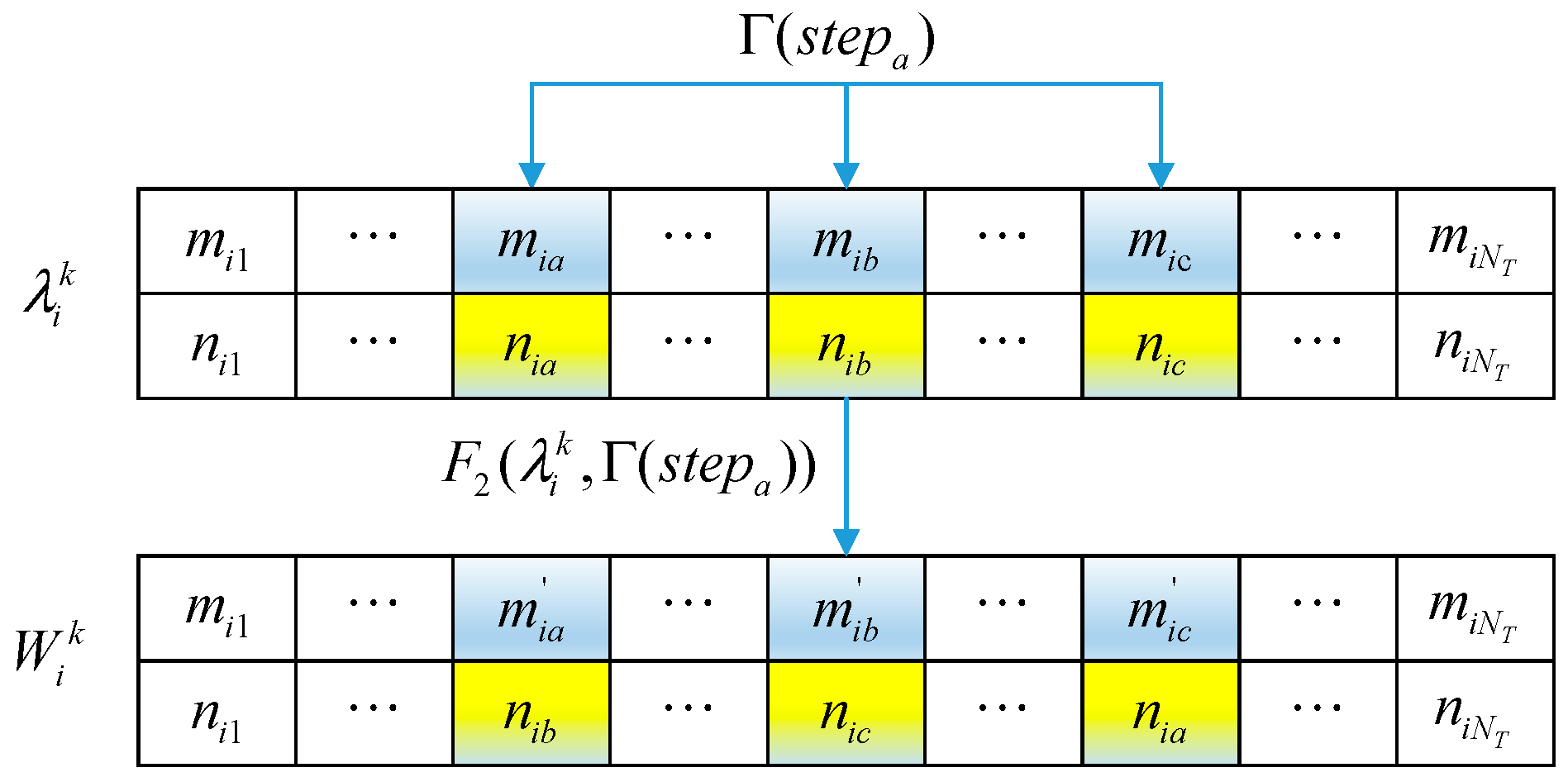
3.2.5. Improvement in Wolf Population Update
| Alorithm 2: POS-GA-DWPA |
 |
4. Experiments of Task Assignment for UAV Swarm Using PSO-GA-DWPA
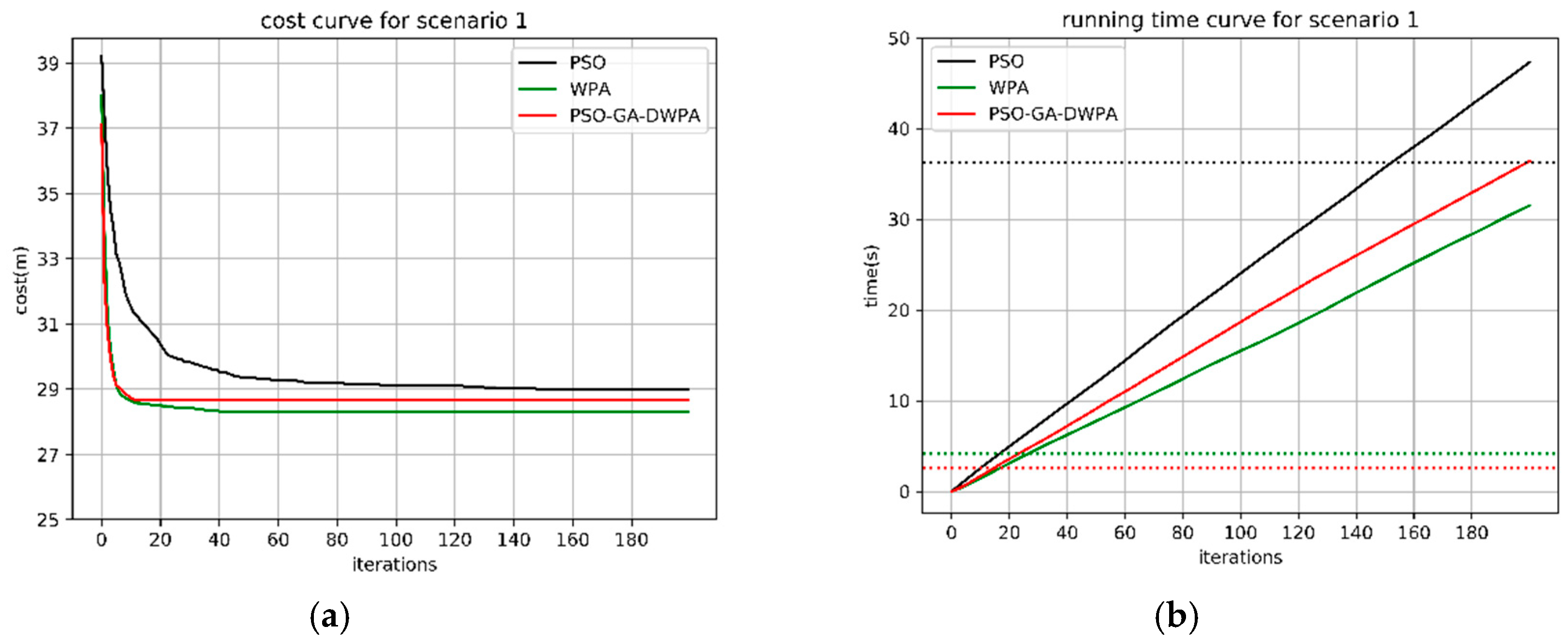
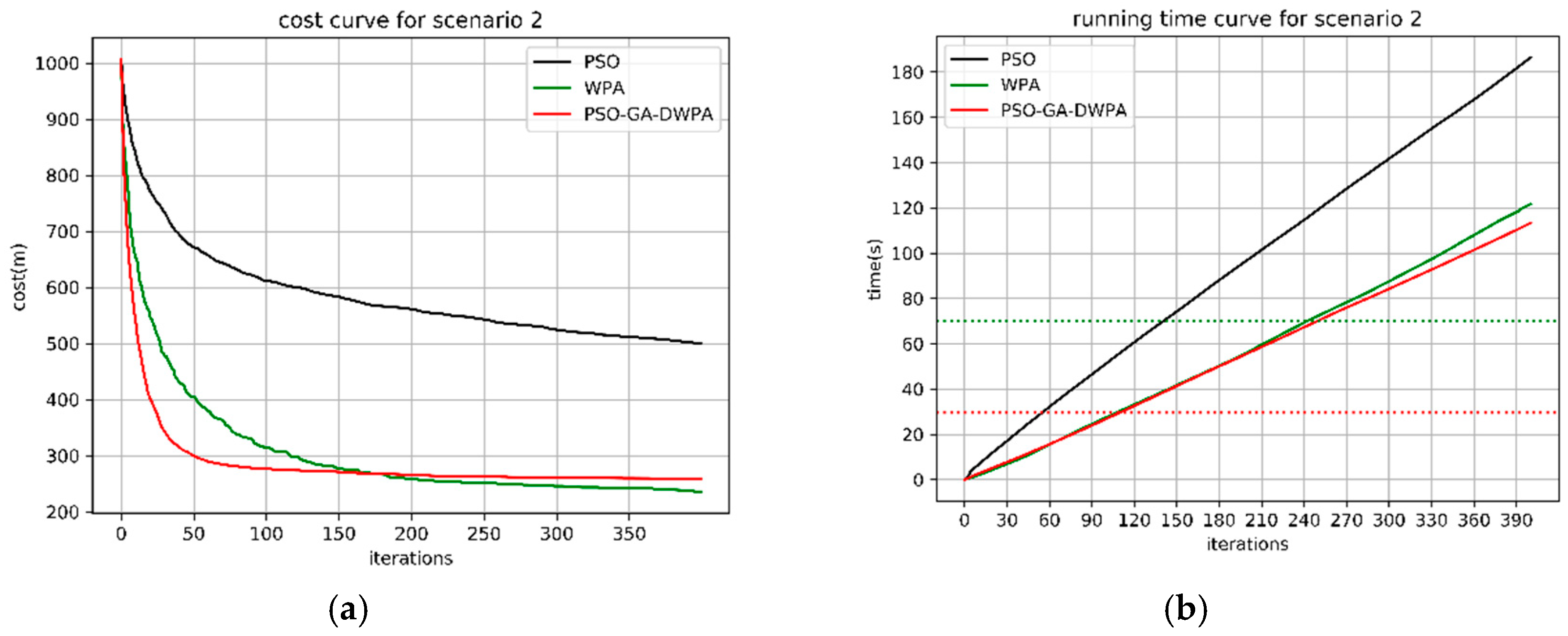
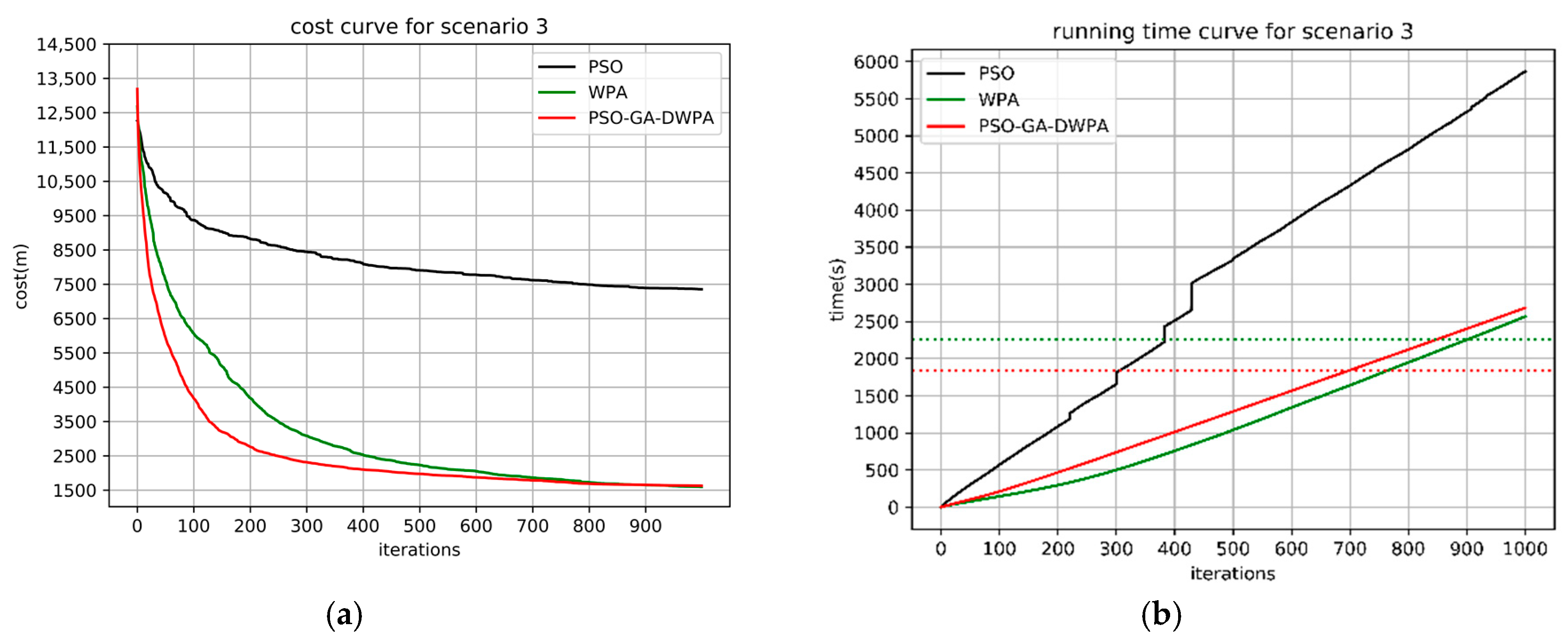
4.1. Monte Carlo Simulation in Different Scenarios
4.2. The Real-Time Analysis of the PSO-GA-DWPA
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peters, J.R.; Surana, A.; Bullo, F. Robust Scheduling and Routing for Collaborative Human/Unmanned Aerial Vehicle Surveillance Missions. J. Aerosp. Inf. Syst. 2018, 15, 1–19. [Google Scholar] [CrossRef]
- Ran, H.; Zhou, R.; Dong, Z. Cooperative guidance of multi aircraft in beyond-visual-range air combat. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 1457–1462. [Google Scholar]
- Cattrysse, D.; van Wassenhove, L. A survey of algorithms for the generalized assignment problem. Eur. J. Oper. Res. 1992, 60, 260–272. [Google Scholar] [CrossRef] [Green Version]
- Drexl, M. Synchronization in vehicle routing-a survey of VRPs with multiple synchronization constraints. Transp. Sci. 2012, 46, 297–316. [Google Scholar] [CrossRef] [Green Version]
- Shima, T.; Rasmussen, S.J.; Sparks, A.G.; Passino, K.M. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2006, 33, 3252–3269. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Shima, T.; Rasmussen, S.J. Tree search algorithm for assigning cooperating UAVs to multiple tasks. Int. J. Robust Nonlinear Control 2008, 18, 135–153. [Google Scholar]
- Alighanbari, M.; How, J. Cooperative task assignment of unmanned aerial vehicles in adversarial environments. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 4661–4666. [Google Scholar]
- Ling, X. The approximate optimal solution of the traveling salesman problem is obtained by the optimal exhaustive method. Comput. Appl. Res. 1998, 15, 82–83. [Google Scholar]
- Lipson, J.D. Newton’s method: A great algebraic algorithm. In Proceedings of the Third ACM Symposium on Symbolic & Algebraic Computation, Yorktown Heights, NY, USA, 10 August 1976; pp. 260–270. [Google Scholar]
- Ji, S.; Ye, J. An accelerated gradient method for trace norm minimization. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 457–464. [Google Scholar]
- Wang, C.; Mu, D.; Zhao, F.; Sutherland, J.W. A parallel simulated annealing method for the vehicle routing problem with simultaneous pickup-delivery and time windows. Comput. Ind. Eng. 2015, 83, 111–122. [Google Scholar] [CrossRef]
- Diaz, J.A.; Fernandez, E. A Tabu search heuristic for the generalized assignment problem. Eur. J. Oper. Res. 2011, 132, 22–38. [Google Scholar] [CrossRef]
- Shima, T.; Rasmussen, S.J.; Sparks, A.G. UAV cooperative multiple task assignments using genetic algorithms. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 2989–2994. [Google Scholar]
- Boveiri, H.R. An incremental ant colony optimization based approach to task assignment to processors for multiprocessor scheduling. Front. Inf. Technol. Electron. Eng. 2017, 18, 498–510. [Google Scholar] [CrossRef]
- Sujit, P.B.; George, J.M.; Beard, R. Multiple UAV task allocation using particle swarm optimization. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; pp. 1–9. [Google Scholar]
- Jia, Z.; Yu, J.; Ai, X.; Xu, X.; Yang, D. Cooperative multiple task assignment problem with stochastic velocities and time windows for heterogeneous unmanned aerial vehicles using a genetic algorithm. Aerosp. Sci. Technol. 2018, 76, 112–125. [Google Scholar] [CrossRef]
- Liang, G.; Kang, Y.; Xing, Z.; Yin, G. UAV Cooperative Multi-task Assignment Based on Discrete Particle Swarm Optimization Algorithm. Comput. Simul. 2018, 35, 22–28. [Google Scholar]
- Su, F. Research on Distributed Online Cooperative Mission Planning for Multiple Unmanned Combat Aerial Vehicles in Dynamic Environment. PhD Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Wu, X. Coordination Tasks Pre-Allocation and Redistribution Studies in UAVs. Master’s Thesis, Nanchang Hangkong University, Nanchang, China, 2018. [Google Scholar]
- Braun, H. On solving travelling salesman problems by genetic algorithms. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 1990; pp. 129–133. [Google Scholar]
- Tuani, A.F.; Keedwell, E.; Collett, M. Heterogenous Adaptive Ant Colony Optimization with 3-opt local search for the Travelling Salesman Problem. Appl. Soft Comput. 2020, 106720, 1–14. [Google Scholar] [CrossRef]
- Matin, H.N.; Yekkehkhany, A.; Nagi, R. Probabilistic Analysis of UAV Routing with Dynamically Arriving Targets. In Proceedings of the 22th International Conference on Information Fusion, Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Di, B.; Rui, Z.; Jiang, W. Distributed coordinated heterogeneous task allocation for unmanned aerial vehicles. Control Decis. 2013, 28, 274–278. [Google Scholar]
- Oh, G.; Kim, Y.; Ahn, J.; Choi, H.-L. Market-Based Task Assignment for Cooperative Timing Missions in Dynamic Environments. J. Intell. Robot. Syst. 2017, 87, 97–123. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Li, F.; Zhou, T. Dynamic Task Assignment Problem of Multi-agent. Electron. Technol. Softw. Eng. 2018, 18, 255–258. [Google Scholar]
- Li, Y.; Dong, Y. Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat. Acta Aeronaut. Et Astronaut. Sin. 2010, 31, 626–631. [Google Scholar]
- Kumar, N.; Vidyarthi, D.P. A novel hybrid PSO-GA metaheuristic for scheduling of DAG with communication on multiprocessor systems. Eng. Comput. 2016, 32, 35–47. [Google Scholar] [CrossRef]
- López LF, M.; Blas, N.G.; Albert, A.A. Multidimensional knapsack problem optimization using a binary particle swarm model with genetic operations. Soft Comput. 2018, 22, 2567–2582. [Google Scholar] [CrossRef]
- Guo, T.; Michalewicz, Z. Inver-over operator for the TSP. In International Conference on Parallel Problem Solving from Nature; Springer: Heidelberg, Germany, 1998; pp. 803–812. [Google Scholar]
- Yan, J.; Li, X.; Liu, B. Cooperative task allocation of multi-UAVs with mixed DPSO-GT algorithm. J. Natl. Univ. Def. Technol. 2015, 37, 165–171. [Google Scholar]
- Wu, H.; Zhang, F.; Wu, L. New Swarm Intelligence Algorithm-Wolf Pack Algorithm. Syst. Eng. Electron. 2013, 35, 2430–2437. [Google Scholar]
- Liu, Y.; Li, W.; Wu, H.; Song, W. Track Planning for Unmanned Aerial Vehicles Based on Wolf Pack Algorithm. J. Syst. Simul. 2015, 27, 1838–1843. [Google Scholar]
- Zhang, L.; Lei, Z.; Liu, S.; Zhou, J. Three-Dimensional Underwater Path Planning Based on Modified Wolf Pack Algorithm. IEEE Access 2017, 5, 22783–22795. [Google Scholar] [CrossRef]




| Parameters | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| iterations | 200 | 400 | 1000 |
| population size | 100 | 100 | 100 |
| 2 | 2 | 2 | |
| 4 | 14 | 70 | |
| 1 | 2 | 2 | |
| 2 | 2 | 2 | |
| 10 | 10 | 10 | |
| 2 | 14 | 70 | |
| 4 | 4 | 4 | |
| 5 | 5 | 5 |
| Scenario | Algorithm | Cost Function | Convergence Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Maximum | Minimum | Mean | Standard Deviation | Maximum | Minimum | Mean | Standard Deviation | ||
| 5 vs. 8 | PSO | 31.69 | 28.72 | 29.49 | 0.78 | 46.77 | 16.23 | 36.31 | 7.8 |
| WPA | 29.7 | 28.72 | 28.92 | 0.37 | 7.47 | 2.64 | 4.22 | 1.43 | |
| PSO-GA-WPA | 30.98 | 28.72 | 29.23 | 0.52 | 4.36 | 1.45 | 2.53 | 0.17 | |
| 20 vs. 30 | PSO | 582.86 | 412.4 | 511.84 | 37 | - | - | - | - |
| WPA | 279.15 | 239.23 | 261.95 | 12.65 | 100.55 | 64.89 | 70.29 | 10.17 | |
| PSO-GA-WPA | 269.84 | 235.28 | 253.6 | 10.2 | 51 | 23.67 | 29.56 | 4.77 | |
| 100 vs. 150 | PSO | 8586 | 7929 | 8212 | 225 | - | - | - | - |
| WPA | 1908 | 1650 | 1783 | 80 | 2508 | 2160 | 2255 | 102 | |
| PSO-GA-WPA | 1880 | 1480 | 1606 | 78 | 1894 | 1784 | 1844 | 27 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Ma, Y.; Wang, J.; Han, L. Task Assignment of UAV Swarm Based on Wolf Pack Algorithm. Appl. Sci. 2020, 10, 8335. https://doi.org/10.3390/app10238335
Lu Y, Ma Y, Wang J, Han L. Task Assignment of UAV Swarm Based on Wolf Pack Algorithm. Applied Sciences. 2020; 10(23):8335. https://doi.org/10.3390/app10238335
Chicago/Turabian StyleLu, Yingtong, Yaofei Ma, Jiangyun Wang, and Liang Han. 2020. "Task Assignment of UAV Swarm Based on Wolf Pack Algorithm" Applied Sciences 10, no. 23: 8335. https://doi.org/10.3390/app10238335





