Hydrogen Intramolecular Stretch Redshift in the Electrostatic Environment of Type II Clathrate Hydrates from Schrödinger Equation Treatment
Abstract
1. Introduction
2. Methodology
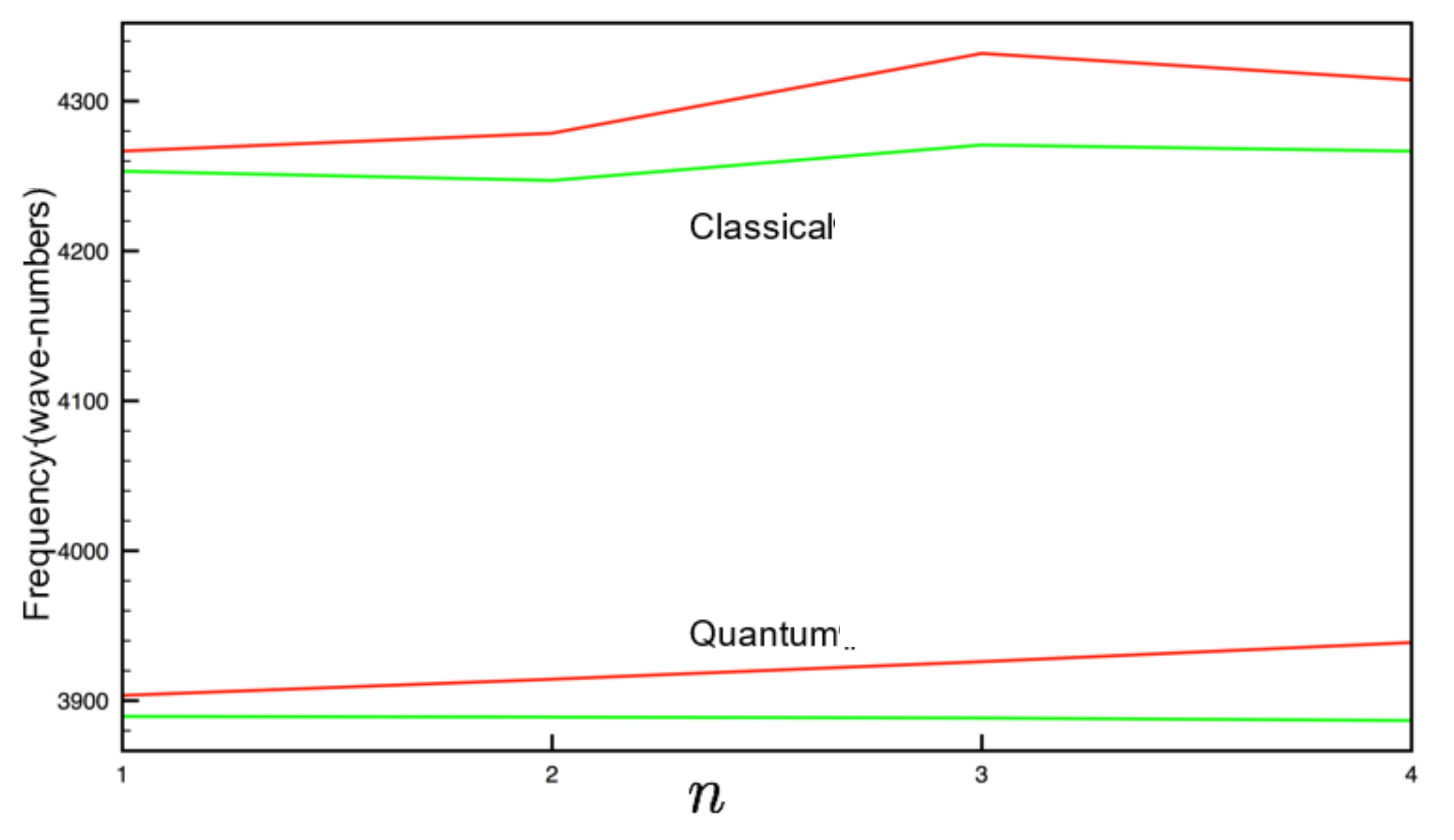
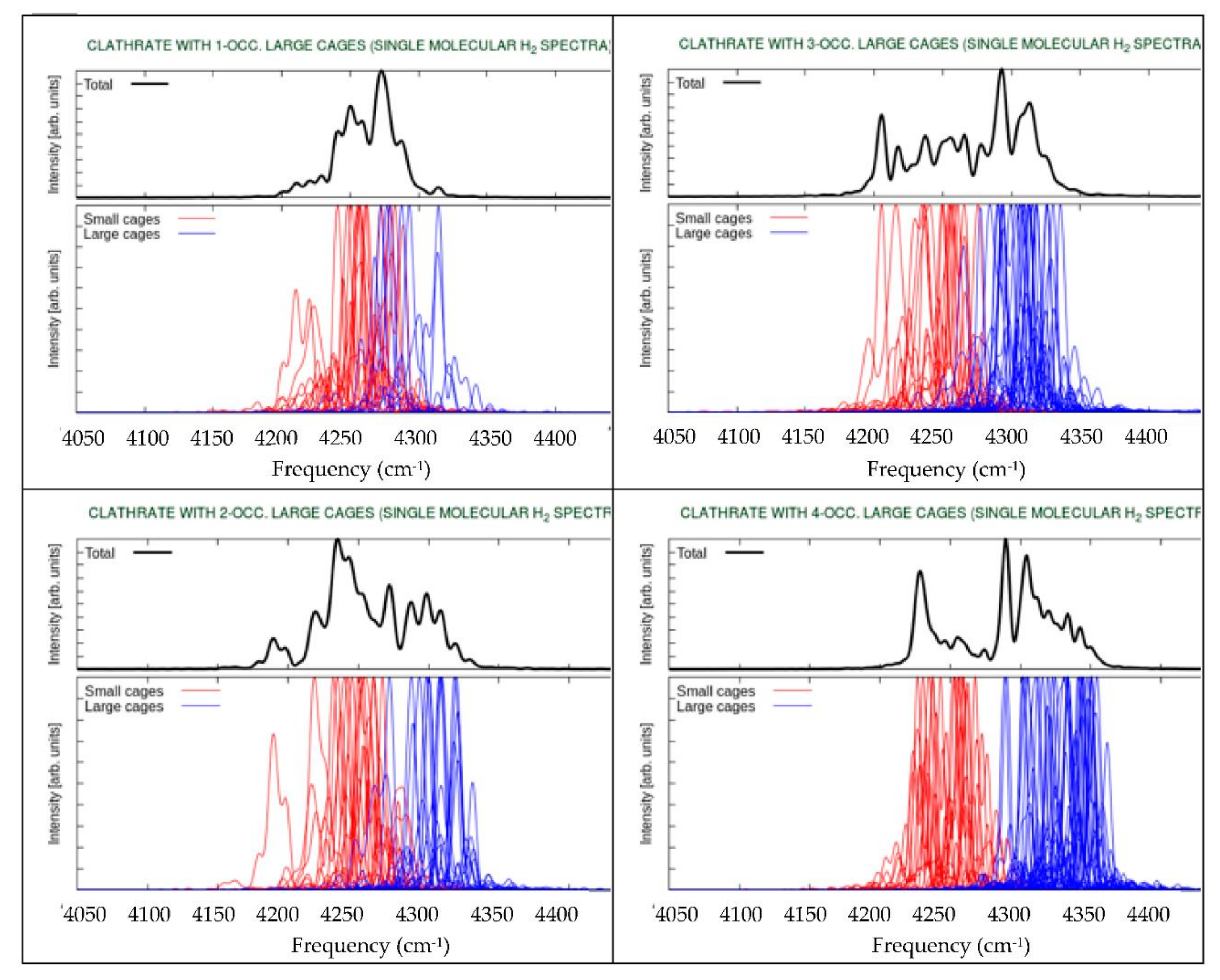
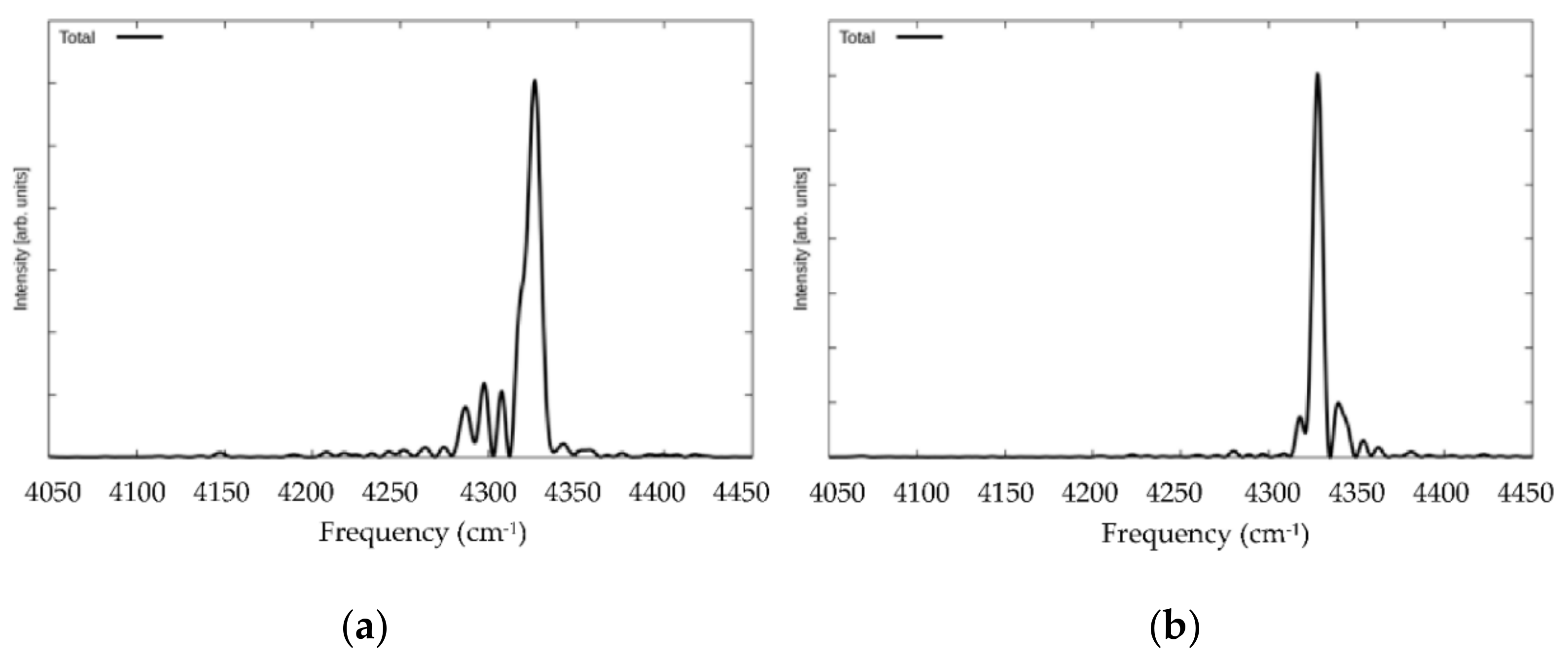
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Makogon, Y.F. Hydrates of Hydrocarbons; Penn Well Books: Tulsa, OK, USA, 1997. [Google Scholar]
- Burnham, C.J.; English, N.J. Free-energy calculations of the intercage hopping barriers of hydrogen molecules in clathrate hydrates. J. Phys. Chem. C 2016, 120, 16561. [Google Scholar] [CrossRef]
- Burnham, C.J.; Futera, Z.; English, N.J. Quantum and classical inter-cage hopping of hydrogen molecules in clathrate hydrate: Temperature and cage-occupation effects. Phys. Chem. Chem. Phys. 2017, 19, 717. [Google Scholar] [CrossRef] [PubMed]
- Burnham, C.J.; Futera, Z.; English, N.J. Study of hydrogen-molecule guests in type II clathrate hydrates using a force-matched potential model parameterised from ab-initio molecular dynamics. J. Chem. Phys. under review. [CrossRef] [PubMed]
- Trinh, T.T.; Waage, M.H.; van Erp, T.S.; Kjelstrup, S. Low barriers for hydrogen diffusion in sII clathrate. Phys. Chem. Chem. Phys. 2015, 7, 13808. [Google Scholar] [CrossRef]
- Cendagorta, J.R.; Powers, A.; Hele, T.J.H.; Marsalek, O.; Bačić, Z.; Tuckerman, M.E. Competing quantum effects in the free energy profiles and diffusion rates of hydrogen and deuterium molecules through clathrate hydrates. Phys. Chem. Chem. Phys. 2016, 18, 32169. [Google Scholar] [CrossRef]
- Cao, H.; English, N.J.; MacElroy, J.M.D. Diffusive hydrogen inter-cage migration in hydrogenand hydrogen-tetrahydrofuran clathrate hydrates. J. Chem. Phys. 2013, 138, 094507. [Google Scholar] [CrossRef]
- Alavi, S.; Ripmeester, J.A. Hydrogen-Gas Migration through Clathrate Hydrate Cages. Angew. Chem. 2007, 46, 6102. [Google Scholar] [CrossRef]
- Frankcombe, T.J.; Kroes, G.-J. Molecular Dynamics Simulations of Type-sII Hydrogen Clathrate Hydrate Close toEquilibrium Conditions. J. Phys. Chem. C 2007, 111, 13044. [Google Scholar] [CrossRef]
- Peters, B.; Zimmerman, N.E.R.; Beckham, G.T.; Tester, J.W.; Trout, B.L. Path Sampling Calculation of Methane Diffusivity in Natural Gas Hydrates from a Water-Vacancy Assisted Mechanism. J. Am. Chem. Soc. 2008, 130, 17342. [Google Scholar] [CrossRef]
- Gorman, P.D.; English, N.J.; MacElroy, J.M.D. Dynamical cage behaviour and hydrogen migration in hydrogen and hydrogen-tetrahydrofuran clathrate hydrates. J. Chem. Phys. 2012, 136, 044506. [Google Scholar] [CrossRef]
- English, N.J.; MacElroy, J.M.D. Perspectives on Molecular Simulation of Clathrate Hydrates: Progress, Prospects and Challenges. Chem. Eng. Sci. 2015, 121, 133. [Google Scholar] [CrossRef]
- Mao, W.L.; Mao, H.K.; Goncharov, A.F.; Struzhkin, V.V.; Guo, Q.; Hu, J.; Shu, J.; Hemley, R.J.; Somayazulu, M.; Zhao, Y. Hydrogen Clusters in Clathrate Hydrate. Science 2002, 297, 2247–2249. [Google Scholar] [CrossRef] [PubMed]
- Alavi, S.; Ripmeester, J.A.; Klug, D.D. Molecular-Dynamics Study of Structure II Hydrogen Clathrate. J. Chem. Phys. 2005, 123, 024507. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.L.; Mao, H.-K. Hydrogen Storage in Molecular Compounds. Proc. Nat. Acad. Sci. USA 2004, 101, 708–710. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Tse, J.S. Thermodynamic Stability of Hydrogen Clathrate. Proc. Nat. Acad. Sci. USA 2003, 100, 14645–14650. [Google Scholar] [CrossRef]
- Lee, J.W.; Yedlapalli, P.; Lee, S. Prediction of Hydrogen Hydrate Equilibrium by Integrating Ab Initio Calculations with Statistical Thermodynamics. J. Phys. Chem. B 2006, 110, 2332–2337. [Google Scholar] [CrossRef]
- Sluiter, M.H.; Adachi, H.F.; Belosludov, R.V.; Belosludov, V.R.; Kawazoe, Y. Ab Initio Study of Hydrogen Storage in Hydrogen Hydrate Clathrate. Mater. Trans. 2004, 45, 1452–1454. [Google Scholar] [CrossRef][Green Version]
- Chattaraj, P.K.; Bandaru, S.; Mondal, S. Hydrogen Storage in Clathrate Hydrates. J. Phys. Chem. A 2011, 115, 187–193. [Google Scholar] [CrossRef]
- Willow, S.Y.; Xantheas, S.S. Enhancement of Hydrogen Storage Capacity in Hydrate Lattices. Chem. Phys. Lett. 2012, 525, 13–18. [Google Scholar] [CrossRef]
- Mao, W.L.; Koh, C.A.; Sloan, E.D. Clathrate Hydrates under Pressure. Phys. Today 2007, 60, 42–47. [Google Scholar] [CrossRef]
- Xu, M.; Elmatad, Y.; Sebastianelli, F.; Moskowitz, J.W.; Bacic, Z. Hydrogen molecule in the small dodecahedral cage of a clathrate hydrate: Quantum five-dimensional calculations of the coupled translation-rotation eigenstates. J. Phys. Chem. B 2006, 110, 24806. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Sebastianelli, F.; Bacic, Z. Quantum dynamics of H2, D2, and HD in the small dodecahedral cage of clathrate hydrate: Evaluating H2-water nanocage interaction potentials by comparison of theory with inelastic neutron scattering experiments. J. Chem. Phys. 2008, 128, 244715. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Sebastianelli, F.; Bacic, Z. Coupled translation-rotation eigenstates of H2, HD, and D2 in the large cage of structure II clathrate hydrate: Comparison with the small cage and rotational Raman spectroscopy. J. Phys. Chem. A 2009, 113, 7601. [Google Scholar] [CrossRef] [PubMed]
- Powers, A.; Marsalek, O.; Xu, M.; Ulivi, L.; Colognesi, D.; Tuckerman, M.E.; Bacic, Z. Impact of the condensed-phase environment on the translation-rotation eigenstates and spectra of a hydrogen molecule in clathrate hydrates. J. Phys. Chem. Lett. 2016, 7, 308. [Google Scholar] [CrossRef]
- Xu, M.; Felker, P.M.; Bacic, Z. Light molecules inside the nanocavities of fullerenes and clathrate hydrates: Inelastic neutron scattering spectra and the unexpected selection rule from rigorous quantum simulations. Int. Rev. Phys. Chem. 2020, 39, 425. [Google Scholar] [CrossRef]
- Xu, M.; Ulivi, L.; Celli, M.; Colognesi, D.; Bačić, Z. Quantum Calculation of Inelastic Neutron Scattering Spectra of a Hydrogen Molecule Inside a Nanoscale Cavity Based on Rigorous Treatment of the Coupled Translation-Rotation Dynamics. Phys. Rev. B 2011, 83, 241403. [Google Scholar] [CrossRef]
- Xu, M.; Ulivi, L.; Celli, M.; Colognesi, D.; Bačić, Z. Rigorous Quantum Treatment of Inelastic Neutron Scattering Spectra of a Heteronuclear Diatomic Molecule in a Nanocavity: HD in the Small Cage of Structure II Clathrate Hydrate. Chem. Phys. Lett. 2013, 563, 1–8. [Google Scholar] [CrossRef]
- Colognesi, D.; Celli, M.; Ulivi, L.; Xu, M.; Bačić, Z. Neutron Scattering Measurements and Computation of the Quantum Dynamics of Hydrogen Molecules Trapped in the Small and Large Cages of Clathrate Hydrates. J. Phys. Chem. A 2013, 117, 7314–7326. [Google Scholar] [CrossRef]
- Celli, M.; Powers, A.; Colognesi, D.; Xu, M.; Bačić, Z.; Ulivi, L. Experimental Inelastic Neutron Scattering Spectrum of Hydrogen Hexagonal Clathrate-Hydrate Compared with Rigorous Quantum Simulations. J. Chem. Phys. 2013, 139, 164507. [Google Scholar] [CrossRef]
- Colognesi, D.; Powers, A.; Celli, M.; Xu, M.; Bačić, Z.; Ulivi, L. The HD Molecule in Small and Medium Cages of Clathrate Hydrates: Quantum Dynamics Studied by Neutron Scattering Measurements and Computation. J. Chem. Phys. 2014, 141, 134501. [Google Scholar] [CrossRef]
- Ulivi, L.; Celli, M.; Giannasi, A.; Ramirez-Cuesta, A.J.; Bull, D.J.; Zoppi, M. Quantum Rattling of Molecular Hydrogen in Clathrate Hydrate Nanocavities. Phys. Rev. B 2007, 76, 161401. [Google Scholar] [CrossRef]
- Giannasi, A.; Celli, M.; Zoppi, M.; Moraldi, M.; Ulivi, L. Experimental and Theoretical Analysis of Rotational Raman Spectrum of Hydrogen Molecules in Clathrate Hydrates. J. Chem. Phys. 2011, 135, 054506. [Google Scholar] [CrossRef] [PubMed]
- Giannasi, A.; Celli, M.; Ulivi, L.; Zoppi, M. Low Temperature Raman Spectra of Hydrogen in Simple and Binary Clathrate Hydrates. J. Chem. Phys. 2008, 129, 084705. [Google Scholar] [CrossRef] [PubMed]
- Sebastianelli, F.; Xu, M.; Bačić, Z. Quantum Dynamics of Small H2 and D2 Clusters in the Large Cage of Structure II Clathrate Hydrate: Energetics, Occupancy, and Vibrationally Averaged Cluster Structures. J. Chem. Phys. 2008, 129, 244706. [Google Scholar] [CrossRef] [PubMed]
- Witt, A.; Sebastianelli, F.; Tuckerman, M.E.; Bačić, Z. Path Integral Molecular Dynamics Study of Small H2 Clusters in the Large Cage of Structure II Clathrate Hydrate: Temperature Dependence of Quantum Spatial Distributions. Z. J. Phys. Chem. C 2010, 114, 20775–20782. [Google Scholar] [CrossRef]
- Felker, P.M. Fully Quantal Calculation of H2 Translation-Rotation States in (p-H2)2@51264 Clathrate Hydrate Inclusion Compounds. J. Chem. Phys. 2014, 141, 184305. [Google Scholar] [CrossRef]
- Valdes, A.; Kroes, G.J. Theoretical investigation of two H2 molecules inside the cages of the structure H clathrate hydrate. J. Phys. Chem. C 2012, 116, 21664. [Google Scholar] [CrossRef]
- Felker, P.M. Fully Quantal Calculation of H2 Translation-Rotation States in (H2)4@51264 Clathrate SII Inclusion Compounds. J. Chem. Phys. 2013, 138, 174306. [Google Scholar] [CrossRef]
- Strobel, T.A.; Sloan, E.D.; Koh, C.A. Raman Spectroscopic Studies of Hydrogen Clathrate Hydrates. J. Chem. Phys. 2009, 130, 014506. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Ripmeester, J.A. Raman Spectroscopy and Cage Occupancy of Hydrogen Clathrate from First Principles Calculations. J. Am. Chem. Soc. 2009, 131, 14132–14133. [Google Scholar] [CrossRef]
- Ramya, K.R.; Venkatnathan, A. Vibrational Raman Spectra of Hydrogen Clathrate Hydrates from Density Functional Theory. J. Chem. Phys. 2013, 138, 124305. [Google Scholar] [CrossRef] [PubMed]
- Plattner, N.; Meuwly, M. The effect of classical and quantum dynamics on vibrational frequency shifts of H2 in clathrate hydrates. J. Chem. Phys. 2014, 140, 02431. [Google Scholar] [CrossRef] [PubMed]
- Zaghloul, M.A.S.; Celli, M.; Salem, N.M.; Elsheikh, S.M.; Ulivi, L. High Pressure Synthesis and In Situ Raman Spectroscopy of H2 and HD Clathrate Hydrates. J. Chem. Phys. 2012, 137, 164320. [Google Scholar] [CrossRef] [PubMed]
- Futera, Z.; Celli, M.; del Rosso, L.; Burnham, C.J.; Ulivi, L.; English, N.J. Vibrational Modes of Hydrogen Hydrates: A First-Principles Molecular-Dynamics and Raman-Spectra Study. J. Phys. Chem. C 2017, 121, 3690–3696. [Google Scholar] [CrossRef]
- Habershon, S.; Manolopoulos, D.E.; Markland, T.E.; Miller, T.F., 3rd. Ring-polymer Molecular Dynamics: Quantum Effects in Chemical Dynamics from Classical Trajectories in an Extended Phase Space. Annu. Rev. Phys. Chem. 2013, 64, 387–413. [Google Scholar] [CrossRef]
- Cao, J.; Voth, G.A. The Formulation of Quantum Statistical Mechanics Based on the Feynman Path Centroid Density. II. Dynamical Properties. J. Chem. Phys. 1994, 100, 5106–5117. [Google Scholar] [CrossRef]
- Craig, I.R.; Manolopoulos, D.E. Quantum Statistics and Classical Mechanics: Real Time Correlation Functions from Ring Polymer Molecular Dynamics. J. Chem. Phys. 2004, 121, 3368–3373. [Google Scholar] [CrossRef]
- Hele, J.H.; Willatt, M.J.; Muolo, A.; Althorpe, S.C. Boltzmann-conserving classical dynamics in quantum time-correlation functions: Matsubara dynamics. J. Chem. Phys. 2015, 142, 134103. [Google Scholar] [CrossRef]
- Hele, T.J.H.; Willatt, M.J.; Muolo, A.; Althorpe, S.C. Communication: Relation of centroid molecular dynamics and ring-polymer molecular dynamics to exact quantum dynamics. J. Chem. Phys. 2015, 142, 191101. [Google Scholar] [CrossRef]
- Lauvergnat, D.; Felker, P.M.; Scribano, Y.; Benoit, D.M.; Bacic, Z. H2, HD and D2 in the small cage of structure II clathrate hydrate: Vibrational frequency shifts from fully coupled quantum six-dimensional calculations of the vibration-translation-rotation eigenstates. J. Chem. Phys. 2019, 150, 154303. [Google Scholar] [CrossRef]
- Felker, P.M.; Bacic, Z. Weakly bound molecular dimers: Intramolecular vibrational fundamentals, overtones, and tunneling splittings from full-dimensional quantum calculations using compact contracted bases of intramolecular and low-energy rigid-monomer intermolecular eigenstates. J. Chem. Phys. 2019, 151, 024305. [Google Scholar] [CrossRef] [PubMed]
- Felker, P.M.; Lauvergnat, D.; Scribano, Y.; Benoit, D.M.; Bacic, Z. Intramolecular stretching vibrational states and frequency shifts of (H2)2 confined inside the large cage of clathrate hydrate from an eight-dimensional quantum treatment using small basis sets. J. Chem. Phys. 2019, 151, 124311. [Google Scholar] [CrossRef] [PubMed]
- Waldron, C.J.; English, N.J. Global-Density Fluctuations in Methane Clathrate Hydrates in Externally-Applied Electromagnetic Fields. J. Chem. Phys. 2017, 147, 024506. [Google Scholar] [CrossRef] [PubMed]
- Waldron, C.J.; English, N.J. System-density fluctuations and electro-dissociation of methane clathrate hydrates in externally-applied static electric fields. J. Chem. Thermo. 2017. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. A density functional for sparse matter. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed]
- Román-Pérez, G.; Soler, J.M. Efficient implementation of a van der Waals density functional: Application to double-wall carbon nanotubes. Phys. Rev. Lett. 2009, 103, 096102. [Google Scholar] [CrossRef]
- Wang, J.; Román-Pérez, G.; Soler, J.M.; Artacho, E.; Fernández-Serra, M.-V. Density, structure, and dynamics of water: The effect of van der Waals interactions. J. Chem. Phys. 2011, 134, 024516. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Galli, G.; Gygi, F.J. Structural and vibrational properties of liquid water from van der Waals density functionals. Chem. Theory Comput. 2011, 7, 3054. [Google Scholar] [CrossRef]
- Corsetti, F.; Artacho, E.; Soler, J.M.; Alexandre, S.S.; Fernández-Serra, M.-V. Room temperature compressibility and diffusivity of liquid water from first principles. J. Chem. Phys. 2013, 139, 194502. [Google Scholar] [CrossRef]
- Bankura, A.; Karmakar, A.; Carnevale, V.; Chandra, A.; Klein, M.L. Structure, dynamics, and spectral diffusion of water from first-principles molecular dynamics. J. Phys. Chem. C 2014, 118, 29401. [Google Scholar] [CrossRef]
- English, N.J. Structural Properties of Liquid Water and Ice Ih from Ab-Initio Molecular Dynamics with a Non-Local Correlation Functional. Energies 2015, 8, 9383. [Google Scholar] [CrossRef]
- Gillan, M.J.; Alfè, D.; Michaelides, A. Perspective: How good is DFT for water? J. Chem. Phys. 2016, 144, 130901. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- Garate, J.-A.; English, N.J.; MacElroy, J.M.D. Human aquaporin 4 gating dynamics in dc and ac electric fields: A molecular dynamics study. J. Chem. Phys. 2011, 134, 055110. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Cond. Matt. 2002, 14, 2745. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987; ISBN 0470-20812-0. [Google Scholar]
- Futera, Z.; English, N.J. Influence of external static and alternating electric fields on water from long-time non-equilibrium ab-initio molecular dynamics. J. Chem. Phys. 2017, 147, 031102. [Google Scholar] [CrossRef]
- Hermansson, K.; Tepper, H. Electric-field effects on vibrating polar molecules: From weak to strong fields. Mol. Phys. 1996, 89, 1291–1299. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burnham, C.J.; Futera, Z.; Bacic, Z.; English, N.J. Hydrogen Intramolecular Stretch Redshift in the Electrostatic Environment of Type II Clathrate Hydrates from Schrödinger Equation Treatment. Appl. Sci. 2020, 10, 8504. https://doi.org/10.3390/app10238504
Burnham CJ, Futera Z, Bacic Z, English NJ. Hydrogen Intramolecular Stretch Redshift in the Electrostatic Environment of Type II Clathrate Hydrates from Schrödinger Equation Treatment. Applied Sciences. 2020; 10(23):8504. https://doi.org/10.3390/app10238504
Chicago/Turabian StyleBurnham, Christian J., Zdenek Futera, Zlatko Bacic, and Niall J. English. 2020. "Hydrogen Intramolecular Stretch Redshift in the Electrostatic Environment of Type II Clathrate Hydrates from Schrödinger Equation Treatment" Applied Sciences 10, no. 23: 8504. https://doi.org/10.3390/app10238504
APA StyleBurnham, C. J., Futera, Z., Bacic, Z., & English, N. J. (2020). Hydrogen Intramolecular Stretch Redshift in the Electrostatic Environment of Type II Clathrate Hydrates from Schrödinger Equation Treatment. Applied Sciences, 10(23), 8504. https://doi.org/10.3390/app10238504





