Multi-Time-Scale Features for Accurate Respiratory Sound Classification

Featured Application

The automated classification of respiratory sound has gained increasing attention in recent years and has been the subject of a growing number of international scientific challenges for the development of accurate classification algorithms to support clinical practice. The COVID-19 pandemic has highlighted an urgent need for such developments. In this work, an accurate algorithm for the classification of respiratory sounds—specifically, crackles, wheezes or a combination of them—is presented.

Abstract

The COVID-19 pandemic has amplified the urgency of the developments in computer-assisted medicine and, in particular, the need for automated tools supporting the clinical diagnosis and assessment of respiratory symptoms. This need was already clear to the scientific community, which launched an international challenge in 2017 at the International Conference on Biomedical Health Informatics (ICBHI) for the implementation of accurate algorithms for the classification of respiratory sound. In this work, we present a framework for respiratory sound classification based on two different kinds of features: (i) short-term features which summarize sound properties on a time scale of tenths of a second and (ii) long-term features which assess sounds properties on a time scale of seconds. Using the publicly available dataset provided by ICBHI, we cross-validated the classification performance of a neural network model over 6895 respiratory cycles and 126 subjects. The proposed model reached an accuracy of $85\%\pm 3\%$ and an precision of $80\%\pm 8\%$, which compare well with the body of literature. The robustness of the predictions was assessed by comparison with state-of-the-art machine learning tools, such as the support vector machine, Random Forest and deep neural networks. The model presented here is therefore suitable for large-scale applications and for adoption in clinical practice. Finally, an interesting observation is that both short-term and long-term features are necessary for accurate classification, which could be the subject of future studies related to its clinical interpretation.

1. Introduction

Respiratory diseases are the third leading cause of death worldwide, accounting for an estimated 3 million deaths each year [1], and their burden is set to increase, especially in 2020 due to the severe acute respiratory syndrome coronavirus 2 epidemic caused by coronavirus disease 2019 (COVID-19) [2]. While the most critical manifestations of COVID-19 include respiratory symptoms and pneumonia of varying severity [3], there are clinically confirmed cases of patients with respiratory symptoms whose chest computed tomography (CT) did not reveal signs of pneumonia [4]. The situation is even more intriguing when considering asymptomatic subjects as they are known to ease the diffusion of the virus but their identification without instrumental examination is extremely challenging [5].

In this context, the development of accurate diagnostic decision support systems for the early detection of respiratory diseases to monitor patient conditions and assess the severity of symptoms is of paramount importance. The role played by artificial intelligence in this field has been thoroughly explored [6,7,8,9]; the identification of useful respiratory sounds, such as crackles or wheezes, allows the detection of abnormal conditions and therefore timely diagnosis. It is worth noting that crackles can be discontinuous and therefore detectable in a limited amount of time by “short-range” features, while wheezes have a prolonged duration and therefore are more suitably characterized by “long-term” features covering an extended time range [10].

Traditionally, sound analyses are based on time–frequency characterizations, such as Fourier transforms (FT) or wavelet transforms [11,12,13,14,15]. More recently, other approaches have shown promising results. For example, cepstral features have been successfully adopted for lung sound classification [16]. A multi-time-scale approach has been adopted based on the principal component analysis of Fourier transforms of signals [17]. Another proposed strategy is the empirical mode decomposition method [18,19,20], which exploits instantaneous frequencies and points toward a local high-dimensional representation. In some sense, these approaches can be considered precursors of the most recent deep learning approaches [21,22,23,24]. However, the high dimensionality of these strategies impairs their statistical robustness; more importantly, deep learning provides models which can be difficult to clinically interpret. In this work, we propose a joint set of multi-time-scale features, where “multi-time-scale” denotes the fact that these features are intrinsically designed to capture sound properties at different time scales, specifically the presence of crackles and wheezes; these features are used to feed a supervised learning framework [25] to accurately detect sound anomalies and gain further insights about the discriminating features between healthy and pathological conditions. The proposed system represents a very promising framework also in the field of telemedicine, because it could become the operational nucleus of a remote diagnostic system that would allow users to examine the respiratory conditions of patients, identifying possible problematic situations that require urgent intervention in real time.

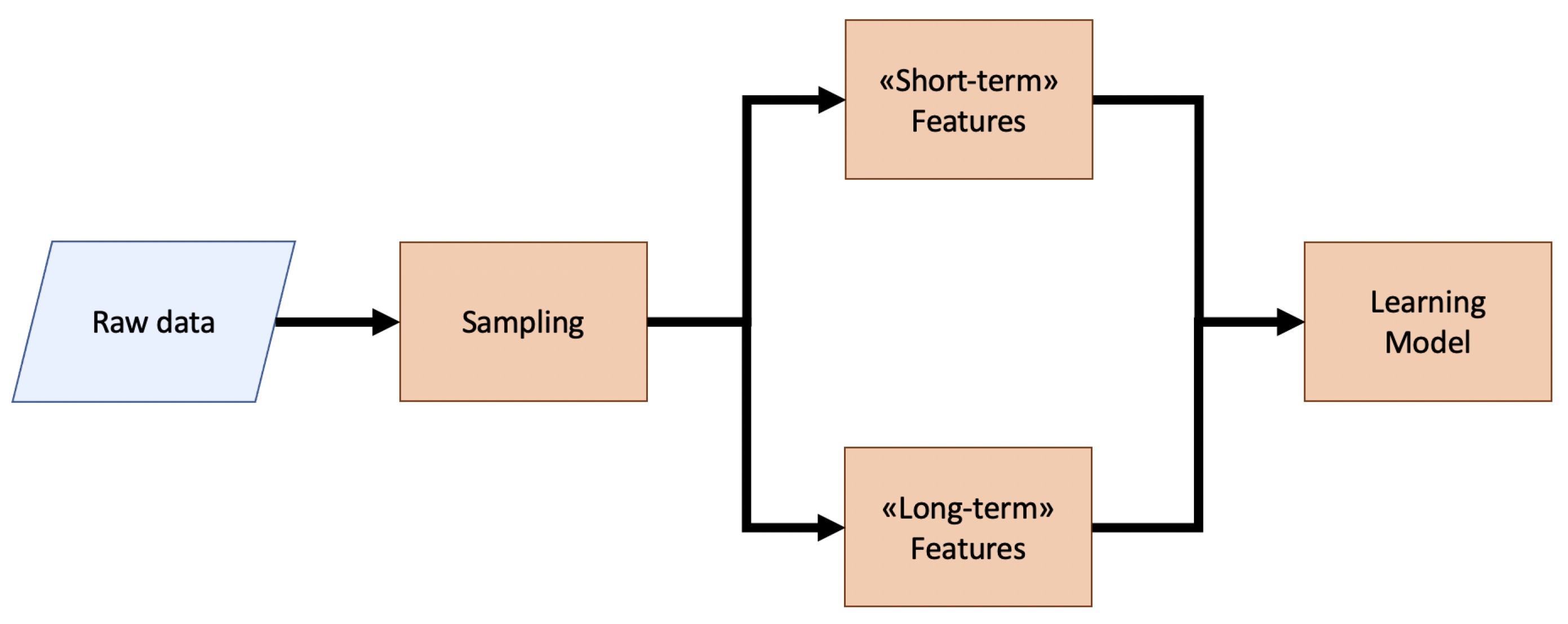
2. Materials and Methods

In this work, we present a novel classification framework for respiratory sounds, specifically aimed at detecting the presence of significant sounds during the respiratory cycle (see Figure 1).

The goal is the development of a diagnostic decision support system for the discrimination of healthy controls from patients with respiratory symptoms. The proposed approach consists of three main steps: (i) data standardization, (ii) multi-time-scale feature extraction and (iii) classification. A detailed description of these steps is provided in the following sections.

2.1. The ICBHI Dataset

The ICBHI Scientific Challenge was launched in 2017 to provide a fair comparison of several respiratory sound classification algorithms [26]. One of the goals of the challenge was the creation of a common large and open dataset for respiratory analyses. The database was collected by two collaborating research teams from Portugal and Greece. The data collection required several years; the final dataset consists of 920 labeled audio tracks from 126 distinct participants and is currently the largest annotated, publicly available dataset. The sounds were collected from six different positions (left/right anterior, posterior and lateral) as illustrated in Figure 2.

The available tracks have two different sampling rates: 44.1 kHz with 24 bits for sampling and 4 kHz with 16 bits for sampling. Metadata, which are not used here, also include sex, age, body-mass index for adults and height and weight for children. We segmented the audio tracks into respiratory cycles in order to increase the sample size; for each cycle, an annotation reporting the presence of significant sounds was available. Of course, we took into account this aspect during cross-validation analyses; respiratory cycles from the same patient were not split between training and validation to prevent a possible overfitting bias. The final dataset consisted of 6895 annotated respiratory cycles, including 321 cycles from healthy patients (HC) and 6574 cycles from patients with respiratory symptoms (RS).

2.2. Multi-Time-Scale Feature Extraction

We applied a multi-level feature extraction approach, where we progressed from a fine-scale representation to a global one through progressive generalizations [27]. The first level of analysis was the short-term level: we initially divided the signal into windows of 0.25 s (called short-term windows), and for each window, we computed 33 physical quantities, called short-term features. For each feature f, the short-term analysis produced a time series of values $F=(f_1,f_2,\dots ,f_L)$; we extracted higher time-scale properties of the signal from the distribution of these values. The duration of the time windows on which short-term features were computed was set to 0.25 s as a compromise between two opposite needs. On the one hand, as the respiratory cycle in rest conditions lasts around two seconds for an inhalation and three seconds for an exhalation, the duration of the signal needed not to be excessive in order to effectively map the two phases of the respiratory cycle in a detailed way. Moreover, the shorter the time window, the higher the number of samples in the distribution of short-term features, and therefore the more meaningful the statistical indicators built from these distributions and used in the long-term analysis. On the other hand, a lower limit on the duration of the short-term time frames is essential to observe meaningful and informative features on the respiratory cycle, since time windows much shorter than the typical duration of the process would provide information that would be affected by noise and difficult to interpret.

The second level of analysis was the long-term level and consisted of the calculation of 10 statistical moments associated with the time series of each of the 33 short-term features. At the end of the extraction process, each track was characterized by a total of 330 features. Figure 3 displays a pictorial representation of the feature extraction procedure.

2.2.1. Short-Term Features

For the short-term analysis, we considered features in the time domain, features in the frequency domain, ceptral features and chroma for a total of 33 short-term features. We divided the input track into short-term windows and defined $x_i\left(n\right)$ with $n=1,\dots ,N$ being the sequence of sound intensities contained in the $i$-th window. In the time domain, we considered the zero crossing rate $ZC{R}_i$ [28]:

$$\begin{array}{c}\hfill ZC{R}_i=\frac{1}{2N}\sum _{n=1}^N|sgn\left[x_i\left(n\right)\right]-sgn\left[x_i(n-1)\right]|\end{array}$$

(1)

with

$$sgn\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x\ge 0\hfill \\ -1\hfill & \mathrm{if}x<0\hfill \end{array}\right.$$

(2)

and the entropy of energy $H_i$ [29]:

$$\begin{array}{c}\hfill H_i=-\sum _{j=1}^K{e}_{j}lo{g}_2{e}_j\end{array}$$

(3)

where $e_j$ is the ratio between the energy of the $j\mathrm{-th}$ interval of K frames in which we divided the i-th short-term window and the energy $E_i$ of the i-th short-term window, defined as [30]:

$$\begin{array}{c}\hfill E_i=\sum _{n=1}^N{\left|x_i\left(n\right)\right|}^2.\end{array}$$

(4)

In the frequency domain, we computed the spectral centroid $C_i$ [31]:

$$\begin{array}{c}\hfill C_i=\frac{{\sum }_{n=1}^{N/2}n{X}_i\left(n\right)}{{\sum }_{n=1}^{N/2}{X}_i\left(n\right)}\end{array}$$

(5)

and its spectral spread $S_i$ [32]:

$$\begin{array}{c}\hfill S_i=\sqrt{\frac{{\sum }_{n=1}^{N/2}{(n-C_i)}^2{X}_i\left(n\right)}{{\sum }_{n=1}^{N/2}{X}_i\left(n\right)}}\end{array}$$

(6)

where $X_i\left(n\right)$, with $n=1,\dots ,N$ being the Fourier coefficients obtained by applying the discrete Fourier transform (DFT) on the i-th short-term window. In addition, we evaluated the spectral entropy $S{H}_i$ [33]:

$$\begin{array}{c}\hfill S{H}_i=-\sum _{j=1}^K{n}_{j}lo{g}_2{n}_j\end{array}$$

(7)

with

$$\begin{array}{c}\hfill n_j=\frac{E_j}{{\sum }_{j=1}^K{E}_j}\end{array}$$

(8)

$E_j$ ($j=1,\dots ,K$) represents the energy estimated on one of the K bins in which we divided the window. Furthermore, we computed the spectral flux $Fl$ [34] as a measure of the spectral variation between two consecutive short-term windows $i-1$ and i:

$$\begin{array}{c}\hfill Fl(i,i-1)=\sum _{n=1}^{N/2}{(E{N}_i\left(n\right)-E{N}_{i-1}\left(n\right))}^2\end{array}$$

(9)

where

$$\begin{array}{c}\hfill E{N}_i\left(n\right)=\frac{X_i\left(n\right)}{{\sum }_{n=1}^{N/2}{X}_i\left(n\right)}.\end{array}$$

(10)

The other considered features that we computed were the spectral roll-off [35], Mel-frequency cespstrum coefficients (MFCCs) [36,37] and the chroma vector [38].

The spectral roll-off R is defined as:

$$\begin{array}{c}\hfill R=C\sum _{n=1}^{N/2}{X}_i\left(n\right)\end{array}$$

(11)

where C is a threshold frequency below which most (typically $90\%$) of the spectral amplitude distribution is concentrated.

MFCCs were derived from a representation of the spectrum in which frequency bands were evenly distributed with respect to the Mel scale. Frequencies $f_{Mel}$ in the Mel scale were related to frequencies in Hz $f_{Hz}$ by the relation

$$\begin{array}{c}\hfill f_{mel}=1127·ln\left(\frac{f_{Hz}}{700}+1\right).\end{array}$$

(12)

MFCCs were computed through the following steps:

• Calculate the DFT of the signal in the short-term window;
• Identify M equally spaced frequencies on the Mel scale and build a bank of triangular spectral filters $F_j$ with $j=1,\dots ,M$ centered on each corresponding M frequency in Hz;
• Evaluate the spectral output powers $O_j$ of each filter $F_j$;
• Estimate MFCCs as

$$\begin{array}{c}\hfill c_m=\sum _{j=1}^{M}log{O}_{j}cos\left[m\left(j-\frac{1}{2}\right)\frac{\pi }{M}\right]\end{array}$$

(13)

with $m=1,\dots ,M$. In the present work, we considered the first 13 MFCCs because they were deemed to contain sufficient discriminatory information in order to perform various classification tasks [27].

The chroma vector is a $12-$element representation of the spectral energy and is calculated by grouping the DFT coefficients of the short-term window into 12 frequency classes related to semitone spacing. For each class q in $1,\dots ,12$, the q-th chroma element ${\nu }_q$ is defined as the following ratio:

$$\begin{array}{c}\hfill {\nu }_q=\sum _{k\in S_q}\frac{X_i\left(k\right)}{N_q}\end{array}$$

(14)

where $S_q$ is the subset of frequencies belonging to class q, and $N_q$ is the number of elements in $S_q$. The last implemented feature is the standard deviation of the 12 components of the chroma vector.

2.2.2. Long-Term Features

From the time distributions of the 33 short-term features, we computed the following 10 statistical moments: the mean, standard deviation, coefficient of variation, skewness, kurtosis, first, second and third quartile, minimum and maximum [39].

2.3. Classification and Performance Assessment

To evaluate the informative content of the designed multi-time-scale features and thus to assess to which extent the performance depended on the feature representation or the classification models, we compared the performance of several classification methods. We used two state of the art classifiers: Random Forest (RF) [40] and the Support Vector Machine (SVM) [41]. Additionally, we explored the use of both an artificial neural network [42] and a fully-connected deep neural network [43].

2.3.1. Learning Models

RF is an ensemble of classification trees built with the bootstrapping of the training data-set. Through an iterative process during the construction of the trees, at each node, a subset of features is randomly selected which implies that the trees of the forest are weakly correlated to each other. In general, RF classifiers are easy to tune, very robust against overfitting and are particularly suitable when the number of features in the model exceeds the number of observations. In our analysis, we implemented a standard configuration in which each forest is grown with 1000 trees and $m=f/3$, with f being the number of features and m the number of features sampled to grow each leaf within a tree. An important property of Random Forest classifiers is that they can estimate the importance of each feature during the training phase of the model. The algorithm can evaluate how much each feature decreases the impurity of a tree. In RF, the impurity decrease due to each variable is obtained from the average on all trees. Node impurity is measured by the Gini index [44].

SVM is a machine learning algorithm that employs mathematical functions, called kernels, to represent data in a new hyperspace that simplifies the representation of complicated patterns present in the data. Suppose it is desired to separate data belonging to two clusters; SVM finds the functional equation to separate the two clusters. When considering more variables, the separation line becomes a plane. By further increasing the variables, the separation becomes a hyperplane, obtained from a subset of points of the two classes, called support vectors. In general, the SVM algorithm finds a hyperplane that separates data into two classes, maximizing the separation. We implemented a default configuration with a linear kernel.

Artificial neural networks (ANNs) are computational networks inspired by the human nervous system that can learn from known examples and generalize to unknown cases. In this work, we used multilayer perceptron networks (MLPs) [45], the most commonly used ANNs, which utilize back-propagation for supervised learning. MLPs are composed of three neural levels: input, hidden and output layers. MLPs starts by feeding a features array to the input layer. The network then passes the input to the next hidden layers through connections, called dendrites; connection weights inhibit or amplify the signal, and neurons add up the input signals and transform them into output signals through an activation function. Our MLP model was composed of two hidden layers with 50 and 15 neurons, respectively, and used the sigmoid as an activation function.

The use of deep learning techniques has seen an exponential increase in the last decade; the reason for this is mainly due to the increasing availability of computing infrastructures that allow the learning of very expensive models from the computational perspective and to the increasing availability of infrastructures for data storage. Deep neural networks (DNNs) expand the architecture of ANNs: they are composed by a hierarchical architecture with many layers that constitute a non-linear information processing unit. The multiple levels of abstraction provide deep neural networks with a huge advantage in complex pattern recognition problems, adding information and analysis to each intermediate level to provide reliable output. The potential and capabilities of deep learning were unthinkable until a few years ago, even if its real advantage over ANNs, especially when the number of input cases is not very large, has been the subject of in-depth analysis and study. In this work, we used a DNN model composed of three hidden layers with 150 neurons in each layer.

2.3.2. Cross-Validation, Balancing and Performance Metrics

The examined dataset is particularly imbalanced in favor of patients; therefore, we adopted a three-fold classification framework to establish enough control in the validation sets. Moreover, it is essential that the numbers of patients and controls analyzed by a classification algorithm are balanced; otherwise, the algorithm could learn to discriminate one class well at the expense of the other classes. Among the simplest methods to balance a dataset are random over-sampling and random under-sampling strategies [46,47].

We performed the random under-sampling of the RS class during training for the machine learning models, while we performed the over-sampling of the HC class for the deep learning algorithm, which usually obtains higher performances with larger sample sizes. The balancing strategies were nested into the cross-validation procedure. Finally, respiratory cycles were randomly split into training and validation sets stratified over the subjects’ identification codes; in this way, the presence of respiratory cycles from the same patient in both training and validation did not occur. We repeated the cross-validation procedure 500 times.

As a measure of performance, we evaluated accuracy, namely the rate of correct classifications, defined as follows:

$$\begin{array}{c}\hfill Acc=\frac{TP+TN}{TP+TN+FP+FN}\end{array}$$

(15)

where $TP$, $TN$, $FP$, $FN$ represent true positives, true negatives, false positives and false negatives, respectively. In addition to accuracy, we also used precision:

$$\begin{array}{c}\hfill Prec=\frac{TP}{TP+FP};\end{array}$$

(16)

classification error of the class HC:

$$\begin{array}{c}\hfill EHC=\frac{FP}{TN+FP};\end{array}$$

(17)

and classification error of class RS:

$$\begin{array}{c}\hfill ERS=\frac{FN}{TP+FN}.\end{array}$$

(18)

All the data processing and statistical analyses were performed in Python version 3.7 (https://www.python.org/downloads/release/python-370/) and R version 3.6.1 (https://www.r-project.org/).

2.3.3. Feature Importance Procedure

To evaluate the robustness of the implemented model with respect to the used features, we applied a feature importance procedure. Initially, we estimated a feature importance ranking through the RF algorithm and the three-fold cross-validation procedure; namely, for each cross-validation cycle, we assigned a weight to each feature according to its importance evaluated by the Gini index, thus obtaining a partial ranking. We obtained an overall ranking by repeating the procedure 500 times averaging over all repetitions.

As an alternative approach, we applied a backward feature selection strategy. First, we considered a model exploiting the informative content of all the available 330 features; then, we removed the least important feature, assessed the classification performance and iterated the procedure until only four features were left. To avoid a double dipping bias, these feature selection analyses were performed within a nested cross-validation framework.

3. Results

3.1. Classification Performances

We evaluated the accuracy and precision of the HC vs. RS classification task and classification errors $EHC$ and $ERS$ for healthy controls and respiratory symptoms, respectively. The performances obtained by means of the implemented machine and deep learning algorithms are shown in Figure 4. An overview of the classification performances is summarized in

Table 1. Summary table of the classification performance measures of the four implemented machine and deep learning models. Accuracy, precision and classification errors are reported with the respective standard deviations. According to a Kruskal–Wallis test, the differences within each column are statistically significant (p-value < 1%) MLP: multi-layer perceptron; SVM: support vector machine; DNN: deep neural network.

Learning Models	Accuracy	Precision	Error HC	Error RS
Random Forest	$0.84\pm 0.04$	$0.84\pm 0.10$	$0.17\pm 0.10$	$0.16\pm 0.04$
MLP	$0.85\pm 0.03$	$0.80\pm 0.08$	$0.20\pm 0.08$	$0.14\pm 0.03$
SVM	$0.81\pm 0.03$	$0.79\pm 0.07$	$0.21\pm 0.07$	$0.19\pm 0.03$
DNN	$0.82\pm 0.02$	$0.87\pm 0.02$	$0.13\pm 0.02$	$0.23\pm 0.02$

.

According to a Kruskal–Wallis test [48], the four methodologies are significantly different despite these differences being quite comparable with the inherent uncertainties for each metric. We also made pairwise comparisons of their predictions (see Figure 5 and Figure A1 in the Appendix A).

Overall, MLP had the best performance; thus, we only report its comparisons in the form of contingency tables. The remaining comparisons can be found in the Appendix A. It is worth noting that, in all three cases, the agreement between the classification models exceeds $76\%$.

3.2. Feature Importance

In the previous section, we showed that there was no significant difference among the four different classification algorithms adopted. Here, we investigate the most important features for classification and evaluate their importance. First of all, we investigated how precision and classification errors varied with the number of features used in the training (see Figure 6).

By applying the procedure described in Section 2.3.3, we observed that classification performance worsens as the number of features used to train the model decreases. Moreover, we investigated feature importance in relation to the feature category (see Figure 7).

The mean decrease of the Gini index reaches a plateau at about 50 features. These 50 features were also categorized by type: $52\%$ of the top 50 features (26 features) were the chrome vector, $14\%$ were MFCCs and roll-off features and $10\%$ were the ZCR and entropy.

4. Discussion

The classification of significant sounds has gained increasing importance in recent years. Several strategies have been proposed, and machine learning strategies account for a huge body of literature [49,50,51,52,53,54,55,56,57]. The plethora of different approaches and strategies address two distinct issues: on one hand, a robust classification for diagnostic purposes; on the other hand, “interpretability”—i.e, the design of specific features for the differential diagnosis of different pathologies. In fact, there is a consolidated consensus about the accuracy of machine learning approaches for sound analyses. Although it is difficult to compare results from different studies, state-of-the-art classification performances reach or exceed $80\%$ accuracy, which compares well with the results obtained by our framework ($81\%\sim 85\%$). The use of different data or the adoption of specific study designs such as different cross-validation strategies (if any) makes comparison difficult in general.

Table 2. Classification performances reported by other studies on the ICBHI data.

Study	Performance	Sensitivity	Specificity
Minami et al. [23]	0.81 (harmonic score)	0.54	0.41
Wu et al. [58]	0.88 (accuracy)	-	0.91
Ma et al. [59]	0.52 (performance score)	-	-
Yang et al. [60]	0.55 (average score)	-	-

presents an overview of recent peer-reviewed published studies using ICBHI data. These studies only occasionally deal with the classification of significant sounds, and their performance measures cannot be directly compared.

The need for an objective comparison between different classification algorithms has led in recent years to the spread of international challenges, especially for machine learning applications, a common trait of whichwas the use of a shared framework for all the participants: a unique dataset for training and a blind test set [61,62,63,64,65]. The data investigated in this work were collected on the occasion of the previously mentioned international ICBHI challenge. Of the 18 different algorithms submitted to the challenge, only two reached the final stage and were presented at the ICBHI 2017. The first was an approach exploiting resonance-based decomposition [66]; the second was a method based on the application of hidden Markov models in combination with Gaussian mixture models [67]. These algorithms were evaluated on the basis of accuracy to detect wheezes, crackles or their simultaneous presence, thus resulting in a four-class classification problem; the test accuracy reported for both algorithms did not exceed $50\%$, which is far below the performances reported in the literature. A possible explanation for this would be that, despite the large sample size, the collected data included some examples which were extremely difficult to classify—a possibility also mentioned by the organizers of the challenge.

The information content provided by the proposed features is encouraging not only for the high level of accuracy obtained but also for its robustness, which we evaluated by comparing several supervised learning frameworks. In fact, we observed that, for all pairwise comparisons, the agreement between the classification models exceeded $76\%$. It is well-known that, for each classification task, it is not possible to determine a priori which is the best classifier, and the impact of a specific classifier on classification performance can be substantial [68]. Nevertheless, we observed that the performances of four different approaches (RF, SVM, MLP and a DNN) differ by a few percentage points. The best-performing methods were the MLP in terms of accuracy and the DNN in terms of precision.

In recent years, deep learning strategies have experienced an exponential growth. Among the many available strategies that might be worth exploring in this setting, two deserve a mention: residual networks (ResNet) and long short-term memory (LSTM) networks [69,70,71,72]. These approaches should be considered especially for further studies that are aimed more at the deep learning domain.

It is also well known that, in general, learning algorithms require a sufficient number or training examples for each class and that unbalanced classes can weaken the learning process [73,74]; besides, the strength of DNN is related to the available sample size—the more the better. Accordingly, we adopted a three-fold cross-validation and different sampling strategies to allow the best operational conditions for each classifier. The use of three-fold instead of a more common five-fold or 10-fold cross-validation was motivated by the exiguous number of HC cases and ensured that the test set contained a representative number of HC examples. As concerns the sample strategies, we used under-sampling with standard machine learning algorithms and over-sampling for DNN. In fact, we observed that the use of under-sampling with DNN resulted in a significant performance deterioration.

Finally, we investigated which features were best at characterizing the presence of significant sounds. We observed that a relatively small amount of features (∼50) was sufficient for an accurate classification. Besides, our findings demonstrated that, in the examined case variations, roughly this number of features results in negligible performance differences (see Figure 6); this is a relevant aspect, considering that using different feature importance thresholds can significantly affect the classification performance. Finally, by grouping these top rank features by type, we observed that the main contribution was given by the chroma vector. The chroma vector is a $12-$dimensional representation of the spectral energy [75]. In general, this descriptor is suitable for music–speech applications when the signal is heavily affected by noise [27,76]; our findings would suggest that they can also be effectively used in the context of significant sound recognition.

5. Conclusions

In this work, we presented a multi-time-scale machine learning framework for the classification of respiratory sounds including crackles and wheezes. The proposed framework can accurately distinguish healthy controls from patients whose respiratory cycles present some significant sounds. Besides, we observed that the informative power of the proposed features is only slightly affected by the classifier choice; with four different classifiers (RF, SVM, MLP and DNN), we obtained accuracy values ranging from 85% for MLP to 81% for SVM. The best performing features among the 330 adopted were the chroma vector components. In this work, we addressed the binary classification problem for HC versus RS; in fact, we ran our analyses at the “patient” level. Future studies could address the recognition of significant sounds at the respiratory cycle level; of course, this problem poses some major difficulties, because it is a a multi-class classification task. Our analysis presents the typical limitations of a feature-based learning approach. In fact, in a feature engineering process, a priori hypotheses are made that might imply that significant aspects of the signal are neglected. More general deep learning approaches such as LSTM and ResNet might be able to improve the classification performance, although this would require further investigation. Nevertheless, the results presented here are promising and deserve further investigation.