Study on the Mechanical Criterion of Ice Lens Formation Based on Pore Size Distribution
Abstract
:1. Introduction
2. Theoretical Model
2.1. Hypotheses
- (1)
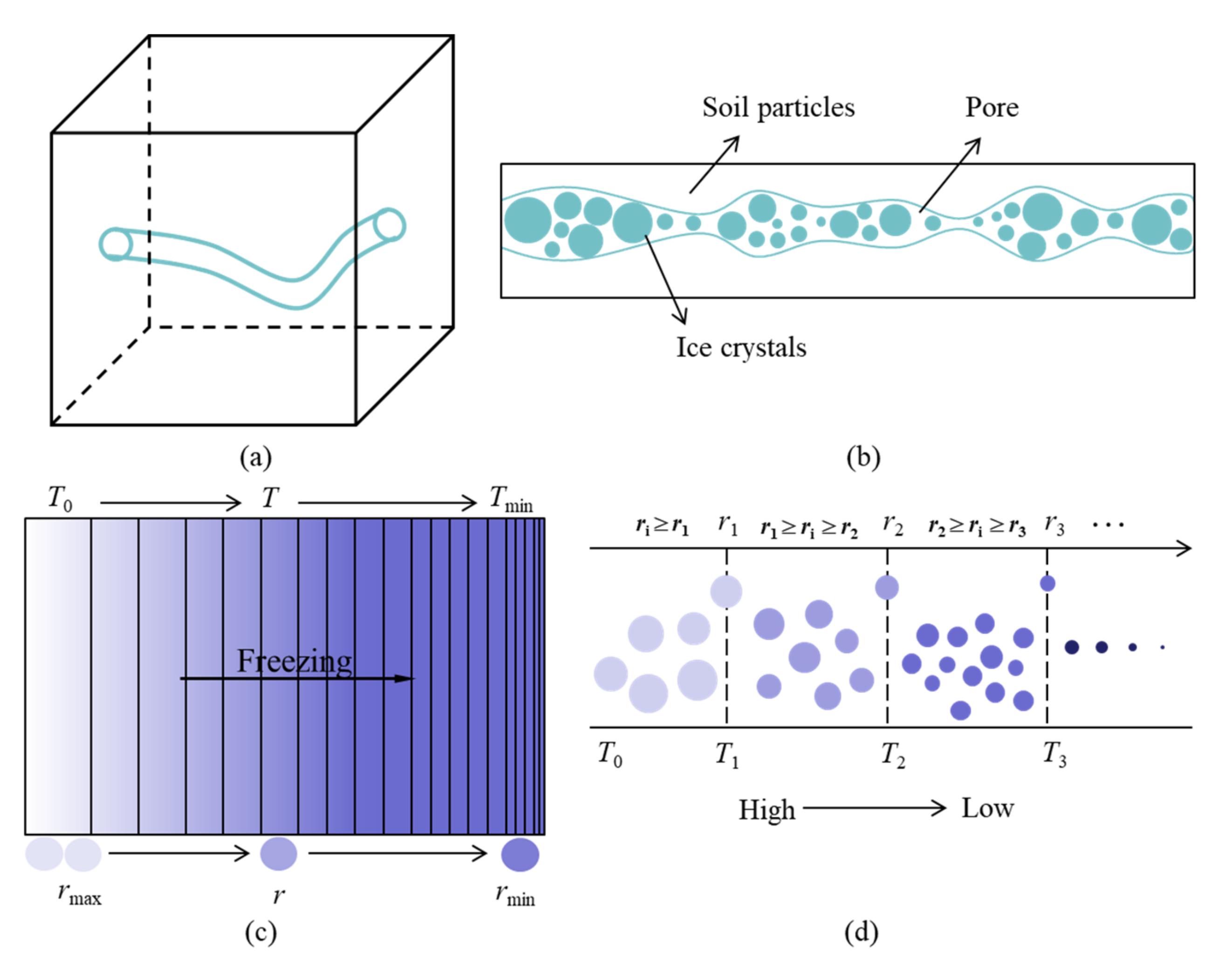
- The pores in soil were simplified as spheres with different radii and connected by cylindrical channels with different radii. Moreover, the cylindrical tubes are fully saturated.
- (2)
- Pores are uniformly distributed in the saturated soil (Figure 2a,b)
- (3)
- The freezing process started from the pores with larger radius (Figure 2c,d).
- (4)
- Spherical crystals with different radii are distributed evenly in the pores.
2.2. Equilibrium of a Single Crystal in a Pore
2.2.1. Chemical Equilibrium
2.2.2. Growth of the Crystal in the Pore
2.2.3. The Crystallization Stress of an Ideal Spherical Crystal
2.3. The Crystallization Stress of True Porous Media
2.4. Determination of Pore Size Distribution from the Soil Freezing Characteristic Curve
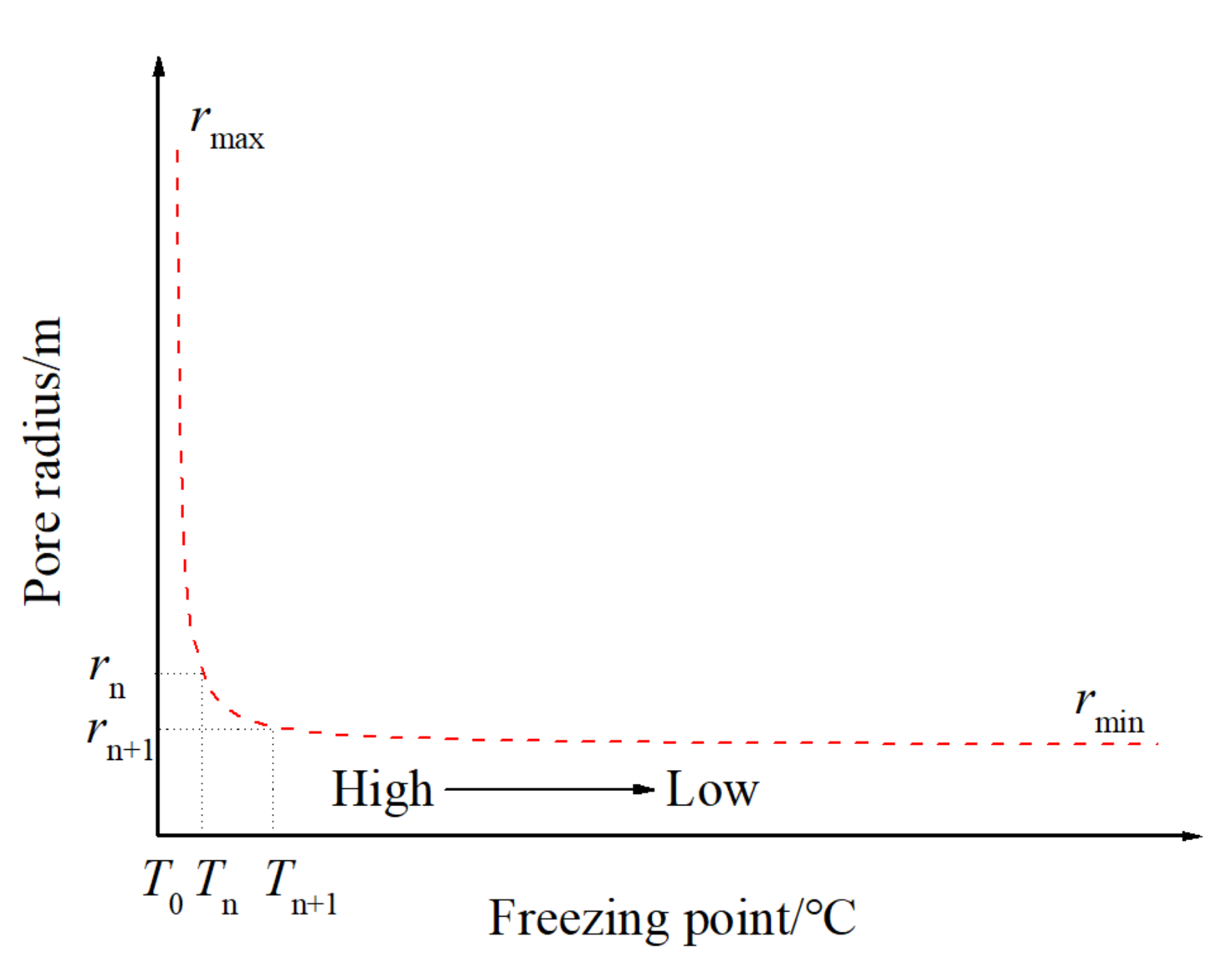
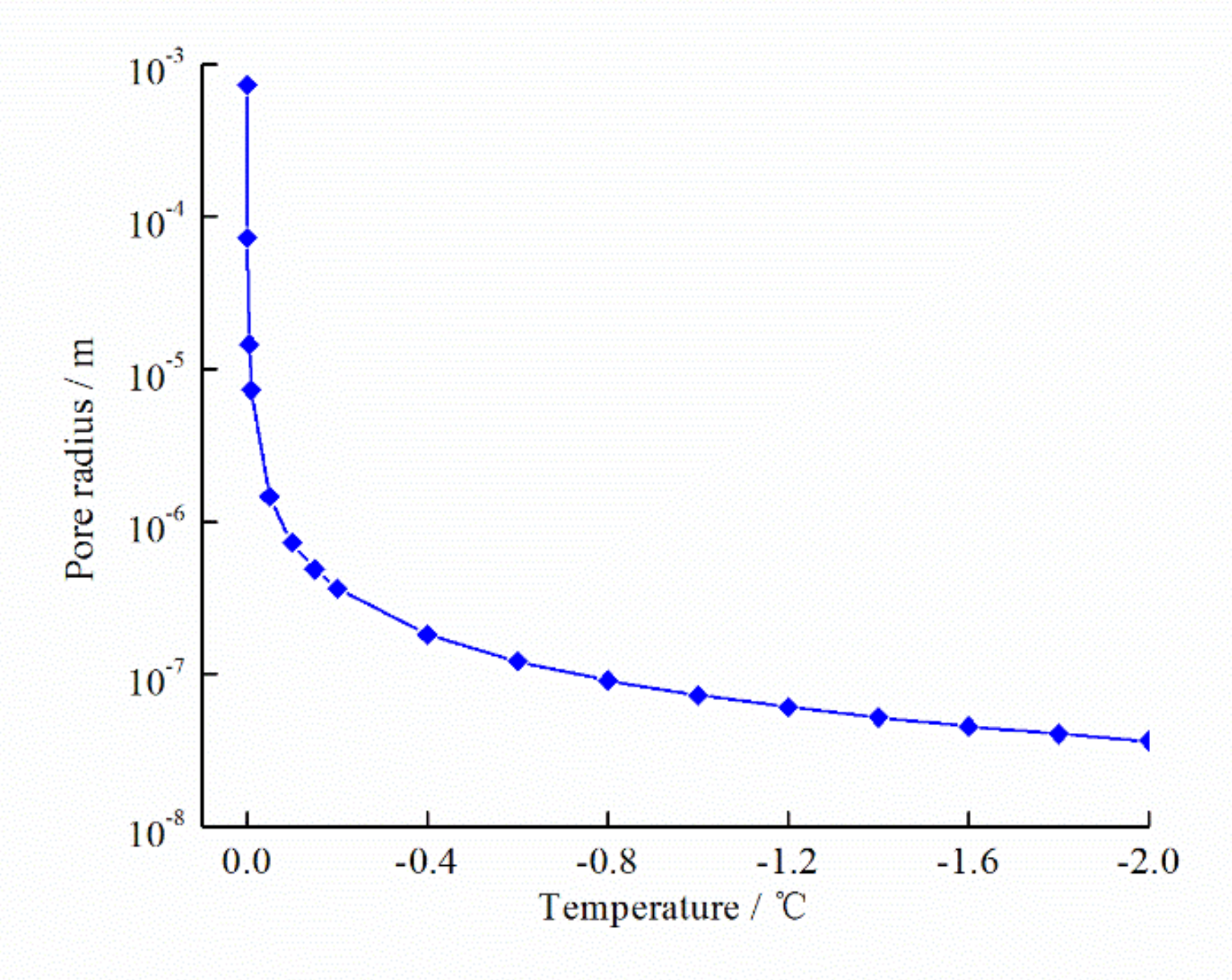
2.4.1. Relationship between Freezing Point and Pore Radius
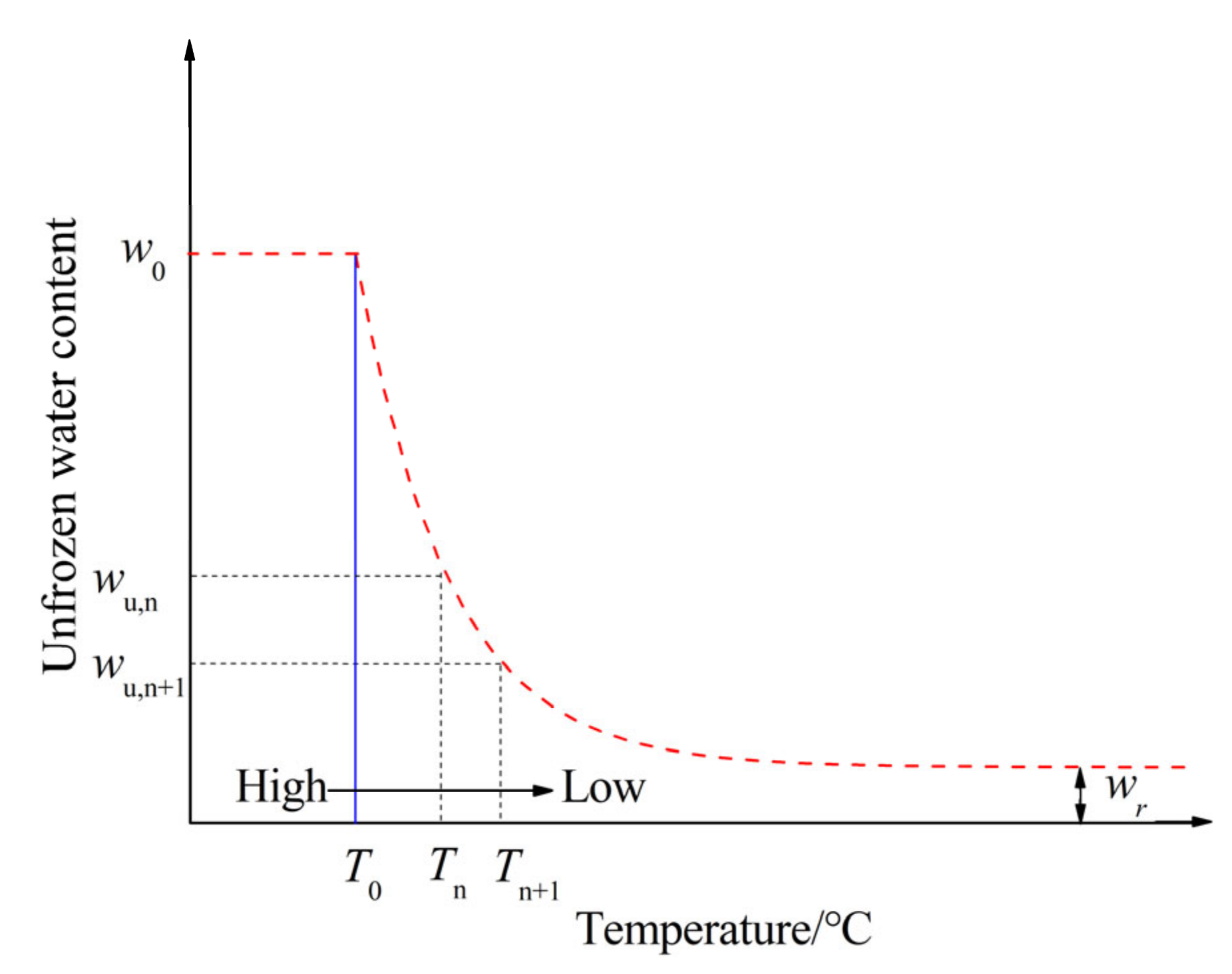
2.4.2. Determination of Pore Size Distribution from the Unfrozen Water Content
2.5. Formation of Ice Lens
2.5.1. Driving Force of Ice Lens Formation
2.5.2. Constraining Force of Ice Lens Formation
2.5.3. The New Criterion of Ice Lens Formation
3. Experiment Design
3.1. Experiment Materials
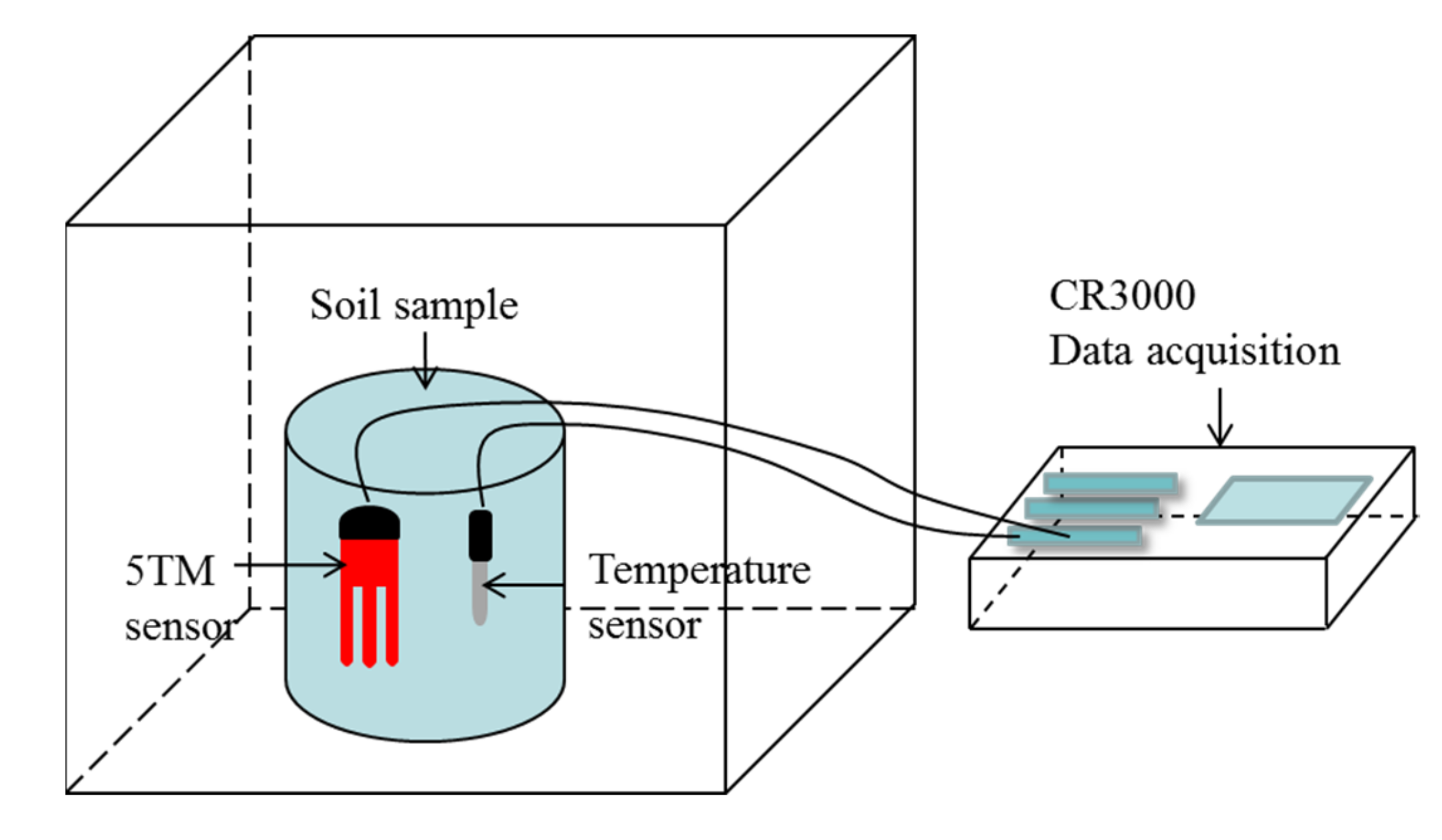
3.2. Experiment Methods
3.2.1. Unfrozen Water Content
3.2.2. Tensile Strength
4. Results and Discussions
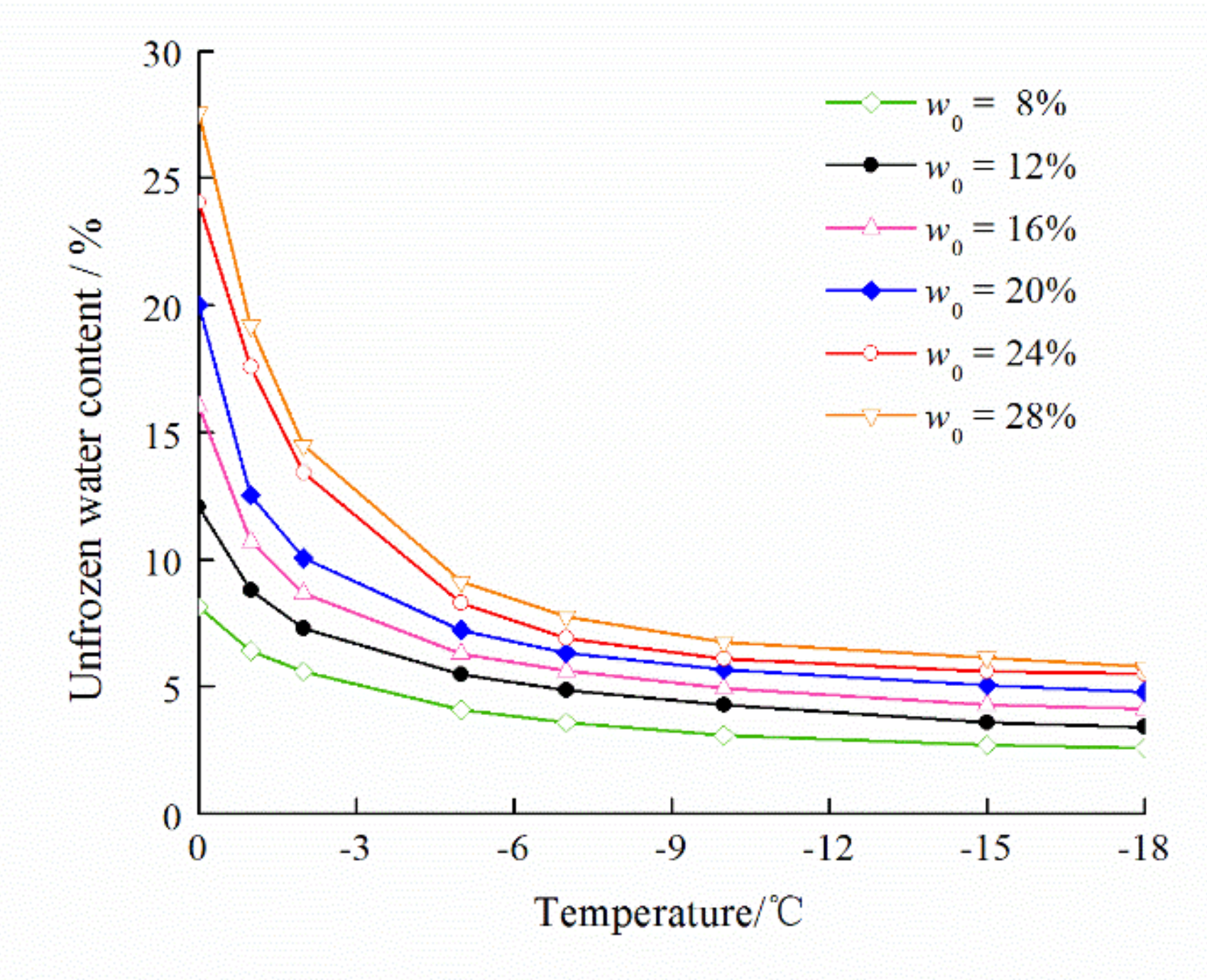
4.1. Unfrozen Water Content
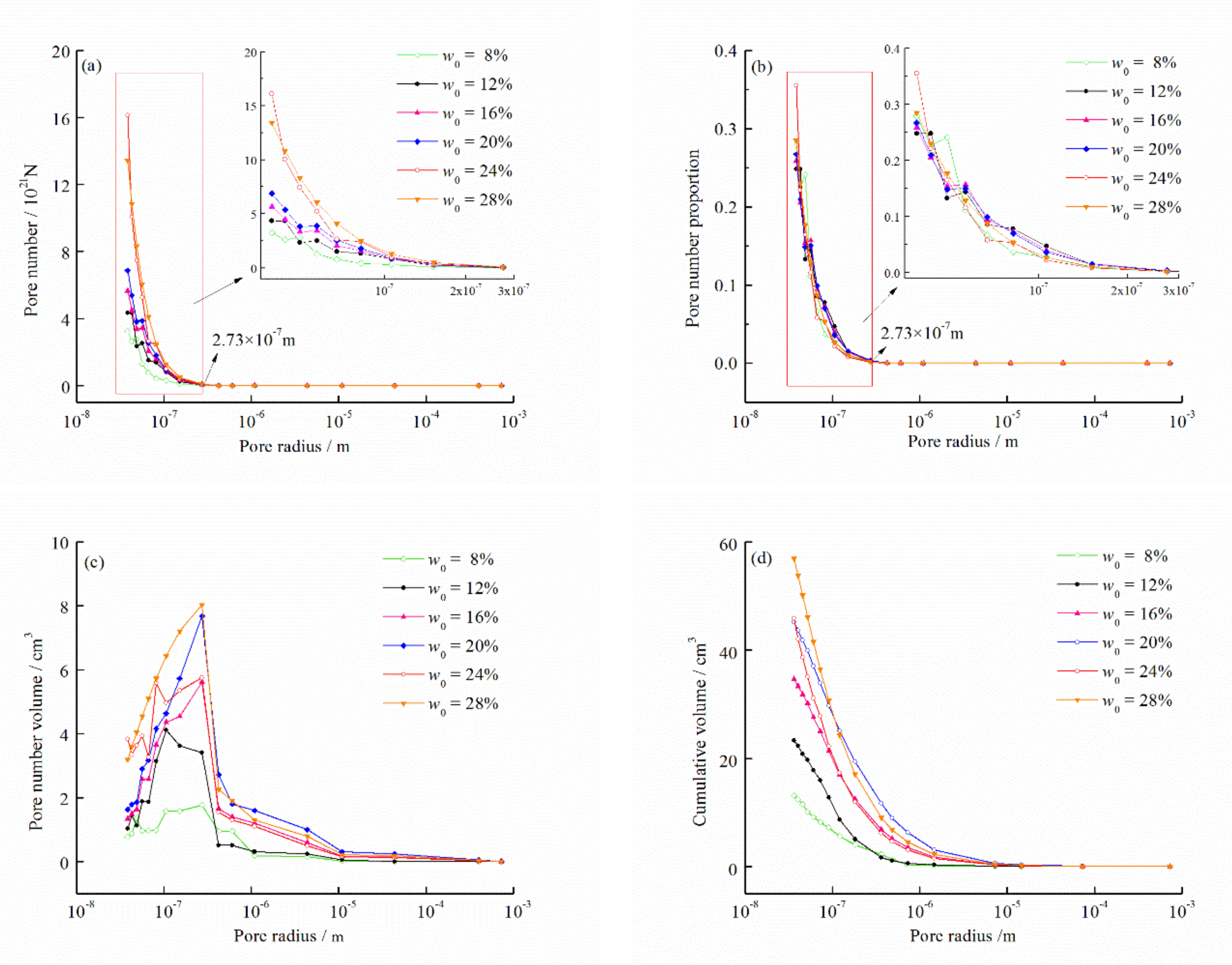
4.2. Pore Size Distribution
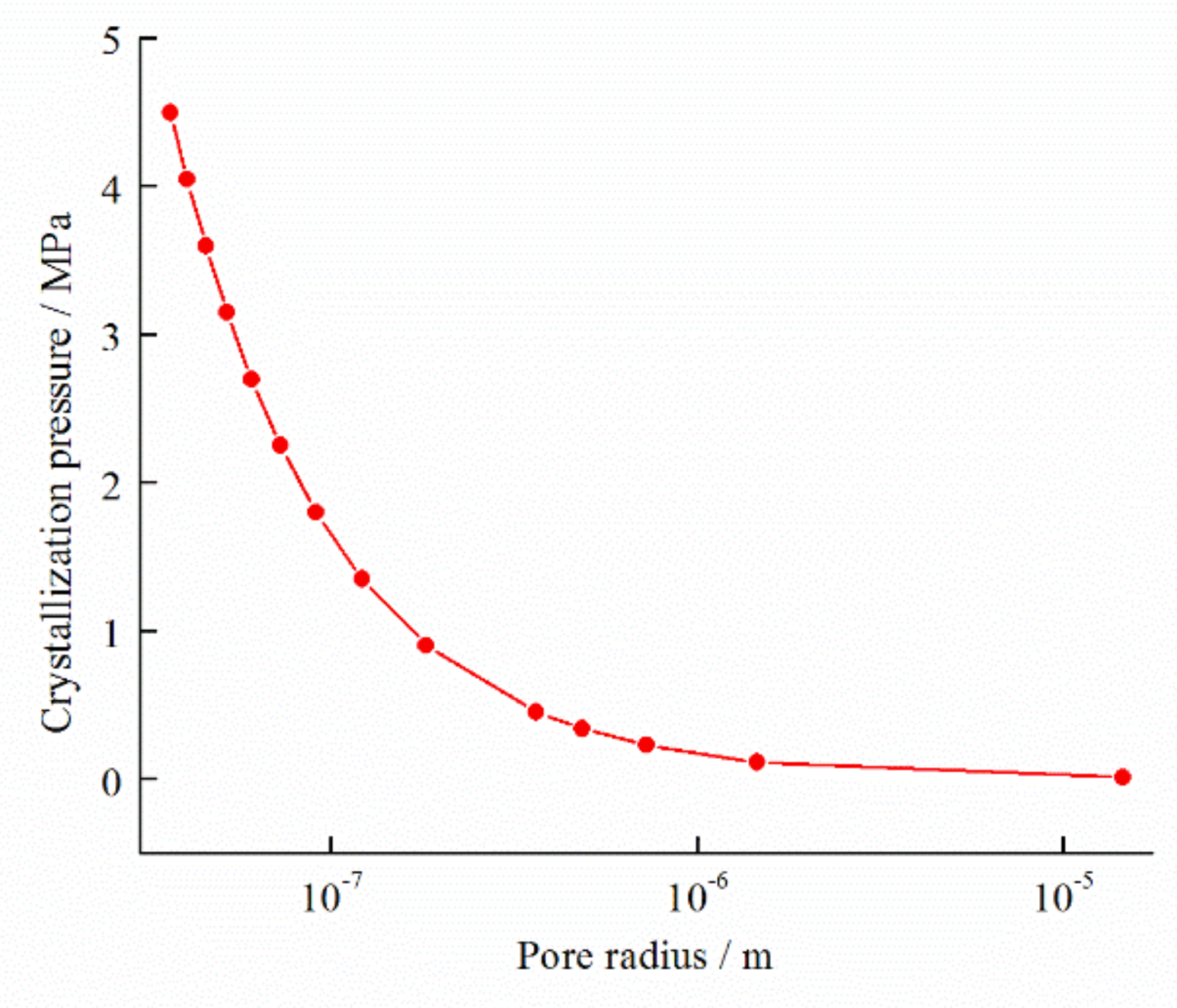
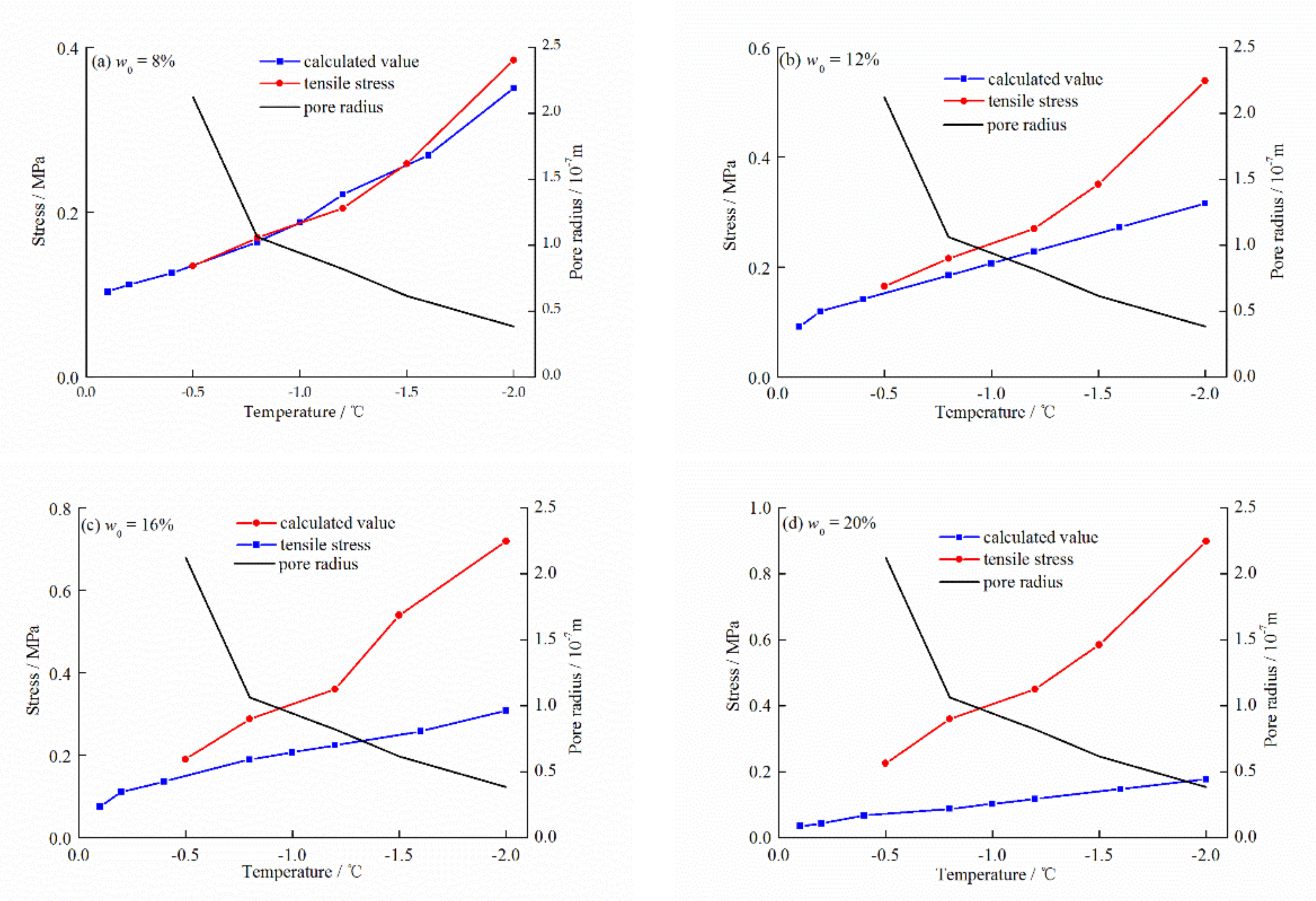
4.3. Microscopic Mean Stress
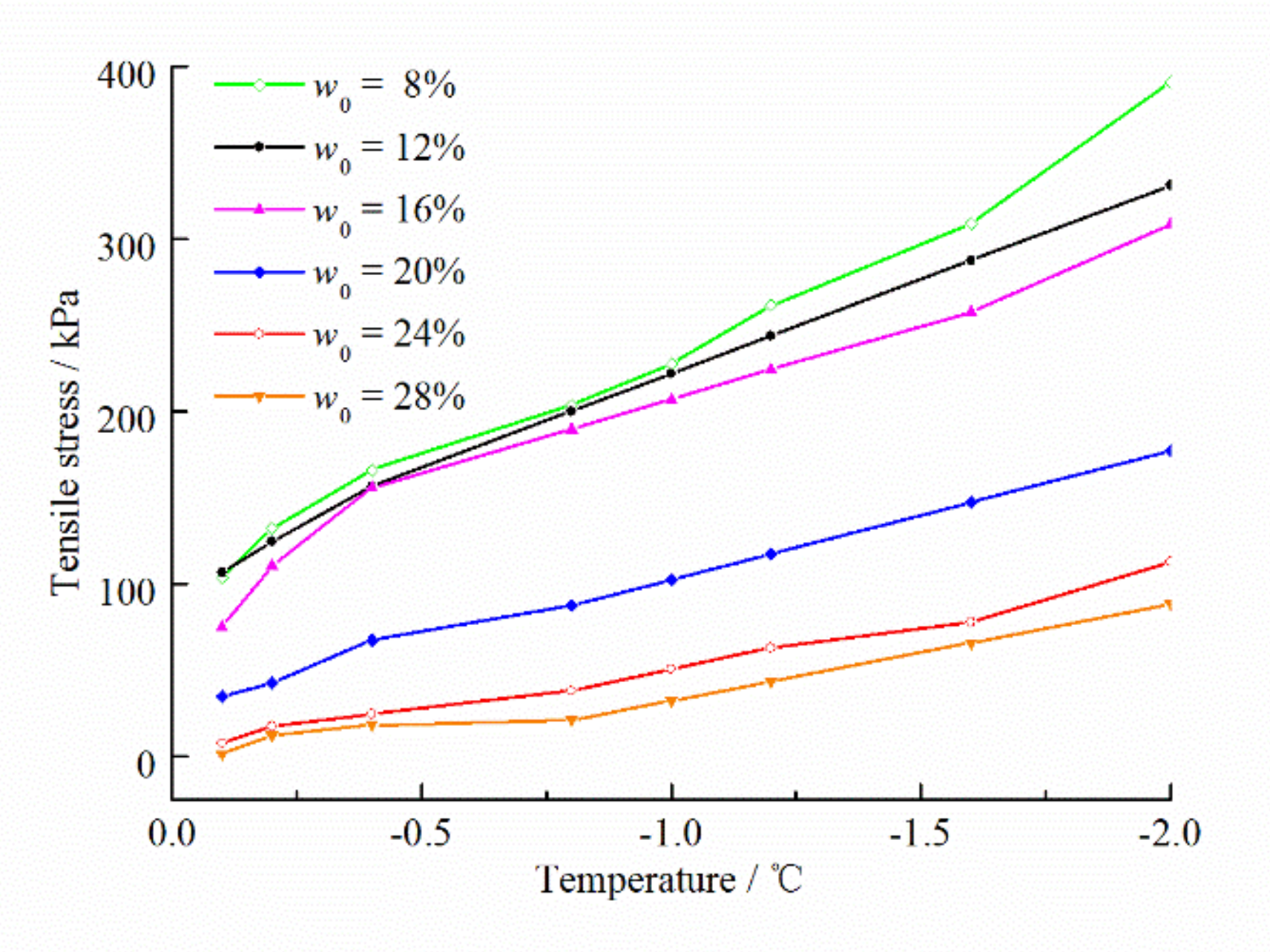
4.4. Tensile Stress
4.5. Comparison of the Mean Stress and the Tensile Strength
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, W.; Niu, F.J.; Mu, Y.H. Basic research on the major permafrost projects in the Qinghai-Tibet Plateau. Adv. Earth Sci. 2012, 27. [Google Scholar] [CrossRef]
- Wang, G.S.; Yu, Q.H.; Guo, L.; You, Y.H.; Wang, S.J.; Yu, Y. Prevention and control of freezing and thawing disasters in electric transmission lines constructed in permafrost regions. J. Glaciol. Geocryol. 2014, 36, 137–143. [Google Scholar] [CrossRef]
- Yu, F.; Qi, J.L.; Lai, Y.M.; Sivasithamparam, N.; Yao, X.L.; Zhang, M.Y.; Liu, Y.Z.; Wu, G.L. Typical embankment settlement/heave patterns of the Qinghai-Tibet highway in permafrost regions: Formation and evolution. Eng. Geol. 2016, 214, 147–156. [Google Scholar] [CrossRef]
- Taber, S. Frost Heaving. J. Geol. 1929, 37, 428–461. [Google Scholar] [CrossRef]
- Thomas, H.R.; Cleall, P.J.; Li, Y. Modelling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 59, 173–184. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, Y.; Li, D.Q. Experimental and theoretical investigations into the formation of ice lenses in deformable porous media. Geosci. J. 2016, 20, 667–679. [Google Scholar] [CrossRef]
- O’Neill, K.; Miller, R.D. Exploration of a rigid ice model of frost heave. Water Resour. Res. 1985, 21, 281–296. [Google Scholar] [CrossRef]
- Rempel, A.W.; Wettlaufer, J.S.; Worster, M.G. Premelting dynamics in a continuum model of frost heave. J. Fluid Mech. 2004, 498, 227–244. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhou, G.Q.; Zhou, J.S.; Wang, J.Z. Ice lens growth process involving coupled moisture and heat transfer during freezing of saturated soil. Chin. J. Geotech. Eng. 2010, 32, 578–585. [Google Scholar]
- Miller, R.D. Lens initiation in secondary heaving. In Proceedings of the International Symposium on Frost Action in Soils, Lulea, Sweden, 16–18 February 1977; pp. 68–74. [Google Scholar]
- Gilpin, R.R. A model for the prediction of ice lensing and frost heave in soils. Water Resour. Res. 1980, 16, 918–930. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Churaev, N.V. The theory of frost heaving. Prog. Surf. Sci. 1993, 67, 391–396. [Google Scholar] [CrossRef]
- Hopke, S.W. A model for frost heave including overburden. Cold Reg. Sci. Technol. 1980, 3, 111–127. [Google Scholar] [CrossRef]
- Sheng, D.C.; Axelsson, K.; Knutsson, S. Frost heave due to ice lens formation in freezing soils1. Theory and verification. Hydrol. Res. 1995, 26, 125–146. [Google Scholar] [CrossRef]
- Chen, F.X. The theoretical frame of multi-phase porous medium for the freezing soil. Chin. J. Geotech. Eng. 2002, 24, 213–217. [Google Scholar] [CrossRef]
- Dash, J.G.; Rempel, A.W.; Wettlaufer, J.S. The physics of premelted ice and its geophysical consequences. Rev. Mod. Phys. 2006, 78, 695–741. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Bing, H. Experimental study of the effect of freezing thawing cycles on porosity characters of silty clay by using mercury intrusion porosimetry. J. Glaciol. Geocryol. 2015, 19, 620–624. [Google Scholar] [CrossRef]
- Lecampion, B. Stress-induced crystal preferred orientation in the poromechanics of in-pore crystallization. J. Mech. Phys. Solids 2010, 58, 1701–1715. [Google Scholar] [CrossRef]
- Zhang, H.M.; Yang, G.S. Damage mechanical characteristics of rock under freeze-thaw and load coupling. Eng. Mech. 2011, 28, 161–195. [Google Scholar]
- Wall, F.T. Chemical Thermodynamics; Freeman: San Francisco, CA, USA, 1965; pp. 157–158. [Google Scholar]
- Scherer, G.W. Freezing gels. J. Non-Cryst. Solids 1993, 155, 1–25. [Google Scholar] [CrossRef]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 5th ed.; John Wiley and Sons: New York, NY, USA, 1967; pp. 379–389. [Google Scholar]
- Adamson, A.W. Physical chemistry of surfaces Wiley. Phys. Chem. Surf. 1990, 524, A467. [Google Scholar] [CrossRef]
- Scherer, G.W. Stress from crystallization of salt. Cem. Concr. Res. 2004. [Google Scholar] [CrossRef]
- Ju, X.D. Study on the Mechanism of Crystallization Damage for the Porous Media of Rocks; Institute of Rock and Soil Mechanics University of Chinese Academy of Sciences: Wuhan, China, 2014. [Google Scholar]
- Ju, X.D.; Feng, W.J.; Zhang, Y.J.; Zhao, H.B. Crystallization stresses in brittle porous media. Chin. J. Geotech. Eng. 2016, 38, 1246–1253. [Google Scholar] [CrossRef]
- Wang, C.; Lai, Y.M.; Zhang, M.Y. Estimating soil freezing characteristic curve based on pore-size distribution. Appl. Therm. Eng. 2017, 124, 1049–1060. [Google Scholar] [CrossRef]
- Xiao, Z.A.; Lai, Y.M.; You, Z.M. Study on the Water and Salt Migration Process and Deformation Mechanism of Daline Freezing Soil; Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences: Lanzhou, China, 2017. [Google Scholar]
- You, Z.M.; Lai, Y.M.; Zhang, M.Y.; Liu, E.L. Quantitative analysis for the effect of microstructure on the mechanical strength of frozen silty clay with different contents of sodium sulfate. Environ. Earth Sci. 2017, 76, 143. [Google Scholar] [CrossRef]
- Watanabe, K.; Mizoguchi, M. Amount of unfrozen water in frozen porous media saturated with solution. Cold Reg. Sci. Technol. 2002, 34, 103–110. [Google Scholar] [CrossRef]
- Anderson, D.M.; Tice, A.R. The unfrozen interfacial phase in frozen soil water systems. In Physical Aspects of Soil Water and Salts in Ecosystems; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar] [CrossRef]
- Everett, D.H. The thermodynamics of frost damage to porous solids. Trans. Faraday Soc. 1961, 57, 1541–1551. [Google Scholar] [CrossRef]
- Konrad, J.M.; Duquennoi, C. A model for water transport and ice lensing in freezing soils. Water Resour. Res. 1993, 29, 3109–3124. [Google Scholar] [CrossRef]
- Dash, J.G.; Fu, H.; Wettlaufer, J.S. The premelting of ice and its environmental consequences. Rep. Prog. Phys. 1995, 58, 115–167. [Google Scholar] [CrossRef]
- Miyata, Y. A thermodynamic study of liquid transportation in freezing porous media. JSME Int. J. 1998, 41, 601–609. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, K.; Mizoguchi, M. Ice configuration near a growing ice lens in a freezing porous medium consisting of micro glass particles. J. Cryst. Growth 2000, 213, 135–140. [Google Scholar] [CrossRef]
- Nixon, J.F. Discrete ice lens theory for frost heave in soils. Can. Geotech. J. 1991, 28, 843–859. [Google Scholar] [CrossRef]
- He, P.; Cheng, G.; Yu, Q.; Zhu, Y.L.; Xu, X.Z. A couple model of heat, water and stress fields of saturated soil during freezing. J. Glaciolgy Geocryol. 2000, 22, 135–138. [Google Scholar]
- Zhang, L.H.; Ma, W.; Yang, C.S.; Yuan, C. Investigation of the pore water pressures of coarse-grained sandy soil during open-system step-freezing and thawing tests. Eng. Geol. 2014, 181, 233–248. [Google Scholar] [CrossRef]
- Wu, D.; Lai, Y.M.; Zhang, M.Y. Thermo-hydro-salt-mechanical coupled model for saturated porous media based on crystallization kinetics. Cold Reg. Sci. Technol. 2017, 133, 94–107. [Google Scholar] [CrossRef]
- Penner, E. Aspects of ice lens growth in soils. Cold Reg. Sci. Technol. 1986, 13, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, K.; Mizoguchi, M.; Ishizaki, T. Experimental study on microstructure near freezing front during soil freezing. Trans. Jpn. Soc. Irrig. Drain. Reclam. Eng. 1997, 65, 53–58. [Google Scholar]
- Zhang, Q. Tests on Evolution of Segregation Ice of Artificial Frozen Soils; China University of Mining and Technology: Xuzhou, China, 2005. (In Chinese) [Google Scholar]






| Soil Type | Maximum Dry Density (g/cm3) | Plastic Limit | Liquid Limit | Plasticity Index | Optimum Water Content |
|---|---|---|---|---|---|
| Loess | 1.76 | 15.60% | 27.20% | 8.40 | 16.00% |
| Experiment Condition | Initial Water Content | Wit Density (g/cm3) | Experiment Temperature (°C) | Soil Sample Diameter (mm) | Soil Sample Height (mm) |
|---|---|---|---|---|---|
| L1 | 8% | 1.95 | −18.00 | 62.00 | 84.76 |
| L2 | 12% | 1.99 | 83.11 | ||
| L3 | 16% | 2.04 | 81.16 | ||
| L4 | 20% | 2.10 | 78.90 | ||
| L5 | 24% | 2.13 | 77.70 | ||
| L6 | 28% | 2.17 | 76.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, D.; Chen, L.; Ming, F. Study on the Mechanical Criterion of Ice Lens Formation Based on Pore Size Distribution. Appl. Sci. 2020, 10, 8981. https://doi.org/10.3390/app10248981
Liu Y, Li D, Chen L, Ming F. Study on the Mechanical Criterion of Ice Lens Formation Based on Pore Size Distribution. Applied Sciences. 2020; 10(24):8981. https://doi.org/10.3390/app10248981
Chicago/Turabian StyleLiu, Yuhang, Dongqing Li, Lei Chen, and Feng Ming. 2020. "Study on the Mechanical Criterion of Ice Lens Formation Based on Pore Size Distribution" Applied Sciences 10, no. 24: 8981. https://doi.org/10.3390/app10248981
APA StyleLiu, Y., Li, D., Chen, L., & Ming, F. (2020). Study on the Mechanical Criterion of Ice Lens Formation Based on Pore Size Distribution. Applied Sciences, 10(24), 8981. https://doi.org/10.3390/app10248981






