Control Design of a Swarm of Intelligent Robots: A Closed-Form H2 Nonlinear Control Approach
Abstract
:1. Introduction
2. Mathematical Model and Tracking Error Dynamics
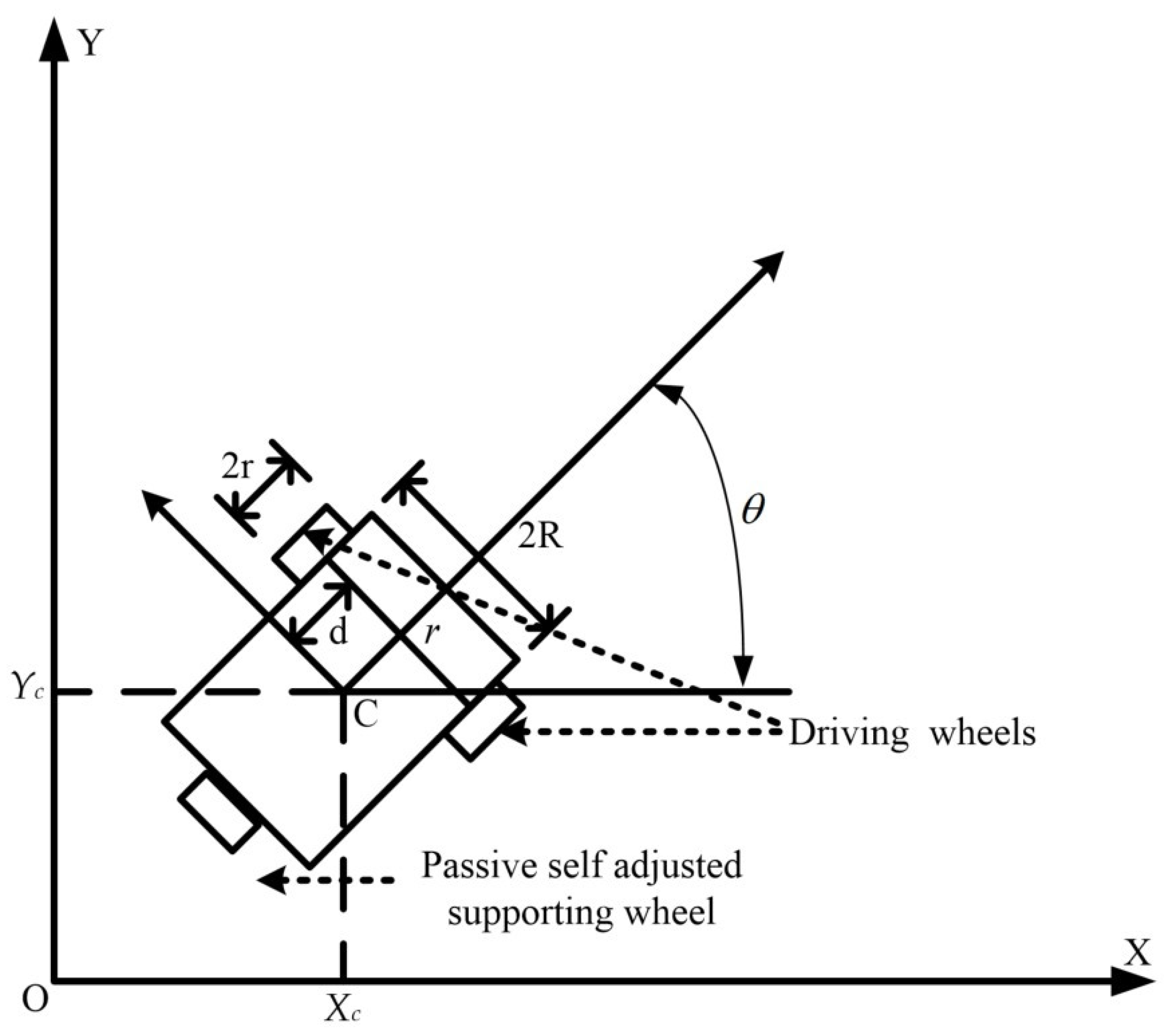
2.1. Dynamic Model of a Swarm of WMRs
2.2. Problem Formulation
3. Problem Formulation and H2 Controller Design
3.1. Nonlinear H2 Trajectory Tracking Problem
3.2. H2 Control Design for a Swarm of WMRs
3.3. Closed-Form Solution of the Nonlinear Time-Varying Riccati-Like Equation
4. Simulation Results and the Practical Implementation
4.1. Set Up of Simulation Environments
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Carelli, R.; Santos-Victor, J.; Roberti, F.; Tosetti, S. Direct visual tracking control of remote cellular robots. Robot. Auton. Syst. 2006, 54, 805–814. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Mitsutake, S.; Isoda, T.; Shi, T. Omni-directional robot and adaptive control method for off-road running. IEEE Trans. Robot. Autom. 2002, 18, 251–256. [Google Scholar] [CrossRef]
- Chwa, D. Sliding-mode tracking control of wheeled mobile robots in polar coordinates. IEEE Trans. Control. Syst. Tech. 2004, 12, 637–644. [Google Scholar] [CrossRef]
- Das, T.; Kar, I.N.; Chaudhury, S. Simple neuron-based adaptive controller for a mobile robot including actuator dynamics. Neurocomputing 2006, 69, 2140–2151. [Google Scholar] [CrossRef]
- Das, T.; Kar, I.N. Design and implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots. IEEE Trans. Control. Syst. Technol. 2006, 14, 501–510. [Google Scholar] [CrossRef]
- Dixon, W.E.; Dawson, D.M.; Zergeroglu, E.; Behal, A. Adaptive tracking control of a wheeled mobile robot via an uncalibrated camera system. IEEE Trans. Syst. Man Cyber. Part-B 2001, 31, 341–352. [Google Scholar] [CrossRef] [Green Version]
- Wai, R.J.; Su, K.H. Adaptive enhanced fuzzy sliding-mode control for electrical servo drive. IEEE Trans. Ind. Electron. 2006, 53, 569–580. [Google Scholar]
- Wai, R.J.; Chang, L.J. Adaptive stabilizing and tracking control for a nonlinear inverted-pendulum system. via sliding-mode technique. IEEE Trans. Ind. Electron. 2006, 53, 674–692. [Google Scholar]
- Defoort, M.; Murakami, T. Sliding-mode control scheme for an intelligent bicycle. IEEE Trans. Ind. Electron. 2009, 56, 3357–3368. [Google Scholar] [CrossRef]
- Park, M.S.; Chwa, D. Swing-up, and stabilization control of inverted pendulum systems via coupled sliding-mode control method. IEEE Trans. Ind. Electron. 2009, 56, 3541–3555. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Chang, P.H.; Choi, C. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control. IEEE Trans. Ind. Electron. 2009, 56, 3593–3601. [Google Scholar]
- Zhang, J.; Xia, Y. Design of static output feedback sliding mode control for uncertain linear systems. IEEE Trans. Ind. Electron. 2010, 57, 2161–2170. [Google Scholar] [CrossRef]
- Kim, D.H.; Oh, J.H. Tracking control of a two-wheeled mobile robot using input-output linearization. Control. Eng. Pract. 1999, 7, 369–373. [Google Scholar] [CrossRef]
- Leith, D.J.; Leithead, W.E. Gain-scheduled, and nonlinear systems: Dynamic analysis by velocity-based linearization families. Int. J. Control. 1998, 70, 289–317. [Google Scholar] [CrossRef]
- Fierro, R.; Lewis, F.V. Control of a mobile robot: Backstepping kinematics into dynamics. J. Robot. Syst. 1997, 14, 149–163. [Google Scholar] [CrossRef]
- Zhang, Q.; Shippen, J.; Jones, B. Robust backstepping and neural network control of a low-quality mobile robot. Int. J. Mach. Tools Manuf. 1999, 39, 1117–1134. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding mode tracking control of surface vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Tai, H.M.; Wang, J.; Ashenayi, K. A neural network-based tracking control system. IEEE Trans. Ind. Electron. 1992, 39, 504–510. [Google Scholar] [CrossRef]
- Wai, R.J. Fuzzy sliding-mode control using adaptive tuning technique. IEEE Trans. Ind. Electron. 2007, 54, 586–594. [Google Scholar] [CrossRef]
- Tsai, C.C.; Huang, H.C.; Lin, S.C. Adaptive neural network control of self-balancing two-wheeled scooter. IEEE Trans. Ind. Electron. 2010, 57, 1420–1428. [Google Scholar] [CrossRef]
- Rigatos, G.G.; Tzafestas, C.S.; Tzafestas, S.G. Mobile robot motion control in partially unknown environments using a sliding-mode fuzzy logic controller. Robot. Auton. Syst. 2000, 33, 1–11. [Google Scholar] [CrossRef]
- Boquete, V.; Garcia, R.; Barea, R.; Mazo, M. Neural control of the movements of a wheelchair. J. Intell. Robot. Syst. 1999, 25, 213–226. [Google Scholar] [CrossRef]
- Marichal, G.N.; Acosta, L.; Moreno, L.; Méndez, J.A.; Rodrigo, J.J.; Sigut, M. Obstacle avoidance for a mobile robot: A neuro-fuzzy approach. Fuzzy Sets Syst. 2001, 124, 171–179. [Google Scholar] [CrossRef]
- Francis, B.A. A Course in H∞ Control Theory. Lect. Notes Control Inf. Sci. Ser. 1987, 88, 101–113. [Google Scholar]
- Baser, T.; Bernhard, P. H∞-Optimal Control and Related Minmax Problems; Birkhauser: Berlin, Germany, 1990; pp. 72–93. [Google Scholar]
- Chen, Y.H.; Li, T.H.S.; Chen, Y.Y. A novel nonlinear control law with trajectory tracking capability for mobile robots: Closed-form solution design. Appl. Math. Inf. Sci. 2013, 7, 749–754. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Chen, Y.H.; Huang, C.Y. Wheeled mobile robot design with robustness properties. Adv. Mech. Eng. 2018, 10, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zhou, K.; Glover, K.; Bodenheimer, B.; Doyle, J. Mixed H2 and H∞ performance objectives I: Robust performance analysis. IEEE Trans. Autom. Control. 1994, 39, 1564–1574. [Google Scholar] [CrossRef]


















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-H.; Lou, S.-J. Control Design of a Swarm of Intelligent Robots: A Closed-Form H2 Nonlinear Control Approach. Appl. Sci. 2020, 10, 1055. https://doi.org/10.3390/app10031055
Chen Y-H, Lou S-J. Control Design of a Swarm of Intelligent Robots: A Closed-Form H2 Nonlinear Control Approach. Applied Sciences. 2020; 10(3):1055. https://doi.org/10.3390/app10031055
Chicago/Turabian StyleChen, Yung-Hsiang, and Shi-Jer Lou. 2020. "Control Design of a Swarm of Intelligent Robots: A Closed-Form H2 Nonlinear Control Approach" Applied Sciences 10, no. 3: 1055. https://doi.org/10.3390/app10031055



