Darcy–Boussinesq Model of Cilia-Assisted Transport of a Non-Newtonian Magneto-Biofluid with Chemical Reactions

Abstract

The model developed in this study presents a mathematical approach to the physiological transport of seminal liquid due to ciliary movements, which are attached with the lumen of the ductile efferent in the male reproductive system. The rheological properties of the seminal liquids were described using the Jeffrey liquid model. The problem described an electromagnetic mixed convective flow of a Jeffrey liquid through a vertical channel with heat and mass transfers. The effects of chemical reactions and the external heat generation were included in the formulation. The flow took place through an active porous medium (due to thick cilia mat and other deposits) and was influenced by the Lorentz magnetic force. Four basic conservation laws of mass, momentum, energy, and concentration were utilized in the mathematical modeling. These are highly nonlinear equations, which were simplified due to a physiologically valid approach known as LAT (lubrication approximation theory). Analytical solutions for temperature, concentration, and velocity profiles were evaluated. The expressions describing the pressure–volume flow rate relationships were also obtained. Analysis of various physical and geometrical factors affecting the pressure–volume (pumping) characteristics was also presented. One of the main findings of our study is that the difference between our calculated values of the flow rate and the estimated values of the flow rate in the ductile efferent was negligibly small. Moreover, our results can be implemented in the artificial cilia pumping systems in microchannels.

1. Introduction

The propulsion mechanisms of cilia-driven flows are of great importance in the proper examination of various biological systems in the human body, locomotion of natural organisms, and biomedical devices. Hair-like microscopic structures, known as cilia, is present in many organs of almost every mammal. Their capabilities of producing wave-like periodic movements help in propelling the surrounding liquids and flagella [1,2,3]. These organelles not only power the cell movements and fluid transport, but also organize and regulate the biophysical forces and act as sensors for many biochemical and biomechanical changes in the body. Their rapid and coordinated beatings are periodic in nature and produce sinusoidal waves known as metachronal waves. In the human body, cilia are present in the brain, kidneys, eyes, lungs, trachea, fallopian tubes, and efferent ducts of the male reproductive system, and their defects can cause a wide range of disorders in the human body, including kidney degeneration, vision impairment, and even some cancers [4,5,6]. Beyond their traditional role in biological systems, the ciliary-induced transport mechanisms are widely implemented in lab-on-a-chip devices that use artificial cilia for inducing fluid flow and mixing [7].

Although cilia were discovered in 1675, an explosion of studies on cilia and its functionality in human development was started after the invention of the electronic microscope in 1960. The early studies on the fluid dynamics of ciliary locomotion was comprehensively reviewed by Brennen and Winet [8]. We shall not repeat the detailed description of the previous studies on the fluid dynamics of ciliary locomotion here; however, interested readers can see these details in References [9,10,11,12,13,14,15]. The related study with heat transfer, thermal behavior, and their applications can be seen in References [16,17,18,19]. The related cilia usually function in large groups and one group of cilia beat (swing) in the opposite direction (out of phase) with respect to a neighboring group of cilia. These coordinated actions of the cilia produce a wave called a metachronal wave propagating all along the surface formed by the cilia tips. In the fields of medical sciences, applications of the electromagnetic effects and heat and mass transfer are recognized in many therapies, for example, hyperthermia and radiofrequency therapies, thermoregulation in testis, hemodialysis, oxygenation, MRI and X-rays, etc. [20,21,22,23]. This phenomenon also has implications regarding the design of magnetic artificial cilia that can be used in nanodrug supply systems, quick disease diagnosis, and daily health monitoring systems [24]. Thermal analysis of biological tissues and various metabolic processes is another hot research area in the medical sciences. In addition, chemical reactions play essential roles in the lives of all humans, producing energy and regulating the growing processes in the body. Research articles by Nadeem [24,25], Sirinivas [26], Akbar [27], and Tripathi [28] present the important roles of electromagnetic body forces, chemical reactions, and heat and mass transfers on various biological flows in the human body. These articles contain many other related citations and we feel that it will not be suitable to repeat them again. The flow through porous (Darcian or non-Darcian) media has wide applications in physiology (also in industry) because such flows are observed in kidneys, lungs, liver, bile ducts, bones, cartilages, etc. Today, most researchers believe that the dissemination of fatty substances in blood vessels and the formation of blood clots in coronary veins can be considered as a porous medium that will provide a resistance to the propulsion of various biological materials [29,30,31,32,33].

In view of the above studies, we investigated the impacts of heat and mass transfers on the propulsion mechanisms of cilia in moving a Jeffrey-type, electromagnetic, viscoelastic fluid through a vertical channel. The effects of heat generations and chemical reactions was also considered. The Jeffrey fluid model is the simplest extension of the classical viscous model describing the viscoelastic behavior of fluids that uses time derivatives instead of convective derivatives and is widely proposed for physiological fluids [34,35,36,37]. A close examination of the literature reveals that very little research work has been conducted on the ciliary-induced transport of viscoelastic fluid through the vertical channels with mixed convection analysis. Such investigations are very rare when the effects of chemical reactions and mixed convections on the transport of magneto-biofluids due to cilia motions are also considered. Our main aim was to formulate mathematical equations for the physical flows of the required problems of ciliary induced transport of seminal fluids through male reproductive systems. The material was assumed to admit the laws of the Jeffrey model. A dense mat of ciliated epithelium was attached to the inner walls of the conduit and was assumed to act as a porous medium (Darcian type) for the flow. The governing mathematical equations were simplified and then solved by employing the valid creeping flow and the long wavelength approaches. The other related work with analytical solutions can be seen in References [38,39,40,41,42,43,44]. In this study, our main focus lay on the volume flow rate, the pressure rise per wavelength, and the pumping characteristics of cilia transport. The physical quantities are presented and discussed graphically.

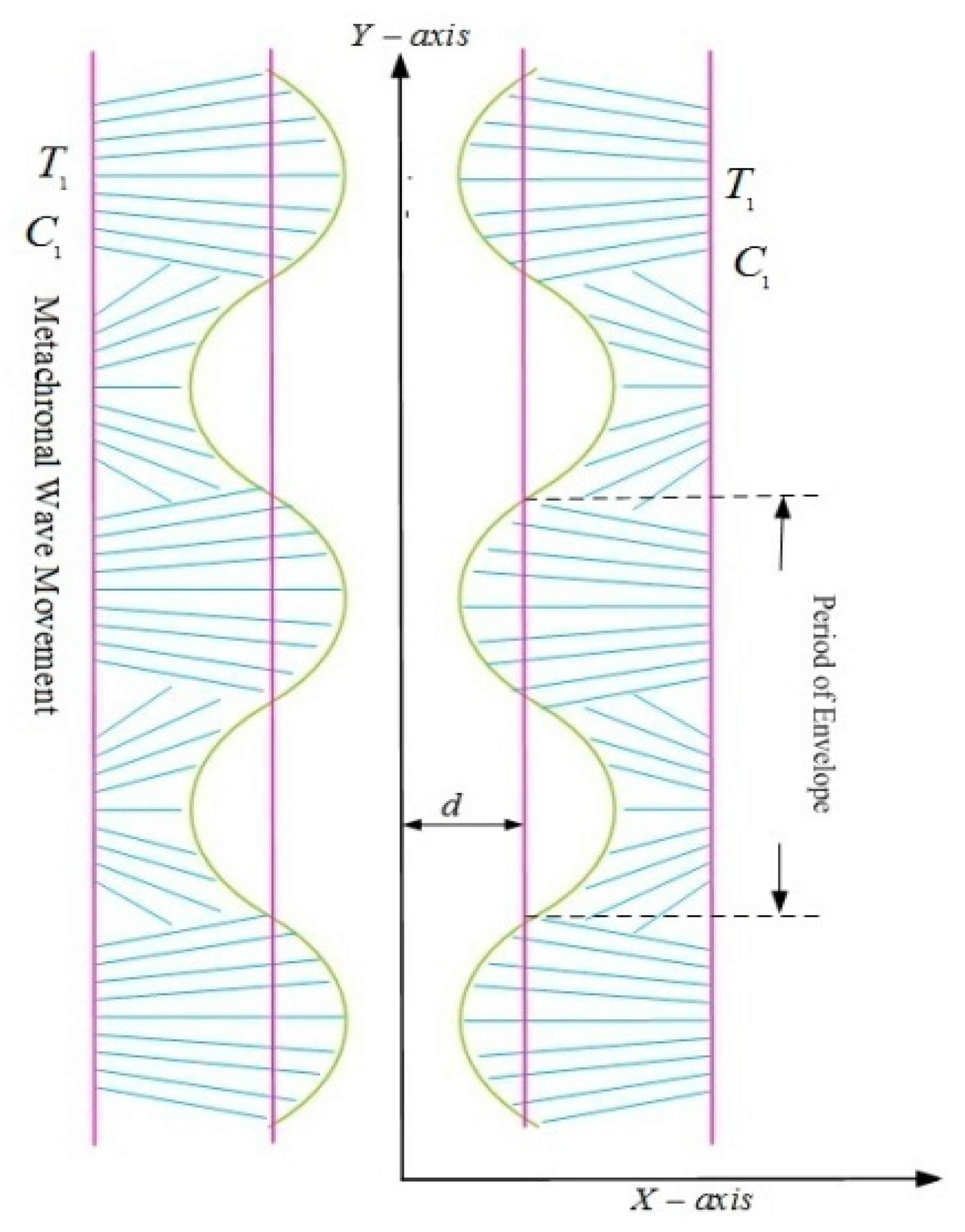
2. Problem Statement

We consider a vertical channel of uniform width and a rectangular coordinate system $\left(\widehat{X},\widehat{Y}\right)$, where the $\widehat{Y}-axis$ of the of the system coincides with its centerline and the $\widehat{X}-axis$ lies along its normal direction. The inner surface was carpeted with a highly dense mat of cilia, which was assumed to behave as a Darcian porous medium [35]. The tips of the cilia performed synchronous periodic beatings and formed a sinusoidal wave called the metachronal wave traveling with a uniform speed $c$ along the surface made by the cilia tips. A magnetized, viscoelastic, Jeffrey-type liquid was placed within the channel under the influence of a magnetic body force. The imposed magnetic field had a constant strength $B_0$ and acted normal to the flow. The geometry of the problem is shown in Figure 1. We neglected the induced magnetic field by taking the magnetic Reynolds number to be very small. The analysis of the heat and mass transfer was also taken into consideration by giving the temperature $T_1$ and concentration $C_1$ on the walls of the channel. The well-known symmetry conditions for both the temperature and concentration fields were employed at the center of the channel. Moreover, the study of thermal effects on biochemical reactions was necessary to examine the various metabolisms taking place within the human body. Therefore, the effects of chemical reactions and heat addition (absorption) were also considered in the present study.

By considering the above assumptions, we defined the mass, momentum, energy, and concentration equations with the usual Boussinesq approximation as:

$$\frac{\partial \widehat{U}}{\partial \widehat{X}}+\frac{\partial \widehat{V}}{\partial \widehat{Y}}=0,$$

(1)

$$\rho \left[\frac{\partial \widehat{U}}{\partial \widehat{t}}+\widehat{U}\frac{\partial \widehat{U}}{\partial \widehat{X}}+\widehat{V}\frac{\partial \widehat{U}}{\partial \widehat{Y}}\right]=-\frac{\partial \widehat{P}}{\partial \widehat{X}}+\frac{\partial S_{\widehat{X}\widehat{X}}}{\partial \widehat{X}}+\frac{\partial S_{\widehat{X}\widehat{Y}}}{\partial \widehat{Y}}+\rho g{\alpha }_T\left(T-T_0\right)+\rho g{\alpha }_m\left(C-C_0\right)-\left(\sigma B_0^2+\frac{\mu }{K_p}\right)\widehat{U},$$

(2)

$$\rho \left[\frac{\partial \widehat{V}}{\partial \widehat{t}}+\widehat{U}\frac{\partial \widehat{V}}{\partial \widehat{X}}+\widehat{V}\frac{\partial \widehat{V}}{\partial \widehat{Y}}\right]=-\frac{\partial \widehat{P}}{\partial \widehat{Y}}+\frac{\partial S_{\widehat{Y}\widehat{X}}}{\partial \widehat{X}}+\frac{\partial S_{\widehat{Y}\widehat{Y}}}{\partial \widehat{Y}}-\frac{\mu }{K_p}\widehat{V},$$

(3)

$$\rho C_p\left[\frac{\partial T}{\partial \widehat{t}}+\widehat{U}\frac{\partial T}{\partial \widehat{X}}+\widehat{V}\frac{\partial T}{\partial \widehat{Y}}\right]=K\left[\frac{{\partial }^{2}T}{\partial {\widehat{X}}^2}+\frac{{\partial }^{2}T}{\partial {\widehat{Y}}^2}\right]+Q_0,$$

(4)

$$\left[\frac{\partial C}{\partial \widehat{t}}+\widehat{U}\frac{\partial C}{\partial \widehat{X}}+\widehat{V}\frac{\partial C}{\partial \widehat{Y}}\right]=D\left[\frac{{\partial }^{2}C}{\partial {\widehat{X}}^2}+\frac{{\partial }^{2}C}{\partial {\widehat{Y}}^2}\right]+\frac{D{K}_T}{T_m}\left[\frac{{\partial }^{2}T}{\partial {\widehat{X}}^2}+\frac{{\partial }^{2}T}{\partial {\widehat{Y}}^2}\right]-K_c\left(C-C_0\right).$$

(5)

In the above equations, $\widehat{U}$, $\widehat{V}$, $\widehat{P}$, and $T$ denote the axial velocity component, the normal velocity component, the fluid pressure, and the fluid temperature, respectively. Moreover, $\rho$ represents the fluid density, $\mu$ denotes the viscosity coefficient, $g$ is the acceleration due to gravity, ${\alpha }_T$ is the thermal expansion coefficient, ${\alpha }_m$ is the concentration expansion coefficient, $\sigma$ is the electrical conductivity, $K_p$ is the permeability of the porous medium, $C_p$ is the specific heat, $K$ is the thermal conductivity, $Q_0$ stands for the constant heat addition (absorption), $D$ represents the mass diffusivity coefficient, $K_T$ is the thermal diffusion ration, $T_m$ is the mean medium temperature, and $K_c$ is the chemical reaction parameter.

The components of the stress tensors $S_{XX}$, $S_{XY}$, $S_{YX}$, and $S_{YY}$ for the Jeffrey fluid model can be determined by using the following constitutive relations [34,35,36,37,38,39]:

$$S=\mu {(1+{\lambda }_1)}^{-1}\left(1+{\lambda }_2\frac{d}{dt}\right)A_1,A_1=\left(\mathrm{grad}V\right)+{\left(\mathrm{grad}V\right)}^{\mathrm{transpose}},$$

(6)

where $\mu$ is the coefficient of shear viscosity, ${\lambda }_1$ is the dimensionless ratio of the relaxation time to the retardation time, ${\lambda }_2$ is the retardation time, $\frac{d}{dt}$ represents the material time derivative, and $A_1$ is the first Rivlin–Ericksen tensor.

The effective and recovery nature of ciliary beatings trace out elliptical courses, which are defined in the following parametric equations [3]:

$$\widehat{X}=f(\widehat{X},\widehat{t})={\widehat{X}}_0+d\delta \epsilon \sin \left(2\pi {\lambda }^{-1}(\widehat{X}-ct)\right),$$

(7)

$$\widehat{Y}=g(\widehat{X},\widehat{t})=\pm \left[d+\epsilon d\cos \left(2\pi {\lambda }^{-1}\left(\widehat{X}-ct\right)\right)\right]=\pm H.$$

(8)

In the above, $d$ measures the average distance measured from the central axis; $\epsilon$ is a dimensionless parameter, which measures the cilia lengths; $\delta$ is the measurement of the eccentricity of the cilia motion; and $\widehat{X}$, ${\widehat{X}}_0$, and $\widehat{Y}$ represent the horizontal position, reference position, and the vertical position of the cilia tips. Furthermore, $\lambda$ is the wavelength and $c$ is the wave speed of the metachronal wave.

The velocities of the cilia tips are defined as:

$$\widehat{U}={\frac{\partial \widehat{X}}{\partial \widehat{t}}|}_{{}_{X_0}}=\frac{\partial f}{\partial \widehat{t}}+\frac{\partial f}{\partial \widehat{X}}\frac{\partial \widehat{X}}{\partial \widehat{t}}=\frac{\partial f}{\partial \widehat{t}}+\frac{\partial f}{\partial \widehat{X}}\widehat{U},$$

(9)

$$\widehat{V}={\frac{\partial \widehat{Y}}{\partial \widehat{t}}|}_{{}_{X_0}}=\frac{\partial g}{\partial \widehat{t}}+\frac{\partial g}{\partial \widehat{X}}\frac{\partial \widehat{X}}{\partial \widehat{t}}=\frac{\partial g}{\partial \widehat{t}}+\frac{\partial g}{\partial \widehat{X}}\widehat{U}.$$

(10)

Upon substituting Equations (7) and (8) into Equations (9) and (10) and solving for $\widehat{U}$ and $\widehat{V}$, we arrive at:

$$\widehat{U}=\frac{-2\pi {\lambda }^{-1}\left(d\delta c\epsilon \cos \left(2\pi {\lambda }^{-1}\left(\widehat{X}-c\widehat{t}\right)\right)\right)}{1-2\pi {\lambda }^{-1}\left(d\delta \epsilon \cos \left(2\pi {\lambda }^{-1}\left(\widehat{X}-c\widehat{t}\right)\right)\right)},\widehat{V}=\frac{2\pi {\lambda }^{-1}\left(dc\epsilon \sin \left(2\pi {\lambda }^{-1}\left(\widehat{X}-c\widehat{t}\right)\right)\right)}{1-2\pi {\lambda }^{-1}\left(d\delta \epsilon \cos \left(2\pi {\lambda }^{-1}\left(\widehat{X}-c\widehat{t}\right)\right)\right)}\mathrm{at}\widehat{Y}=\pm H.$$

(11)

It is convenient to analyze the steady-state solutions of the present problem. Therefore, we converted our equations from $(\widehat{X},\widehat{\mathsf{Y}})$, i.e., the fixed frame, to $\left(x,y\right)$, i.e., the wave frame, which will travel with a speed $c$. The variables in these two frames are connected through the following relations:

$$x=\widehat{X}-ct,y=\widehat{Y},u=\widehat{U}-c,v=\widehat{V},P(x)=P(\widehat{X},t).$$

(12)

In the wave frame, the boundary conditions will become:

$$\frac{\partial u}{\partial y}=0\left(\mathrm{regularity}\mathrm{condition}\right),v=0\mathrm{at}y=0,$$

(13)

$$u+c=\frac{-2\pi {\lambda }^{-1}\left(d\delta c\epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right)}{1-2\pi {\lambda }^{-1}\left(d\delta \epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right)},\mathrm{at}y=\pm H=d\left(1+\epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right),$$

(14)

$$v=\frac{2\pi {\lambda }^{-1}\left(dc\epsilon \sin \left(2\pi {\lambda }^{-1}x\right)\right)}{1-2\pi {\lambda }^{-1}\left(d\delta \epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right)},\mathrm{at}y=\pm H=d\left(1+\epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right),$$

(15)

$$\frac{\partial T}{\partial y}=0,\frac{\partial C}{\partial y}=0,\left(\mathrm{symmetry}\mathrm{conditions}\right)\mathrm{at}y=0,$$

(16)

$$T=T_1,C=C_1,\mathrm{at}y=\pm H=d\left(1+\epsilon \cos \left(2\pi {\lambda }^{-1}x\right)\right).$$

(17)

Now, we introduce the following dimensionless quantities:

$$\begin{array}{l}{t}^{*}=\frac{ct}{\lambda },y^{*}=\frac{y}{d},x^{*}=\frac{x}{\lambda },u^{*}=\frac{u}{\beta c},v^{*}=\frac{v}{c},h^{*}=\frac{H}{d},p^{*}=\frac{d^{2}p}{c\lambda \mu },\beta =\frac{d}{\lambda },S_{ij}^{*}=\frac{a}{\mu c}{S}_{ij}^{*},\\ {\theta }^{*}=\frac{T-T_0}{T_1-T_0},{\phi }^{*}=\frac{C-C_0}{C_1-C_0},\mathrm{Re}=\frac{\rho cd}{c\mu },S_t=\frac{Q_0{d}^2}{K(T_1-T_0)},g_t=\frac{g\rho {\alpha }_T{d}^2\left(T_1-T_0\right)}{\mu c},\\ g_c=\frac{g\rho {\alpha }_m{d}^2\left(C_1-C_0\right)}{\mu c},S_c=\frac{\mu }{\rho D_m},S_r=\frac{D{K}_T}{C_0{T}_m},M=\frac{d^2\rho K_1}{\mu },H_a^2=\frac{\sigma B_0^{2}d}{\mu },D_a=\frac{K_p}{d^2},Q^{*}=\frac{Q}{dc}.\end{array}$$

(18)

For the low speed flow, we took the Reynolds number ($Re$) equal to zero. Furthermore, if we assume that the wavelength of the metachronal wave is larger than the mean width of the conduit, i.e., $\beta \ll 1$, considerable simplifications are achieved in the governing equations, which help to formulate an analytical analysis of the flow mechanism. Thus, we need to solve the following simplified system of the governing equations after dropping the asterisks, which are:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(19)

$${\left(1+{\lambda }_1\right)}^{-1}\frac{{\partial }^{2}u}{\partial y^2}-\left(H_a^2+\frac{1}{D_a}\right)\left(u+1\right)+g_t\theta +g_s\phi =\frac{\partial p}{\partial x},$$

(20)

$$\frac{\partial p}{\partial y}=0,$$

(21)

$$\frac{{\partial }^2\theta }{\partial y^2}+S_t=0,$$

(22)

$$\frac{1}{S_c}\frac{{\partial }^2\phi }{\partial y^2}-M\phi +S_r\frac{{\partial }^2\theta }{\partial y^2}=0.$$

(23)

The conditions will become:

$$\frac{\partial u}{\partial y}=0,\frac{\partial \theta }{\partial y}=0,\frac{\partial \phi }{\partial y}=0,\mathrm{at}y=0,$$

(24)

$$u=-1-\frac{2\pi \epsilon \delta \beta \cos \left(2\pi x\right)}{1-2\pi \epsilon \delta \beta \cos \left(2\pi x\right)},\theta =1,\phi =1,\mathrm{at}y=h=1+\epsilon \cos \left(2\pi x\right).$$

(25)

In the above equations, $g_t$ is the thermal Grashof number; $g_c$ is the concentration Grashof number; $H_a$ and $D_a$ are the Hartmann and the Darcy numbers, respectively; $S_t$ is the heat generation (absorption) parameter; $S_c$ is the Schmidt number; $S_r$ is the Soret number; and $M$ is the chemical parameter.

3. Solution of the Problem

The boundary value problem given in Equations (19)–(25) admits the closed form analytical solutions for the temperature, concentration, and velocity profiles in the following way

Using Equations (22) and the boundary conditions for $\theta$ defined in Equations (24) and (25), we obtain the following expression for the temperature distribution:

$$\theta =1-\frac{S_t}{2}\left(y^2-h^2\right).$$

(26)

Differentiating Equation (26) twice with respect to $y$ and using the result in Equation (23), we obtain:

$$\frac{1}{S_c}\frac{{\partial }^2\phi }{\partial y^2}-M\phi -S_r{S}_t=0,$$

(27)

which leads to the following solution satisfying the relevant boundary for $\phi$:

$$\phi =\frac{\cosh \left(\sqrt{M{S}_c}y\right)}{\cosh \left(\sqrt{M{S}_c}h\right)}\left(1+\frac{S_r{S}_t}{M}\right)-\frac{S_r{S}_t}{M}.$$

(28)

Upon using Equations (26) and (28) and boundary conditions, the axial velocity distribution $u$ from Equation (20) is formulated as:

$$\begin{array}{l}u=\left(-1-\frac{2\pi \epsilon \alpha \beta \cos \left(2\pi x\right)}{1-2\pi \epsilon \alpha \beta \cos \left(2\pi x\right)}\right)\frac{\cosh \left(\sqrt{X_1}y\right)}{\cosh \left(\sqrt{X_1}h\right)}+X_3\left(\frac{\cosh \left(\sqrt{X_1}y\right)}{\cosh \left(\sqrt{X_1}h\right)}-\frac{\cosh \left(\sqrt{M{S}_c}y\right)}{\cosh \left(\sqrt{M{S}_c}h\right)}\right)+\left[X_4+X_5\frac{dp}{dx}\right]\left(\frac{\cosh \left(\sqrt{X_1}y\right)}{\cosh \left(\sqrt{X_1}h\right)}-1\right)+X_6\left(y^2-h^2\right)\end{array}$$

(29)

where $X_1=\left(1+{\lambda }_1\right)\left(H_a^2+\frac{1}{D_a}\right)$, $X_2=X_1+\left(1+{\lambda }_1\right)\frac{g_c{S}_r{S}_t}{M}$, $X_3=\frac{\left(1+{\lambda }_1\right)g_c}{\left(M{S}_c-X_1\right)}\left(1+\frac{S_r{S}_t}{M}\right)$, $X_4=\frac{X_2+g_t{S}_t(1+{\lambda }_1)}{X_1}$, $X_5=\frac{\left(1+{\lambda }_1\right)}{\left(M{S}_c-X_1\right)}$, and $X_6=\frac{-\left(1+{\lambda }_1\right)g_t{S}_t}{2X_1}$.

In order to determine the unknown pressure gradient in Equation (28), we used the following relation:

$$q={\displaystyle \underset{0}{\overset{h}{\int }}udy},$$

(30)

which upon utilizing Equation (29) and then solving for $\frac{dp}{dx}$, takes the following form:

$$\frac{dp}{dx}=\frac{1}{\tanh \sqrt{X_1}h-\sqrt{X_1}h}\left[\frac{\sqrt{X_1}q}{X_5}-\frac{X_6\tanh \sqrt{X_1}h}{X_5}-\frac{X_3\tanh \sqrt{X_1}h}{X_5}+\frac{X_3\sqrt{X_1}\tanh \sqrt{M{S}_c}h}{X_5\sqrt{M{S}_c}}\right],$$

(31)

where $q$ is the volume flow rate, which is interconnected with $Q$ (the nondimensional time mean volume flow rate) as follows:

$$q=Q-1.$$

(32)

Upon integrating Equation (31), we obtain $\mathsf{\Delta }p$ (the pressure rise or drop) over one wavelength as:

$$\mathsf{\Delta }p={\displaystyle \underset{0}{\overset{1}{\int }}\frac{dp}{dx}}dx=a_{11}\left(Q-1\right)I_1-a_{12}{I}_2-a_{13}{I}_3+a_{14}{I}_4.$$

(33)

From the above relation, we could determine the formula for $Q$ as:

$$Q=1+\frac{1}{a_{11}{I}_1}\left(a_{12}{I}_2+a_{12}{I}_3-a_{12}{I}_4-\mathsf{\Delta }p\right),$$

(34)

where $I_1={\displaystyle \underset{0}{\overset{1}{\int }}\frac{dx}{\tanh \left(\sqrt{X_1}h\right)-\sqrt{X_1}h}}$, $I_2={\displaystyle \underset{0}{\overset{1}{\int }}\left(-1-\frac{2\pi \epsilon \delta \beta \cos \left(2\pi x\right)}{\left(1-2\pi \epsilon \delta \beta \cos \left(2\pi x\right)\right)}\right)}\frac{\tanh \left(\sqrt{X_1}h\right)dx}{\tanh \left(\sqrt{X_1}h\right)-\sqrt{X_1}h}$, $I_3={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\tanh (\sqrt{X_1}h)dx}{\tanh (\sqrt{X_1}h)-\sqrt{X_1}h}}$, $I_4={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\tanh (\sqrt{M{S}_c}h)dx}{\tanh (\sqrt{X_1}h)-\sqrt{X_1}h}}$, $a_{11}=\frac{\sqrt{X_1}}{X_5}$, $a_{12}=\frac{X_1}{X_5}$, $a_{13}=\frac{X_3}{X_5}$, and $a_{14}=\frac{X_3\sqrt{X_1}}{X_5\sqrt{M{S}_c}}$.

4. Discussions

This section contains an assessment of the physical behaviors of various key parameters on the transport characteristics of the semen in the human ductuli efferentes due to cilia transport. For brevity, we confine our attention to analyzing the effects of ${\lambda }_1$ (the Jeffery liquid parameter), $H_a$ (the Hartmann number), $D_a$ (the Darcy number), $S_t$ (the heat source parameter), $g_t$ (the Grashof number), and $\epsilon$ (the cilia length parameter) on $u(y)$ (the axial velocity), $Q$ (the volume flow rate), and $\mathsf{\Delta }p$ (pressure rise per wave length).

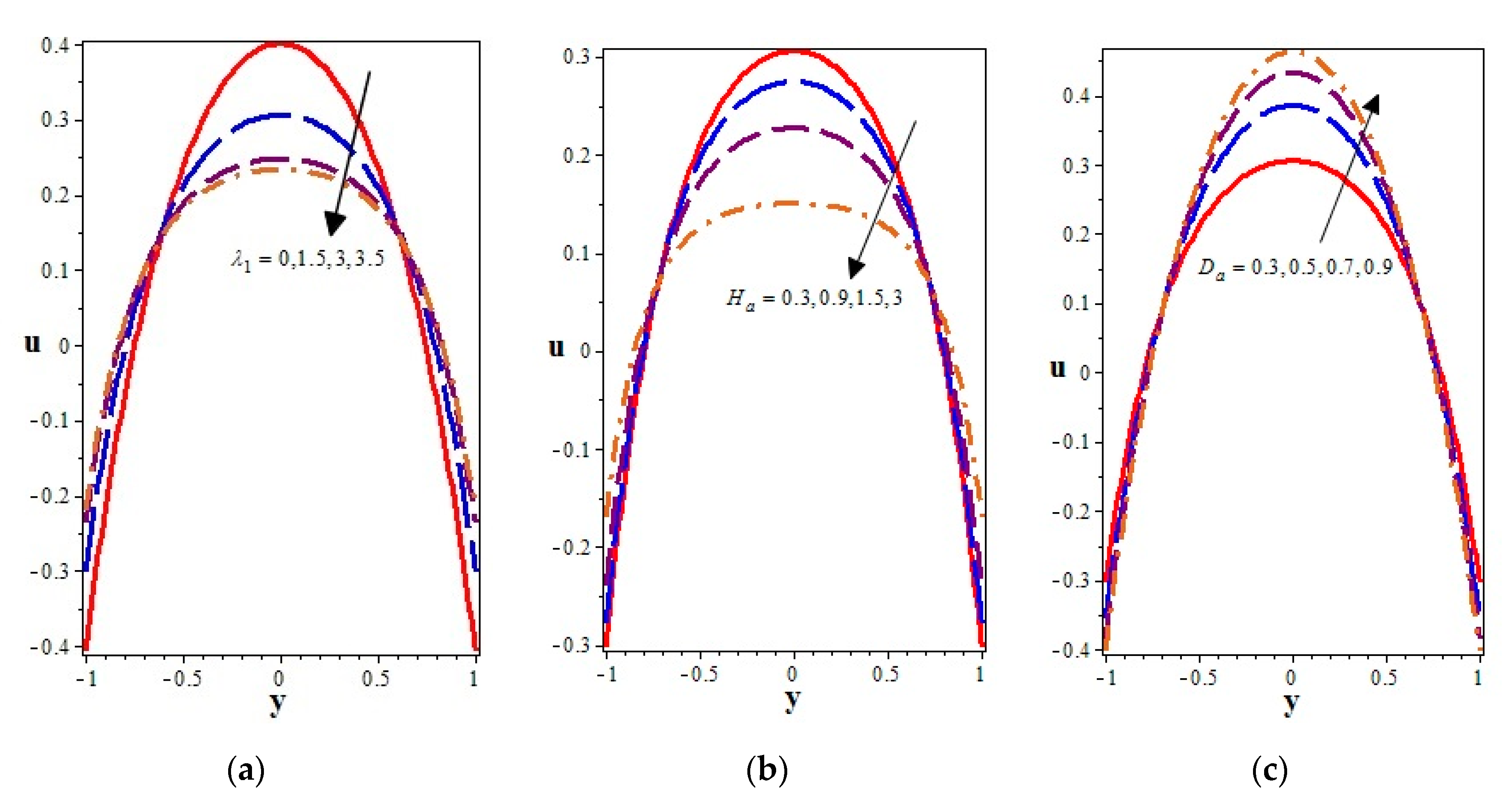
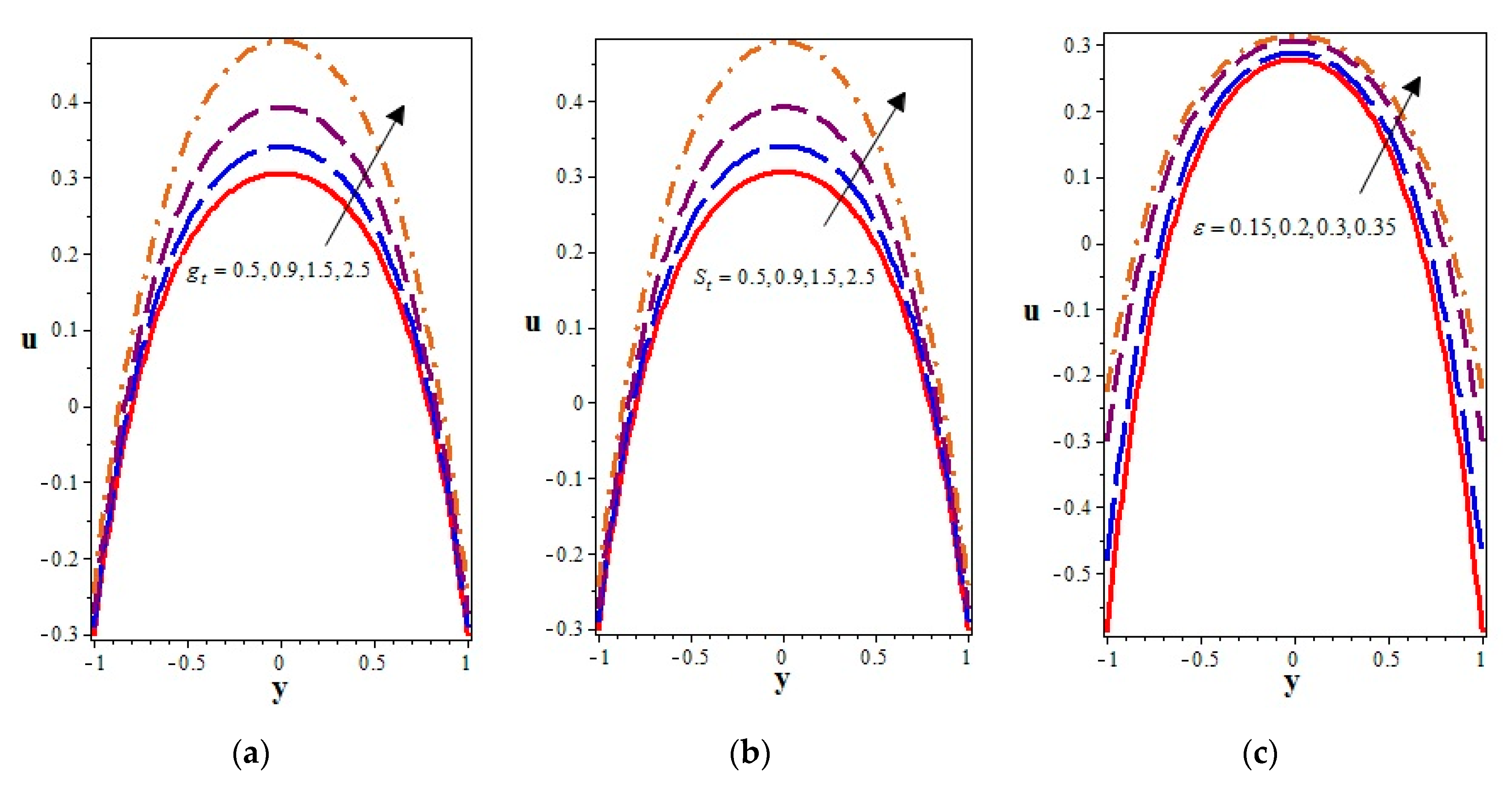
4.1. Velocity Profiles

The graphs in Figure 2a demonstrate the influence of ${\lambda }_1$ on the velocity $u(y)$. The velocity decreased in the central part of the channel, while it increased near the walls when we increased the values of the viscoelastic parameter ${\lambda }_1$. Similar effects of ${\lambda }_1$ on the velocity profiles were also reported by Akbar, Tripathi, and Nadeem in their articles [34,35,36,37]. Thus, the role of the parameter ${\lambda }_1$ on viscoelastic fluids was to decelerate the flow. Figure 2b demonstrates that the velocity profiles showed a qualitatively similar view under the impacts of the Hartman number $H_a$ as that of the parameter ${\lambda }_1$. The velocity decreased within the core part and increased in the vicinity of the boundaries of the channel. However, a strong deceleration was noted in velocity at the core region and a comparatively lower increase was observed near the channel walls. Physically, this behavior explained the retarding nature of the electromagnetic forces in the flow regime. Figure 2c depicts that the velocity profile admitted a nonuniform behavior under the influence of the Darcy number $D_a$, that is, the velocity increased in the central regions, whereas it fell near the ciliated boundaries for higher values of $D_a$. These observations confirmed the fact that the velocity showed increasing behaviors as the porosity of the medium was widened. This was physically realistic due the fact that at the walls of the channel, the ciliated epithelium was very thick and dense and provided more resistance to the flow compared to the central part of the channel. The graphs in Figure 3a,b illustrate that the velocity accelerated due to the enhancement in the heat transfer effects (the Grashof number and the heat source or sink parameter). Figure 3c explains the velocity rises when we increased the value of the parameter $\epsilon$. The overall features of the velocity profile in the present study for all cases were in good agreement with the existing studies in the literature [17,18,19,20,21,22,23,24,25,26,27,28]; for instance, the flow was symmetric, the velocity profiles exhibited parabolic graphs, their maximum values were almost near the central region and decreased as we moved from center to the walls of the channel. This validates the correctness and generality of our model.

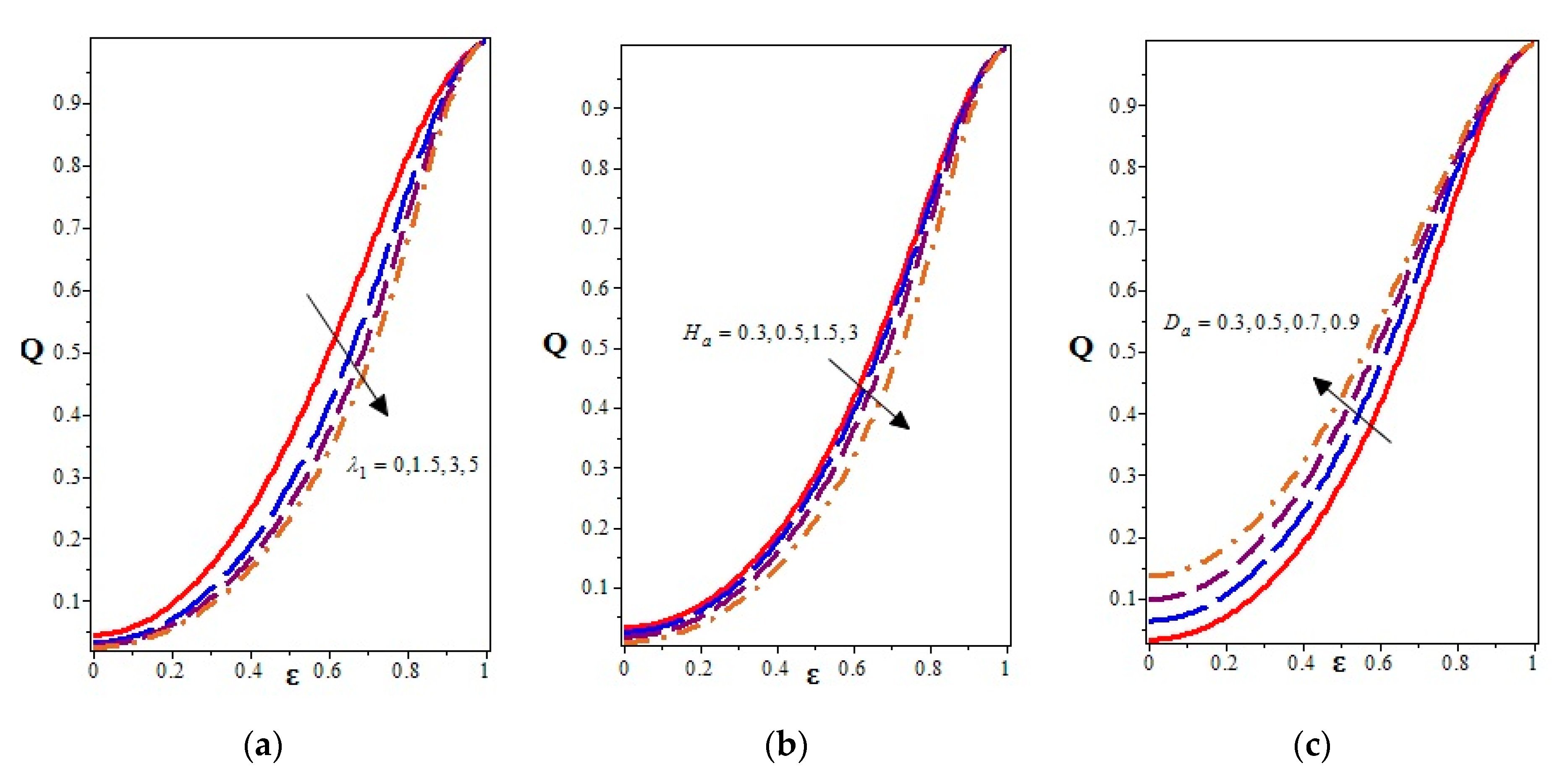
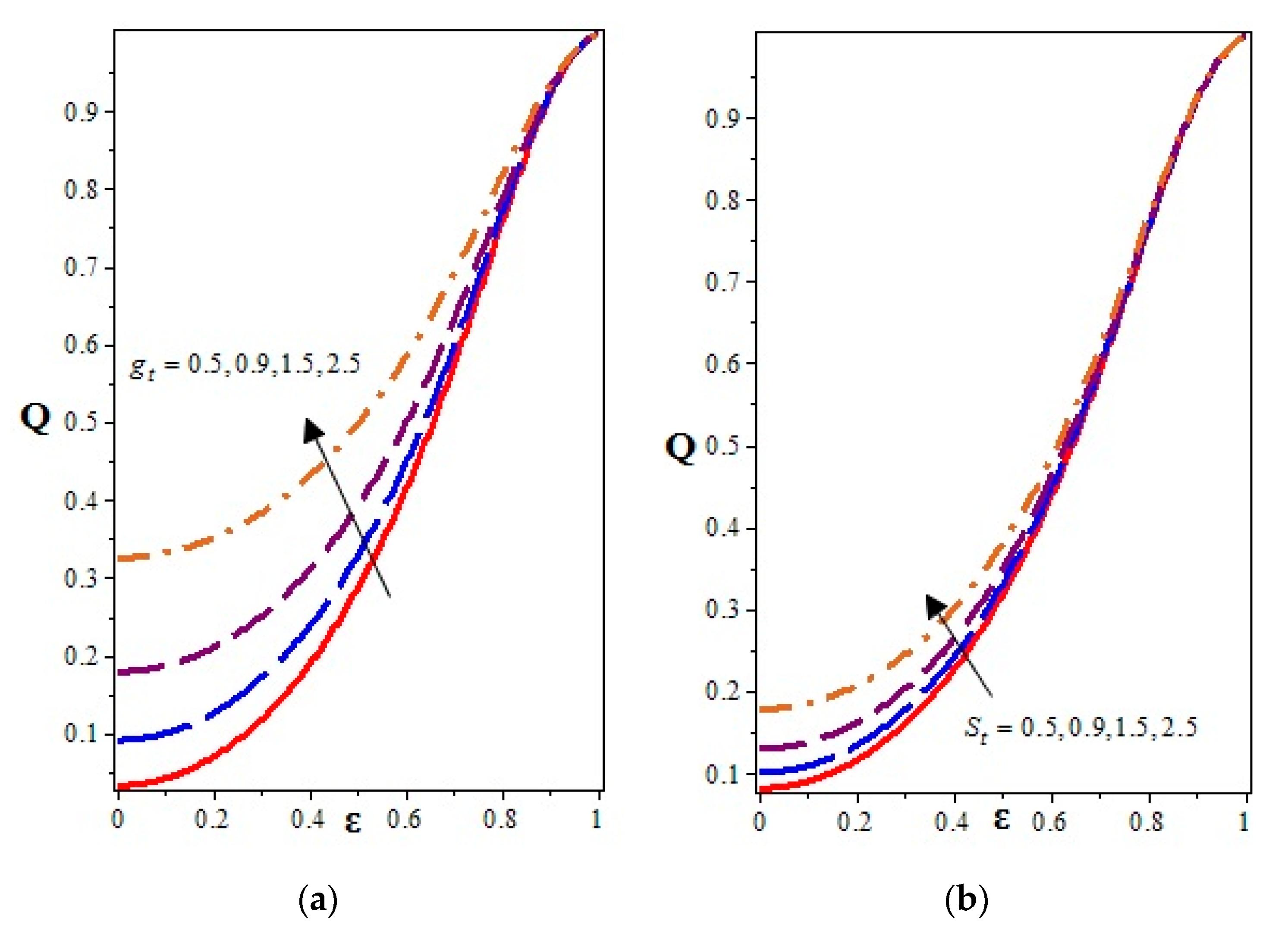
4.2. Volume Flow Rate

The impacts of the key parameters ${\lambda }_1$, $H_a$, $D_a$, $S_t$, $g_t$, and $M$ on the volume flow rate $Q$ were examined and the results are presented in this subsection. Figure 4 and Figure 5 were plotted to see the variations in $Q$ versus $\epsilon$. The graphs in Figure 4a,b shows that higher values of ${\lambda }_1$ and $H_a$ tended to diminish the volume flow rate along the channel length. However, Figure 4c shows an opposite behavior of $Q$ under the influence of the porosity parameter $D_a$, i.e., the increasing values of $D_a$ assisted the flow rate. This was physically verified because increasing values of $D_a$ means enlarging the porosity of the medium, which allows more fluid to pass through it (as observed in References [24,25,26,27,28,29]). We see in Figure 5a that the higher values of the Grash of number $g_t$ tended to enhance $Q$. In fact, as the Grashof number became larger, the impact of the buoyancy force became stronger, which supported the flow of the fluid and caused an enhancement in the volume flow rate. We can notice from Figure 5b that with increasing the values of $S_t$, the flow rate increased. It is interesting to note in these graphs that the volume flow rate was an increasing function of the cilia length parameter $\epsilon$ over the range $0<\epsilon <1$. When $\epsilon =0$, we obtain a peristaltic pumping problem, which is not under discussion in this study. The variations in $Q$ versus $\delta$ (the eccentricity parameter) are sketched in Figure 6 and Figure 7. In Figure 6a, we see that the flow rate declined when we increased the values of $M$ (chemical reaction parameter). Physically, the chemical reactions could cause an increase in the internal resistance within the fluid, which resulted in the reduction of the flow rate. Figure 6b shows that the graphs of $Q$ versus $\delta$ were straight lines with positive slopes, which indicated that the flow rate increased in a linear way with the eccentricity parameter $\delta$. These graphs also indicate that the flow rate gradually rose with the pressure drop (i.e., $\mathsf{\Delta }p<0$) and declined with the pressure rise (i.e., $\mathsf{\Delta }p>0$). This is a well-known observation in a peristaltic pumping system that also remains valid in ciliary pumping. Figure 7a,b shows that the volume flow rate reduced with increasing the values of $H_a$, whereas it increased with increasing values of $D_a$. These graphical results were in accord with our previous results, as shown in Figure 4 and Figure 5. It is worthwhile to note that these observations were in close agreement with the previous studies of References [23,24,25,26,27,28,29,30,31,32], where the authors noted that the effects of heat transfer may cause an increase in the volume flow rate.

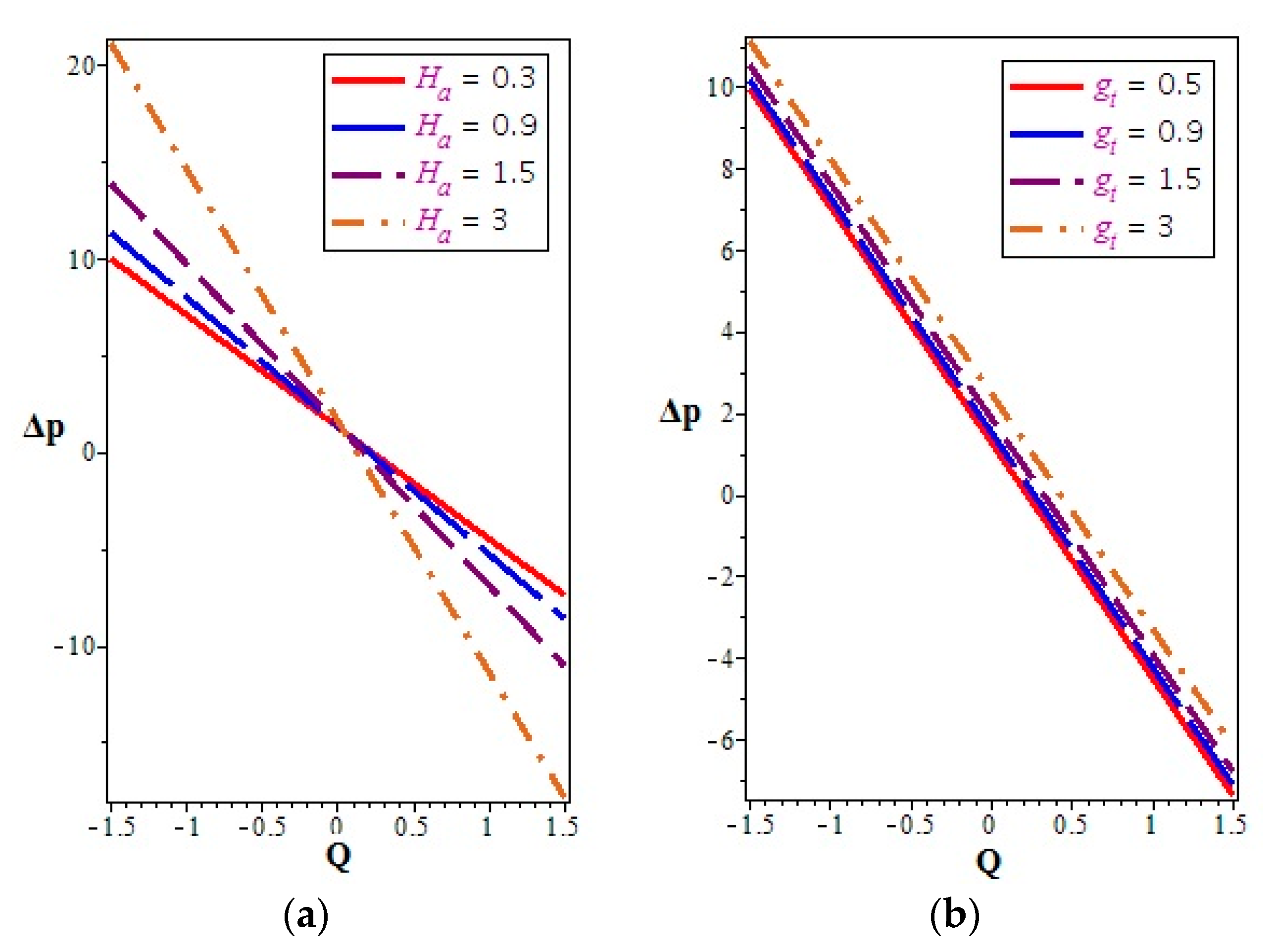
4.3. Pressure Distribution

It is obvious that the pressure distribution exhibits a fundamental influence on the pumping characteristics of both peristaltic and cilia motions. Figure 8a,b shows the behavior of $\mathsf{\Delta }p$ versus $Q$ (i.e., pressure–volume characteristics) under the effects of key parameters. From these graphs, we note that the impacts of the parameters ${\lambda }_1$, $H_a$, $D_a$, $S_t$, $g_t$, and $M$ on the pressure rise were strongly controlled by the amount of volume flow rate of the moving fluids. In other words, their impacts on $\mathsf{\Delta }p$ produced opposite actions before and after some critical values of $Q$. Figure 8a shows that when the flow rate was less than a certain value, i.e., $Q<0.3$, the pressure rise decreased due to increasing values of the parameter ${\lambda }_1$ and it showed an opposite trend when $Q>0.3$. In the same way, Figure 7b and Figure 8a show that the impacts of the Darcy number $D_a$ and the Hartmann number $H_a$ on the pressure rise were highly influenced by the amount of flow rate that was passed through the channel. The pressure rise decreased with the increasing values of the Darcy number $D_a$, whereas it reduced with increasing the magnitude of $H_a$ whenever the flow rate was less than some certain value. It is also noted that a higher magnetic field assisted the development of a higher pressure rise in the channel when the volume flow rate was above the critical value i.e., when $Q>0.3$. These characteristics of the magnetic field have useful applications in controlling the excessive bleeding during critical surgeries. It is noted from Figure 8b that $\mathsf{\Delta }p$ increased whenever $g_t$ attained higher values (a similar behavior is also noted in References [19,20,21,22,23,24,25,26,27,28]). It is remarkable to note that the classical pressure–volume flow rate characteristics of peristalsis ($\epsilon =0$) was also observed for the ciliary induced transport ($\epsilon \ne 0$) in the present study.

5. Applications in Physiology

The physical explanation of the previously obtained results can predict the transport of various physiological fluids, such as blood, semen, mucus, etc., in smaller vessels of the body. In the male reproductive system, ductile efferences are microsized tubules that connect the rete testis to the epididymis and are composed of columnar ciliated cells. These ciliated cells serve to transport human semen. The volume flow rate of human semen is estimated to be 0.006 mL/h in Lardner and Shack [3]. This value was predicted by many scientists and was based on many experiments conducted for the flow rates of semen in various animals, such as the rete testis of rat, ram, and bull. However, Lardner and Shack correlated these values with a mathematical model [3]. They utilized a viscous fluid model to estimate and compare their theoretical values with the experimental value of the flow rate in the human reproductive system. According to their calculations, the following values were used in the model.

$$d=50\mu m,c=200\mu /\sec ,\epsilon =0.1,\delta =1.0,\mathrm{and}\beta =0.1.$$

According to their calculations, the approximate value of $Q$ (i.e., the dimensionless volume flow rate) was 0.022 and the approximate value of $Q^{*}$ (i.e., the dimensional volume flow rate) was 0.00012 mL/h. For the present model, we display the numerical values of $Q$ and its dimensional counterpart $Q^{*}=(\pi d^{2}c\times Q)$ for various values of the key parameters in

Table 1. Numerical results for the dimensional flow rate $Q$ and non-dimensional flow rate $Q^{*}=(Q\times 2\pi d^{2}c)$ when $\delta =0.1$, $\epsilon =0.1$, $\beta =1.0$, and $\mathsf{\Delta }p=0$.

${\mathit{\lambda }}_1$	${\mathit{H}}_{\mathit{a}}$	${\mathit{D}}_{\mathit{a}}$	${\mathit{S}}_{\mathit{t}}$	${\mathit{g}}_{\mathit{t}}$	$\mathit{M}$	$\mathit{Q}$	${\mathit{Q}}^{*}$
0.1	0.5	0.3	0.5	0.5	0.5	0.367313	0.002003
0.5	0.5	0.3	0.5	0.5	0.5	0.356839	0.001946
1.5	0.5	0.3	0.5	0.5	0.5	0.341044	0.001860
2.0	0.5	0.3	0.5	0.5	0.5	0.336095	0.001833
0.5	1.5	0.3	0.5	0.5	0.5	0.305248	0.001666
0.5	2.0	0.3	0.5	0.5	0.5	0.277866	0.001515
0.5	3.0	0.3	0.5	0.5	0.5	0.235197	0.001282
0.1	0.5	0.4	0.5	0.5	0.5	0.399765	0.002181
0.1	0.5	0.5	0.5	0.5	0.5	0.426126	0.002324
0.1	0.5	0.7	0.5	0.5	0.5	0.468452	0.002555
0.1	0.5	0.5	1.5	3.5	1.5	1.062621	0.005795
0.1	0.5	0.5	1.5	3.5	3.5	1.055827	0.005758
0.1	0.5	0.5	1.5	3.5	5.0	1.052525	0.005740
0.5	0.5	0.5	1.5	4.0	1.5	1.013808	0.005529
0.5	0.5	0.5	1.5	4.5	1.5	1.098599	0.005992
0.5	0.5	0.5	1.5	5.0	1.5	1.183390	0.006454

. These numerical results demonstrate the fact that the viscoelastic parameter and the Hartmann number had reducing effects on the volume flow rate, whereas the Darcy number had an opposite effect on the flow rate. The effect of the Grashof number was to accelerate the flow rate, while the chemical reaction parameter decelerated it. Indeed, these observations are consistent with many other studies on peristaltic and cilia transport mechanisms [23,30,31]. Here, we point out that the results obtained in References [3,20] for a Newtonian fluid could be recovered from our model by setting ${\lambda }_1,H_a,S_t,g_t,S_c,g_c$ and $M$ equal to zero and $D_a\to \infty$. However, the difference between these values and the experimentally estimated values of the volume flow rate of human semen (i.e., 0.006 mL/h) was not minor. This indicates a need for further improvements, both theoretically and experimentally. The drawbacks and limitations of the present model can be evaluated by considering other main physiological factors involving in these mechanisms. We hope that the present results are reasonably utilized in investigating the physiological flows inside the human vessels and in producing the magnetically actuated artificial cilia in lab-on-chip devices.

6. Conclusions

In the human body, various physiological liquids, such as blood, mucus, semen, etc., contain hemoglobin and other elemental compounds that are influenced by the extracorporeal electromagnetic fields. These electromagnetic body forces cause various metabolisms and chemical reactions to take place in the organs of human body. Moreover, the deposition of fatty materials in the small vessels causes many cardiovascular and arterial diseases, and requires the special attention of physiologists and biomedical researchers. In light of these key features, the present article discusses the effects of heat and mass transfer on the propulsion of a viscoelastic fluid through a vertical channel due to a mixed convection in the presence of a transverse magnetic field. The inner surface of the channel was covered with a highly dense mat known as cilia, which in this study, was simulated as a Darcian porous medium. The theoretical results of the current model were used to examine the propulsion of epididymal fluids through ductili efferentes. Some of the leading outcomes were:

• The velocity distribution clearly admitted parabolic profiles, which were at a maximum at the central part of the channel and gradually decreased toward the boundary.
• The axial velocity was diminished with an increasing Jeffery first viscoelastic parameter (ratio of relaxation to retardation times) in the central part of the channel, whereas a converse behavior was shown near the walls.
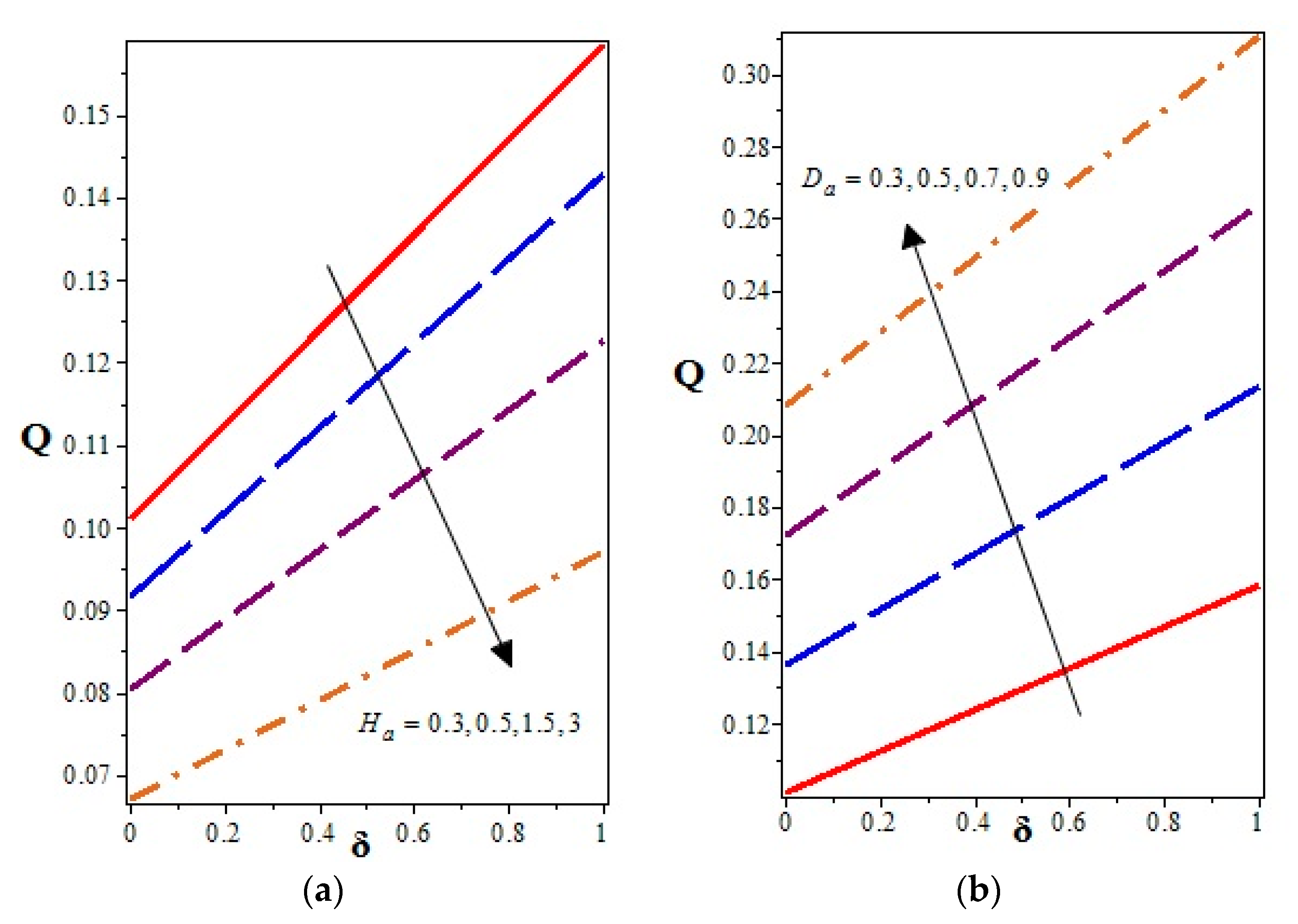
• The increasing strength in the magnetic body force inhibited the axial velocity of the fluid in the central part, while it was promoted toward the walls of the channel. However, the effects of the Darcy number on the axial velocity were quite opposite to that of the magnetic field parameter (i.e., the Hartmann number).
• The axial velocity of the flow field was increased due to the increasing values of the heat transfer parameters (the Grashof number and the heat source number). Another important observation made from this study was that the cilia with higher lengths provided a boost in the axial velocity and hence accelerated the flow in the axial direction.
• The viscoelastic fluid moved slowly compared to the linear viscous fluid in the central region of the channel. This shows that the viscous forces had stronger influences in the central part compared to the boundary of the channel.
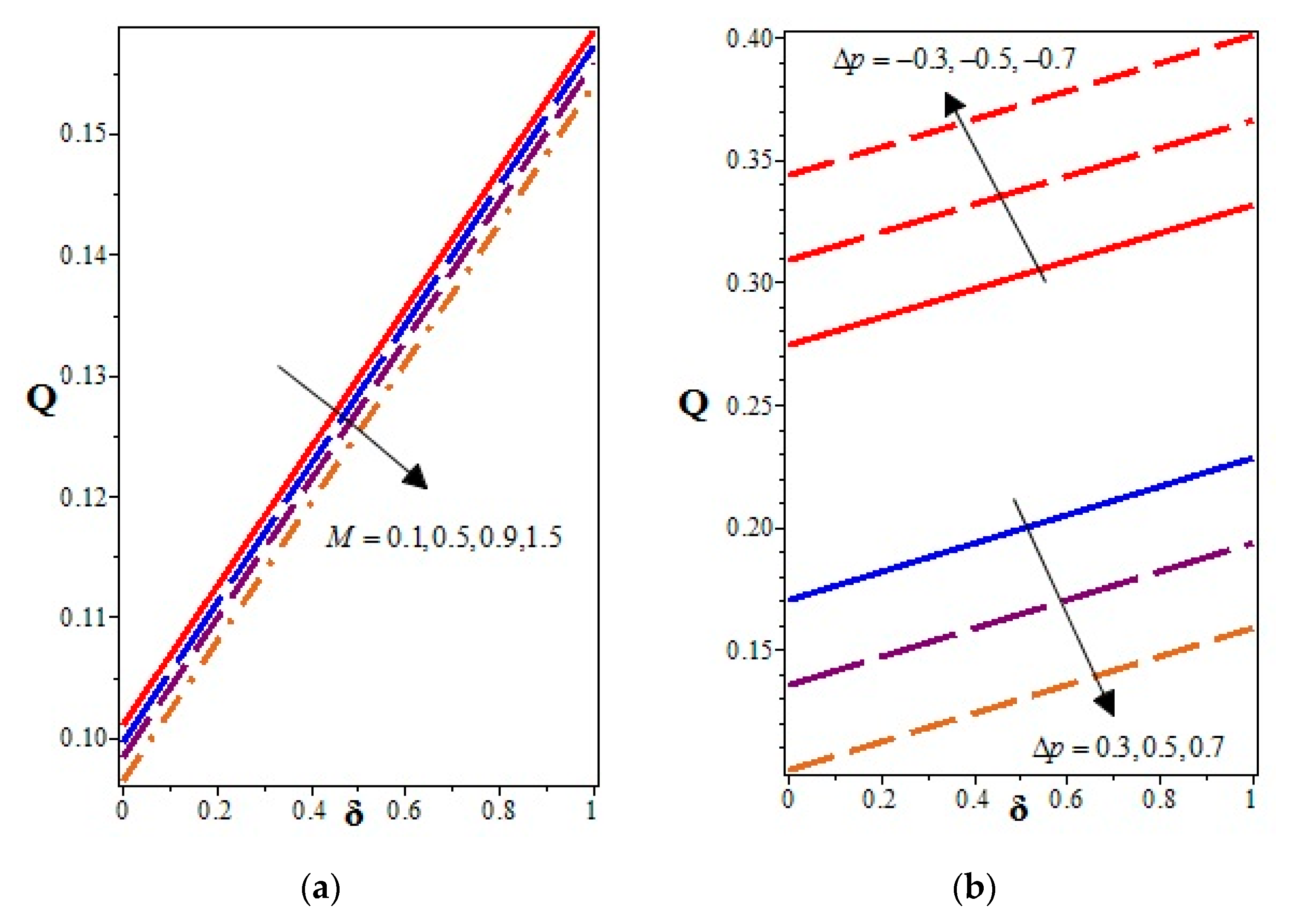
• The time mean flow volume of a viscoelastic fluid (semen, i.e., ${\lambda }_1\ne 0$) was less than that of the Newtonian fluid (${\lambda }_1=0$) under similar conditions.
• The time mean volume flow rate was strongly influenced by the cilia height, i.e., flow volume of the semen increased gradually with the increase in cilia height.
• Due to an increase in the eccentricity parameter of cilia paths, a rise in the flow volume of the semen was observed.
• The volume flow rate decreased due to increasing values of the parameters ${\lambda }_1$, $H_a$, and $M$ (chemical reaction parameter), while it decreased with increasing $D_a$, $g_t$, and $S_t$.
• It was concluded that heat transfer generally aids the propulsion mechanism of ciliary motion.

Here, we remark that the theoretical model has many limitations and is a small part the total scenario, but without it we cannot understand and interpret the physical processes fully.