Analysis of the Quantization Noise in Discrete Wavelet Transform Filters for 3D Medical Imaging

Abstract

Denoising and compression of 2D and 3D images are important problems in modern medical imaging systems. Discrete wavelet transform (DWT) is used to solve them in practice. We analyze the quantization noise effect in coefficients of DWT filters for 3D medical imaging in this paper. The method for wavelet filters coefficients quantizing is proposed, which allows minimizing resources in hardware implementation by simplifying rounding operations. We develop the method for estimating the maximum error of 3D grayscale and color images DWT with various bits per color (BPC). The dependence of the peak signal-to-noise ratio (PSNR) of the images processing result on wavelet used, the effective bit-width of filters coefficients and BPC is revealed. We derive formulas for determining the minimum bit-width of wavelet filters coefficients that provide a high (PSNR ≥ 40 dB for images with 8 BPC, for example) and maximum (PSNR = ∞ dB) quality of 3D medical imaging by DWT depending on wavelet used. The experiments of 3D tomographic images processing confirmed the accuracy of theoretical analysis. All data are presented in the fixed-point format in the proposed method of 3D medical images DWT. It is making possible efficient, from the point of view of hardware and time resources, the implementation for image denoising and compression on modern devices such as field-programmable gate arrays and application-specific integrated circuits.

1. Introduction

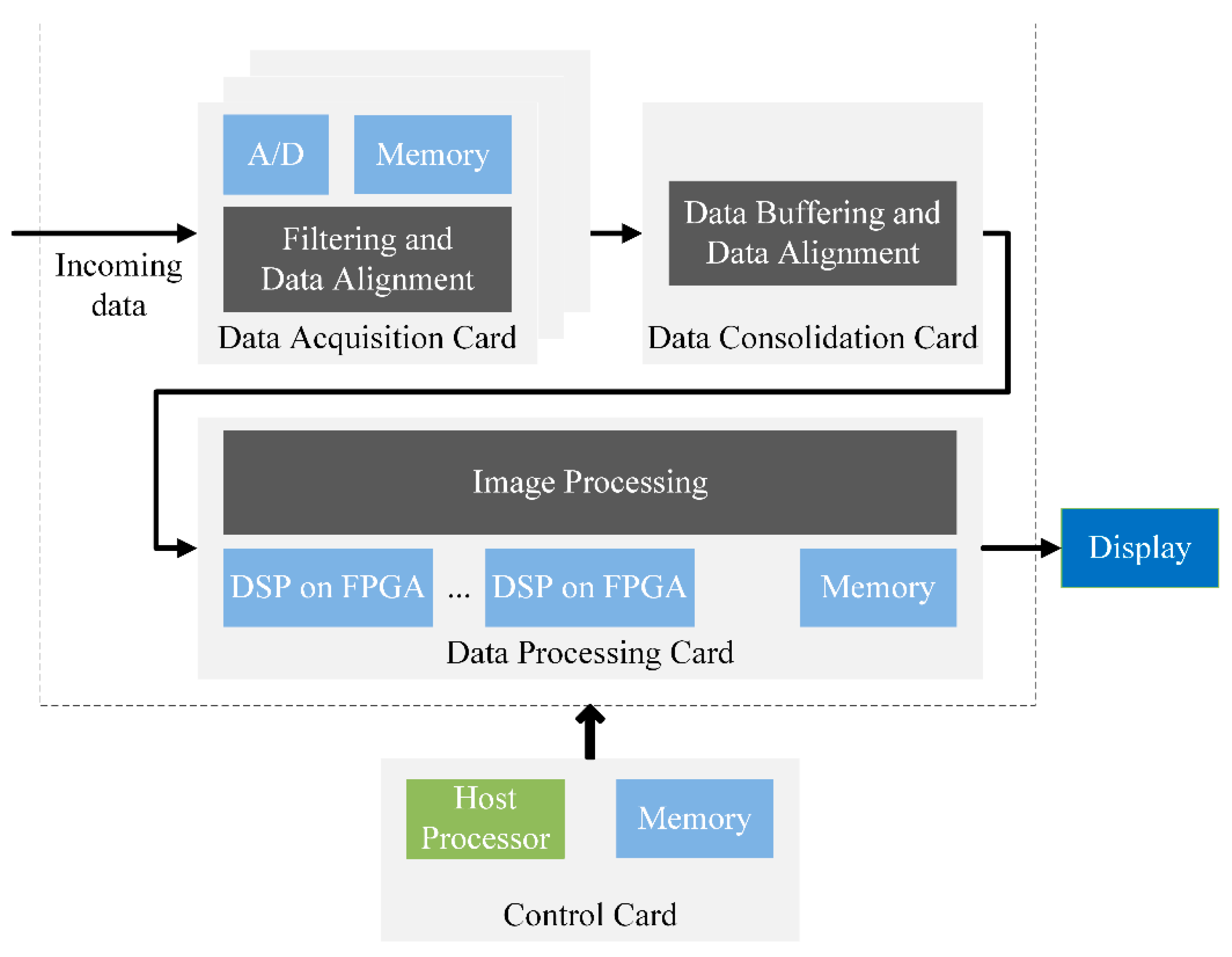
Medical imaging uses many different methods such as magnetic resonance (MR) imaging [1,2,3,4,5,6,7,8], radiography [4,9,10,11], radionuclide [8,12], optical [11,13,14], ultrasound [1,15] and medical robotics [16,17]. The typical medical imaging system consists of three components (Figure 1): data acquisition, data consolidation and data processing. The data acquisition card, which filters incoming data, is the most cost-sensitive system card. Usually, a diagnostic imaging system will consist of multiple data acquisition cards. Once the data is compensated and filtered in scanners, it is sent to the data consolidation card for buffering and data alignment. Once the data has been collected, it is sent to the image processing cards [18]. These cards perform heavy-duty filtering and the most algorithm-intensive image reconstruction. Modern field-programmable gate array (FPGA) devices are widely used in data consolidation, and image processing for sophisticated application algorithms implementation including pattern recognition, image enhancement and data compression [19,20].

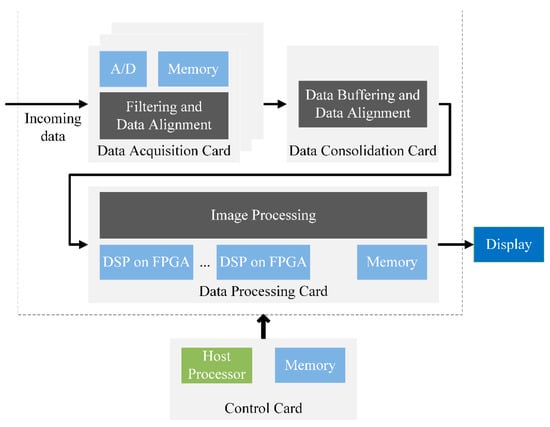
Figure 1. The typical medical imaging system.

Denoising of 2D and 3D medical images is an important problem in modern medical imaging systems. The noisy pattern is not always bad in medical images, but in most cases is a problem. MR images are inherently noisy and thus filtering methods are required to improve the data quality [5]. Rheological methods of increasing MR elastography resolution determine viscoelastic properties through wave inversion, which is highly ill posed and sensitive to noise [1]. In radiology using computed tomography (CT) or related morphological imaging modalities, noise affects the analysis of anatomical structures and thus impedes diagnostic applications [11]. Low dose radiation exposure for patient safety leads to noisy and low-contrast fluoroscopic sequences [11]. The reconstruction process of the positron emission tomography images includes inherent multiplicative noise, which prevents the analysis of visual data [12]. In optical CT for retinal imaging as another example use case, noise limits the measurement of structural features in the human eye, e.g., retinal layer properties [11]. Denoising facilitates visual data interpretation from echocardiography [15].

Medical imaging systems produce increasingly accurate images with improved quality using higher spatial resolutions and bit-depths with advances in scanning technology and digital devices. Such improvements increase the amount of information that needs to be processed, transmitted and stored. This is especially true when using 3D scanning technology [4]. For example, four sets of positron emission tomography medical images of one patient may require more than 4 GB of storage space [21]. Video recording of a relatively short retinal peeling procedure may require over 40 GB of memory storage [14]. The capacity of hard drives is on average 1–2 TB with the current level of storage technology development. Thus, the compression of 3D medical images is also an important problem in modern medical imaging systems.

Various transforms are used to solve problems of 2D and 3D medical images denoising and compression in practice. The most common of them are discrete Fourier transform (DFT) [3,7,14,22] and discrete wavelet transform (DWT) [1,9,11,14]. DFT is widely used in the frequency domain but the domain characteristics disappeared after it. We cannot determine the time position and the degree of intensity after signal DFT. It is not possible to describe the local properties of the time domain of the image. DWT solves these problems because it allows obtaining both frequency and time information about a signal [23,24]. 2D and 3D images DWT is performed by convolution with a pair of lowpass and highpass wavelet filters of filter bank that highlight main and detailed information respectively. Denoising and compression of images are performed by detailed information manipulating in modern algorithms such as set partitioning in hierarchical trees (SPIHTs) [25] and embedded zerotrees of wavelet transforms (EZWs) [26]. The convolution operation has high computational complexity. Hardware implementation on modern microelectronic devices such as field-programmable gate arrays (FPGAs) and application-specific integrated circuits (ASICs) working with fixed-point numbers is one of the ways to improve its characteristics [27,28,29]. Quantization noise occurs when converting wavelet filters coefficients into this format, due to which convolution is performed with an error. The question arises about the accuracy of wavelet filters coefficients representation in the device’s memory, which is efficient in terms of resources and enough to achieve the required quality of image processing. A novel area-efficient high-throughput 3D DWT architecture for real-time medical imaging based on distributed arithmetic is proposed by the authors [30]. The design and implementation of 3D Haar wavelet transform with transpose based computation and dynamic partial reconfiguration for 3D medical image compression are presented in [31]. The implementation of positron emission tomography using DWT on FPGA is proposed by authors [32]. In paper [33] described the architecture based on the use of DWT for biomedical signals compression. The design and implementation of context-based adaptive variable length coding and comparative analysis of trade-off offered by DWT for 3D medical image compression systems are described by authors [34]. In [35] presented the design and implementation of 3D DWT with a transpose-based method for medical image compression on FPGA. Experimental results from [36] showed that the system constructed a 1D DWT system based on FPGA can filter the noise and extract the electroencephalogram (EEG) signal well. The design and implementation on FPGA of 3D DWT using Daubechies wavelets with a transpose-based method for medical image compression are presented in [37]. The design and implementation of distributed arithmetic architectures of 3D DWT with a hybrid method for medical image compression are presented in [38]. Authors [39] presented the FPGA-based embedded system design using DWT and its evaluation for a pre-processing stage of EEG signal analysis. A detailed review of FPGA and ASIC architectures for DWT implementation in biomedical and intelligent applications, which can be designed either for higher-accuracy or for low-power consumption is provided by the authors [29]. In [40], the authors showed that DWT along with Gaussian filtering shows better results in removing the noise and smoothes the electrocardiogram signals. Authors [41] described the design and implement a complete hardware model based on DWT for EEG data compression and reconstruction on FPGA. A framework is offered in [42] based on DWT using linear and non-linear classifiers for detecting an epileptic seizure from EEG data recorded from normal subjects and an epileptic patient. There are no references to selected bit-width of wavelet filters coefficients in the materials studied about the hardware implementation of medical images DWT on FPGA and ASIC [29,30,31,32,34,35,36,37,38,39,40,41,42]. Authors [33] quantized wavelet filters coefficients by 16 bits, but there is no rationale for this choice. The problem of analyzing the quantization noise effect in wavelet filters coefficients for 2D grayscale and color images DWT with 8 bits per color (BPC) was solved in [43].

Analysis of 3D medical images DWT result quality dependence on noise arising from filters coefficients quantizing of wavelet with compact support is the purpose of this work. Particular attention is paid to determining the minimum bit-width of wavelet filters coefficients, at which this noise does not have a significant impact on the 3D medical images DWT result $(PSNR\ge 40$ dB for images with 8 BPC, for example$)$, or does not affect it at all $\left(PSNR=\infty \right)$. The values $PSNR\ge 40$ dB describes the difference between the two images with 8 BPC almost imperceptible for human eyes [44,45]. The value $PSNR=\infty$ for identical images.

2. Materials and Methods

DWT is a signal transform using a filter bank, which is a convolution of the input data with wavelet filters that translate them from a time representation into a time-frequency domain. Wavelet filters $F$ of filter bank consist of coefficients $f_{F,i}$, where $i=1,\dots ,k$ and $k$ is the number of coefficients. Coefficients of lowpass and highpass wavelet filters of decomposition $\left(LD,HD\right)$ and reconstruction $\left(LR,HR\right)$ are related by equation [27]

$$f_{HD,i}={(-1)}^{i+1}{f}_{LD,k-1-i}, f_{LR,i}=f_{LD,k-1-i}, f_{HR,i}={(-1)}^i{f}_{LD,i}.$$

(1)

We shall consider only wavelets with compact support [46]. Daubechies wavelets $db\left(k/2\right)$ (where $db1$ with $k=2$ is Haar wavelet), symlets $sym\left(k/2\right)$ and coiflets $coif\left(k/6\right)$ are the most common ones.

Consider a 3D digital medical image $I$ of $X$ rows, $Y$ columns and $Z$ frames as a function $I\left(x,y,z\right)$, where $0\le x\le X-1$, $0\le y\le Y-1$ and $0\le z\le Z-1$ are the spatial coordinates of $I$. Thus, voxel values (analogues of 2D pixels for 3D space) are represented as $I\left(x,y,z\right)$ for grayscale images and as $I\left(x,y,z,c\right)$ for color images, where $c$ is the color number (for example, $c=1,2,3$—red, green and blue colors respectively for RGB images). We assumed that all image voxels are isotropic [47], hereinafter.

Convolution of a 3D image with wavelet filters is performed by formulas

$$I^{\prime }\left(x,y,z\right)={\displaystyle \sum _{i=1}^{k}I\left(x-i,y,z\right)\cdot f_{F,i}}, I^{″}\left(x,y,z\right)={\displaystyle \sum _{i=1}^k{I}^{\prime }\left(x,y-i,z\right)\cdot f_{F,i}},$$

$$I^{‴}\left(x,y,z\right)={\displaystyle \sum _{i=1}^k{I}^{″}\left(x,y,z-i\right)\cdot f_{F,i}},$$

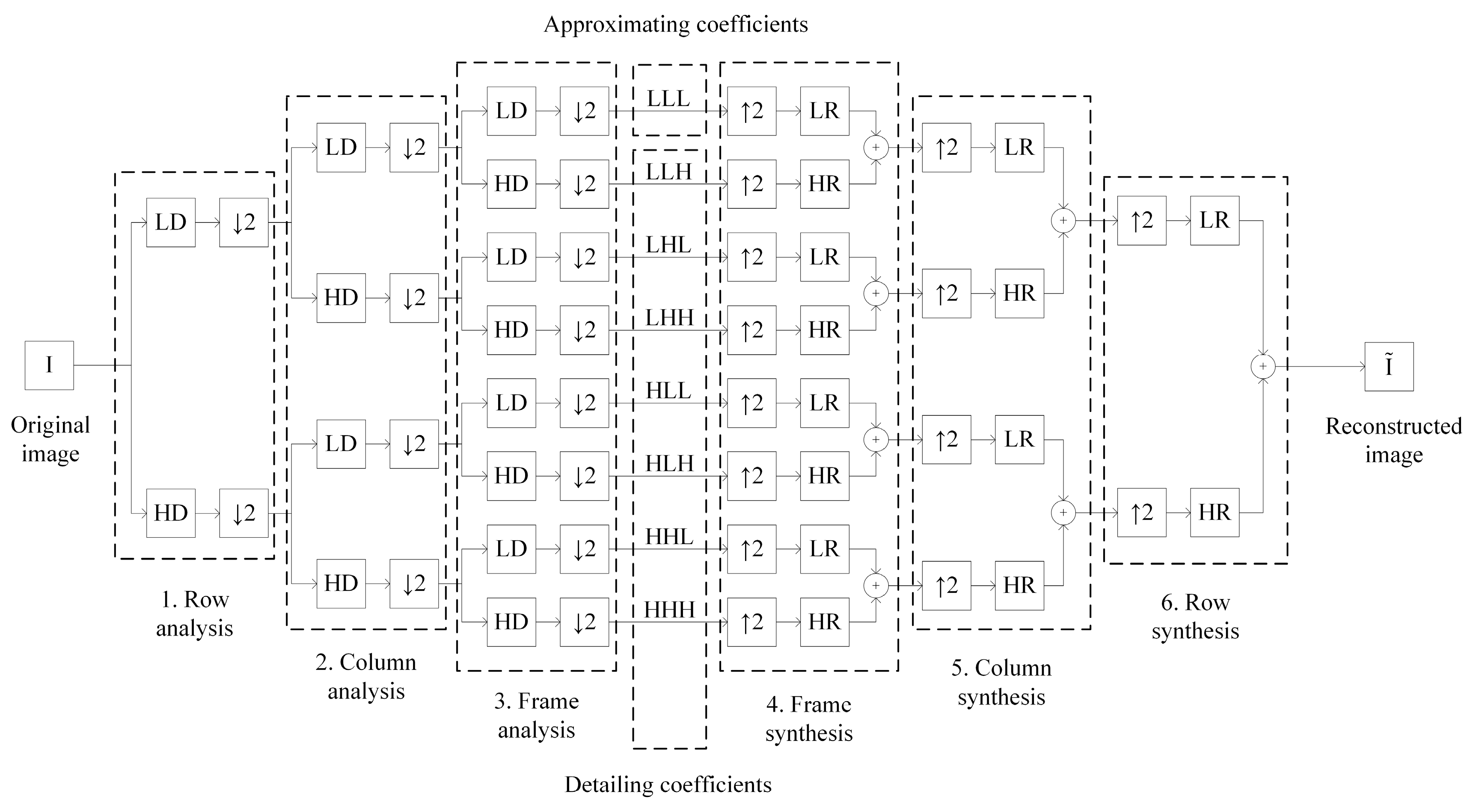
where $I^{\prime }$, $I^{″}$ and $I^{‴}$ is the convolution results by strings, columns and frames respectively. 3D image DWT is performed by sequential convolution with wavelet filters (Figure 2) in the steps below.

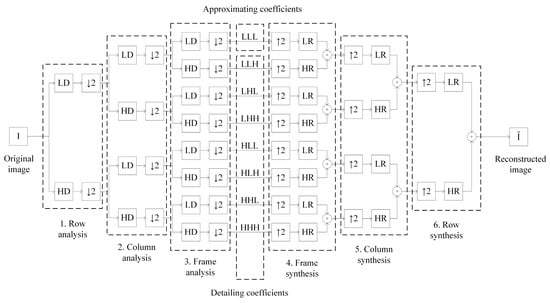
Figure 2. The scheme of 3D image discrete wavelet transform (DWT).

• Row analysis is performed by decomposing the original image $I$ by rows with lowpass $LD$ and highpass $HD$ wavelet filters and downsampling, indicated by the symbol $\downarrow 2$ (for example, the array $\left[2,8,5,1,-1,3\right]$ is transformed into an array $\left[2,5,-1\right]$ after the operation $\downarrow 2$).
• Column analysis is performed by columns similar to the row analysis for coefficients obtained at stage 1.
• Frame analysis is performed by frames similar to the row analysis for coefficients obtained at stage 2.

We get 8 sets of coefficients, $LLL,LLH,LHL,LHH,HLL,HLH,HHL$ and $HHH$, of image decomposition as a result of original image $I$ analysis. These sets can be divided into approximating $\left(LLL\right)$ and detailing $(LLH,LHL,LHH,HLL,HLH,HHL$ and $HHH).$ Approximating coefficients correspond to the lowpass part of the signal and contain main information about the image $I$. Detailing coefficients to correspond to the highpass part of the signal and contain detailed information about the image $I$. 3D image denoising and compression are carried out by manipulating detailing coefficients $(LLH,LHL,LHH,HLL,HLH,HHL$ and $HHH)$ of image decomposition.

4.

Frame synthesis is performed by upsampling, indicated by the symbol $\uparrow 2$ (for example, the array $\left[2,5,-1\right]$ is transformed into an array $\left[2,0,5,0,-1,0\right]$ after the operation $\uparrow 2$), of image decomposition coefficients by frames, reconstructing with lowpass $LR$ and highpass $HR$ wavelet filters and summation of the corresponding results.

5.

Column synthesis is performed by columns similar to the frame synthesis for coefficients obtained at Stage 4.

6.

Row synthesis is performed by rows similar to the frame synthesis for coefficients obtained at Stage 5.

We get the reconstructed image $\tilde{I}$ as a result of image decomposition coefficients synthesis. Theoretically, the original image should be fully reconstructed since the scheme in Figure 2 has the perfect reconstruction property [48]. However, quantization noise occurs due to the digital format of wavelet filters coefficients representation in practice. Quantization noise distorts all image decomposition coefficients $LLL,LLH,LHL,LHH,HLL,HLH,HHL$ and $HHH$ as well as reconstructed image $\tilde{I}$. The images DWT result may have a quality unacceptable for the task depending on the magnitude of quantization noise.

The question arises about the minimum bit-width of wavelet filters coefficients $f_{F,i}$, necessary for efficient software and hardware implementation of 3D images DWT on modern devices and enough for high-quality images processing. The speed of operations with a fixed-point number is higher than with a floating-point number on modern devices. This can be used to develop 3D medical imaging devices. Therefore, wavelet filters coefficients are quantized and converted into a fixed-point format in the proposed method by scaling by $2^n$ and rounding up

$$f_{F,i}^{*}=\lceil 2^n{f}_{F,i}\rceil .$$

(2)

Bit-width $r$ of quantized wavelet filters coefficients $f_{F,i}^{*}$ can be determined by the formula $r=n+1$ in this case. The digital image $I^{\ast }$ processed according to the scheme in Figure 2 using quantized wavelet filters coefficients $f_{F,i}^{*}$. Voxel values of an image $I^{\ast }$ should be normalized by scaling by $2^{-6n}$ ($2^{-n}$ for each convolution, according to the scheme from Figure 2) and rounding down

$$\tilde{I}=\lfloor 2^{-6n}{I}^{\ast }\rfloor .$$

(3)

We get only integers as a result of images DWT with unquantized coefficients. The quantization error of the wavelet filters coefficients rounded up is strictly redundant. Rounding down of the DWT results minimizes this error and cannot cause an error by itself. Rounding up and down operations are performed by discarding the fractional part of the number with the addition of one in the case of rounding up an integer. The rounding errors will have different signs and partially compensate each other for rounding in different directions. Rounding operations in this order require fewer resources for hardware implementation than rounding operations to the nearest integer. This is due to the fact wavelet filter coefficients are known a priori and their quantization with rounding up can be made in advance. Thus, wavelet filters coefficients will be used in the form of constants in the software and hardware part. The convolution is performed using arithmetic logic devices, and its result is rounded down by simply discarding the fractional part and does not require additional hardware and time costs.

We used the peak signal-to-noise ratio $\left(PSNR\right)$ between two images (original image $I$ and processed image $\tilde{I}$) to quantify the image processing quality. The $PSNR$ logarithmic nature makes it possible to clearly interpret results that differ slightly from each other. Other metrics usually only show a big difference. This characteristic is measured in decibels (dB) and is calculated by the following formula [49]

$$PSNR=10{\log }_{10}\left(\frac{{\left(2^B-1\right)}^2}{MSE}\right)=10{\log }_{10}\left(\frac{M^2}{MSE}\right),$$

where: $B$ is the image BPC; $M$ is the maximum brightness of the image voxels (for example, $B=8$ and $M=2^8-1=255$ for 8-bit grayscale image and 24-bit RGB image); $MSE$ is the mean square error of brightness, which is calculated for grayscale $(MS{E}_{grayscale})$ [50] and color $(MS{E}_{color})$ [51] 3D images by formulas

$$MS{E}_{grayscale}={\displaystyle \sum _{x=0}^{X-1}{\displaystyle \sum _{y=0}^{Y-1}{\displaystyle \sum _{z=0}^{Z-1}\frac{{\left(I\left(x,y,z\right)-\tilde{I}\left(x,y,z\right)\right)}^2}{X\cdot Y\cdot Z}}}},$$

$$MS{E}_{color}=\frac{1}{C}{\displaystyle \sum _{c=1}^C{\displaystyle \sum _{x=0}^{X-1}{\displaystyle \sum _{y=0}^{Y-1}{\displaystyle \sum _{z=0}^{Z-1}\frac{{\left(I\left(x,y,z,c\right)-\tilde{I}\left(x,y,z,c\right)\right)}^2}{X\cdot Y\cdot Z}}}}}.$$

The value $PSNR=\infty$ for identical images. The image processing quality is considered high if $PSNR\ge Q$, where $Q$ describes the difference between the two images almost imperceptible for human eyes. $Q=40$ dB for images with 8 BPC [44,45]. We propose to generalize $Q$ to the case of images with 12 and 16 BPC using formula

$$Q=5B.$$

(4)

Thus, $Q$ is equal 40 dB, 60 dB and 80 dB for images with 8, 12 and 16 BPC respectively.

3. Results

3.1. Theoretical Analysis of the Maximum Error of the 3D Medical Images DWT

The error of 3D medical images DWT occurs as a result of wavelet filters coefficients conversion (quantization noise) by Formula (2). Convolutions, upsampling and the summing of convolution results cause an increase in this error. Rounding down normalized voxel values of the restored image also has an effect. Note the important facts.

• The analyzing and synthesizing wavelet filters consist of the same coefficients, according to Formula (1), hence, the limited absolute errors of computations will also be equal. Therefore, within the framework of theoretical calculations, wavelet filters are classified only into lowpass $L$ and highpass $H$ ones.
• The sums of the lowpass and highpass wavelet filter coefficients are equal ${\displaystyle \sum _{i=1}^k{f}_{L,i}}=\sqrt{2}$ and ${\displaystyle \sum _{i=1}^k{f}_{L,i}}=\sqrt{2}$, respectively [27].

We introduce the following notation.

• $E_{j,F}$—limited absolute error (LAE) of calculating the value of the coefficient at the $j$-th stage, resulting from convolution with a sequence of wavelet filters $F$.
• $S_F$—the exact value of the sum of the coefficients of the wavelet filter $F$.
• $T_{j,F}$—the exact value of the calculations in the $j$-th stage, after convolution with a sequence of wavelet filters $F$.

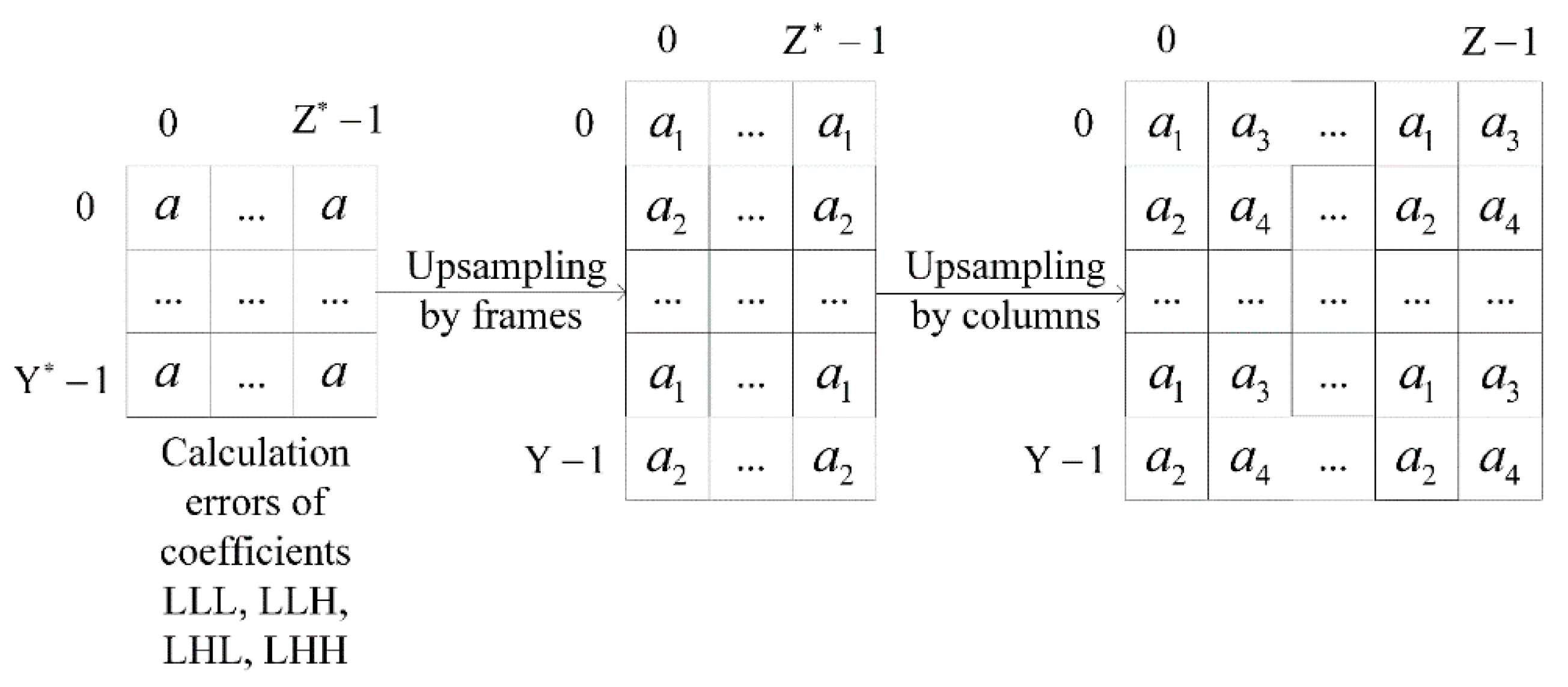
The errors $a$ of all image decomposition coefficients $LLL,LLH,LHL,LHH,HLL,HLH,HHL$ and $HHH$ are separated into two groups $a_{\epsilon }$ $\left(\epsilon =1,2\right)$ as a result of upsampling $\uparrow 2$. Figure 3 shows an example of the errors separation $a_{\epsilon }$ $\left(\epsilon =1,2,3,4\right)$ at the upsampling by frames and columns, where $Y^{\ast }=\left(Y+k\right)/2-1$ and $Z^{\ast }=\left(Z+k\right)/2-1$. This situation is similar for upsampling by strings. Upsampling is applied three times during image restoration. We got eight groups of errors $a_{\epsilon }$ $\left(\epsilon =1,2,3,4,5,6,7,8\right)$ as a result. Thus, we would add an additional index $\epsilon$ to the introduced notations, which denotes calculations by the spatial characteristics of wavelet filters coefficients.

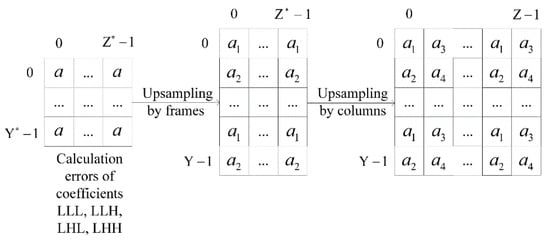
Figure 3. The scheme of the errors separation with upsampling by frames and columns.

Next, we carried out analysis calculations for an estimation of the maximum error of the 3D medical images DWT.

Stage 1. Wavelet filters coefficients quantization. Let us calculate the exact values of the coefficients sums $S_F$, $S_{F,\epsilon }$ and errors $E_{1,F}$, $E_{1,F,\epsilon }$ of rounding up filters $L$ and $H$ scaled coefficients.

$$S_L={\displaystyle \sum _{i=1}^k{2}^n{f}_{L,i}}=2^n{\displaystyle \sum _{i=1}^k{f}_{L,i}}=2^n\cdot \sqrt{2}=2^{n+\frac{1}{2}},S_H={\displaystyle \sum _{i=1}^k{2}^n{f}_{H,i}}=2^n{\displaystyle \sum _{i=1}^k{f}_{H,i}}=2^n\cdot 0=0,$$

$$S_{L,1}={\displaystyle \sum _{i=1}^{\frac{k}{2}}{2}^n{f}_{L,2(i-1)}},S_{L,2}={\displaystyle \sum _{i=1}^{\frac{k}{2}}{2}^n{f}_{L,2i-1}},S_{H,1}={\displaystyle \sum _{i=1}^{\frac{k}{2}}{2}^n{f}_{H,2(i-1)}},S_{H,2}={\displaystyle \sum _{i=1}^{\frac{k}{2}}{2}^n{f}_{H,2i-1}},$$

$$E_{1,L}={\displaystyle \sum _{i=1}^k\left(\lceil 2^n{f}_{L,i}\rceil -2^n{f}_{L,i}\right)},E_{1,H}={\displaystyle \sum _{i=1}^k\left(\lceil 2^n{f}_{H,i}\rceil -2^n{f}_{H,i}\right)},$$

$$E_{1,L,1}={\displaystyle \sum _{i=1}^{\frac{k}{2}}\left(\lceil 2^n{f}_{L,2(i-1)}\rceil -2^n{f}_{L,2(i-1)}\right)},E_{1,L,2}={\displaystyle \sum _{i=1}^{\frac{k}{2}}\left(\lceil 2^n{f}_{L,2i-1}\rceil -2^n{f}_{L,2i-1}\right)},$$

$$E_{1,H,1}={\displaystyle \sum _{i=1}^{\frac{k}{2}}\left(\lceil 2^n{f}_{H,2(i-1)}\rceil -2^n{f}_{H,2(i-1)}\right)},E_{1,H,2}={\displaystyle \sum _{i=1}^{\frac{k}{2}}\left(\lceil 2^n{f}_{H,2i-1}\rceil -2^n{f}_{H,2i-1}\right)}.$$

Stage 2. Row decomposition. Let us calculate the exact values $T_{2,F}$ and errors $E_{2,F}$ of row decomposition with filters $L$ and $H$.

$$T_{2,L}=S_L\cdot M,E_{2,L}=E_{1,L}\cdot M,E_{2,H}=E_{1,H}\cdot M.$$

All convolution results $T_{j,F}$ with filter $H$ are zero since $T_{i,F}$ for all voxels are equal and ${\displaystyle \sum _{i=0}^{k-1}{f}_{H,i}}=0$ [27].

Stage 3. Column decomposition. Let us calculate the exact values $T_{3,F}$ and errors $E_{3,F}$ of column decomposition with filters $L$ and $H$.

$$T_{3,LL}=T_{2,L}\cdot S_L,E_{3,LL}=\left(T_{2,L}+E_{2,L}\right)\left(S_L+E_{1,L}\right)-T_{3,LL},$$

$$E_{3,LH}=\left(T_{2,L}+E_{2,L}\right)E_{1,H},E_{3,HL}=E_{2,H}\left(S_L+E_{1,L}\right),E_{3,HH}=E_{2,H}{E}_{1,H}.$$

Stage 4. Frame decomposition. Let us calculate the exact values $T_{4,F}$ and errors $E_{4,F}$ of frame decomposition with filters $L$ and $H$.

$$T_{4,LLL}=T_{3,LL}\cdot S_L,E_{4,LLL}=\left(T_{3,LL}+E_{3,LL}\right)\left(S_L+E_{1,L}\right)-T_{4,LLL},$$

$$E_{4,LLH}=\left(T_{3,LL}+E_{3,LL}\right)E_{1,H},E_{4,LHL}=E_{3,LH}\left(S_L+E_{1,L}\right),$$

$$E_{4,LHH}=E_{3,LH}\cdot E_{1,H},E_{4,HLL}=E_{3,HL}\left(S_L+E_{1,L}\right),E_{4,HLH}=E_{3,HL}\cdot E_{1,H},$$

$$E_{4,HHL}=E_{3,HH}\left(S_L+E_{1,L}\right),E_{4,HHH}=E_{3,HH}\cdot E_{1,H}.$$

Stage 5. Frame reconstruction. Let us calculate the exact values $T_{5,F,l}$ and errors $E_{5,F,l}$ of frame reconstruction with filters $L$ and $H$, $\epsilon =1,2$.

$$T_{5,LLLL,\epsilon }=T_{4,LLL}\cdot S_{L,\epsilon },E_{5,LLLL,\epsilon }=\left(T_{4,LLL}+E_{4,LLL}\right)\left(S_{L,\epsilon }+E_{1,L,\epsilon }\right)-T_{5,LLLL,\epsilon },$$

$$E_{5,LLHH,\epsilon }=E_{4,LLH}\left(S_{H,\epsilon }+E_{1,H,\epsilon }\right),E_{5,LHLL,\epsilon }=E_{4,LHL}\left(S_{L,\epsilon }+E_{1,L,\epsilon }\right),$$

$$E_{5,LHHH,\epsilon }=E_{4,LHH}\left(S_{H,\epsilon }+E_{1,H,\epsilon }\right),E_{5,HLLL,\epsilon }=E_{4,HLL}\left(S_{L,\epsilon }+E_{1,L,\epsilon }\right),$$

$$E_{5,HLHH,\epsilon }=E_{4,HLH}\left(S_{H,\epsilon }+E_{1,H,\epsilon }\right),E_{5,HHLL,\epsilon }=E_{4,HHL}\left(S_{L,\epsilon }+E_{1,L,\epsilon }\right),$$

$$E_{5,HHHH,\epsilon }=E_{4,HHH}\left(S_{H,\epsilon }+E_{1,H,\epsilon }\right).$$

Stage 6. Frame summation. Let us calculate the errors $E_{6,F,\epsilon }$ of sums $E_{5,F,\epsilon }$, $\epsilon =1,2$.

$$E_{6,LL,\epsilon }=E_{5,LLLL,\epsilon }+E_{5,LLHH,\epsilon },E_{6,LH,\epsilon }=E_{5,LHLL,\epsilon }+E_{5,LHHH,\epsilon },$$

$$E_{6,HL,\epsilon }=E_{5,HLLL,\epsilon }+E_{5,HLHH,\epsilon },E_{6,HH,\epsilon }=E_{5,HHLL,\epsilon }+E_{5,HHHH,\epsilon }.$$

Stage 7. Column reconstruction. Let us calculate the errors $T_{7,F,\epsilon }$ and errors $E_{7,F,\epsilon }$ of column reconstruction with filters $L$ and $H$.

$$T_{7,LL,1}=T_{5,LLLL,1}\cdot S_{L,1},T_{7,LL,2}=T_{5,LLLL,2}\cdot S_{L,1},T_{7,LL,3}=T_{5,LLLL,1}\cdot S_{L,2},T_{7,LL,4}=T_{5,LLLL,2}\cdot S_{L,2},$$

$$E_{7,LL,1}=\left(T_{5,LLLL,1}+E_{6,LL,1}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{7,LL,1},E_{7,LL,2}=\left(T_{5,LLLL,2}+E_{6,LL,2}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{7,LL,2},$$

$$E_{7,LL,3}=\left(T_{5,LLLL,1}+E_{6,LL,1}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{7,LL,3},E_{7,LL,4}=\left(T_{5,LLLL,2}+E_{6,LL,2}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{7,LL,4},$$

$$E_{7,LH,1}=E_{6,LH,1}\left(S_{H,1}+E_{1,H,1}\right),E_{7,LH,2}=E_{6,LH,2}\left(S_{H,1}+E_{1,H,1}\right),E_{7,LH,3}=E_{6,LH,1}\left(S_{H,2}+E_{1,H,2}\right),$$

$$E_{7,LH,4}=E_{6,LH,2}\left(S_{H,2}+E_{1,H,2}\right),E_{7,HL,1}=E_{6,HL,1}\left(S_{L,1}+E_{1,L,1}\right),E_{7,HL,2}=E_{6,HL,2}\left(S_{L,1}+E_{1,L,1}\right),$$

$$E_{7,HL,3}=E_{6,HL,1}\left(S_{L,2}+E_{1,L,2}\right),E_{7,HL,4}=E_{6,HL,2}\left(S_{L,2}+E_{1,L,2}\right),E_{7,HH,1}=E_{6,HH,1}\left(S_{H,1}+E_{1,H,1}\right),$$

$$E_{7,HH,2}=E_{6,HH,2}\left(S_{H,1}+E_{1,H,1}\right),E_{7,HH,3}=E_{6,HH,1}\left(S_{H,2}+E_{1,H,2}\right),E_{7,HH,4}=E_{6,HH,2}\left(S_{H,2}+E_{1,H,2}\right).$$

Stage 8. Column summation. Let us calculate the errors $E_{8,F,\epsilon }$ of sums $E_{7,F,\epsilon }$, $\epsilon =1,2,3,4$.

$$E_{8,L,\epsilon }=E_{7,LL,\epsilon }+E_{7,LH,\epsilon },E_{8,H,\epsilon }=E_{7,HL,\epsilon }+E_{7,HH,\epsilon }.$$

Stage 9. Row reconstruction. Let us calculate the errors $T_{9,\epsilon }$ and errors $E_{9,F,\epsilon }$ of column reconstruction with filters $L$ and $H$.

$$T_{9,1}=T_{7,LL,1}\cdot S_{L,1},T_{9,2}=T_{7,LL,2}\cdot S_{L,1},T_{9,3}=T_{7,LL,3}\cdot S_{L,1},T_{9,4}=T_{7,LL,4}\cdot S_{L,1},$$

$$T_{9,5}=T_{7,LL,1}\cdot S_{L,2},T_{9,6}=T_{7,LL,2}\cdot S_{L,2},T_{9,7}=T_{7,LL,3}\cdot S_{L,2},T_{9,8}=T_{7,LL,4}\cdot S_{L,2},$$

$$E_{9,L,1}=\left(T_{7,LL,1}+E_{8,L,1}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{9,1},E_{9,L,2}=\left(T_{7,LL,2}+E_{8,L,2}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{9,2},$$

$$E_{9,L,3}=\left(T_{7,LL,3}+E_{8,L,3}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{9,3},E_{9,L,4}=\left(T_{7,LL,4}+E_{8,L,4}\right)\left(S_{L,1}+E_{1,L,1}\right)-T_{9,4},$$

$$E_{9,L,5}=\left(T_{7,LL,1}+E_{8,L,1}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{9,5},E_{9,L,6}=\left(T_{7,LL,2}+E_{8,L,2}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{9,6},$$

$$E_{9,L,7}=\left(T_{7,LL,3}+E_{8,L,3}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{9,7},E_{9,L,8}=\left(T_{7,LL,4}+E_{8,L,4}\right)\left(S_{L,2}+E_{1,L,2}\right)-T_{9,8},$$

$$E_{9,H,1}=E_{8,H,1}\left(S_{H,1}+E_{1,H,1}\right),E_{9,H,2}=E_{8,H,2}\left(S_{H,1}+E_{1,H,1}\right),E_{9,H,3}=E_{8,H,3}\left(S_{H,1}+E_{1,H,1}\right),$$

$$E_{9,H,4}=E_{8,H,4}\left(S_{H,1}+E_{1,H,1}\right),E_{9,H,5}=E_{8,H,1}\left(S_{H,2}+E_{1,H,2}\right),E_{9,H,6}=E_{8,H,2}\left(S_{H,2}+E_{1,H,2}\right),$$

$$E_{9,H,7}=E_{8,H,3}\left(S_{H,2}+E_{1,H,2}\right),E_{9,H,8}=E_{8,H,4}\left(S_{H,2}+E_{1,H,2}\right).$$

Stage 10. Row summation. Let us calculate the errors $E_{10,\epsilon }$ of sums $E_{9,F,\epsilon }$, $\epsilon =1,2,3,4,5,6,7,8.$

$$E_{10,\epsilon }=E_{9,L,\epsilon }+E_{9,H,\epsilon }.$$

Stage 11. Normalizing. Let us calculate the errors $E_{11,\epsilon }$ of rounding downscaled $E_{10,\epsilon }$ by $2^{-6n},$ $\epsilon =1,2,3,4,5,6,7,8$.

$$E_{11,\epsilon }=\lfloor 2^{-6n}{E}_{10,\epsilon }\rfloor .$$

The obtained values $E_{11,\epsilon }$ $\left(\epsilon =1,2,3,4,5,6,7,8\right)$ represent the resulting error of the method and allow for the calculation of the PSNR

$$PSNR=10{\log }_{10}\left(8M^2/{\displaystyle \sum _{\epsilon =1}^8{{\displaystyle E}}_{11,\epsilon }^2}\right),$$

(5)

where $MS{E}_{grayscale}=MS{E}_{color}=\frac{1}{8}{\displaystyle \sum _{\epsilon =1}^8{{\displaystyle E}}_{11,\epsilon }^2}$.

Formula (5) allows determining the minimum quality of a 3D image $db3$, obtained as a result of DWT of the original image $I$, depending on the maximum brightness and selected bit-width $r=n+1$ of wavelet filters coefficients $f_{F,i}$.

Calculations results ($PSNR$, dB) obtained by using our method of wavelet filters coefficients quantizing and final Formula (5) for 3D medical grayscale and color images DWT with various BPC, various bit-width $r$ and numbers $k=2,4,6,\dots ,20$ of wavelets $db\left(k/2\right)$ filters coefficients are presented in Table 1, Table 2 and Table 3. The cells in bold correspond to the minimum bit-widths of the filter coefficients, at which the processing quality achieves a high level according to the formula (4).

Table 1. Calculation results ($PSNR$, dB) of 3D medical images (with 8 BPC) DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
10	36.79	36.67	29.87	30.08	31.59	24.60	22.29	24.46	22.19	22.08
11	44.15	43.36	39.68	34.58	36.67	32.22	28.80	31.17	28.58	27.60
12	57.16	48.71	44.15	41.85	43.36	39.68	34.58	37.82	35.26	35.34
13	$\infty$	$\infty$	51.14	51.14	51.14	47.16	43.18	43.36	43.36	39.68
14	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	57.16	51.14	51.14	51.14	47.16
15	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 2. Calculation results ($PSNR$, dB) of 3D medical images (with 12 BPC) DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
12	49.43	45.01	42.18	40.05	41.80	38.21	33.76	36.69	34.47	34.40
13	57.46	52.38	49.10	46.76	46.46	44.76	41.11	41.99	41.92	39.07
14	71.28	61.23	54.39	52.38	52.27	50.35	47.91	47.73	47.65	44.90
15	70.86	71.28	61.11	59.15	57.68	57.46	55.52	52.38	53.27	52.27
16	$\infty$	81.28	71.28	64.37	63.79	63.79	63.15	57.97	59.85	56.33
17	$\infty$	$\infty$	$\infty$	70.86	75.26	71.28	68.49	67.30	64.37	63.79
18	$\infty$	$\infty$	$\infty$	$\infty$	81.28	81.28	75.26	75.26	75.26	71.28
19	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	81.28
20	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 3. Calculation results ($PSNR$, dB) of 3D medical images (with 16 BPC) DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
16	77.35	76.55	67.85	63.56	61.94	63.27	61.70	57.52	59.24	55.92
17	93.90	77.35	76.91	68.05	71.33	67.85	66.49	65.34	63.50	62.62
18	102.35	88.73	80.42	77.35	75.56	73.79	71.69	71.42	71.36	69.35
19	105.36	95.36	85.19	86.02	81.76	81.86	78.48	76.46	78.34	75.56
20	$\infty$	99.34	92.35	91.56	90.05	87.96	85.19	83.84	84.87	83.46
21	$\infty$	$\infty$	99.34	105.36	99.34	99.34	92.57	91.38	93.45	87.88
22	$\infty$	$\infty$	$\infty$	$\infty$	105.36	$\infty$	105.36	99.34	105.36	95.36
23	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	105.36
24	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Calculations results ($PSNR$, dB) obtained by using our method of wavelet filters coefficients quantizing and final Formula (5) for 3D medical grayscale and color images DWT with various BPC, various bit-width $r$ and numbers $k=2,4,6,\dots ,20$ of wavelets $sym\left(k/2\right)$ filters coefficients are presented in Table 4, Table 5 and Table 6.

Table 4. Calculation results ($PSNR$, dB) of 3D medical images (with 8 BPC) DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
10	36.79	36.67	29.87	30.08	26.15	26.07	24.53	24.46	21.15	22.08
11	44.15	43.36	39.68	34.58	32.46	32.22	30.83	31.17	26.75	26.15
12	57.16	48.71	44.15	41.85	41.85	36.99	35.04	37.82	34.71	32.46
13	$\infty$	$\infty$	51.14	51.14	51.14	43.18	44.15	43.18	43.18	41.85
14	$\infty$	$\infty$	$\infty$	$\infty$	57.16	51.14	57.16	48.71	51.14	47.16
15	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 5. Calculation results ($PSNR$, dB) of 3D medical images (with 12 BPC) DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
13	57.46	52.38	49.10	46.76	46.46	41.18	42.09	41.03	40.87	39.89
14	71.28	61.23	54.39	52.38	50.44	49.10	50.46	45.91	47.65	44.90
15	70.86	71.28	61.11	61.23	57.68	59.46	56.80	51.56	52.38	53.13
16	$\infty$	81.28	71.28	72.82	63.79	67.47	63.87	57.97	58.07	59.37
17	$\infty$	$\infty$	$\infty$	81.28	71.28	75.26	71.28	64.37	65.96	67.30
18	$\infty$	$\infty$	$\infty$	$\infty$	81.28	81.28	81.28	72.82	72.82	75.26
19	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 6. Calculation results ($PSNR$, dB) of 3D medical images (with 16 BPC) DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
16	77.35	76.55	67.85	70.44	63.48	65.06	63.18	57.52	57.46	58.27
17	93.90	77.35	76.91	76.55	67.96	70.97	69.20	63.56	64.39	64.31
18	102.35	88.73	80.42	79.43	74.14	73.79	73.90	70.41	70.39	71.33
19	105.36	95.36	85.19	83.84	81.76	77.89	78.48	77.35	76.46	76.35
20	$\infty$	99.34	92.35	91.56	90.05	85.19	86.02	83.84	86.02	82.16
21	$\infty$	$\infty$	99.34	105.36	95.36	92.57	92.57	90.05	91.56	90.05
22	$\infty$	$\infty$	$\infty$	$\infty$	105.36	105.36	99.34	96.91	99.34	95.36
23	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	105.36
24	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Calculations results ($PSNR$, dB) obtained by using our method of wavelet filters coefficients quantizing and final Formula (5) for 3D medical grayscale and color images DWT with various BPC, various bit-width $r$ and numbers $k=6,12,18,24,30$ of wavelets $coif\left(k/6\right)$ filters coefficients are presented in Table 7, Table 8 and Table 9.

Table 7. Calculation results ($PSNR$, dB) of 3D medical images (with 8 BPC) DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
11	36.99	29.87	29.48	26.07	25.60
12	41.85	36.99	37.82	33.72	32.40
13	48.71	47.16	43.18	39.68	37.82
14	$\infty$	51.14	48.71	47.16	44.37
15	$\infty$	$\infty$	$\infty$	57.16	57.16
16	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 8. Calculation results ($PSNR$, dB) of 3D medical images (with 12 BPC) DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
14	54.39	47.96	45.87	44.09	43.24
15	61.11	56.08	52.38	50.35	49.69
16	71.28	63.79	58.82	57.46	54.94
17	81.28	75.26	65.96	63.79	60.67
18	$\infty$	81.28	72.82	68.49	68.49
19	$\infty$	$\infty$	$\infty$	75.26	75.26
20	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 9. Calculation results ($PSNR$, dB) of 3D medical images (with 16 BPC) DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
17	73.79	70.97	64.39	61.91	59.42
18	83.54	73.79	69.56	67.24	66.49
19	87.96	80.42	77.35	73.19	72.10
20	92.35	85.19	84.87	80.42	77.96
21	99.34	95.36	91.56	87.88	86.02
22	$\infty$	$\infty$	99.34	95.36	91.38
23	$\infty$	$\infty$	$\infty$	105.36	99.34
24	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Let us compile Table 10, Table 11 and Table 12 based on Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 with the minimum values of $r$, at which the result of 3D medical images DWT with Daubechies wavelets, symlets and coiflets reach a high and maximum quality. For example, the result of 3D medical images (with 8 BPC) DWT with Daubechies wavelet $db8$ reaches high quality at $r=13$ $(PSNR=43.36$ dB$)$ and maximum quality at $r=15$ $\left(PSNR=\infty \right)$ according to Table 1. The remaining cells are filled in the same way.

Table 10. Minimum values of $r$, at which the result of 3D medical images DWT with Daubechies wavelets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
8	40	11	11	12	12	12	13	13	13	13	14
	$\infty$	13	13	14	14	14	15	15	15	15	15
12	60	14	14	15	16	16	16	16	17	17	17
	$\infty$	16	17	17	18	19	19	19	19	19	20
16	80	17	18	18	19	19	19	20	20	20	20
	$\infty$	20	21	22	22	23	22	23	23	23	24

Table 11. Minimum values of $r$, at which the result of 3D medical images DWT with symlets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
8	40	11	11	12	12	12	13	13	13	13
	$\infty$	13	13	14	14	15	15	15	15	15
12	60	14	14	15	15	16	16	17	17	17
	$\infty$	16	17	17	18	19	19	19	19	19
16	80	17	18	18	19	19	20	20	20	20
	$\infty$	20	21	22	22	23	23	23	23	24

Table 12. Minimum values of $r$, at which the result of 3D medical images DWT with coiflets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
8	40	12	13	13	14	14
	$\infty$	14	15	15	16	16
12	60	15	16	17	17	17
	$\infty$	18	19	19	20	20
16	80	18	19	20	20	21
	$\infty$	22	22	23	24	24

We could make the following conclusions based on calculation results presented in the Table 10, Table 11 and Table 12.

• Minimum bit-width $r$ of wavelet filters coefficients at which the result of 3D medical images with 8 BPC DWT does not contain visible distortions $(PSNR\ge 40$ dB$)$ can be determined by a formula

  $$r=11+\lfloor \sqrt{\frac{k}{2}}\rfloor ,$$

  (6)

  where $k$ is the number of wavelet filters coefficients.
• Minimum bit-width $r$ of wavelet filters coefficients at which the result of 3D medical images with 12 BPC DWT does not contain visible distortions $(PSNR\ge 60$ dB$)$ can be determined by a formula

  $$r=15+\lfloor \sqrt{\frac{k}{4}}\rfloor .$$

  (7)
• Minimum bit-width $r$ of wavelet filters coefficients at which the result of 3D medical images with 16 BPC DWT does not contain visible distortions $(PSNR\ge 80$ dB$)$ can be determined by a formula

  $$r=18+\lfloor \sqrt{\frac{k}{3}}\rfloor .$$

  (8)
• Minimum bit-width $r$ of wavelet filters coefficients at which the result of 3D medical images DWT does not contain distortions $\left(PSNR=\infty \right)$ can be determined by a formula

  $$r=5+B+\lfloor \sqrt{\frac{k}{2}-1}\rfloor ,$$

  (9)

  where $B$ is the image BPC.

Formulas (6)–(9) are an approximate since the values $r$ obtained at their use are sometimes redundant, that is, exceed values presented in Table 10, Table 11 and Table 12. However, they allow one to accurately calculate the non-redundant bit-width of the quantized wavelet filters coefficients in most cases. These formulas are applicable to both grayscale and color images.

3.2. Experiments of the 3D Medical Tomographic Images DWT

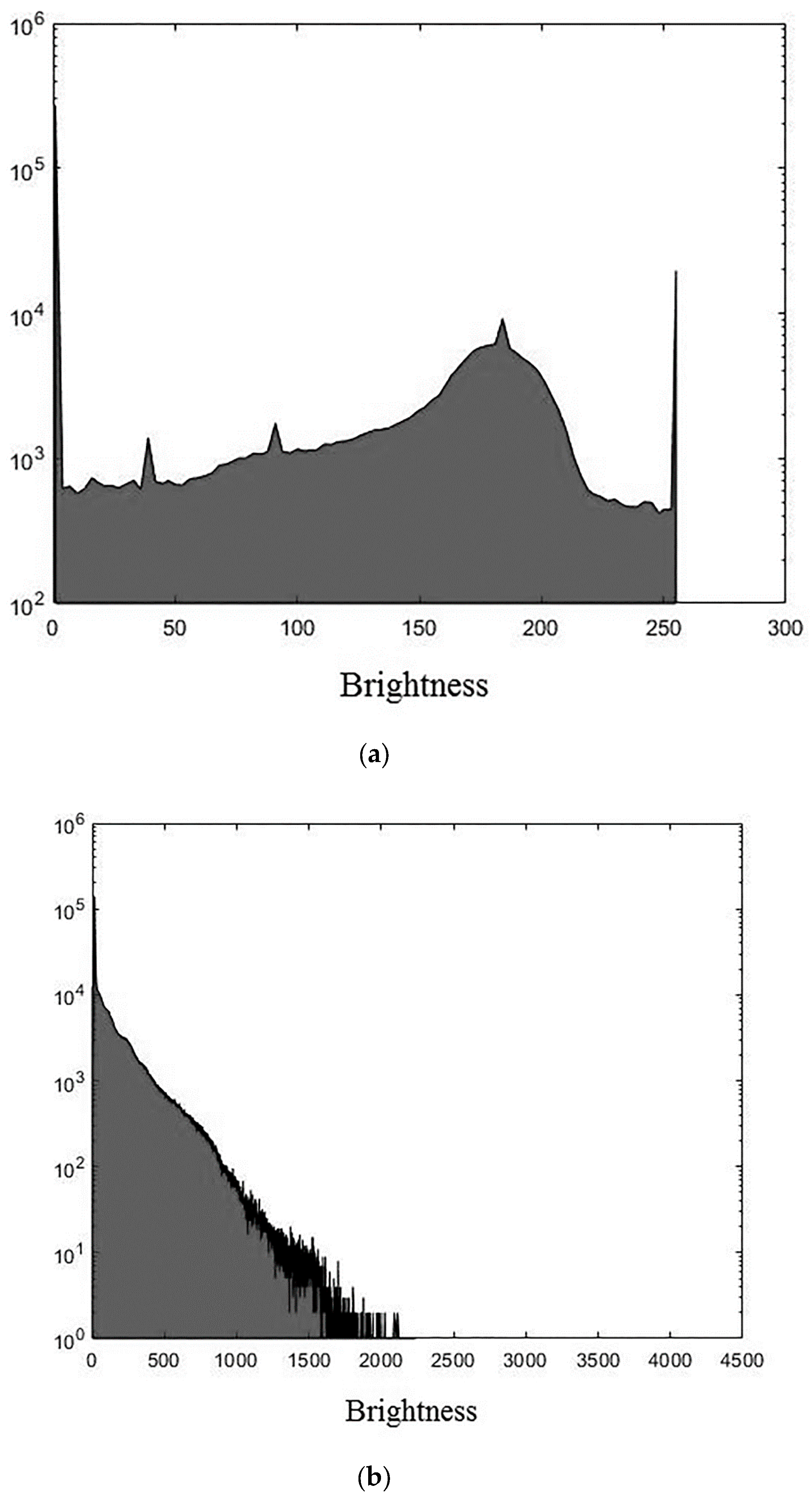
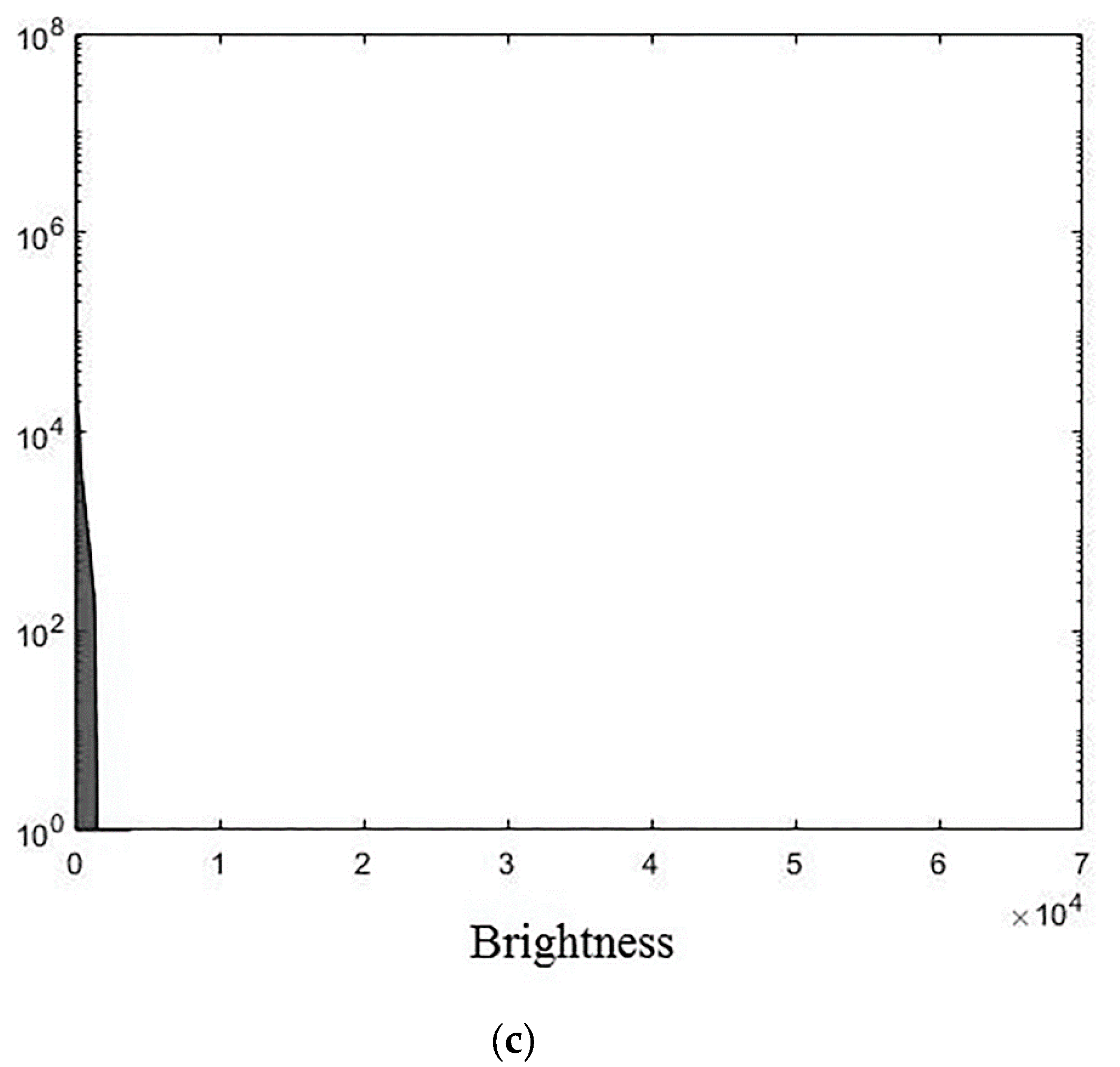
The experiments were conducted using MatLab software version R2018b for the three 3D medical tomographic grayscale images: “wmri” is the 8-bit image of size $128\times 128\times 27$; “Trufi_COR” is the 12-bit image of size $320\times 320\times 30$ and “Body_1.0” is the 16-bit image of size $512\times 512\times 507$. These images have the following histograms (Figure 4). The larger the image bitness, the lower its ratio of the average voxel brightness to the maximum allowed. We show the influence of this factor on the image processing quality further.

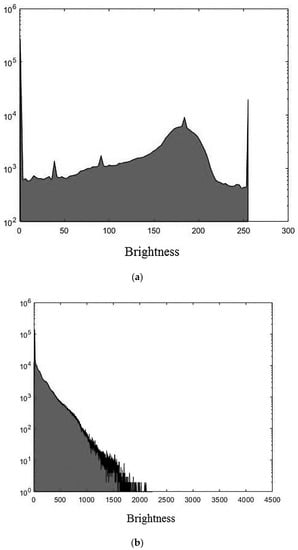
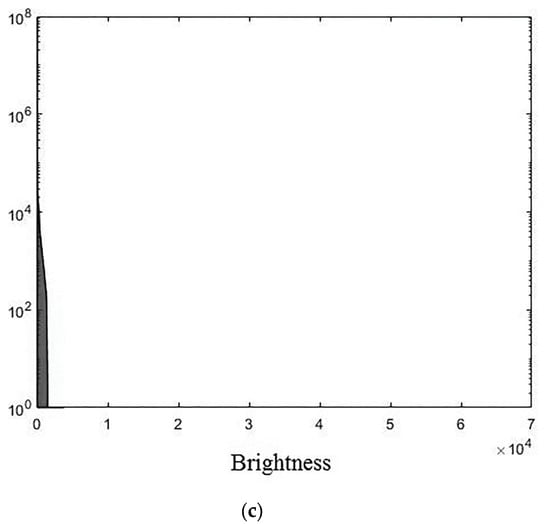
Figure 4. Histograms of used images: (a) “wmri”, average brightness $63.276$; (b) “Trufi_COR”, average brightness $129.796$ and (c) “Body_1.0”, average brightness $21.053$.

Images DWT performed as follows: filters coefficients $f_{F,i}$ of the Daubechies wavelets $db\left(k/2\right)$ $\left(k=2,4,6,\dots ,20\right)$, symlets $sym\left(k/2\right)$ $\left(k=2,4,6,\dots ,20\right)$ and coiflets $coif\left(k/6\right)$ $\left(k=6,12,18,24,30\right)$ were obtained, quantized by multiplying by $2^n$ $(n=1,2,3,\dots ,25)$ and rounding up according to Formula (2) and converted to fixed-point format; DWT of 3D images implemented; the voxels brightness values of the restored images were scaled by dividing by $2^{6n}$ and rounding down according to Formula (3) and converted to fixed-point format.

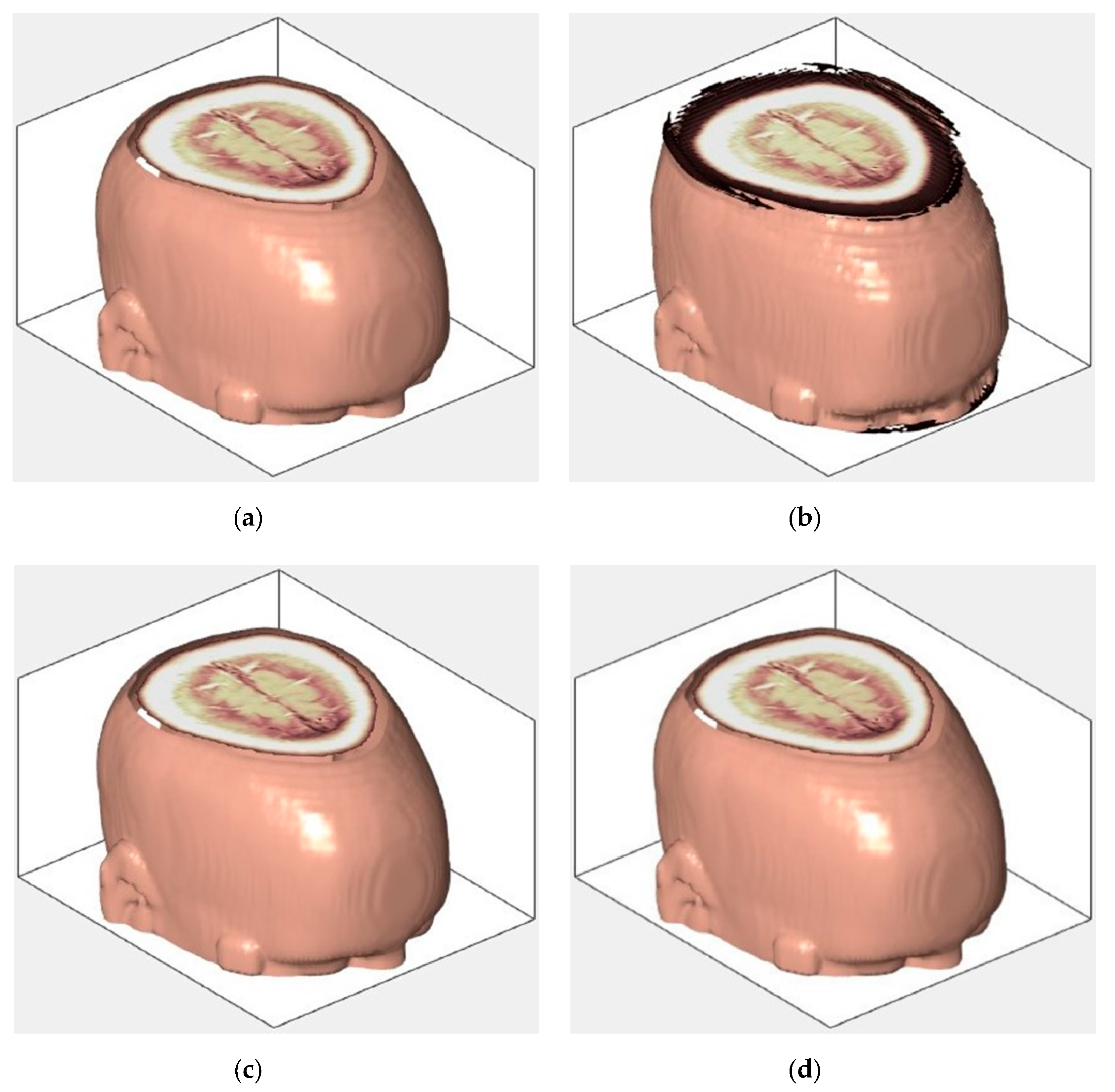
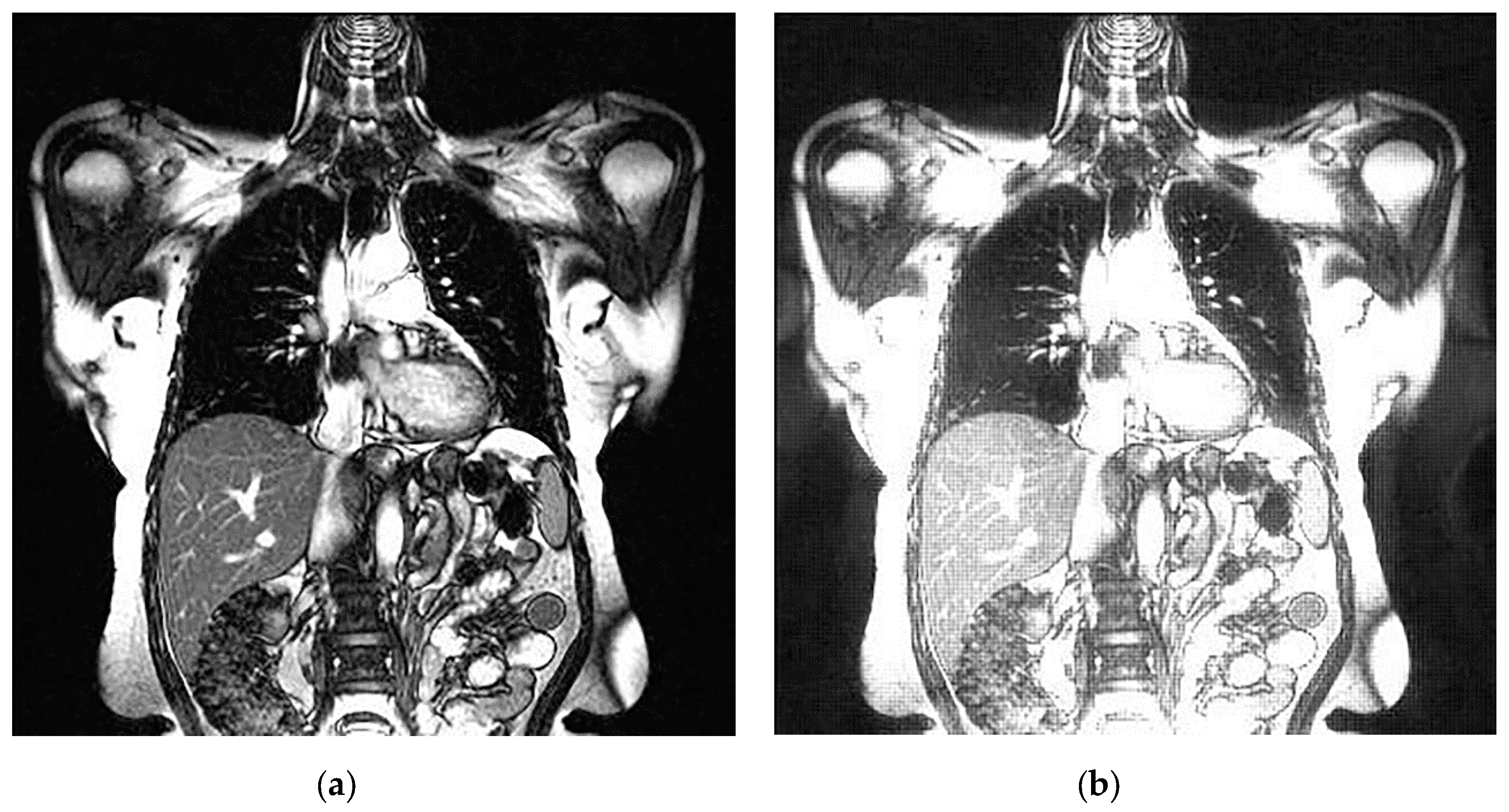
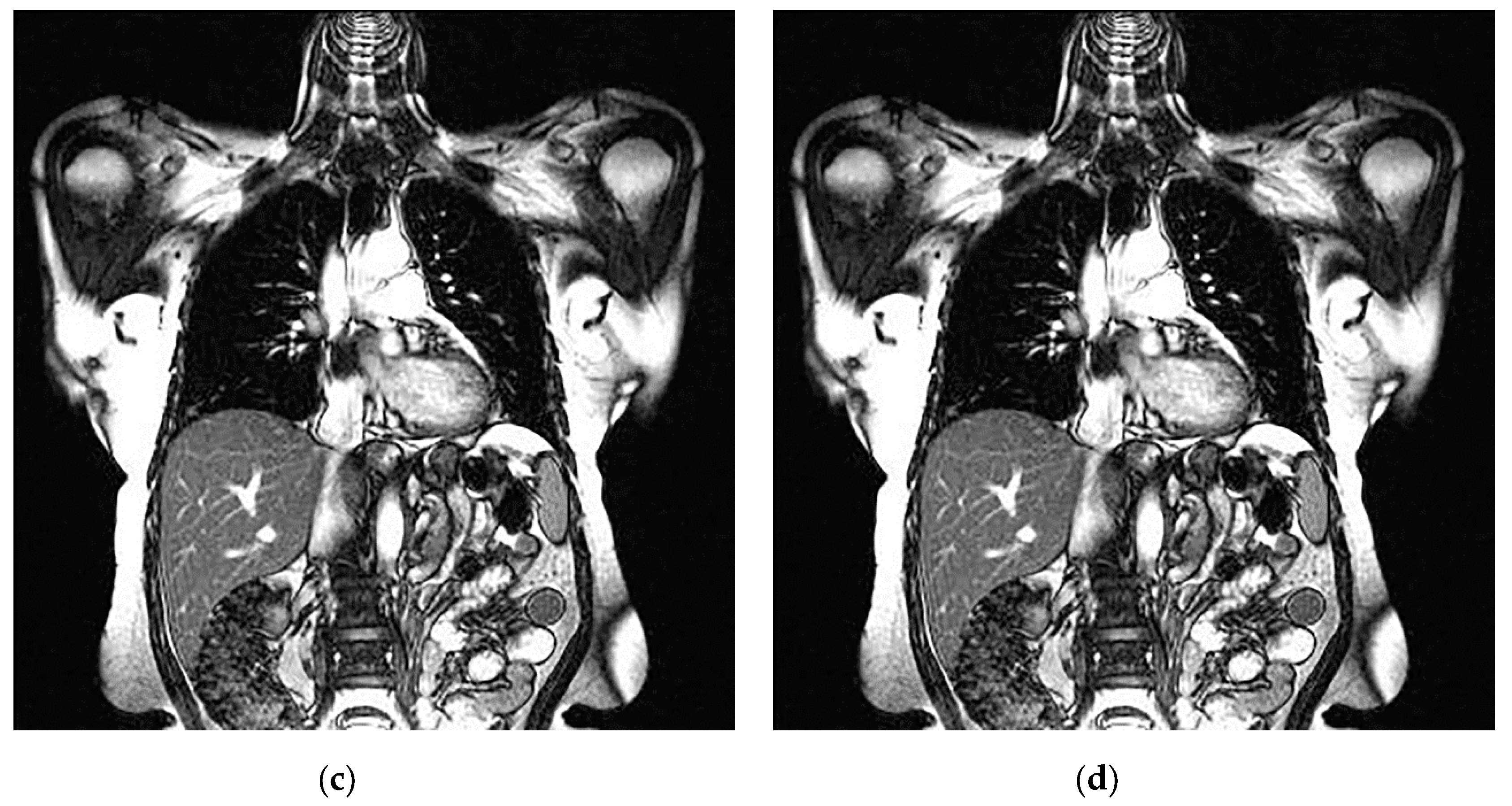
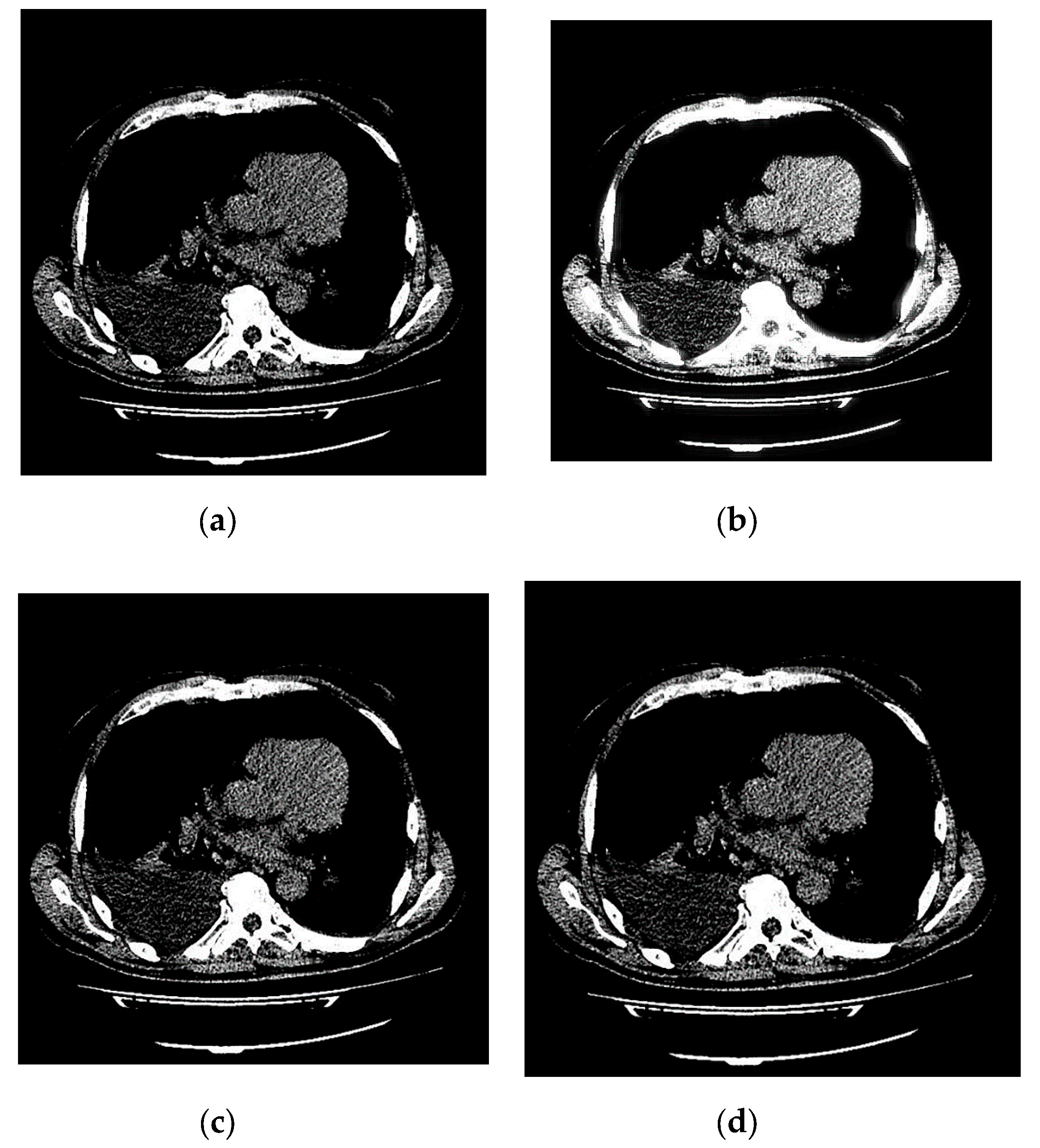
An example of 3D tomographic images “wmri”, “Trufi_COR” and “Body_1.0” DWT with wavelet $db8$ is shown in Figure 5, Figure 6 and Figure 7 respectively. Frames in Figure 6 and Figure 7 are selected to illustrate the error effect on the image processing result. Figures show a gradual improvement in the quality of processing with an increase the bit-width $r$: in Figure 5b, Figure 6b and Figure 7b visible distortion (Figure 5b is darkened in places, and Figure 6b and Figure 7b are lighted); in Figure 5c, Figure 6c and Figure 7c processed images are indistinguishable by eye from the original images; in Figure 5d, Figure 6d and Figure 7d processed images are identical to the corresponding originals. Experimental results are of higher quality compared with the calculation results. The values $PSNR=47.11$ dB and $PSNR=\infty$ at $r=12$ and $r=15$ respectively (Figure 5) obtained after 8-bit image “wmri” DWT with wavelet $db8$ exceed the corresponding calculated values $PSNR=37.82$ dB and $PSNR=\infty$ at $r=12$ and $r=15$ respectively (Table 1). The values $PSNR=64.57$ dB and $PSNR=\infty$ at $r=12$ and $r=17$ respectively (Figure 6) obtained after 12-bit image “Trufi_COR” DWT with wavelet $db8$ exceed the corresponding calculated values $PSNR=36.67$ dB, $PSNR=67.30$ dB at $r=12$ and $r=17$ respectively (Table 2). Similarly, for “Body_1.0”.

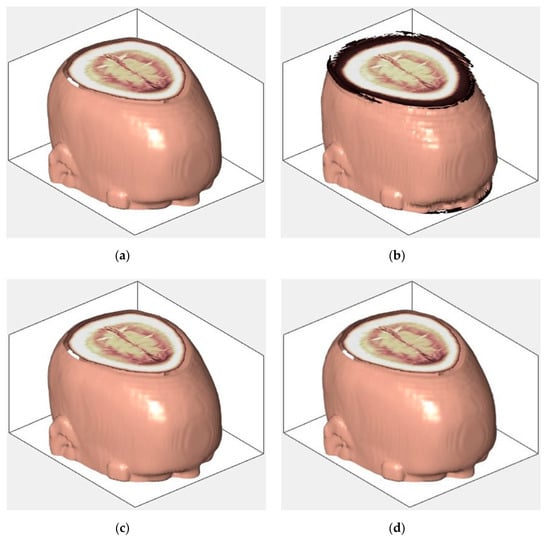
Figure 5. Example of 3D tomographic 8-bit image “wmri” DWT by $db8$ wavelet: (a) original image; processed image: (b) $r=9$, $PSNR=27.62$ dB; (c) $r=12$, $PSNR=47.11$ dB and (d) $r=15$, $PSNR=\infty$.

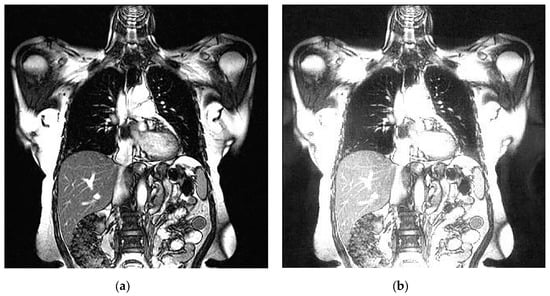
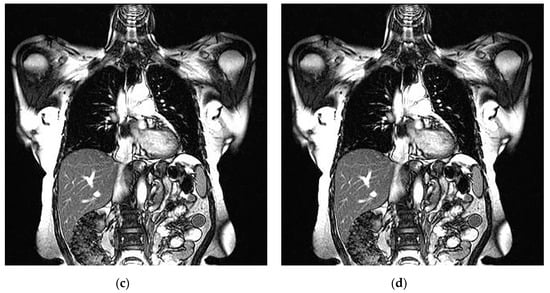
Figure 6. Example of 3D tomographic 12-bit image “Trufi_COR” (15-th frame) DWT by $db8$ wavelet: (a) original image; processed image: (b) $r=7$, $PSNR=30.27$ dB; (c) $r=12$, $PSNR=64.57$ dB and (d) $r=17$, $PSNR=\infty$.

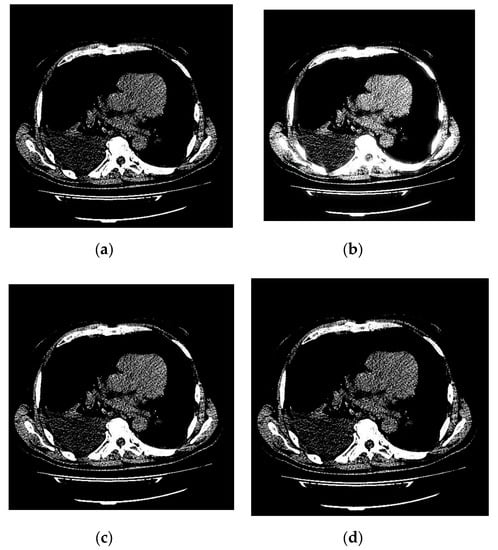
Figure 7. Example of 3D tomographic 16-bit image “Body_1.0” (1-st frame) DWT by $db8$ wavelet: (a) original image; processed image: (b) $r=7$, $PSNR=64.05$ dB; (c) $r=10$, $PSNR=85.30$ dB and (d) $r=17$, $PSNR=\infty$.

The image processing results were analyzed using $PSNR$ and structure similarity $(SSIM$) [52], calculating by formula

$$SSIM\left(I,\tilde{I}\right)=\frac{\left(2{\mathsf{\mu }}_I{\mathsf{\mu }}_{\tilde{I}}+c_1\right)\left(2{\mathsf{\sigma }}_{I\tilde{I}}+c_2\right)}{\left({\mathsf{\mu }}_I^2+{\mathsf{\mu }}_{\tilde{I}}^2+c_1\right)\left({\mathsf{\sigma }}_I^2+{\mathsf{\sigma }}_{\tilde{I}}^2+c_2\right)},$$

where: ${\mathsf{\mu }}_I$ is the average of $I$; ${\mathsf{\mu }}_{\tilde{I}}$ is the average of $\tilde{I}$; ${\mathsf{\sigma }}_I^2$ is the variance of $I$; ${\mathsf{\sigma }}_{\tilde{I}}^2$ is the variance of $\tilde{I}$; $c_1={\left(0.01\cdot M\right)}^2$; $c_2={\left(0.03\cdot M\right)}^2$ and $M$ is the maximum brightness of the image voxels. Experimental results ($PSNR$, dB; $SSIM$) of DWT of 3D tomographic grayscale images “wmri” (8-bit), “Trufi_COR” (12-bit) and “Body_1.0” (16-bit) for various bit-width $r$ and numbers $k=2,4,6,\dots ,20$ of wavelets $db\left(k/2\right)$ filters coefficients are presented in Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18. The cells in bold correspond to the minimum bit-widths of the filter coefficients, at which the processing quality achieves a high level according to the formula (4).

Table 13. Experimental results ($PSNR$, dB) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
9	37.77	37.51	31.59	31.45	33.45	27.81	25.33	27.62	24.16	25.03
10	44.78	44.47	38.16	37.95	40.21	32.98	30.81	32.95	30.76	30.67
11	52.66	52.44	48.29	42.84	44.97	41.03	37.43	39.59	37.37	36.48
12	69.55	56.29	53.32	50.66	52.88	48.64	43.25	47.11	44.52	44.44
13	$\infty$	$\infty$	70.86	60.74	60.36	56.92	52.47	53.42	53.32	50.09
14	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	93.45	65.73	64.80	64.10	57.65
15	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 14. Experimental results ($SSIM$) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
9	0.9998	0.9998	0.9991	0.9990	0.9993	0.9975	0.9953	0.9969	0.9936	0.9943
10	1.0000	1.0000	0.9998	0.9998	0.9998	0.9993	0.9987	0.9991	0.9985	0.9984
11	1.0000	1.0000	1.0000	0.9999	0.9999	0.9999	0.9997	0.9998	0.9997	0.9996
12	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	1.0000	0.9999	0.9999
13	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Table 15. Experimental results ($PSNR$, dB) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
9	55.35	55.15	49.64	49.52	51.56	46.10	43.74	46.08	42.62	43.54
10	61.94	61.74	55.93	55.74	58.14	51.13	49.08	51.29	49.14	49.10
11	69.03	69.02	65.33	60.46	62.66	58.84	55.49	57.68	55.53	54.82
12	77.25	72.30	69.89	67.43	69.64	65.88	61.00	64.57	62.24	62.33
13	88.60	81.40	78.04	75.10	75.33	73.56	69.22	70.48	70.39	67.51
14	118.20	96.42	85.23	82.51	82.65	80.99	77.38	77.57	77.62	74.43
15	129.34	119.88	99.48	93.90	90.03	91.05	88.62	84.20	85.12	84.30
16	$\infty$	$\infty$	$\infty$	110.99	105.34	109.92	105.08	94.67	98.96	91.61
17	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	121.21	117.93
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 16. Experimental results ($SSIM$) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
9	0.9996	0.9995	0.9981	0.9979	0.9986	0.9948	0.9902	0.9939	0.9864	0.9884
10	0.9999	0.9999	0.9996	0.9996	0.9997	0.9985	0.9972	0.9982	0.9968	0.9967
11	1.0000	1.0000	1.0000	0.9999	0.9999	0.9998	0.9994	0.9996	0.9993	0.9991
12	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	0.9999	0.9999	0.9999
13	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Table 17. Experimental results ($PSNR$, dB) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
7	77.99	77.69	70.86	68.90	68.96	65.38	65.39	64.05	62.04	59.98
8	87.98	81.65	78.77	76.46	76.54	71.53	70.89	72.11	68.08	68.88
9	88.22	88.00	82.85	82.90	84.95	79.80	77.67	79.97	76.69	77.63
10	94.84	94.62	89.15	88.98	91.67	84.80	83.03	85.30	83.27	83.27
11	101.92	101.93	98.64	93.87	96.45	92.39	89.47	91.69	89.76	89.16
12	109.95	105.14	103.17	100.98	103.38	99.76	94.87	98.86	96.63	96.80
13	120.74	114.03	111.17	108.38	108.91	107.49	103.36	104.87	104.83	102.16
14	167.56	127.71	118.07	115.86	116.02	115.25	111.44	111.96	112.20	109.24
15	166.77	169.11	131.41	126.83	122.99	125.99	123.36	119.26	119.89	119.63
16	$\infty$	$\infty$	$\infty$	144.12	138.29	145.66	140.29	130.67	135.37	128.20
17	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	172.79	161.13
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 18. Experimental results ($SSIM$) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of Daubechies wavelets filters coefficients.

$\mathit{r}$	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{7}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{9}$	$\mathit{d}\mathit{b}\mathbf{10}$
7	0.9999	0.9999	0.9996	0.9994	0.9994	0.9987	0.9986	0.9982	0.9970	0.9953
8	1.0000	1.0000	0.9999	0.9999	0.9999	0.9997	0.9996	0.9997	0.9992	0.9993
9	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	0.9999	0.9999	0.9999	0.9999
10	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Experimental results ($PSNR$, dB; $SSIM$) of DWT of 3D tomographic grayscale images “wmri” (8-bit), “Trufi_COR” (12-bit) and “Body_1.0” (16-bit) for various bit-width $r$ and numbers $k=2,4,6,\dots ,20$ of wavelets $sym\left(k/2\right)$ filters coefficients are presented in Table 19, Table 20, Table 21, Table 22, Table 23 and Table 24.

Table 19. Experimental results ($PSNR$, dB) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
9	37.77	37.51	31.59	31.35	27.75	29.25	26.23	25.01	22.24	24.91
10	44.78	44.47	38.16	38.01	34.33	34.16	32.84	32.72	29.60	30.54
11	52.66	52.44	48.29	42.69	41.11	41.00	39.51	39.38	35.37	34.59
12	69.55	56.29	53.32	50.35	50.34	45.38	44.43	46.72	43.12	41.43
13	$\infty$	$\infty$	70.86	60.35	60.06	52.29	53.30	52.18	52.18	50.82
14	$\infty$	$\infty$	$\infty$	$\infty$	87.43	74.66	79.40	59.06	63.68	57.27
15	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 20. Experimental results ($SSIM$) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
9	0.9998	0.9998	0.9991	0.9990	0.9979	0.9982	0.9967	0.9954	0.9917	0.9944
10	1.0000	1.0000	0.9998	0.9998	0.9995	0.9995	0.9992	0.9992	0.9984	0.9985
11	1.0000	1.0000	1.0000	0.9999	0.9999	0.9999	0.9998	0.9998	0.9996	0.9995
12	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	1.0000	0.9999	0.9999
13	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Table 21. Experimental results ($PSNR$, dB) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
9	55.35	55.15	49.64	49.35	45.83	47.40	44.46	43.29	40.55	43.33
10	61.94	61.74	55.93	55.82	52.32	52.11	50.96	50.87	47.78	48.86
11	69.03	69.02	65.33	60.22	58.78	58.74	57.42	57.33	53.42	52.74
12	77.25	72.30	69.89	67.03	67.23	62.83	61.88	64.07	60.87	59.29
13	88.60	81.40	78.04	74.82	75.01	68.86	70.12	68.84	68.94	67.90
14	118.20	96.42	85.23	82.14	80.24	78.63	80.16	74.73	76.99	73.83
15	129.34	119.88	99.48	97.83	90.32	93.04	89.60	82.15	83.43	84.56
16	$\infty$	$\infty$	$\infty$	$\infty$	109.58	115.30	107.15	93.49	93.67	94.62
17	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	117.03	119.88	119.49
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 22. Experimental results ($SSIM$) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
9	0.9996	0.9995	0.9981	0.9980	0.9955	0.9964	0.9932	0.9905	0.9825	0.9886
10	0.9999	0.9999	0.9996	0.9996	0.9990	0.9989	0.9984	0.9983	0.9966	0.9968
11	1.0000	1.0000	1.0000	0.9999	0.9998	0.9998	0.9997	0.9997	0.9991	0.9988
12	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	0.9999	0.9999	0.9998	0.9998
13	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Table 23. Experimental results ($PSNR$, dB) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
7	77.99	77.69	70.86	66.59	68.20	66.55	62.15	62.64	61.78	61.58
8	87.98	81.65	78.77	74.26	74.19	74.41	71.33	70.33	68.46	69.41
9	88.22	88.00	82.85	82.52	79.09	80.85	77.89	76.90	74.25	77.28
10	94.84	94.62	89.15	89.03	85.67	85.47	84.57	84.48	81.44	82.83
11	101.92	101.93	98.64	93.36	92.14	92.21	91.01	90.95	87.22	86.66
12	109.95	105.14	103.17	100.15	100.63	96.34	95.53	97.87	94.76	93.33
13	120.74	114.03	111.17	107.82	108.37	102.48	103.73	102.57	102.98	102.12
14	167.56	127.71	118.07	114.95	113.49	112.18	113.78	108.50	111.20	108.03
15	166.77	169.11	131.41	129.65	123.55	126.81	123.10	115.96	117.59	118.94
16	$\infty$	$\infty$	$\infty$	$\infty$	142.56	147.12	140.64	127.84	128.64	129.62
17	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	151.00	160.08	159.78
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 24. Experimental results ($SSIM$) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of symlets filters coefficients.

$\mathit{r}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{3}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{5}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{7}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{9}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
7	0.9999	0.9999	0.9996	0.9991	0.9994	0.9990	0.9974	0.9976	0.9970	0.9969
8	1.0000	1.0000	0.9999	0.9998	0.9998	0.9998	0.9997	0.9996	0.9993	0.9994
9	1.0000	1.0000	1.0000	1.0000	0.9999	1.0000	0.9999	0.9999	0.9998	0.9999
10	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

Experimental results ($PSNR$, dB; $SSIM$) of DWT of 3D tomographic grayscale images “wmri” (8-bit), “Trufi_COR” (12-bit) and “Body_1.0” (16-bit) for various bit-width $r$ and numbers $k=6,12,18,24,30$ of wavelets $coif\left(k/6\right)$ filters coefficients are presented in Table 25, Table 26, Table 27, Table 28, Table 29 and Table 30.

Table 25. Experimental results ($PSNR$, dB) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
9	33.91	27.72	24.02	20.62	21.25
10	40.58	34.26	30.54	27.99	27.35
11	44.93	38.35	38.25	34.55	35.28
12	50.59	45.41	46.59	43.00	41.96
13	61.35	55.11	52.12	48.07	48.21
14	$\infty$	66.81	58.76	56.43	56.52
15	$\infty$	$\infty$	$\infty$	99.82	96.81
16	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 26. Experimental results ($SSIM$) of 3D tomographic 8-bit image “wmri” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
9	0.9995	0.9976	0.9940	0.9870	0.9873
10	0.9999	0.9995	0.9987	0.9973	0.9966
11	1.0000	0.9998	0.9998	0.9994	0.9994
12	1.0000	1.0000	1.0000	0.9999	0.9999
13	1.0000	1.0000	1.0000	1.0000	1.0000

Table 27. Experimental results ($PSNR$, dB) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
10	58.14	52.30	48.76	46.38	45.24
11	62.21	56.20	56.34	52.78	53.00
12	67.16	62.90	64.06	60.82	59.41
13	75.02	71.54	68.84	65.25	64.93
14	85.17	77.12	74.73	72.81	72.40
15	99.11	87.99	83.32	81.23	80.64
16	126.33	103.94	95.26	92.00	88.75
17	$\infty$	$\infty$	121.68	109.44	101.44
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 28. Experimental results ($SSIM$) of 3D tomographic 12-bit image “Trufi_COR” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
10	0.9998	0.9989	0.9972	0.9944	0.9918
11	0.9999	0.9996	0.9995	0.9988	0.9986
12	1.0000	0.9999	0.9999	0.9998	0.9997
13	1.0000	1.0000	1.0000	0.9999	0.9999
14	1.0000	1.0000	1.0000	1.0000	1.0000

Table 29. Experimental results ($PSNR$, dB) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
8	78.19	71.20	70.48	65.46	64.87
9	84.76	79.33	76.10	73.01	73.31
10	91.16	85.79	82.46	80.39	79.40
11	95.23	89.68	90.16	86.87	87.29
12	100.21	96.41	97.92	94.99	93.71
13	107.91	105.11	102.80	99.41	99.41
14	117.81	110.61	108.67	107.14	107.07
15	130.24	121.55	117.33	115.73	115.45
16	171.54	136.59	129.87	128.02	124.92
17	$\infty$	$\infty$	168.53	146.89	138.98
18	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$

Table 30. Experimental results ($SSIM$) of 3D tomographic 16-bit image “Body_1.0” DWT by using bit-width $r$ of coiflets filters coefficients.

$\mathit{r}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
8	0.9999	0.9997	0.9996	0.9986	0.9983
9	1.0000	0.9999	0.9999	0.9997	0.9997
10	1.0000	1.0000	1.0000	1.0000	0.9999
11	1.0000	1.0000	1.0000	1.0000	1.0000

Calculation results from Table 10, Table 11 and Table 12 supplemented by experimental results from Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, Table 24, Table 25, Table 26, Table 27, Table 28, Table 29 and Table 30 and the difference between them is presented in Table 31, Table 32 and Table 33.

Table 31. Minimum values of $r$, at which the result of 3D tomographic images DWT by Daubechies wavelets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	Results	$\mathit{d}\mathit{b}\mathbf{1}$	$\mathit{d}\mathit{b}\mathbf{2}$	$\mathit{d}\mathit{b}\mathbf{3}$	$\mathit{d}\mathit{b}\mathbf{4}$	$\mathit{d}\mathit{b}\mathbf{5}$	$\mathit{d}\mathit{b}\mathbf{6}$	$\mathit{d}\mathit{b}\mathbf{8}$	$\mathit{d}\mathit{b}\mathbf{10}$
8	40	Calculation	11	11	12	12	12	13	13	14
		Experimental	10	10	11	11	10	11	12	12
		Difference	1	1	1	1	2	2	1	2
	$\infty$	Calculation	13	13	14	14	14	15	15	15
		Experimental	13	13	14	14	14	15	15	15
		Difference	0	0	0	0	0	0	0	0
12	60	Calculation	14	14	15	16	16	16	17	17
		Experimental	10	10	11	11	11	12	12	12
		Difference	4	4	4	5	5	4	5	5
	$\infty$	Calculation	16	17	17	18	19	19	19	20
		Experimental	16	16	16	17	17	17	17	18
		Difference	0	1	1	1	2	2	2	2
16	80	Calculation	17	18	18	19	19	19	20	20
		Experimental	8	8	9	9	9	10	10	10
		Difference	9	10	9	10	10	9	10	10
	$\infty$	Calculation	20	21	22	22	23	22	23	24
		Experimental	16	16	16	17	17	17	17	18
		Difference	4	5	6	5	6	5	6	6

Table 32. Minimum values of $r$, at which the result of 3D tomographic images DWT by symlets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	Results	$\mathit{s}\mathit{y}\mathit{m}\mathbf{1}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{2}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{4}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{6}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{8}$	$\mathit{s}\mathit{y}\mathit{m}\mathbf{10}$
8	40	Calculation	11	11	12	13	13	13
		Experimental	10	10	11	11	12	12
		Difference	1	1	1	2	1	1
	$\infty$	Calculation	13	13	14	15	15	15
		Experimental	13	13	14	15	15	15
		Difference	0	0	0	0	0	0
12	60	Calculation	14	14	15	16	17	17
		Experimental	10	10	11	12	12	13
		Difference	4	4	4	4	5	4
	$\infty$	Calculation	16	17	18	19	19	19
		Experimental	16	16	16	17	18	18
		Difference	0	1	2	2	1	1
16	80	Calculation	17	18	19	20	20	20
		Experimental	8	8	9	9	10	10
		Difference	9	10	10	11	10	10
	$\infty$	Calculation	20	21	22	23	23	24
		Experimental	16	16	16	17	18	18
		Difference	4	5	6	6	5	6

Table 33. Minimum values of $r$, at which the result of 3D tomographic images DWT by coiflets reaches high and maximum quality.

BPC	$\mathit{P}\mathit{S}\mathit{N}\mathit{R}$, dB	Results	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{1}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{2}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{3}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{4}$	$\mathit{c}\mathit{o}\mathit{i}\mathit{f}\mathbf{5}$
8	40	Calculation	12	13	13	14	14
		Experimental	10	12	12	12	12
		Difference	2	1	1	2	2
	$\infty$	Calculation	14	15	15	16	16
		Experimental	14	15	15	16	16
		Difference	0	0	0	0	0
12	60	Calculation	15	16	17	17	17
		Experimental	11	12	12	12	13
		Difference	4	4	5	5	4
	$\infty$	Calculation	18	19	19	20	20
		Experimental	17	17	18	18	18
		Difference	1	2	1	2	2
16	80	Calculation	18	19	20	20	21
		Experimental	9	10	10	10	11
		Difference	9	9	10	10	10
	$\infty$	Calculation	22	22	23	24	24
		Experimental	17	17	18	18	18
		Difference	5	5	5	6	6

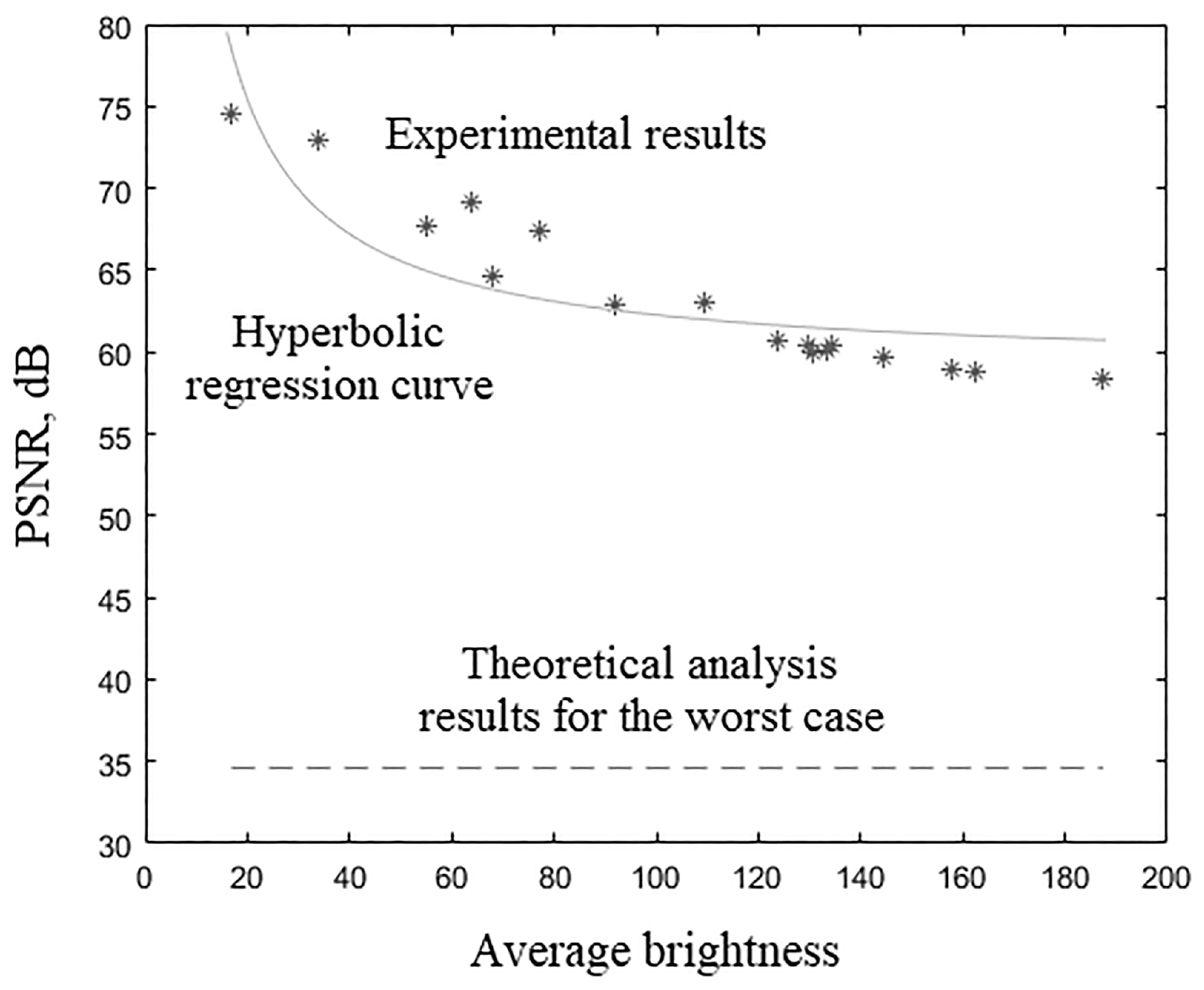
Experimental results ($PSNR$, dB) of various 3D tomographic 12-bit grayscale images DWT by wavelet $db4$ with bit-width $r=11$ of filters coefficients are presented in Table 34 and in Figure 8.

Table 34. Experimental results ($PSNR$, dB) of 3D tomographic images DWT by wavelet $db4$ with bit-width $r=11$ of filters coefficients.

Image Name	Average Brightness	PSNR, dB
SUB_1st pass	16.89	74.57
cor shared echo_SUB_MIP_COR	33.92	72.87
MIP thin cor first phase	55.16	67.63
mra highres.ce_S47_DIS2D	63.74	69.07
cor thin mips ist pass	67.92	64.58
mra highres.ce_S48_DIS2D	77.29	67.32
sag timing run-flash_MIP_SAG	91.71	62.81
cine_retro_normal_lvot	109.46	63.07
cine_retro_normal_rvot	123.87	60.63
Trufi_COR	129.80	60.46
Trufi_SAG	130.79	59.97
cine_retro_normal_sa	133.50	60.17
cine_retro_normal_lvla	134.35	60.41
cine_retro_normal_hla	144.48	59.72
cine_retro_aortic valve	157.94	58.87
Trufi_TRANS	162.25	58.83
t1_fl2d_cor_pre-post	187.42	58.39

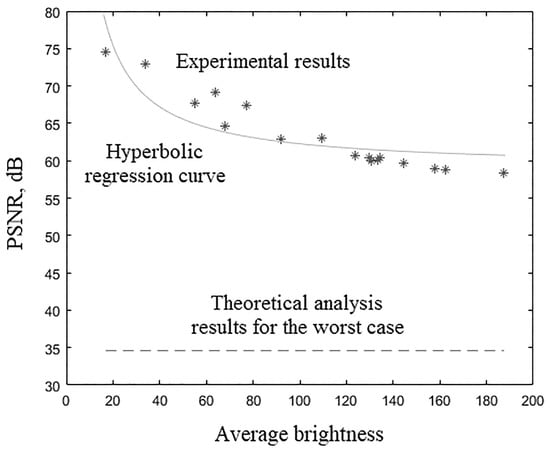
Figure 8. Experimental results of 3D tomographic 12-bit images DWT by wavelet $db4$ with bit-width $r=11$ of filters coefficients.

The nonlinear hyperbolic regression [53] curve for the data from Table 34 was plotted in Figure 8 and has the equation $PSNR=58.98+328.78/A$, where $A$ is the average brightness of the image voxels. The $F$-test value [54] for constructed nonlinear hyperbolic regression curve is $F=42.24$ actually observed. The $F$-test critical value [55] for false-rejection probability $0.001$ with degrees of freedom $k_1=p-1=2-1=1$ and $k_2=m-p=17-2=15$ is $F_{0.001;1,15}=16.59$, where $p$ is the regression equation estimated parameters number and $m$ is the images number from Table 34. Since $F>F_{0.001;1,15}$ resulting regression equation is significant at false-rejection probability $0.001$. Equation asymptote exceeds the corresponding theoretical calculations values.

4. Discussion

Experimental results, the main of which are presented in Table 31, Table 32 and Table 33, show that all $PSNR$ values obtained as calculation results were not bigger than the $PSNR$ values obtained as experimental results. This confirms the accuracy of theoretical analysis. Thus, the derived Formulas (6)–(9) could be used for determining the minimum bit-width of wavelet filters coefficients, at which the result of 3D medical tomographic images DWT reaches high ($PSNR\ge 40$ dB for images with 8 BPC, $PSNR\ge 60$ dB for images with 12 BPC and $PSNR\ge 80$ dB for images with 16 BPC according to Formula (4)$)$ and maximum $\left(PSNR=\infty \right)$ quality respectively. Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, Table 24, Table 25, Table 26, Table 27, Table 28, Table 29 and Table 30 show that $SSIM$ values obtained as a calculation result were set to one when using 4 decimal places in simulating 8-, 12- and 16-bit images when the $PSNR$ was approximately 45, 65 and 80 dB, respectively. Thus, both $PSNR$ and $SSIM$ metrics used confirm high-quality image processing. The experiment of 3D 8-bit medical tomographic image DWT required 1–2 bits less for wavelet filters coefficients than the calculations require for high-quality processing since the worst case was predicted in theoretical analysis. An even greater decrease in the bit-width of wavelet filter coefficients led to even greater savings in hardware resources. The difference between the obtained theoretical and experimental values increased significantly in the case of 12-bit and 16-bit images. The 12-bit tomographic image required 4–5 bits and 1–2 bits less for wavelet filters coefficients to achieve high and maximum processing quality respectively. This difference increased to 9–10 and 5–6 bits respectively in the case of a 16-bit image. This is because the range of voxel brightness values significantly increased in 12- and 16-bit images. The average brightness of the image voxels varied insignificantly at this time (was within the 8-bit range) since the high-order bits were rarely used. Thus, the ratio of the average voxel brightness to the maximum allowable value of $M$ decreased with increasing BPC of images, which were demonstrated by histograms in Figure 4. This led to much faster achievement of high and maximum quality compared with the theoretical analysis results.

The darkening and lighting in Figure 5, Figure 6 and Figure 7 were due to the low accuracy of wavelet filters coefficients quantization used for image processing. The excessive character of quantization error led to an increase in the voxels brightness values of the processed images. Figure 6b and Figure 7b turned out to be lighted since 12- and 16-bit images had a brightness margin, which is shown by the histograms in Figure 4b,c. However, the range of brightness values of the 8-bit image was fully utilized (Figure 4a) and the quantization error led to the computational range overflow. The voxels brightness values that exceeded the range went to zero as a result of this.

Table 34 and Figure 8 show the dependence of the 12-bit medical tomographic images processing quality of their average voxels brightness. This dependence had a nonlinear hyperbolic regression form. Equation asymptote exceeded the corresponding theoretical calculation values. The processing quality by $PSNR$ metric (from 74.57 to 58.39) decreased with an increase in the average voxels brightness (from 16.89 to 187.42). The difference in the image processing quality with the minimum and maximum values of the average brightness according to Table 34 was more than 15 dB. It was commensurate with the difference in the processing quality of the same image by the same wavelet with filter coefficients bit-width that differ by two, according to Table 15, Table 21 and Table 27. That is, we would need 2 bits less for wavelet filter coefficients for high-quality processing of a 12-bit image with an average brightness of 16.89 than for processing a 12-bit image with an average brightness of 187.42. The average voxels brightness of the medical image can vary in different ranges depending on many factors: from the medical image modalities; from the analyzing device type; from specific device settings; from the analyzed organ or group of organs; etc. Thus, the requirements for the digit capacity of wavelet filter coefficients can be relaxed, depending on the ability to take into account many factors related to the nature of the images obtained as a result of medical tests. Summarizing, the quality of 3D medical tomographic images DWT primarily depends on their bits per color, on average voxels brightness, on the number of wavelet filters coefficients and to a lesser extent on the type of wavelet.

Minimum bit-width $r$ of wavelet filters coefficients for 3D medical tomographic images DWT is defined as follows: determine BPC of images (for example, 8, 12 or 16 BPC); select a quality threshold of image processing (for example, $PSNR=40$ dB, $PSNR=60$ dB, $PSNR=80$ dB or $PSNR=\infty$); choose the wavelet with the number of coefficients $k$; calculate bit-width $r$ of wavelet filters coefficients by Formulas (5)–(9) depending on the quality threshold of image processing selected.

5. Conclusions

The problem of analyzing the quantization noise effect in coefficients of DWT filters for 3D medical imaging was solved. The method was proposed for wavelet filters coefficients quantizing, which allows minimizing resources in hardware implementation. The method was developed for estimating the maximum error of 3D grayscale and color images DWT with various BPC. The derived Formula (5) allows determining the minimum quality of 3D medical images DWT depending on the wavelet used, bit-width of wavelet filters coefficients and BPC. We proved that Formulas (6)–(9) can be used to determine the minimum bit-width of wavelet filters coefficients for which the result of 3D images DWT reaches high ($PSNR\ge 40$ dB for images with 8 BPC, $PSNR\ge 60$ dB for images with 12 BPC and $PSNR\ge 80$ dB for images with 16 BPC) and maximum $\left(PSNR=\infty \right)$ quality respectively depending on the wavelet used. The experiments of the 3D tomographic images DWT showed that the bit-width of wavelet filters coefficients could be significantly reduced for high-quality medical imaging compared to theoretical analysis results. All data were presented in a fixed-point format and rounding operations were simplified in the proposed method of 3D images DWT.

The proposed DWT method could be used in a wide range of applications for denoising and compression of 3D medical images. Given the need to improve the efficiency of medical visual data processing methods, further research can be expected in this direction.