Experimental Study on the Cyclic Behavior of Integrated Panels for Cold-Formed Steel Shear Wall System
Abstract
:1. Introduction
1.1. Research Background
1.2. Literature Review
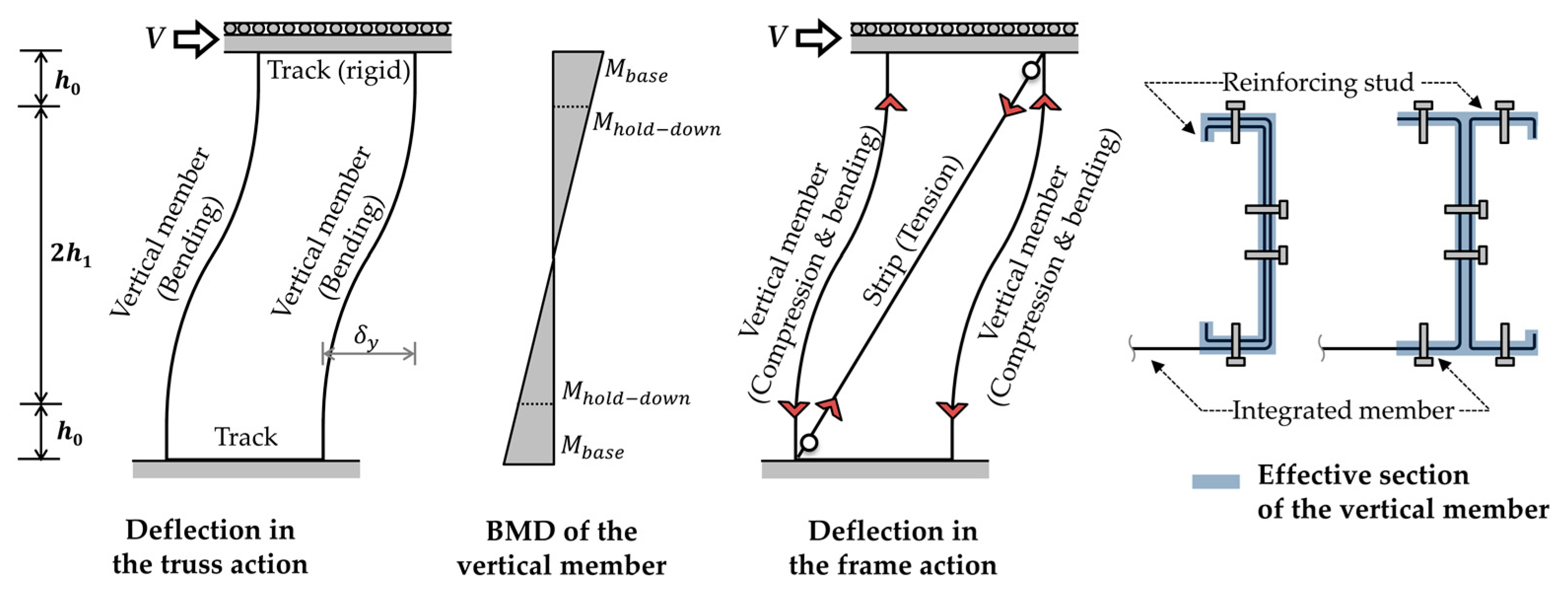
1.3. Nominal Strength of an Integrated Panel Under Combined Bending and Shear According to AISI S100-16
1.4. Objective and Scope of Research
2. Experimental Test
2.1. Test Protocol
2.2. Material Properties
3. Experimental Results
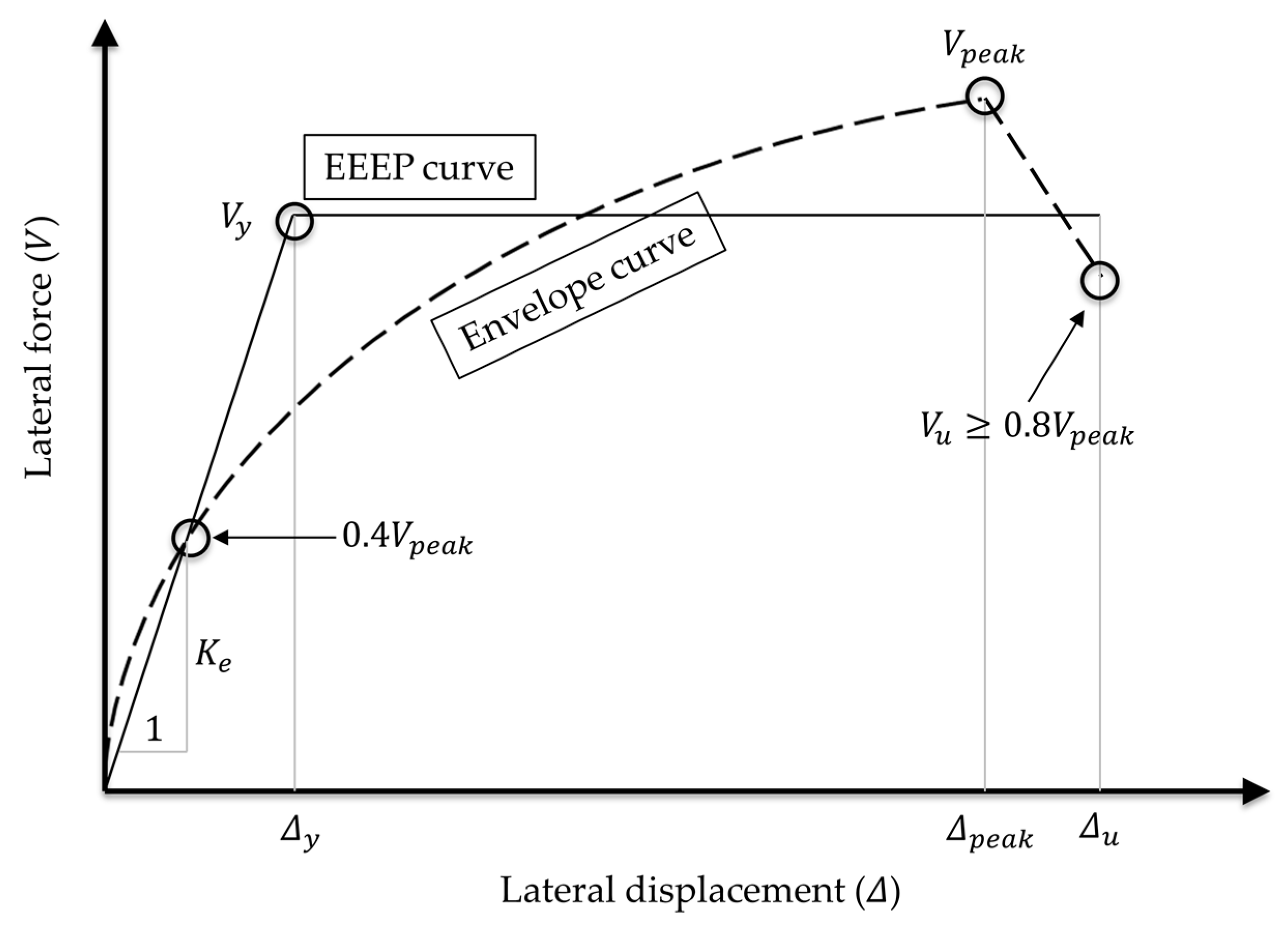
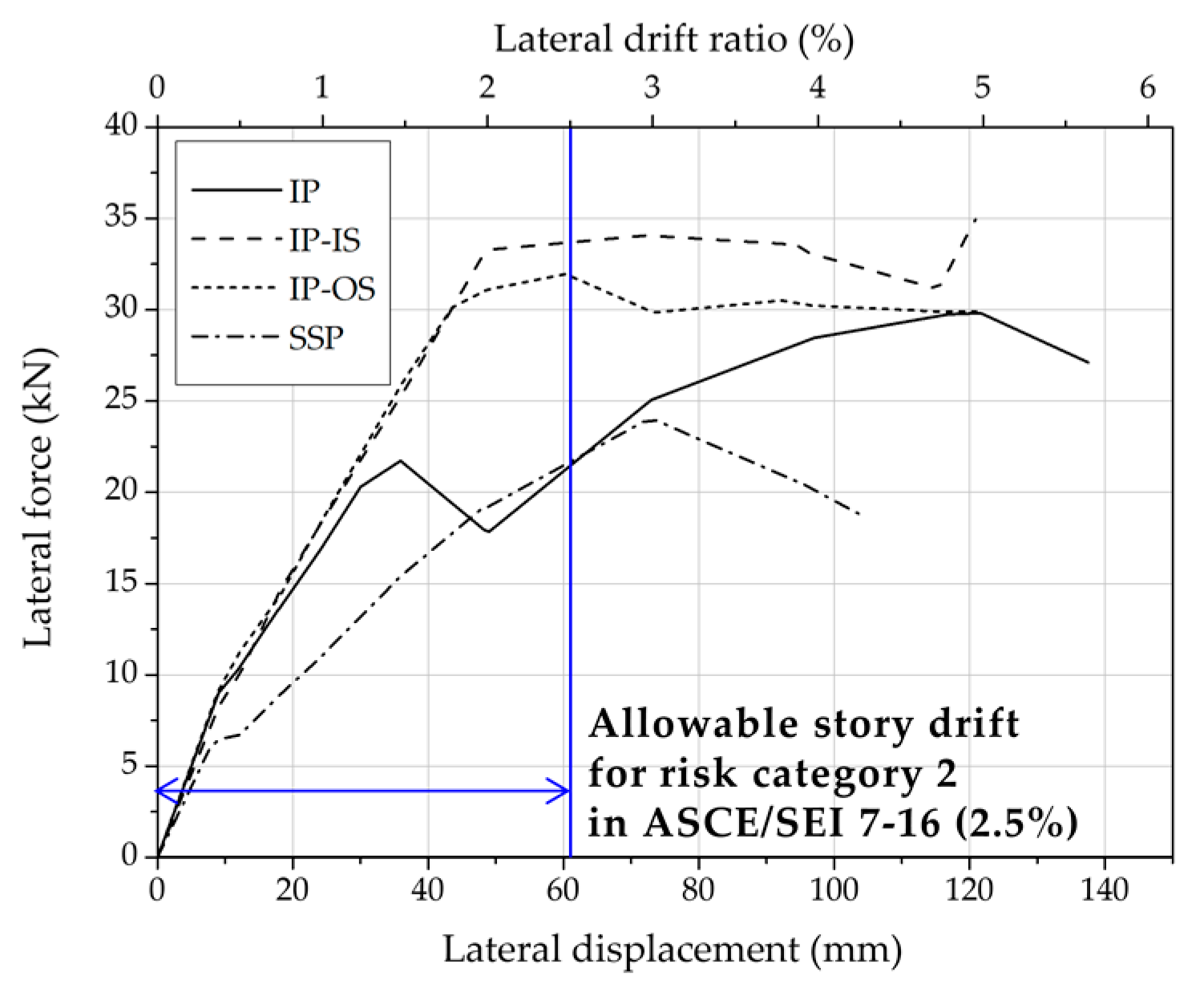
3.1. Lateral Load–Displacement Relationship and Failure Modes
3.2. Analysis and Comparison of Experimental Results
3.2.1. Load-Carrying Capacity
3.2.2. Yield Stiffness
3.2.3. Deformation Capacity
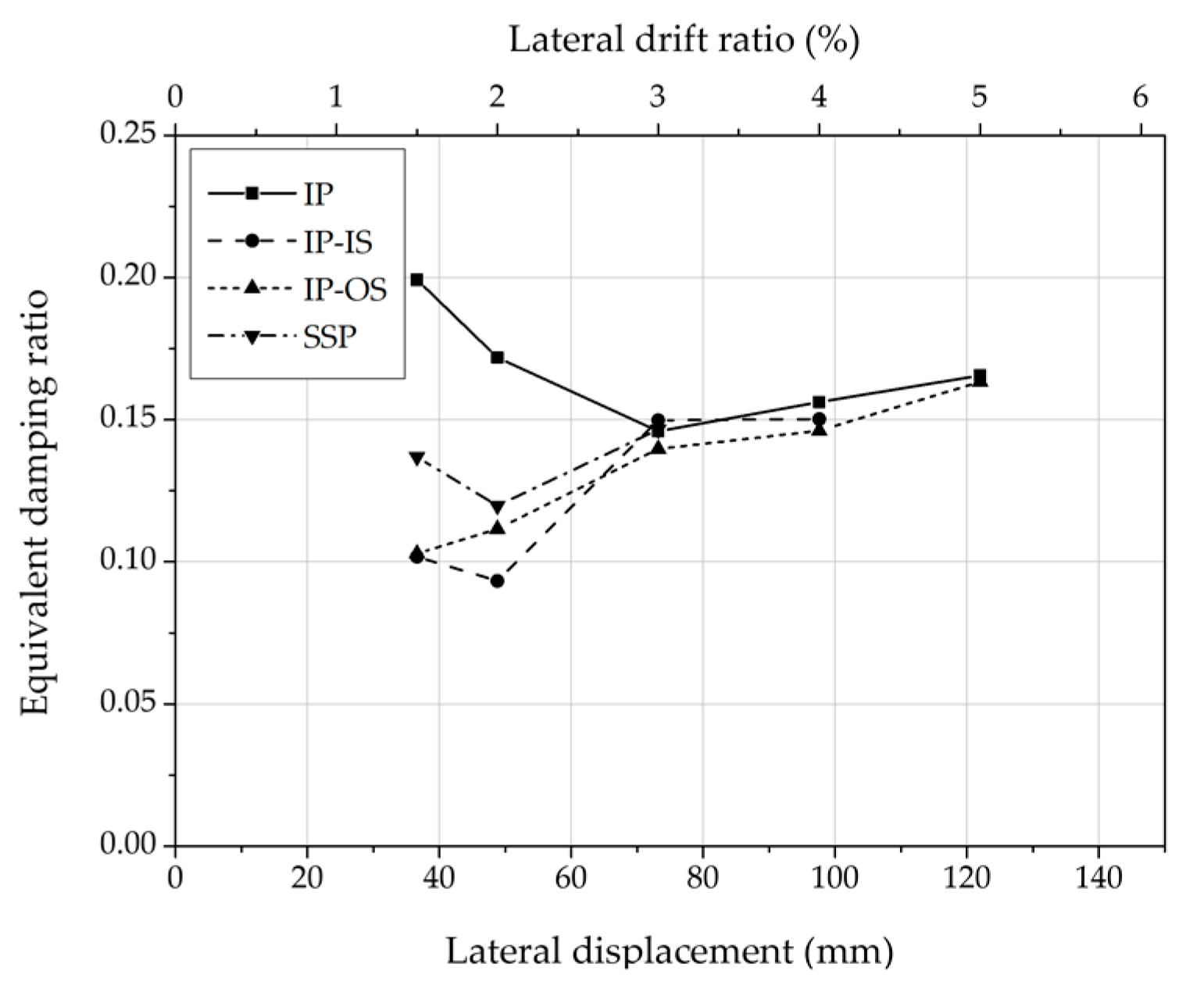
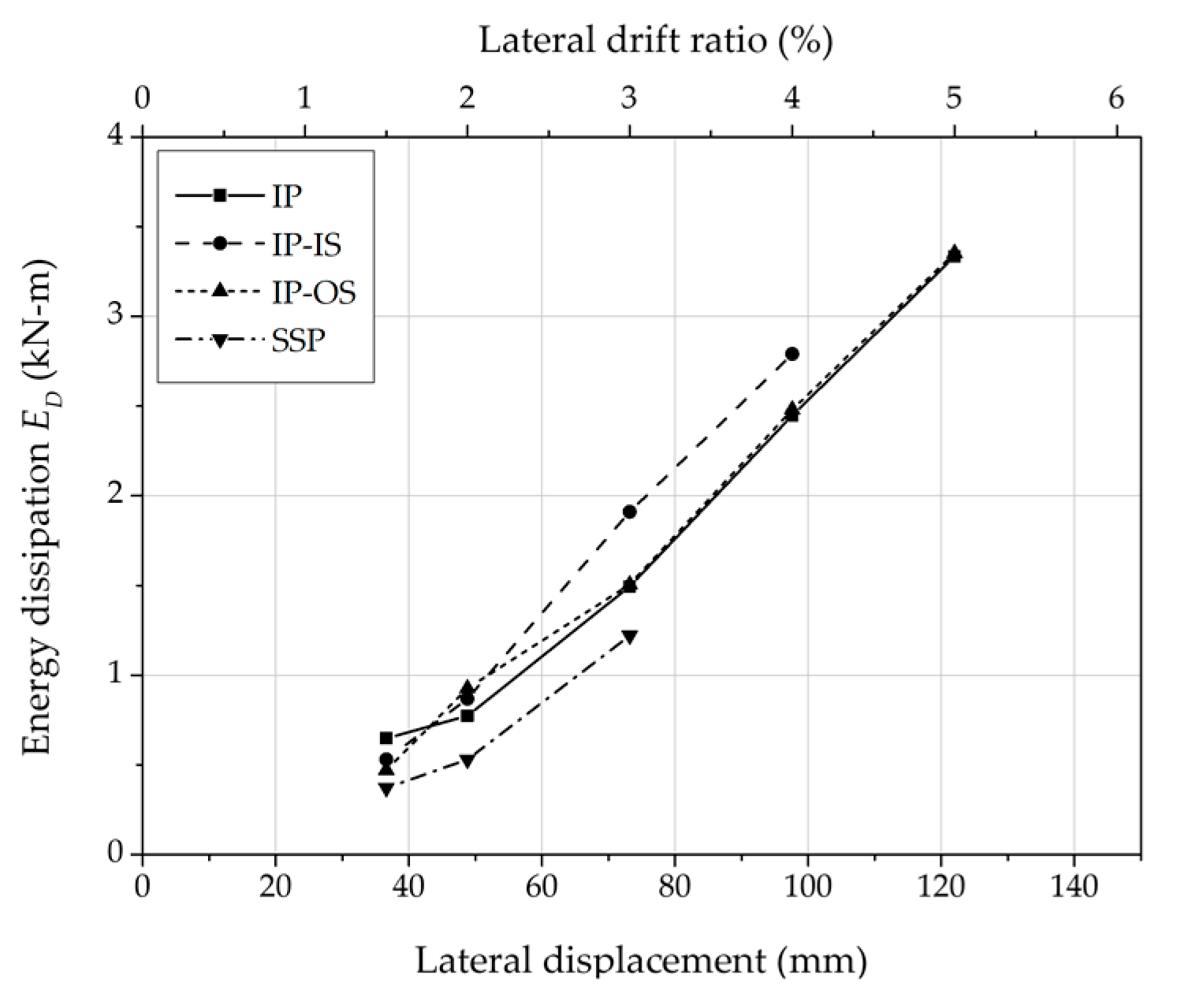
3.2.4. Equivalent Damping Ratio Per Load Cycle
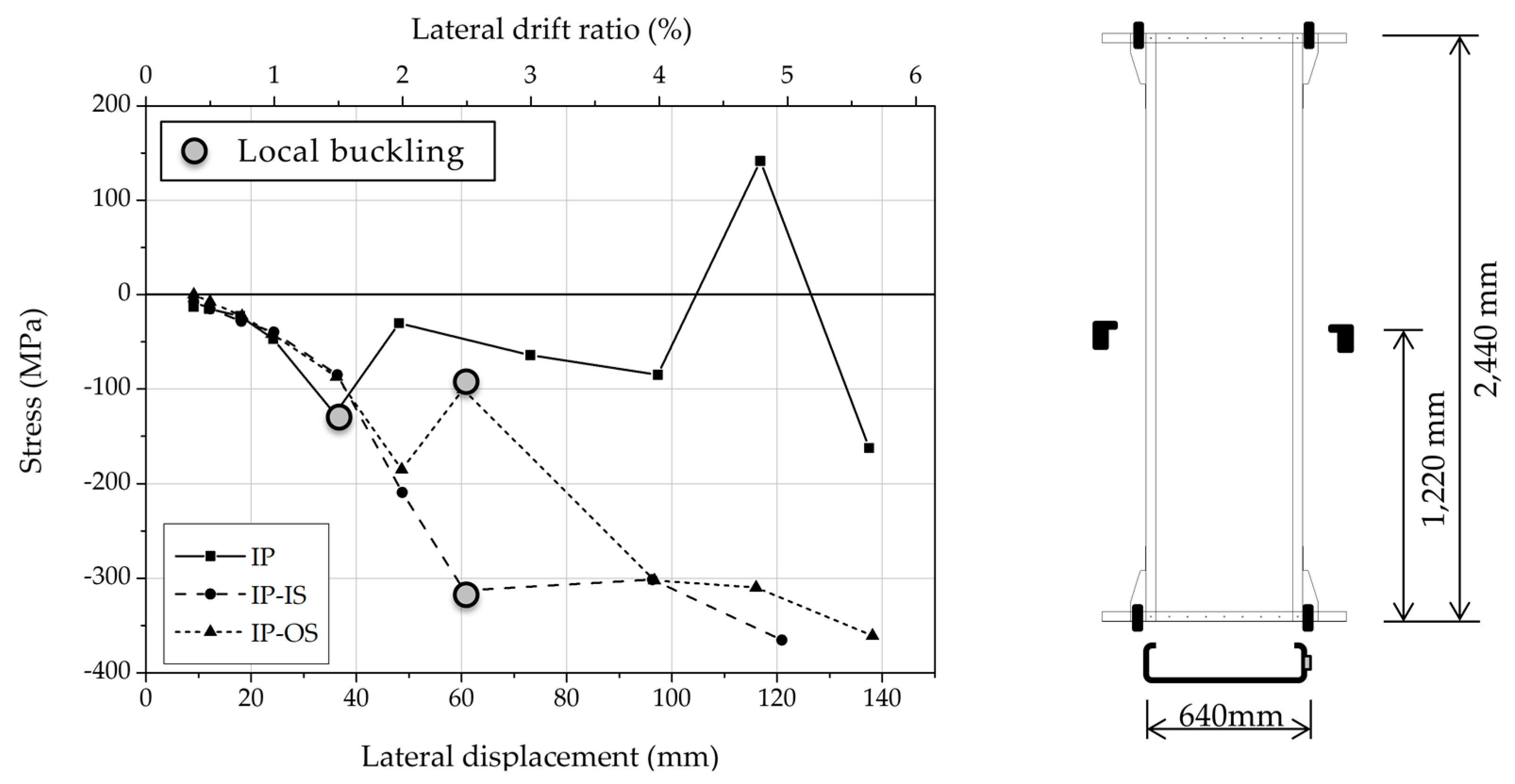
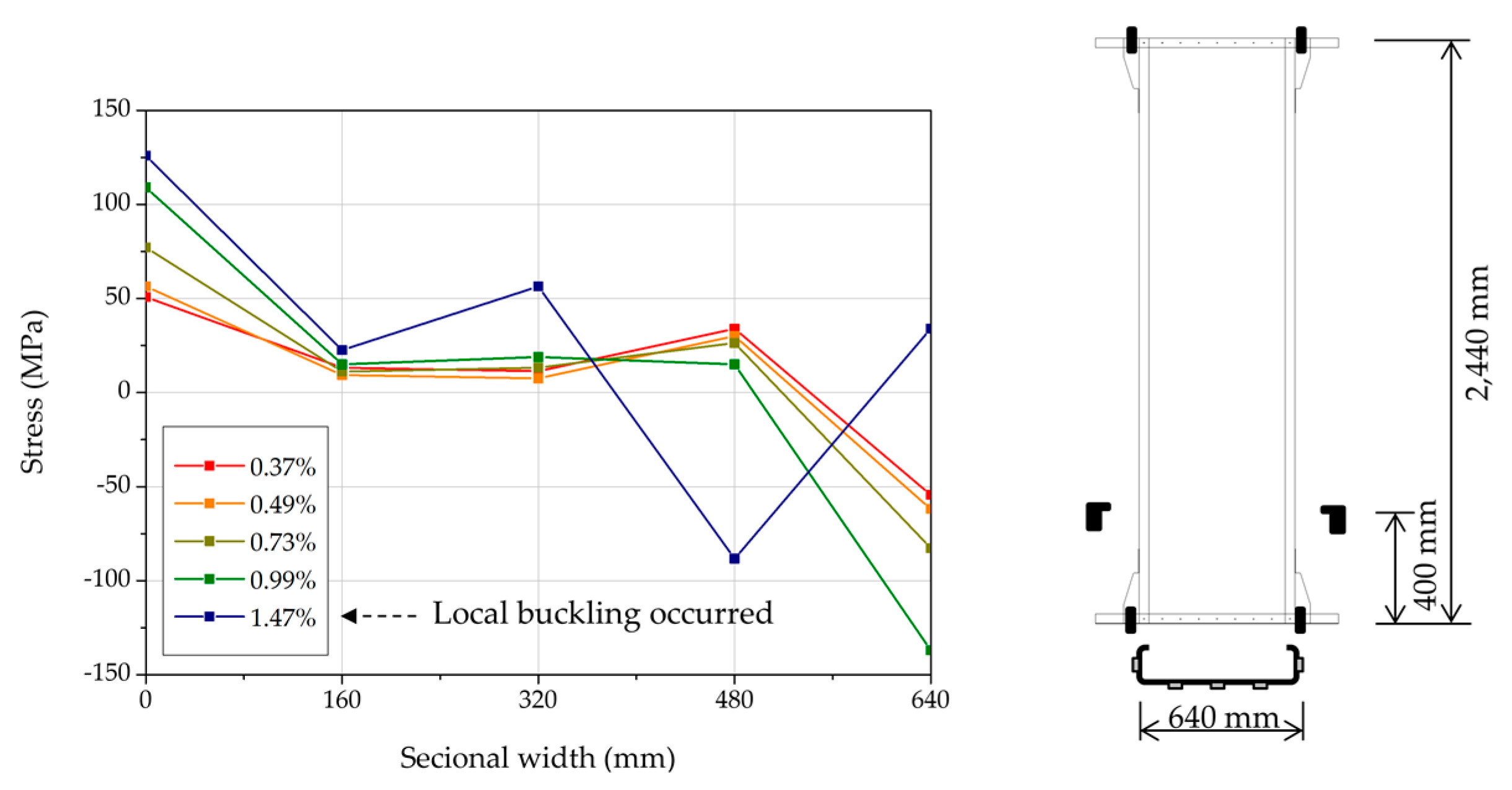
3.2.5. Strain Gauges Attached to the Integrated Member
4. Proposed Method for Calculating Nominal Strength of an Integrated Panel with Reinforced Studs
4.1. Draft Prediction Equation for the Nominal Strength of an Integrated Panel with Reinforced Studs
4.2. Comparison of Prediction Equation and Test Results for the Integrated Panel with Reinforced Studs
5. Summary and Conclusions
- The yield strength , maximum strengths , elastic stiffness , ductility and equivalent damping ratio of SSP, IP, IP-IS and IP-OS specimens were compared. The IP specimen showed better structural performance than the SSP specimen. Considering the allowable story drift, reinforcing integrated members with studs can increase the yield strength, and local buckling occurred at high drift ratios. When reinforcing the integrated member with studs, it is recommended to reinforce the studs inside, not outside of, the integrated member, so that the studs behave in combination.
- Assuming that the integrated member behaves like a cantilever beam, the nominal strengths of the IP, IP-IS and IP-OS specimens were 83%, 145% and 160% of the yield strengths , respectively. The nominal strength of the IP specimens appeared to be similar to the yield strength , although the web slenderness of the integrated member was nearly 400. Since the nominal strength of the stud-reinforced specimens (IP-IS and IP-OS) were 45% and 60% higher than the yield strength , respectively, the assumption that the integrated panel behaves like a cantilever beam, was found to be incorrect.
- To predict the nominal strength of the integrated panel with reinforced stud, a draft prediction equation was proposed. The proposed nominal strength coincided with the average yield strength at the yield displacement when the values of the coefficient that reflects the changes in the effective moment of inertia when loaded are 0.09 and 0.24 in the IS-IS and IP-OS specimens, respectively. The cross-section of the integral member, the cross-section of the reinforcing studs, and the position of the reinforcing studs, are considered to be factors influencing the coefficient . The proposed equation is meaningful, as it reflects the failure aspects of the specimens, such as the location of local buckling. A finite element analysis of the various models may help to accurately define the coefficient .
Author Contributions
Funding
Conflicts of Interest
References
- Chini, S.A.; Gupta, K. A comparison between steel and wood residential framing systems. J. Construct. Educ. Summer 1997, 2, 133–145. [Google Scholar]
- Yang, W.; Yang, Q. Study on the dynamic characteristics of light steel residential structural system. Engineering 2017, 9, 591–598. [Google Scholar] [CrossRef] [Green Version]
- Yong, Y.; Yunpeng, C.; Yongjun, D.; Bin, X.; Xiaoyan, G. Numerical simulation of the cold-formed thin-walled steel structure system. Build. Struct. 2011, 2, 41–45. [Google Scholar]
- Barton, A.D. Performance of Steel Framed Domestic Structures Subject to Earthquake Loads. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 1997. [Google Scholar]
- Von Karman, T. The strength of thin plates in compression. Trans. ASME 1932, 54, 53–57. [Google Scholar]
- Winter, G. Strength of thin steel compression flanges. Trans. ASCE 1947, 112, 527. [Google Scholar]
- AISI S100. North American Specification for the Design of Cold-Formed Steel Structural Members; American Iron and Steel Institute: Washington, DC, USA, 2016. [Google Scholar]
- Winter, G. Commentary on the 1968 Edition of the Specification for the Design of Cold-Formed Steel Structural Members; American Iron and Steel Institute: New York, NY, USA, 1970. [Google Scholar]
- LaBoube, R.A.; Yu, W.W. Structural behavior of beam webs subjected primarily to shear stress. In Civil Eng. Study Struct. Ser.; Department of Civil Engineering, University of Missouri: Rolla, MS, USA, 1978; Volume 78–2. [Google Scholar]
- LaBoube, R.A.; Yu, W.W. Structural behavior of beam webs subjected to a combination of bending and shear. In Civil Eng. Study Struct. Ser.; Department of Civil Engineering, University of Missouri: Rolla, MS, USA, 1978; Volume 78–3. [Google Scholar]
- LaBoube, R.A.; Yu, W.W. Bending strength of webs of cold-formed steel beams. J. Struct. Divis. 1982, 108, 1589–1604. [Google Scholar]
- Hetrakul, N.; Yu, W.W. Structural behavior of beam webs subjected to web crippling and a combination of web crippling and bending. In Civil Eng. Study Struct. Ser.; Department of Civil Engineering, University of Missouri: Rolla, MS, USA, 1978; Volume 78–4. [Google Scholar]
- Hetrakul, N.; Yu, W.W. Cold formed steel I-beams subjected to combined bending and web crippling. In Proceedings of the International Conference (2nd ed.), University of Strathclyde, Glasgow, UK, 3–6 April 1979; pp. 413–426. [Google Scholar]
- Phung, N.; Yu, W.W. Structural behavior of longitudinally reinforced beam webs. In Civil Eng. Study Struct. Ser.; Department of Civil Engineering, University of Missouri: Rolla, MS, USA, 1978; Volume 78–6. [Google Scholar]
- Phung, N.; Yu, W.W. Structural behavior of transversely reinforced beam webs. In Civil Eng. Study Struct. Ser.; Department of Civil Engineering, University of Missouri: Rolla, MS, USA, 1978; Volume 78–5. [Google Scholar]
- DaBreo, J.; Rogers, C.A. Steel Sheathed Shear Walls Subjected to Combined Lateral and Gravity Loads; Department of Civil Engineering and Applied Mechanics, McGill University: Montreal, Canada, 2012. [Google Scholar]
- DaBreo, J.; Balh, N.; Ong-Tone, C.; Rogers, C.A. Steel sheathed cold-formed steel framed shear walls subjected to lateral and gravity loading. Thin-Walled Struct. 2014, 74, 232–245. [Google Scholar] [CrossRef]
- Ong-Tone, C. Tests and Evaluation of Cold-Formed Steel Frame; Department of Civil Engineering and Applied Mechanics, McGill University: Montreal, Australia, 2009. [Google Scholar]
- Rogers, C.A.; Balh, N.; Ong-Tone, C.; Shamim, I.; DaBreo, J. Development of seismic design provisions for steel sheet sheathed shear walls. In Proceedings of the Structures Congress 2011, Las Vegas, NV, USA, 14–16 April 2011; pp. 676–687. [Google Scholar]
- Hong, S.G.; Cho, B.H.; Chung, K.S.; Moon, J.H. Behavior of framed modular building system with double skin steel panels. J. Construct. Steel Res. 2011, 67, 936–946. [Google Scholar] [CrossRef]
- Tian, H.W.; Li, Y.Q.; Yu, C. Testing of steel sheathed cold-formed steel trussed shear walls. Thin-Walled Struct. 2015, 94, 280–292. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Xiao, Y.; Yu, B. Cyclic test and numerical analytical assessment of cold-formed thin-walled steel shear walls using tube truss. Thin-Walled Struct. 2019, 134, 442–459. [Google Scholar] [CrossRef]
- AISI. Specification for the Design of Cold-formed Steel Structural Members; American Iron and Steel Institute: Washington, DC, USA, 1989. [Google Scholar]
- Zeynalian, M.; Ronagh, H.R.; Hatami, S. Seismic characteristics of K-braced cold-formed steel shear walls. J. Construct. Steel Res. 2012, 77, 23–31. [Google Scholar] [CrossRef]
- Mirzaei, A.; Sangree, R.H.; Velchev, K.; Comeau, G.; Balh, N.; Rogers, C.A.; Schafer, B.W. Seismic capacity-based design of narrow strap-braced cold-formed steel walls. J. Construct. Steel Res. 2015, 115, 81–91. [Google Scholar] [CrossRef]
- Moghimi, H.; Ronagh, H.R. Performance of light-gauge cold-formed steel strap-braced stud walls subjected to cyclic loading. Eng. Struct. 2009, 31, 69–83. [Google Scholar] [CrossRef]
- AISI S213. North American Standard for Cold-Formed Steel framing—Lateral Design; American Iron and Steel Institute: Washington, DC, USA, 2009. [Google Scholar]
- Clark, P.; Frank, K.; Krawinkler, H.; Shaw, R. Protocol for Fabrication, Inspection, Testing, and Documentation of Beam-Column Connection Tests and Other Experimental Specimens; Rep. No. SAC/BD-97; SAC Joint Venture: Berkeley, CA, USA, 1997. [Google Scholar]
- ASTM E2126-19. Standard Test Methods for Cyclic (Reversed) Load Test for Shear Resistance of Vertical Elements of the Lateral Force Resisting Systems for Buildings; ASTM International: West Conshohocken, PA, USA, 2019. [Google Scholar]
- Yanagi, N.; Yu, C. Effective strip method for the design of cold-formed steel framed shear wall with steel sheet sheathing. J. Struct. Eng. 2013, 140, 04013101. [Google Scholar] [CrossRef]
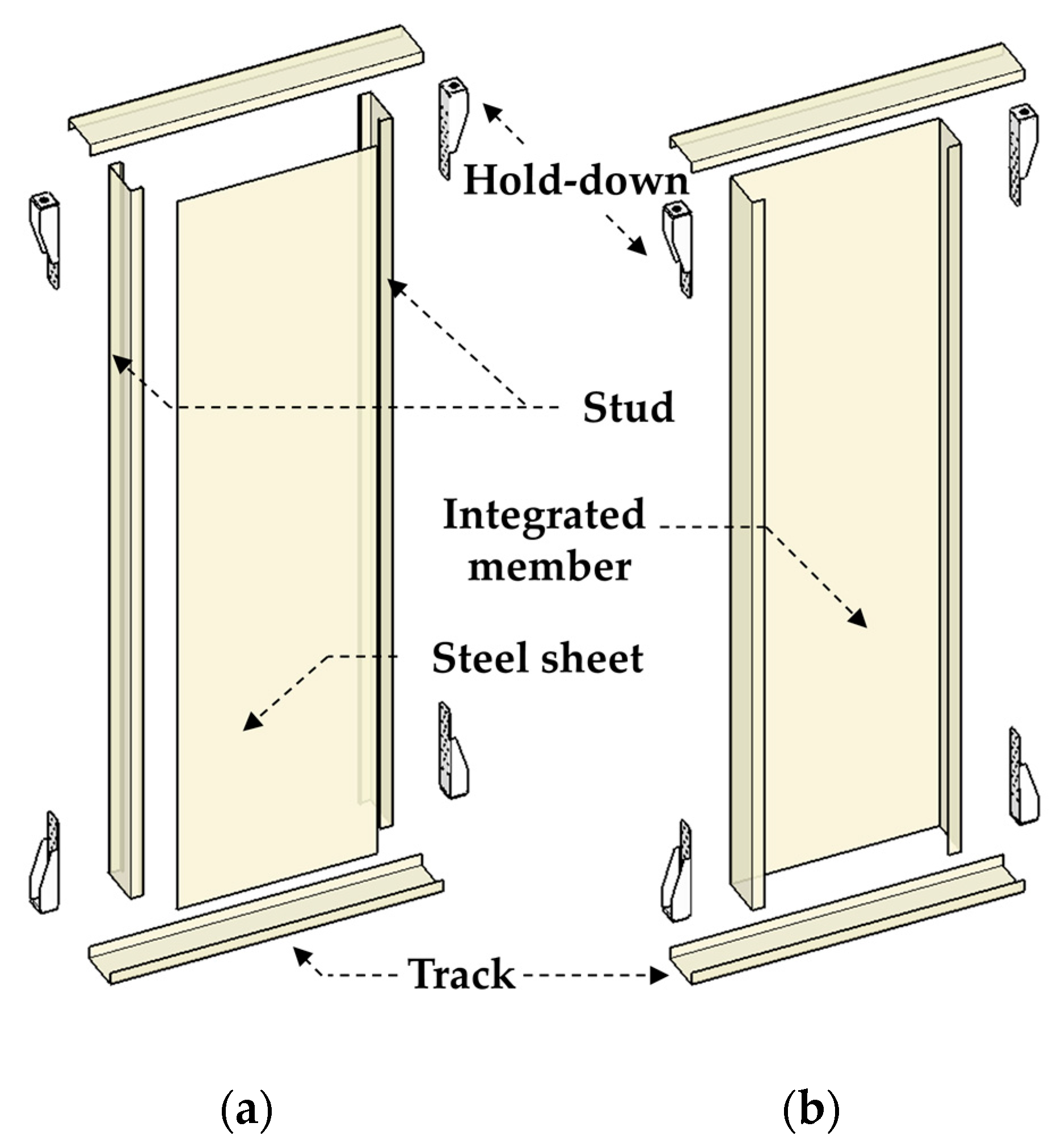


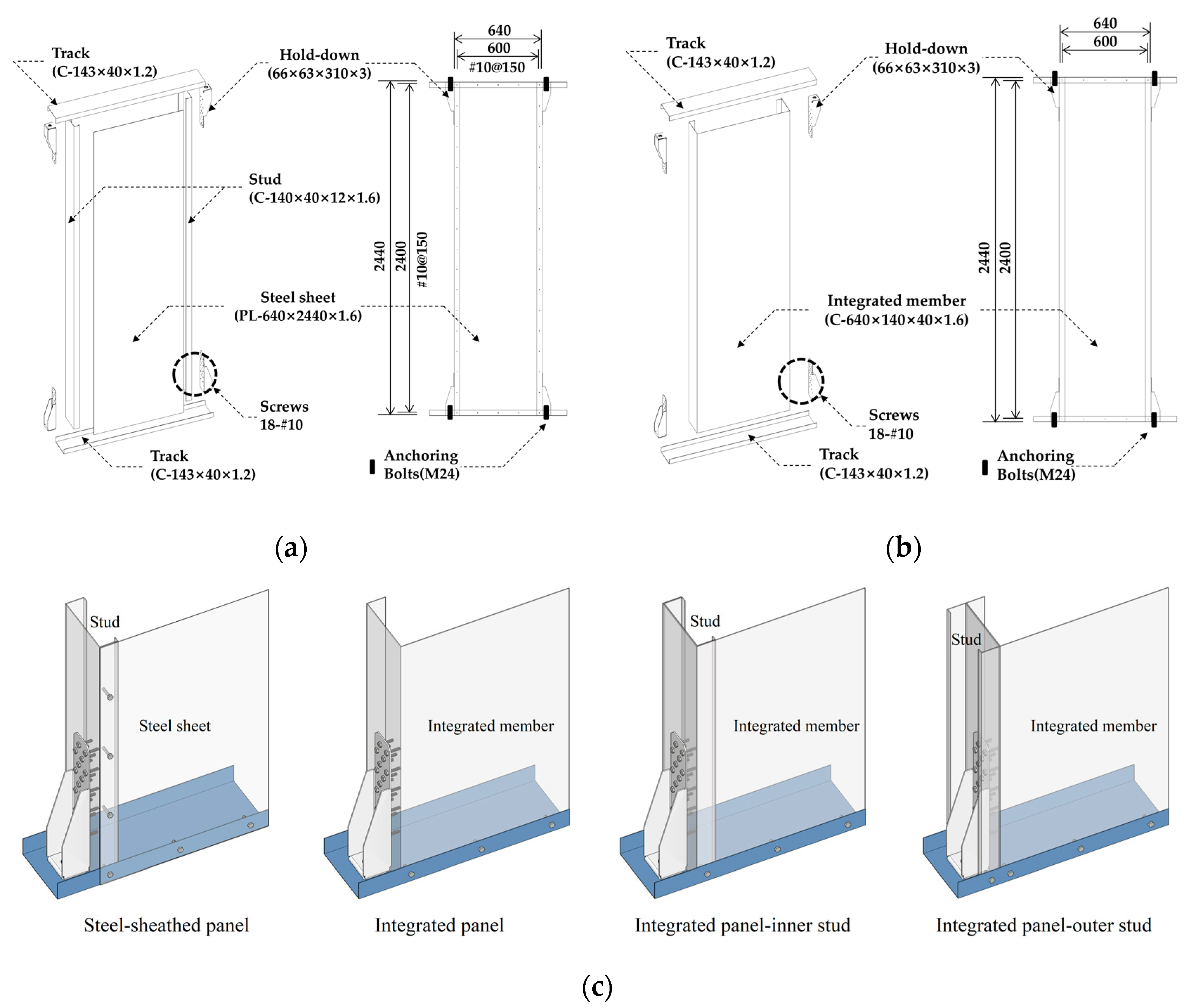




| Specimens | Main Component | Stud |
|---|---|---|
| SSP (Steel-sheathed panel) | Steel sheet (PL – 640 × 2440 × 1.6) | C – 140 × 40 × 12 × 1.6 |
| IP (integrated panel) | Integrated member (C – 640 × 140 × 40 × 1.6) | - |
| IP-IS (integrated panel-inner stud) | Inner Stud (C – 137 × 40 × 12 × 1.6) | |
| IP-OS (integrated panel-outer stud) | Outer Stud (C – 140 × 40 × 12 × 1.6) |
| Steel | Number of Coupon Tests | Thickness (mm) | Maximum Yield/Tensile Strengths (MPa) | Minimum Yield/Tensile Strengths (MPa) | Average Yield/Tensile Strengths (MPa) |
|---|---|---|---|---|---|
| Track | 3 | 1.2 | 324.4/352.6 | 323.6/352.3 | 323.9/352.4 |
| Integrated member, steel sheet, and stud | 3 | 1.6 | 324.6/375.0 | 323.1/374.9 | 324.0/374.9 |
| Specimens | Test Results | Prediction | Comparison | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (kN) | (kN) | (mm (%)) | (mm (%)) | (mm (%)) | (kN/mm) | (kN) | ||||
| SSP | + | 20.1 | 23.5 | 49.7 (2.0) | 72.8 (3.0) | 103.7 (4.3) | 0.40 | 2.09 | - | - |
| - | 23.9 | 24.6 | 46.0 (1.9) | 73.0 (3.0) | 81.2 (3.3) | 0.52 | 1.76 | |||
| IP | + | 23.7 | 28.1 | 38.1 (1.6) | 120.0 (4.9) | 137.5 (5.6) | 0.62 | 3.61 | 20.6 | 0.87 |
| - | 26.2 | 31.8 | 27.1 (1.1) | 124.4 (5.1) | 121.6 (5.0) | 0.97 | 4.48 | 0.79 | ||
| IP-IS | + | 34.4 | 36.9 | 52.7 (2.2) | 61.8 (2.5) | 120.9 (5.0) | 0.65 | 2.29 | 48.1 | 1.40 |
| - | 32.1 | 34.9 | 36.4 (1.5) | 48.7 (2.0) | 115.4 (4.7) | 0.88 | 3.17 | 1.50 | ||
| IP-OS | + | 29.9 | 32.6 | 50.9 (2.1) | 61.6 (2.5) | 138.2 (5.7) | 0.59 | 2.72 | 48.4 | 1.62 |
| - | 30.6 | 35.0 | 26.6 (1.1) | 44.1 (1.8) | 121.0 (5.0) | 1.15 | 4.55 | 1.58 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-Y.; Cho, B.-H.; Jung, D.-I.; Lee, J.-S.; Lee, K.-W. Experimental Study on the Cyclic Behavior of Integrated Panels for Cold-Formed Steel Shear Wall System. Appl. Sci. 2020, 10, 1649. https://doi.org/10.3390/app10051649
Lee D-Y, Cho B-H, Jung D-I, Lee J-S, Lee K-W. Experimental Study on the Cyclic Behavior of Integrated Panels for Cold-Formed Steel Shear Wall System. Applied Sciences. 2020; 10(5):1649. https://doi.org/10.3390/app10051649
Chicago/Turabian StyleLee, Doo-Yong, Bong-Ho Cho, Dam-I Jung, Jae-Sub Lee, and Keun-Woo Lee. 2020. "Experimental Study on the Cyclic Behavior of Integrated Panels for Cold-Formed Steel Shear Wall System" Applied Sciences 10, no. 5: 1649. https://doi.org/10.3390/app10051649
APA StyleLee, D.-Y., Cho, B.-H., Jung, D.-I., Lee, J.-S., & Lee, K.-W. (2020). Experimental Study on the Cyclic Behavior of Integrated Panels for Cold-Formed Steel Shear Wall System. Applied Sciences, 10(5), 1649. https://doi.org/10.3390/app10051649





