An Exact Method for Calculating the Eigenvector Sensitivities
Abstract
1. Introduction
2. The Classical Exact Methods
2.1. Modal Superposition Method
2.2. Nelson’s Method
3. The New Exact Method for Eigenvector Sensitivities
4. Numerical Examples
4.1. A Truss Structure
4.2. A Spring-Mass System
4.3. A System with Similar Eigenvalues
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| , | structural stiffness and mass matrices |
| , | the th eigenvalue and eigenvector |
| the th design parameters | |
| the number of degrees of freedom | |
| , | the first-order eigenvalue and eigenvector sensitivities |
| , | the second-order eigenvalue and eigenvector sensitivities |
References
- Soong, T.; Michalakis, C. (Eds.) Passive and Active Structural Vibration Control in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 345. [Google Scholar]
- El-Ganaini, W.A. Duffing Oscillator Vibration Control via Suspended Pendulum. Appl. Math. Inf. Sci. 2018, 12, 203–215. [Google Scholar] [CrossRef]
- Li, N.; Zheng, Z.; Tian, Y.; Sun, J.-Y.; He, X.-T.; Lu, Y. Stochastic nonlinear vibration and reliability of orthotropic membrane structure under impact load. Thin-Walled Struct. 2017, 119, 247–255. [Google Scholar] [CrossRef]
- Hamed, Y.S.; Alharthi, M.R.; AlKhathami, H.K. Active Vibration Control of a Dynamical System Subjected to Simultaneous Excitation Forces. Int. J. Appl. Eng. Res. 2017, 12, 434–442. [Google Scholar]
- Saidi, A.; Zizouni, K.; Kadri, B.; Fali, L.; Bousserhane, I.K. Adaptive Sliding Mode Control for Semi-Active Structural Vibration Control. Stud. Inform. Control. 2019, 28, 371–380. [Google Scholar] [CrossRef]
- Yong, W. Research Status and Prospect of Structural Vibration Control. Int. Core J. Eng. 2019, 5, 142–144. [Google Scholar]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient optimization design method using kriging model. J. Aircr. 2005, 42, 413–420. [Google Scholar] [CrossRef]
- Lingyun, W.; Mei, Z.; Guangming, W. Truss optimization on shape and sizing with frequency constraints based on genetic algorithm. Comput. Mech. 2005, 35, 361–368. [Google Scholar] [CrossRef]
- Yang, Q.W. Fast and Exact Algorithm for Structural Static Reanalysis Based on Flexibility Disassembly Perturbation. AIAA J. 2019, 57, 3599–3607. [Google Scholar] [CrossRef]
- Bartilson, D.T.; Jang, J.; Smyth, A.W. Finite element model updating using objective-consistent sensitivity-based parameter clustering and Bayesian regularization. Mech. Syst. Signal Process. 2019, 114, 328–345. [Google Scholar] [CrossRef]
- Yu, K.; Liang, P.; Silva, T.; Yu, K.; Mottershead, J. Parameter selection for model updating with global sensitivity analysis. Mech. Syst. Signal Process. 2019, 115, 483–496. [Google Scholar]
- Altunişik, A.C.; Karahasan, O.Ş.; Genç, A.F.; Okur, F.Y.; Gunaydin, M.; Adanur, S. Sensitivity-Based Model Updating of Building Frames using Modal Test Data. KSCE J. Civ. Eng. 2018, 22, 4038–4046. [Google Scholar]
- Deng, Z.; Guo, Z. Interval identification of structural parameters using interval overlap ratio and Monte Carlo simulation. Adv. Eng. Softw. 2018, 121, 120–130. [Google Scholar] [CrossRef]
- Rubio, P.-B.; Louf, F.; Chamoin, L. Fast model updating coupling Bayesian inference and PGD model reduction. Comput. Mech. 2018, 62, 1485–1509. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, C.; Li, N.; Wang, W.; Liu, Y. Enhanced Singular Value Truncation Method for Non-Destructive Evaluation of Structural Damage Using Natural Frequencies. Materials 2019, 12, 1021. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.W. A mixed sensitivity method for structural damage detection. Commun. Numer. Methods Eng. 2009, 25, 381–389. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, J. A coupled method for structural damage identification. J. Sound Vib. 2006, 296, 401–405. [Google Scholar] [CrossRef]
- Fox, R.L.; Kapoor, M.P. Rates of change of eigenvalues and eigenvectors. AIAA J. 1968, 6, 2426–2429. [Google Scholar] [CrossRef]
- Nelson, R.B. Simplified calculation of eigenvector derivatives. AIAA J. 1976, 14, 1201–1205. [Google Scholar] [CrossRef]
- Lim, K.B.; Junkins, J.L.; Wang, B.P. Re-examination of eigenvector derivatives. J. Guid. Control. Dyn. 1987, 10, 581–587. [Google Scholar] [CrossRef]
- Zhang, O.; Zerva, A. Iterative method for calculating derivatives of eigenvectors. AIAA J. 1996, 34, 1088–1090. [Google Scholar] [CrossRef]
- Zhang, O.; Zerva, A. Accelerated iterative procedure for calculating eigenvector derivatives. AIAA J. 1997, 35, 340–348. [Google Scholar] [CrossRef]
- Balmes, E. Efficient sensitivity analysis based on finite element model reduction. In Proceedings of the 16th International Modal Analysis Conference, Santa Barbara, CA, USA, 8 February 1998. [Google Scholar]
- Zeng, Q.-H. Highly accurate modal method for calculating eigenvector derivatives in viscous damping systems. AIAA J. 1995, 33, 746–751. [Google Scholar] [CrossRef]
- Sondipon, A. Derivative of eigensolutions of nonviscously damped linear systems. AIAA J. 2002, 40, 2061–2069. [Google Scholar]
- Adhikari, S. Calculation of derivative of complex modes using classical normal modes. Comput. Struct. 2000, 77, 625–633. [Google Scholar] [CrossRef]
- Van Der Aa, N.P.; Ter Morsche, H.G.; Mattheij, R.R. Computation of eigenvalue and eigenvector derivatives for a general complex-valued eigensystem. Electron. J. Linear Algebra 2007, 16, 1. [Google Scholar] [CrossRef]
- Lin, R.M.; Lim, M.K. Structural sensitivity analysis via reduced-order analytical model. Comput. Methods Appl. Mech. Eng. 1995, 121, 345–359. [Google Scholar] [CrossRef]
- Lin, R.M.; Wang, Z.; Lim, M.K. A practical algorithm for the efficient computation of eigenvector sensitivities. Comput. Methods Appl. Mech. Eng. 1996, 130, 355–367. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I. Calculation of eigensolution derivatives for nonviscously damped systems. AIAA J. 2006, 44, 1799–1806. [Google Scholar] [CrossRef]
- Wu, B.; Xu, Z.; Li, Z. Improved Nelson’s Method for computing eigenvector derivatives with distinct and repeated eigenvalues. AIAA J. 2007, 45, 950–952. [Google Scholar] [CrossRef]
- Guedria, N.; Chouchane, M.; Smaoui, H. Second-order eigensensitivity analysis of asymmetric damped systems using Nelson’s method. J. Sound Vib. 2007, 300, 974–992. [Google Scholar] [CrossRef]
- Wang, P.; Dai, H. Calculation of eigenpair derivatives for asymmetric damped systems with distinct and repeated eigenvalues. Int. J. Numer. Methods Eng. 2015, 103, 501–515. [Google Scholar] [CrossRef]
- Wang, P.; Dai, H. Eigensensitivity of symmetric damped systems with repeated eigenvalues by generalized inverse. J. Eng. Math. 2016, 96, 201–210. [Google Scholar] [CrossRef]
- Ruiz, D.; Bellido, J.; Donoso, A. Eigenvector sensitivity when tracking modes with repeated eigenvalues. Comput. Methods Appl. Mech. Eng. 2017, 326, 338–357. [Google Scholar] [CrossRef]
- Lin, R.; Ng, T. Eigenvalue and eigenvector derivatives of fractional vibration systems. Mech. Syst. Signal Process. 2019, 127, 423–440. [Google Scholar] [CrossRef]
- Friswell, M.I. Calculation of second and higher order eigenvector derivatives. J. Guid. Control. Dyn. 1995, 18, 919–921. [Google Scholar] [CrossRef]
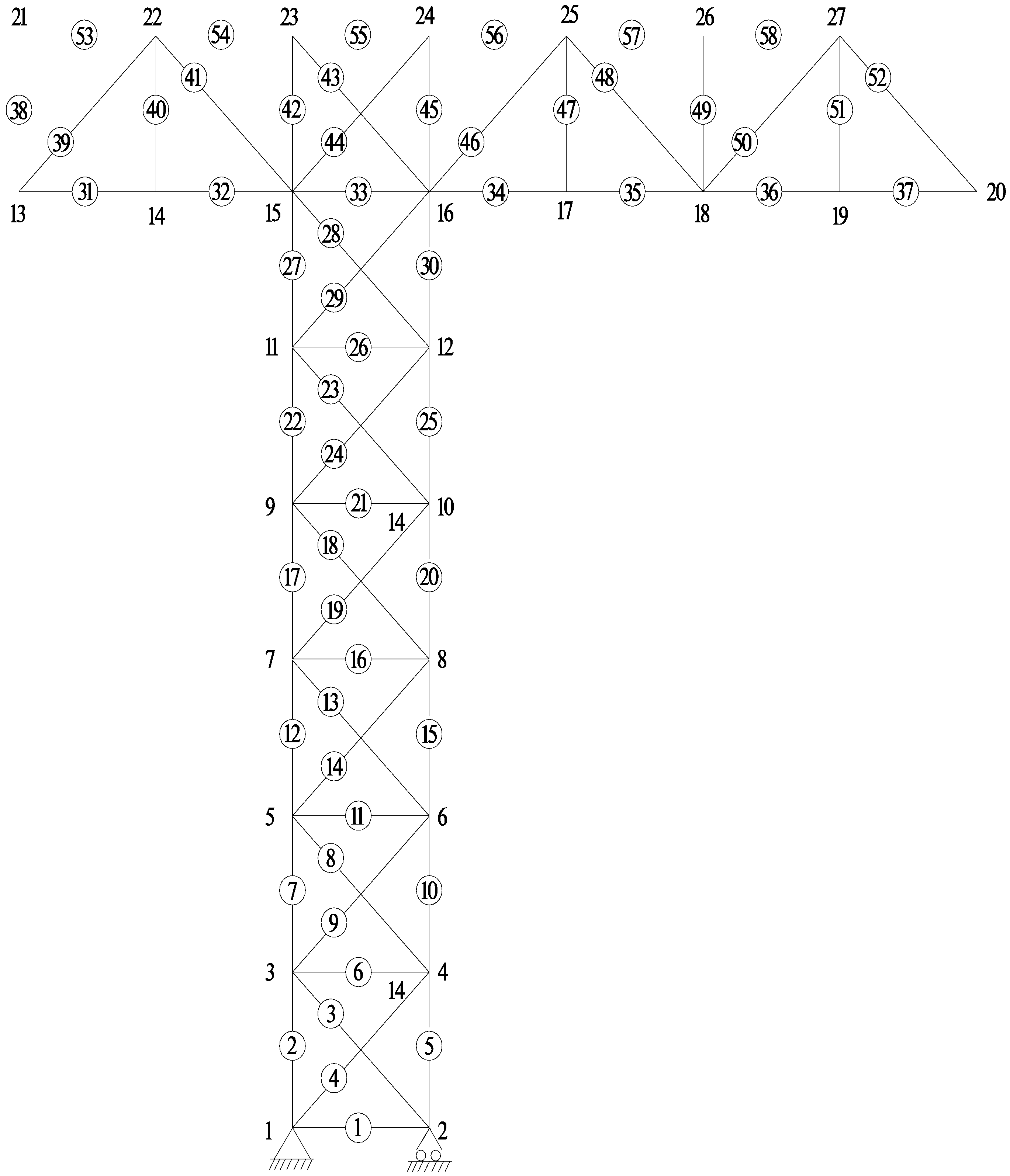
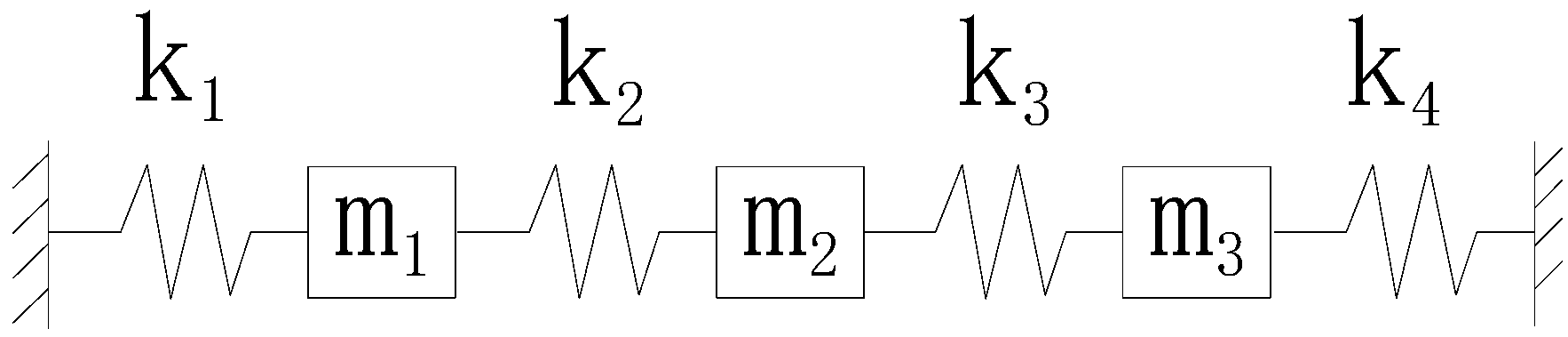
| DOF Number | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.3 | 0.3 | −0.5 | −0.5 | −0.1 | −0.1 | 0.1 | 0.1 |
| 2 | 0.1 | 0.1 | 1.1 | 1.1 | 0.4 | 0.4 | 0.5 | 0.5 |
| 3 | −0.0 | −0.0 | 3 | 3 | −0.1 | −0.1 | 0.1 | 0.1 |
| 4 | 0.1 | 0.1 | 0.8 | 0.8 | 0.3 | 0.3 | 0.6 | 0.6 |
| 5 | −0.0 | −0.0 | 0.3 | 0.3 | −0.1 | −0.1 | 0.1 | 0.1 |
| 6 | 0.1 | 0.1 | 2.9 | 2.9 | 0.3 | 0.3 | 0.5 | 0.5 |
| 7 | −0.0 | −0.0 | 2.4 | 2.4 | −0.1 | −0.1 | 0.1 | 0.1 |
| 8 | 0.1 | 0.1 | 2.9 | 2.9 | 0.3 | 0.3 | 0.5 | 0.5 |
| 9 | −0.0 | −0.0 | 0.9 | 0.9 | −0.1 | −0.1 | 0.1 | 0.1 |
| 10 | 0.1 | 0.1 | 3.8 | 3.8 | 0.3 | 0.3 | 0.4 | 0.4 |
| 11 | −0.0 | −0.0 | 1.9 | 1.9 | −0.1 | −0.1 | 0.1 | 0.1 |
| 12 | 0.1 | 0.1 | 3.7 | 3.7 | 0.3 | 0.3 | 0.4 | 0.4 |
| 13 | −0.0 | −0.0 | 1.4 | 1.4 | −0.1 | −0.1 | 0.1 | 0.1 |
| 14 | 0.1 | 0.1 | 3.7 | 3.7 | 0.2 | 0.2 | 0.3 | 0.3 |
| 15 | −0.0 | −0.0 | 1.6 | 1.6 | −0.1 | −0.1 | 0.1 | 0.1 |
| 16 | 0.1 | 0.1 | 3.7 | 3.7 | 0.2 | 0.2 | 0.3 | 0.3 |
| 17 | −0.0 | −0.0 | 1.8 | 1.8 | −0.0 | −0.0 | 0.1 | 0.1 |
| 18 | 0.1 | 0.1 | 3.0 | 3.0 | 0.2 | 0.2 | 0.2 | 0.2 |
| 19 | −0.0 | −0.0 | 1.3 | 1.3 | −0.1 | −0.1 | 0.0 | 0.0 |
| 20 | 0.1 | 0.1 | 3.0 | 3.0 | 0.2 | 0.2 | 0.2 | 0.2 |
| DOF Number | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 1.5 | −1.1 | −1.1 | −0.5 | −0.5 | 0.8 | 0.8 |
| 2 | 0.8 | 0.8 | 1.3 | 1.3 | 2.3 | 2.3 | 3.6 | 3.6 |
| 3 | −0.2 | −0.2 | 5.5 | 5.5 | −0.6 | −0.6 | 0.6 | 0.6 |
| 4 | 0.7 | 0.7 | 0.5 | 0.5 | 1.8 | 1.8 | 4.4 | 4.4 |
| 5 | −0.2 | −0.2 | 1.2 | 1.2 | −0.4 | −0.4 | 1.1 | 1.1 |
| 6 | 0.6 | 0.6 | 3.0 | 3.0 | 1.7 | 1.7 | 3.3 | 3.3 |
| 7 | −0.2 | −0.2 | 4.1 | 4.1 | −0.7 | −0.7 | 0.3 | 0.3 |
| 8 | 0.6 | 0.6 | 3.1 | 3.1 | 1.8 | 1.8 | 3.2 | 3.2 |
| 9 | −0.1 | −0.1 | 2.9 | 2.9 | −0.3 | −0.3 | 1.1 | 1.1 |
| 10 | 0.4 | 0.4 | 2.5 | 2.5 | 1.3 | 1.3 | 2.2 | 2.2 |
| 11 | −0.3 | −0.3 | 3.1 | 3.1 | −0.8 | −0.8 | 0.2 | 0.2 |
| 12 | 0.5 | 0.5 | 2.5 | 2.5 | 1.3 | 1.3 | 2.2 | 2.2 |
| 13 | −0.1 | −0.1 | 3.9 | 3.9 | −0.3 | −0.3 | 1.2 | 1.2 |
| 14 | 0.2 | 0.2 | 0.4 | 0.4 | 0.7 | 0.7 | 1.0 | 1.0 |
| 15 | −0.3 | −0.3 | 2.5 | 2.5 | −0.8 | −0.8 | 0.2 | 0.2 |
| 16 | 0.3 | 0.3 | 0.4 | 0.4 | 0.7 | 0.7 | 1.0 | 1.0 |
| 17 | −0.1 | −0.1 | 4.5 | 4.5 | −0.3 | −0.3 | 1.2 | 1.2 |
| 18 | 0.0 | 0.0 | −2.4 | −2.4 | 0.1 | 0.1 | −0.1 | −0.1 |
| 19 | −0.3 | −0.3 | 2.4 | 2.4 | −0.8 | −0.8 | 0.3 | 0.3 |
| 20 | 0.1 | 0.1 | −2.3 | −2.3 | 0.2 | 0.2 | −0.0 | −0.0 |
| DOF Number | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) | (The Proposed Method) | (Modal Superposition Method) |
|---|---|---|---|---|---|---|
| 1 | −0.0000 | −0.0000 | 0.3640 | 0.3640 | −0.3677 | −0.3677 |
| 2 | −0.0494 | −0.0494 | −0.3677 | −0.3677 | −0.3640 | −0.3640 |
| 3 | 0.0000 | 0.0000 | −0.0347 | −0.0347 | 0.0352 | 0.0352 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Peng, X. An Exact Method for Calculating the Eigenvector Sensitivities. Appl. Sci. 2020, 10, 2577. https://doi.org/10.3390/app10072577
Yang Q, Peng X. An Exact Method for Calculating the Eigenvector Sensitivities. Applied Sciences. 2020; 10(7):2577. https://doi.org/10.3390/app10072577
Chicago/Turabian StyleYang, Qiuwei, and Xi Peng. 2020. "An Exact Method for Calculating the Eigenvector Sensitivities" Applied Sciences 10, no. 7: 2577. https://doi.org/10.3390/app10072577
APA StyleYang, Q., & Peng, X. (2020). An Exact Method for Calculating the Eigenvector Sensitivities. Applied Sciences, 10(7), 2577. https://doi.org/10.3390/app10072577





