Designing Parallel Adaptive Laplacian Smoothing for Improving Tetrahedral Mesh Quality on the GPU

Abstract

Mesh quality is a critical issue in numerical computing because it directly impacts both computational efficiency and accuracy. Tetrahedral meshes are widely used in various engineering and science applications. However, in large-scale and complicated application scenarios, there are a large number of tetrahedrons, and in this case, the improvement of mesh quality is computationally expensive. Laplacian mesh smoothing is a simple mesh optimization method that improves mesh quality by changing the locations of nodes. In this paper, by exploiting the parallelism features of the modern graphics processing unit (GPU), we specifically designed a parallel adaptive Laplacian smoothing algorithm for improving the quality of large-scale tetrahedral meshes. In the proposed adaptive algorithm, we defined the aspect ratio as a metric to judge the mesh quality after each iteration to ensure that every smoothing improves the mesh quality. The adaptive algorithm avoids the shortcoming of the ordinary Laplacian algorithm to create potential invalid elements in the concave area. We conducted 5 groups of comparative experimental tests to evaluate the performance of the proposed parallel algorithm. The results demonstrated that the proposed adaptive algorithm is up to 23 times faster than the serial algorithms; and the accuracy of the tetrahedral mesh is satisfactorily improved after adaptive Laplacian mesh smoothing. Compared with the ordinary Laplacian algorithm, the proposed adaptive Laplacian algorithm is more applicable, and can effectively deal with those tetrahedrons with extremely poor quality. This indicates that the proposed parallel algorithm can be applied to improve the mesh quality in large-scale and complicated application scenarios.

1. Introduction

The finite element method (FEM) is one of the most popular numerical simulation methods, which is commonly used to address many science and engineering problems. The core idea of the FEM is to discretize a continuum into a set of finite size elements to solve continuum mechanics problems. Generally, a two-dimensional model is discretized into a triangular or quadrilateral mesh; and a three-dimensional model is discretized into a tetrahedral or hexahedral mesh. The mesh is the basis of discretization in the numerical analysis of FEM. Thus, the quality of meshes plays a key role on the computational accuracy and efficiency of final results [1,2,3]. To obtain a high-quality mesh, numornous mesh generation methods [3,4,5,6] have been proposed. However, the generated initial meshes are in general have poor quality, and cannot be directly used for numerical computation. Therefore, it is necessary to further optimize the mesh to improve its quality after initial generation.

There are two main approaches used to optimize meshes [7,8]. One is to improve the mesh quality by encrypting, removing, or inserting mesh nodes [9], which changes the topology of the mesh [10,11]; the other is to change the locations of the mesh nodes, which is called mesh smoothing [12,13,14,15]. Mesh smoothing is more widely used because it does not change the connectivity of the mesh; one of the popular approaches is Laplacian mesh smoothing [16,17,18].

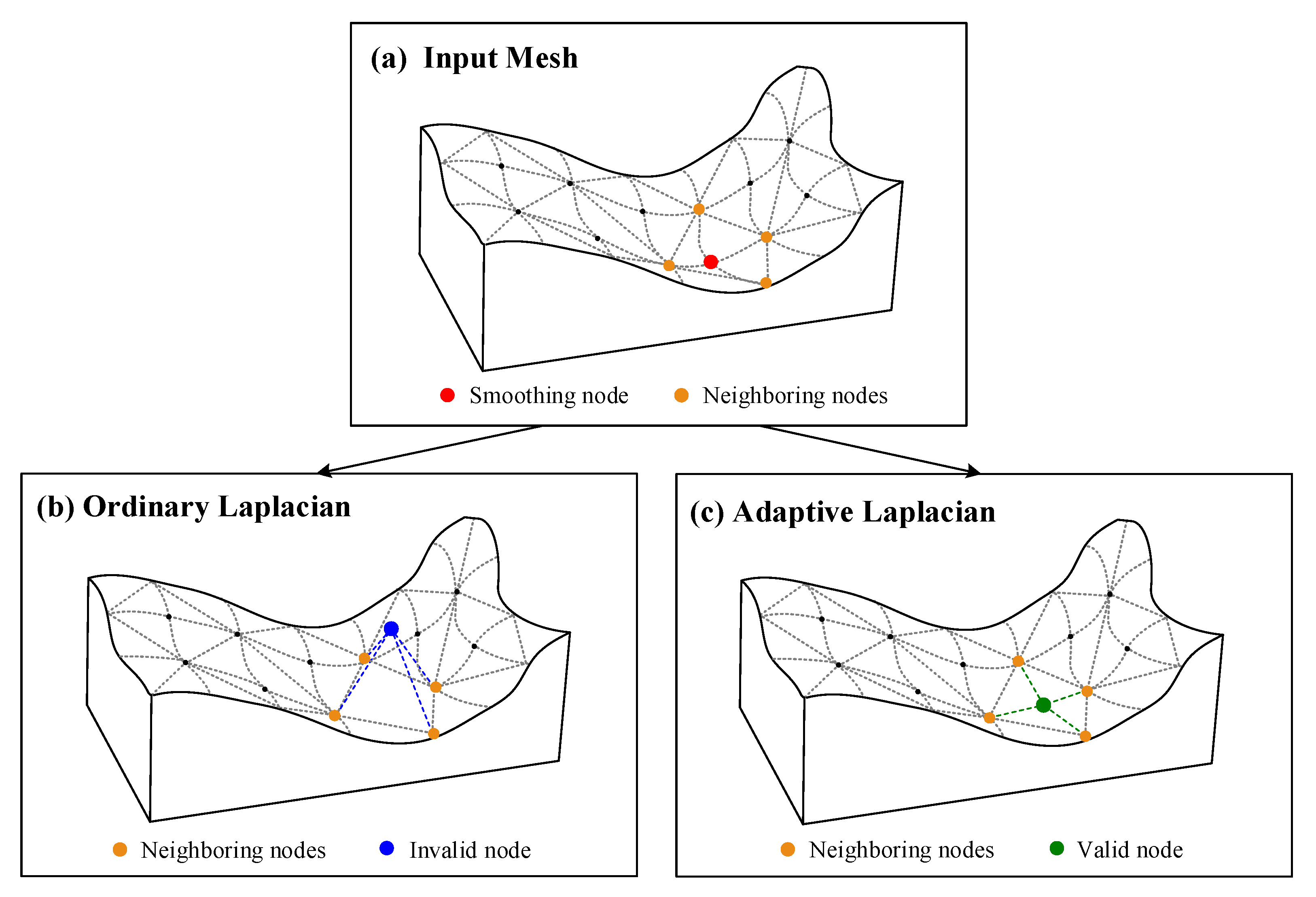
The process of Laplacian mesh smoothing is straightforward, requiring only that the locations of mesh nodes be updated to the geometric center of their neighbors during each iteration. In this case, the mesh topology will not be changed. However, in large-scale and complicated application scenarios, the computational models consist of a large number of nodes and elements, which means that in tetrahedral or hexahedral mesh models, a large number of tetrahedrons or hexahedrons need to be involved in the iterative computations. In this case, the complex iteration process will result in expensive computational costs when using Laplacian mesh smoothing. The use of parallel computing is an effective strategy to improve the efficiency of the Laplacian mesh smoothing algorithm; the powerful parallelism features of a modern graphics processing unit (GPU) can be utilized.

Currently, parallel computing on GPUs has been widely used in numerical computing, artificial intelligence, and other applications [19,20,21,22]. In Laplacian mesh smoothing, when the input mesh changes from a simple triangular mesh to a complex tetrahedral or hexahedral mesh, there are obviously larger number of tetrahedrons need to be calculated, Laplacian mesh smoothing process in serial calculation will become extremely long, and the experimental cost will be expensive. Therefore, it is necessary to accelerate Laplacian mesh smoothing algorithm on a GPU.

Several feasible algorithms accelerated on the GPU have been proposed to optimize mesh quality. For example, Mei et al. [23] proposed an ordinary Laplacian mesh smoothing algorithm accelerated on the GPU; Dahal and Newman [24] proposed three efficient parallel algorithms to improve finite element meshes based on the Laplacian smoothing. In addition, other parallel optimization strategies have been proposed for various types of meshes. For example, Jiao, X et al. [25] presented a parallel approach for optimizing surface meshes by redistributing vertices on a feature-aware higher-order reconstruction of a triangulated surface. Antepara, O et al. [26] described a parallel adaptive mesh refinement strategy for two-phase flows using tetrahedral meshes. Shang Mengmeng [27] proposed a multithreaded parallel version of a sequential quality improvement algorithm for tetrahedral meshes, which combined mesh smoothing operations and local reconnection operations.

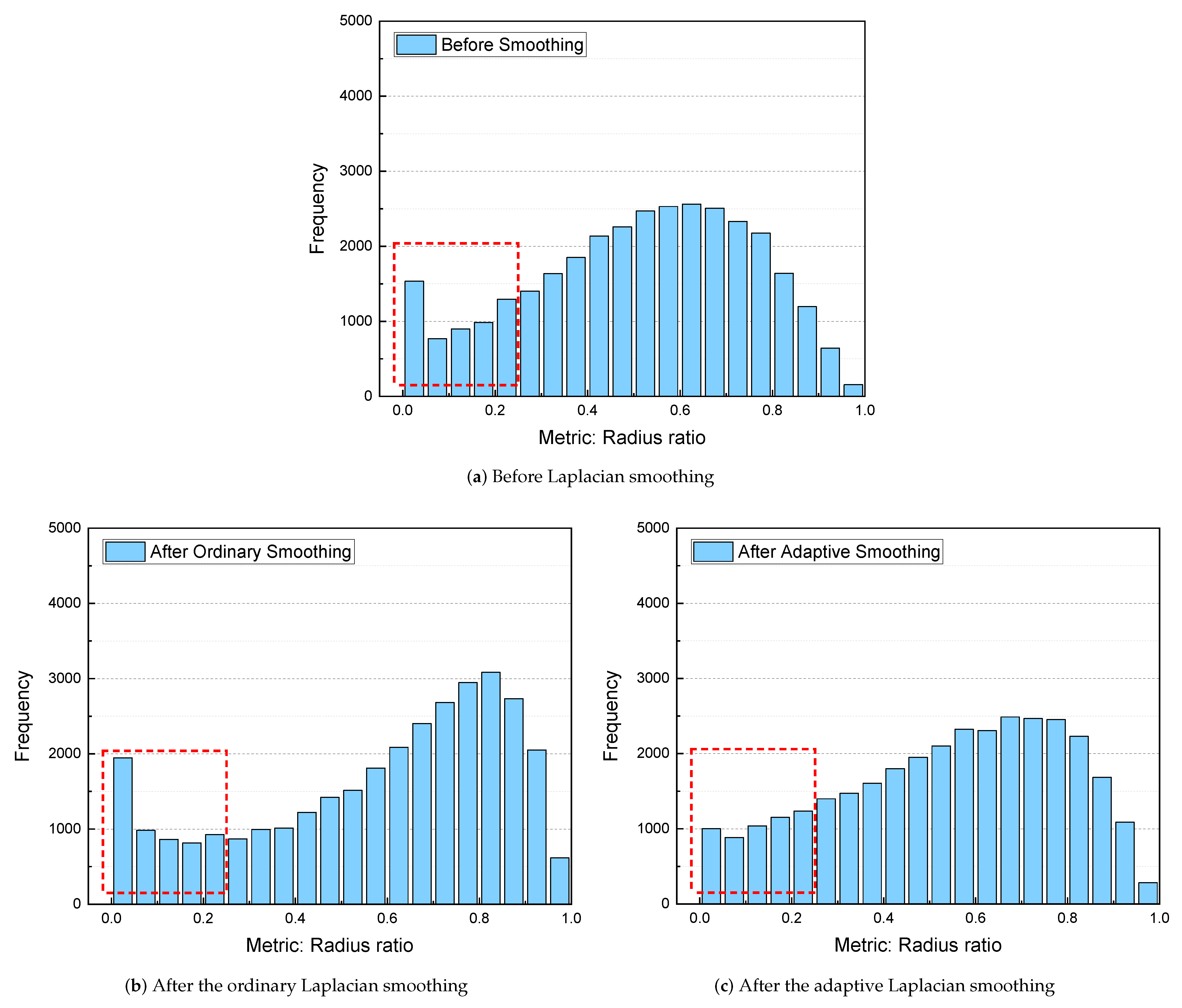
In our previous research, we developed parallel Laplacian mesh smoothing algorithms for triangular meshes accelerated on the GPU [23,28]. Moreover, a parallel ordinary Laplacian mesh smoothing for tetrahedral mesh accelerated on the GPU [29] has been presented. However, there is a shortcoming in the previously proposed ordinary Laplacian mesh smoothing algorithm. Specifically, the potential invalid nodes will be created in the concave area of the mesh. In FEM, the creation of invalid nodes will lead to distorted elements, which will strongly reduce the computational accuracy [30,31,32,33]. For example, Freitag L.A [18] found that approximately 30 percent of the Laplacian smoothing steps will result in an invalid mesh when using the ordinary algorithm compared with approximately 3 percent when using an improved swapping approach. Moreover, Vollmer J [33] found that the ordinary Laplacian algorithm shrinks meshes. Huang Lili et al. [4] reported that there are still severely distorted elements after using Laplacian smoothing. Therefore, it is necessary to propose improved Laplacian mesh smoothing algorithms.

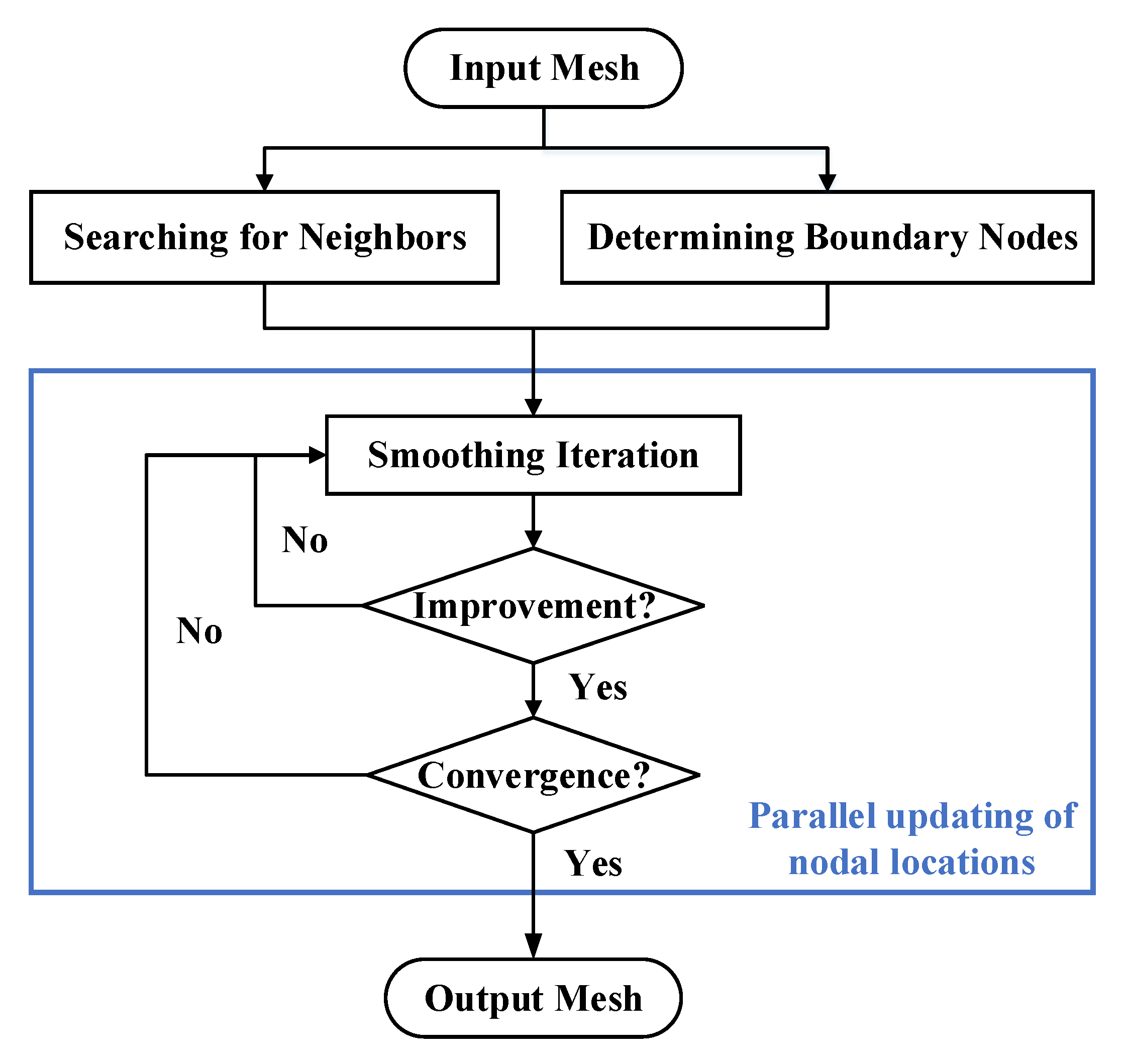
To address the above problem, in this paper, we specifically designed a parallel adaptive Laplacian smoothing algorithm for improving the quality of large-scale tetrahedral meshes by exploiting the parallelism features of the GPU. In the proposed algorithm, we added a judgment of tetrahedral mesh quality in the Laplacian smoothing process, and the new smoothing location is retained only if it improves the mesh quality. Furthermore, we changed the method of searching for neighboring nodes and compared the impact of different data layouts and iteration forms on the running performance and compared the efficiency on the GPU when using a single block and multiple blocks. The results are compared and analyzed with the serial version and ordinary Laplacian smoothing.

The rest of the paper is organized as follows: Section 2 provides a background introduction to Laplacian mesh smoothing and GPU computing. Section 3 introduces the proposed parallel adaptive Laplacian mesh smoothing in detail. Section 4 describes the experimental test and results. Section 5 discusses the advantages and shortcomings of the proposed parallel algorithm and outlines future work. Finally, Section 6 concludes this work.

2. Background

2.1. Laplacian Mesh Smoothing

2.1.1. Ordinary Laplacian Mesh Smoothing

Laplacian mesh smoothing is one of the most widely used smoothing methods. The core idea of Laplacian mesh smoothing is straightforward. First, the first-order domain [29] of every internal node is determined in the mesh. Second, the coordinate of each internal node is updated iteratively to the center of mass of its first-order neighboring nodes until the result converges. Laplacian mesh smoothing does not change the topology of the mesh; and the iterative calculation of nodes in the algorithm is easy to parallelize; thus, it is easy to exploit in practical applications. Figure 1 briefly compares a tetrahedral mesh before and after Laplacian smoothing.

2.1.2. Adaptive Laplacian Mesh Smoothing

Adaptive Laplacian mesh smoothing is proposed based on ordinary Laplacian mesh smoothing. Generally, in ordinary Laplacian mesh smoothing, invalid elements may be created in the concave areas of the mesh, which results in a mesh quality that does not improve. To solve this problem, adaptive Laplacian mesh smoothing [23] adds a step to judge whether the mesh quality improves after every update of the nodal location. If the new smoothing location improves the mesh quality, the new location is retained; if not, it is recalculated. This approach provides a guarantee for improving the mesh quality compared with ordinary mesh smoothing.

The quality of an entire mesh model depends on the quality of all tetrahedrons in the mesh; and the quality of a tetrahedron can be defined by different metrics, such as mean ratio, aspect ratio, dihedral angle, circumradius-shortest edge ratio, etc. According to these defined metrics, the adaptive Laplacian algorithm will automatically determine whether the new node is invalid. This mechanism of checking can avoid invalid iterative calculations compared with the ordinary Laplacian algorithm. Figure 2 illustrates the smoothed positions of a sample node in the concave area of a tetrahedral mesh when using ordinary Laplacian mesh smoothing and adaptive Laplacian mesh smoothing.

2.1.3. Two Forms of Smoothing Iteration

In Laplacian mesh smoothing, there are two forms to select the coordinates of neighboring nodes when iteratively calculating the smoothing coordinate of a vertex: Form A and Form B. For example, when updating the smoothing coordinates of vertices in iteration pass (q + 1), Form A completely select the old coordinates of neighboring nodes calculated in the previous iteration pass q, while Form B need not only the old coordinates of neighboring nodes calculated in the previous iteration pass q but also the new coordinates of neighboring nodes calculated in the current iteration pass (q + 1). It is clear that Form A is a special case of Form B when the number of neighboring nodes derived from iteration pass (q + 1) is 0.

Form A:

$$\overline{x_i^{q+1}}=\frac{1}{N}\sum _{j=1}^N{x}_j^q$$

(1)

Form B:

$$\overline{x_i^{q+1}}=\frac{1}{N}\left(\sum _{j=1}^{N_q}{x}_j^q+\sum _{k=1}^{N_{q+1}}{x}_k^{q+1}\right),\left\{\begin{array}{c}0\le N_q\le N\\ 0\le N_{q+1}\le N\\ N_q+N_{q+1}=N\end{array}\right.$$

(2)

where N is the total quantity of neighboring nodes of computing node; $\overline{x_i^{q+1}}$ is the new location calculated in the iteration (q + 1); $N_q$ is the number of neighbors derived from the iteration q; $N_{q+1}$ is the number of neighbors derived from the iteration (q + 1); $x_j^q$ is the old location calculated in the iteration q for $N_q$ nodes; $x_k^{q+1}$ is the old location calculated in the iteration (q + 1) for $N_{q+1}$ nodes. Form A is a special case of Form B where $N_{q+1}$ = 1.

2.2. Data Layouts in GPU Computing

Data layout takes the form of storing and accessing data in memory. In GPU computing, there are two main data layouts [34]: Array of Structures (AoS) and Structure of Arrays (SoA). The selection of the data layout is an important step, and an appropriate data layout can significantly improve GPU computing efficiency.

In the AoS data layout, the data will be misaligned, which will cause merging problems. This is because multidimensional and multivalued data containers lead to stridden memory access in the one-dimensional address space. Therefore, organizing data in the AoS layout cannot make full use of the memory bandwidth, resulting in a waste of memory space.

SoA data layout is more appropriate in most cases. Compared with the AoS data layout, organizing the data in the SoA layout can avoid data interleaving to make full use of the memory bandwidth.

Whether the data layout can achieve better performance depends on its underlying algorithm, and the specific algorithm should match the specific data layout. Generally, the SoA data layout is more suitable for single instruction multiple data (SIMD) units, and the AoS data layout is more suitable for commonly used language syntax and standard container types. Different types of data layouts can be converted into each other; for example, in the paper by Strzodka R [35], the conversion of two data layouts in C++ was realized. Taking the storage of node A containing four neighboring nodes as an example, Figure 3 briefly illustrates the different ways of storing the coordinates of its neighbors.

3. Parallel Adaptive Laplacian Mesh Smoothing on the GPU

3.1. Overview

In this paper, we proposed a parallel adaptive Laplacian smoothing algorithm for improving the quality of large-scale tetrahedral mesh, the proposed algorithm consists of three main steps. (1) The first step is to determine the first-order domain of all nodes in the input tetrahedral mesh. This step includes searching for the first-order neighboring nodes of each vertex and initializing the mass of each adjacent tetrahedral element. (2) The second step is to determine the constraints, i.e., which nodes are internally smoothable and which are constrained. (3) The third step is to iteratively calculate the smoothing location of each node until the iteration converges, and the end of every iteration needs a quality judgment of neighboring tetrahedrons. The above steps are implemented in parallel on the GPU. The shortcomings and advantages are described in detail in Section 5.3. The entire workflow of the proposed algorithm is illustrated in Figure 4.

3.2. Step 1: Searching for First-Order Neighbors of Nodes

The new smoothing position of a node depends entirely on its neighboring nodes. For a tetrahedral mesh, a single tetrahedron is a basic unit, and each node of the tetrahedron is a neighbor of the other three nodes. All neighbors form the first-order domain of the vertex. The center of mass of the first-order domain is taken as the new nodal location during the iteration. The general method of obtaining neighbors is to allocate an array for each node to store its neighboring coordinates, and then to find the neighbors of that node by traversing each neighboring tetrahedron in turn [36]. There are two major disadvantages of this approach. First, the length of the array of neighboring nodes cannot be determined at the time of initial creation, and it should only be opened up gradually at a later stage of storage, which will lead to data conflicts during writing operations. Second, the work of finding neighbors is carried out in the order of nodes; thus, it is impossible to determine all the neighbors of nodes at the same time.

Based on this approach, we have proposed a new search method in our previous research [36], where the data traversal unit is changed from a node to each side of a triangle. The specific implementation procedures are as follows.

1.

Search for the sideline segments of each triangle in the tetrahedral mesh by multithreading, and the corresponding values of the start node and the end node of each edge are stored in two integer arrays;

2.

Copy two integer arrays where store all sideline segments in reverse;

3.

Sort by the value of the first integer array that stores the starting node of all the sideline segments in parallel;

4.

Remove duplicate integer pairs with unique operations in parallel and perform segmented scans to quickly find the index of all neighboring nodes of each vertex.

It is clear that neighbors of all the nodes can be found simultaneously through the above method, and the number of neighboring nodes can also be determined in advance. In the proposed method, there is no complex data structure, and only an integer array is needed; therefore, it is easy to execute efficiently on a GPU. Figure 5 briefly illustrates the process of searching for neighbors.

3.3. Step 2: Determining Boundary Nodes

There are two types of nodes in a tetrahedral mesh: boundary nodes and internal nodes. Only the internal nodes are involved in the smoothing iteration, and the boundary nodes are used as mesh constraints to fix their coordinates. Therefore, it is necessary to determine which nodes are boundary nodes before iterating. The core idea of determining boundary nodes is straightforward. The face in a tetrahedral mesh shared by two tetrahedrones at the same time is an internal face, and all three nodes on the internal face are internal nodes, while the face that has only been used once is the boundary face, and the nodes that make up the boundary face are boundary nodes. The specific procedure to determine boundary nodes is as follows.

1.

Invoke all threads in the thread grid to traverse each tetrahedron in the mesh, and the node indices of four faces in each tetrahedron are stored from small to large in memory;

2.

Sort all the faces in the array from small to large in parallel;

3.

Compare each face in the array with its adjacent face in parallel to choose the boundary face that has been used only once and mark all three nodes of the boundary face as internal nodes saved in the CUDA kernel.

Through the above operations, we add a new attribute value for all nodes in memory to facilitate the subsequent iterative calculation.

3.4. Step 3: Adaptive Smoothing Iteration

When optimizing the tetrahedral meshes using adaptive Laplacian mesh smoothing, the last step is to judge the mesh node locations iteratively until convergence. For adaptive Laplacian mesh smoothing to tetrahedral meshes, the standard for judging tetrahedral mesh quality is the minimum value of the mass of all adjacent tetrahedrons of the node [22]. If the minimum value of the mass obtained in this iteration is greater than the minimum value of the mass calculated in the previous iteration, then we terminate the iteration and keep the smoothing results in this iteration; otherwise, we need to continue the iteration.

In this paper, we chose the aspect ratio as a metric to evaluate the quality of the tetrahedral meshes, where the aspect ratio is the radius ratio of the inscribed sphere and the circumscribed sphere. The maximum aspect ratio of the tetrahedron is 1/3, that is, the regular tetrahedron. For the convenience of statistical analysis, we have expanded all the mesh masses by three times, and the numerical range of the radius ratio is controlled between 0 ∼ 1, where 1 represents the tetrahedral element with the best quality, and 0 represents the tetrahedral element with the worst quality. The calculations of the inscribed sphere radius and circumscribed sphere radius are shown in Equations (3) and (4). Figure 6 simply shows the relationship between a tetrahedron and its inscribed sphere and circumscribed sphere.

Radius of inscribed sphere $R_1$:

$$R_1=\frac{3V}{S}$$

(3)

where V is the volume of the tetrahedron and S is the sum of the side areas of the tetrahedron.

Radius of circumscribed sphere $R_2$:

$$R_2=\frac{\sqrt{(a+b+c)\ast (a+b-c)\ast (a+c-b)\ast (b+c-a)}}{24V}$$

(4)

where a, b, and c are the products of three pairs of opposite edges of the tetrahedron and V is the volume of the tetrahedron.

There is a clear data dependency in the iteration process. In the smoothing iteration, the q + 1 iteration calculation requires the results of the q iteration, and the computation must ensure that all nodes in the mesh have completed the q iteration before the q + 1 iteration can be performed. However, in GPU computing, there are no synchronization barriers in a block, and it is not always guaranteed that the current iteration must have started after all nodes have completed the previous calculation. A practical solution to this problem is to distribute only one block for a single iteration. Each thread in the block is responsible for the smoothing calculation of several nodes in this iteration, including (1) updating the locations of nodes and (2) updating the mass value of all neighboring tetrahedrons in memory by the new node coordinates and determining whether the mass minimum has increased.

Obviously, when distributing a block for a location updating process, it is guaranteed that the q + 1 iteration must start after the q iteration completely finishes. However, this iteration method cannot make efficient use of the parallel computing power of GPUs. In this paper, we adopted a multiple block iterative method [29] where the multiple blocks complete an iteration at the same time. The maximum number of threads allowed on the GPU is 1024 at the moment; thus, all simultaneous starts of multiple blocks can achieve the maximum parallel strategy. In the implementation, we distribute a thread to each node to complete its smoothing calculation. If there are a total of 4096 internal nodes in the mesh that need to be calculated, when 1024 threads are allocated to a block, 4 blocks need to be designed to work at the same time. Figure 7 briefly illustrates the process of the single block iteration and the multiple block iteration.

4. Results

4.1. Experimental Setup

In this paper, we implemented the proposed adaptive Laplacian mesh smoothing algorithm for tetrahedral mesh with CUDA11.0 on a workstation computer. The specifications and details of the workstation used for the experiments are shown in

Table 1. Specifications and details of the workstation computer.

Specifications	Details
Compiler	VS2017 Community
CUDA version (GHz)	V11.0
CPU	Intel Xeon Gold
CPU Frequency	2.30 GHz
CPU RAM	128 GB
CPU cores	48
GPU	NVIDIA Quadro P6000
GPU core	3840
GPU Memory	24 GB

.

In order to evaluate the performance of the proposed parallel adaptive algorithm, we conducted five groups of experimental tests, which are implemented on CPU and GPU, respectively. And the CPU version is implemented serially. The test data includes five sets of tetrahedral meshes: 5k, 10k, 59k, 77k, and 109k vertices; among them, the test of 77k vertices is supplemented by a slope model. The experimental data are shown in

Table 2. Experimental data.

Model	Number of Nodes	Number of Tetrahedrons
1	5000(5k)	32,978
2	10,000(10k)	66,542
3	59,261(59k)	391,220
4	76,928(77k)	388,428
5	109,260(109k)	727,088

. The input mesh is created as follows. First, the equidistant nodes were distributed in a user-specified multidimensional data set. Second, random nodes were created in this space. Third, Delaunay meshes for these discrete point sets were established by using the TetGen library [37,38]. As shown in Figure 8, we displayed the surface and internal structure of experimental mesh models with 59k nodes and 77k nodes.

4.2. Experimental Results

In this paper, we recorded the running times of five groups of experiments. The results were conducted to test the impact of different data layouts in the two iterative methods of Form A and Form B and the effect of using a single block or multiple blocks in the iterative process on the GPU computational performance.

Table 3. Running time of the proposed algorithm when using Form A.

	Running Time (ms)
Number of Nodes	CPU	GPU-AoS		GPU-SoA
		Single Block	Multiple Blocks	Single Block	Multiple Blocks
5k	1473	450	467	151	139
10k	3745	537	535	775	331
59k	8452	799	954	986	1254
77k	15,825	3252	1675	3505	2231
109k	36,592	5811	4866	6718	4140

and

Table 4. Running time of the proposed algorithm when using Form B.

	Running Time (ms)
Number of Nodes	CPU	GPU-AoS		GPU-SoA
		Single Block	Multiple Blocks	Single Block	Multiple Blocks
5k	1473	169	155	130	96
10k	3745	542	304	287	389
59k	8452	763	502	726	654
77k	15,825	1184	705	1263	1180
109k	36,592	3566	1618	4362	2230

show the running time of Form A and Form B in the adaptive Laplacian mesh smoothing for tetrahedral mesh, and

Table 5. Speedup of the proposed algorithm over serial algorithm when using Form A.

	Speedup
Number of Nodes	GPU-AoS		GPU-SoA		Max Speedup
	Single Block	Multiple Blocks	Single Block	Multiple Blocks
5k	3.273	3.154	9.755	10.597	10.597
10k	6.974	7.004	4.832	11.310	11.31
59k	10.576	8.857	8.570	6.740	10.576
77k	4.866	9.448	4.515	7.093	9.448
109k	6.297	7.520	5.447	8.839	8.839

and

Table 6. Speedup of the proposed algorithm over serial algorithm when using Form B.

	Speedup
Number of Nodes	GPU-AoS		GPU-SoA		Max Speedup
	Single Block	Multiple Blocks	Single Block	Multiple Blocks
5k	8.716	9.503	11.331	15.344	15.344
10k	6.906	12.319	13.049	9.627	13.049
59k	11.075	16.833	11.639	12.920	16.833
77k	13.366	22.447	12.530	13.411	22.447
109k	10.261	22.620	8.389	16.409	22.620

show the speedups of Form A and Form B in the parallel adaptive Laplacian mesh smoothing over a corresponding serial version of the algorithm for tetrahedral meshes.

All the experimental results indicated that (1) the algorithm with Form B is faster than Form A; (2) the algorithm with AoS data layout is slightly faster than SoA data layout; and (3) the running time of the algorithm that distributed multiple blocks during the GPU iteration is faster than the algorithm with a single block. In the five experiments, for a tetrahedral mesh with 100k nodes, the proposed mesh optimization algorithm can achieve a maximum acceleration of 22.620 times compared with the serial version.

5. Discussion

5.1. Efficiency of the Parallel Adaptive Laplacian Mesh Smoothing

5.1.1. Efficiency Analysis of Data Layouts

Figure 9a,b show the running time of the different data layouts when using Form A and Form B, respectively. It can be clearly seen that: (1) for Form A, when the number of nodes is smaller than 5k, the running time of the SoA version is shorter than that of the AoS version; and when the number of nodes is larger than 5k, AoS version shows better performance than SoA version with a max speedup of 1.44; (2) for Form B, when the number of nodes is smaller than 59k, SoA version shows a better performance; and when the number of nodes is larger than 59k, AoS version shows a better performance with a max speedup of 1.23.

The above results illustrate that the AoS is more efficient than SoA for mesh models with a large number of nodes. This is consistent with our previous studies [23,28,29]; the GPU version with AoS data layout has better performance is due to the aligned global memory accesses. Therefore, in complex application scenarios, we recommend using AoS data layout when accelerating the Laplacian mesh smoothing algorithm on the GPU.

5.1.2. Efficiency Analysis of Iteration Forms

As shown in Figure 10, the algorithm when using the Form B iteration always runs faster than Form A, both in the AoS data layout version and the SoA data layout version. In total, Form B runs 1.2 to 3.1 times faster than Form A. There are two main reasons why the Form B iteration is more efficient. First, Form A needs to exchange intermediate node coordinates during the iteration process; thus, it needs to access global memory more frequently and allocate additional memory to store the updated coordinates for each iteration, which greatly reduces the GPU computing power. Second, the iterative convergence rate of Form A is much lower than Form B. As the scale of test data becomes larger, the number of iterations of Form A becomes larger, and the running times become longer. Therefore, when running the adaptive Laplacian mesh smoothing algorithm on the GPU for tetrahedral meshes, it is more logical to use the Form B iteration method.

5.1.3. Efficiency Analysis of Multiple Block Iteration

In this paper, we analyzed and compared the performance of the kernel with a single block and multiple blocks based on a GPU with the CPU version. As seen in Figure 11, the GPU version runs faster than the CPU version, up to approximately 20 times faster, and the multiple block version runs faster than the single block version overall. In addition, we compared the single block version and the multiple block version individually. The results are shown in Figure 12. The performance advantage of the multiple block version becomes more apparent as the size of the experimental data increases. When the input mesh has 109k nodes, the speed can reach approximately 2.0 times. Thus, it can be seen that a kernel with multiple block can significantly improve iteration efficiency and make full use of the efficient parallel performance of the GPU.

However, it is important to note that although multiple block iteration is more efficient, this kernel design method does not always guarantee that there will be no data conflicts between the q iteration and the q + 1 iteration; thus, in practical applications, how to choose the iteration method will depend on the user’s requirements. For simple mesh models with few nodes, the kernel with a single block has better performance, and for complex and multinode meshes, the kernel with multiple blocks more easily ensures computational efficiency.

5.2. Comparative Analysis of Mesh Quality

To verify the accuracy of the proposed algorithm, we evaluated the quality of the original input mesh (Figure 13a), the mesh after ordinary Laplacian smoothing (Figure 13b), and the mesh after adaptive Laplacian smoothing (Figure 13b).The experimental results show that the mesh quality is significantly improved after adaptive Laplacian smoothing, and the value of the aspect ratio of the mesh tetrahedrons is approximately 0.15 times higher than the input mesh overall.

As shown in Figure 13b, it should be noted that the ordinary Laplacian smoothing algorithm cannot improve the quality of tetrahedrones with a radius ratio between 0∼0.2, which leads to the quality distribution of the smoothing mesh not being continuous. It is clearly in Figure 13b, there are approximately 2000 tetrahedrons with aspect ratios close to 0.0. However, the number of tetrahedrons with very poor quality in the input mesh is only approximately 1500, proving that the ordinary Laplacian mesh smoothing algorithm cannot improve the quality of very poor tetrahedrons.

However, the proposed adaptive algorithm in this paper is very obvious for improving the tetrahedrons with very poor quality, and the quantity of these tetrahedrons was reduced to approximately 1000. As shown in Figure 13c, the tetrahedron mesh quality after adaptive smoothing is relatively continuous. Therefore, the adaptive Laplacian smoothing algorithm for tetrahedral mesh proposed in this paper is very efficient to mesh tetrahedrons with very poor quality, which also means that the proposed algorithm in this paper has a wider range of applications.

5.3. Shortcomings and Advantages of Parallel Adaptive Laplacian Mesh Smoothing

One of the essential ideas behind the Laplacian mesh smoothing is to update the new positions of vertices to the geometric center of neighboring nodes. However, in practical application scenarios, the influence proportion of each neighboring node is different. Thus it is unreasonable to simply select the geometric center as the new vertical coordinate. Moreover, in the proposed adaptive parallel Laplacian mesh smoothing algorithm, the aspect ratio was used as a metric to evaluate the quality of the tetrahedral meshes during the smoothing iteration process. Different metrics have different computing methods and criteria, which will have some impact on the computational efficiency of the mesh smoothing algorithm and the optimized results of the mesh model. Therefore, more metrics should be employed and evaluated for careful consideration.

Overall, experimental results demonstrated that the proposed adaptive Laplacian mesh smoothing achieved better efficiency and accuracy compared with the baseline algorithm, and compared with the ordinary Laplacian algorithm, the adaptive algorithm is more applicable, which can effectively improve tetrahedrons with extremely poor quality.

5.4. Outlook and Future work

In future work, we will propose an appropriate metric to judge the influence weight of each neighboring node of the calculating vertex, and more metrics for mesh quality will be discussed. Moreover, we will further expand the application scopes of the adaptive Laplacian mesh smoothing algorithm accelerated on the GPU for more complex and irregular hexahedral mesh models. In fact, hexahedral meshes have higher accuracy and applicability; at present, the generation and optimization technologies of tetrahedral meshes are relatively mature, but because studies on hexahedral mesh less common, we will focus on the optimization of hexahedral meshes in the future.

6. Conclusions

In this paper, by exploiting the parallelism features of the GPU, we specifically designed a parallel adaptive Laplacian smoothing algorithm for improving the quality of large-scale tetrahedral mesh models. In the proposed parallel adaptive Laplacian smoothing, we added a judgment of tetrahedral mesh quality in the Laplacian smoothing process. The adaptive algorithm avoids the shortcoming of the ordinary Laplacian algorithm to create potential invalid elements in the concave area. In this paper, we conducted five groups of comparative experimental tests and compared and analyzed the operational performance of the two iteration methods and two data layouts. Moreover, we analyzed the efficiency of the iteration of a kernel with a single block and a kernel with multiple blocks. We found that (1) the proposed algorithm is up to 23 times faster than serial algorithms; (2) the accuracy of the tetrahedral mesh is improved after the proposed adaptive Laplacian smoothing; and (3) the proposed adaptive Laplacian mesh smoothing has broader applicability than ordinary Laplacian smoothing. This indicates that the proposed parallel algorithm can be applied to improve the mesh quality in large-scale and complicated application scenarios.