Multiparametric Analysis of a Gravity Retaining Wall
Abstract
:1. Introduction
2. Mathematical Model of a Gravity Retaining Wall
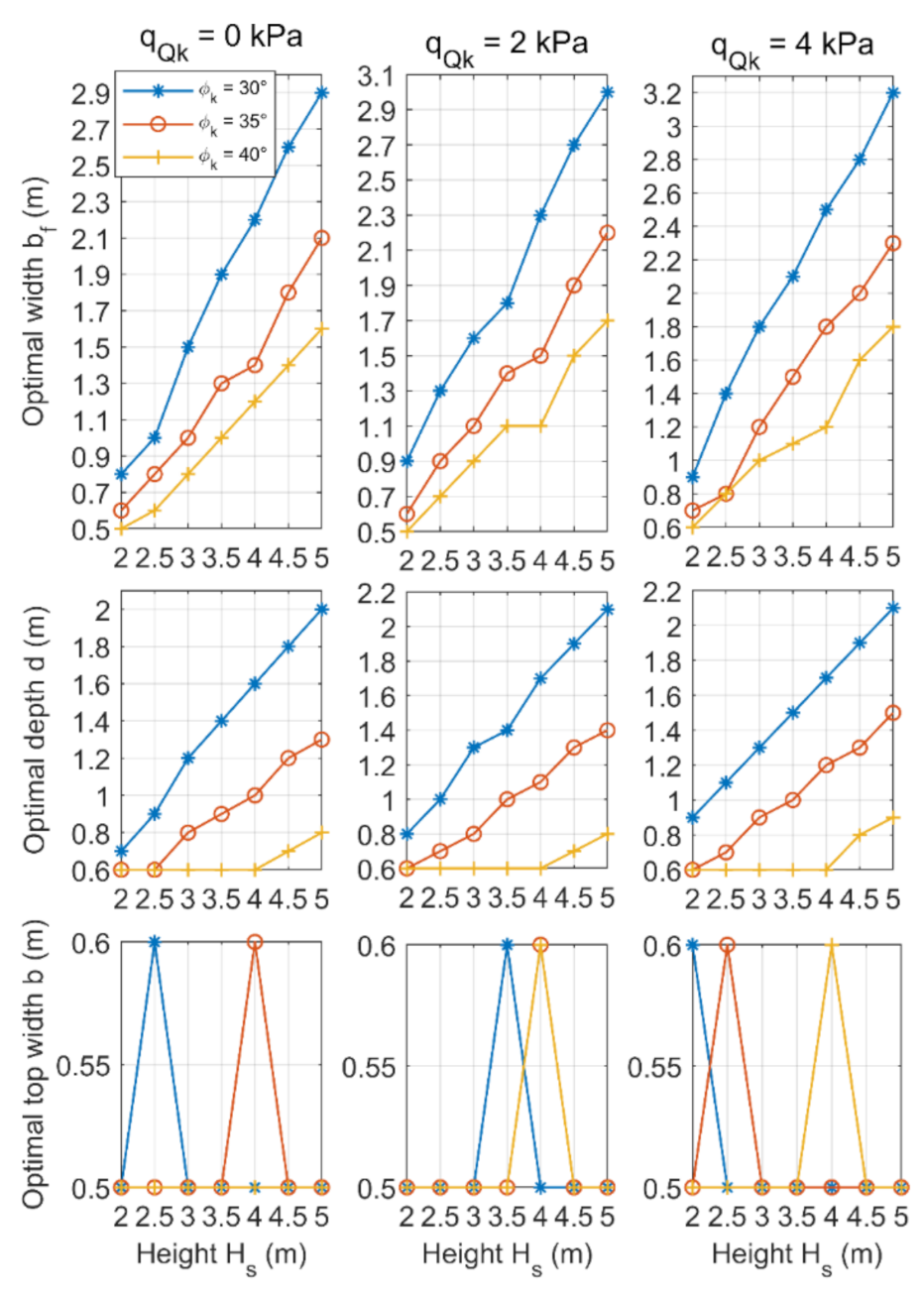
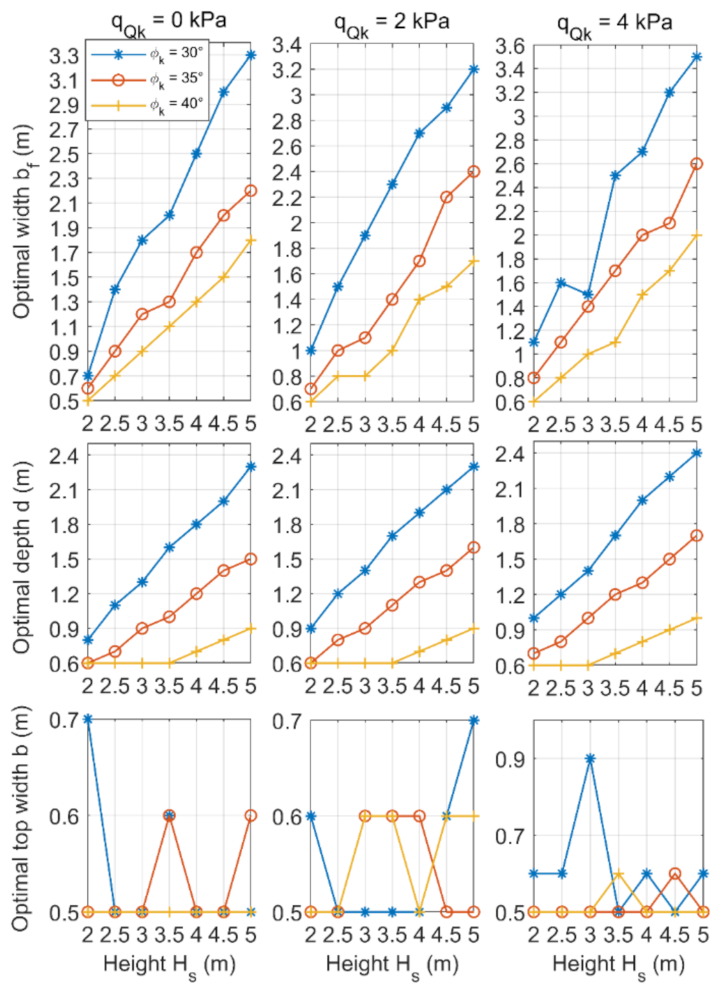
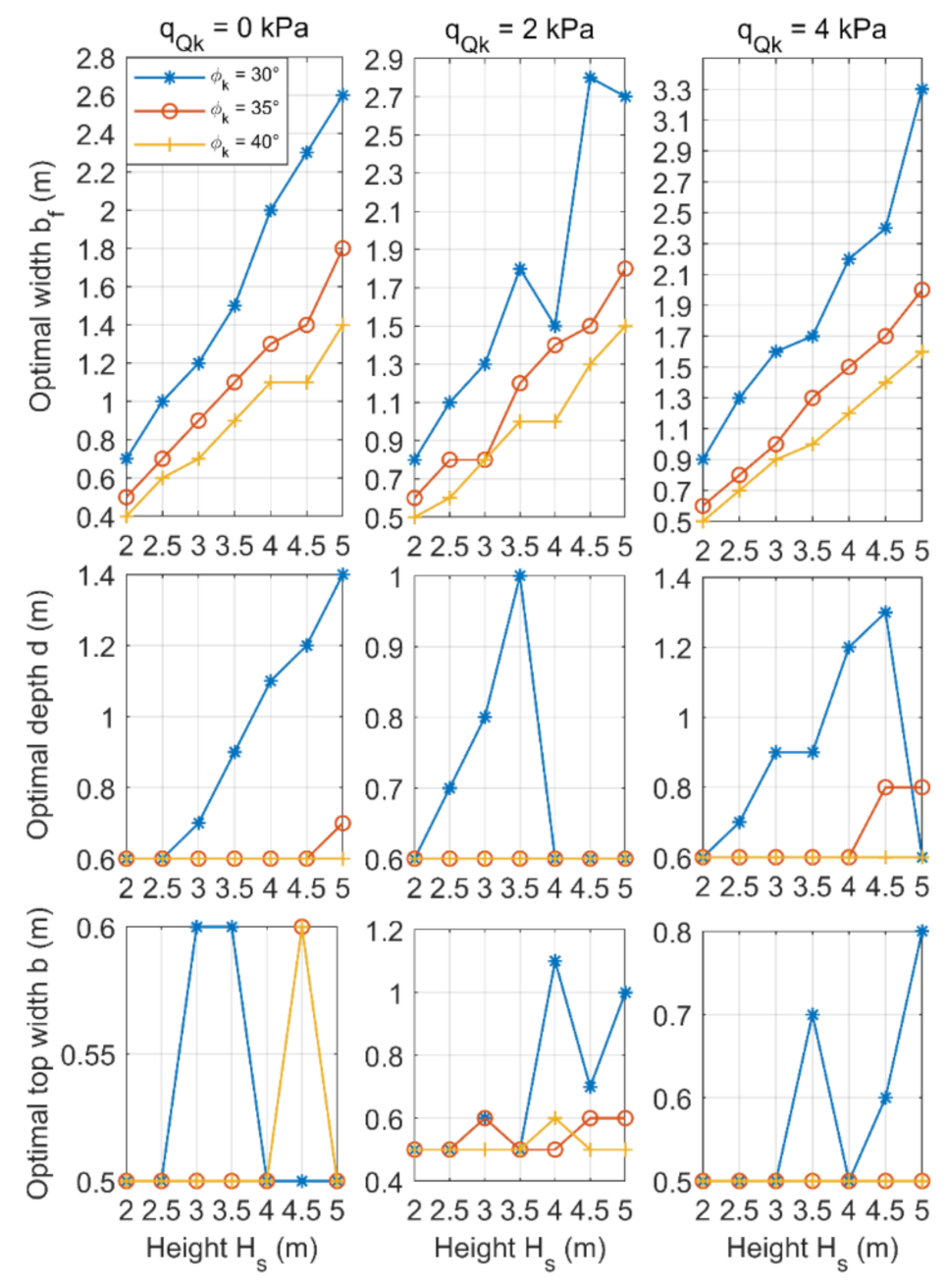
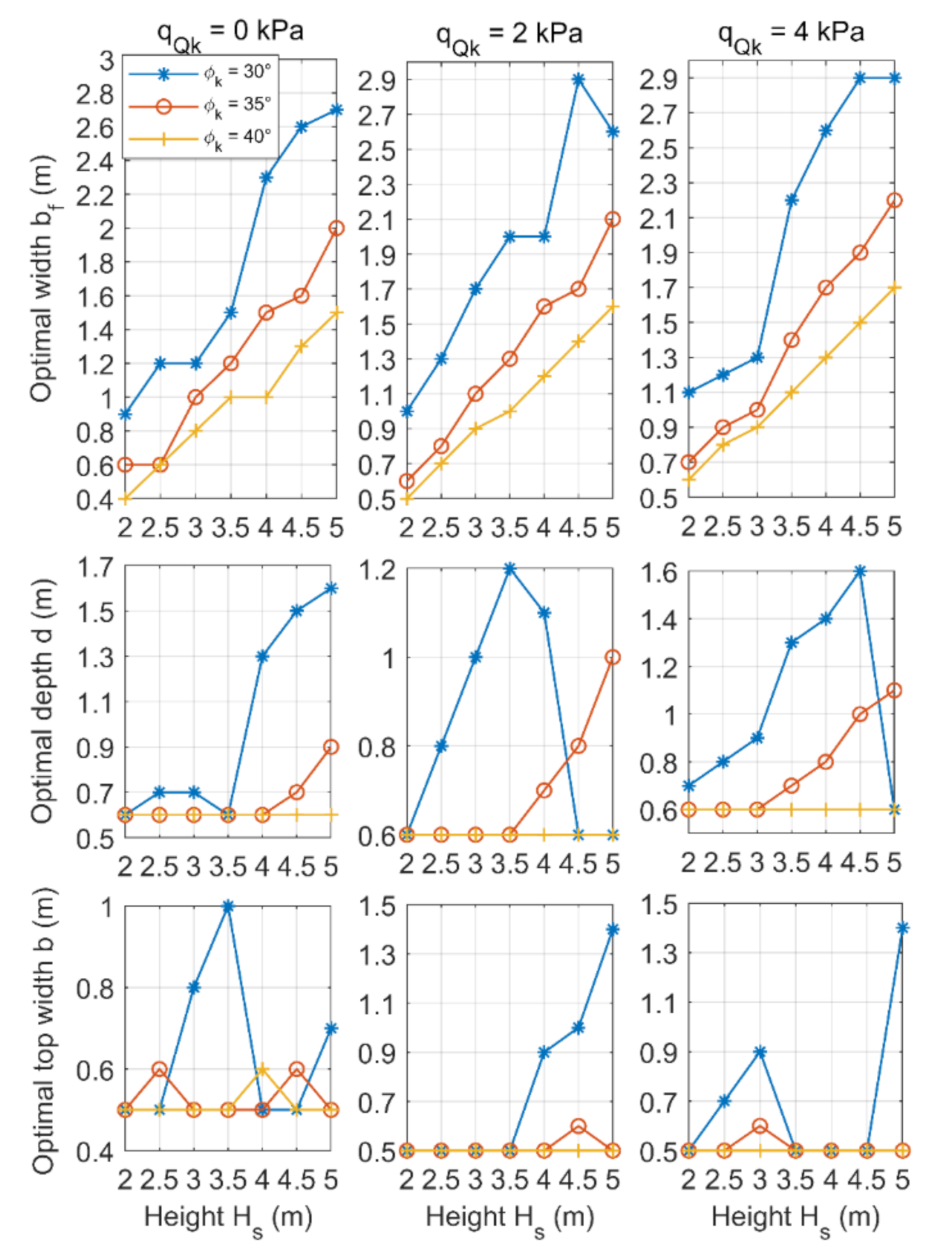
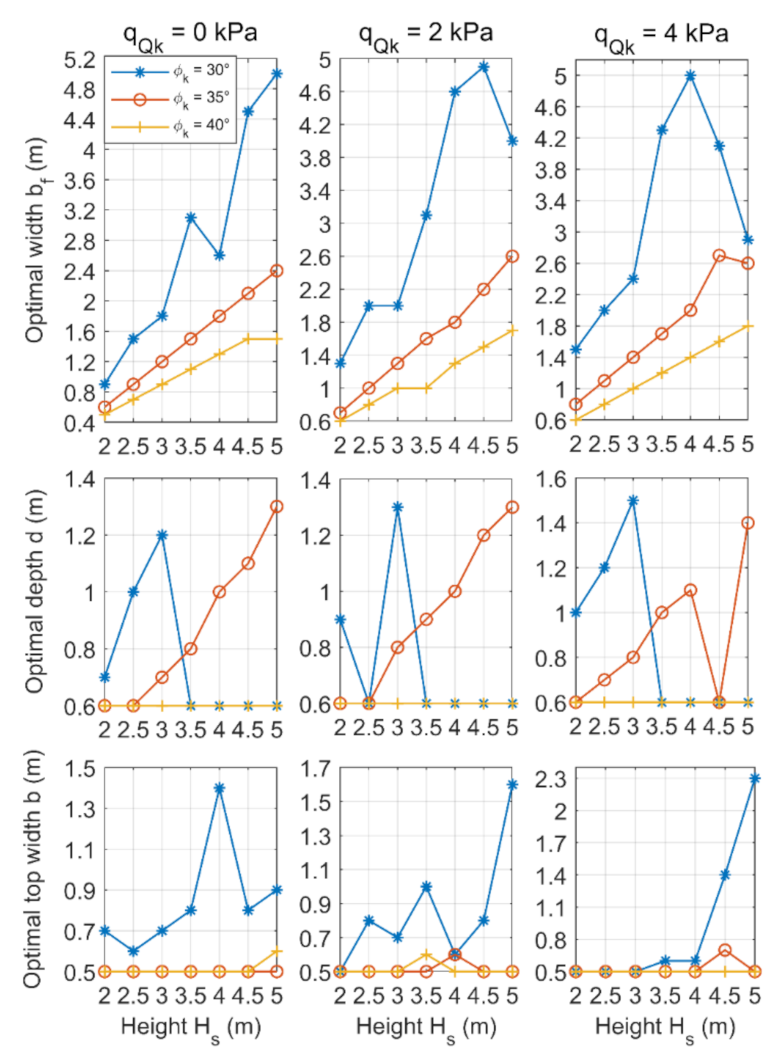
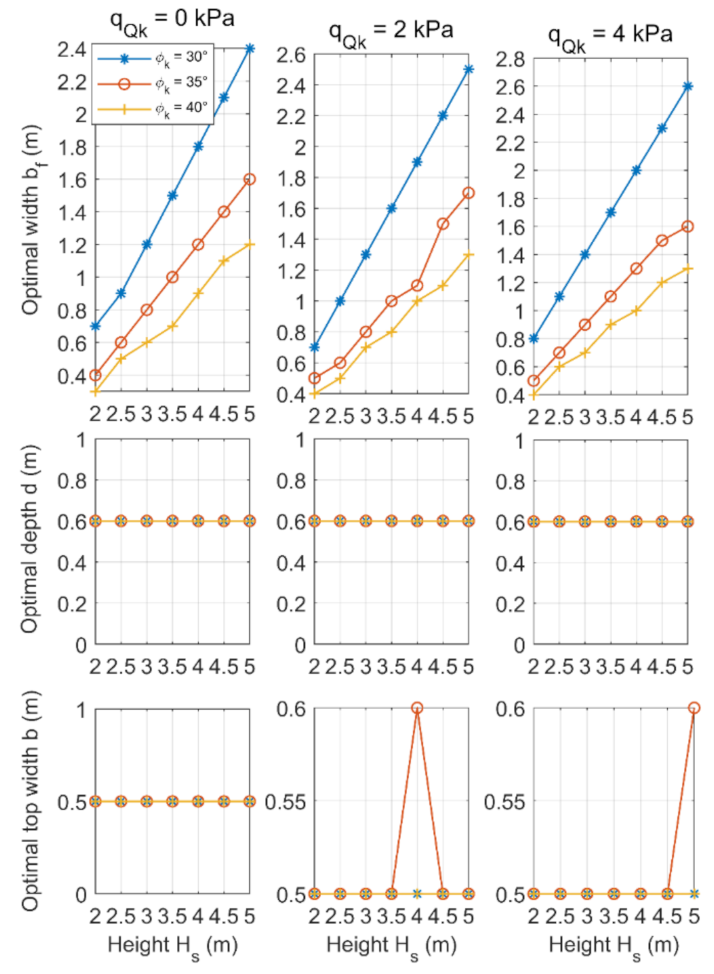
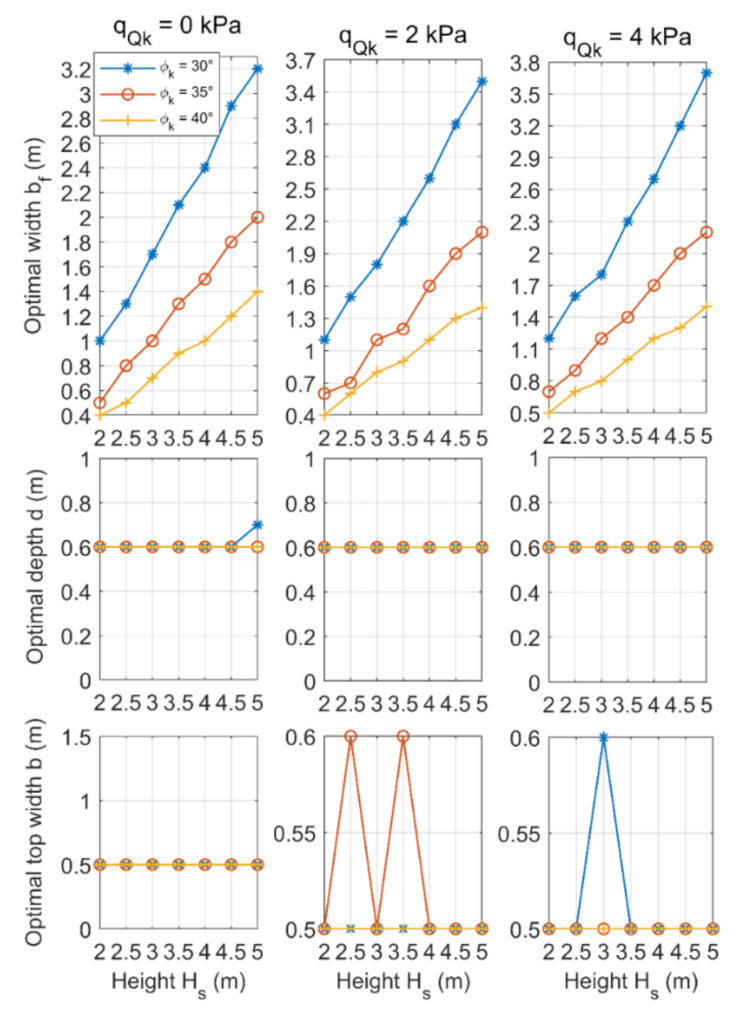
3. Parametric Analysis of a Gravity Retaining Wall
| 2, 2.5, 3, 3.5, 4, 4.5 and 5 m; |
| 30, 35 and 40°; |
| 1/2, 2/3 and 1; |
| 0, 10 and 20°; |
| 0, 2 and 4 kPa. |
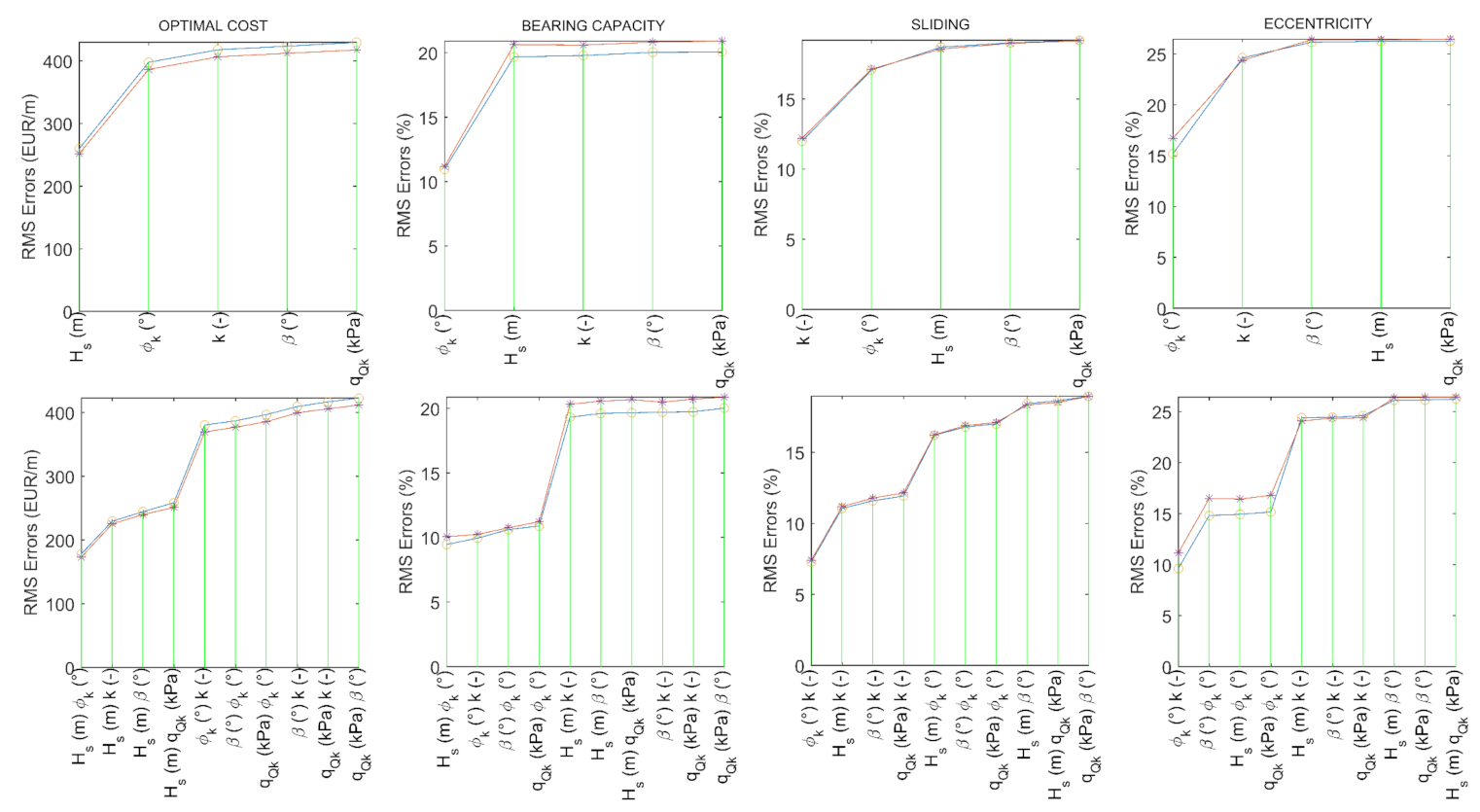
4. Sensitivity Analysis
5. Conclusions
- The optimal width of the front wall section bf reached the highest values among all dimensions of the wall, while the optimal width of the rear wall section bb was found to be 0 m at all different combinations of parameters.
- The most important parameter for the optimal cost of the gravity retaining wall is the height of the retained ground, followed by the shear angle of the soil, the soil–wall interaction coefficient, the slope angle and the variable surcharge load.
- The shear angle of the soil is most relevant to the bearing capacity and eccentricity condition, while the interaction coefficient is most relevant to the sliding condition.
- Given the unfavorable site characteristics and project data (φk = 30°, k = 0.5, β = 20°, qQk = 0 kPa), doubling the height of the retaining wall (from 2.5 to 5 m) increases the cost from 653.7 to 2510.7 EUR/m, almost four times the cost of a smaller wall.
- Gravity retaining walls are usually sloped toward the earth mass behind them to counteract the force of gravity acting against them, which is called “setback”. Based on the parametric analysis, the optimum angle of this slope ranges from 7 to 47°, with an average value of about 18° (slope ratio HD/VD = 1:3).
- The depth of the foundation for a gravity retaining wall depends on the height of the wall. Based on the parametric analysis, the optimum depth of the retaining wall is between 10 and 40% of the height of the wall, with an average value of 20% (one-fifth of its height below ground level).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EN 1997-1. Eurocode 7: Geotechnical Design Part 1, General Rules. 2004. Available online: https://www.ngm2016.com/uploads/2/1/7/9/21790806/eurocode_7_-_geotechnical_designen.1997.1.2004.pdf (accessed on 20 May 2021).
- Brady, K.C.; O’Reilly, M.; Bevc, L.; Žnidarič, A.; O’Brien, E.; Jordan, R. COST 345. Working Group 1. Report on the Current Stock of Highway Structures in European Countries, the Cost of Their Replacement and the Annual Costs of Maintaining, Repairing and Renewing Them. Available online: http://cost345.zag.si/Reports/COST_345_WG1.pdf (accessed on 25 May 2021).
- Kaveh, A.; Hamedani, K.B.; Bakhshpoori, T. Optimal Design of Reinforced Concrete Cantilever Retaining Walls Utilizing Eleven Meta-Heuristic Algorithms: A Comparative Study. Period. Polytech. Civ. Eng. 2020, 64, 156–168. [Google Scholar] [CrossRef]
- Kaveh, A.; Soleimani, N. CBO and DPSO for optimum design of reinforced concrete cantilever retaining walls. Asian J. Civ. Eng. 2015, 16, 751–774. [Google Scholar]
- Kaveh, A.; Behnam, A.F. Charged System Search Algorithm for the Optimum Cost Design of Reinforced Concrete Cantilever Retaining Walls. Arab. J. Sci. Eng. 2013, 38, 563–570. [Google Scholar] [CrossRef]
- Konstandakopoulou, F.; Tsimirika, M.; Pnevmatikos, N.; Hatzigeorgiou, G.D. Optimization of Reinforced Concrete Retaining Walls Designed According to European Provisions. Infrastructures 2020, 5, 46. [Google Scholar] [CrossRef]
- Sarıbaş, A.; Erbatur, F. Optimization and Sensitivity of Retaining Structures. J. Geotech. Eng. 1996, 122, 649–656. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Economic design of retaining wall using particle swarm optimization with passive congregation. Aust. J. Basic Appl. Sci. 2010, 4, 5500–5507. [Google Scholar]
- Camp, C.V.; Akin, A. Design of Retaining Walls Using Big Bang–Big Crunch Optimization. J. Struct. Eng. 2012, 138, 438–448. [Google Scholar] [CrossRef]
- Moayyeri, N.; Gharehbaghi, S.; Plevris, V. Cost-Based Optimum Design of Reinforced Concrete Retaining Walls Considering Different Methods of Bearing Capacity Computation. Mathematics 2019, 7, 1232. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.N.; Suribabu, C.R. Optimal design of cantilever retaining wall using differential evolution algorithm. Iran Univ. Sci. Technol. 2017, 7, 433–449. [Google Scholar]
- Talatahari, S.; Sheikholeslami, R.; Shadfaran, M.; Pourbaba, M. Optimum Design of Gravity Retaining Walls Using Charged System Search Algorithm. Math. Probl. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Sadoglu, E. Design optimization for symmetrical gravity retaining walls. Acta Geotech. Slov. 2014, 11, 71–79. [Google Scholar]
- Zhuang, J.; Chen, J. Stability Analysis of Gravity Retaining Walls with Different Wall-back Types under Equal Section Area. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 2020 International Conference on Innovative Solutions in Hydropower and Environmental and Civil Engineering, Beijing, China, 11–13 December 2020; IOP Publishing: Bristol, UK, 2021; Volume 668. [Google Scholar]
- Nama, S.; Saha, A.K.; Ghosh, S. Parameters Optimization of Geotechnical Problem Using Different Optimization Algorithm. Geotech. Geol. Eng. 2015, 33, 1235–1253. [Google Scholar] [CrossRef]
- Qiong, G.; Meng-Gang, Y.; Jian-Dong, Q. A multi-parameter optimization technique for prestressed concrete cable-stayed bridges considering prestress in girder. Struct. Eng. Mech. 2017, 64, 567–577. [Google Scholar] [CrossRef]
- Rumpf, M.; Grohmann, M.; Eisenbach, P.; Hauser, S. Structural Surface—Multi parameter structural optimization of a thin high performance concrete object. In Proceedings of the International Association for Shell and Spatial Structures (IASS), Amsterdam, The Netherlands, 17–20 August 2015. [Google Scholar]
- Jelusic, P.; Kravanja, S. Optimal design of timber-concrete composite floors based on the multi-parametric MINLP optimization. Compos. Struct. 2017, 179, 285–293. [Google Scholar] [CrossRef]
- Kravanja, S.; Žula, T.; Klanšek, U. Multi-parametric MINLP optimization study of a composite I beam floor system. Eng. Struct. 2017, 130, 316–335. [Google Scholar] [CrossRef]
- Chen, C.; Mao, F.; Zhang, G.; Huang, J.; Zornberg, J.; Liang, X.; Chen, J. Settlement-Based Cost Optimization of Geogrid-Reinforced Pile-Supported Foundation. Geosynth. Int. 2021, 1–39, online ahead of print. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal design of piled embankments with basal reinforcement. Geosynth. Int. 2018, 25, 150–163. [Google Scholar] [CrossRef]
- Nguyen, D.D.C.; Kim, D.-S.; Jo, S.-B. Parametric study for optimal design of large piled raft foundations on sand. Comput. Geotech. 2014, 55, 14–26. [Google Scholar] [CrossRef]
- Leung, Y.F.; Klar, A.; Soga, K. Theoretical Study on Pile Length Optimization of Pile Groups and Piled Rafts. J. Geotech. Geoenviron. Eng. 2010, 136, 319–330. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Determining optimal designs for conventional and geothermal energy piles. Renew. Energy 2020, 147, 2633–2642. [Google Scholar] [CrossRef]
- Alberdi-Pagola, M.; Poulsen, S.E.; Jensen, R.L.; Madsen, S. A case study of the sizing and optimisation of an energy pile foundation (Rosborg, Denmark). Renew. Energy 2020, 147, 2724–2735. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal Design of Reinforced Pad Foundation and Strip Foundation. Int. J. Geeomeech. 2018, 18, 04018105. [Google Scholar] [CrossRef]
- Wang, Y.; Kulhawy, F.H. Economic Design Optimization of Foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 1097–1105. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Determining optimal designs for geosynthetic-reinforced soil bridge abutments. Soft Comput. 2020, 24, 3601–3614. [Google Scholar] [CrossRef]
- Balasbaneh, A.T.; Yeoh, D.; Juki, M.I.; Ibrahim, M.H.W.; Abidin, A.R.Z. Assessing the life cycle study of alternative earth-retaining walls from an environmental and economic viewpoint. Environ. Sci. Pollut. Res. 2021, in press. [Google Scholar] [CrossRef]
- Damians, I.P.; Bathurst, R.J.; Adroguer, E.G.; Josa, A.; Lloret, A. Sustainability assessment of earth-retaining wall structures. Environ. Geotech. 2018, 5, 187–203. [Google Scholar] [CrossRef]
- Giri, R.K.; Reddy, K.R. Sustainability Assessment of Two Alternate Earth-Retaining Structures. In Proceedings of the IFCEE 2015; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 2836–2845. [Google Scholar]
- Deep, K.; Singh, K.P.; Kansal, M.; Mohan, C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Appl. Math. Comput. 2009, 212, 505–518. [Google Scholar] [CrossRef]
- Kalasin, T.; Wood, D.M. Seismic analysis of retaining walls within plasticity framework. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Wood, D.M.; Kalasin, T. Macroelement for study of dynamic response of gravity retaining walls. In Proceedings of the International Conference on Cyclic Behaviour of Soils and Liquefaction Phenomena, Bochum, Germany, 31 March 2004. [Google Scholar]
- Javanmard, M.; Angha, A.R. Seismic Behavior of Gravity Retaining Walls. GeoFlorida 2010, 2021, 2263–2270. [Google Scholar] [CrossRef]




| The cost objective function of a gravity retaining wall: | |||||||
| (1) | |||||||
| Geotechnical constraints and the corresponding equations: | |||||||
| (2) | (2a) | ||||||
| (2b) | (2c) | ||||||
| (2d) | (2e) | ||||||
| (2f) | (2g) | ||||||
| (2h) | (2i) | ||||||
| (2j) | (2k) | ||||||
| (2l) | (2m) | ||||||
| (2n) | (2o) | ||||||
| (2p) | (2q) | ||||||
| (2r) | (2s) | ||||||
| (2t) | (2u) | ||||||
| (2v) | (2w) | ||||||
| (2aa) | (2ab) | ||||||
| (2ac) | (2ad) | ||||||
| (2ae) | |||||||
| (3) | (3a) | ||||||
| (3b) | (3c) | ||||||
| (3d) | (3e) | ||||||
| (3f) | (3g) | ||||||
| (3h) | (3i) | ||||||
| (3j) | (3k) | ||||||
| (3l) | (3m) | ||||||
| (4) | (4a) | ||||||
| (4b) | (4c) | ||||||
| (4d) | (4e) | ||||||
| (4f) | (4g) | ||||||
| (4h) | (4i) | ||||||
| (4j) | (4k) | ||||||
| (4l) | (5) | ||||||
| Design constraints: | |||||||
| (6) | ; | (6a) | |||||
| (6b) | |||||||
| Discrete alternatives of the retaining wall dimensions: | |||||||
| Variable | Minimum | Increment (step) | Maximum | Number of alternatives | |||
| bf (m) | 0.0 | 0.1 | 5.0 | 51 | |||
| b (m) | 0.5 | 0.1 | 5.0 | 46 | |||
| bb (m) | 0.0 | 0.1 | 5.0 | 51 | |||
| d (m) | 0.6 | 0.1 | 5.0 | 45 | |||
| cfound,k | Cohesion of the Foundation Soil | 0 kPa |
| cret,k | cohesion of the retained earth | 0 kPa |
| γfound,k | unit weight of the foundation soil | 18 kN/m3 |
| γwall | unit weight of the wall | 23.5 kN/m3 |
| dmin | minimum depth of the embedded gravity wall | 0.6 m |
| Cstone | unit price of crushed stone from carbonate rocks bound with concrete | 85 EUR/m3 |
| Cexc | unit price of ground excavation | 10 EUR/m3 |
| Cfill | unit price of fill soil | 18 EUR/m3 |
| Cdrain | unit price of drainage pipes | 10 EUR/m |
| SFG | partial safety factor for permanent actions | 1.0 |
| SFG,fav | partial safety factor for favourable permanent actions | 1.0 |
| SFQ | partial safety factor for variable actions | 1.3 |
| SFφ | partial safety factor for the shear angle | 1.25 |
| SFc | partial safety factor for the cohesion | 1.25 |
| SFRv | partial safety factor for the bearing resistance | 1.0 |
| SFRh | partial safety factor for the sliding resistance | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varga, R.; Žlender, B.; Jelušič, P. Multiparametric Analysis of a Gravity Retaining Wall. Appl. Sci. 2021, 11, 6233. https://doi.org/10.3390/app11136233
Varga R, Žlender B, Jelušič P. Multiparametric Analysis of a Gravity Retaining Wall. Applied Sciences. 2021; 11(13):6233. https://doi.org/10.3390/app11136233
Chicago/Turabian StyleVarga, Rok, Bojan Žlender, and Primož Jelušič. 2021. "Multiparametric Analysis of a Gravity Retaining Wall" Applied Sciences 11, no. 13: 6233. https://doi.org/10.3390/app11136233
APA StyleVarga, R., Žlender, B., & Jelušič, P. (2021). Multiparametric Analysis of a Gravity Retaining Wall. Applied Sciences, 11(13), 6233. https://doi.org/10.3390/app11136233






