Ab Initio Study of Martensitic Transformation in NiTiPt High Temperature Shape Memory Alloys
Abstract
:1. Introduction
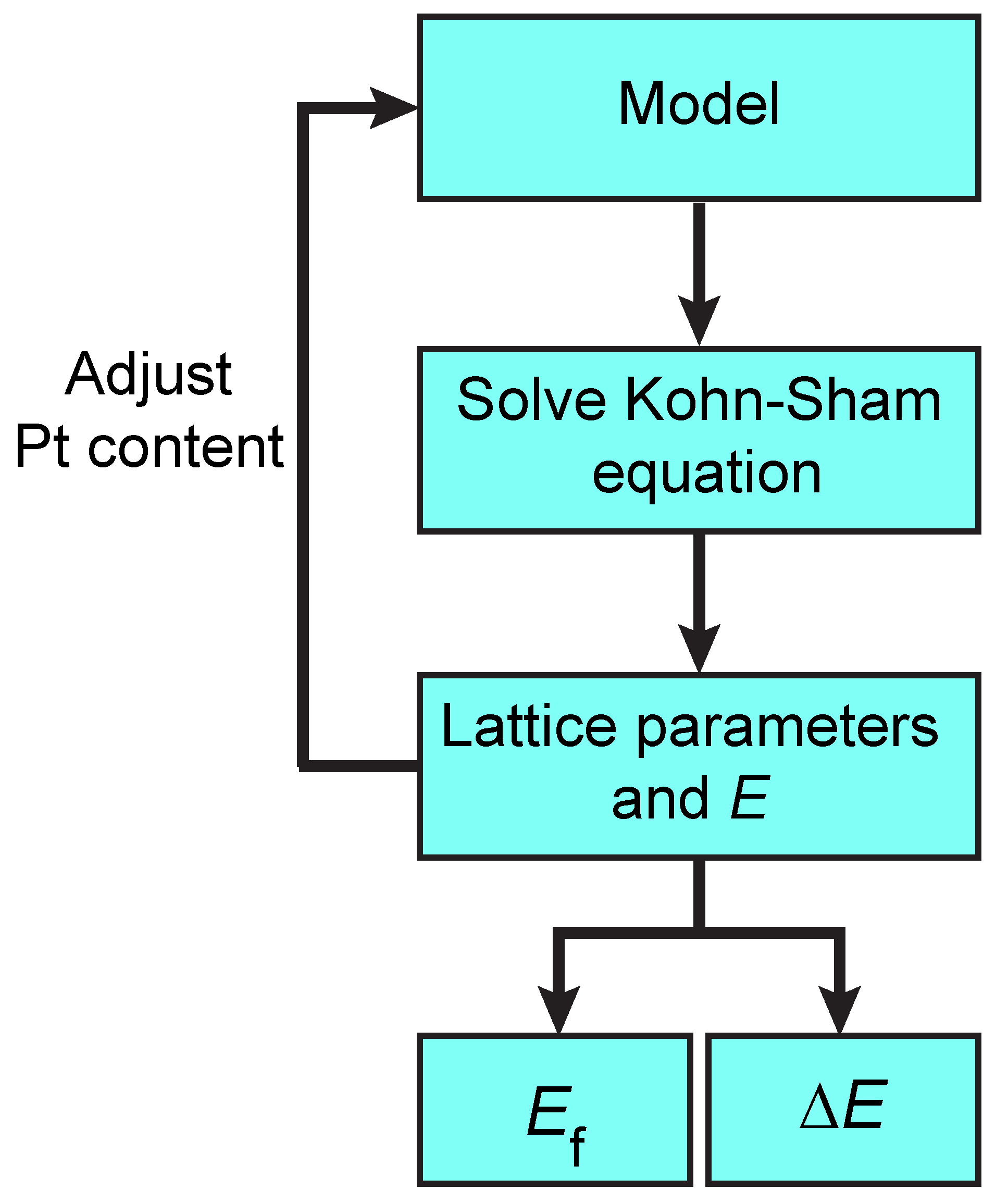
2. Model and Methodology
3. Results and Discussion
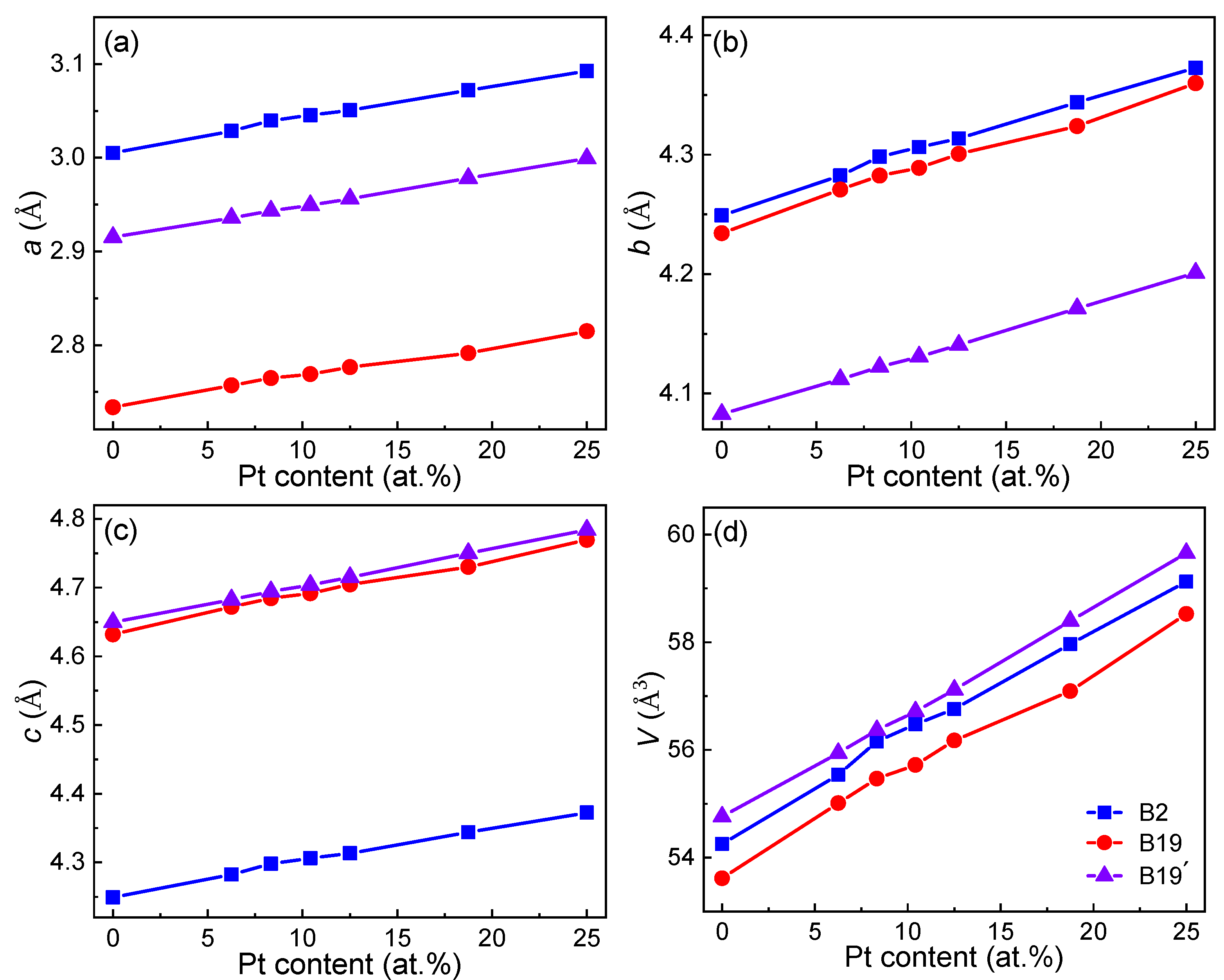
3.1. Crystal Structures of TiNiPt Alloys
3.2. Phase Stabilities of TiNiPt Alloys
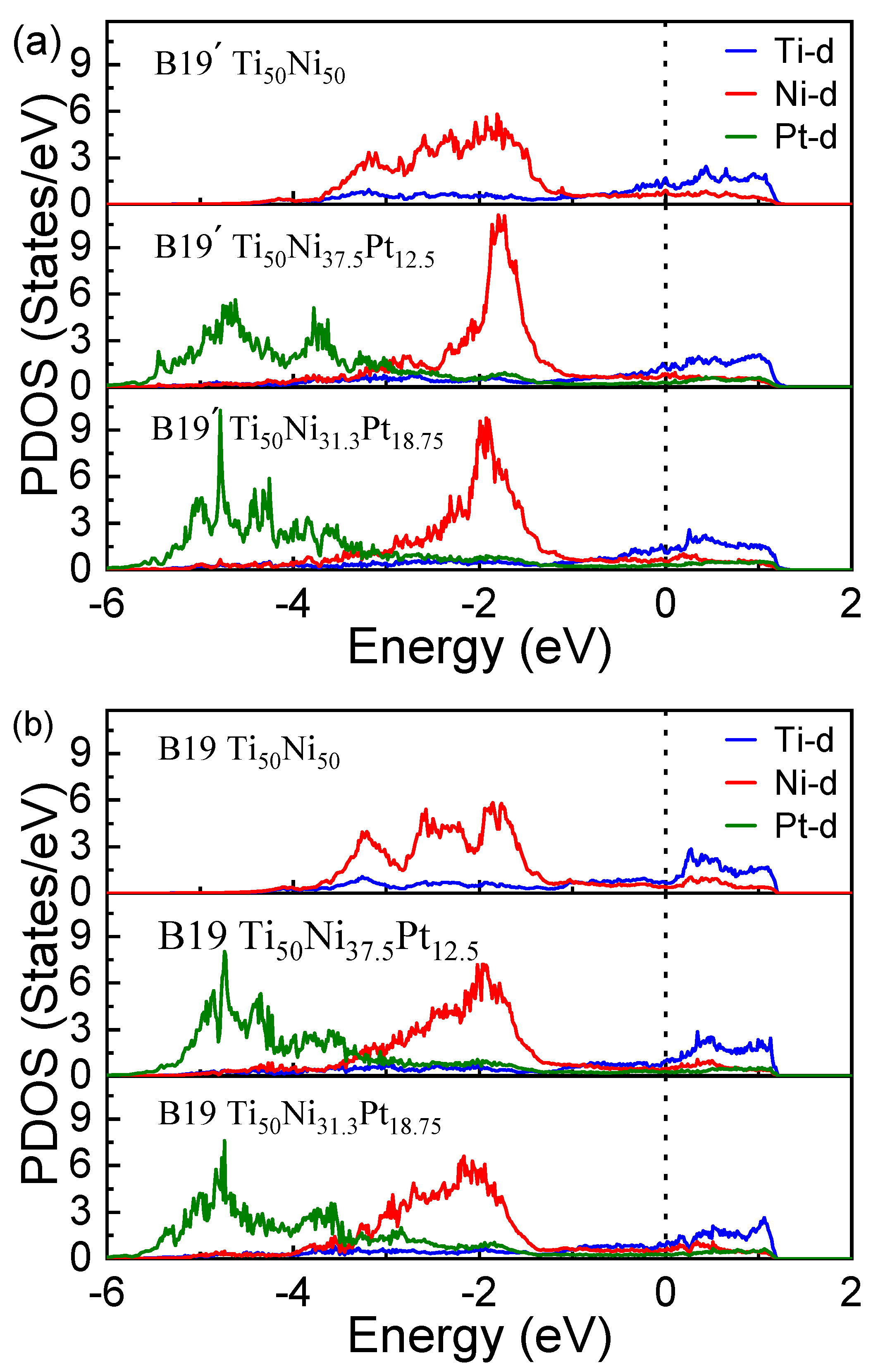
3.3. Electronic Structures
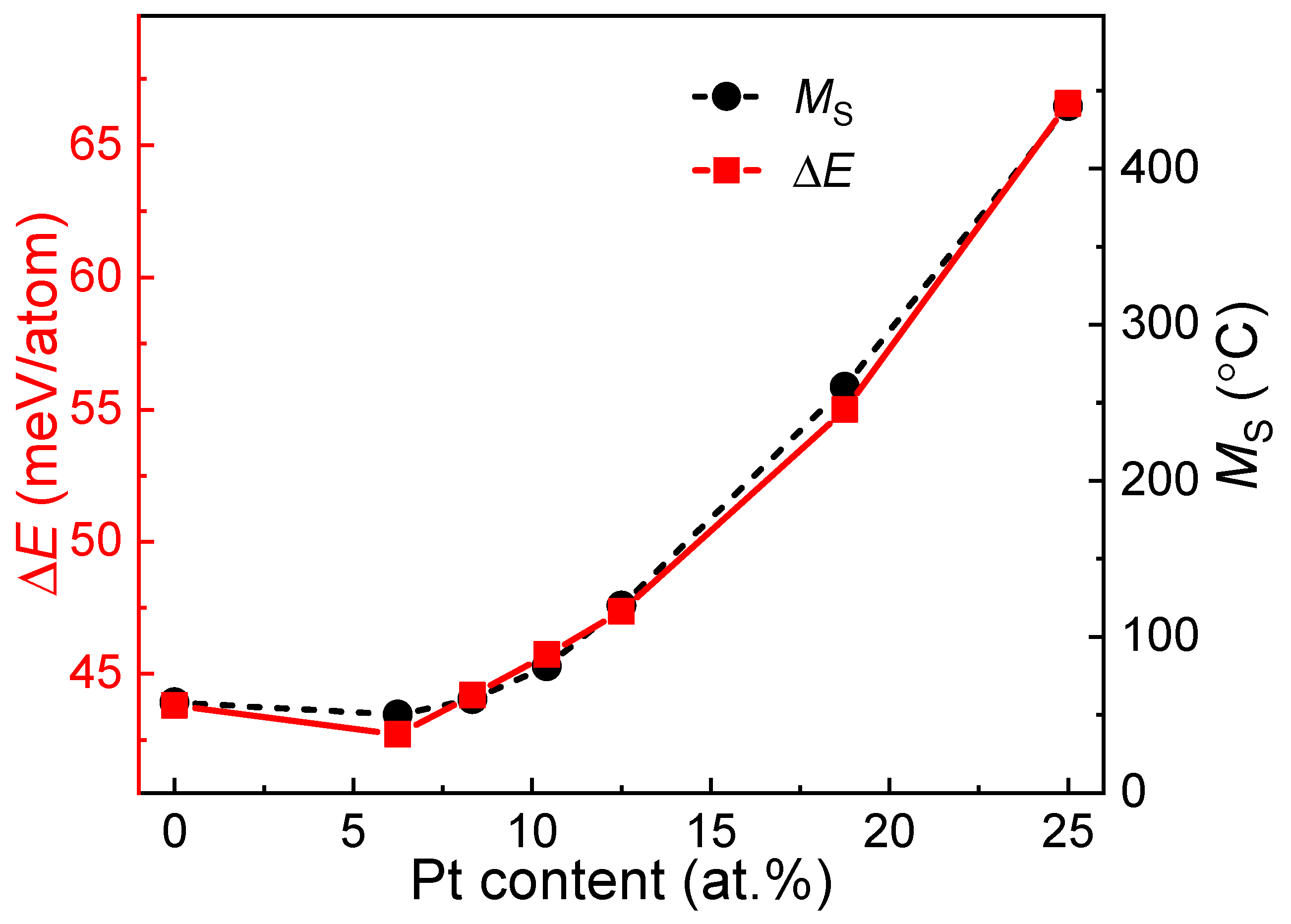
3.4. Energy Differences between the Austenite and Martensite
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buehler, W.J.; Wiley, R.C. TiNi-ductile intermetallic compound. ASM-Trans. 1962, 55, 269–276. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Guda Vishnu, K.; Strachan, A. Size effects in NiTi from density functional theory calculations. Phys. Rev. B 2012, 85, 014114. [Google Scholar] [CrossRef] [Green Version]
- Haskins, J.B.; Lawson, J.W. Finite temperature properties of NiTi from first principles simulations: Structure, mechanics, and thermodynamics. J. Appl. Phys. 2017, 121, 205103. [Google Scholar] [CrossRef]
- Kumar, P.; Waghmare, U.V. First-principles phonon-based model and theory of martensitic phase transformation in NiTi shape memory alloy. Materialia 2020, 9, 100602. [Google Scholar] [CrossRef]
- Lang, L.; Payne, A.; Valencia-Jaime, I.; Verstraete, M.J.; Bautista-Hernández, A.; Romero, A.H. Assessing Nickel Titanium Binary Systems Using Structural Search Methods and Ab Initio Calculations. J. Phys. Chem. C 2021, 125, 1578–1591. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Stable atomic structure of NiTi austenite. Phys. Rev. B 2014, 90, 060102. [Google Scholar] [CrossRef] [Green Version]
- Frenzel, J.; Wieczorek, A.; Opahle, I.; Maaß, B.; Drautz, R.; Eggeler, G. On the effect of alloy composition on martensite start temperatures and latent heats in Ni-Ti-based shape memory alloys. Acta Mater. 2015, 90, 213–231. [Google Scholar] [CrossRef]
- Bozzolo, G.; Noebe, R.D.; Mosca, H.O. Site preference of ternary alloying additions to NiTi: Fe, Pt, Pd, Au, Al, Cu, Zr and Hf. J. Alloys Compd. 2005, 389, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Karaman, I.; Noebe, R.D. High temperature shape memory alloys. Int. Mater. Rev. 2010, 55, 257–315. [Google Scholar] [CrossRef]
- Zarinejad, M.; Liu, Y.; White, T.J. The crystal chemistry of martensite in NiTiHf shape memory alloys. Intermetallics 2008, 16, 876–883. [Google Scholar] [CrossRef]
- Bigelow, G.S.; Padula, S.A.; Garg, A.; Gaydosh, D.; Noebe, R.D. Characterization of Ternary NiTiPd High-Temperature Shape-Memory Alloys under Load-Biased Thermal Cycling. Metall. Mater. Trans. A 2010, 41, 3065–3079. [Google Scholar] [CrossRef] [Green Version]
- Inoue, S.; Sawada, N.; Namazu, T. Effect of Zr content on mechanical properties of Ti-Ni-Zr shape memory alloy films prepared by dc magnetron sputtering. Vacuum 2009, 83, 664–667. [Google Scholar] [CrossRef]
- Bozzolo, G.; Mosca, H.O.; del Grosso, M.F. Energy of formation, lattice parameter and bulk modulus of (Ni, X)Ti alloys with X = Fe, Pd, Pt, Au, Al, Cu, Zr, Hf. Intermetallics 2008, 16, 668–675. [Google Scholar] [CrossRef]
- Mosca, H.O.; Bozzolo, G.; del Grosso, M.F. Atomistic modeling of ternary additions to NiTi and quaternary additions to Ni-Ti-Pd, Ni-Ti-Pt and Ni-Ti-Hf shape memory alloys. Phys. B Conden. Matter 2012, 407, 3244–3247. [Google Scholar] [CrossRef]
- Potapov, P.L.; Shelyakov, A.V.; Gulyaev, A.A.; Svistunov, E.L.; Matveeva, N.M.; Hodgson, D. Effect of Hf on the structure of Ni-Ti martensitic alloys. Mater. Lett. 1997, 32, 247–250. [Google Scholar] [CrossRef]
- Suresh, K.S.; Kim, D.I.; Bhaumik, S.K.; Suwas, S. Evolution of microstructure and texture in Ni49.4Ti38.6Hf12 shape memory alloy during hot rolling. Intermetallics 2013, 42, 1–8. [Google Scholar] [CrossRef]
- Hsieh, S.F.; Wu, S.K. A Study on Ternary Ti-rich TiNiZr Shape Memory Alloys. Mater Charact. 1998, 41, 151–162. [Google Scholar] [CrossRef]
- Koenig, D.; Zarnetta, R.; Savan, A.; Brunken, H.; Ludwig, A. Phase transformation, structural and functional fatigue properties of Ti-Ni-Hf shape memory thin film. Acta Mater. 2011, 59, 3267–3275. [Google Scholar] [CrossRef]
- Meng, X.L.; Cai, W.; Chen, F.; Zhao, L.C. Effect of aging on martensitic transformation and microstructure in Ni-rich TiNiHf shape memory alloy. Scr. Mater. 2006, 54, 1599–1604. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Seyedein, S.H.; Salehi, M.T.; Aboutalebi, M.R. Age-induced multi-stage transformation in a Ni-rich NiTiHf alloy. Acta Mater. 2013, 61, 2583–2594. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, F.; Tian, B.; Li, L.; Zheng, Y. Microstructure and martensitic transformation of Ti49Ni51−xHfx high temperature shape memory alloys. Mater. Lett. 2009, 63, 1869–1871. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, Y.; Miao, J. Phase transformation in NiTiHf shape memory alloy thin films. Thin Solid Films 2008, 516, 5393–5396. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, Y.; Miao, J.; Zhao, L. Characterization of a nanocrystalline NiTiHf high temperature shape memory alloy thin film. Scr. Mater. 2005, 52, 983–987. [Google Scholar] [CrossRef]
- Acar, E.; Karaca, H.E.; Tobe, H.; Noebe, R.D.; Chumlyakov, Y.I. Characterization of the shape memory properties of a Ni45.3Ti39.7Hf10Pd5 alloy. J. Alloys Compd. 2013, 578, 297–302. [Google Scholar] [CrossRef]
- Belbasi, M.; Salehi, M.T.; Mousavi, S.A.A.A.; Ebrahimi, S.M. A study on the mechanical behavior and microstructure of NiTiHf shape memory alloy under hot deformation. Mater. Sci. Eng. A 2013, 560, 96–102. [Google Scholar] [CrossRef]
- Meng, X.L.; Cai, W.; Fu, Y.D.; Li, Q.F.; Zhang, J.X.; Zhao, L.C. Shape-memory behaviors in an aged Ni-rich TiNiHf high temperature shape-memory alloy. Intermetallics 2008, 16, 698–705. [Google Scholar] [CrossRef]
- Meng, X.L.; Zheng, Y.F.; Cai, W.; Zhao, L.C. Two-way shape memory effect of a TiNiHf high temperature shape memory alloy. J. Alloys Compd. 2004, 372, 180–186. [Google Scholar] [CrossRef]
- Saghaian, S.M.; Karaca, H.E.; Tobe, H.; Souri, M.; Noebe, R.; Chumlyakov, Y.I. Effects of aging on the shape memory behavior of Ni-rich Ni50.3Ti29.7Hf20 single crystals. Acta Mater. 2015, 87, 128–141. [Google Scholar] [CrossRef]
- Karaca, H.E.; Saghaian, S.M.; Ded, G.; Tobe, H.; Basaran, B.; Maier, H.J.; Noebe, R.D.; Chumlyakov, Y.I. Effects of nanoprecipitation on the shape memory and material properties of an Ni-rich NiTiHf high temperature shape memory alloy. Acta Mater. 2013, 61, 7422–7431. [Google Scholar] [CrossRef]
- Meng, X.L.; Cai, W.; Zheng, Y.F.; Zhao, L.C. Phase transformation and precipitation in aged Ti-Ni-Hf high-temperature shape memory alloys. Mater. Sci. Eng. A 2006, 438-440, 666–670. [Google Scholar] [CrossRef]
- Santamarta, R.; Arróyave, R.; Pons, J.; Evirgen, A.; Karaman, I.; Karaca, H.E.; Noebe, R.D. TEM study of structural and microstructural characteristics of a precipitate phase in Ni-rich Ni-Ti-Hf and Ni-Ti-Zr shape memory alloys. Acta Mater. 2013, 61, 6191–6206. [Google Scholar] [CrossRef]
- Yang, F.; Coughlin, D.R.; Phillips, P.J.; Yang, L.; Devaraj, A.; Kovarik, L.; Noebe, R.D.; Mills, M.J. Structure analysis of a precipitate phase in an Ni-rich high-temperature NiTiHf shape memory alloy. Acta Mater. 2013, 61, 3335–3346. [Google Scholar] [CrossRef]
- Yang, F.; Kovarik, L.; Phillips, P.J.; Noebe, R.D.; Mills, M.J. Characterizations of precipitate phases in a Ti-Ni-Pd alloy. Scr. Mater. 2012, 67, 145–148. [Google Scholar] [CrossRef]
- Rios, O.; Noebe, R.D.; Biles, T.; Garg, A.; Palczer, A.; Scheiman, D.; Seifert, H.J.; Kaufman, M. Characterization of Ternary NiTiPt High-Temperature Shape Memory Alloys. Proc. SPIE 2005, 5761, 376–387. [Google Scholar]
- Zarnetta, R.; Takahashi, R.; Young, M.L.; Savan, A.; Furuya, Y.; Thienhaus, S.; Maaß, B.; Rahim, M.; Frenzel, J.; Brunken, H.; et al. Identification of quaternary shape memory alloys with near-zero thermal hysteresis and unprecedented functional stability. Adv. Funct. Mater. 2010, 20, 1917–1923. [Google Scholar] [CrossRef]
- Zhang, Z.; James, R.D.; Müller, S. Energy barriers and hysteresis in martensitic phase transformations. Acta Mater. 2009, 57, 4332–4352. [Google Scholar] [CrossRef] [Green Version]
- Meisner, L.L.; Sivokha, V.P. The effect of applied stress on the shape memory behavior of TiNi-based alloys with different consequences of martensitic transformations. Phys. B Conden. Matter 2004, 344, 93–98. [Google Scholar] [CrossRef]
- Smialek, J.L.; Humphrey, D.L.; Noebe, R.D. Comparative Oxidation Kinetics of a NiPtTi High Temperature Shape Memory Alloy. Oxid. Met. 2010, 74, 125–144. [Google Scholar] [CrossRef]
- Chovan, D.; Nolan, M.; Tofail, S.A.M. First principles simulations of elastic properties of radiopaque NiTiPt. J. Alloys Compd. 2015, 630, 54–59. [Google Scholar] [CrossRef]
- Tan, C.L.; Tian, X.H.; Ji, G.J.; Gui, T.L.; Cai, W. Elastic property and electronic structure of TiNiPt high-temperature shape memory alloys. Solid State Commun. 2008, 147, 8–10. [Google Scholar] [CrossRef]
- Gou, L.; Liu, Y.; Ng, T.Y. An investigation on the crystal structures of Ti50Ni50−xCux shape memory alloys based on density functional theory calculations. Intermetallics 2014, 53, 20–25. [Google Scholar] [CrossRef]
- Hu, Q.M.; Yang, R.; Lu, J.M.; Wang, L.; Johansson, B.; Vitos, L. Effect of Zr on the properties of (TiZr)Ni alloys from first-principles calculations. Phys. Rev. B 2007, 76, 224201. [Google Scholar] [CrossRef]
- Ma, L.; Wang, X.; Shang, J.X. Effect of Pd in NiTi on the martensitic transformation temperatures and hysteresis: A first-principles study. Acta Phys. Sin. 2014, 63, 233103. [Google Scholar]
- Singh, N.; Talapatra, A.; Junkaew, A.; Duong, T.; Gibbons, S.; Li, S.; Thawabi, H.; Olivos, E.; Arróyave, R. Effect of ternary additions to structural properties of NiTi alloys. Comput. Mater. Sci. 2016, 112, 347–355. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.L.; Cai, W.; Tian, X.H. First-principles study on the effect of Hf content on martensitic transformation temperature of TiNiHf alloy. Chin. Phys. 2006, 15, 2718–2723. [Google Scholar]
- Yang, X.; Ma, L.; Shang, J. Martensitic transformation of Ti50(Ni50−xCux) and Ni50(Ti50−xZrx) shape-memory alloys. Sci. Rep. 2019, 9, 3221. [Google Scholar] [CrossRef] [Green Version]
- Kibey, S.; Sehitoglu, H.; Johnson, D.D. Energy landscape for martensitic phase transformation in shape memory NiTi. Acta Mater. 2009, 57, 1624–1629. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Shang, J.; Xu, H. First principles calculations on martensitic transformation and phase instability of Ni-Mn-Ga high temperature shape memory alloys. Appl. Phys. Lett. 2006, 89, 231921. [Google Scholar] [CrossRef]
- Alonso, P.; Rubiolo, G. Relative stability of bcc structures in ternary alloys with Ti50Al25Mo25 composition. Phys. Rev. B 2000, 62, 237. [Google Scholar] [CrossRef]
- Holec, D.; Friák, M.; Dlouhy, A.; Neugebauer, J. Ab initio study of point defects in NiTi-based alloys. Phys. Rev. B 2014, 89, 014110. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, K.; Ishida, S.; Asano, S. Electron concentration and structural transformation of Ni2MnGa-based shape memory alloys. Mater. Trans. 2002, 43, 846–851. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, A.; Biswas, C.; Banik, S.; Dhaka, R.S.; Shukla, A.K.; Barman, S.R. Influence of Ni doping on the electronic structure of Ni2MnGa. Phys. Rev. B 2005, 72, 073103. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Shang, J.X.; Wang, F.H.; Chen, Y. Origin of the strain glass transition in Ti50(Ni50−xDx) alloys. J. Alloys Compd. 2016, 678, 325–328. [Google Scholar] [CrossRef]
- Huang, X.; Ackland, G.J.; Rabe, K.M. Crystal structures and shape-memory behaviour of NiTi. Nat. Mater. 2003, 2, 307–311. [Google Scholar] [CrossRef] [PubMed]
- Kudoh, Y.; Tokonami, M.; Miyazaki, S.; Otsuka, K. Crystal-structure of the martensite in Ti-49.2at%Ni alloy analyzed by the single-crystal X-ray-diffration method. Acta Metall. 1985, 33, 2049–2056. [Google Scholar] [CrossRef]
- Philip, T.; Beck, P.A. CsCl-type ordered structures in binary alloys of transition elements. Trans. AIME J. Metal. 1957, 209, 1269–1271. [Google Scholar] [CrossRef]
- Zhang, J.M.; Guo, G.Y. Microscopic Theory of the Shape Memory Effect in TiNi. Phys. Rev. Lett. 1997, 78, 4789–4792. [Google Scholar] [CrossRef]
- Simon, A. Intermetallic Compounds and the Use of Atomic Radii in Their Description. Angew. Chem. Int. Ed. 1983, 22, 95–113. [Google Scholar] [CrossRef]
- Zarinejad, M.; Liu, Y. Dependence of Transformation Temperatures of NiTi-based Shape-Memory Alloys on the Number and Concentration of Valence Electrons. Adv. Funct. Mater. 2008, 18, 2789–2794. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Recent developments in the research of shape memory alloys. Intermetallics 1999, 7, 511–528. [Google Scholar] [CrossRef]
- Ye, Y.; Chan, C.; Ho, K. Structural and electronic properties of the martensitic alloys TiNi, TiPd, and TiPt. Phys. Rev. B 1997, 2, 8–22. [Google Scholar] [CrossRef] [Green Version]



| n | Pt Content (at.%) | Site Occupation of Pt |
|---|---|---|
| 3 | 6.25 | 8, 11, 24 |
| 4 | 8.33 | 8, 11, 24, 18 |
| 5 | 10.42 | 5, 8, 11, 24, 18 |
| 6 | 12.50 | 2, 5, 8, 11, 24, 18 |
| 9 | 18.75 | 3, 5, 8, 9, 11, 16, 17, 22, 24 |
| 12 | 25.00 | 3, 5, 6, 8, 10, 11, 14, 16, 17, 19, 22, 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Shang, J. Ab Initio Study of Martensitic Transformation in NiTiPt High Temperature Shape Memory Alloys. Appl. Sci. 2021, 11, 6878. https://doi.org/10.3390/app11156878
Yang X, Shang J. Ab Initio Study of Martensitic Transformation in NiTiPt High Temperature Shape Memory Alloys. Applied Sciences. 2021; 11(15):6878. https://doi.org/10.3390/app11156878
Chicago/Turabian StyleYang, Xiaolan, and Jiaxiang Shang. 2021. "Ab Initio Study of Martensitic Transformation in NiTiPt High Temperature Shape Memory Alloys" Applied Sciences 11, no. 15: 6878. https://doi.org/10.3390/app11156878
APA StyleYang, X., & Shang, J. (2021). Ab Initio Study of Martensitic Transformation in NiTiPt High Temperature Shape Memory Alloys. Applied Sciences, 11(15), 6878. https://doi.org/10.3390/app11156878





