COVID-19 Lesion Segmentation Using Lung CT Scan Images: Comparative Study Based on Active Contour Models

Abstract

Pneumonia is a lung infection that threatens all age groups. In this paper, we use CT scans to investigate the effectiveness of active contour models (ACMs) for segmentation of pneumonia caused by the Coronavirus disease (COVID-19) as one of the successful methods for image segmentation. A comparison has been made between the performances of the state-of-the-art methods performed based on a database of lung CT scan images. This review helps the reader to identify starting points for research in the field of active contour models on COVID-19, which is a high priority for researchers and practitioners. Finally, the experimental results indicate that active contour methods achieve promising results when there are not enough images to use deep learning-based methods as one of the powerful tools for image segmentation.

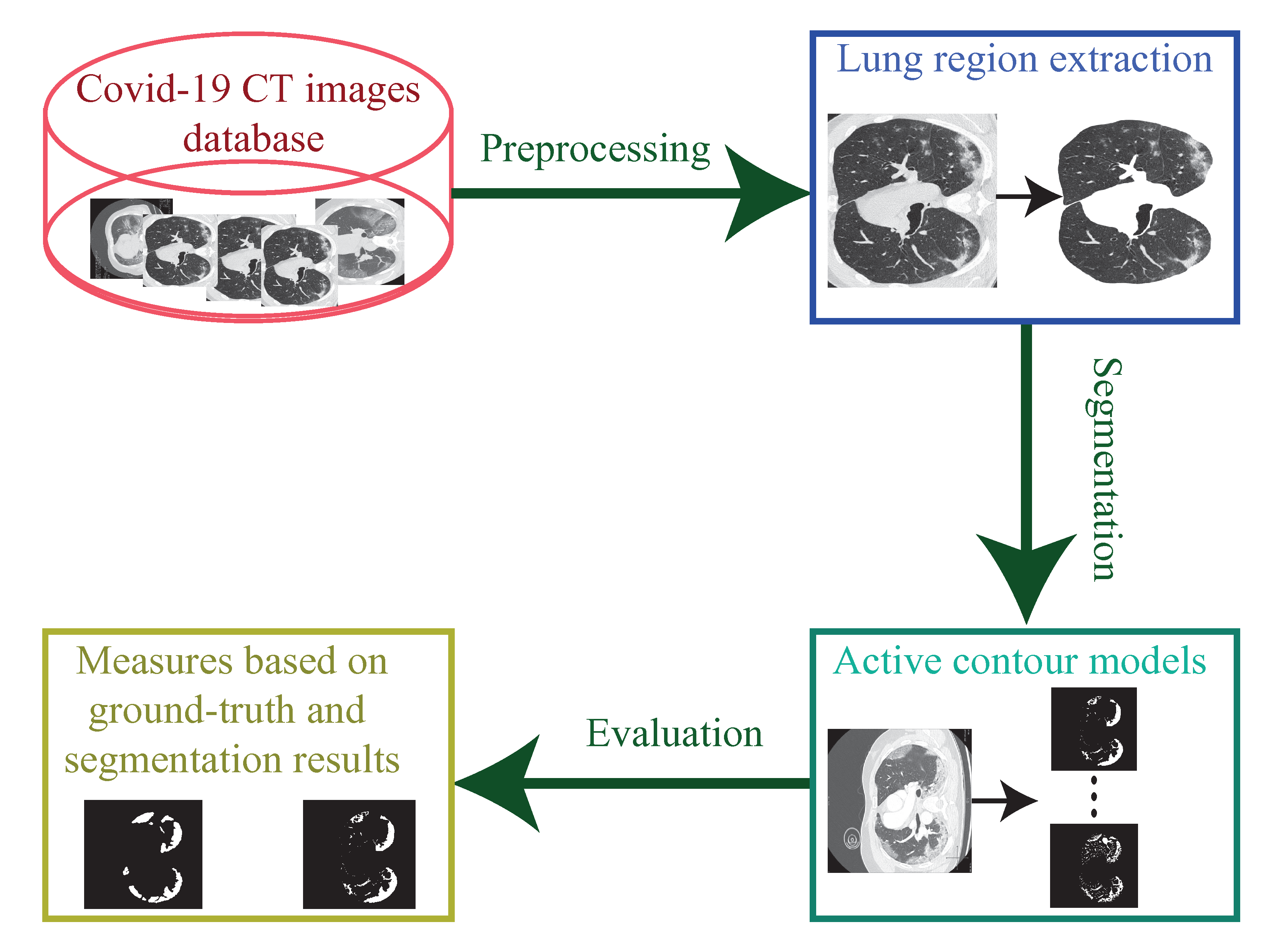
1. Introduction

The new 2019 coronavirus, named COVID-19 by the World Health Organization (WHO), is attracting a lot of attention lately because it is a new type of coronavirus that is highly contagious and has not been seen in humans before [1]. As of 20 August 2021, 209,201,939 confirmed cases of COVID-19, including 4,390,467 deaths, have been reported by the WHO (https://covid19.who.int/ (accessed on 20 August 2021)). The current standard golden diagnostic method for COVID-19 cases is the detection of viral nucleic acids by Reverse Transcription Polymerase Chain Reaction (RT-PCR). Due to the lower sensitivity of some tests leading to false-negative results, other methods may be considered to aid in COVID-19 diagnosis. To facilitate COVID-19 diagnosis, medical radiological imaging is used as a valuable supplemental diagnostic tool to evaluate the infectious process. Radiologic imaging such as radiographs is usually performed in patients with clinical symptoms suggestive of pulmonary infection [1]. The authors of [2] showed that CT scan tests have higher sensitivity than RT-PCR tests. This point is also confirmed by the fact that CT scans and RT-PCR tests have sensitivities of 98% and 71%, respectively. However, the duration of diagnosis remains the major limitation of CT scans. Even experienced radiologists need about 21.5 min to analyze the test results of each case [2,3].

Therefore, identifying the region of infection can help reduce the time radiologists spend analyzing examination results. Automatic segmentation of the infection region can be achieved by effective segmentation algorithms. Currently, there are several segmentation algorithms in the literature that show accurate and robust segmentation results. In general, they can be divided into four categories, the clustering-based [4,5], the graph-cut-based [6,7], neural network-based (for example, deep learning methods) [8,9] and the active-contour-based methods [10,11,12,13,14]. The clustering-based methods use clustering algorithms such as Kmeans and fuzzy C-means, which are based on the assumption that each pixel can be assigned to pixels belonging to the same class because they have a certain distribution. The clustering-based methods have high efficiency but are sensitive to the initial clustering centers and require manual adjustment of the clustering number. In the graph cut-based methods, the pixel correlation is considered and the segmentation problem is converted into a graph partition problem where a cut energy model is constructed and the segmentation curve is the cut that minimizes the energy. The drawback of this method is the difficulty in constructing accurate weights for the correlations between pixels, which usually leads to over-segmentation or under-segmentation problems, especially in complicated regions. The neural network-based semantic segmentation solutions [8,9] require a large set of images to train the network, and also lack fine segmentation for tiny regions, which is very important in medical image analysis. One of the methods that ensures stable performance is the active contour model (snake model). This method grants closed boundaries and has proven to be effective and widely used. The general idea behind ACMs is to apply partial differential equations (PDEs) to iteratively evolve the initial contour toward object boundaries by minimizing a given energy function [15,16], which is a function of the internal and external energies of the contour.

Since our goal is to investigate the effectiveness of active contouring methods for segmenting COVID-19 infected regions from the CTSI, current methods for segmenting COVID-19 pneumonia using the CTSI are examined below. It should be noted that the segmentation methods in COVID-19 applications can be mainly divided into two categories, namely, the lung region-oriented methods and the lung lesion-oriented methods. The lung region-oriented methods aim to separate the lung regions, i.e., the entire lung and the lobe of the lung, from other (background) regions in CT or X-ray images, which is considered a prerequisite in COVID-19 applications [17,18,19,20,21,22,23,24,25,26]. To the best of our knowledge, most COVID-19 pneumonia segmentation methods are based on deep learning networks, including the classic U-Net [17,18,19,20,21,22], UNet++ [22,23], VB-Net [24]. UNet and its variants achieved reasonable segmentation results in images COVID-19. For example, Jin et al. [23] used the UNet++ network to segment the lung region from CT images. Then, the damaged region of the lung is separated. This process is challenging because the damaged area may have different shapes and textures. The authors of [21] developed an automatic AI-based analysis of CT images using a deep learning approach to classify CT images into coronavirus and non-coronavirus cases. They reused a system previously used to detect small opacities and nodules in the lungs and used UNet to segment lung images. To detect coronavirus abnormalities, they used the CNN architecture Resnet-50, which consists of 50 layers, to classify images into normal and abnormal cases. One of the most important approaches to visually interpret and explain medical imaging is Gradient Weighted Class Activation Mapping (Grad-CAM) [27]. Therefore, many studies have been conducted to segment COVID-19 infected regions based on activation mapping [28,29]. Finally, for more detail, the reader is referred to several comprehensive reviews of all works on this topic, including deep learning methods [30,31,32,33].

The aim of this work is to compare current active contour methods for detecting COVID-19 pneumonia infections using CTSI, as shown in Figure 1. Our proposed segmentation experiments are performed using the COVID-CS database [34], which contains one hundred CT COVID-19 images with dimensions of $512\times 512\times 1$ pixels, and all images are associated with the Ground-Truth Image (GTI). In this paper, we present the state-of-the-art methods that have been selected between 2008 and 2020 and have achieved the best results in medical image segmentation. Moreover, these methods were compared in terms of robustness to initialization.

This paper deals with CT COVID-19 image segmentation. The main contributions of this paper are described as follows:

• A survey of active contour models: One of the most important aspects of detecting diseases such as pneumonia from medical images is identifying the region of infection. Although deep learning methods are well suited for this goal, if there are not enough images to train deep learning methods, the experimental results of the paper show that active contour methods achieve promising results. Therefore, our main contribution is to verify whether the active contour model-based image processing methods can be useful when only one image is available;
• Study on COVID-19 as a current topic: To the best of the authors’ knowledge, this paper is the first attempt to study active contour models and comparisons on images of the disease;
• Pointing out a line of research for the next researchers: We examine different methods and show which of them are effective for the topic and where the problems lie.

The remainder of this paper is organised as follows: Section 2 presents our methodology, including the methodological background and the database description. Section 3 presents the experimental results, Section 4 discusses the results, and Section 5 concludes the paper.

2. Methodology

In this section, we describe the details of the ACM methods used in our experiments, including traditional and the state-of-the-art methods. We also explain the database to which the methods are applied. The main idea of ACM is to segment an image based on an initial contour by minimizing the energy associated with the sum of internal and external energy. Depending on the contour representation (parametric or level set) and object boundary description (edge-based or region-based), ACMs can be classified into four categories: parametric representation with edge-based description [15,35], parametric representation with region-based description [36,37], level set representation with edge-based description [38,39] and level set representation with region-based description [40,41]. In parametric ACM, the contour is explicitly represented as polynomials or splines [42,43]. Given an initial contour, the external energies drive the evolution of a parametric ACM, while the internal energies maintain the shape of the contour. The parametric ACM is capable of extracting a single object given a single initial contour. Its strength is that the parametric snakes have a limited capture range, i.e., the range where the external forces are is strong enough to drive the contour evolution. Therefore, they must be initialized near the object contour. Another problem is that the parametric snakes are not able to accurately capture concave shapes. In the ACMs with level set, the contour is implicitly represented in the zero level set. In this method, the deformation of the level set function leads to contour evolution. Compared to the parametric ACMs, the level set model can capture multiple objects by a single initial contour and complex geometry. However, since the level set models require the deformation of a higher dimensional function, these methods are generally slower than parametric methods [39]. Moreover, for many applications, such as medical image processing, it is necessary to extract only a single object [44] and therefore, in such situations, the parametric representation is preferred over the level set representation. To solve the contour evolution equation, each representation scheme must select appropriate numerical methods. The finite element method [45] is used for parametric snake models, while the finite difference method [46] is used for level set models. Boundary-based segmentation methods for describing object boundaries based on the external force include region-based and edge-based models. Region-based models use more global information to define object boundaries. To control the evolution, region-based models use the statistical information inside and outside the contour [40,41]. In the region-based approach, the deformation of ACM is based on an energy minimization algorithm. In the region-based method, many functions were considered as an edge stop function (ESF) [41], such as a signed pressure function (SPF). Edge-based models use image gradients to construct an ESF [39,42], which is used to stop contour evolution at object boundaries. Using the ESF, the boundary points can be characterized by a differential property with respect to the image gradient. It should be noted that hybrid description approaches have been used recently to take advantage of edge-based and region-based methods and avoid their drawbacks [47]. Two important challenges in using ACMs are initialization and convergence. For example, some parametric ACMs are affected by saddle point and stationary point problems that lead to convergence failure [39]. ACM models respond quickly to initial conditions, so a poor initial contour can lead to a poor result, as shown in Figure 2, which shows the initialization of the contour outside, overlapping (cross), or inside the image.

The region-based methods are more efficient than the edge-based methods in detecting the outer and interior boundaries because they are less sensitive to the location of the initial contour. However, for weak edges and concave shapes, the edge-based methods are more successful than the region-based descriptions.

2.1. Background of ACMS

In this subsection, a background knowledge of ACMs is presented by briefly explaining traditional ACMs, geometric ACM models, and deep learning methods with loss functions based on ACMs.

2.1.1. Traditional ACM

The earliest active contour or snake, which was a parametric representation with edge-based description, was proposed by Kass et al. (1988) [42]. Active contours are declared as an energy minimization process. The energy functional is a function of contour’s internal energy ($E_{int}$) addition to the external energy ($E_{ext}$). These energies are two functions of the set of points ($x\left(s\right),y\left(s\right)$), which make up a snake $c\left(s\right)=\left(x\right(s),y(s\left)\right)$. The energy functional denoted by $E_{Snake}$ is computed as follows:

$$\begin{array}{c}\hfill E_{\mathrm{Snake}}={\int }_0^1\left[E_{\mathrm{int}}\left(c\left(s\right)\right)+E_{\mathrm{ext}}\left(c\left(s\right)\right)\right]ds,\end{array}$$

(1)

where $s\in [0,1]$ is the normalized length around the snake and to control the behavior of the snake naturally, $E_{int}$ is defined as follows:

$$\begin{array}{c}\hfill E_{int}=\frac{\alpha \left(s\right){\left|c^{\prime }\left(s\right)\right|}^2+\beta \left(s\right){\left|c^{″}\left(s\right)\right|}^2}{2},\end{array}$$

(2)

where the first and the second derivatives of $c\left(s\right)$ are shown by $c^{\prime }\left(s\right)$ and $c^{″}\left(s\right)$ with respect to s and $\alpha$ and $\beta$ called elasticity and rigidity parameters, respectively, which are the weighting parameters of contour. The term of external energy, $E_{ext}$, attracts a snake to the chosen low-level features (such as edge points) such that it has smaller value near the object boundary and bigger value in other areas.

Limit capture range and poor convergence to the concave regions are two major issues in ACM. Figure 3 shows an example of concave regions which has not been captured.

2.1.2. Geometric Active Contours (Gac) Models

One of the most popular level set representations with edge-based models is the Geometric active contours (GAC) model [38]. This model utilizes image gradient to construct an ESF. Usually, a positive, decreasing and regular ESF such as $g\left(t\right)$ is used such that ${lim}_{t\to \infty }g\left(t\right)=0$. For instance, $g\left(\right|\nabla I\left|\right)$ can be computed using the following formula:

$$\begin{array}{c}\hfill g\left(\right|\nabla I\left|\right)=\frac{1}{1+{\left|\nabla G_{\sigma }\ast I\right|}^2},\end{array}$$

(3)

where $G_{\sigma }\ast I$ shows the convolution of Gaussian kernel (standard deviation of $\sigma$) and image I. The GAC model suffers some major disadvantages as follows:

• High computational cost due to computation of gradient of the curvature approximation of the current level set at each iteration;
• Since the GAC model is in terms of the curvature and the gradient, only local boundary information is used. This leads to the GAC model being affected by input noise. This problem is shown in Figure 4.

2.1.3. The C-V Model

The C-V model is a parametric representation with region-based description presented by Chan and Vese [40]. For a given image I in domain $\Omega$, the C-V model is formulated (parametric) by minimizing the following energy functional:

$$\begin{array}{cc}\hfill E_{C-V}=& {\lambda }_1{\int }_{\mathrm{inside}\left(c\right)}{\left|I\left(x\right)-c_1\right|}^{2}dx\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & +{\lambda }_2{\int }_{\mathrm{outside}\left(C\right)}{\left|I\left(x\right)-c_2\right|}^{2}dx,x\in \Omega \hfill \end{array}$$

(5)

where $c_1$ and $c_2$ show the average intensities inside and outside the contour, respectively. Two major disadvantages of C-V model are as follows:

• Similar to GAC model, C-V model also needs to calculate the curvature approximation $\delta \left(\varphi \right)$, which has a high computational expense;
• Despite power of global segmentation of the C-V model with a proper initial contour, it cannot extract the interior contour without setting the initial contour inside the object and fails to extract all the objects. This problem has been shown in Figure 5.

2.1.4. Deep Learning Approaches

Deep learning models showed better results, but are limited to pixel-wise adaptations of the segmentation map. This limitation can be addressed by considering the size of the boundaries and the areas inside and outside the region of interest during the learning process. This can be achieved by using an active contour loss function inspired by ACMs. This new loss function combines geometric information with region similarity to enable more accurate segmentation. The ACM loss function is used as a loss function in many deep learning models, as in [48,49,50,51].

2.2. The State-of-the-Art Methods

In this section, we review some of the best proposed ACMs and present the main advantages and disadvantages.

2.2.1. Magnetostatic Active Contour (MAC) Model

The magnetostatic active contour (MAC) model is based on the level set representation with edge-based description [39]. MAC represents the active contour using an implicit model in which the contour, c, is defined as follows:

$$\begin{array}{c}\hfill c=\left\{\overline{x}\right|\varphi \left(\overline{x}\right)=0\},\end{array}$$

(6)

where $\varphi :{\mathbb{R}}^2\to \mathbb{R}$. For image segmentation MAC considers the following PDE:

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial t}=\alpha s\left(\overline{x}\right)\nabla \left(\frac{\nabla \varphi }{|\nabla \varphi |}\right)|\nabla \varphi |-(1-\alpha )F\left(\overline{x}\right)\nabla \varphi ,\end{array}$$

(7)

where $\alpha$, $s\left(\overline{x}\right)$, and $F\left(\overline{x}\right)$ are a real constant, the stopping function (Sobel filter), and the magnetostatic force, respectively. The advantages of MAC compared to other related works are as follows:

• Significant improvement in initialization invariance;
• Significant improvement in convergence capability; the contour attracts into deep concave regions;
• Is not affected by stationary point and saddle point problems;
• It is able to capture complex geometries;
• It is able to capture multiple objects with a single initial contour.

2.2.2. Online Region-Based Active Contour Model (Oracm)

The ORACM is introduced as representing the level set with region-based ACM. The models do not require any parameters. Compared to traditional ACMs, the ORACM requires less time without a change in the segmentation accuracy. In each iteration, the ORCAM performs block thresholding. Rigorous boundaries and small particles that do not belong to the object and are produced outside of this process. To tackle this problem, morphological operations such as closing and opening are applied. The level set function, $\varphi \left(x\right)$, is initialized to constants, which have different signs such as $-1$ and $+1$ inside and outside the contour. A simple and efficient level set updating formulation is used in ORACM as follows:

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial t}=H(SPF\left(I\left(x\right)\right))·\varphi \left(x\right),\end{array}$$

(8)

where $H(.)$ is the Heaviside function, and $SPF(.)$ is the signed pressure function defined as follows:

$$\begin{array}{c}\hfill SPF\left(I(x,y)\right)=\frac{I(x,y)-\frac{c_1-c_2}{2}}{max\left(\right|I(x,y)-\frac{c_1-c_2}{2}\left|\right)},\end{array}$$

(9)

where I and $\varphi$ show an input image and the current level set, respectively. Two parameters, $c_1$ and $c_2$, have the same definitions as (20) and (21), respectively. The advantages of ORACM are as follows:

• Decreasing efficiency without changing the accuracy of the image segmentation process;
• Accurate segmentation of all object regions in both inside and outside for medical, real, and synthetic images with holes, complex backgrounds, weak edges, and high noise.

The disadvantage of ORACM is that it supports only bimodal segmentation of piecewise constant intensity distribution. Therefore, the application of ORACM is limited to the cases satisfied the above constraints. It should be noted that two types of ORACM have been conducted by researchers called ORACM1 and ORACM2 which consider ORACM without or with the morphological operations, respectively.

2.2.3. Selective Binary and Gaussian Filtering Regularized Level Set (Sbgfrls)

The SBGFRLS [47] is an ACM based on level set representation with a region-based description. This model uses both global and local information. At the initialization step, a user-defined active contour is determined and it is continuously updated by a region-based signed pressure function (SPF) defined by (25). Unlike the C-V method, obtaining $c_1$ and $c_2$ using (20) and (21), SBGFRLS uses the H Heaviside function described in (22) only with $\epsilon =0$. The SPF function tunes the signs of the pressure force inside and outside the region of interest. For example, the contour shrinks and expands based on whether it is outside or inside the object. The SBGFRLS obtains the corresponding variation level set by:

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial t}=SPF\left(I\left(x\right)\right)·\alpha .|\nabla \varphi |,\end{array}$$

(10)

where, to control the speed, a constant $\alpha$ is used. The advantages of SBGFRLS are as follows:

• Robust against noise because the image statistical information is used to stop the curve evolution on the desired boundaries;
• Good performance on images with weak edges or even without edges;
• Initial curve can be defined anywhere to extract the interior boundaries of the objects

However, the disadvantages of the ACM with SBGFRLS include the following cases:

• Difficult to use ACM with SBGFRLS on different images because it needs to be tuned according to the image which is why it cannot be used on real-time video images;
• The slowness of the method caused by propagating the SPF function results in the boundary of the level set function only using $|\nabla \varphi |$ at the level set. Updating only the boundary of the level set is the main cause of the slowness.

2.2.4. Level Set Active Contour Model (Lsacm)

The LSACM is a level set method that relies on the region for image segmentation in the presence of intensity inhomogeneity. This method models the inhomogeneous objects as Gaussian distributions of different means and variances. Using a sliding window, the original image is mapped into another domain. In this area, every object’s intensity distribution is still Gaussian but more distinct. It is possible to approximate the means of the Gaussian distributions in the transformed domain by multiplying a bias field with the original signal inside the window. A functional energy of maximum likelihood is then defined in the entire image region, which combines the bias field, the level set function, and the partly constant function which approximates the true image signal [10].

The method works by combining information from neighbouring pixels that belong to the same class. In this approach, the desired object is separated from its background. Given $N{R}_x$, a neighboring region centered at location x, i.e., $N{R}_x=\left\{y\right||y-x|\le \rho \}$, where for the region $N{R}_x$, $\rho$ is its radius. The whole image domain $\Omega$ can be represented as $\Omega ={\cup }_{i=1,\dots ,n}{\Omega }_i$ with ${\Omega }_i\cap {\Omega }_i=\varnothing$, for all $i\ne j$, where ${\Omega }_i$ is the $ith$ object region. A mapping $\mathcal{T}:I(\mathbf{x}|{\theta }_i,B)\to \mathcal{I}(\mathbf{x}|{\theta }_i,B)$ from original image intensity domain $ID\left(\mathcal{T}\right)$ to another domain $RD\left(\mathcal{T}\right)$ by averaging image intensities is defined as

$$\begin{array}{c}\hfill \mathcal{I}(\mathbf{x}|{\theta }_i,B)=\frac{1}{L_i\left(\mathbf{x}\right)}{\int }_{{\Omega }_i\cap N{R}_x}I(\mathbf{y}|{\theta }_i,B,\mathbf{x})d\mathbf{y}\end{array}$$

(11)

where the number of pixels in region ${\Omega }_i\cap N{R}_x$ is obtained with $L_i\left(x\right)=\left|{\Omega }_i\cap N{R}_x\right|$. The intensity of pixel x is assumed to be independently distributed with a Gaussian distribution, that is, $P\left(\mathcal{I}\right(\mathbf{x}|{\theta }_i,B\left)\right)=\mathcal{N}(I|U_i\left(\mathbf{x}\right),\frac{{\sigma }_i^2}{L_i\left(\mathbf{x}\right)})$ where $U_i$ and ${\sigma }_i$ are the spatial varying mean and the standard deviation subject to the object in region ${\Omega }_i$, for all $\mathcal{I}\left(\mathbf{x}\right|{\theta }_i)\in RD\left(\mathcal{I}\right)$.

The advantages of this method are: it achieves soft classification, it is robust against noise and it mitigates the over-smoothing of object boundaries problem.

The disadvantages are: only the neighbouring intensities belonging to the same class contribute to each class and the overlapping parts of the statistical distributions among different classes of intensities are suppressed.

2.2.5. Region-Scalable Fitting and Optimized Laplacian of Gaussian Energy (Rsfolge)

The RSFOLGE applies a LoG energy term optimized by an energy functional. Then, it integrates the optimized LoG energy term with the region-scalable fitting energy term. The advantage of this is that it makes use of of local region information to drive the curve towards the boundaries. The advantage of the RSFOLGE model is that it achieves accurate image segmentation and it is insensitive to the positions of initial contour [11]. The energy functional used to optimize the LoG of the image is as follows:

$$\begin{array}{cc}\hfill E^{LQG}\left(L\right)=& \underset{\Omega }{\int \int }g\left([\nabla I]\right)\times {(L-0)}^2+(1-g(|\nabla I|\left)\right)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \times {(L-\beta \times \Delta (G_{\sigma }\ast I\left)\right)}^{2}dxdy\hfill \end{array}$$

(13)

where the value of optimized LoG of the image is represented with L, and $g(\nabla I)=e^{-a|\nabla G_o\ast I},a,\beta$ are positive constants. A edge indicator is defined by $g(\nabla I)$. The values of $g(\nabla I)$ are small and approximately equal to 0 at the locations near the object boundaries. $\Delta (G_{\sigma }\ast I)$ is:

$$\begin{array}{c}\hfill \Delta (G_{\sigma }\ast I)=\left[\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial x^2}+\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial y^2}\right]\ast I(x,y)\end{array}$$

(14)

where $G_{\sigma }(x,y)$ is a Gaussian kernel function with standard deviation $\sigma$.

The advantages of this method are that it develops the robustness of initialization and it has accurate segmentation results compared with the original region scalable fitting (RSF) method. Moreover, the optimization process is applied to the edge stopping function which used in edge-based ACMs.

The disadvantage of this method is that it fails when objects inside the image have significantly different intensity values which can be tackled by using multi-phase segmentation.

A simple and universal method of improving the robustness of initial contour for these local fitting-based models is presented [12]. The core idea of proposed method is exchanging the fitting values on the two sides of contour, so that the fitting values inside the contour are always larger (or smaller) than the values outside the contour in the process of curve evolution. In this way, the whole curve will evolve along the inner (or outer) boundaries of object and is less likely to be stuck in the object or background.

2.2.6. Adaptive Local-Fitting (Alf) Method

The ALF model pushes the initial contour towards the object boundary using adaptive local fitting energy and regularization energy. This method shows an accurate way to separate the region of interest. The traditional methods assume that the intensities in the local region are constant; however, the LBF method finds an optimal solution by fitting the original image using an adaptive technique [52].

The ALF method improves on the local binary fitting method. The energy function of the ALF is:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill E^{ALF}=& \int \sum _{i=1}^N({\kappa }_i\int w^x(x-y){\left|I\left(y\right)-{\mu }_i\left(x\right)-\lambda \left(x\right)\overline{\sigma }\left(y\right)\right|}^2\hfill \\ \hfill & \times M_i\left(\Phi \left(y\right)\right)dy)dx\hfill \\ \hfill & +\beta \int \frac{1}{2}{\left(\right|\nabla \Phi \left(x\right)|-1)}^{2}dx+v\int \delta \left(\Phi \left(x\right)\right)|\nabla \Phi \left(x\right)|dx\hfill \end{array}\end{array}$$

(15)

where $w^x$ is a truncated weight function, $\overline{\sigma }$ is an appropriate estimation to $\sigma$ and $M_i\left(\Phi \left(y\right)\right)$ is a membership function satisfying:

$$\begin{array}{c}\hfill M_i\left(\Phi \left(y\right)\right)=\left\{\begin{array}{c}1,y\in {\Omega }_i\hfill \\ 0,\mathrm{else}\hfill \end{array}\right.\end{array}$$

(16)

In Equation (27), when $\lambda \left(x\right)=0$ or $\overline{\sigma }\left(y\right)=0$, it is the same as the LBF model. So, the LBF model can be seen as special case of the proposed ALF model. Nevertheless, LBF discards the local information about intensity variance Despite the necessity to improve the efficiency of the method, the model can extract more details and performs robustly with regard to to intensity inhomogeneity and noises.

2.2.7. Fuzzy Region-Based Active Contour Model (Frbacm)

The FRBACM is driven by weighting global and local fitting energy, wherein fuzzy region energy with local spatial image information is proposed. The segmentation results of this method are independent of initialization. To extract object boundaries while maintaining its distance, an initial evolving curve of pseudo level set function (LSF) followed by the pseudo-LSF and further smoothed by edge energy is proposed. This method consists of fuzzy region energy which is formulated with local spatial image information and edge energy which use the evolving curve to stop the object boundaries. The fuzzy region energy is strictly convex and used to drive the motion of the evolving curves. To minimize the energy functional, the fuzzy region energy directly calculates the change in the fuzzy region energy instead of using the Euler–Lagrange equation [53].

This proposed model succeeds in extracting objects in different situations such as images with noise and images with intensity inhomogeneity; however, this model fails when the similarity between the object and its background is high.

2.2.8. Global and Local Signed Energy-Based Pressure Force (Glsepf)

The GLSEPF uses the energy difference between the inner and outer energies to obtain the contour of the object. This model will improve the initial curve robustness. The local signed energy-based pressure force (LSEPF) is determined by means of the pixel-by-pixel energy difference within the local neighborhood region. This LSEPF can handle images with depth inhomogeneity and noise. Global image information and local energy information are used, respectively, for global and local force propagation functions. Global and local variances are used to balance the weights of GSEPF and LSEPF automatically, which can solve the problem of parameter setting. In the meantime, a regularization term and a penalty term are added in order to prevent re-initialization during iterations and smooth the level set function [54]. The level set formulation of the GSEPF model is written as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{GSEPF}\mathrm{model}:\frac{\partial \varphi }{\partial t}=& \frac{\Delta E^g\left(I\left(x\right)\right)}{max\left(\left|\Delta E^g\left(I\left(x\right)\right)\right|\right)}·\left|c_1-c_2\right|·\nabla \varphi \hfill \\ \hfill & +\mu \delta \left(\varphi \right)·div\left(\frac{\nabla \varphi }{|\nabla \varphi |}\right)\hfill \\ \hfill & +v({\nabla }^2\varphi -div(\frac{\nabla \varphi }{|\nabla \varphi |}\left)\right)\hfill \end{array}\end{array}$$

(17)

where $\Delta E^g\left(I\left(x\right)\right)$ is the global energy. Objects in images with noise and intensity can be detected by incorporation of the global and local image information; however, for color images, the segmentation is poor because only the intensity information is used.

In next subsection, we explain the database that the methods are applied to.

2.3. Database

In this paper, the COVID-19 pneumonia image database of [34] was considered to test the performance of the proposed image processing method. This database consists of 100 CTI with dimensions of $512\times 512\times 1$ pixels, and all the available images are associated with corresponding Ground-Truth Images (GTI). The overall distribution of patients is shown in

Table 1. The overall distribution of samples used in the database.

Range of ages of patients	32–86 (years)
No. of total patients (men + women + NA)	49 (=27 + 11 + 11)
Minimum no. of COVID-19 CT images per patient	1
Maximum no. of COVID-19 CT images per patient	13
Total no. of COVID-19 CT images	100

. Figure 6 also shows examples of COVID-19 CT images and the corresponding ground truth. As can be seen in the figure, the ground truth is a binary image where the white parts are infection regions. The segmentation step aims to divide the images of CT into black and white regions. The segmentation results are compared with the ground truth to evaluate the performance of the method.

3. Evaluation

In this section, we present the experimental results of the active contour methods defined in the previous section for comparison purposes. We also explain the implementation of the methods. To evaluate the effectiveness of the active contour methods, seven suitable measures applied, namely: Dice, Jaccard, Bfscore, Precision, Recall, Iteration and Time. If the first five measures score better (closer to one or closer to 100%), then the implemented disease investigation scheme is confirmed as a better procedure. If $I_O$ and $I_{GT}$ represent the binary output image of the segmentation result and the binary image of the ground truth, respectively, the measures are defined as follows:

$$\begin{array}{c}\hfill \mathrm{Precision}=\frac{TP}{TP+FP},\end{array}$$

(18)

$$\begin{array}{c}\hfill \mathrm{Recall}=\frac{TP}{TP+FN},\end{array}$$

(19)

$$\begin{array}{c}\hfill \mathrm{Jaccard}=\frac{\left|I_o\cap I_g\right|}{\left|I_o\cup I_g\right|},\end{array}$$

(20)

$$\begin{array}{c}\hfill \mathrm{Dice}=\frac{2\left|I_o\cap I_g\right|}{\left|I_o\right|+\left|I_g\right|},\end{array}$$

(21)

$$\begin{array}{c}\hfill \mathrm{Bfscore}=\frac{2\times Precision\times Recall}{Recall+Precision},\end{array}$$

(22)

where TP, FP and FN are true positive, false positive and false negative rates.

3.1. Lung Region Extraction

In this work, we first removed the artifacts such as bones and other body segments from the test image using a threshold filter in [55]. This threshold filter separates the test image into two sections based on a chosen threshold. We plotted the Receiver Operating Characteristic (ROC) curve (the TP part against the FP part) by changing the threshold value, as shown in Figure 7. This method obtained an area under curve (AUC) value of 0.94. We chose the threshold value when TP = 0.9 and FP = 0.045, and then we obtained the accuracy of the lung region extraction step for each image with respect to the ground truth. We assumed that the method failed for each image if the accuracy was less than 95 %. Therefore, we manually separated the part of images. A total of 12 images of the database (12 %) failed and were processed manually. The results obtained with the threshold filter are shown in Figure 8.

3.2. Comparison the Active Contour Methods

In this section, the performances of the mentioned methods in the previous sections have been compared. We performed all simulations in MATLAB R2018a. All experiments were run on a 64-bit operating system with a CPU E5-2690 v3 @ 2.60 GHz, 64.0 GB of RAM, and a single NVIDIA GTX TITAN X. In order to implement the methods, their codes have been provided by authors: the C-V, SBGFRLS, and ORACM (available at http://iys.inonu.edu.tr /webpanel/dosyalar/1348/file/OnlineSeg.rar (accessed on 20 August 2021)), LSACM (available at http://www.comp.polyu.edu.hk/~cslzhang/LSACM/%MDPI:changedlikethisformat,pleaseconfirm.Thedatehasbeenadded.LSACM.htm (accessed on 20 August 2021)), RSFOLGE (available at https://github.com/dingkeyan93/Active-Contour-Model-Matlab-Code-Set (accessed on 20 August 2021)), ALF (available at https://github.com/madd2014/ALF (accessed on 20 August 2021)), FRAGL (available at https://github.com/fangchj2002/FRAGL (accessed on 20 August 2021)), GLSEPF (available at https://github.com/HuaxiangLiu/GLSEPF/ (accessed on 20 August 2021)) methods were implemented in MATLAB code and the MAC method (available at http://csvision.swan.ac.uk/public_html_XX/snakes/mac/index.html (accessed on 20 August 2021)) was implemented in JAVA code. For all of the methods used on the database, the default parameters mentioned in their codes were retained. The experimental results confirm that the proposed methods provide the mean value of infection rate for further evaluation. The comparative analysis was performed for CT COVID-19 images. To test the robustness of initialization, three initial contours were considered: inside, outside, and overlapping (cross) the target object. However, some methods failed on the initial contours (when the inner contour cannot be extracted and the method is forced to infinite loop), as shown in

Table 2. Success of active contour methods in obtaining infection area in terms of initial contour.

Initial Contour	C-V	SBGFRLS	MAC	ORACM	LSACM	RSFOLGE	ALF	FRAGL	GLSEPF
Inside	Failed	Failed	Done	Done	Failed	Failed	Failed	Failed	Failed
Outside	Failed	Failed	Done	Done	Failed	Done	Done	Failed	Failed
Cross	Done	Failed	Done	Done	Done	Done	Failed	Done	Done

.

3.3. Result

The quality of the results of the methods is shown in Figure 9. The quantitative results related to the metrics from the database are presented in

Table 3. Detailed evaluation of seven metrics based on COVID-19 CT images.

Measure	C-V	MAC	ORACM	LSACM	RSFOLGE	ALF	FRAGL	GLSEPF
Dice (%)	93.55	95.94	96.30	95.77	89.88	92.12	96.44	95.60
Jaccard (%)	88.31	92.32	93.06	92.01	82.49	85.70	93.21	91.77
Bfscore (%)	66.82	61.40	74.13	60.46	63.50	57.05	65.55	71.96
Precision (%)	84.44	92.37	77.73	96.89	73.03	93.33	91.33	68.24
Recall (%)	58.15	48.25	72.41	45.67	61.44	43.34	53.18	78.81
Iteration	158	8500	5	200	250	8	10	30
Time (s)	55	700	1.4	12	41.40	100	1.8	5.5

. According to the evaluations, the quantitative and qualitative results are promising in segmentation, but the results should help the researchers to improve the results in sensitive application.

The quantitative results in terms of Dice, Jaccard, Bfscore, Precision, Recall, Iteration and Time measured using the database are shown in Table 3.

Figure 9 shows some binary results processed with six sample images from the CT database. The six images were randomly selected for qualitative evaluation. The authors reviewed the images based on the results of each method compared to the corresponding ground truth.

To show the effectiveness of active contour methods, we compared the best active contour method (GLSEPF), which achieves the best results among all methods in the database based on Table 3, with deep learning methods. Due to the different structure of the two sets of methods, the comparison is not fair. However, it can show the effectiveness of the active contour methods.

Table 4. Comparison of the best active contour method with deep learning methods in terms of the Recall measure.

MiniSeg	MobileNet	Inf-Net	DeepLabv3+	EfficientNet	EDANet	ENet	ESPNetv2	GLSEPF (ACM)
84.95	81.19	76.50	79.58	80.25	82.86	81.26	77.84	78.81

shows the comparison in terms of recall measure. The deep learning methods consist of 8 popular methods, namely MiniSeg [56], MobileNet [57], Inf-Net [58], DeepLabv3+ [59], EfficientNet [60], EDANet [61], ENet [62], and ESPNetv2 [63].

4. Discussion

In this section, we elaborate on the results section. As shown in Table 2, ORACM can perform the final segmentation based on the three initial contours in two cases: the MAC of both methods. Additionally, LSACM failed only on one of the initial contours and the remaining methods succeeded only on one of the initial contours. It should be noted that some methods (Figure 9) failed for at least one of the initial contours, which is why we report the best results of each method. In the overall evaluation, it can be seen that ORACM performs best in both quantitative and qualitative evaluations compared to the other methods.

In the quantitative evaluation, Table 3 shows that ORACM performs significantly better than all other methods in terms of Bfscore, iteration and time and performs as well as the FRAGL method in terms of Dice and Jaccard measures. Therefore, as shown in the table, FRAGL ranks first in terms of the DICE and Jaccard measures. Compared to the other methods, LSACM reaches the highest score in terms of accuracy, followed by ALF and MAC, which rank second and third, respectively. While GLSEPF ranks first in terms of recall measure, ORACM scores second and the other methods do not have promising results in this measure. As can be seen from the low value of time and iteration, ORACM and ALF are also faster than the others. Since the Bfscore measures how well the predicted boundary of an object matches the true boundary, ORACM preserves the boundaries better than other methods. Moreover, Jaccard and Dice similarities of 100% imply that the segmentations in the two images match perfectly. FRAGL and ORACM achieve the best matching images compared to other methods.

As the qualitative evaluation in Figure 9 shows, RSFOLGE, MAC and C-V methods achieve clean binary images. However, the results of the ORACM, FRAGL and GLSEPF methods are more effective and can efficiently produce higher visual quality from the input image with a dark shadow. In qualitative evaluation, as shown in the figure, ORACM is able to keep the boundaries in the patterns smooth. As shown, ORACM, FRAGL and GLSEPF methods are successful in delineating the area of infection, which serves as the foreground, from the background, but they also fail in maintaining thin strokes. Nevertheless, the methods achieve the best visual quality for the coronal and axial view database samples.

Finally, the comparison with deep learning methods shows that the active contour methods are competitive with deep learning methods, although the results show that deep learning methods are better overall.

5. Conclusions

This study is an introduction to the automatic investigation of infection COVID-19 with CTSI. Finding a collection of clinical quality images is a difficult task due to the sudden onset of the disease. In this work, active contour methods are applied to the 2D lung scans CT to automatically extract the infected sections. In this work, methods from 2008 to 2020 were tested, which are divided into four classes belonging to contour representation and object boundary description categories. In addition to a brief explanation of the methods, this paper also examined the advantages and disadvantages of the methods. Furthermore, a comparison between the methods in terms of computational cost and accuracy has been carried out. Based on the experimental results, ORACM2 (online region-based active contour model with the morphological operations) has the best overall performance in terms of speed and accuracy.

In the future, we plan to test more segmentation methods in other categories such as the graph-cut-based and the clustering-based methods. We will also propose to implement the following: (i) automatic detection and classification of COVID-19 cases into mild, moderate, and severe classes; (ii) automatic detection of disease progression; and (iii) automatic classification of CTSI slices into normal and COVID-19 pneumonia classes.