A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals
Abstract
1. Introduction
- The proposed MP-ORPD is envisaged from the point of view of a power system operator; in this case, a single objective function is not pursued as such, but instead a set of goals regarding the minimization of deviations from desired operational values are considered;
- The main goal of the MP-ORPD is guaranteeing operative feasibility throughout a given time horizon, while minimizing the number of maneuvers carried out in reactive power devices and transformers taps, preserving their useful life and reducing eventual maintenance costs;
- Instead of considering all buses to enforce voltage limit constraints, only a set of pilot nodes are taken into account. Furthermore, dynamic limits are considered in these buses to mimic real-life operation. This results in low computational effort, which encourages real-life applications of the methodology.
2. Proposed Mathematical Modeling
2.1. Objective Function
2.2. Equality Constraints
2.3. Inequality Constraints
2.3.1. Generators Constraints
2.3.2. Voltage Angle Constraints
2.3.3. Transformer Constraints
2.3.4. Shunt Constraints
2.3.5. Security Constraints
2.3.6. Operating Times Constraints
3. Tests and Results
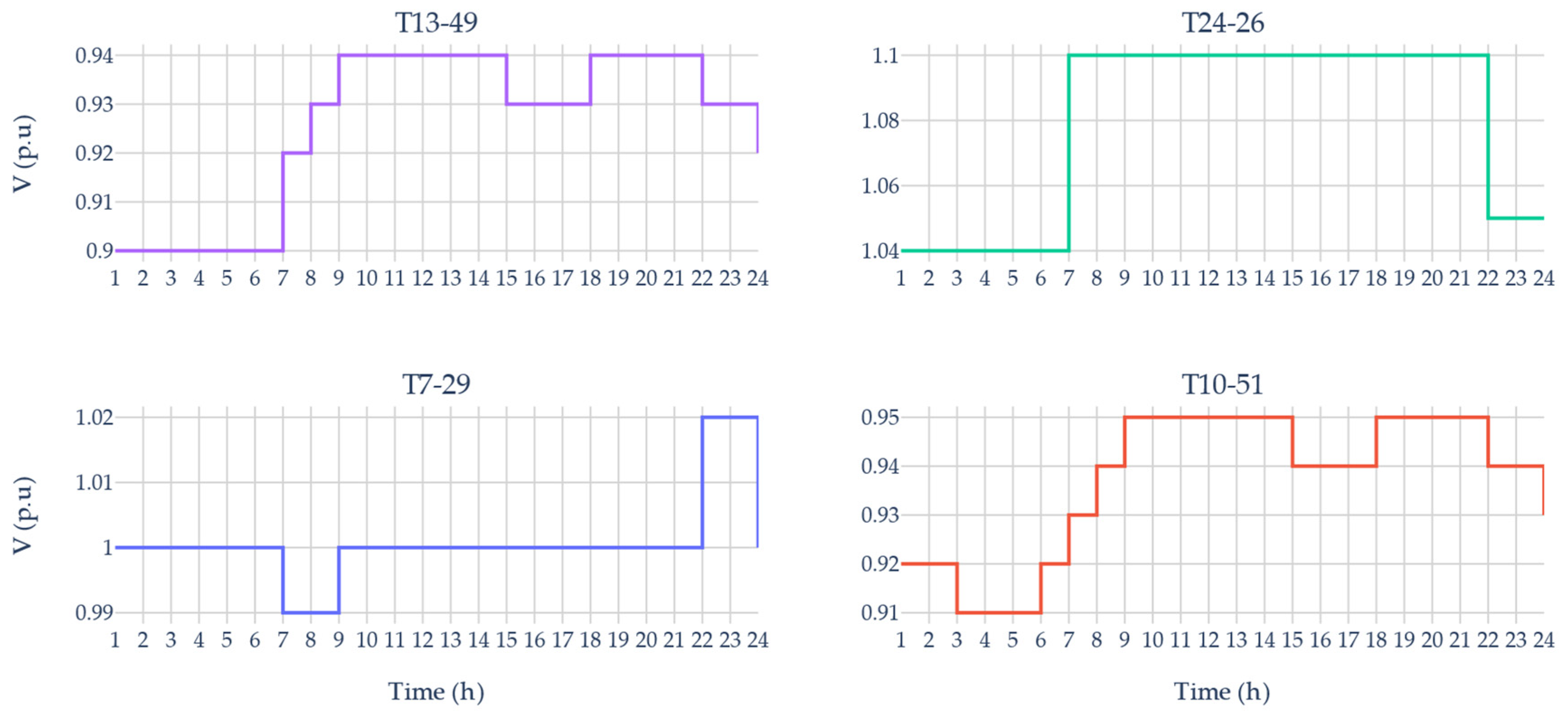
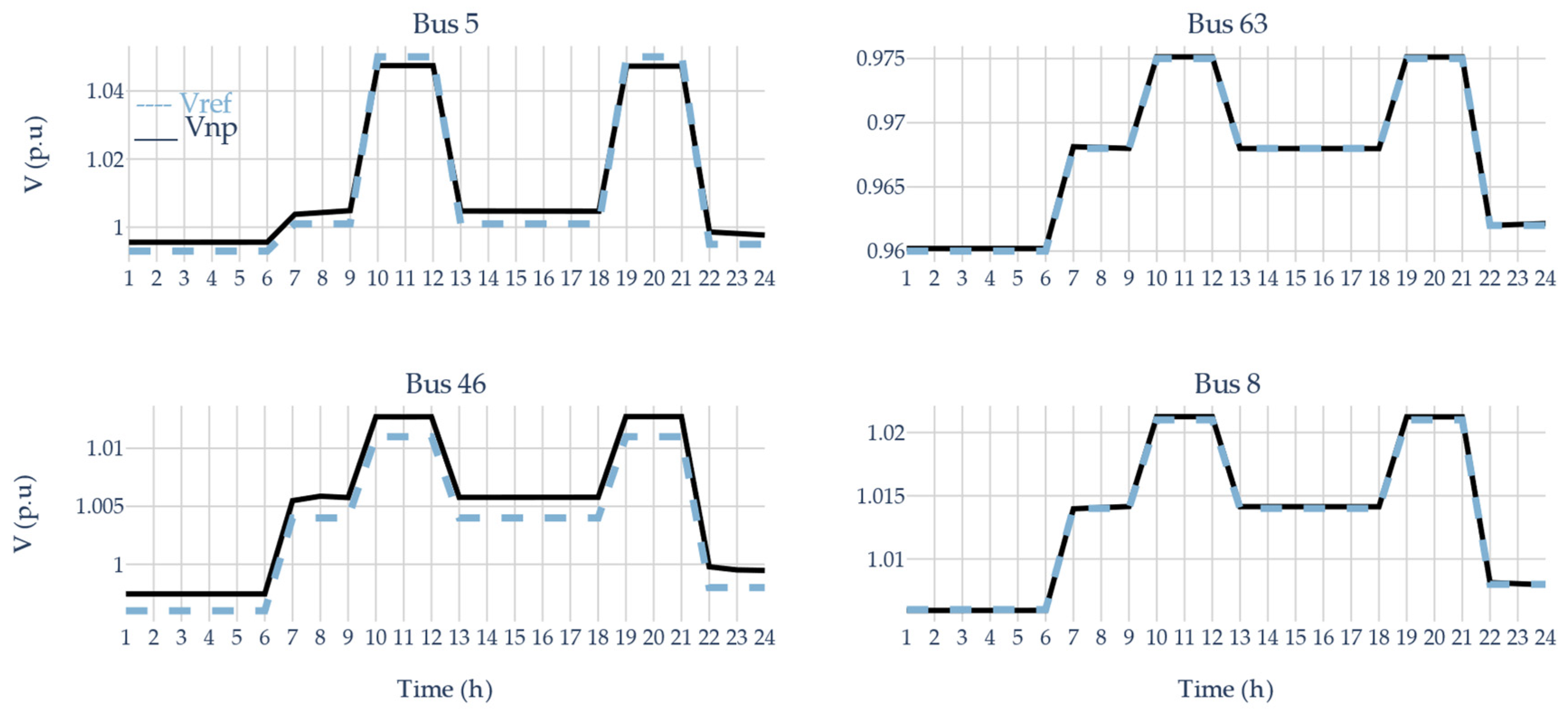
3.1. Pilot Nodes
3.2. Test Systems
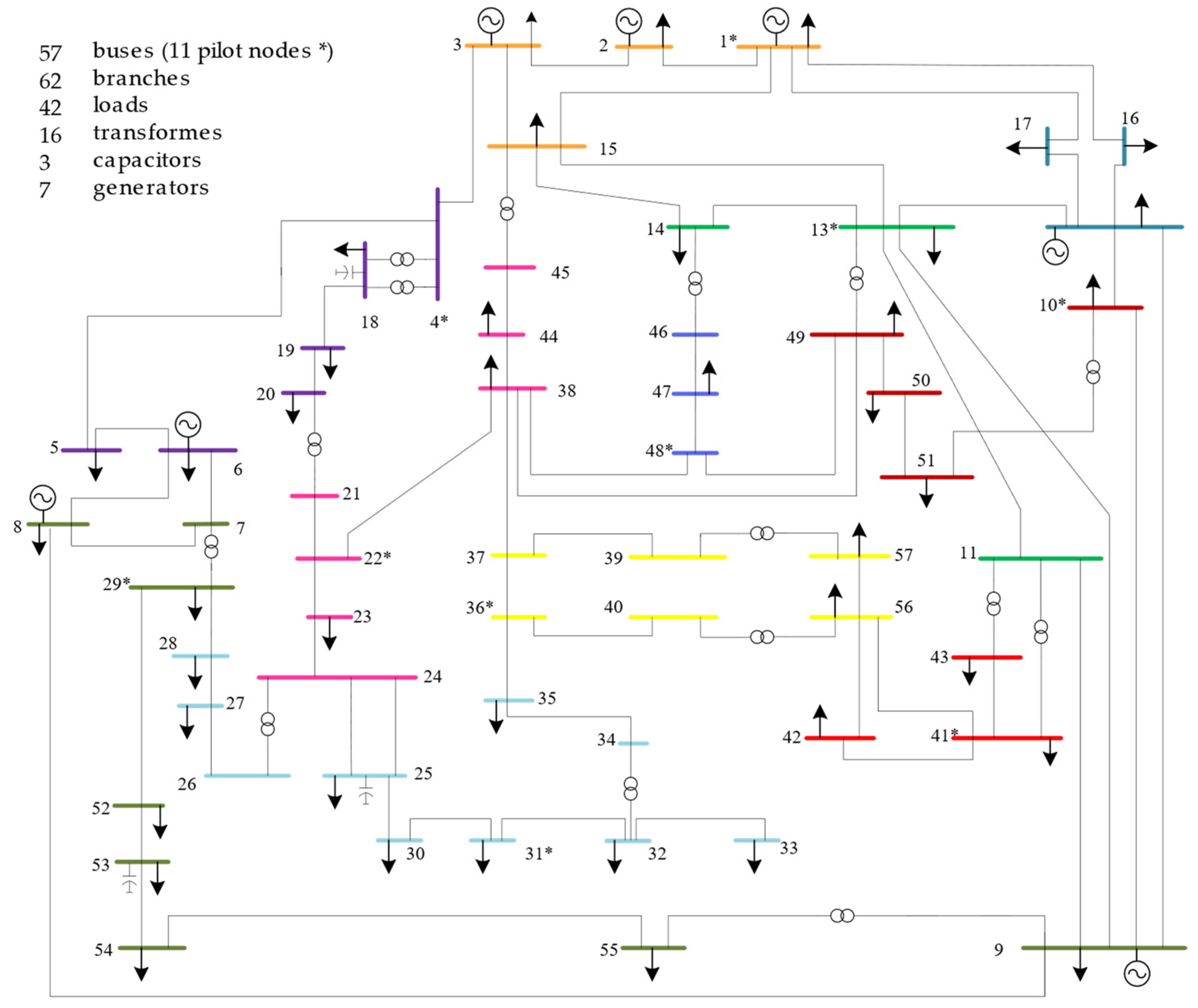
3.2.1. IEEE 57-Bus Test System
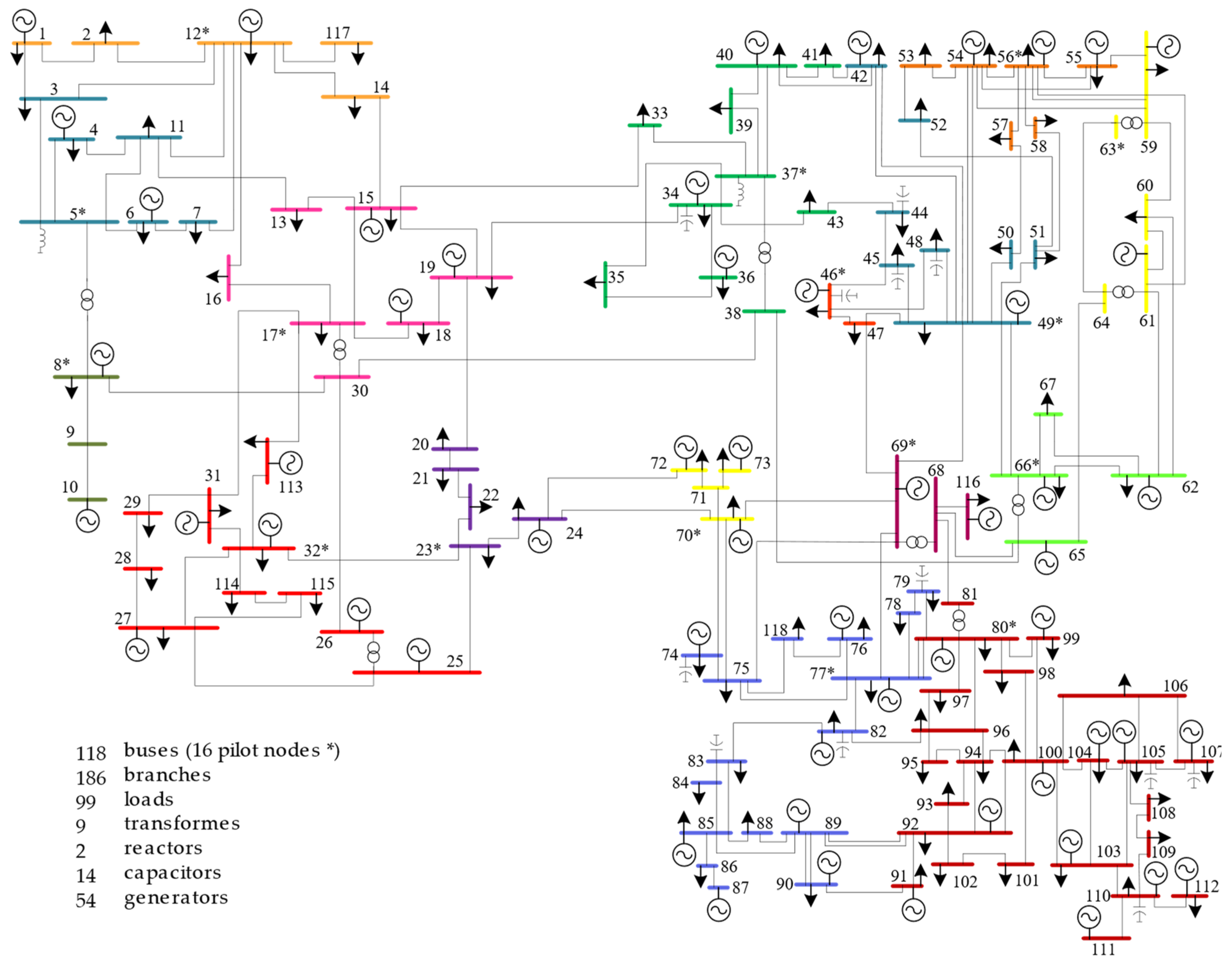
3.2.2. IEEE 118-Bus Test Case
3.3. Results
3.3.1. IEEE 57-Bus Test System
3.3.2. IEEE 118-Bus Test System
3.4. Sensibility of Objective Function Components
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Nomenclature
Appendix A.1. Sets
| Set of buses in the transmission network | |
| Set of generators in the transmission network | |
| Set of connections in the transmission network | |
| Set of interfaces | |
| Set of periods | |
| Set of branches in the transmission network | |
| Set of transformers with tap charge belonging to set of branches | |
| Set of maneuverable shunt elements | |
| Set of nonmaneuverable shunt elements | |
| Subset of generators connected to bus | |
| Subset of generators connected to slack bus | |
| Subset of maneuverable shunt elements connected to bus | |
| Subset of lines belonging to interface | |
| Subset of nodes belonging to pilot nodes |
Appendix A.2. Parameters
| Conductance and susceptance on line | |
| Shunt conductance and susceptance at bus | |
| Branch charging susceptance and angle on line | |
| Reference voltage at bus for period | |
| Shunt susceptance of shunt element | |
| Maximum number of steps of element | |
| Real and reactive power demand at bus for period | |
| Lower and upper active power injection limits of generator | |
| Lower and upper reactive power injection limits of generator | |
| Voltage magnitude lower and upper limits at bus | |
| Lower and upper limit tap positionof transformer | |
| Real power limit on line | |
| Real power limit on interface | |
| Status of generator in period | |
| Maximum number of maneuvers allowed in set of periods | |
| Penalty factors associated to objective function |
Appendix A.3. Variables
| Maneuver on tap transformer in period (1: Control action performed) | |
| Maneuver on shunt element in period (1: Control action performed) | |
| Voltage at bus in period | |
| Angle at bus in period | |
| Ratio of tap transformer in period | |
| Step number of shunt element in period | |
| Active and reactive power flowing on line in period | |
| Active and reactive power generated by generator in period |
Appendix B. MP-ORPD Schedule
| (a) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shnt | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |||||||
| 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | 5.9 | |
| 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | 6.3 | |
| (b) | ||||||||||||||||||||||||
| Trf | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | |
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.02 | 1.02 | 1.00 | |
| 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.01 | 1.08 | 1.07 | 1.06 | 1.10 | 1.10 | 1.10 | 1.06 | 1.06 | 1.07 | 1.07 | 1.07 | 1.06 | 1.10 | 1.10 | 1.10 | 0.97 | 0.99 | 1.01 | |
| 0.92 | 0.92 | 0.91 | 0.91 | 0.91 | 0.92 | 0.93 | 0.94 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 | 0.94 | 0.94 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 | 0.94 | 0.93 | |
| 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.98 | 0.97 | 0.97 | 0.97 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | |
| 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.98 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.92 | 0.93 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | 0.93 | 0.93 | 0.94 | 0.94 | 0.94 | 0.94 | 0.93 | 0.93 | 0.92 | |
| 0.93 | 0.93 | 0.92 | 0.92 | 0.92 | 0.93 | 0.91 | 0.91 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.91 | 0.90 | 0.90 | 0.91 | 0.90 | 0.91 | 0.90 | 0.90 | 0.91 | |
| 0.98 | 0.99 | 1.00 | 1.03 | 1.02 | 0.98 | 1.02 | 0.98 | 0.94 | 0.94 | 0.94 | 0.94 | 0.95 | 0.95 | 0.96 | 0.97 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.93 | 0.95 | 0.99 | |
| 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | |
| 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.10 | 1.05 | 1.05 | 1.05 | |
| 0.97 | 0.97 | 0.98 | 0.98 | 0.98 | 0.96 | 1.05 | 1.02 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 | 1.00 | 0.97 | 0.98 | 0.97 | |
| 0.90 | 0.90 | 0.90 | 0.91 | 0.91 | 0.91 | 0.92 | 0.96 | 0.97 | 0.97 | 0.98 | 0.97 | 0.97 | 0.97 | 0.96 | 0.96 | 0.96 | 0.97 | 0.97 | 0.97 | 0.97 | 0.98 | 0.96 | 0.96 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.92 | 0.94 | 0.95 | 0.95 | 0.95 | 0.94 | 0.94 | 0.93 | 0.93 | 0.93 | 0.94 | 0.94 | 0.95 | 0.94 | 0.95 | 0.93 | 0.91 | |
| (c) | ||||||||||||||||||||||||
| Gen | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 0.964 | 0.963 | 0.962 | 0.961 | 0.962 | 0.964 | 1.003 | 1.003 | 1.004 | 1.024 | 1.024 | 1.024 | 1.004 | 1.004 | 1.003 | 1.003 | 1.003 | 1.004 | 1.024 | 1.024 | 1.024 | 0.974 | 0.973 | 0.973 | |
| 0.956 | 0.956 | 0.955 | 0.955 | 0.955 | 0.956 | 0.995 | 0.996 | 0.999 | 1.019 | 1.019 | 1.019 | 0.999 | 0.998 | 0.997 | 0.997 | 0.997 | 0.998 | 1.018 | 1.019 | 1.018 | 0.968 | 0.967 | 0.965 | |
| 0.944 | 0.944 | 0.944 | 0.944 | 0.944 | 0.944 | 0.984 | 0.985 | 0.986 | 1.007 | 1.007 | 1.007 | 0.986 | 0.986 | 0.985 | 0.985 | 0.985 | 0.986 | 1.006 | 1.006 | 1.006 | 0.955 | 0.955 | 0.954 | |
| 0.938 | 0.938 | 0.937 | 0.937 | 0.937 | 0.939 | 0.975 | 0.984 | 0.994 | 1.017 | 1.018 | 1.017 | 0.992 | 0.991 | 0.989 | 0.988 | 0.989 | 0.991 | 1.013 | 1.016 | 1.013 | 0.966 | 0.96 | 0.949 | |
| 0.947 | 0.947 | 0.947 | 0.947 | 0.947 | 0.948 | 0.984 | 0.99 | 0.999 | 1.02 | 1.021 | 1.02 | 0.997 | 0.996 | 0.994 | 0.992 | 0.994 | 0.996 | 1.018 | 1.019 | 1.018 | 0.969 | 0.966 | 0.957 | |
| 0.933 | 0.934 | 0.934 | 0.935 | 0.935 | 0.933 | 0.972 | 0.974 | 0.976 | 0.998 | 0.998 | 0.998 | 0.975 | 0.975 | 0.975 | 0.974 | 0.975 | 0.975 | 0.997 | 0.997 | 0.997 | 0.945 | 0.944 | 0.941 | |
| 0.944 | 0.944 | 0.944 | 0.945 | 0.945 | 0.944 | 0.985 | 0.985 | 0.984 | 1.003 | 1.003 | 1.003 | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 1.004 | 1.003 | 1.004 | 0.954 | 0.954 | 0.955 | |
| (a) | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shnt | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | -40 | |||||||
| 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | |||||||||
| -25 | -25 | -25 | -25 | -25 | -25 | -25 | -25 | -25 | ||||||||||||||||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | ||||||||||
| 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | |||||||||||
| 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | ||||||||||
| 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | |||||||||
| 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | |||||||
| 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | |
| 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | |
| (b) | ||||||||||||||||||||||||
| Trf | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.93 | 0.93 | 0.93 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.93 | 0.93 | 0.93 | 0.98 | 0.98 | 0.98 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.92 | 0.93 | 1.00 | 1.00 | 1.00 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 1.00 | 1.00 | 1.00 | 0.93 | 0.92 | 0.90 | |
| 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.94 | 0.95 | 0.98 | 0.99 | 0.98 | 0.95 | 0.95 | 0.94 | 0.94 | 0.94 | 0.95 | 0.98 | 0.98 | 0.98 | 0.95 | 0.94 | 0.93 | |
| 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.96 | 0.97 | 1.00 | 1.00 | 1.00 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 1.00 | 1.00 | 1.00 | 0.96 | 0.94 | 0.93 | |
| 1.03 | 1.03 | 1.03 | 1.04 | 1.03 | 1.01 | 1.00 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.99 | 1.00 | 1.00 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.95 | 0.96 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | 0.96 | 0.95 | 0.96 | 0.96 | |
| 0.91 | 0.91 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.91 | 0.92 | 0.93 | 0.93 | 0.93 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 | 0.92 | 0.91 | 0.90 | |
| 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.94 | 0.95 | 0.95 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | 0.96 | 0.95 | 0.94 | 0.93 | |
| 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.91 | 0.91 | 0.91 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.90 | 0.91 | 0.91 | 0.91 | 0.90 | 0.90 | 0.90 | |
| (c) | ||||||||||||||||||||||||
| Gen | Period | |||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| 0.965 | 0.965 | 0.965 | 0.965 | 0.965 | 0.965 | 0.973 | 0.971 | 0.971 | 0.983 | 0.983 | 0.983 | 0.971 | 0.971 | 0.971 | 0.970 | 0.971 | 0.971 | 0.983 | 0.983 | 0.983 | 0.964 | 0.966 | 0.967 | |
| 0.992 | 0.992 | 0.992 | 0.992 | 0.992 | 0.992 | 1.001 | 1.001 | 1.001 | 1.042 | 1.042 | 1.042 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.001 | 1.042 | 1.042 | 1.042 | 0.995 | 0.995 | 0.995 | |
| 0.980 | 0.980 | 0.980 | 0.980 | 0.980 | 0.981 | 0.989 | 0.989 | 0.989 | 1.011 | 1.011 | 1.011 | 0.989 | 0.989 | 0.989 | 0.989 | 0.989 | 0.989 | 1.011 | 1.011 | 1.011 | 0.983 | 0.983 | 0.983 | |
| 1.006 | 1.006 | 1.006 | 1.006 | 1.006 | 1.006 | 1.014 | 1.014 | 1.014 | 1.021 | 1.021 | 1.021 | 1.014 | 1.014 | 1.014 | 1.014 | 1.014 | 1.014 | 1.021 | 1.021 | 1.021 | 1.008 | 1.008 | 1.008 | |
| 1.080 | 1.080 | 1.080 | 1.079 | 1.079 | 1.080 | 1.089 | 1.087 | 1.086 | 1.099 | 1.099 | 1.099 | 1.086 | 1.086 | 1.086 | 1.086 | 1.086 | 1.086 | 1.099 | 1.099 | 1.099 | 1.080 | 1.081 | 1.083 | |
| 0.978 | 0.978 | 0.978 | 0.978 | 0.978 | 0.978 | 0.986 | 0.985 | 0.984 | 0.999 | 0.999 | 0.999 | 0.984 | 0.985 | 0.985 | 0.985 | 0.985 | 0.985 | 0.999 | 0.999 | 0.999 | 0.979 | 0.979 | 0.980 | |
| 0.967 | 0.968 | 0.968 | 0.968 | 0.968 | 0.967 | 0.975 | 0.973 | 0.973 | 0.981 | 0.981 | 0.981 | 0.973 | 0.973 | 0.972 | 0.972 | 0.972 | 0.973 | 0.981 | 0.981 | 0.981 | 0.966 | 0.968 | 0.969 | |
| 0.964 | 0.964 | 0.964 | 0.964 | 0.964 | 0.964 | 0.971 | 0.970 | 0.970 | 0.977 | 0.977 | 0.977 | 0.970 | 0.970 | 0.969 | 0.969 | 0.969 | 0.970 | 0.977 | 0.977 | 0.977 | 0.964 | 0.965 | 0.965 | |
| 0.962 | 0.962 | 0.962 | 0.963 | 0.962 | 0.961 | 0.969 | 0.967 | 0.967 | 0.975 | 0.975 | 0.975 | 0.967 | 0.967 | 0.967 | 0.967 | 0.967 | 0.967 | 0.975 | 0.975 | 0.975 | 0.961 | 0.962 | 0.963 | |
| 0.986 | 0.986 | 0.986 | 0.985 | 0.986 | 0.986 | 0.995 | 0.998 | 0.999 | 1.008 | 1.008 | 1.008 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 1.008 | 1.008 | 1.008 | 0.993 | 0.992 | 0.989 | |
| 1.023 | 1.023 | 1.022 | 1.022 | 1.022 | 1.023 | 1.032 | 1.033 | 1.034 | 1.035 | 1.035 | 1.035 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.028 | 1.026 | 1.026 | |
| 0.938 | 0.938 | 0.937 | 0.937 | 0.937 | 0.938 | 0.950 | 0.969 | 0.979 | 1.042 | 1.043 | 1.042 | 0.977 | 0.976 | 0.975 | 0.973 | 0.975 | 0.976 | 1.040 | 1.042 | 1.040 | 0.971 | 0.960 | 0.942 | |
| 0.957 | 0.957 | 0.957 | 0.956 | 0.956 | 0.957 | 0.964 | 0.964 | 0.963 | 0.970 | 0.970 | 0.970 | 0.963 | 0.963 | 0.964 | 0.964 | 0.964 | 0.963 | 0.970 | 0.970 | 0.970 | 0.958 | 0.958 | 0.958 | |
| 0.945 | 0.945 | 0.945 | 0.945 | 0.945 | 0.945 | 0.953 | 0.953 | 0.952 | 0.959 | 0.959 | 0.959 | 0.952 | 0.952 | 0.952 | 0.953 | 0.952 | 0.952 | 0.960 | 0.959 | 0.960 | 0.947 | 0.947 | 0.947 | |
| 0.955 | 0.955 | 0.955 | 0.955 | 0.955 | 0.955 | 0.963 | 0.963 | 0.963 | 0.970 | 0.970 | 0.970 | 0.963 | 0.963 | 0.963 | 0.963 | 0.963 | 0.963 | 0.970 | 0.970 | 0.970 | 0.957 | 0.957 | 0.957 | |
| 0.979 | 0.979 | 0.979 | 0.979 | 0.979 | 0.979 | 0.987 | 0.988 | 0.987 | 0.995 | 0.995 | 0.995 | 0.987 | 0.987 | 0.987 | 0.987 | 0.987 | 0.987 | 0.995 | 0.995 | 0.995 | 0.981 | 0.982 | 0.981 | |
| 0.974 | 0.974 | 0.974 | 0.975 | 0.974 | 0.974 | 0.982 | 0.983 | 0.982 | 0.990 | 0.990 | 0.990 | 0.982 | 0.982 | 0.982 | 0.983 | 0.982 | 0.982 | 0.990 | 0.990 | 0.990 | 0.977 | 0.977 | 0.976 | |
| 0.961 | 0.962 | 0.962 | 0.962 | 0.962 | 0.961 | 0.967 | 0.967 | 0.973 | 0.983 | 0.983 | 0.983 | 0.973 | 0.972 | 0.971 | 0.970 | 0.971 | 0.972 | 0.982 | 0.982 | 0.982 | 0.966 | 0.960 | 0.962 | |
| 0.972 | 0.973 | 0.973 | 0.973 | 0.973 | 0.972 | 0.979 | 0.977 | 0.985 | 0.995 | 0.995 | 0.995 | 0.984 | 0.984 | 0.983 | 0.981 | 0.983 | 0.984 | 0.994 | 0.995 | 0.994 | 0.977 | 0.971 | 0.973 | |
| 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 0.997 | 1.005 | 1.006 | 1.006 | 1.013 | 1.013 | 1.013 | 1.006 | 1.006 | 1.006 | 1.006 | 1.006 | 1.006 | 1.013 | 1.013 | 1.013 | 1.000 | 1.000 | 0.999 | |
| 1.010 | 1.010 | 1.010 | 1.011 | 1.011 | 1.010 | 1.018 | 1.017 | 1.017 | 1.024 | 1.024 | 1.024 | 1.017 | 1.017 | 1.017 | 1.017 | 1.017 | 1.017 | 1.024 | 1.024 | 1.024 | 1.011 | 1.011 | 1.012 | |
| 0.948 | 0.948 | 0.948 | 0.948 | 0.948 | 0.948 | 0.956 | 0.956 | 0.956 | 0.962 | 0.962 | 0.962 | 0.956 | 0.956 | 0.956 | 0.956 | 0.956 | 0.956 | 0.962 | 0.962 | 0.962 | 0.950 | 0.950 | 0.950 | |
| 0.944 | 0.944 | 0.944 | 0.944 | 0.944 | 0.944 | 0.952 | 0.953 | 0.953 | 0.960 | 0.960 | 0.960 | 0.953 | 0.953 | 0.953 | 0.953 | 0.953 | 0.953 | 0.960 | 0.960 | 0.960 | 0.947 | 0.947 | 0.946 | |
| 0.946 | 0.946 | 0.946 | 0.946 | 0.946 | 0.947 | 0.955 | 0.955 | 0.955 | 0.962 | 0.962 | 0.962 | 0.955 | 0.955 | 0.955 | 0.955 | 0.955 | 0.955 | 0.962 | 0.962 | 0.962 | 0.949 | 0.949 | 0.949 | |
| 0.948 | 0.948 | 0.947 | 0.947 | 0.947 | 0.950 | 0.960 | 0.965 | 0.964 | 0.974 | 0.974 | 0.974 | 0.964 | 0.964 | 0.965 | 0.966 | 0.965 | 0.964 | 0.975 | 0.974 | 0.975 | 0.959 | 0.957 | 0.953 | |
| 1.032 | 1.032 | 1.031 | 1.030 | 1.031 | 1.001 | 1.007 | 1.015 | 1.016 | 1.025 | 1.025 | 1.025 | 1.016 | 1.016 | 1.016 | 1.017 | 1.016 | 1.016 | 1.025 | 1.025 | 1.025 | 1.011 | 1.006 | 0.999 | |
| 1.029 | 1.028 | 1.028 | 1.027 | 1.027 | 1.004 | 1.010 | 1.017 | 1.017 | 1.025 | 1.025 | 1.025 | 1.017 | 1.017 | 1.017 | 1.018 | 1.017 | 1.017 | 1.025 | 1.025 | 1.025 | 1.012 | 1.008 | 1.003 | |
| 0.962 | 0.962 | 0.961 | 0.960 | 0.961 | 0.964 | 0.975 | 0.984 | 0.989 | 1.005 | 1.006 | 1.005 | 0.988 | 0.988 | 0.987 | 0.987 | 0.987 | 0.988 | 1.003 | 1.005 | 1.003 | 0.982 | 0.974 | 0.968 | |
| 1.043 | 1.043 | 1.043 | 1.043 | 1.043 | 1.043 | 1.051 | 1.052 | 1.052 | 1.059 | 1.059 | 1.059 | 1.052 | 1.052 | 1.051 | 1.051 | 1.051 | 1.052 | 1.058 | 1.059 | 1.058 | 1.046 | 1.045 | 1.045 | |
| 1.025 | 1.025 | 1.025 | 1.025 | 1.025 | 1.025 | 1.033 | 1.034 | 1.034 | 1.041 | 1.041 | 1.041 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.034 | 1.041 | 1.041 | 1.041 | 1.028 | 1.028 | 1.027 | |
| 0.975 | 0.975 | 0.976 | 0.976 | 0.976 | 0.975 | 0.983 | 0.983 | 0.983 | 0.991 | 0.991 | 0.991 | 0.983 | 0.983 | 0.983 | 0.983 | 0.983 | 0.983 | 0.991 | 0.991 | 0.991 | 0.977 | 0.977 | 0.977 | |
| 0.973 | 0.972 | 0.971 | 0.969 | 0.970 | 0.974 | 0.984 | 0.990 | 0.992 | 1.003 | 1.003 | 1.003 | 0.991 | 0.991 | 0.991 | 0.990 | 0.991 | 0.991 | 1.003 | 1.003 | 1.003 | 0.985 | 0.983 | 0.978 | |
| 0.968 | 0.967 | 0.966 | 0.964 | 0.965 | 0.969 | 0.979 | 0.984 | 0.984 | 0.991 | 0.991 | 0.991 | 0.984 | 0.984 | 0.983 | 0.983 | 0.983 | 0.984 | 0.991 | 0.991 | 0.991 | 0.978 | 0.976 | 0.973 | |
| 0.961 | 0.962 | 0.963 | 0.964 | 0.964 | 0.960 | 0.966 | 0.962 | 0.966 | 0.973 | 0.973 | 0.973 | 0.965 | 0.965 | 0.965 | 0.966 | 0.965 | 0.965 | 0.973 | 0.973 | 0.973 | 0.959 | 0.957 | 0.960 | |
| 0.953 | 0.954 | 0.955 | 0.957 | 0.956 | 0.951 | 0.955 | 0.949 | 0.949 | 0.957 | 0.957 | 0.957 | 0.949 | 0.948 | 0.948 | 0.949 | 0.948 | 0.948 | 0.956 | 0.957 | 0.956 | 0.942 | 0.945 | 0.949 | |
| 1.002 | 1.002 | 1.002 | 1.002 | 1.002 | 1.001 | 1.009 | 1.008 | 1.007 | 1.014 | 1.014 | 1.014 | 1.007 | 1.008 | 1.008 | 1.008 | 1.008 | 1.008 | 1.014 | 1.014 | 1.014 | 1.002 | 1.002 | 1.003 | |
| 1.027 | 1.027 | 1.026 | 1.026 | 1.026 | 1.027 | 1.036 | 1.037 | 1.037 | 1.044 | 1.045 | 1.044 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.044 | 1.044 | 1.044 | 1.031 | 1.030 | 1.030 | |
| 1.011 | 1.010 | 1.009 | 1.007 | 1.008 | 1.012 | 1.025 | 1.018 | 1.020 | 1.025 | 1.026 | 1.025 | 1.019 | 1.019 | 1.018 | 1.017 | 1.018 | 1.019 | 1.023 | 1.024 | 1.023 | 1.013 | 1.021 | 1.019 | |
| 1.013 | 1.011 | 1.006 | 1.002 | 1.004 | 1.017 | 1.035 | 1.035 | 1.046 | 1.053 | 1.054 | 1.053 | 1.043 | 1.041 | 1.039 | 1.036 | 1.039 | 1.041 | 1.048 | 1.051 | 1.048 | 1.035 | 1.038 | 1.027 | |
| 1.029 | 1.028 | 1.026 | 1.024 | 1.025 | 1.030 | 1.042 | 1.032 | 1.036 | 1.041 | 1.042 | 1.041 | 1.035 | 1.034 | 1.033 | 1.032 | 1.033 | 1.034 | 1.039 | 1.040 | 1.039 | 1.028 | 1.036 | 1.035 | |
| 1.007 | 1.006 | 1.004 | 1.003 | 1.004 | 1.008 | 1.017 | 1.003 | 1.004 | 1.008 | 1.009 | 1.008 | 1.003 | 1.003 | 1.002 | 1.001 | 1.002 | 1.003 | 1.006 | 1.007 | 1.006 | 0.997 | 1.009 | 1.011 | |
| 1.014 | 1.013 | 1.012 | 1.010 | 1.011 | 1.016 | 1.026 | 1.014 | 1.018 | 1.022 | 1.023 | 1.022 | 1.016 | 1.015 | 1.014 | 1.013 | 1.014 | 1.015 | 1.020 | 1.021 | 1.020 | 1.010 | 1.019 | 1.020 | |
| 1.021 | 1.021 | 1.019 | 1.018 | 1.019 | 1.022 | 1.032 | 1.020 | 1.024 | 1.029 | 1.029 | 1.029 | 1.022 | 1.022 | 1.021 | 1.020 | 1.021 | 1.022 | 1.027 | 1.028 | 1.027 | 1.016 | 1.025 | 1.026 | |
| 1.028 | 1.028 | 1.027 | 1.026 | 1.027 | 1.029 | 1.037 | 1.028 | 1.035 | 1.042 | 1.043 | 1.042 | 1.033 | 1.032 | 1.031 | 1.029 | 1.031 | 1.032 | 1.039 | 1.041 | 1.039 | 1.026 | 1.029 | 1.031 | |
| 1.025 | 1.025 | 1.024 | 1.023 | 1.024 | 1.026 | 1.033 | 1.021 | 1.029 | 1.036 | 1.037 | 1.036 | 1.027 | 1.025 | 1.024 | 1.022 | 1.024 | 1.025 | 1.032 | 1.034 | 1.032 | 1.019 | 1.023 | 1.027 | |
| 1.022 | 1.021 | 1.020 | 1.019 | 1.020 | 1.022 | 1.028 | 1.012 | 1.025 | 1.033 | 1.035 | 1.033 | 1.022 | 1.020 | 1.017 | 1.014 | 1.017 | 1.020 | 1.027 | 1.031 | 1.027 | 1.013 | 1.016 | 1.022 | |
| 1.016 | 1.016 | 1.015 | 1.014 | 1.015 | 1.017 | 1.021 | 1.002 | 1.016 | 1.024 | 1.026 | 1.024 | 1.012 | 1.010 | 1.007 | 1.004 | 1.007 | 1.010 | 1.017 | 1.021 | 1.017 | 1.003 | 1.007 | 1.016 | |
| 1.018 | 1.017 | 1.016 | 1.016 | 1.016 | 1.018 | 1.022 | 1.002 | 1.017 | 1.025 | 1.028 | 1.025 | 1.013 | 1.011 | 1.008 | 1.004 | 1.008 | 1.011 | 1.019 | 1.023 | 1.019 | 1.004 | 1.008 | 1.017 | |
| 1.016 | 1.015 | 1.015 | 1.014 | 1.014 | 1.016 | 1.019 | 0.997 | 1.019 | 1.028 | 1.031 | 1.028 | 1.014 | 1.011 | 1.006 | 1.001 | 1.006 | 1.011 | 1.020 | 1.026 | 1.020 | 1.002 | 1.004 | 1.014 | |
| 1.015 | 1.014 | 1.013 | 1.012 | 1.012 | 1.016 | 1.020 | 1.003 | 1.024 | 1.034 | 1.037 | 1.034 | 1.019 | 1.016 | 1.012 | 1.007 | 1.012 | 1.016 | 1.025 | 1.031 | 1.025 | 1.008 | 1.007 | 1.015 | |
| 1.025 | 1.024 | 1.022 | 1.020 | 1.021 | 1.027 | 1.033 | 1.019 | 1.042 | 1.051 | 1.055 | 1.051 | 1.036 | 1.033 | 1.028 | 1.023 | 1.028 | 1.033 | 1.042 | 1.048 | 1.042 | 1.025 | 1.022 | 1.027 | |
| 1.005 | 1.004 | 1.003 | 1.002 | 1.002 | 1.005 | 1.009 | 0.993 | 1.019 | 1.029 | 1.032 | 1.029 | 1.012 | 1.009 | 1.004 | 0.998 | 1.004 | 1.009 | 1.019 | 1.025 | 1.019 | 1.000 | 0.994 | 1.004 | |
| 0.980 | 0.980 | 0.980 | 0.979 | 0.979 | 0.980 | 0.989 | 0.990 | 0.991 | 0.998 | 0.998 | 0.998 | 0.991 | 0.991 | 0.991 | 0.991 | 0.991 | 0.991 | 0.998 | 0.998 | 0.998 | 0.985 | 0.984 | 0.983 | |
| 0.963 | 0.962 | 0.961 | 0.960 | 0.961 | 0.964 | 0.975 | 0.983 | 0.989 | 1.004 | 1.005 | 1.004 | 0.987 | 0.987 | 0.986 | 0.986 | 0.986 | 0.987 | 1.002 | 1.003 | 1.002 | 0.981 | 0.974 | 0.968 | |
References
- Bingane, C.; Anjos, M.F.; Le Digabel, S. Tight-and-cheap conic relaxation for the optimal reactive power dispatch problem. IEEE Trans. Power Syst. 2019, 34, 4684–4693. [Google Scholar] [CrossRef]
- Villa-Acevedo, W.M.; López-Lezama, J.M.; Valencia-Velásquez, J.A. A novel constraint handling approach for the optimal reactive power dispatch problem. Energies 2018, 11, 2352. [Google Scholar] [CrossRef]
- Constante, F.S.G.; Lopez, J.C.; Rider, M.J. Optimal reactive power dispatch with discrete controllers using a branch-and-bound algorithm: A semidefinite relaxation approach. IEEE Trans. Power Syst. 2021. [Google Scholar] [CrossRef]
- Masoud Mohseni-Bonab, S.; Rabiee, A. Optimal reactive power dispatch: A review, and a new stochastic voltage stability constrained multi-objective model at the presence of uncertain wind power generation. IET Gener. Transm. Distrib. 2017, 11, 815–829. [Google Scholar] [CrossRef]
- Davoodi, E.; Babaei, E.; Mohammadi-Ivatloo, B.; Rasouli, M. A novel fast semidefinite programming-based approach for optimal reactive power dispatch. IEEE Trans. Ind. Inform. 2020, 16, 288–298. [Google Scholar] [CrossRef]
- Cai, G.; Ren, Z.; Yu, T. Optimal reactive power dispatch based on modified particle swarm optimization considering voltage stability. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampla, FL, USA, 24–28 June 2007. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. Determining generator contributions to transmission system using parallel vector evaluated particle swarm optimization. IEEE Trans. Power Syst. 2005, 20, 1765–1774. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. A comparative study on particle swarm optimization for optimal steady-state performance of power systems. IEEE Trans. Power Syst. 2006, 21, 1718–1728. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Raja, M.A.Z.; Jamal, R.; Muhammad, Y. Design of fractional particle swarm optimization gravitational search algorithm for optimal reactive power dispatch problems. IEEE Access 2020, 8, 146785–146806. [Google Scholar] [CrossRef]
- Gutiérrez, D.; Villa, W.M.; López-Lezama, J.M. Flujo óptimo reactivo mediante optimización por enjambre de partículas. Inf. Tecnológica 2017, 28, 215–224. [Google Scholar] [CrossRef][Green Version]
- Devaraj, D. Improved genetic algorithm for multi-objective reactive power dispatch problem. Eur. Trans. Electr. Power 2007, 17, 569–581. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Varadarajan, M.; Swarup, K.S. Differential evolution approach for optimal reactive power dispatch. Appl. Soft Comput. 2008, 8, 1549–1561. [Google Scholar] [CrossRef]
- Niu, M.; Xu, N.Z.; Dong, H.N.; Ge, Y.Y.; Liu, Y.T.; Ngin, H.T. Adaptive Range Composite Differential Evolution for Fast Optimal Reactive Power Dispatch. IEEE Access 2021, 9, 20117–20126. [Google Scholar] [CrossRef]
- El Ela, A.A.A.; Abido, M.A.; Spea, S.R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Rueda, J.L.; Erlich, I. Optimal dispatch of reactive power sources by using MVMOs optimization. In Proceedings of the IEEE Symposium on Computational Intelligence Applications in Smart Grid, CIASG, Singapore, 16–19 April 2013; pp. 29–36. [Google Scholar] [CrossRef]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar] [CrossRef]
- Chen, G.; Liu, L.; Huang, S. Enhanced GSA-based optimization for minimization of power losses in power system. Math. Probl. Eng. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Sinsuphan, N.; Leeton, U.; Kulworawanichpong, T. Optimal power flow solution using improved harmony search method. Appl. Soft Comput. 2013, 13, 2364–2374. [Google Scholar] [CrossRef]
- Ghasemi, M.; Taghizadeh, M.; Ghavidel, S.; Aghaei, J.; Abbasian, A. Solving optimal reactive power dispatch problem using a novel teaching–learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal reactive power dispatch using chaotic bat algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y. Multi-objective optimal reactive power dispatch of power systems by combining classification-based multi-objective evolutionary algorithm and integrated decision making. IEEE Access 2020, 8, 38198–38209. [Google Scholar] [CrossRef]
- Elsayed, S.K.; Kamel, S.; Selim, A.; Ahmed, M. An improved heap-based optimizer for optimal reactive power dispatch. IEEE Access 2021, 9, 58319–58336. [Google Scholar] [CrossRef]
- Wu, T.; Zhao, C.; Zhang, Y.J. Distributed AC-DC optimal power dispatch of VSC-based energy routers in smart microgrids. IEEE Trans. Power Syst. 2021, 11, 6242. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H. A novel nature inspired meta-heuristic optimization approach of gwo optimizer for optimal reactive power dispatch problems. IEEE Access 2020, 8, 202596–202610. [Google Scholar] [CrossRef]
- Kanna, B.; Singh, S.N. Towards reactive power dispatch within a wind farm using hybrid PSO. Int. J. Electr. Power Energy Syst. 2015, 69, 232–240. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H.; Raja, M.A.Z.; Muhammad, Y. Application of shannon entropy implementation into a novel Fractional Particle Swarm Optimization Gravitational Search Algorithm (FPSOGSA) for optimal reactive power dispatch problem. IEEE Access 2021, 9, 2715–2733. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimal reactive power dispatch using hybrid Nelder–Mead simplex based firefly algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
- Gutiérrez, D.; López, J.M.; Villa, W.M. Metaheuristic techniques applied to the optimal reactive power dispatch: A review. IEEE Lat. Am. Trans. 2016, 14, 2253–2263. [Google Scholar] [CrossRef]
- Decompositions, O.C.; Rabiee, A.; Member, S.; Parniani, M.; Member, S. Voltage security constrained multi-period optimal reactive power flow using benders. IEEE Trans. Power Syst. 2013, 28, 696–708. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Liu, Z.; Liu, Y.; Jiang, Q. Dynamic optimal reactive power dispatch based on parallel particle swarm optimization algorithm. Comput. Math. Appl. 2009, 57, 1835–1842. [Google Scholar] [CrossRef]
- Sharif, S.S.; Taylor, J.H. Dynamic optimal reactive power flow. In Proceedings of the American Control Conference IEEE, Philadelphia, PA, USA, 26 June 1998; Volume 6, pp. 3410–3414. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I Formulations and deterministic methods. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, W.; Liang, J.; Cong, P.; Cai, Y. Coordinated day-ahead reactive power dispatch in distribution network based on real power forecast errors. IEEE Trans. Power Syst. 2016, 31, 2472–2480. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; El-Dabah, M.A.; Khurshaid, T.; Dominguez-Garcia, J.L. Optimal reactive power dispatch with time-varying demand and renewable energy uncertainty using Rao-3 algorithm. IEEE Access 2021, 9, 23264–23283. [Google Scholar] [CrossRef]
- Yang, N.; Yu, C.W.; Wen, F.; Chung, C.Y. An investigation of reactive power planning based on chance constrained programming. Int. J. Electr. Power Energy Syst. 2007, 29, 650–656. [Google Scholar] [CrossRef]
- Zhao, J.; Ju, L.; Dai, Z.; Chen, G. Voltage stability constrained dynamic optimal reactive power flow based on branch-bound and primal–dual interior point method. Int. J. Electr. Power Energy Syst. 2015, 73, 601–607. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Wu, Q.H. Fully decentralized multiarea reactive power optimization considering practical regulation constraints of devices. Int. J. Electr. Power Energy Syst. 2019, 105, 351–364. [Google Scholar] [CrossRef]
- Theologi, A.M.; Ndreko, M.; Rueda, J.L.; Van Der Meijden, M.A.M.M.; Gonzalez-Longatt, F. Optimal management of reactive power sources in far-offshore wind power plants. In Proceedings of the 2017 IEEE Manchester PowerTech, Powertech 2017, Manchester, UK, 18–22 June 2017. [Google Scholar] [CrossRef]
- Tang, L.; Ferris, M. Collection of Power Flow Models: Mathematical Formulations; University of Wisconsin: Madison, WI, USA, 2015. [Google Scholar]
- Park, B.; Tang, L.; Ferris, M.C.; Demarco, C.L. Examination of three different ACOPF formulations with generator capability curves. IEEE Trans. Power Syst. 2017, 32, 2913–2923. [Google Scholar] [CrossRef]
- Yang, S.; Wang, W.; Liu, C.; Huang, Y. Optimal reactive power dispatch of wind power plant cluster considering static voltage stability for low-carbon power system. J. Mod. Power Syst. Clean Energy 2015, 3, 114–122. [Google Scholar] [CrossRef]
- Gómez Bedoya, D.A. Metodología para el Análisis de Estabilidad de Tensión Mediante la División de Redes en Áreas de Control. Licentiate Thesis, Facultad de Ingenierías Eléctrica, Electrónica, Física y Ciencias de la Computación, Universidad Tecnológica de Pereira, Pereira, Colombia, 2014. [Google Scholar]
- Lakkaraju, T. Selection of Pilot Buses for VAR Support and Voltage Stability Risk Analysis. Licentiate Thesis, West Virginia University, Morgantown, WV, USA, 2006. [Google Scholar] [CrossRef]
- FlameJaguar/MP-ORPD: Multi-Period Optimal Reactive Power Dispatch Data Files. Available online: https://github.com/FlameJaguar/MP-ORPD (accessed on 17 August 2021).
- coin-or/Bonmin: Basic Open-Source Nonlinear Mixed INteger Programming. Available online: https://github.com/coin-or/Bonmin (accessed on 2 September 2021).
- Grigg, C.; Wong, P. The IEEE reliability test system -1996 a report prepared by the reliability test system task force of the application of probability methods subcommittee. IEEE Trans. Power Syst. 1999, 14, 1010–1020. [Google Scholar] [CrossRef]
- El-Araby, E.-S.E.; Yorino, N. Reactive power reserve management tool for voltage stability enhancement. IET Gener. Transm. Distrib. 2018, 12, 1879–1888. [Google Scholar] [CrossRef]




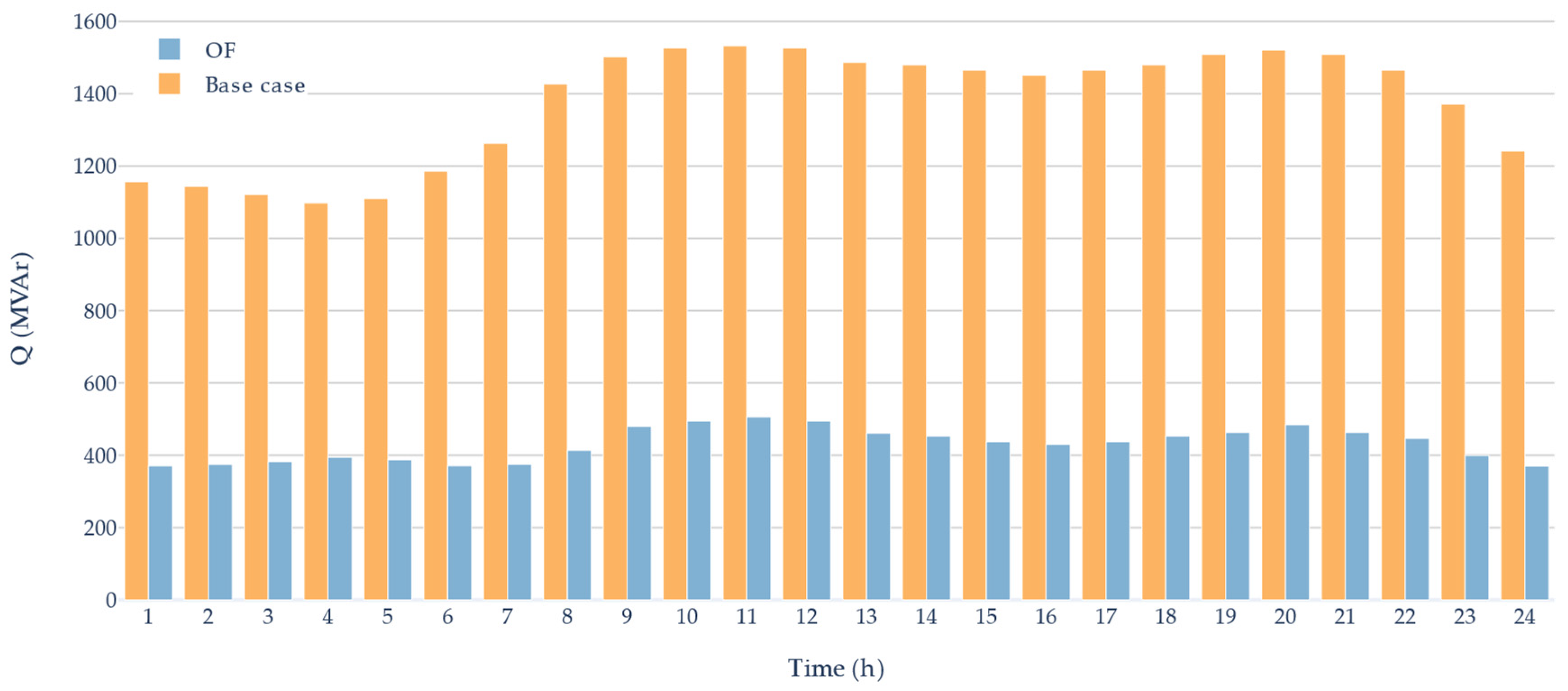
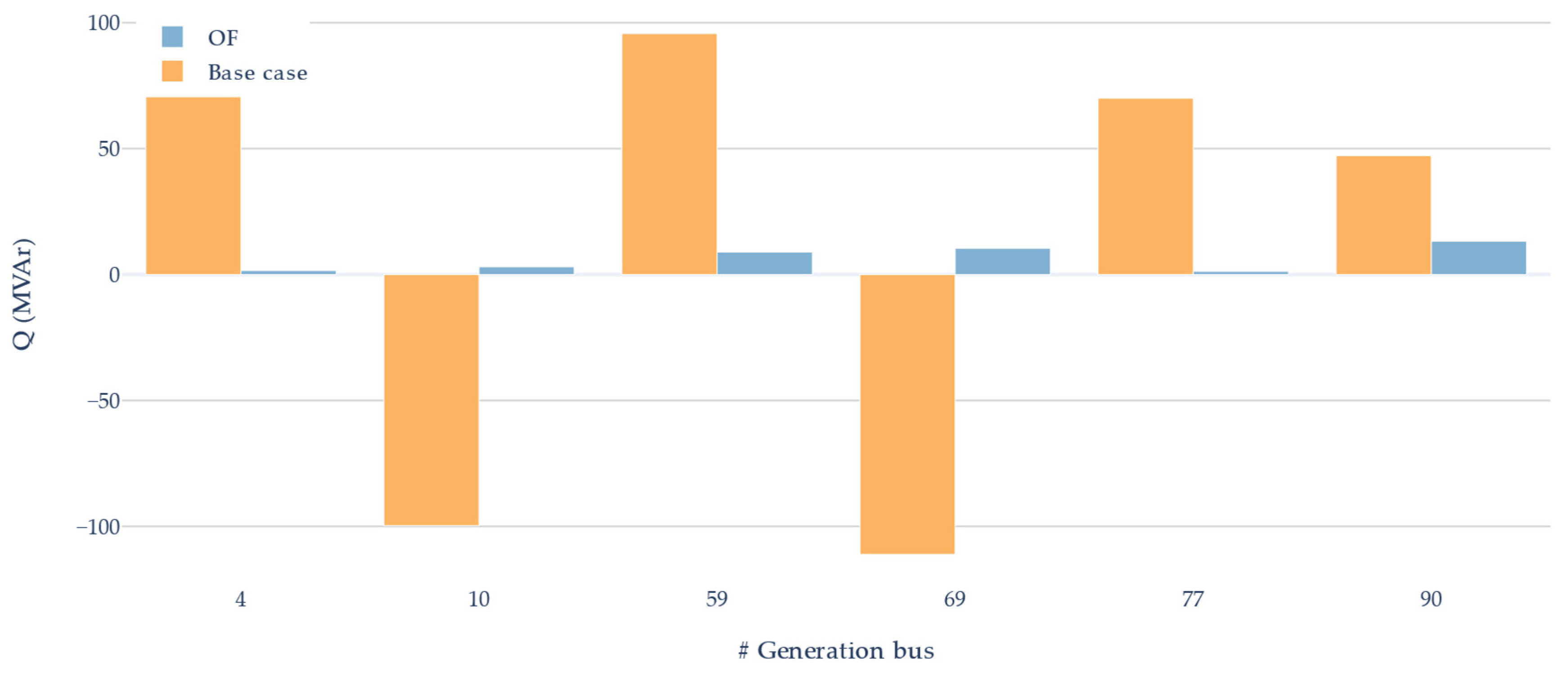
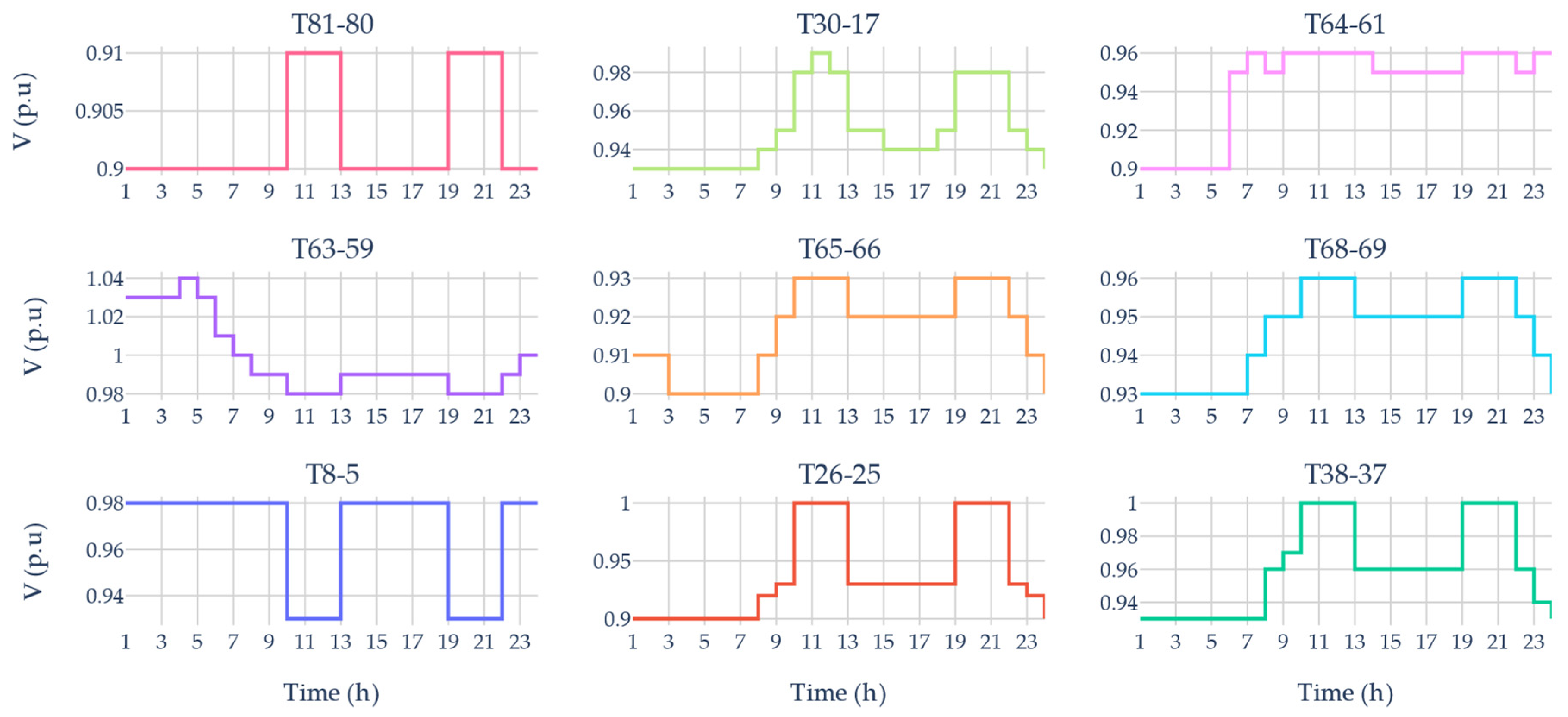
| Pilot Node | Lower Voltage Limit (p.u) | Shunt | MVAr |
|---|---|---|---|
| 0.9097 | 10 | ||
| 0.9177 | 25 | ||
| 0.9244 | 53 | ||
| 0.9252 | |||
| 0.9039 | |||
| 0.8927 | |||
| 0.9274 | |||
| 0.8500 | |||
| 0.8640 | |||
| 0.9119 | |||
| 0.9038 |
| Pilot Node | Lower Voltage Limit (p.u) | Shunt | MVAr |
|---|---|---|---|
| 0.935 | −40 | ||
| 0.9481 | 14 | ||
| 0.9276 | −25 | ||
| 0.9427 | 10 | ||
| 0.9349 | 10 | ||
| 0.90 | 10 | ||
| 0.9341 | 15 | ||
| 0.90 | 12 | ||
| 0.932 | 20 | ||
| 0.9434 | 20 | ||
| 0.90 | 10 | ||
| 0.90 | 20 | ||
| 0.954 | 6 | ||
| 0.9655 | 6 | ||
| 0.9542 | |||
| 0.90 |
| Case Base | TQG | TQD | TVD | TQG+ TQD | TQG+ TVD | TVD+ TQD | TQG+ TVD + TQD | |
|---|---|---|---|---|---|---|---|---|
| 0 | 117 | 51 | 141 | 118 | 118 | 135 | 118 | |
| 0 | 0 | 0 | 4 | 0 | 1 | 0 | 1 | |
| 4757 | 3928 | 4588 | 6965 | 3928 | 5101 | 7080 | 5101 | |
| 10.56 | 29.94 | 10.97 | 0.18 | 29.9 | 1.69 | 0.2 | 1.69 |
| Case Base | TQG | TQD | TVD | TQG+ TQD | TQG+ TVD | TVD+ TQD | TQG+ TVD + TQD | |
|---|---|---|---|---|---|---|---|---|
| 0 | 85 | 20 | 51 | 72 | 71 | 54 | 78 | |
| 0 | 13 | 0 | 20 | 14 | 19 | 0 | 17 | |
| 33037 | 4493 | 35997 | 36509 | 4494 | 10337 | 37000 | 10341 | |
| 18.22 | 20.98 | 7.37 | 8E-06 | 20.98 | 0.66 | 4E-12 | 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morán-Burgos, J.A.; Sierra-Aguilar, J.E.; Villa-Acevedo, W.M.; López-Lezama, J.M. A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals. Appl. Sci. 2021, 11, 8535. https://doi.org/10.3390/app11188535
Morán-Burgos JA, Sierra-Aguilar JE, Villa-Acevedo WM, López-Lezama JM. A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals. Applied Sciences. 2021; 11(18):8535. https://doi.org/10.3390/app11188535
Chicago/Turabian StyleMorán-Burgos, Jairo A., Juan E. Sierra-Aguilar, Walter M. Villa-Acevedo, and Jesús M. López-Lezama. 2021. "A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals" Applied Sciences 11, no. 18: 8535. https://doi.org/10.3390/app11188535
APA StyleMorán-Burgos, J. A., Sierra-Aguilar, J. E., Villa-Acevedo, W. M., & López-Lezama, J. M. (2021). A Multi-Period Optimal Reactive Power Dispatch Approach Considering Multiple Operative Goals. Applied Sciences, 11(18), 8535. https://doi.org/10.3390/app11188535







