Enhancement of Convection Heat Transfer in Air Using Ultrasound
Abstract
:Featured Application
Abstract
1. Introduction
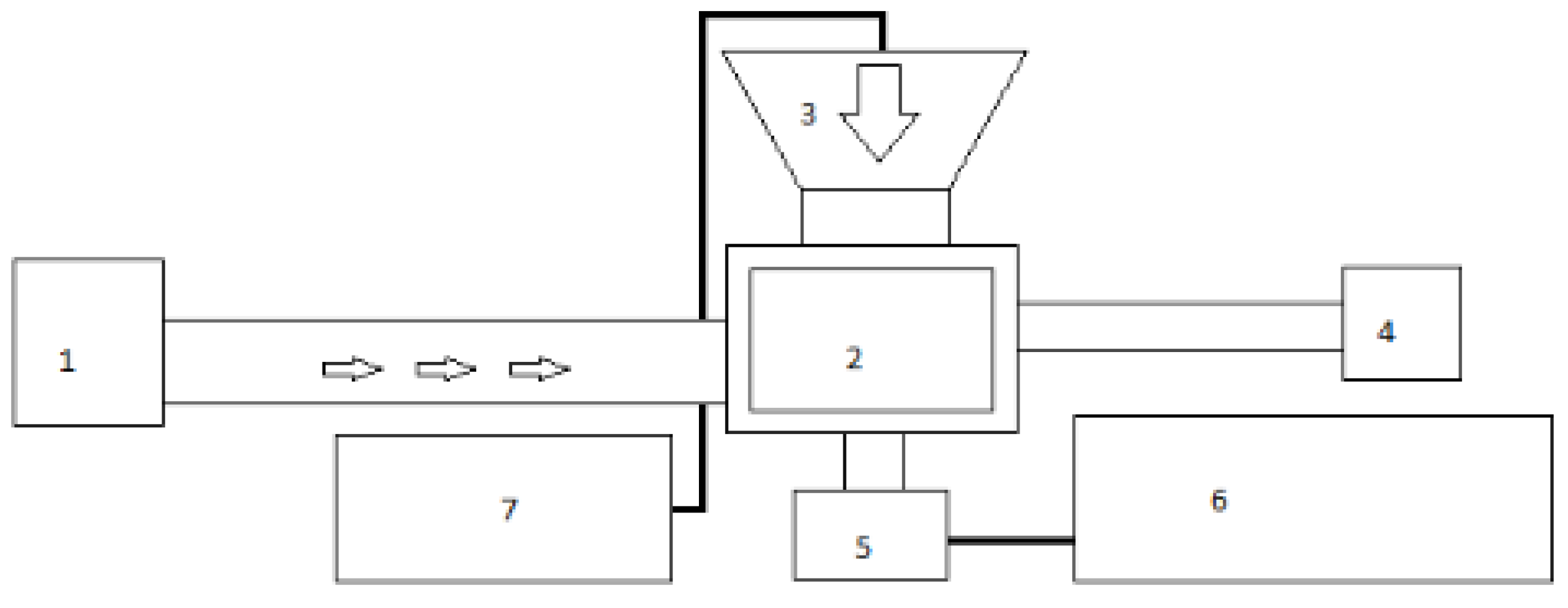
2. Materials and Methods
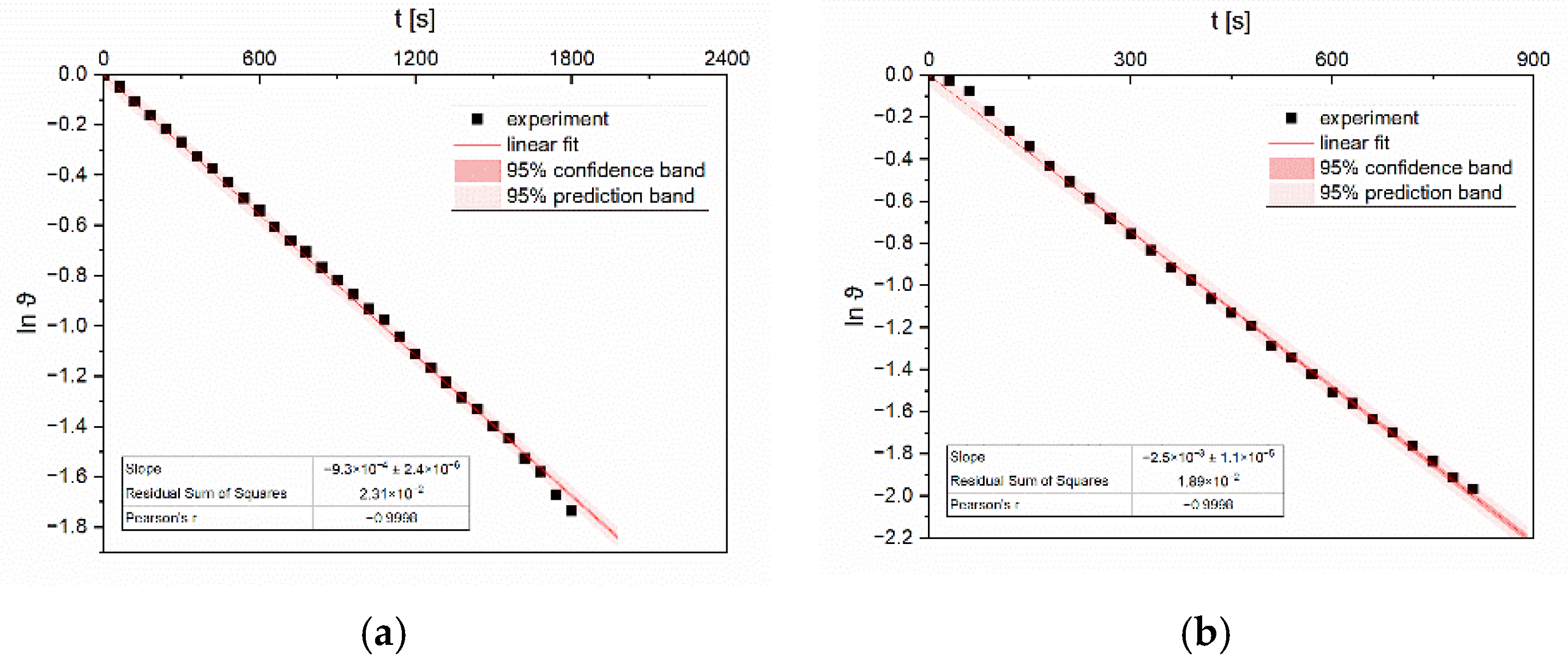
3. Mathematical Model
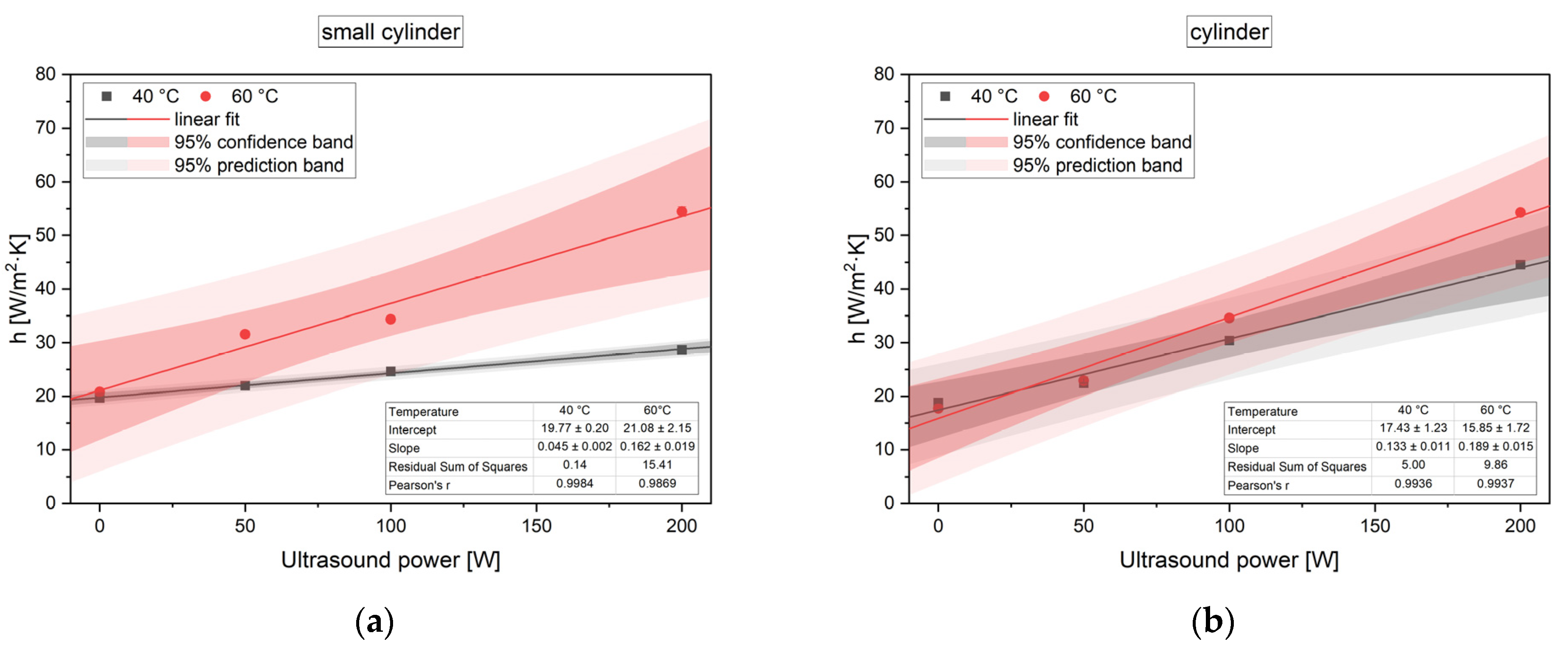
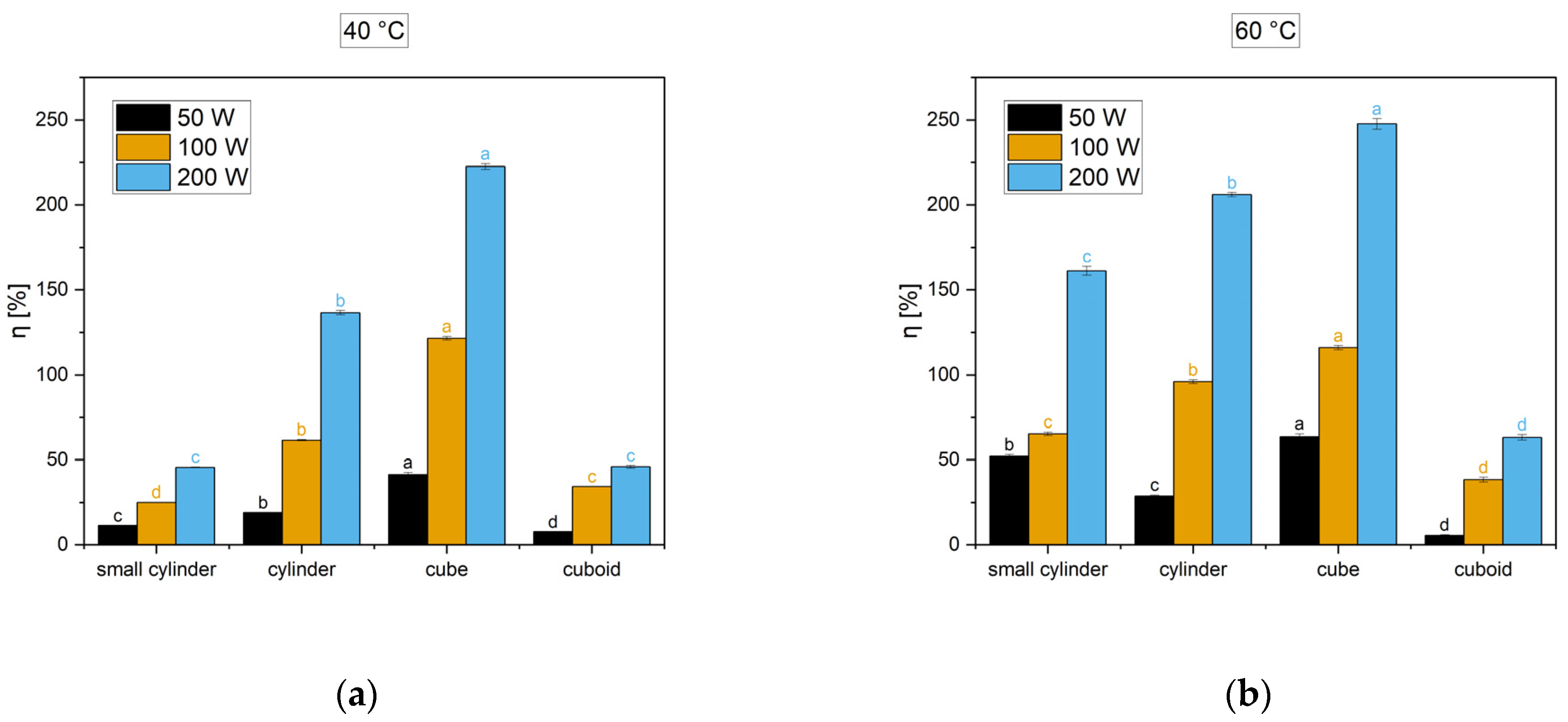
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kudra, T.; Mujumdar, A.S. Special Drying Techniques and Novel Dryers. In Handbook of Industrial Drying, 4th ed.; Mujumdar, A.S., Ed.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2015; pp. 433–489. [Google Scholar]
- Kudra, T.; Mujumdar, A.S. Advanced Drying Technologies, 2nd ed.; Taylor & Francis Group: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Siucińska, K.; Konopacka, D. Application of Ultrasound to Modify and Improve Dried Fruit and Vegetable Tissue—A Review. Dry. Technol. 2014, 32, 1360–1368. [Google Scholar] [CrossRef]
- Musielak, G.; Mierzwa, D.; Kroehnke, J. Food Drying Enhancement by Ultrasound. Trends Food Sci. Technol. 2016, 56, 126–141. [Google Scholar] [CrossRef]
- Muralidhara, H.S.; Ensminger, A.; Putnam, A. Acoustic Dewatering and Drying (Low and High Frequency): State of the Art Review. Dry Technol. 1985, 3, 529–566. [Google Scholar] [CrossRef]
- Cárcel, J.A.; García-Pérez, J.V.; Riera, E.; Mulet, A. Influence of High Intensity Ultrasound on Drying Kinetics of Persimmon. Dry Technol. 2007, 25, 185–193. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Riera, E.; de la Fuente Blanco, S.; Rodríguez-Corral, G.; Acosta- Aparicio, V.M.; Blanco, A. Application of High-Power Ultrasound for Dehydration of Vegetables: Processes and Devices. Dry Technol. 2007, 25, 1893–2007. [Google Scholar] [CrossRef]
- García-Pérez, J.V.; Cárcel, J.A.; Riera, E.; Rosselló, C.; Mulet, A. Intensification of Low-Temperature Drying by Using Ultrasound. Dry Technol. 2012, 30, 1199–1208. [Google Scholar] [CrossRef] [Green Version]
- García-Pérez, J.V.; Cárcel, J.A.; Simal, S.; García-Alvarado, M.A.; Mulet, A. Ultrasonic Intensification of Grape Stalk Convective Drying: Kinetic and Energy Efficiency. Dry Technol. 2013, 31, 942–950. [Google Scholar] [CrossRef]
- Sabarez, H.T.; Gallego-Juárez, J.A.; Riera, E. Ultrasonic-Assisted Convective Drying of Apple Slices. Dry Technol. 2012, 30, 989–997. [Google Scholar] [CrossRef]
- Cárcel, J.A.; García-Pérez, J.V.; Riera, E.; Mulet, A. Improvement of Convective Drying of Carrot by Applying Power Ultrasound. Influence of Mass Load Density. Dry Technol. 2011, 29, 174–182. [Google Scholar] [CrossRef]
- Ortuño, C.; Pérez-Munuera, I.; Puig, A.; Riera, E.; García-Pérez, J.V. Influence of Power Ultrasound Application on Mass Transport and Microstructure of Orange Peel during Hot Air Drying. Phys. Procedia 2010, 3, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Puig, A.; Pérez- Munuera, I.; Cárcel, J.A.; Hernando, I.; García-Pérez, J.V. Moisture Loss Kinetics and Microstructural Changes in Eggplant (Solanum melongena L.) during Conventional and Ultrasonically Assisted Convective Drying. Food Bioprod. Process. 2012, 90, 624–632. [Google Scholar] [CrossRef]
- Rodríguez, J.; Mulet, A.; Bon, J. Influence of High-Intensity Ultrasound on Drying Kinetics in Fixed Beds of High Porosity. J. Food Eng. 2014, 127, 93–102. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Pawłowski, A.; Szadzińska, J.; Łechtańska, J.; Stasiak, M. High Power Airborne Ultrasound Assist in Combined Drying of Raspberries. Innov. Food Sci. Emerg. Technol. 2016, 34, 225–233. [Google Scholar] [CrossRef]
- Szadzińska, J.; Kowalski, S.J.; Stasiak, M. Microwave and Ultrasound Enhancement of Convective Drying of Strawberries: Experimental and Modeling Efficiency. Int. J. Heat Mass Transf. 2016, 103, 1065–1074. [Google Scholar] [CrossRef]
- Szadzińska, J.; Łechtańska, J.; Kowalski, S.J.; Stasiak, M. The Effect of High Power Airborne Ultrasound and Microwaves on Convective Drying Effectiveness and Quality of Green Pepper. Ultrason. Sonochem. 2017, 34, 531–539. [Google Scholar] [CrossRef] [PubMed]
- Aversa, M.; Van der Voort, A.-J.; de Heij, W.; Tournois, B.; Curcio, S. An Experimental Analysis of Acoustic Drying of Carrots: Evaluation of Heat Transfer Coefficients in Different Drying Conditions. Dry. Technol. 2011, 29, 239–244. [Google Scholar] [CrossRef]
- Stasiak, M.; Musielak, G.; Mierzwa, D. Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Process. Energies 2020, 13, 6577. [Google Scholar] [CrossRef]
- Bantle, M.; Hanssler, J. Ultrasonic Convective Drying Kinetics of Clipfish during the Initial Drying Period. Dry. Technol. 2013, 31, 1307–1316. [Google Scholar] [CrossRef]
- Kowalski, S.J. Ultrasound in Wet Materials Subjected to Drying: A Modeling Study. Int. J. Heat Mass Transf. 2015, 84, 998–1007. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Mierzwa, D. US-Assisted Convective Drying of Biological Materials. Dry Technol. 2015, 33, 1601–1613. [Google Scholar] [CrossRef]
- García-Pérez, J.V.; Cárcel, J.A.; Riera, E.; Mulet, A. Influence of the Applied Acoustic Energy on the Drying of Carrots and Lemon Peel. Dry Technol. 2009, 27, 281–287. [Google Scholar] [CrossRef]
- García-Pérez, J.V.; Ozuna, C.; Ortuño, C.; Cárcel, J.A.; Mulet, A. Modeling Ultrasonically Assisted Convective Drying of Eggplant. Dry Technol. 2011, 29, 1499–1509. [Google Scholar] [CrossRef]
- Clemente, G.; Sanjuán, N.; Cárcel, J.A.; Mulet, A. Influence of Temperature, Air Velocity, and Ultrasound Application on Drying Kinetics of Grape Seeds. Dry Technol. 2014, 32, 68–76. [Google Scholar] [CrossRef]
- Fernandes, F.A.N.; Rodrigues, S.; Cárcel, J.A.; García-Pérez, J.V. Ultrasound-Assisted Air Drying of Apple (Malus domestica L.) and Its Effects on the Vitamin of the Dried Product. Food Bioprocess Technol. 2015, 8, 1503–1511. [Google Scholar] [CrossRef]
- Wong, S.W.; Chon, W.Y. Effects of Ultrasonic Vibrations on Heat Transfer to Liquids by Natural Convection and by Boiling. AIChE 1969, 15, 281–288. [Google Scholar] [CrossRef] [Green Version]
- Iida, Y.; Tsutsui, K. Effect of Ultrasonic Waves on Natural Convection, Nucleate Boiling, and Film Boiling Heat Transfer to a Saturated Liquid. Exp. Therm. Fluid Sci. 1992, 5, 108–115. [Google Scholar] [CrossRef]
- Loh, B.-G.; Lee, D.-R. Heat Transfer Characteristics of Acoustic Streaming by Longitudinal Ultrasonic Vibration. J. Thermophys. Heat Transf. 2004, 18, 94–99. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Kim, Y.G.; Kang, B.H. Enhancement of natural convection and pool boiling heat transfer via ultrasonic vibration. Int. J. Heat Mass Transf. 2004, 47, 2831–2840. [Google Scholar] [CrossRef]
- Hyun, S.; Lee, D.-R.; Loh, B.-G. Investigation of Convective Heat Transfer Augmentation Using Acoustic Streaming Generated by Ultrasonic Vibrations. Int. J. Heat Mass Transf. 2005, 48, 703–718. [Google Scholar] [CrossRef]
- Monnot, A.; Gondrexon, A.P.; Boldo, N.; Bontemps, N. Enhancement of Cooling Rate by Means of High Frequency Ultrasound. Heat Transf. Eng. 2007, 28, 3–8. [Google Scholar] [CrossRef]
- Dhanalakshmi, N.P.; Nagarajan, R.; Sivagaminathan, N.; Prasad, B.V.S.S.S. Acoustic Enhancement of Heat Transfer in Furnace Tubes. Chem. Eng. Process. 2012, 59, 36–42. [Google Scholar] [CrossRef]
- Kiani, H.; Sun, D.-W.; Zhang, Z. The Effect of Ultrasound Irradiation on the Convective Heat Transfer Rate during Immersion Cooling of a Stationary Sphere. Ultrason. Sonochem. 2012, 19, 1238–1245. [Google Scholar] [CrossRef] [PubMed]
- Baffigi, F.; Bartoli, C. Influence of the Ultrasound on the Heat Transfer in Single Phase Free Convection and in Saturated Pool Boiling. Exp. Therm. Fluid Sci. 2012, 36, 12–21. [Google Scholar] [CrossRef]
- Rahimi, M.; Dehbani, M.; Abolhasani, M. Experimental Study on the Effects of Acoustic Streaming of High Frequency Ultrasonic Waves on Convective Heat Transfer: Effects of Transducer Position and Wave Interference. Int. Commun. Heat Mass Transf. 2012, 39, 720–725. [Google Scholar] [CrossRef]
- Tajik, B.; Abbassi, A.; Saffar-Avval, M.; Abardeh, R.H. Heat Transfer Enhancement by Acoustic Streaming in a Closed Cylindrical Enclosure Filled with Water. Int. J. Heat Mass Transf. 2013, 60, 230–235. [Google Scholar] [CrossRef]
- Dehbani, M.; Rahimi, M.; Abolhasani, M.; Maghsoodi, A.; Afshar, P.G.; Dodmantipi, A.R.; Alsairafi, A.A. CFD Modeling of Convection Heat Transfer Using 1.7 MHz and 24 kHz Ultrasonic Waves: A Comparative Study. Heat Mass Transf. 2014, 50, 1319–1333. [Google Scholar] [CrossRef]
- Li, B.; Han, X.; Wan, Z.; Wang, X.; Tang, Y. Influence of Ultrasound on Heat Transfer of Copper Tubes with Different Surface Characteristics in Sub-Cooled Boiling. Appl. Therm. Eng. 2016, 92, 93–103. [Google Scholar] [CrossRef]
- Zheng, M.; Li, B.; Wan, Z.; Wu, B.; Tang, Y.; Li, J. Ultrasonic heat transfer enhancement on different structural tubes in LiBr solution. Appl. Therm. Eng. 2016, 106, 625–633. [Google Scholar] [CrossRef]
- Talebi, M.; Setareh, M.; Saffar-Avval, M.; Abardeh, R.H. Numerical Investigation of Natural Convection Heat Transfer in a Cylindrical Enclosure Due to Ultrasonic Vibrations. Ultrasonics 2017, 76, 52–62. [Google Scholar] [CrossRef]
- Cheeke, J.D.M. Fundamentals and Applications of Ultrasonic Waves, 2nd ed.; Taylor & Francis Group: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kroehnke, J.; Szadzińska, J.; Stasiak, M.; Radziejewska-Kubzdela, E.; Biegańska-Marecik, R.; Musielak, G. Ultrasound- and Microwave-Assisted Convective Drying of Carrots—Process Kinetics and Product’s Quality Analysis. Ultrason. Sonochem. 2018, 48, 249–258. [Google Scholar] [CrossRef]



| Sample | Diameter (mm) | Height (mm) | Sample | Length (mm) | Width (mm) | Height (mm) |
|---|---|---|---|---|---|---|
| Small cylinder | 20 | 20 | Cube | 30 | 30 | 30 |
| Cylinder | 30 | 30 | Cuboid | 120 | 20 | 30 |
| Parameter | Series I | Series II |
|---|---|---|
| Air velocity (m/s) | 0.40 ± 0.11 | |
| Air temperature (°C) | 40 ± 0.3 | 60 ± 0.3 |
| Ultrasound power P (W) | 0 | 0 |
| 50 | 50 | |
| 100 | 100 | |
| 200 | 200 | |
| Applied US Power | 0 W | 50 W | ||
| h(W/K·m2) | h(W/K·m2) | |||
| Small cylinder | 19.68 ± 0.10 | - | 21.93 ± 0.08 | 0.14 ± 0.09 |
| Cylinder | 18.81 ± 0.17 | - | 22.43 ± 0.10 | 0.07 ± 0.04 |
| Cube | 17.72 ± 0.09 | - | 24.97 ± 0.68 | 0.17 ± 0.03 |
| Cuboid | 14.35 ± 0.08 | - | 15.43 ± 0.08 | 0.06 ± 0.02 |
| Applied US Power | 100 W | 200 W | ||
| h(W/K·m2) | (W) | h(W/K·m2) | (W) | |
| Small cylinder | 24.60 ± 0.15 | 0.26 ± 0.12 | 28.65 ± 0.14 | 0.46 ± 0.02 |
| Cylinder | 30.40 ± 0.16 | 0.46 ± 0.06 | 44.55 ± 0.34 | 0.96 ± 0.10 |
| Cube | 39.21 ± 0.25 | 0.75 ± 0.16 | 57.12 ± 0.46 | 1.85 ± 0.09 |
| Cuboid | 19.26 ± 0.04 | 0.75 ± 0.02 | 20.92 ± 0.42 | 1.67 ± 0.05 |
| Applied US Power | 0 W | 50 W | ||
| h(W/K·m2) | h(W/K·m2) | |||
| Small cylinder | 20.78 ± 0.24 | - | 31.58 ± 0.63 | 0.061 ± 0.04 |
| Cylinder | 17.73 ± 0.05 | - | 22.87 ± 0.72 | 0.039 ± 0.011 |
| Cube | 16.17 ± 0.20 | - | 26.39 ± 0.65 | 0.037 ± 0.009 |
| Cuboid | 10.68 ± 0.27 | - | 11.27 ± 0.58 | 0.16 ± 0.03 |
| Applied US Power | 100 W | 200 W | ||
| h(W/K·m2) | (W) | h(W/K·m2) | (W) | |
| Small cylinder | 34.34 ± 0.53 | 0.11 ± 0.05 | 54.44 ± 0.93 | 0.33 ± 0.09 |
| Cylinder | 34.60 ± 0.55 | 0.05 ± 0.01 | 54.28 ± 0.12 | 0.78 ± 0.17 |
| Cube | 34.96 ± 0.75 | 0.08 ± 0.01 | 56.32 ± 0.63 | 1.12 ± 0.25 |
| Cuboid | 14.71 ± 0.51 | 0.23 ± 0.03 | 17.61 ± 0.55 | 0.92 ± 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musielak, G.; Mierzwa, D. Enhancement of Convection Heat Transfer in Air Using Ultrasound. Appl. Sci. 2021, 11, 8846. https://doi.org/10.3390/app11198846
Musielak G, Mierzwa D. Enhancement of Convection Heat Transfer in Air Using Ultrasound. Applied Sciences. 2021; 11(19):8846. https://doi.org/10.3390/app11198846
Chicago/Turabian StyleMusielak, Grzegorz, and Dominik Mierzwa. 2021. "Enhancement of Convection Heat Transfer in Air Using Ultrasound" Applied Sciences 11, no. 19: 8846. https://doi.org/10.3390/app11198846
APA StyleMusielak, G., & Mierzwa, D. (2021). Enhancement of Convection Heat Transfer in Air Using Ultrasound. Applied Sciences, 11(19), 8846. https://doi.org/10.3390/app11198846






