1. Introduction
Additive manufacturing (AM) techniques have been widely used in scientific, engineering, medical, and other applications [
1,
2,
3]. An AM process is composed of three stages: geometrical modelling, G-code generation, and 3D printing [
2,
3]. The resultant geometric models, G-code programs, and physical objects consume valuable resources, including human efforts, computing costs, energies, and raw materials. If these contents are illegally distributed, reproduced, and modified, the owners may encounter significant economic losses [
4,
5], and they will hesitate to invest additional resources in AM. Consequently, the innovation and progression of AM industries will be in danger. In some volunteer AM communities, their members are willing to share their work and knowledge with others. Thus, ownership protection is not a concern [
6,
7,
8]. However, in this situation, authentication and annotation of contents are still required to avoid misusage of the products.
Watermarking procedures had long been used to enhance the securities of digital data, including texts, music, images, and videos [
9,
10,
11]. By analogy, in AM industries, people inserted identification signals into digital and physical models to secure their intellectual properties [
12,
13,
14]. Nonetheless, mechanisms for protecting G-code programs were seldom discussed in these publications. In an AM process, the quality of the resultant object is mainly decided by the G-code program. Thus, we spend a lot of efforts to decide the printing direction, construct the supporting structures, slice the geometric model, select the hatching patterns, and schedule the toolpaths before generating the G-code program. Besides, to ensure a high-quality 3D printing, we must also conduct experiments, calculations, and simulations to obtain feasible printing parameters, including the nozzle temperature, raw material type, printing speed, etc. Therefore, for the sake of economy, G-code programs are valuable properties. Furthermore, well-tuned G-code programs can be used to repeatedly produce physical models to reduce production costs. Thus, G-code programs are one of the key gradients for mass-production in AM applications. Based on these reasons, G-code programs should be carefully protected too.
In most of the published watermarking algorithms, the digital models are presumed to be expressed in polygonal representations, for example, stereolithography (STL) and OBJ formats [
2,
3,
4,
5]. However, tissues and organs, segmented from 3D medical image data, are composed of voxels [
15]. They are not polygonal models and cannot be watermarked by using these conventional methods. To protect or authenticate them, we must invent new watermarking techniques. In some conventional watermarking procedures, watermarks are created on the surfaces of digital models. These watermarks could be damaged in the G-code generation, printing, and post-processing stages and become hard to verify [
4,
5]. Some other researchers proposed to insert watermarks inside digital models [
16,
17]; thus, the printing and post-processing processes would not remove these signals. However, these algorithms possess weakness too. For example, the geometrical complexities of the regions for inserting watermarks are usually simple. Secondly, these methods lack the techniques to uncover watermarks in digital models, thought they are capable to reveal watermarks in printed results. Thirdly, special facilities are required to uncover and verify watermarks. Hence, it will be beneficial to design an adaptive watermarking scheme which can insert fingerprints anywhere in digital and physical models and can adjust the encoding process to accommodate the shapes of the target models, the underlying 3D printing platforms, and the intended applications of the products.
Methodology Overview
In this article, we propose a watermarking method for AM. The proposed approach is composed of the following steps. At first, the input geometric model is converted into a distance field. At the second step, the watermark is inserted into a region of interest (ROI) by using self-organizing mapping (SOM). Finally, the watermarked model is converted into a G-code program by using a specialized slicer, and thus the watermark is implicitly encoded into the G-code program. If the G-code program is executed by a 3D printer to manufacture an object, the printed part will contain the watermark too.
Compared with conventional watermarking methods, our algorithm possesses the following advantages. First, it protects not only digital and physical models but also G-code programs. Second, it can embed watermarks into both polygonal and volumetric models. Third, our method is capable of inserting watermarks inside the interiors or on the surfaces of complex objects. Fourth, the watermark can appear in various forms, for example, signature strings, randomly distributed cavities, embossed bumps, and engraved textures.
Various verification methods are also developed in this work to authenticate digital and analog contents. If the target is a G-code program, we emulate it by using a simulator to generate a volume model at first. Then, the result is rendered to search for a trace of watermark. If a watermark is found, we extract it and compare it with the recorded watermark to verify the G-code program. When dealing with a geometric model, we first render the content to confirm the existence of a watermark. Then, this watermark is retrieved from the model and compared with the recorded one to evaluate the genuineness of the geometric model. If the target is a physical part, we illuminate the object by using light rays to uncover the watermark. Then, the revealed watermark is compared with the recorded watermark to authenticate the physical part.
The rest of this article is organized as follows.
Section 2 describes the embedding and detecting procedures. The test results are given in
Section 3. Discussion and analysis of this research are presented in
Section 4. Comparisons with others’ methods and future work are also included in
Section 4. This article ends with a conclusion in
Section 5.
2. Materials and Methods
The flowchart of the proposed watermarking procedure is illustrated in
Figure 1. It includes the steps of voxelization, distance field transformation, region-of-interest creation, watermark embedding, and G-code generation. Details of these computations are presented in this section. Besides the encoding procedure, we also design various verification methods for digital and physical contents. These algorithms are also formulated in this section.
2.1. Voxelization and Distance Field Computation
In the proposed watermarking method, the input model is presumed to be contained in a volumetric space, composed of voxels. In case that the model is expressed in a traditional polygonal representation, a voxelization computation [
18] is triggered to decompose it into voxels. To achieve this goal, we enclose the model by using an axis-aligned bounding box (AABB). Then, the AABB is divided into voxels by using a regular grid. At the following step, the voxels are classified into two types: model voxels and void voxels. A voxel is regarded as a model voxel if it is in the interior of the model or intersected with the model’s boundaries. Otherwise, it is regarded as a void voxel. After the classification process, the intensities of the void and model voxels are set to zero and one, respectively.
At the following stage, we construct a distance field
D(
x,
y,
z) in the AABB to record the shortest distances from the model surface to all the voxels.
D(
x,
y,
z) expands like a wave, originating at the model surface Γ(
x,
y,
z) and propagating inwards and outwards. Its travelling speed is proportional to the inverse of its gradient magnitude. Hence, the distance function is governed by the eikonal equation [
19],
where
f is the propagation speed of the distance field. We compute the distance field by using the revised fast marching method (RFMM), developed in the research of [
20]. In the computation, all the voxels in the AABB are grouped into three sets: DONE, CLOSE, and FAR. DONE contains those voxels, whose final distances are computed. CLOSE keeps the voxels, which are adjacent to the voxels of DONE. Other voxels are stored in FAR.
Initially, the voxels belonging to the model’s boundary, Γ(
x,
y,
z), are inserted into DONE and their distances are set to a purposefully selected value, for example zero. Then, the voxels adjacent to DONE are searched and stored in CLOSE. When inserting a voxel into CLOSE, we apply forward and backward differences to approximate the partial derivatives of Equation (1) and use the distances of its neighbors in DONE to convert Equation (1) into a quadratic polynomial. Then, the voxel’s distance is set to the larger root of this quadratic polynomial. To speed up the computation, CLOSE is implemented by using a priority queue [
21], such that the voxel belonging to CLOSE and having the smallest distance is always at the top-most position of CLOSE. Since the voxels in FAR do not contact any voxels of DONE, their distances are set to infinite at the initial stage.
Then, the computation is iteratively carried out. At each iteration, the top-most voxel of CLOSE is removed and inserted into DONE. Subsequently, those of its neighbors, which are in CLOSE or FAR, are searched and new distances of these neighboring voxels are calculated by using the method mentioned in the previous paragraph. If the new distance of a neighbor is shorter than its current one, the distance of this neighbor is replaced by the new distance. After this updating procedure, the neighbors, which were in FAR before the updating, are removed from FAR and inserted into CLOSE. Along with each distance modification and voxel insertion, positions of voxels in CLOSE are adjusted according to their distance values to ensure the top-most voxel always has the shortest distance in this set. These calculations are repeated until CLOSE becomes empty. The details of the RFMM can be found in the paper of [
20]. The paper of [
19] provides an alternative method for computing distance fields.
Figure 2 shows some results, generated by the voxelization and distance field computation. The input model, displayed in part (a), is a bowl, formed by triangles. After the voxelization process, it becomes a volume model, as revealed in part (b). In the following step, the model is transformed into a distance field. A section, cut from this model, is portraited in part (c) to uncover the characteristics of the distance field. As the image shows, the distance field contains multiple layers of iso-surfaces [
18,
19]. Since voxels in these individual iso-surfaces belong to different distance levels, we can peel this model level-by-level and insert signatures in selected levels.
2.2. ROI Segmentation
After converting the input geometric model into a distance field, the proposed watermarking procedure extracts some adjacent levels from the distance field. These distance levels are confined by the following constraint:
When t1 and t2 are the lower and upper bounds of the adjacent levels. Then, an oriented bounding box (OBB) is manually constructed by the users via a graphical user interface. Those voxels, belonging to these distance levels and the OBB, are automatically collected by the encoder to form a region of interest (ROI). They will be utilized to carry the watermark in a latter computation.
An example is shown in part (a) of
Figure 3 to demonstrate the ROI construction process. The input model is a bowl, rendered in white color. The green edges reveal the OBB of the ROI; the light blue region is the resultant ROI.
2.3. Digital Model Watermarking
Traditional watermarking methods are designed to insert fingerprints into geometries of polygons or parametric meshes [
22,
23]. Nonetheless, in this work, the target contents are volume models comprised with voxels. They lack connectivity and topological information, and thus conventional watermark embedding methods are not applicable for them. To overcome this problem, we develop a self-organizing mapping (SOM) procedure to encode watermarks for these models. The fundamental concept of this procedure is depicted in
Figure 4. At first, the watermark is rasterized in a 2D lattice of nodes. Hence, this lattice forms a binary image of the watermark; some of its nodes are watermarked while others remain intact. Then, an iterative correspondence training process is triggered to create links between the lattice nodes and the ROI voxels. Finally, the watermark is placed inside the ROI via these correspondent relations. The iterative correspondence training and embedding computations are described in the following contexts.
2.3.1. Iterative Correspondence Training
The correspondence training process is conducted as follows. Initially, each lattice node is given a random weight vector
w = (
wx,
wy,
wz). Then, at each iteration, a voxel is randomly selected from the ROI. Assume this voxel is indexed by
I = (
i,
j,
k) in the AABB. At the following step, the lattice node, whose weight vector
w is most similar to
I, is searched. This node is the
winner node and its weight vector is revised by
where
δ(
t) is a learning factor, shrinking with time
t. After the weight vector of the winner is revised, the weight vectors of its neighbors within the
vicinity are also modified as follows,
where
wj is the weight vector of the
j-th neighbor,
dj is the distance between the winner and this neighbor, and
γ is a scaling factor proportional to the inverse of
dj. The vicinity is defined by a circle, centered at the winner node. Its radius is shrunk with time to ensure the convergence of the SOM. The above training procedure repeats until the weight vectors of all the lattice nodes converge or the number of iterations exceeds a predefined limit. The fundamental principles of SOM can be found in the researches of [
24,
25].
2.3.2. Watermark Embedding
Then, for each model voxel in the ROI and with index I, we find the lattice node possessing the most similar weight vector w, i.e., w ≈ I. If the lattice node was watermarked in the rasterization step, the distance of this voxel was disturbed or replaced by a special value. Otherwise, its distance is unchanged. After completing the watermarking process, the model is volume-rendered in several view angles to reveal the embedded watermark. One of the resultant images is recorded and will be used in the future to authenticate G-code programs, geometric models, and printed parts.
An example of the SOM watermarking scheme is demonstrated in
Figure 3. The watermarked ROI and the extracted image are shown in parts (b) and (c), respectively. The watermark image is taken in the top view angle.
2.4. G-Code and Physical Part Watermarking
After being watermarked, the digital model is converted into a G-code program by using a specially designed
slicer. This slicer is capable of translating voxel models into G-code programs. Its algorithms, data structures, and operational procedures can be found in [
26]. During the G-code generation procedure, the space occupied by watermarked voxels is treated as void spaces or filled with different hatch patterns or materials, depending on the characteristics of the underlying 3D-printing platforms and the applications of the model. Hence, the watermark is implicitly embedded in the G-code program. By using this G-code program to layered-manufacture a physical part, the resultant object will contain the watermark and is under protection too.
2.5. Recorded Information
Some essential data of the watermarking process are secretly recorded and will be used in the authentication processes. These data are listed in
Table 1. The first item is the watermark image taken in the encoding stage. It is called the
recorded watermark hereafter. This signal will be used to verify digital models, G-code programs, and printed parts. The second and third items are the disturbance value and the ROI. This information helps us to locate and capture watermarks in digital and physical models. The last recorded parameter is the view angle in which we generate the recorded watermark.
Besides keeping these data, a physical model might be manufactured too. This printed object contains the watermark and will serve as the standard model for verifying printed parts in the future.
2.6. Watermark Detection Procedures
Since watermarks may be embedded into digital models, G-code programs, and physical parts, different decoding methods are derived to handle these contents accordingly. Their flowcharts are illustrated in
Figure 5. The procedures for verifying G-code programs and digital models are similar. They rely on virtual manufacturing, volume rendering, and similarity evaluation to achieve their goals. On the other hand, the authentication procedure for physical parts invokes physical manufacturing, image capturing, and visual comparison. These three watermark detection algorithms are described in this subsection.
The method dedicated to authenticating a G-code program is shown in part (a) of
Figure 5. At first, the G-code program is emulated by using a simulator to generate a voxel model. The design, implementation, and functionalities of this simulator are presented in [
27]. Then, the model is volume-rendered to search for a trace of watermark. If a watermark appears in the resultant images, we extract the watermark by using the recorded view angle and ROI. At the following step, the similarity between this watermark and the recorded one is computed by using the dHash method of [
28]. If the resultant dHash value is higher than a predefined threshold, we assume that this G-code is genuine.
To examine a digital model, we volume-render this model to confirm the existence of a watermark. Then, this watermark is retrieved by using the recorded ROI and view parameter. At the following step, the extracted watermark is compared with the recorded one by using the dHash method. If the similarity index is higher than the predefined threshold, this digital model passes the authentication test.
The verification procedure for a physical part in depicted in part (b) of
Figure 5. At first, we retrieve the standard model, fabricated in the encoding process. At the second step, we illuminate the physical part and the standard model by using a bright light source to uncover their watermarks. Then, the revealed watermarks are visually compared. If an image capture device is available, we can generate watermark images from both objects and make comparisons by using the dHash method.
3. Experimental Results
Based on the proposed embedding and detecting schemes, we built a watermarking system aiming to enhance the security of AM. The major components of this system include an encoder and a decoder. The former is responsible for embedding watermarks, while the latter is utilized to verify contents. Besides these two programs, the slicer and simulator, developed in the researches of [
26,
27], are also employed to translate voxel models into G-code programs and to convert G-code programs into voxel models, respectively. Many experiments had been designed and conducted to test the system. Some of the test results are presented and analyzed in this section.
3.1. Watermarking Experiments
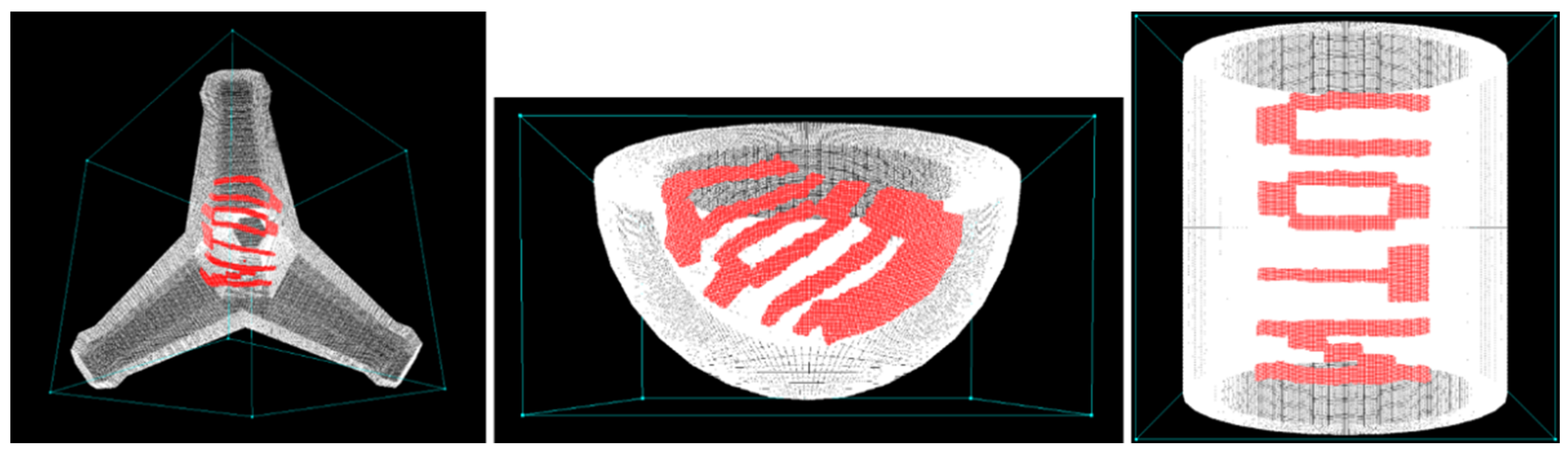
The first experiment was designed to test the encoder. The input models are originally expressed in STL format. The encoder converted the input models into voxel models at first. Then, it transformed these voxel models into distance fields and embedded watermarks there. The watermarked models are shown in
Figure 6, including a tetrapod, a bowl, and a mug. The string, “NTOU”, was served as the watermarks. The results were produced by a volume-rendering subroutine. To high-light the watermarks, the model boundaries were shaded in transparent white color while the watermarks were rendered in opaque red color. We cut off a portion of the bowl by using a clipping plane to better illustrate its internal structures. Among these three models, the tetrapod possesses a complicated structure, and hence its watermark is twisted. On the other hand, the watermark in the mug suffers less distortion because of the mug’s simple shape.
Conventionally, watermarks are inserted in imperceptible positions to enhance security. In this experiment, we purposely embed the watermarks into large curvy spaces in the test models to evaluate the capability of our encoding procedure. As the resultant images show, the watermarks blend well with their host models. The watermarks originate from a flat 2D pattern and the ROIs are comprised with voxels, scattering in curvy distance levels. There are enormous geometric and topological imparities between these two types of media. The experimental results show that the SOM subroutine bridges the gaps and successfully inserts the watermark into these voxel models.
Besides watermarking the test models, blank-and-white images of the watermarks are produced and recorded for authentication purpose. These watermark images are displayed in the upper row of
Figure 7. The watermarks of the tetrapod and mug are rendered in the front view while the watermark of the bowl is imaged through the left upper corner of the AABB. After being watermarked, the digital models were converted into G-code programs by using the slicer. The resultant G-code programs would generate fingerprinted contents if they were interpreted by simulators or executed by 3D printers.
3.2. Watermark Detection for G-Code Programs and Voxel Models
After testing the encoder, we conducted another experiment to evaluate the decoder: At first, we fed the G-code programs to the simulator and virtually manufacture three voxel models. These contents were then processed by the decoder to extract the hidden watermarks. The extracted watermarks are displayed in the lower row of
Figure 7. At the following step, the decoder calculated the dHash values between the extracted and recorded watermarks. The dHash values were represented by 128-bit binary strings. Finally, the similarities between the extracted and recorded watermarks were computed by using the dHash values, based on Hamming distances [
28]. The results are presented in
Table 2.
The test models are not the original ones but reproduced by using the G-code programs. However, the G-code programs are genuine, and thus the test models should be regarded as legitimate copies of the raw models. As the test results shown in
Table 2, the similarities between the detected and recorded watermarks are high. Therefore, our decoder successfully verifies these contents. Furthermore, the genuineness of the G-code programs is also implicitly asserted in this experiment. The efficacy of our decoder on authenticating G-code programs and geometric models were proven in this experiment.
Among the test models, the mug generates the highest similarity while the tetrapod produces the lowest score. The tetrapod is relatively complex. The G-code generation and virtual manufacturing process induces more geometric noises into its virtual model. Thus, the similarity between the extracted and recorded watermarks is decreased. On the other hand, the mug has a simple shape, such that the watermark preserves its pattern after the digital-to-analog and analog-to-digital conversions. Hence, the captured and recorded watermarks of this model are more similar.
3.3. Watermark Verification for Printed Parts
In the third experiment, we assessed the capacities of our verification method for printed parts. At first, we watermarked a plate and utilized the slicer to translate it into a G-code program. Then, we fabricated physical copies of the plate and the mug by using a Fusion Decomposition Modelling (FDM) printer. The plate was printed using acrylonitrile butadiene styrene (ABS) filament while the mug was manufactured with polylactic acid (PLA) thermal plastic. Since we did not have any thermal imaging facilities to retrieve watermarks, we illuminated the physical parts by using bright light sources and captured photos of these printed models by using a cellular phone camera.
The results are presented in
Figure 8. The photos show that the watermarks are invisible under ordinary lighting conditions (the left images of parts (a) and (b)). As the light sources are intensified, the watermarks show up and can be visually evaluated (the right images pf parts (a) and (b)). Based on several test results, we find that the visual detection procedure is greatly influenced by the raw materials. Since the ABS filament possesses higher transparency than the PLA thermal plastic, it is easier to detect the watermark in the plate than the mug.
3.4. Placing Watermarks on Model Surfaces
In the fourth experiment, we used the encoder to create embossed and engraved watermarks on the surfaces of the plate, the bowl, and a round cube. At first, a ROI was created in each of these test object. This ROI contains the surface layer and five consecutive distance levels adjacent to the surface of its host model. To create an embossed watermark, these adjacent levels were selected from the void space outside the model. On the other hand, the adjacent levels were extracted inside the model for generating an engraved watermark. Then, we invoked the SOM procedure to embed the watermark “NTOU” into the ROI. During the encoding process, the SOM procedure converted watermarked void voxels into model voxels (for embossed signatures) or replaced watermarked model voxels with void voxels (for engraved marks). Then, the watermarked models were manufactured by using the FDM printer. The printed parts of the plate were fabricated by using ABS while the bowl and the cube were printed with PLA. The heights and depths of the embossed and engraved patterns are about 1 mm.
The images of the physical objects are displayed in
Figure 9. As the images show, the encoder successfully generates these fingerprints on the models’ surfaces. They can be visually evaluated without using any photographic equipment. In some hobbyist and volunteer communities, people are willing to share their work. Therefore, copyright infringement is not a concern. Instead, they need an efficient way to quickly identify products [
6,
7,
8]. This experiment ensures that our watermarking system can be employed to accomplish this goal.
4. Discussion and Analysis
Imperceptibility and resilience against attacks are essential in designing watermarking methods. In this section, the protective mechanisms offered by the proposed watermarking method are presented and analyzed. In the past decades, many watermarking algorithms had been developed to protect intellectual properties in AM. To our knowledge, these methods are dedicated for protecting either polygonal models or physical products. On the other hand, our watermarking system is designed to enhance the securities of geometric models, G-code programs, and printed parts. Thus, the application scope of our approach is wider. In addition, the computational spaces and fundamental methodology of our method are different from those of the conventional approaches. These issues should be outlined and compared. In this research, we developed new techniques to watermark voxel models. The potential usage of these algorithms also deserves discussion.
4.1. Encryption Using Distance Fields
During the watermarking process, our encoder encrypts the digital model by transforming it into a distance field. To attack the watermark, the attackers must obtain full knowledge about this encryption procedure. Otherwise, they are not able to comprehend the volume data and be aware of the digital model. Thus, our method offers an extra layer of security against malicious accesses.
Conventional G-code generators cannot translate encrypted models into G-code programs. Thus, encrypted models must be decoded before being processed. After the decryption, the input models are not protected and may be illegally copied and distributed. Hence, encryption was not favored in protecting digital models in AM [
4,
5]. On the other hand, our slicer is capable of directly converting encrypted and watermarked voxel models into G-code programs, as shown in the experiments. Therefore, encryption using distance field is pragmatic and increases the strength of watermarking.
4.2. Resilience and Imperceptibilty
In the encoding process, the ROI, disturbance value, and view angle are essential for embedding the watermark and generating the watermark image. They are vital for protecting the contents; thus, we keep them in secret. Without knowing these parameters, it is hard for an outsider to locate and reveal the watermark. In our decoding process, the watermark is captured by means of volume-rendering. It seems that the attackers can utilize volume-rendering tools to uncover the watermark too. However, the attackers must obtain these secret keys and be aware of the distance encryption so that they can filter out irrelevant voxels and high-light the watermark in the volume visualization process. Otherwise, they have to extract the watermark by trial-and-error.
Besides the ROI, disturbance, and view angle, the watermark image is also secretly recorded. For the sake of clarity, we used a simple and large string as watermarks in the presented experiments so that we could easily recognize the fingerprints. If these identification signals were composed of randomly scattered and irregular patterns, it would be difficult to comprehend them, even they had been revealed by volume rendering tools.
4.3. G-Code Program Protection
After a watermarked model was translated into a G-code program, our decoder did not explicitly embed any signatures into the result. It seems that this content is not protected. However, the G-code program contains instructions, which generate the watermark. To remove the watermark from printed parts, the attackers have to figure out these instructions first and remove or modify them later. It is impossible to identify these instructions by browsing the G-code program. Using a simulator to emulate the printing process might offer some clues. Nonetheless, beside the simulator invoked by our decoder, most G-code interpreters can display only the toolpaths and resultant model by drawing thick lines or solid tubes [
29,
30]. If the watermark is irregular or small, it is very unlikely to comprehend the watermark during the simulation process, not to mention locating the G-codes.
Even when these G-codes were discovered, removing or editing them may produce profound damages in the G-code program. As a result, the G-code program becomes useless and no physical part can be manufactured.
4.4. Flexibility and Other Issues
Some researchers proposed to attach fingerprints on the surface of a model or to slightly alter the vertex coordinates or mesh connectivity of the model surface to prevent copyright violation [
31,
32,
33,
34]. Nonetheless, these protection mechanisms may be un-intentionally damaged in the G-code generation, 3D printing, and post-processing stages. As a result, the decoder may fail to accept the watermark in the verification process [
4,
5]. Hiding the watermark inside the model and printing it by using different materials, layer thickness, or filling patterns alleviate this problem [
34,
35]. Using the intrinsic characteristics of the 3D printer can offer some help too [
36]. However, detecting and evaluating hidden and subtly arranged watermarks require special facilities, for example high-resolution scanners and powerful reconstruction software [
4,
5]. In this research, we employ the SOM procedure to embed watermarks. This procedure allows us to plant watermarks inside the input model or to create embossed and engraved patterns on the model surface. Thus, our approach is flexible and can accommodate different 3D printing platforms and applications.
In the presented test results, we utilized strong light sources to reveal watermarks hidden in printed parts, since the raw materials are semi-transparent. This strategy fails if the raw materials are opaque. Using thermal photography and radiation imaging methods may enhance the detection process [
16,
17]. In the work of [
31], watermarks are created by using magnetic materials or RFID chips and can be captured by sensors regardless of their positions. These methods were pragmatic if the slicers had been extended to generate G-codes for multi-material printing and chip insertion.
Besides the watermark embedding methodology, watermark-design deserves some attentions too. This issue is seldom discussed in literatures, except the survey papers of [
4,
5]. A regular and large watermark is easier to verify, but it is prone to be uncovered. On the other hand, a small and irregular watermark is more imperceptible. Nonetheless, it may suffer from damages caused by the slicer and the 3D printer, especially when the underlying 3D printer is a low-end machine. As a result, the watermark could fail to be accepted by the decoder. By performing watermarking in a voxel-space, it is relatively easier to adjust the sizes, patterns, and locations of watermarks. Thus, we can gain extra flexibility in designing watermarks to fit the 3D printers and applications.
4.5. Future Work
In this research, we transform the input model into distance field by using the eikonal equation. It is possible to deduce advanced encryption methods for volume models, based on the distance field computation. For example, varying the propagation speed, f, in some voxels in the AABB will distort the distance field, making it harder to segment the model from the volume data. Besides, the initial distance field value on the model surface can be kept in secret such that comprehending the data set would become more difficult.
In this research, the SOM procedure helps us to embed watermarks. It is capable of creating cavities inside models and generating engraved and embossed patterns on model surfaces. We plan to further exploit this technology and build editing tools for volume models such that we can carve and reshape simple models to create complex objects that are difficult to create by means of polygonal-based or parametric-mesh modelling methods. Therefore, we can create a geometric modeler for voxel models.
Recently, some researchers proposed to build compliant mechanisms and 4D-printing models using AM [
37,
38]. The resultant objects can change shapes, produce motions, transport energies, and bear workloads when encountering external influences, such as water, forces, electricity, magnet, heat, chemical solutions, etc. They possess great applications in industries. Material and mechanic properties differentiate from one position to another inside these types of structures. These parameters are hard to specify in polygonal representations. However, by converting geometric models into volume data sets and encoding these characteristics into the voxels, we can create objects with non-uniform internal properties. We plan to extend the proposed watermark scheme, especially the SOM routine, to adjust structural, material, and mechanic properties inside geometric models to accomplish this functionality.
Some researchers proposed to design models of anisotropic materials [
39,
40,
41]. The SOM embedding module of our watermarking program can be used to define material properties and printing directions for individual voxels. Hence, this functionality can be achieved in the modelling stage. However, we need to revise the G-code generating method to realize anisotropic printing. New experiments also have to be carried out so that a robust manufacturing procedure can be built.
5. Conclusions
In this article, we propose a watermarking scheme which prevents infringements of intellectual properties in AM industries. Our algorithm embedded watermarks into digital and physical contents, including geometric models, G-code programs, and printed parts. Hence, it widens the scope of copyright protection in AM. In the proposed watermarking method, the input geometric models can be expressed in polygonal formats as well as volumetric representations. Therefore, voxel models can be protected too. Besides embedding fingerprints, our encoder transforms digital models into distance fields. As a result, the contents obtain extra security. Because of using the SOM technique, our encoder is able to insert watermarks inside complex models and attach embossed as well as engraved signatures on the model surfaces. Thus, the proposed watermarking method is more flexible and adaptive than conventional ones.
Experimental results validate the efficacy of the proposed watermarking scheme. The proposed procedure can embed and detect watermarks in models with complex shapes, for example, a tetrapod. In some experiments, we employed the encoder to create embossed and engraved marks on model surfaces such that quick verification of printed parts is possible. This functionality helps volunteers and hobbyists to share their creations and innovations. Other tests revealed that our method is able to insert watermarks in large curvy layers inside complicated objects. Hence, the watermarks are more resilient to attacks. In the proposed procedure, watermarks are implicitly encoded into G-code programs to protect these valuable properties. Hence, people can distribute their G-code programs to massively produce physical models. We presented three test cases to evaluate the efficiency of the watermark-detection methods. In all the test results, we found that the similarities between extracted and embedded watermarks are high even though the models had gone through digital-to-analog and analog-to-digital conversions. With these experiments, we showed that both the encoder and the decoder achieve the target goals of this research.
The proposed watermarking process is performed in a voxel space. It invokes several specialized algorithms, including the SOM method, distance field computation, volume rendering, and virtual manufacturing procedures. These techniques possess potential applications in 3D modelling, 4D printing, and compliance mechanism creation. We plan to apply these algorithms in our future work to develop advanced modeling tools and mechanical facilities.