Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization
Abstract
1. Introduction
2. Related Works
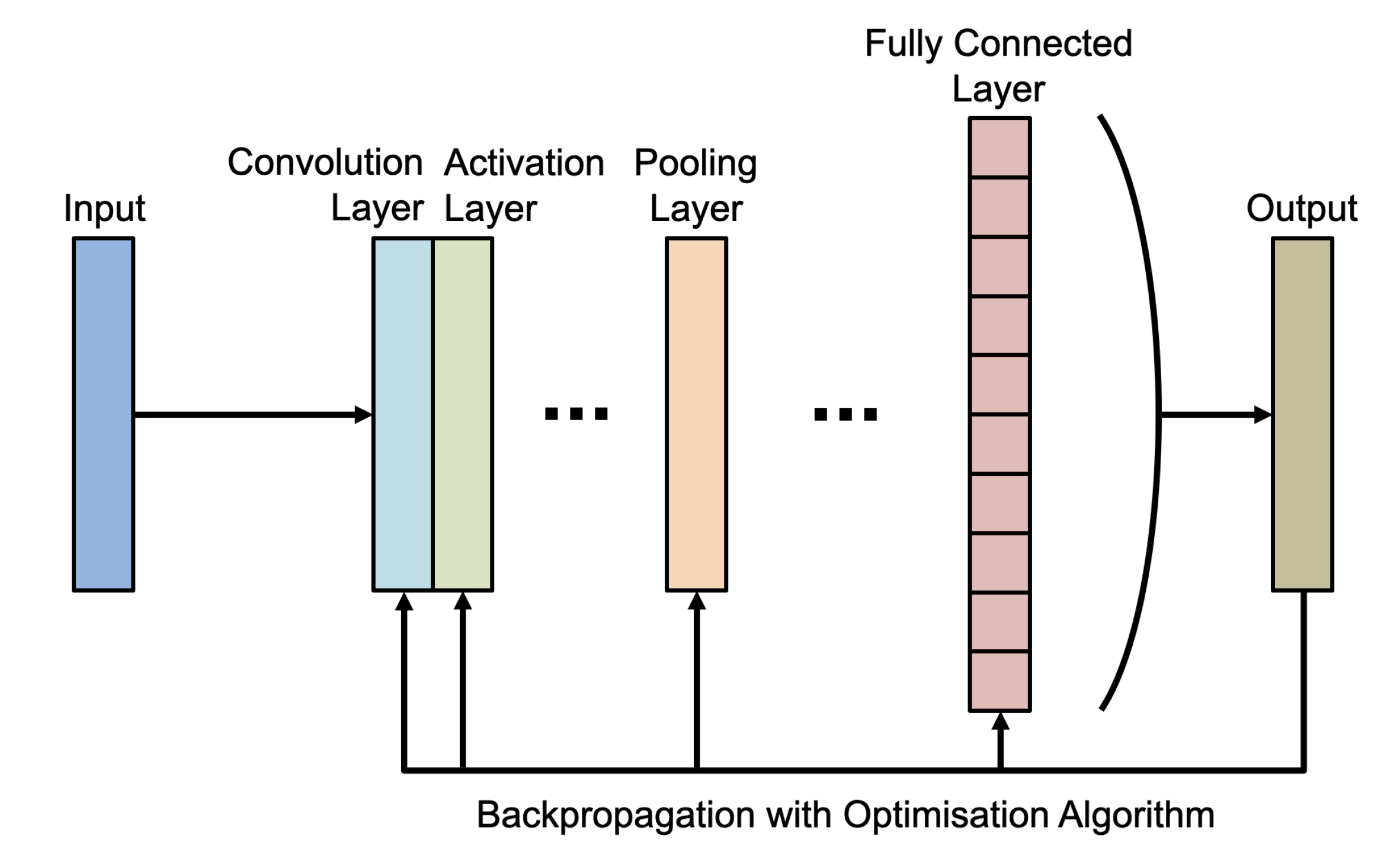
2.1. Convolutional Neural Networks
2.2. Hyperparameters
2.3. Network Architecture Search
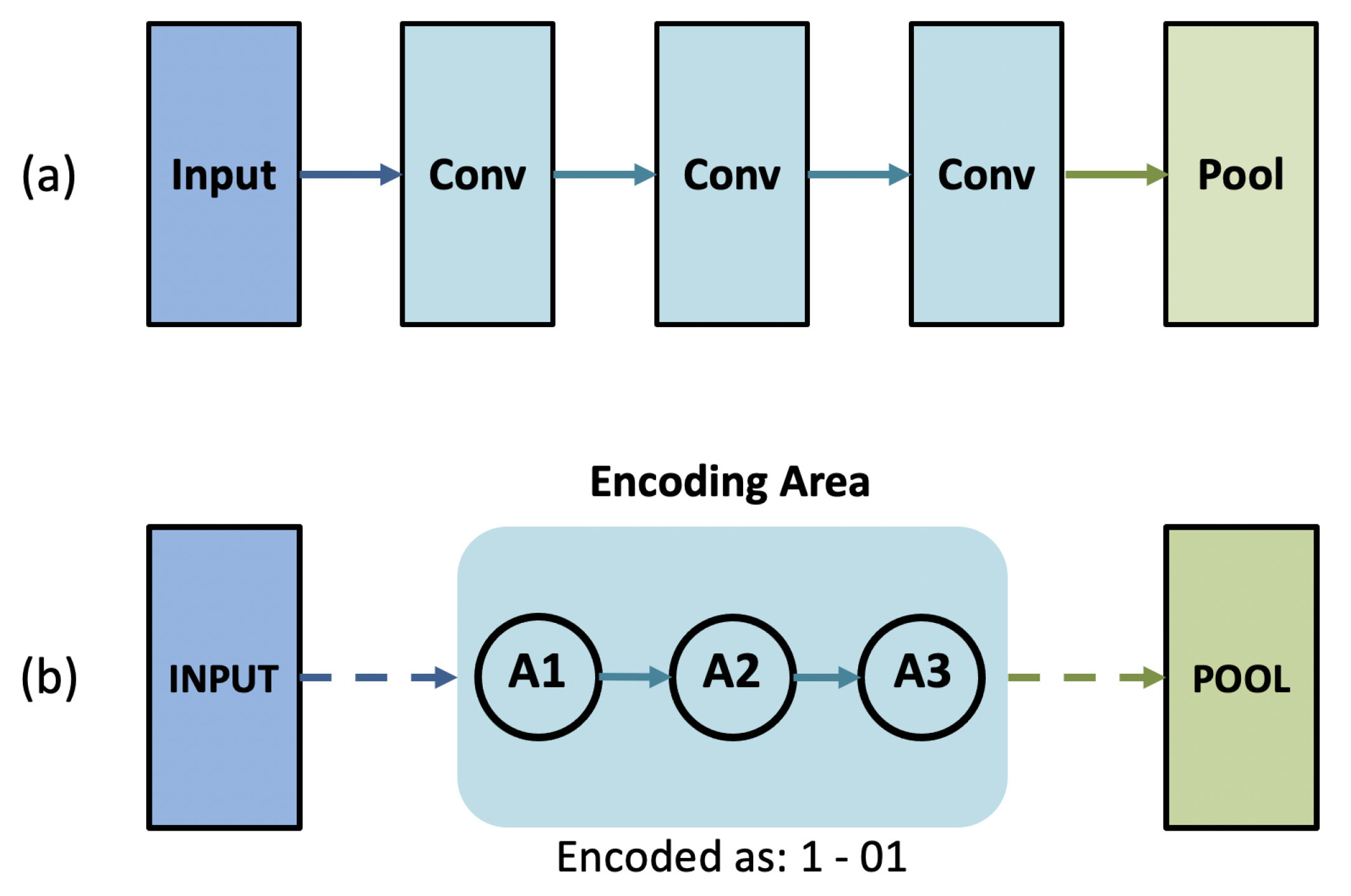
2.4. Genetic CNN
3. Model Optimisation
3.1. Structure of the Algorithm
3.2. Dataset
4. Results and Discussion
4.1. Experiment Settings
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roychaudhuri, R.; Yang, M.; Hoshi, M.M.; Teplow, D.B. Amyloid β-Protein Assembly and Alzheimer Disease. J. Biol. Chem. 2009, 284, 4749–4753. [Google Scholar] [CrossRef] [PubMed]
- Yoder, K.K. Basic PET Data Analysis Techniques. In Positron Emission Tomography-Recent Developments in Instrumentation, Research and Clinical Oncological Practice; IntechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Higaki, A.; Uetani, T.; Ikeda, S.; Yamaguchi, O. Co-authorship network analysis in cardiovascular research utilizing machine learning (2009–2019). Int. J. Med. Inform. 2020, 143, 104274. [Google Scholar] [CrossRef] [PubMed]
- Myszczynska, M.A.; Ojamies, P.N.; Lacoste, A.M.B.; Neil, D.; Saffari, A.; Mead, R.; Hautbergue, G.M.; Holbrook, J.D.; Ferraiuolo, L. Applications of machine learning to diagnosis and treatment of neurodegenerative diseases. Nat. Rev. Neurol. 2020, 16, 440–456. [Google Scholar] [CrossRef] [PubMed]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning Transferable Architectures for Scalable Image Recognition. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8697–8710. [Google Scholar]
- Zhi, H.; Liu, S. Face recognition based on genetic algorithm. J. Vis. Commun. Image Represent. 2019, 58, 495–502. [Google Scholar] [CrossRef]
- Xie, L.; Yuille, A. Genetic CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1388–1397. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Curry, H.B. The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 1944, 2, 258–261. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd Int. Conf. Learn. Representat, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training Very Deep Networks. In Advances in Neural Information Processing Systems 28; Curran Associates, Inc.: Montreal, QC, Canada, 7–10 December 2015; pp. 2377–2385. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 22–25 July 2017; pp. 2261–2269. [Google Scholar]
- Mohandes, M.; Codrington, C.W.; Gelfand, S.B. Two adaptive stepsize rules for gradient descent and their application to the training of feedforward artificial neural networks. In Proceedings of the 1994 IEEE International Conference on Neural Networks, Orlando, FL, USA, 28 June–2 July 1994; Volume 1, pp. 555–560. [Google Scholar]
- Weir, M.K. A method for self-determination of adaptive learning rates in back propagation. Neural Netw. 1991, 4, 371–379. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30th Int. Conf. Mach. Learn, Atlanta, GA, USA, 17–19 June 2013. [Google Scholar]
- Hannun, A.Y.; Case, C.; Casper, J.; Catanzaro, B.; Diamos, G.; Elsen, E.; Prenger, R.; Satheesh, S.; Sengupta, S.; Coates, A.; et al. Deep Speech: Scaling up end-to-end speech recognition. arXiv 2014, arXiv:abs/1412.5567. [Google Scholar]
- Bottou, L. Online Learning and Stochastic Approximations. In On-Line Learning in Neural Networks; Publications of the Newton Institute, Cambridge University Press: Cambridge, UK, 1999; pp. 9–42. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5—RmsProp: Divide the gradient by a running average of its recent magnitude. In COURSERA: Neural Networks for Machine Learning; COURSERA: San Diego, CA, USA, 2012. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd Int. Conf. Learn. Representat, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural Architecture Search: A Survey. J. Mach. Learn. Res. 2019, 20, 1–21. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural Architecture Search with Reinforcement Learning. arXiv 2017, arXiv:cs.LG/1611.01578. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable Architecture Search. arXiv 2019, arXiv:cs.LG/1806.09055. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Simple And Efficient Architecture Search for Convolutional Neural Networks. arXiv 2017, arXiv:stat.ML/1711.04528. [Google Scholar]
- Kandasamy, K.; Neiswanger, W.; Schneider, J.; Poczos, B.; Xing, E.P. Neural Architecture Search with Bayesian Optimisation and Optimal Transport. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 2020–2029. [Google Scholar]
- Kang, H.; Kim, W.G.; Yang, G.S.; Kim, H.W.; Jeong, J.E.; Yoon, H.J.; Cho, K.; Jeong, Y.J.; Kang, D.Y. VGG-based BAPL Score Classification of 18F-Florbetaben Amyloid Brain PET. Biomed. Sci. Lett. 2018, 24, 418–425. [Google Scholar] [CrossRef]
- Kang, H.; Park, J.S.; Cho, K.; Kang, D.Y. Visual and Quantitative Evaluation of Amyloid Brain PET Image Synthesis with Generative Adversarial Network. Appl. Sci. 2020, 10, 2628. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1106–1114. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50× fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:cs.CV/1602.07360. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Autoencoders. In Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]





| Image Type | NII Images | |
|---|---|---|
| Classes | Number of Subjects | Number of Images |
| Train Set | ||
| AD | 159 | 10,812 |
| MCI | 130 | 8840 |
| NC | 85 | 5780 |
| Test Set | ||
| AD | 17 | 1156 |
| MCI | 14 | 952 |
| NC | 9 | 612 |
| Activation Function | Optimization Algorithm | ||
|---|---|---|---|
| Hyperparameter | Bit Representation | Hyperparameter | Bit Representation |
| ReLU | 00 | SGDM | 00 |
| Leaky ReLU | 01 | RMSProp | 01 |
| Clipped ReLU | 11 | Adam | 11 |
| Number of Generations | Accuracy (%) | Best Combination of Network Structure and Hyperparameters | ||
|---|---|---|---|---|
| Maximum | Minimum | Average | ||
| 0 | 46.45 | 40.89 | 43.61 | 0-11 | 1-01-111 | 1-01-110-1101 | 10 | 00 |
| 1 | 46.45 | 38.25 | 42.78 | 0-11 | 1-01-111 | 1-01-110-1101 | 10 | 00 |
| 2 | 47.81 | 44.89 | 46.68 | 0-11 | 1-10-111 | 1-01-110-1101 | 10 | 00 |
| 5 | 47.81 | 48.63 | 48.24 | 0-11 | 1-10-111 | 1-01-110-1101 | 10 | 00 |
| 10 | 64.64 | 58.49 | 61.56 | 1-01 | 1-10-111 | 1-01-110-1101 | 01 | 01 |
| 20 | 71.48 | 67.86 | 69.67 | 1-01 | 0-11-010 | 1-01-101-1101 | 10 | 00 |
| 50 | 82.64 | 80.84 | 81.74 | 1-11 | 1-10-111 | 1-11-011-0111 | 10 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, J.; Kang, H.; Kang, D.-Y.; Park, J. Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization. Appl. Sci. 2021, 11, 744. https://doi.org/10.3390/app11020744
Lee S, Kim J, Kang H, Kang D-Y, Park J. Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization. Applied Sciences. 2021; 11(2):744. https://doi.org/10.3390/app11020744
Chicago/Turabian StyleLee, Sanghyeop, Junyeob Kim, Hyeon Kang, Do-Young Kang, and Jangsik Park. 2021. "Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization" Applied Sciences 11, no. 2: 744. https://doi.org/10.3390/app11020744
APA StyleLee, S., Kim, J., Kang, H., Kang, D.-Y., & Park, J. (2021). Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization. Applied Sciences, 11(2), 744. https://doi.org/10.3390/app11020744






