A Hybrid Approach for Time-Varying Harmonic and Interharmonic Detection Using Synchrosqueezing Wavelet Transform
Abstract
1. Introduction
2. Review of Synchrosqueezing Wavelet Transform
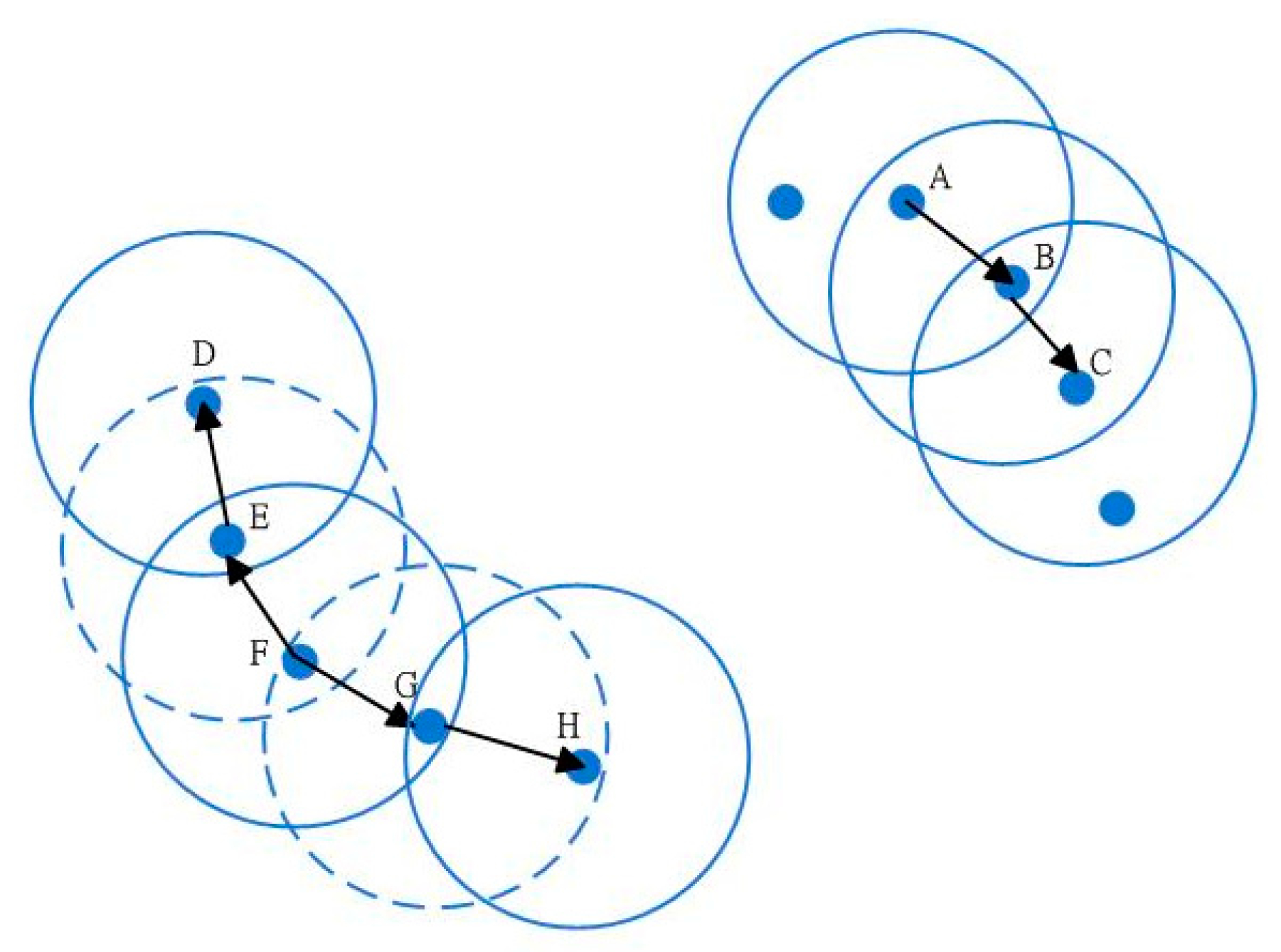
3. DBSCAN Clustering Method
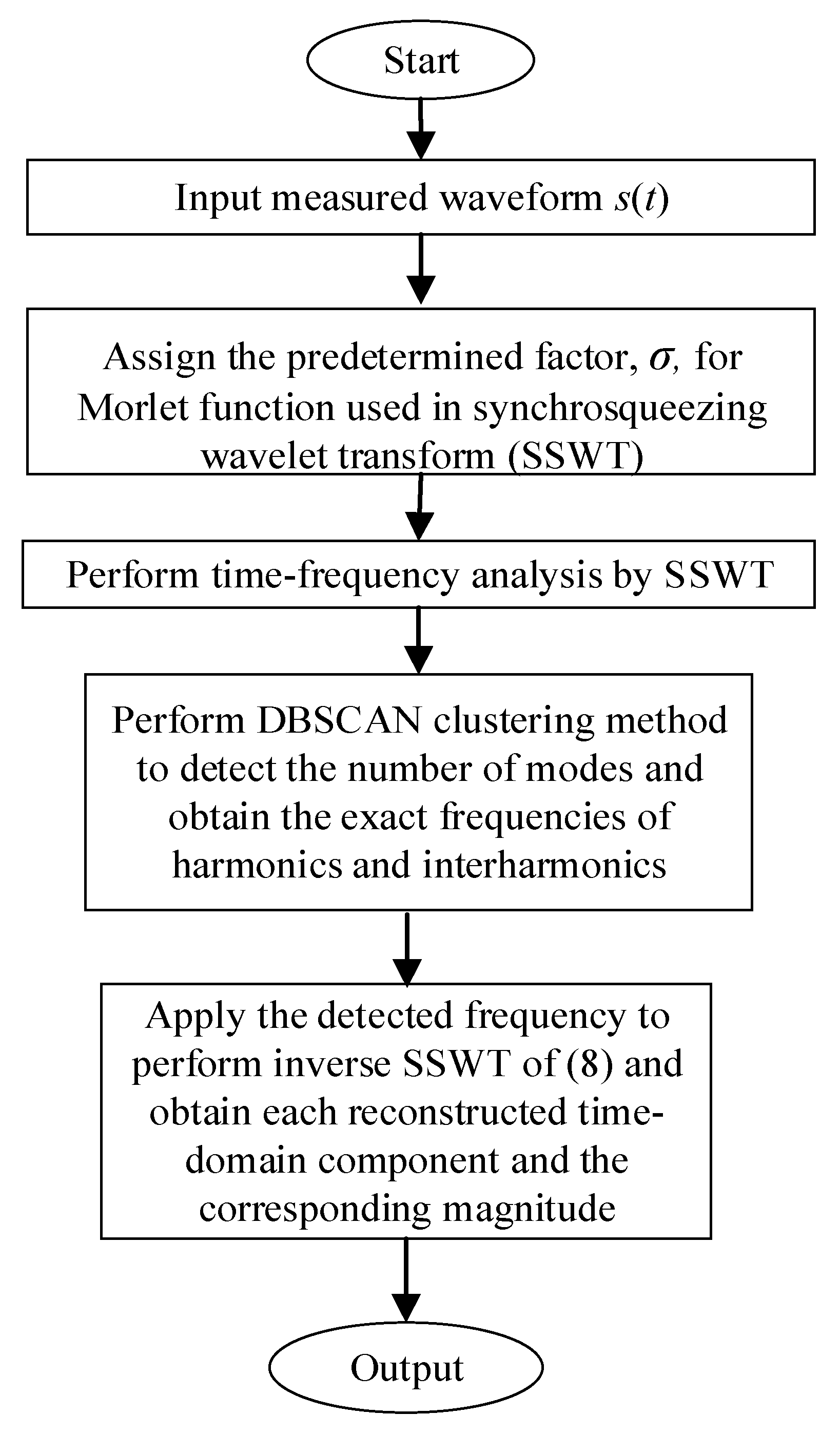
4. Proposed Solution Procedure for Harmonic and Interharmonic Detection
4.1. Setting the Value of Parameter σ for Time–Frequency Analysis
4.2. Solution Procedure of Proposed Harmonic and Interharmonic Detection Method
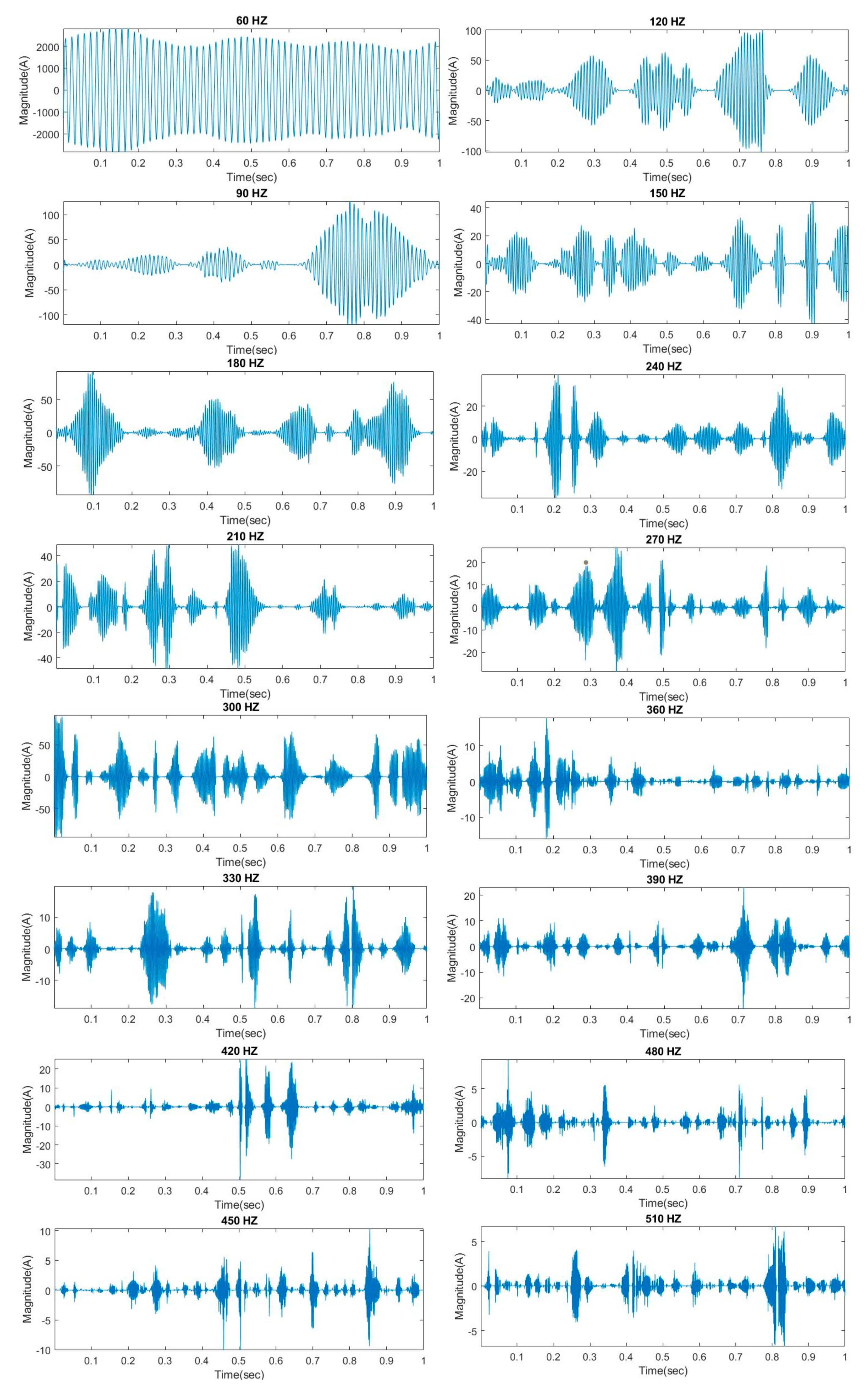
5. Case Studies
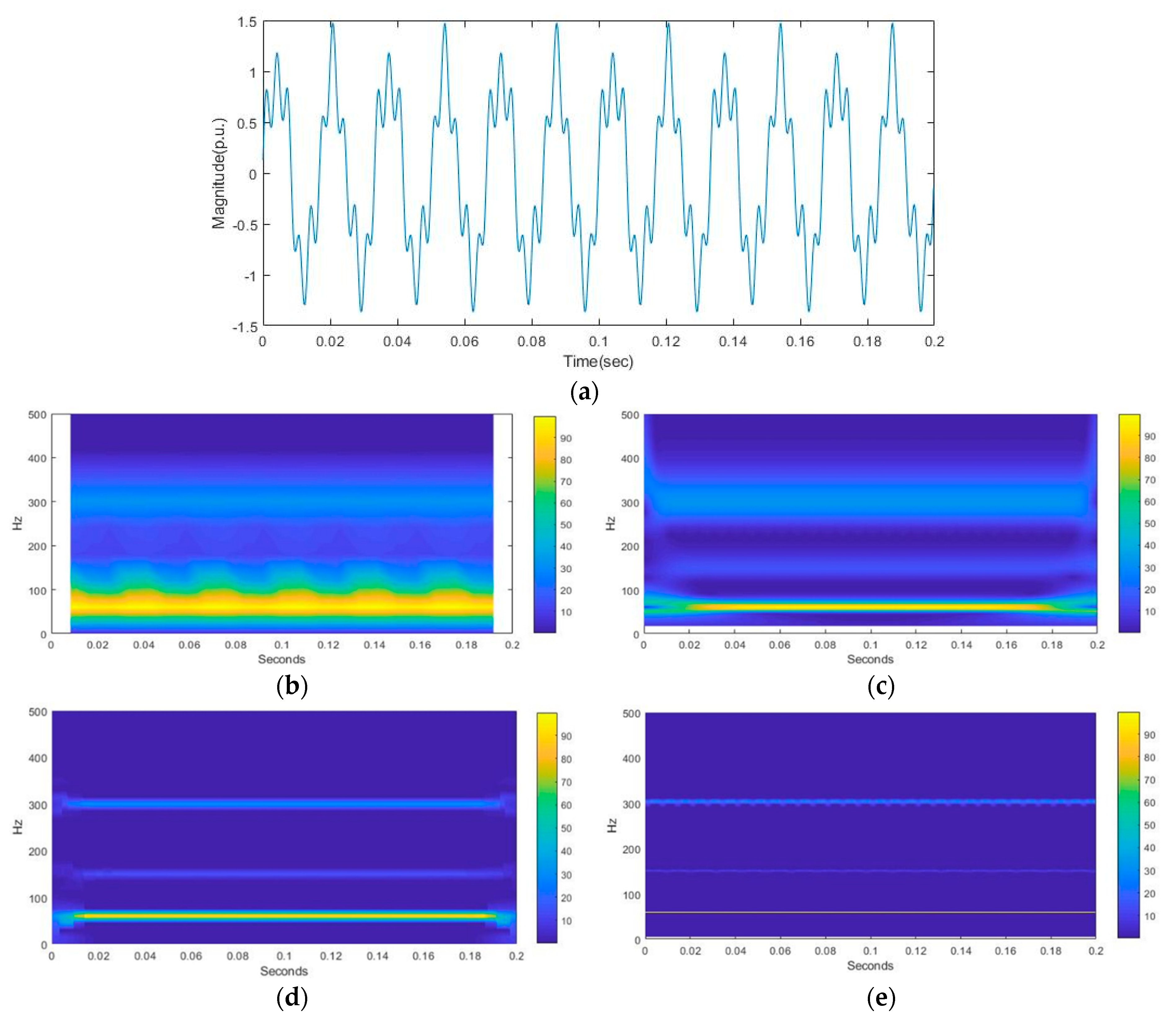
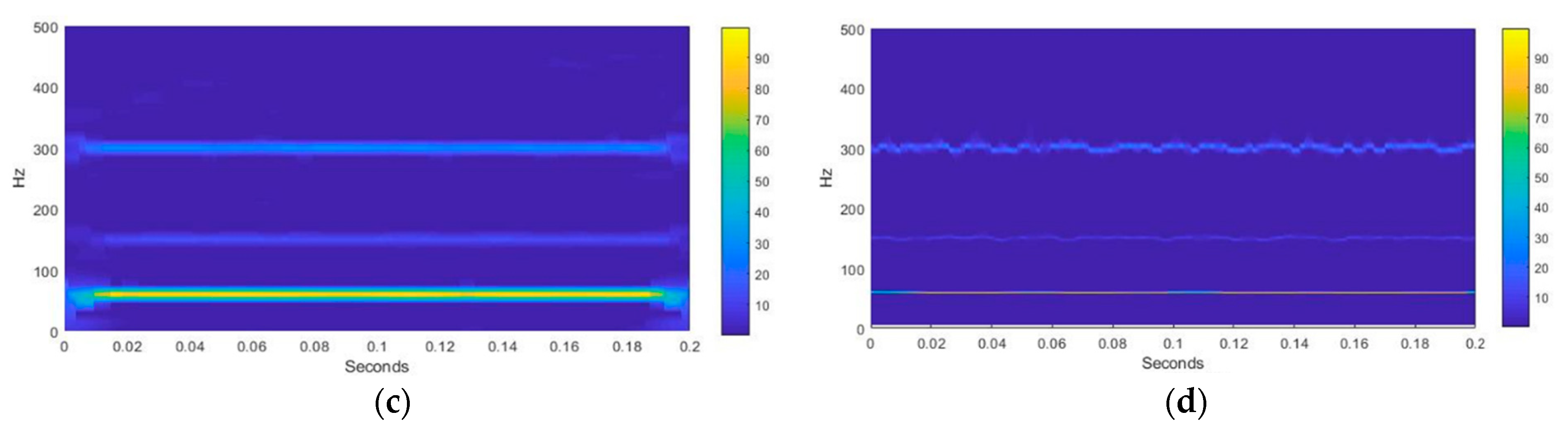
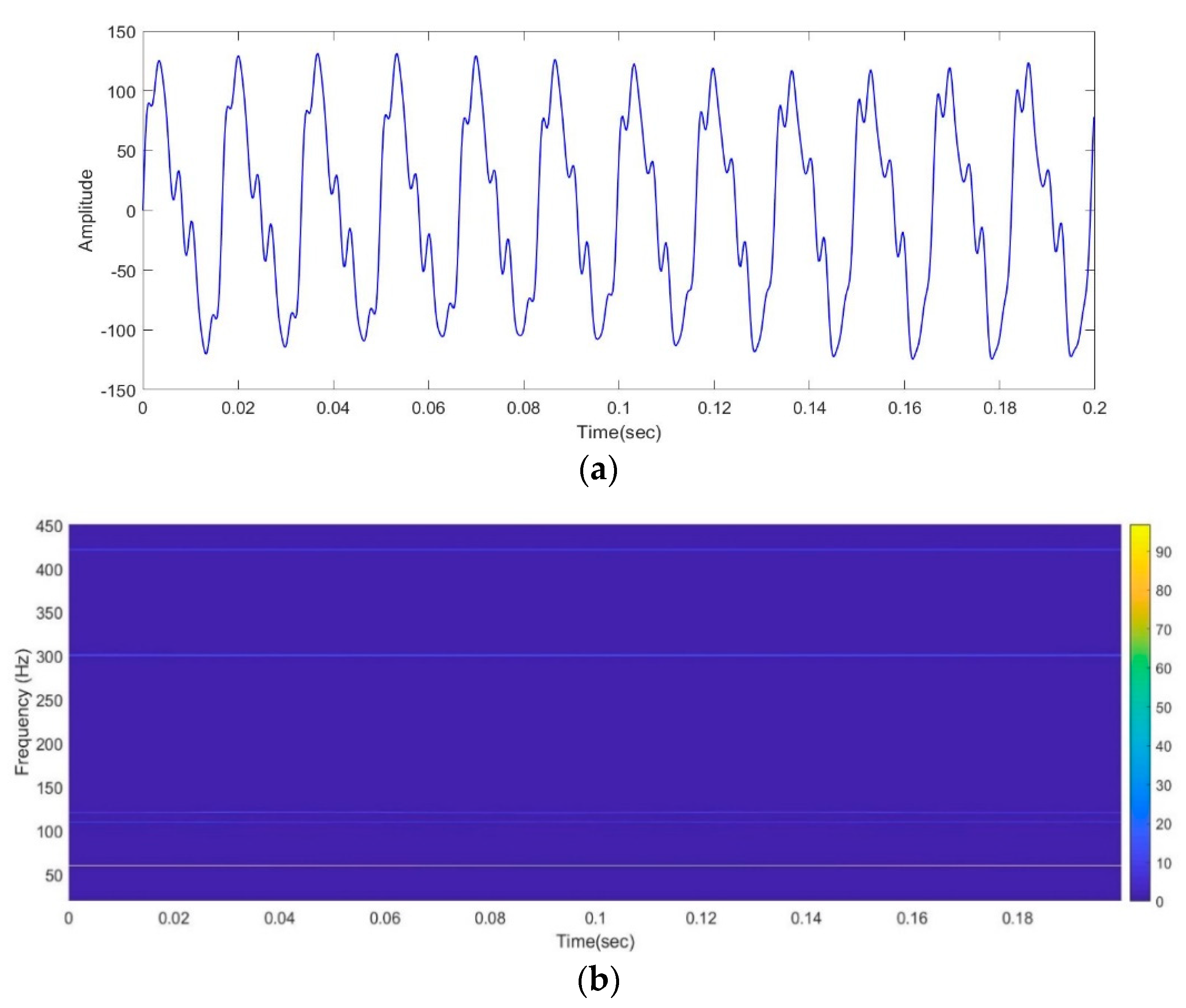
5.1. Effect of Multiple Frequency-Modulated Detection
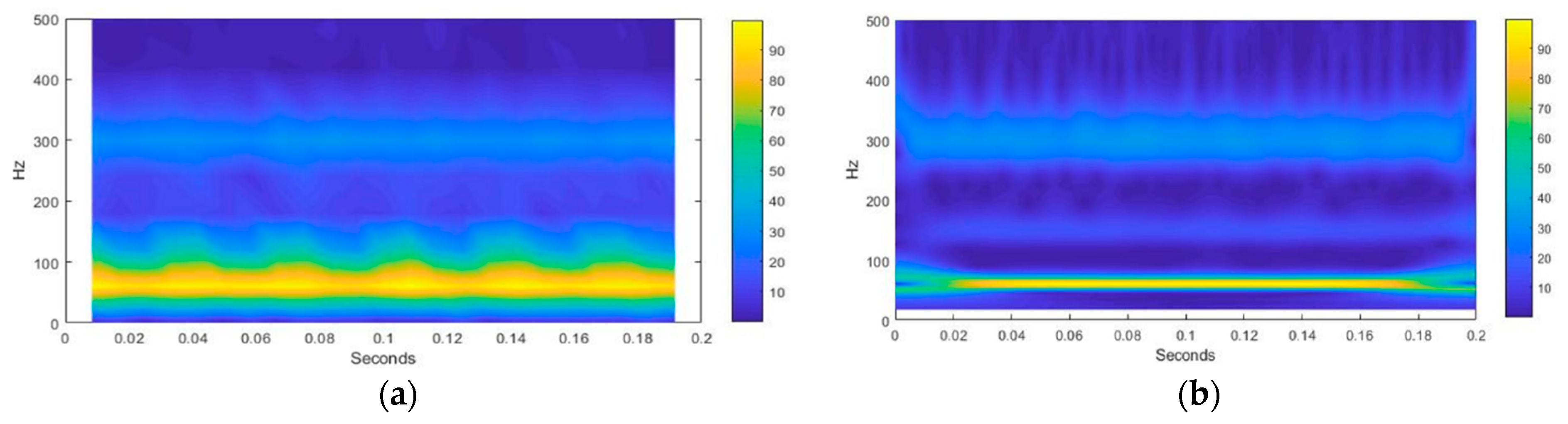
5.2. Impact of Noise Included in the Measured Signal
5.3. Impact of Fundamental Frequency Variations
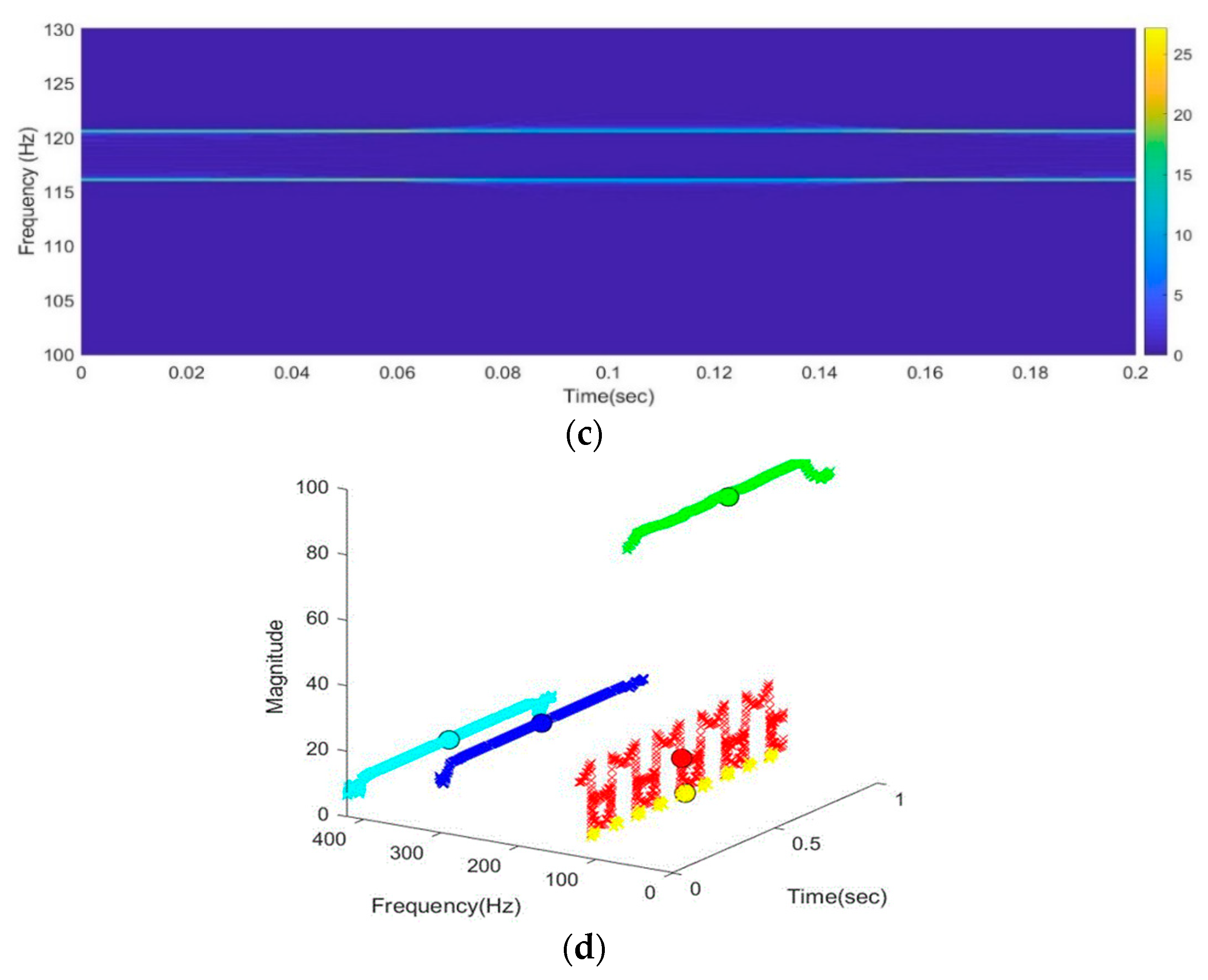
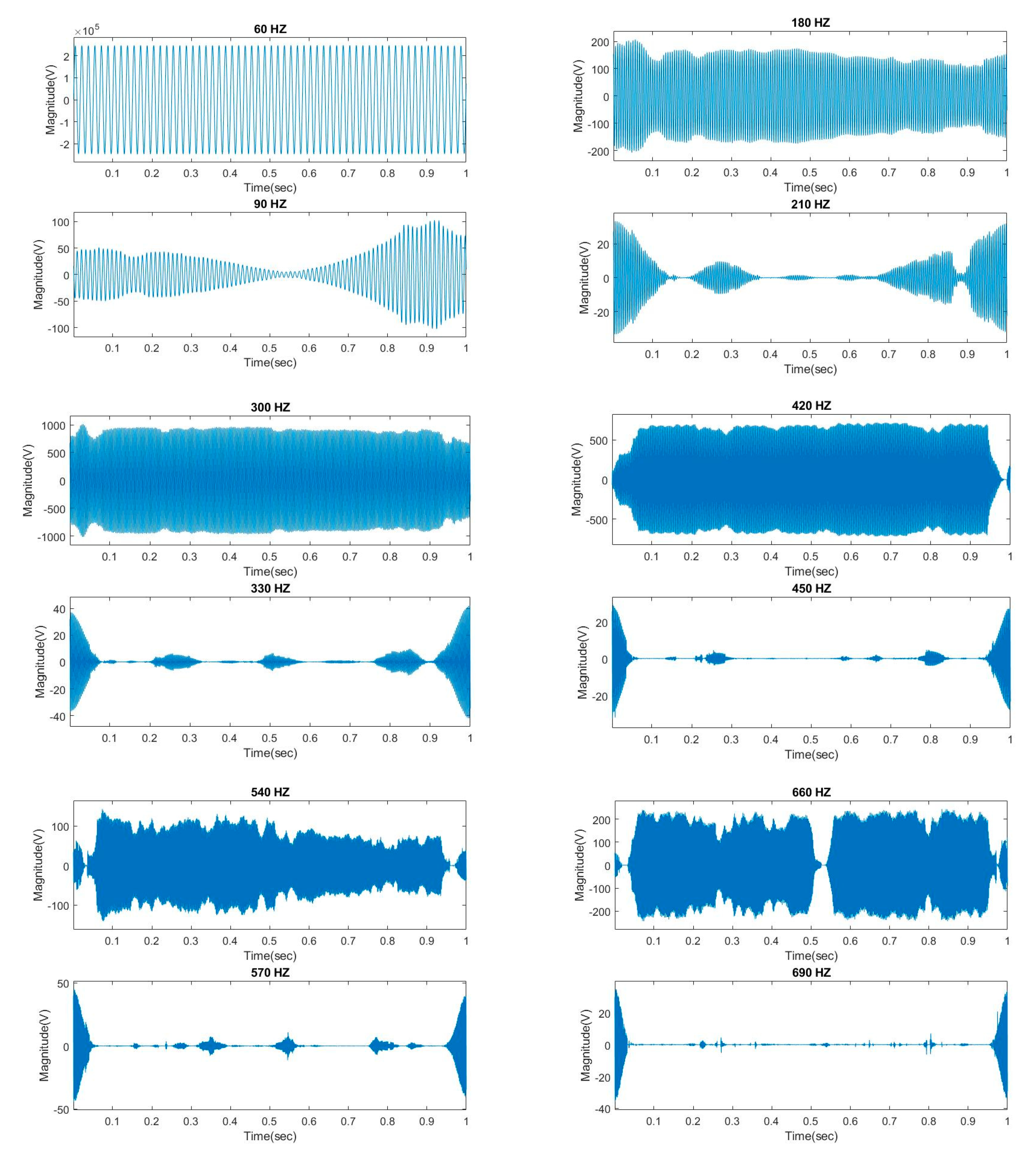
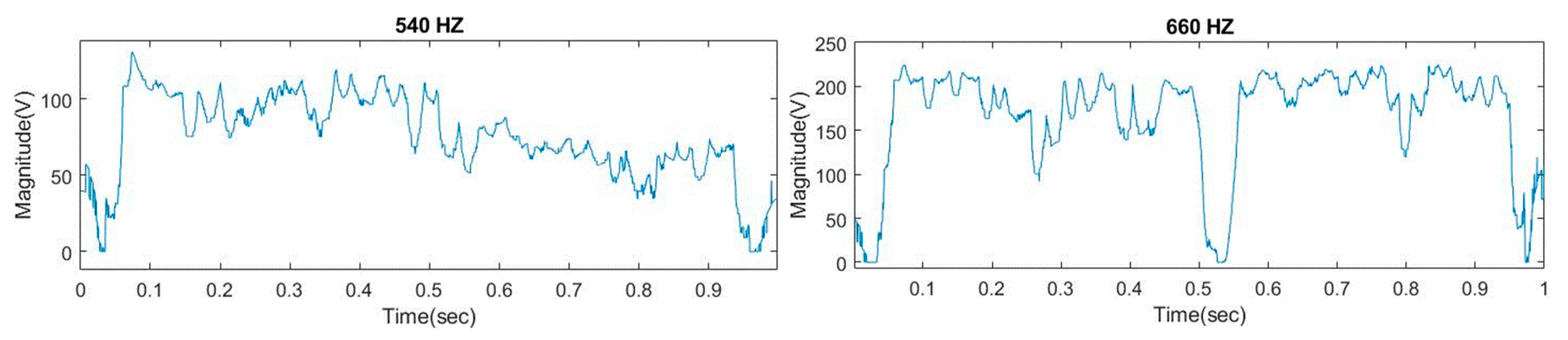
5.4. Effects Due to Proximity of Two Frequencies of Harmonics and Interharmonics
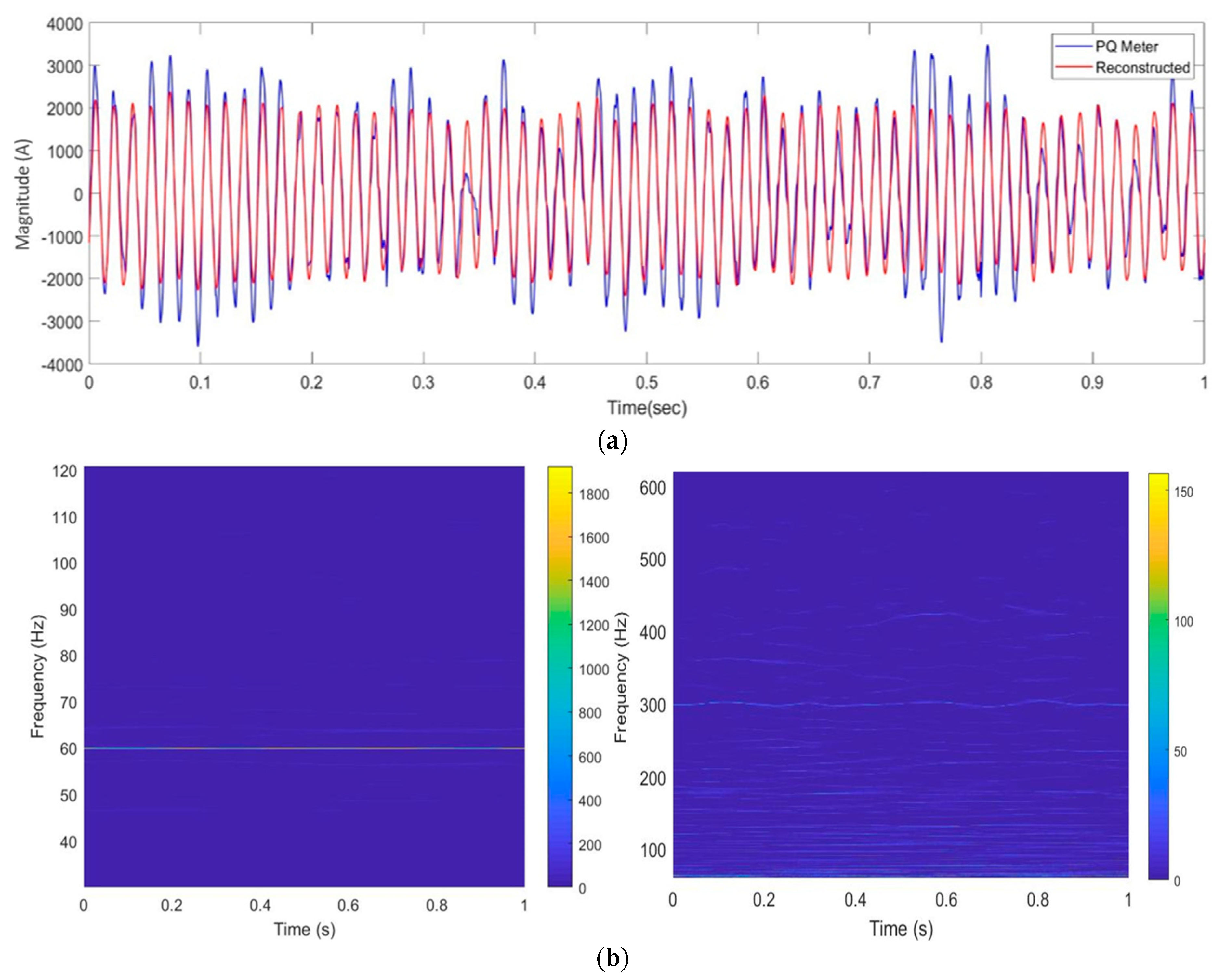
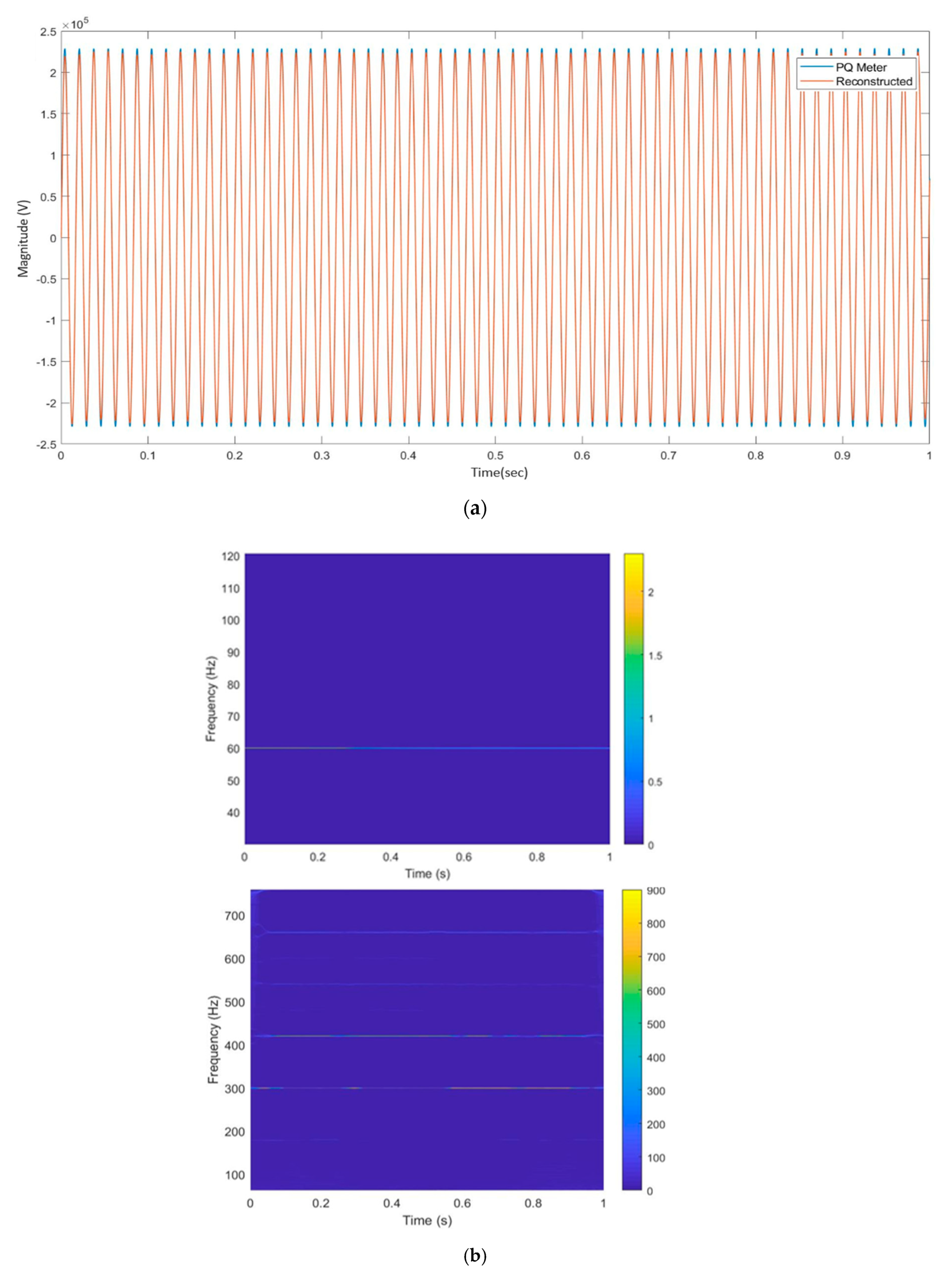
5.5. Performance Verification with Power-Quality Analyzer
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hidalgo, R.M.; Fernandez, J.G.; Rivera, R.R.; Larrondo, H.A. A simple adjustable window algorithm to improve FFT measurements. IEEE Trans. Instrum. Meas. 2002, 51, 31–36. [Google Scholar] [CrossRef]
- Agrez, D. Weighted multipoint interpolated DFT to improve amplitude estimation of multifrequency signal. IEEE Trans. Instrum. Meas. 2002, 51, 287–292. [Google Scholar] [CrossRef]
- Testa, A.; Gallo, D.; Langella, R. On the Processing of Harmonics and Interharmonics: Using Hanning Window in Standard Framework. IEEE Trans. Power Deliv. 2004, 19, 28–34. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; Carpinelli, G. Adaptive Prony method for waveform distortion detection in power systems. Int. J. Electr. Power Energy Syst. 2007, 29, 371–379. [Google Scholar] [CrossRef]
- Su, T.; Yang, M.; Jin, T.; Flesch, R.C.C. Power harmonic and interharmonic detection method in renewable power based on Nuttall double-window all-phase FFT algorithm. IET Renew. Power Gener. 2018, 12, 953–961. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Low-Order Dominant Harmonic Estimation Using Adaptive Wavelet Neural Network. IEEE Trans. Ind. Electron. 2013, 61, 428–435. [Google Scholar] [CrossRef]
- Enayati, J.; Moravej, Z. Real-time harmonics estimation in power systems using a novel hybrid algorithm. IET Gener. Transm. Distrib. 2017, 11, 3532–3538. [Google Scholar] [CrossRef]
- Sheshyekani, K.; Fallahi, G.; Hamzeh, M.; Kheradmandi, M. A General Noise-Resilient Technique Based on the Matrix Pencil Method for the Assessment of Harmonics and Interharmonics in Power Systems. IEEE Trans. Power Deliv. 2017, 32, 2179–2188. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Maximum-Likelihood Frequency and Phasor Estimations for Electric Power Grid Monitoring. IEEE Trans. Ind. Inform. 2017, 14, 167–177. [Google Scholar] [CrossRef]
- Prado, T.D.A.; Barros, A.M.; Guarneri, G.A. An Algorithm Based on Sparse Decomposition for Estimating Harmonic and Interharmonic Components of Stationary Signals in Power Systems. IEEE Access 2019, 7, 163958–163968. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. Measurement of harmonics/inter-harmonics of time-varying frequencies. IEEE Trans. Power Deliv. 2005, 20, 23–31. [Google Scholar] [CrossRef]
- Lin, H.C. Fast Tracking of Time-Varying Power System Frequency and Harmonics Using Iterative-Loop Approaching Algorithm. IEEE Trans. Ind. Electron. 2007, 54, 974–983. [Google Scholar] [CrossRef]
- Chen, C.I.; Chang, G.W.; Hong, R.C.; Li, H.M. Extended Real Model of Kalman Filter for Time-Varying Harmonics Estimation. IEEE Trans. Power Deliv. 2010, 25, 17–26. [Google Scholar] [CrossRef]
- Dash, P.K.; Krishnanand, K.R.; Patnaik, R.K. Dynamic phasor and frequency estimation of time-varying power system signals. Int. J. Electr. Power Energy Syst. 2013, 44, 971–980. [Google Scholar] [CrossRef]
- Jain, S.K. Algorithm for dealing with time-varying signal within sliding-window for harmonics estimation. IET Sci. Meas. Technol. 2015, 9, 1023–1031. [Google Scholar] [CrossRef]
- Narduzzi, C.; Bertocco, M.; Frigo, G.; Giorgi, G. Fast-TFM—Multifrequency Phasor Measurement for Distribution Networks. IEEE Trans. Instrum. Meas. 2018, 67, 1825–1835. [Google Scholar] [CrossRef]
- Balouji, E.; Bäckström, K.; McKelvey, T.; Salor, Ö. Deep-Learning-Based Harmonics and Interharmonics Predetection Designed for Compensating Significantly Time-Varying EAF Currents. IEEE Trans. Ind. Appl. 2020, 56, 3250–3260. [Google Scholar] [CrossRef]
- Ashouri, M.; Silva, F.F.D.; Bak, C.L. Application of short-time Fourier transform for harmonic-based protection of meshed VSC-MTDC grids. J. Eng. 2019, 2019, 1439–1443. [Google Scholar] [CrossRef]
- Ravindran, V.; Busatto, T.; Rönnberg, S.K.; Meyer, J.; Bollen, M.H.J. Time-Varying Interharmonics in Different Types of Grid-Tied PV Inverter Systems. IEEE Trans. Power Deliv. 2020, 35, 483–496. [Google Scholar] [CrossRef]
- Mishra, S.; Bhende, C.N.; Panigrahi, B.K. Detection and Classification of Power Quality Disturbances Using S-Transform and Probabilistic Neural Network. IEEE Trans. Power Deliv. 2007, 23, 280–287. [Google Scholar] [CrossRef]
- Ashrafian, A.; Mirsalim, M. On-line recursive method of phasor and frequency estimation for power system monitoring and relaying. IET Gener. Transm. Distrib. 2016, 10, 2002–2011. [Google Scholar] [CrossRef]
- Santoso, S.; Grady, W.M.; Powers, E.J.; Lamoree, J.; Bhatt, S.C. Characterization of distribution power quality events with Fourier and wavelet transforms. IEEE Trans. Power Deliv. 2000, 15, 247–254. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. The fourier-based synchrosqueezing transform. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar]
- Li, C.; Liang, M. A generalized synchrosqueezing transform for enhancing signal time–frequency representation. Signal Process. 2012, 92, 2264–2274. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.-H.; McLaughlin, S. On Demodulation, Ridge Detection, and Synchrosqueezing for Multicomponent Signals. IEEE Trans. Signal Process. 2017, 65, 2093–2103. [Google Scholar] [CrossRef]
- Arlia, D.; Coppola, M. Experiments in Parallel Clustering with DBSCAN. In Proceedings of the 7th International Euro-Par Conference on Parallel Processing, Manchester, UK, 28–31 August 2001; pp. 28–31. [Google Scholar]
- Singh, A.K.; Fozdar, M. DBSCAN-based coherency identification of generators using complex wavelet transform. J. Eng. 2019, 2019, 4780–4784. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Tong, C.; Zhao, Z. Matching Synchrosqueezing Wavelet Transform and Application to Aeroengine Vibration Monitoring. IEEE Trans. Instrum. Meas. 2017, 66, 360–372. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, X.; Liang, M. Iterative generalized synchrosqueezing transform for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Mech. Syst. Signal Process. 2015, 52–53, 360–375. [Google Scholar] [CrossRef]
- Estevez, P.G.; Marchi, P.; Galarza, C.G.; Elizondo, M. Non-Stationary Power System Forced Oscillation Analysis using Synchrosqueezing Transform. IEEE Trans. Power Syst. 2020. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 2007, 452, 155–176. [Google Scholar] [CrossRef]
- Nikolaou, N.; Antoniadis, I. Demodulation of vibration signals generated by defects in rolling element bearings using complex shifted Morlet wavelets. Mech. Syst. Signal Process. 2002, 16, 677–694. [Google Scholar] [CrossRef]
- Wavelet Synchrosqueezing. Available online: https://www.mathworks.com/help/wavelet/gs/wavelet-synchrosqueezing.html (accessed on 15 April 2020).
- Time Frequency Representations. Available online: http://py-biomedical.lancs.ac.uk/ (accessed on 15 April 2020).
- DBSCAN Clustering Algorithm. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52905-dbscan-clustering-algorithm (accessed on 25 April 2020).





| When Δt Is Large | When Δt Is Small |
|---|---|
| Large scaling factor(|a|), low frequency | Small scaling factor(|a|), high frequency |
| Good frequency resolution | Poor frequency resolution |
| Poor time resolution | Good time resolution |
| Actual Frequency (Hz) | f1 60.3 | f2 116 | f3 120.6 | f4 301.5 | f5 421.1 | |
|---|---|---|---|---|---|---|
| DBSCAN | Detected | 60.2465 | 116.0265 | 120.5671 | 301.7181 | 421.3898 |
| Absolute Error | 0.0535 | 0.0265 | 0.0329 | 0.2181 | 0.2898 | |
| FFT | Detected | 60 | 115 | 120 | 300 | 420 |
| Absolute Error | 0.3 | 1 | 0.6 | 1.5 | 1.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, G.W.; Lin, Y.-L.; Liu, Y.-J.; Sun, G.H.; Yu, J.T. A Hybrid Approach for Time-Varying Harmonic and Interharmonic Detection Using Synchrosqueezing Wavelet Transform. Appl. Sci. 2021, 11, 752. https://doi.org/10.3390/app11020752
Chang GW, Lin Y-L, Liu Y-J, Sun GH, Yu JT. A Hybrid Approach for Time-Varying Harmonic and Interharmonic Detection Using Synchrosqueezing Wavelet Transform. Applied Sciences. 2021; 11(2):752. https://doi.org/10.3390/app11020752
Chicago/Turabian StyleChang, Gary W., Yu-Luh Lin, Yu-Jen Liu, Gary H. Sun, and Johnson T. Yu. 2021. "A Hybrid Approach for Time-Varying Harmonic and Interharmonic Detection Using Synchrosqueezing Wavelet Transform" Applied Sciences 11, no. 2: 752. https://doi.org/10.3390/app11020752
APA StyleChang, G. W., Lin, Y.-L., Liu, Y.-J., Sun, G. H., & Yu, J. T. (2021). A Hybrid Approach for Time-Varying Harmonic and Interharmonic Detection Using Synchrosqueezing Wavelet Transform. Applied Sciences, 11(2), 752. https://doi.org/10.3390/app11020752




