Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation
Abstract
1. Introduction
2. Problem Formulation
2.1. Objective Functions
2.1.1. Minimizing the Total Harmonic Distortion (f1)
2.1.2. Improving the Voltage Profile (f2)
2.1.3. Minimizing the Cost of the Total Active Power Loss and That of the Filter Investment Cost (f3)
2.2. Constraints
- (1)
- Voltage limits:where,
- (2)
- Power balance constraints:PL and QL are active and reactive power losses, respectively. Pd and Qd are load demand active and reactive powers. PGi and QGi are active and reactive power at ith DG unit, respectively.
- (3)
- Generation operating limits:
- (4)
- Harmonic distortion limits:where THDmax and IHDmax are the maximum allowable total harmonic distortion and individual harmonic distortion at each bus, which have values equal to (5% and 3%), respectively, according to the IEEE-519’s standard [3]. Note that the THD as low as possible can be considered as a preventive action to protect the system from any future increase in harmonic sources. If we design the filters to only meet the standard, it needs to redesign the filters with each increase in the harmonic emissions. Added to that, we considered two conflicting objectives (Minimizing the THD and the filter investment cost) to guarantee the optimal economic solution.
3. Optimization Algorithm and Electric Scheme Representation
3.1. Water Cycle Optimization Algorithm
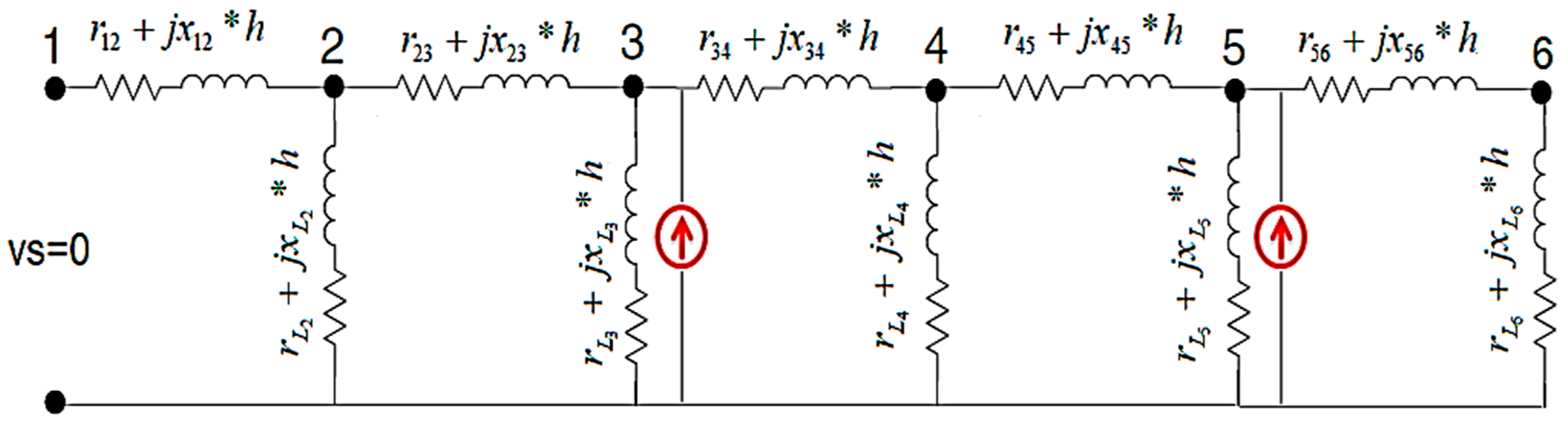
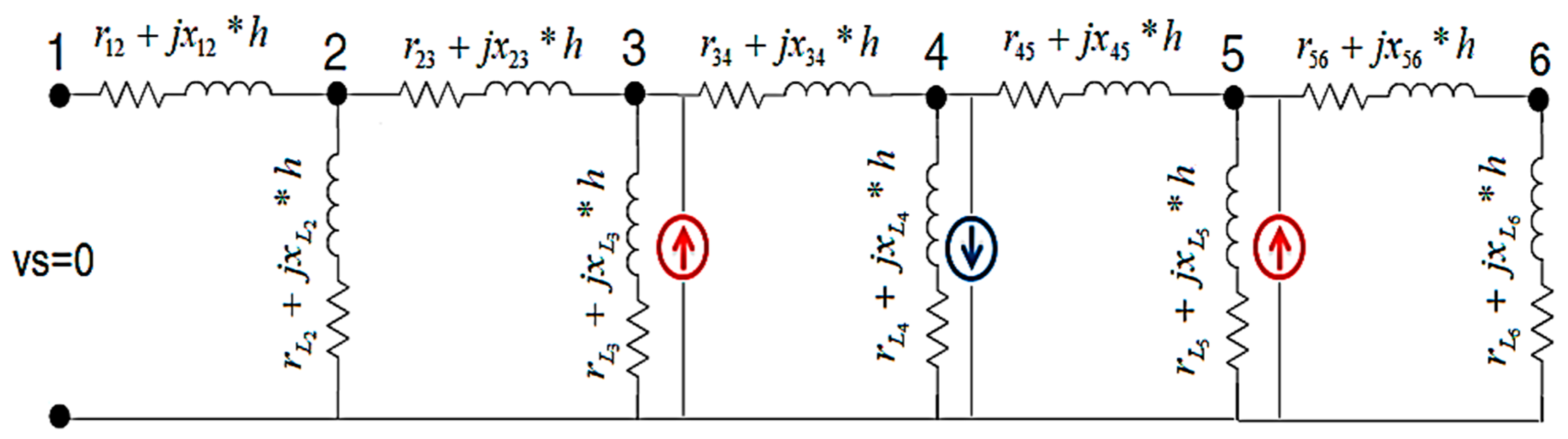
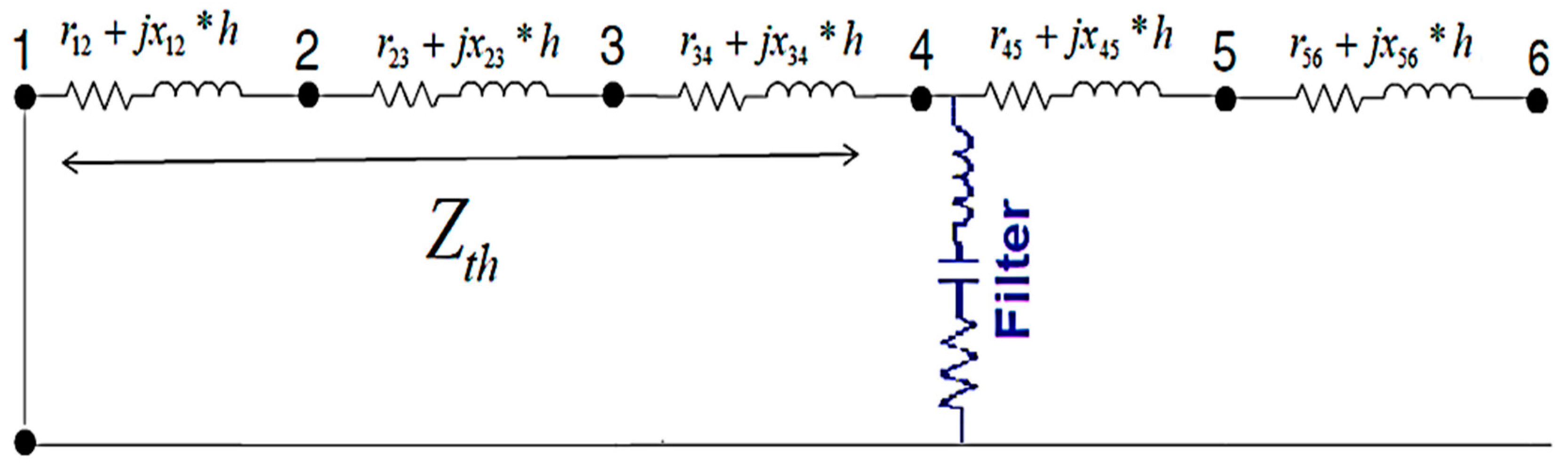
3.2. Electric Scheme and Single Tuned Filter Representation
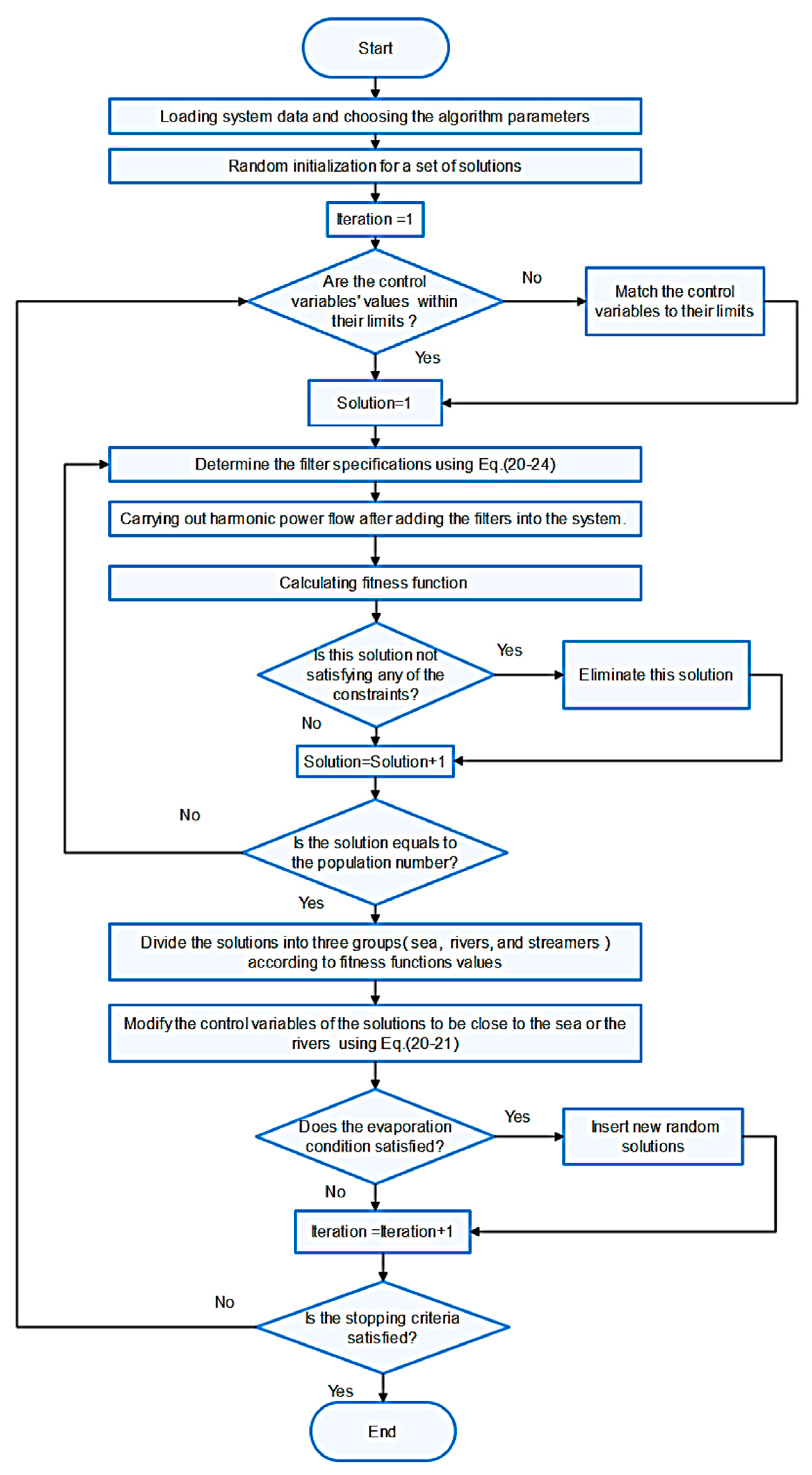
4. Proposed Filters Planning Procedure
- (1)
- Carrying out harmonic power flow calculation based on the backward/forward sweep power flow for balanced radial distribution feeders [35], Power flow analyses are carried before and after adding the filters into the system.
- (2)
- Calculating fitness function using the harmonic power flow results.
- (3)
- Checking the buses’ voltage, THD, and IHD constraints. If any solution doesn’t satisfy any of the constraints, putting the value of its fitness function equals infinity. So, it will not be selected as a minimum solution.
5. Applications
6. Simulation Results and Discussion
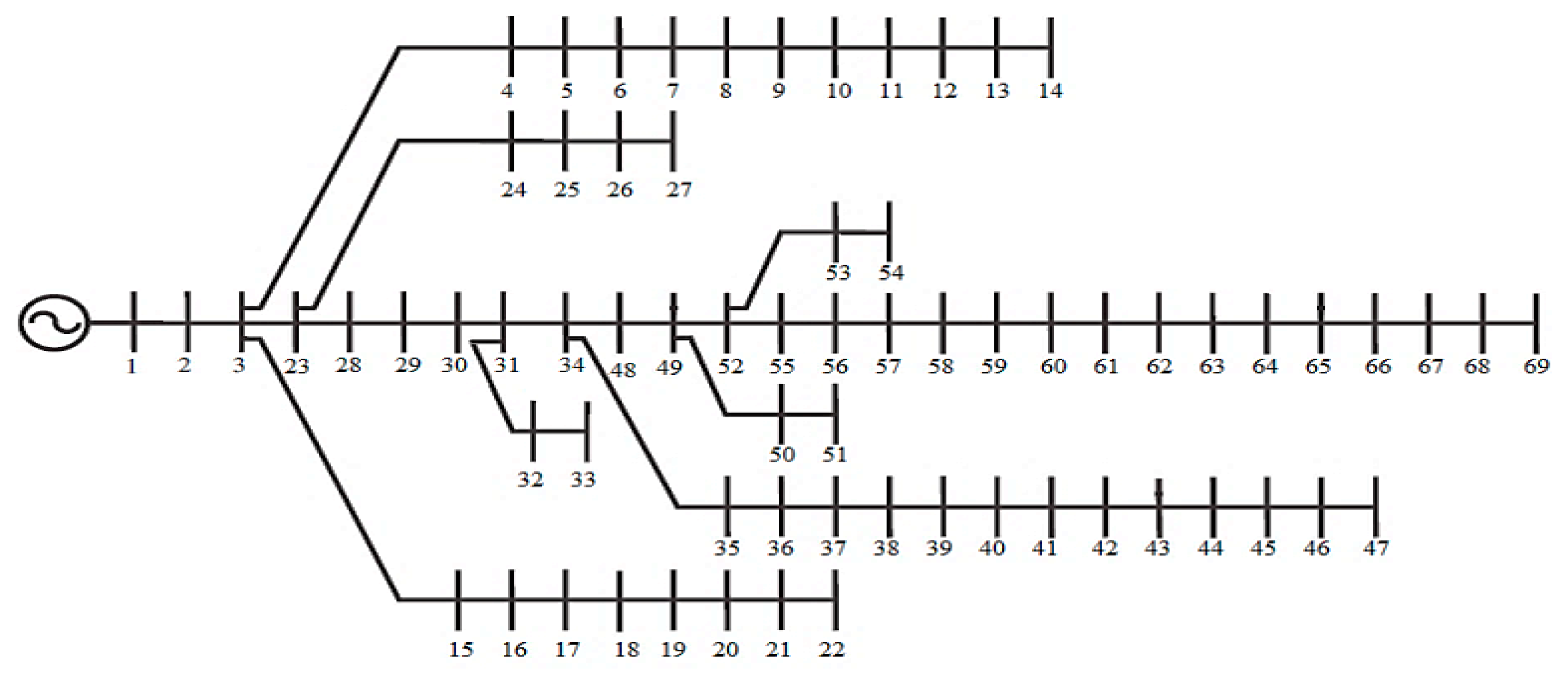
6.1. Test Distribution Systems
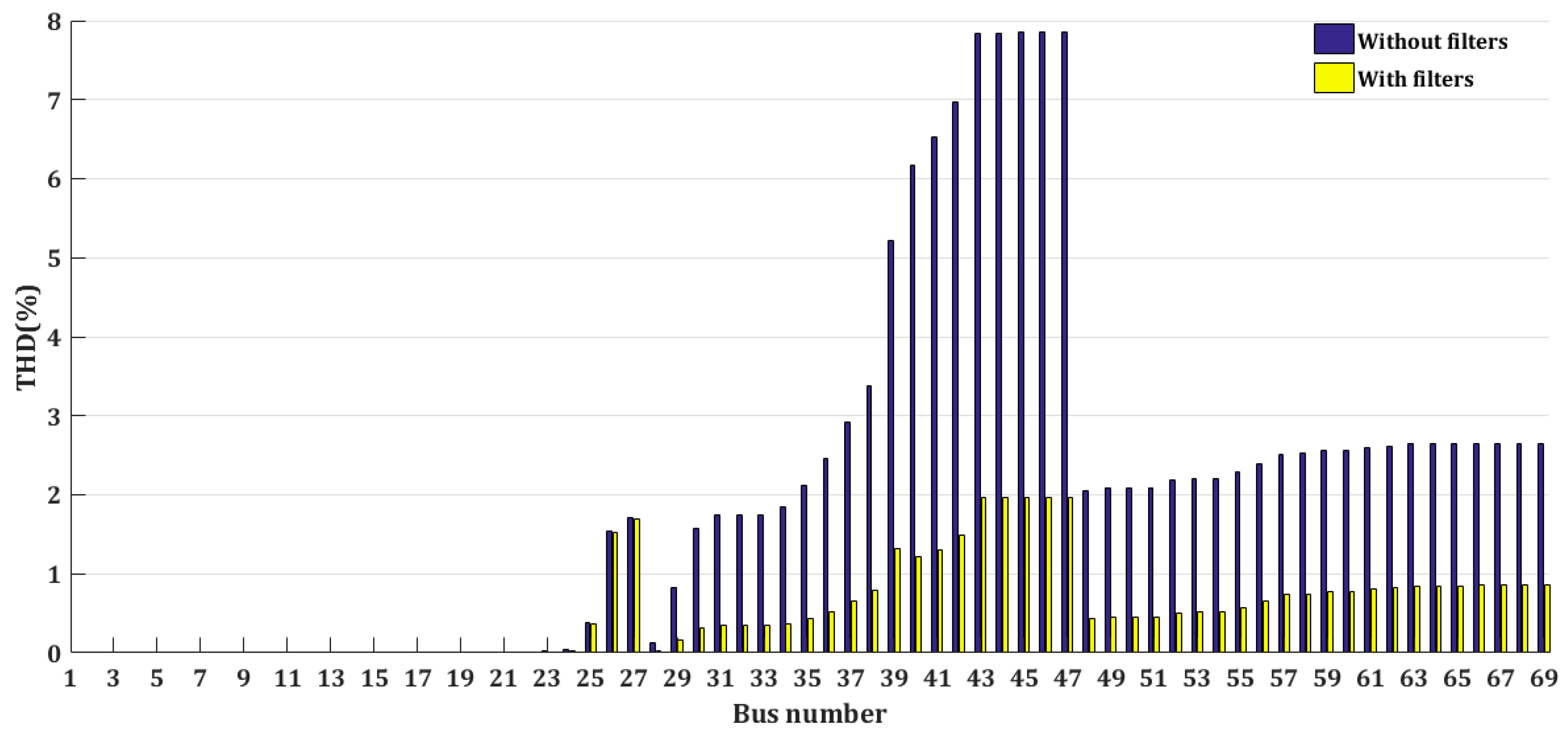
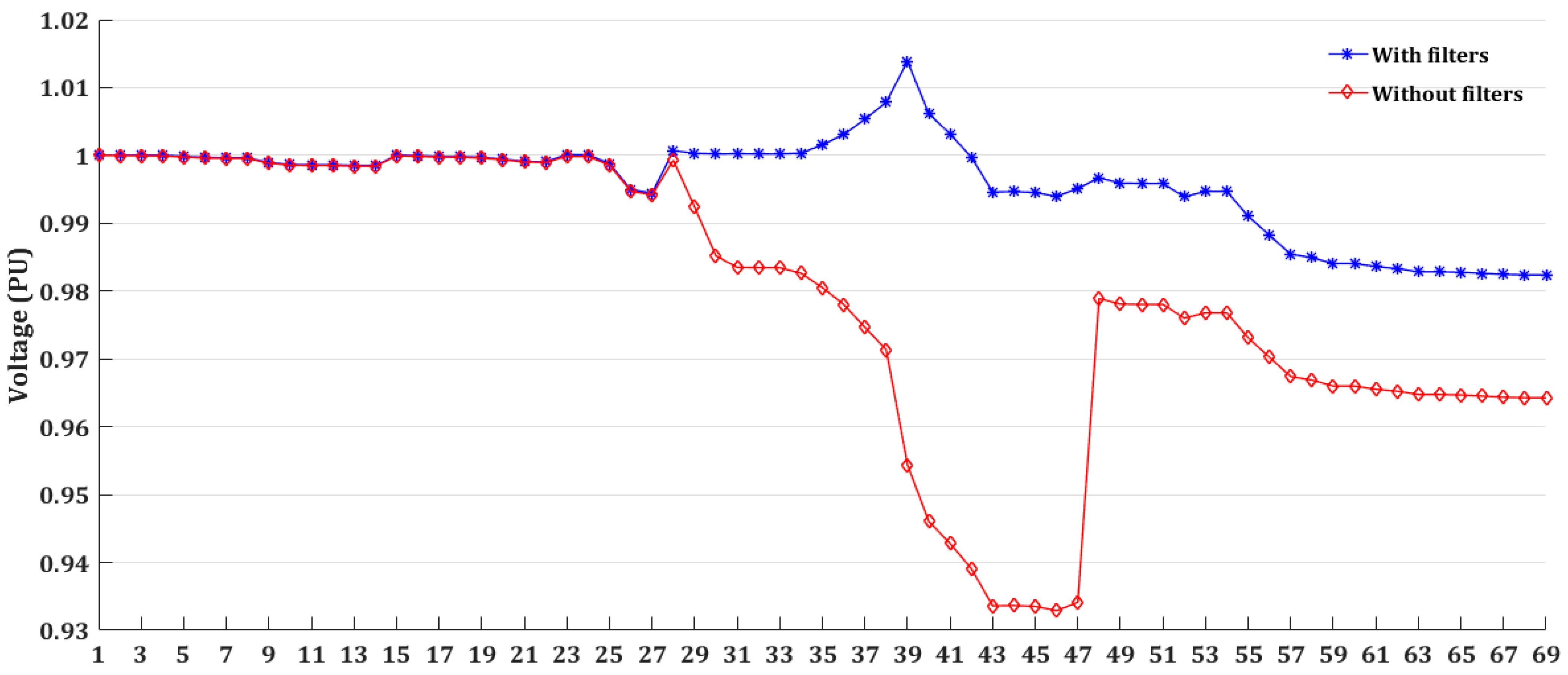
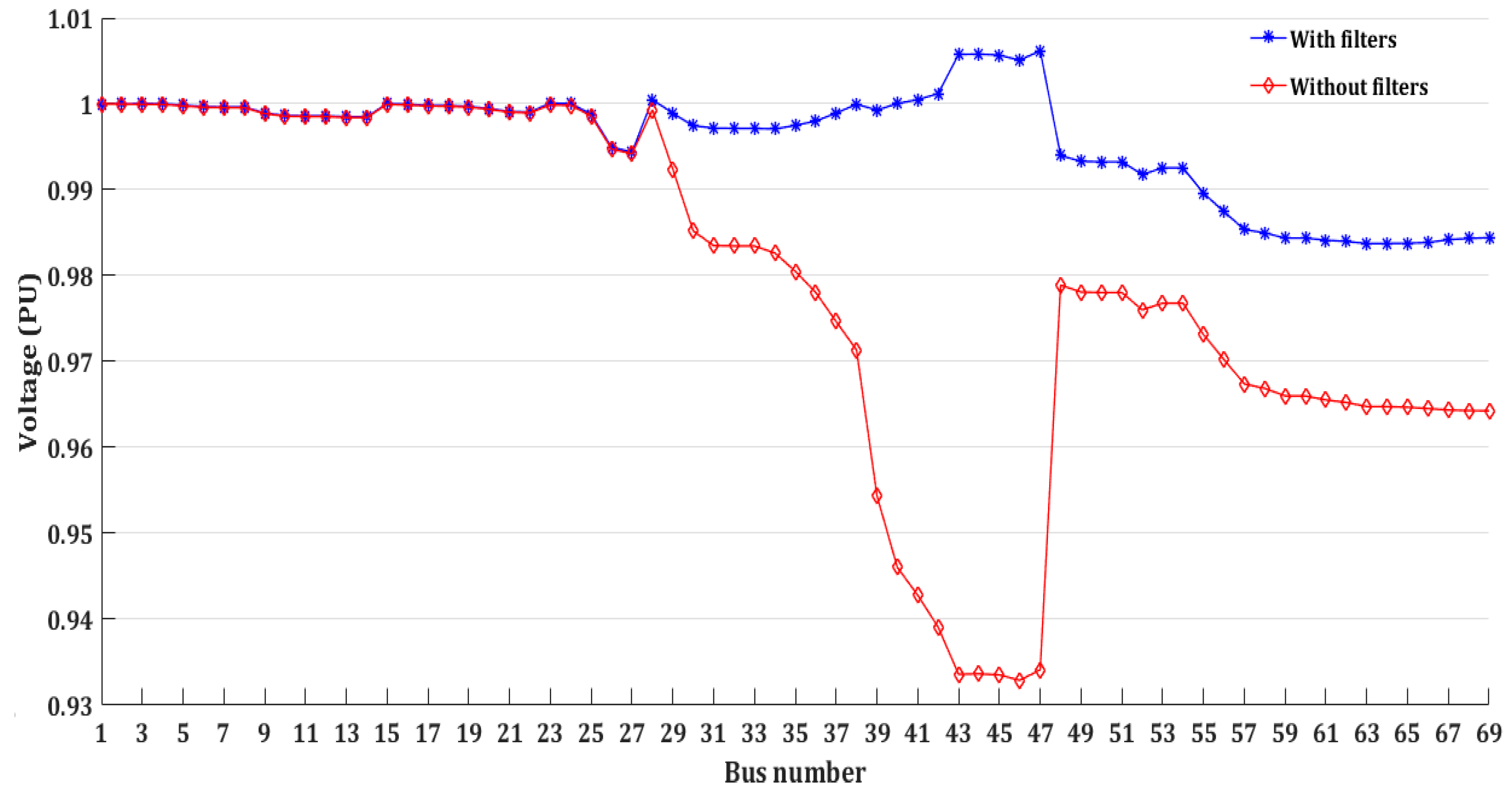
6.2. Simulation Results of Case 1
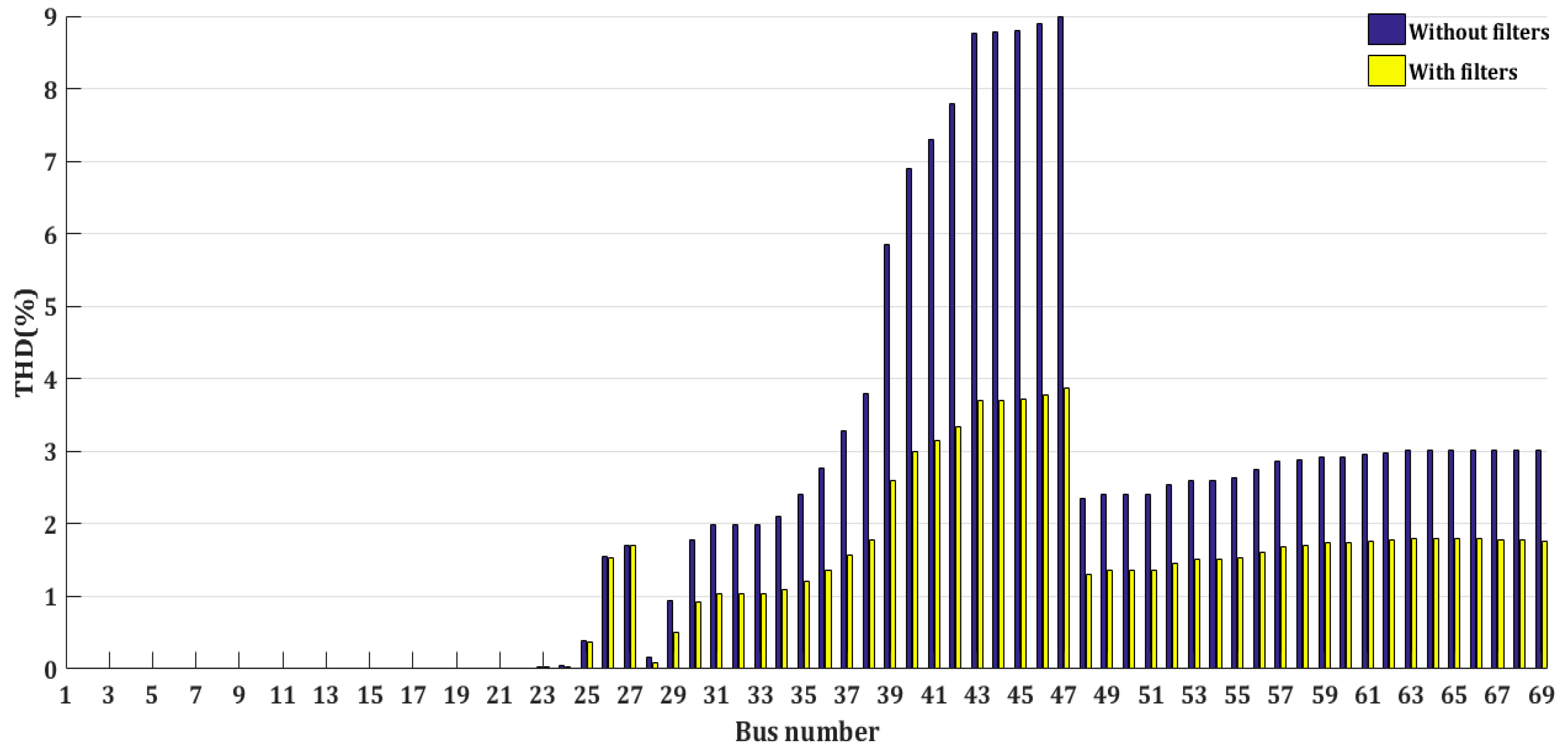
6.3. Simulation Results of Case 2
7. Conclusions
- The effectiveness of the proposed filter planning method in achieving multi-dimensional objectives with the aid of WCA.
- The WCA is efficient with good convergence characteristics in simultaneously determining the optimal design, placement, and the number of the STF.
- The proposed method not only reduces the THD and improves the voltage profile but also reduces the power loss and filter costs.
- Inverter-based DGs have shown a considerable effect on the harmonic distortion in distribution systems which increases the THD by about 14%.
- By using the proposed method, THD in a 69-bus system has reduced by 75% without considering the harmonic distortion of the DGs, and reduced by 56.5% without considering the harmonic distortion of the DGs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Solatialkaran, D.; Zare, F.; Saha, T.K.; Sharma, R. A Novel Approach in Filter Design for Grid-Connected Inverters Used in Renewable Energy Systems. IEEE Trans. Sustain. Energy 2020, 11, 154–164. [Google Scholar] [CrossRef]
- Shukl, P.; Singh, B. Delta-Bar-Delta Neural-Network-Based Control Approach for Power Quality Improvement of Solar-PV-Interfaced Distribution System. IEEE Trans. Ind. Inform. 2020, 16, 790–801. [Google Scholar] [CrossRef]
- IEEE. IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 1993; IEEE Std 519-1992. [Google Scholar]
- Almohaimeed, S.; Abdel-Akher, M. Power Quality Issues and Mitigation for Electric Grids with Wind Power Penetration. Appl. Sci. 2020, 10, 8852. [Google Scholar] [CrossRef]
- Sakar, S.; Balci, M.E.; Aleem, S.H.A.; Zobaa, A.F. Increasing PV hosting capacity in distorted distribution systems using passive harmonic filtering. Electr. Power Syst. Res. 2017, 148, 74–86. [Google Scholar] [CrossRef]
- Li, L.; Mu, H.; Li, N.; Li, M. Economic and environmental optimization for distributed energy resource systems coupled with district energy networks. Energy 2016, 109, 947–960. [Google Scholar] [CrossRef]
- El Ela, A.A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Shalaby, A.S. Application of the crow search algorithm for economic environmental dispatch. In Proceedings of the IEEE 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 78–83. [Google Scholar]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal Placement and Sizing of Distributed Generation and Capacitor Banks in Distribution Systems Using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. A novel adequate bi-level reactive power planning strategy. Int. J. Electr. Power Energy Syst. 2016, 78, 897–909. [Google Scholar] [CrossRef]
- Hu, H.; Shi, Q.; He, Z.; He, J.; Gao, S. Potential Harmonic Resonance Impacts of PV Inverter Filters on Distribution Systems. IEEE Trans. Sustain. Energy 2014, 6, 151–161. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Meyer, J.; Moller, F.; Stiegler, R.; Djokic, S.Z. Experimental-Based Evaluation of PV Inverter Harmonic and Interharmonic Distortion Due to Different Operating Conditions. IEEE Trans. Instrum. Meas. 2016, 65, 2221–2233. [Google Scholar] [CrossRef]
- Abaza, A.; Fawzy, A.; El-Sehiemy, R.A.; Alghamdi, A.S.; Kamel, S. Sensitive reactive power dispatch solution accomplished with renewable energy allocation using an enhanced coyote optimization algorithm. Ain. Shams Eng. J. 2020. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Iracheta-Cortez, R.; Lecheppe, V.; Salgado, O.A.J. Modelling and Validation of a Grid-Connected DFIG by Exploiting the Frequency-Domain Harmonic Analysis. Appl. Sci. 2020, 10, 9014. [Google Scholar] [CrossRef]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A.; Elkadeem, M.R.; Wang, S. Adequate Topology for Efficient Energy Resources Utilization of Active Distribution Networks Equipped with Soft Open Points. IEEE Access 2019, 7, 99003–99016. [Google Scholar] [CrossRef]
- Shaheen, E.A.M.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium optimization algorithm for net-work reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]
- Abbas, A.S.; Ali, E.S.; El-Sehiemy, R.A.; El-Ela, A.A.A.; Fetyan, K.M. Comprehensive Parametric Analysis of Single Tuned Filter in Distribution Systems. In Proceedings of the IEEE 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 465–472. [Google Scholar]
- Khan, U.N.; Sidhu, T.S. A Phase-Shifting Transformer Protection Technique Based on Directional Comparison Approach. IEEE Trans. Power Deliv. 2014, 29, 2315–2323. [Google Scholar] [CrossRef]
- Bai, S.; Lukic, S.M. New Method to Achieve AC Harmonic Elimination and Energy Storage Integration for 12-Pulse Diode Rectifiers. IEEE Trans. Ind. Electron. 2012, 60, 2547–2554. [Google Scholar] [CrossRef]
- Boontua, S.; Chaithanakulwat, A.; Savangboon, T. Power Quality Improvement with Mitigation of Harmonic Distortion in Three-phase System Based on Shunt Active Power Filter Mechanism. Int. J. Eng. Appl. 2019, 7, 188. [Google Scholar] [CrossRef]
- Zeineldin, H.; Zobaa, A. Particle Swarm Optimization of Passive Filters for Industrial Plants in Distribution Net-works. Electr. Power Compon. Syst. 2011, 39, 1795–1808. [Google Scholar] [CrossRef]
- Ertay, M.M.; Tosun, S.; Zengin, A.; Tosun, S. Simulated annealing based passive power filter design for a medium voltage power system. In Proceedings of the IEEE 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012; pp. 1–5. [Google Scholar]
- El-Ela, A.A.; Allam, S.; El-Arwash, H. An optimal design of single tuned filter in distribution systems. Electr. Power Syst. Res. 2008, 78, 967–974. [Google Scholar] [CrossRef]
- Chang, G.W.; Wang, H.-L.; Chuang, G.-S.; Chu, S.-Y. Passive Harmonic Filter Planning in a Power System with Considering Probabilistic Constraints. IEEE Trans. Power Deliv. 2008, 24, 208–218. [Google Scholar] [CrossRef]
- Stone, P.E.C.; Wang, J.; Shin, Y.-J.; Dougal, R.A. Efficient Harmonic Filter Allocation in an Industrial Distribution System. IEEE Trans. Ind. Electron. 2011, 59, 740–751. [Google Scholar] [CrossRef]
- Au, M.; Milanovic, J. Planning Approaches for the Strategic Placement of Passive Harmonic Filters in Radial Dis-tribution Networks. IEEE Trans. Power Deliv. 2007, 22, 347–353. [Google Scholar] [CrossRef]
- Chang, Y.-P.; Low, C.; Hung, S.-Y. Integrated feasible direction method and genetic algorithm for optimal planning of harmonic filters with uncertainty conditions. Expert Syst. Appl. 2009, 36, 3946–3955. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rozbahani, A.; Montazeri, M. Multi criteria simultaneous planning of passive filters and dis-tributed generation simultaneously in distribution system considering nonlinear loads with adaptive bacterial foraging opti-mization approach. Int. J. Electr. Power Energy Syst. 2016, 79, 253–262. [Google Scholar] [CrossRef]
- Ghaffarzadeh, N.; Sadeghi, H. A new efficient BBO based method for simultaneous placement of inverter-based DG units and capacitors considering harmonic limits. Int. J. Electr. Power Energy Syst. 2016, 80, 37–45. [Google Scholar] [CrossRef]
- Kawann, C.; Emanuel, A. Passive shunt harmonic filters for low and medium voltage: A cost comparison study. IEEE Trans. Power Syst. 1996, 11, 1825–1831. [Google Scholar] [CrossRef]
- El-Sayed, M.M.; El-Ela, A.A.; El-Sehiemy, R.A. Effect of photovoltaic system on power quality in electrical distribution networks. In Proceedings of the IEEE Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 1005–1012. [Google Scholar]
- Eajal, A.A.; El-Hawary, M.E. Optimal Capacitor Placement and Sizing in Unbalanced Distribution Systems with Harmonics Consideration Using Particle Swarm Optimization. IEEE Trans. Power Deliv. 2010, 25, 1734–1741. [Google Scholar] [CrossRef]
- Leite, J.C.; Abril, I.P.; Azevedo, M.S. Capacitor and passive filter placement in distribution systems by non-dominated sorting genetic algorithm-II. Electr. Power Syst. Res. 2017, 143, 482–489. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Kersting, W. Distribution System Modeling and Analysis, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Teng, J.-H.; Chang, C.-Y. Backward/Forward Sweep Based Harmonic Analysis Method for Distribution Sys-tems. IEEE Trans. Power Deliv. 2007, 22, 1665–1667. [Google Scholar] [CrossRef]



| Harmonic Order | 1 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 25 |
| Value (%) | 100 | 42 | 14.3 | 7.9 | 3.2 | 3.7 | 2.3 | 2.3 | 1.4 |
| Harmonic Order | Magnitude % | Phase (deg.) | Harmonic Order | Magnitude % | Phase (deg.) |
|---|---|---|---|---|---|
| 1 | 100 | −2.34 | 9 | 8 | 140.36 |
| 3 | 20 | −15.29 | 11 | 5 | 65.54 |
| 5 | 15 | −20.74 | 13 | 3 | 42.62 |
| 7 | 10 | −30.85 | 15 | 2 | 153.28 |
| Filter No. | Placement | ft | Qc (MVar) | R (Ω) | L (mH) | C (µF) |
|---|---|---|---|---|---|---|
| 1 | 39 | 7 | 2.3303 | 0.0655 | 0.0015 | 138.84 |
| Parameter | Without Filter | With Filter | |
|---|---|---|---|
| Vmax (p.u) | 1 | 1.0139 | |
| Vmin (p.u) | 0.9329 | 0.9824 | |
| Ploss (kW) | 51.561 | 29.83 | |
| THDmax (%) | 7.87 | 2 | |
| Fitness Functions | |||
| F1 | F2 | F3 | Ftotal |
| 1.9679 | 0.4545 | 2.8657 × 104 | 0.2284 |
| Filter No. | Placement | ft | Qc (MVar) | R (Ω) | L (mH) | C (µF) |
|---|---|---|---|---|---|---|
| 1 | 69 | 3 | 0.1 | 3.5617 | 0.1890 | 6 |
| 2 | 43 | 3 | 1.82 | 0.1952 | 0.0104 | 108.7 |
| Parameter | Without Filter | With Filter | |
|---|---|---|---|
| Vmax (p.u) | 1 | 1.0062 | |
| Vmin (p.u) | 0.9329 | 0.9837 | |
| Ploss (kW) | 53.622 | 32.29 | |
| THDmax (%) | 9 | 3.87 | |
| Fitness Functions | |||
| F1 | F2 | F3 | Ftotal |
| 3.8657 | 0.4131 | 3.0866 × 104 | 0.3076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.S.; El-Sehiemy, R.A.; Abou El-Ela, A.; Ali, E.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Appl. Sci. 2021, 11, 774. https://doi.org/10.3390/app11020774
Abbas AS, El-Sehiemy RA, Abou El-Ela A, Ali ES, Mahmoud K, Lehtonen M, Darwish MMF. Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Applied Sciences. 2021; 11(2):774. https://doi.org/10.3390/app11020774
Chicago/Turabian StyleAbbas, Ahmed S., Ragab A. El-Sehiemy, Adel Abou El-Ela, Eman Salah Ali, Karar Mahmoud, Matti Lehtonen, and Mohamed M. F. Darwish. 2021. "Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation" Applied Sciences 11, no. 2: 774. https://doi.org/10.3390/app11020774
APA StyleAbbas, A. S., El-Sehiemy, R. A., Abou El-Ela, A., Ali, E. S., Mahmoud, K., Lehtonen, M., & Darwish, M. M. F. (2021). Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Applied Sciences, 11(2), 774. https://doi.org/10.3390/app11020774









