Analysis and Experimental Verification of Mechanical Errors in Nine-Link Type Double-Toggle Mold/Die Clamping Mechanisms
Abstract
:Featured Application
Abstract
1. Introduction
2. Position Analysis
3. Mechanical Error Analysis
3.1. Analysis of the Lower Sub-Mechanism
3.2. Analysis of the Upper Sub-Mechanism
3.3. The Evaluation Indices
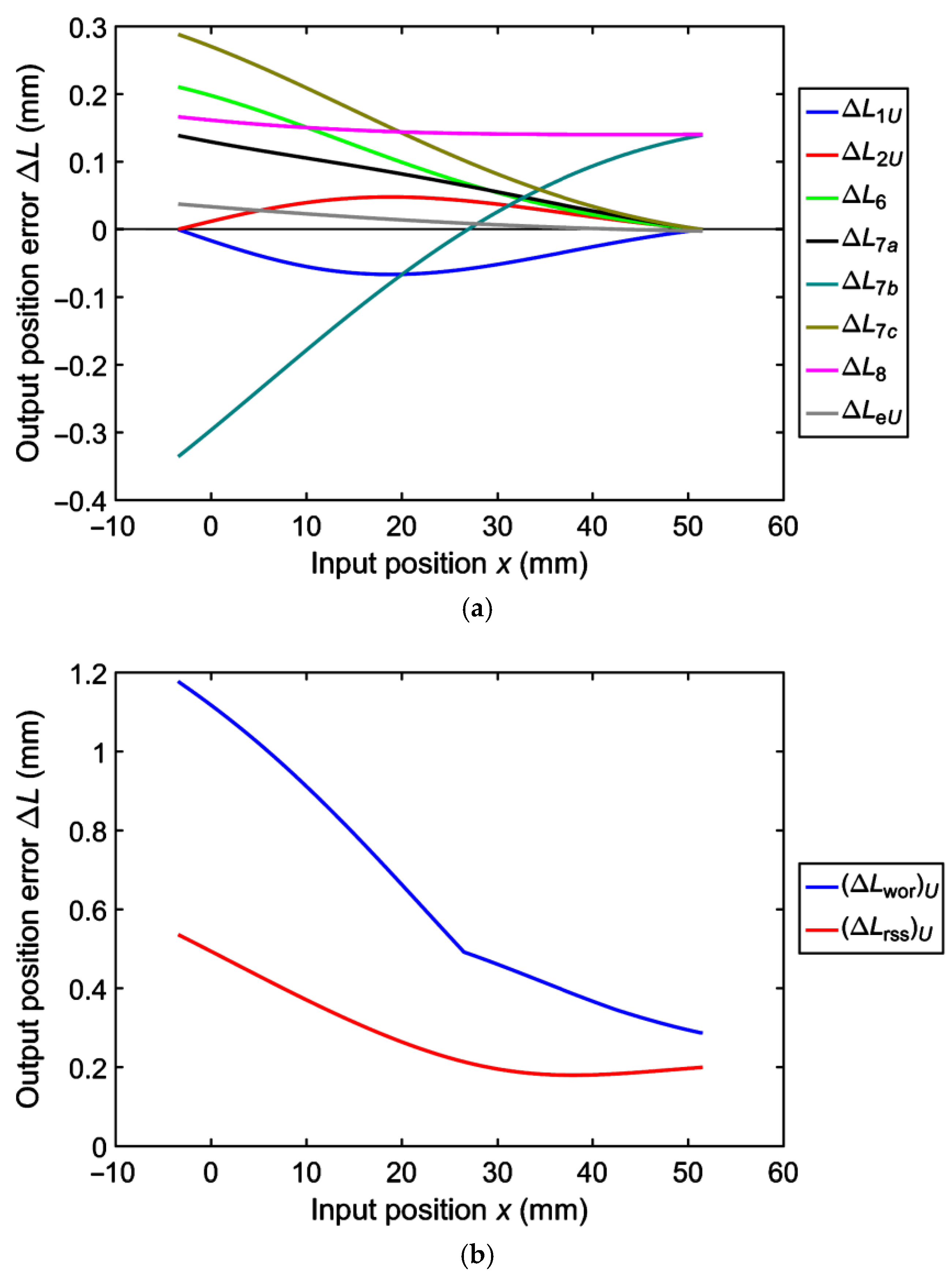
3.4. Case Study
4. Prototype for Experimental Evaluation
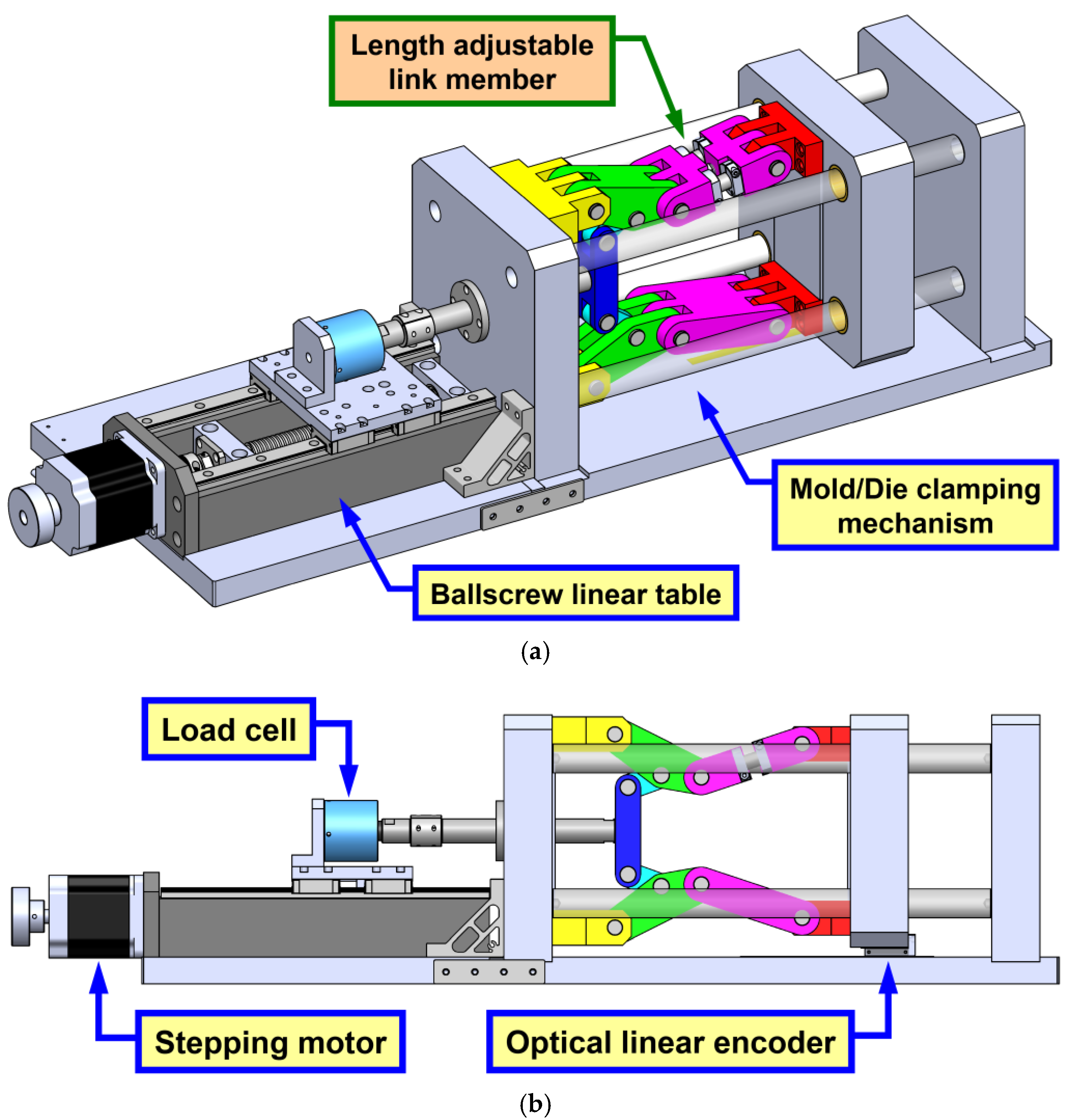
4.1. Conceptual Design
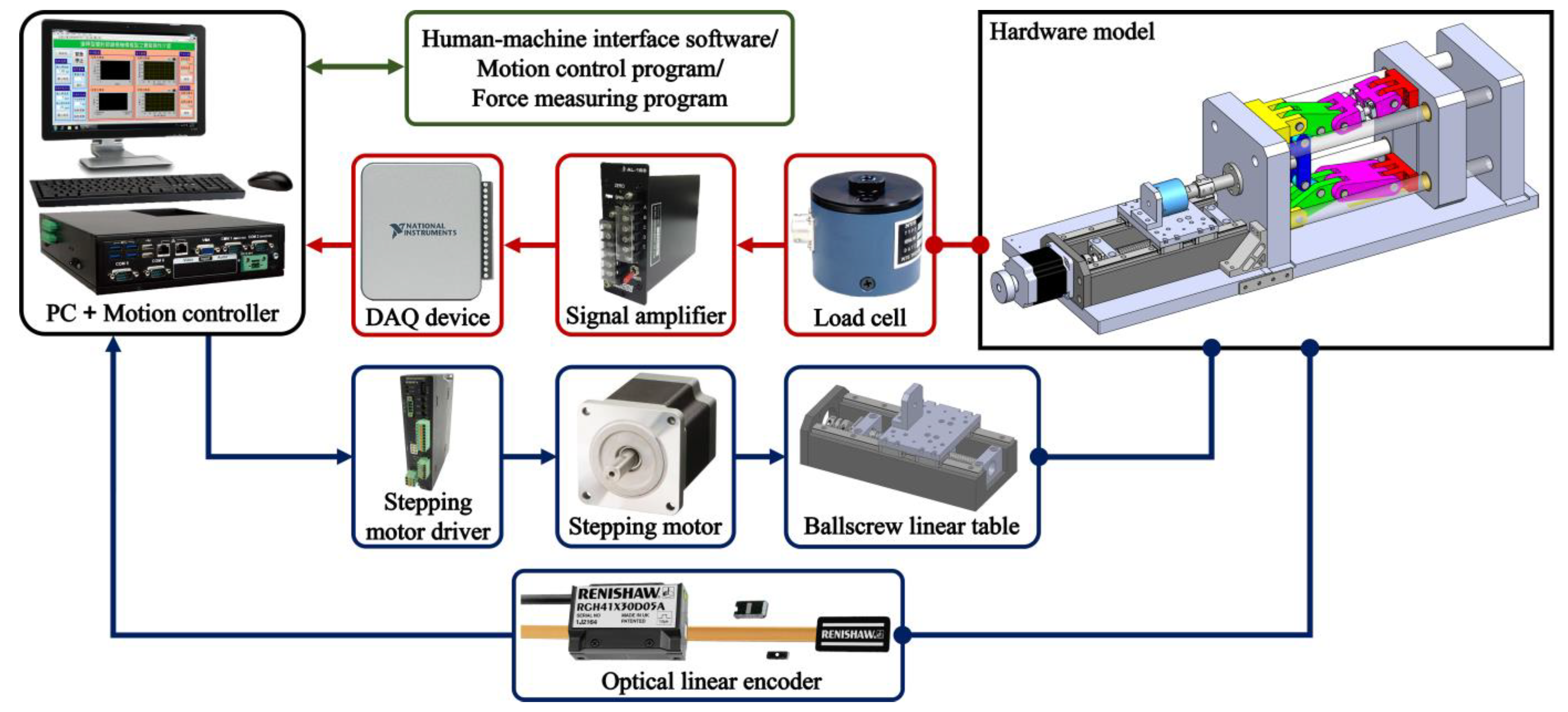
4.2. Hardware Construction and Integration
5. Experimental Results and Discussion
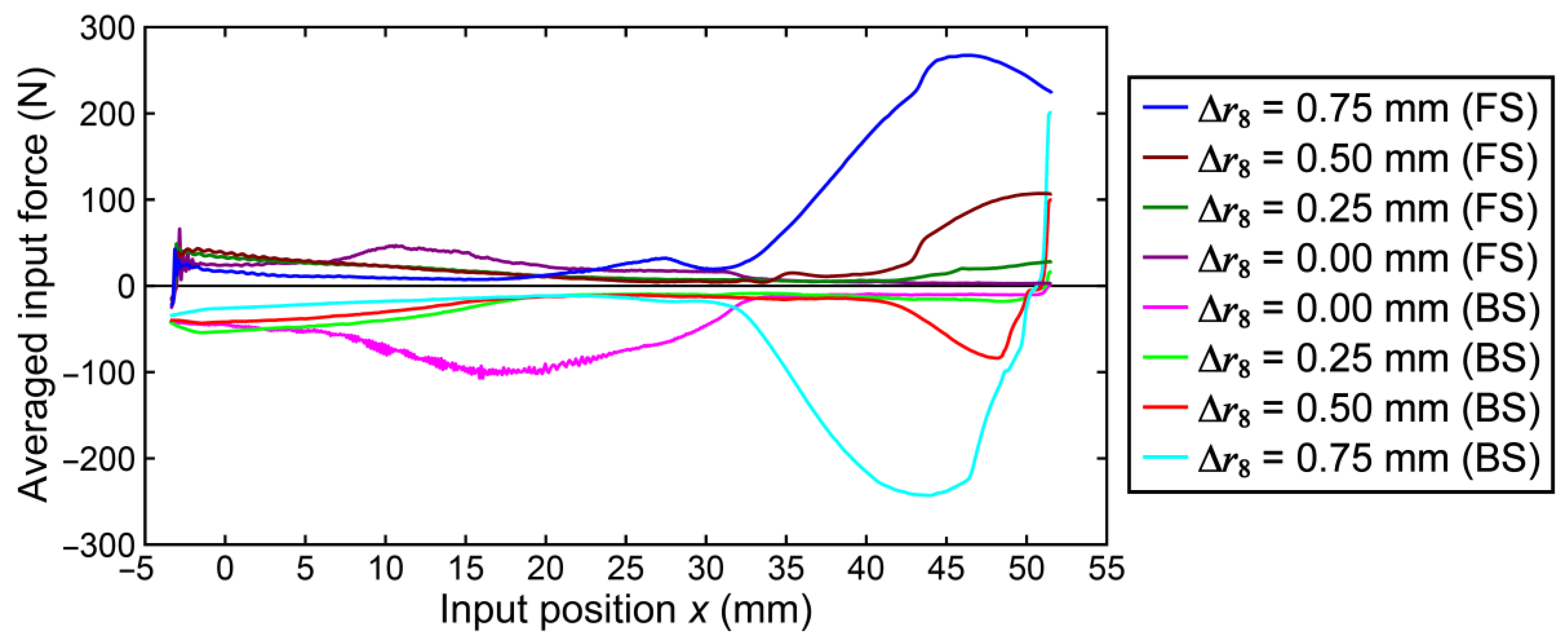
5.1. Experimental Results
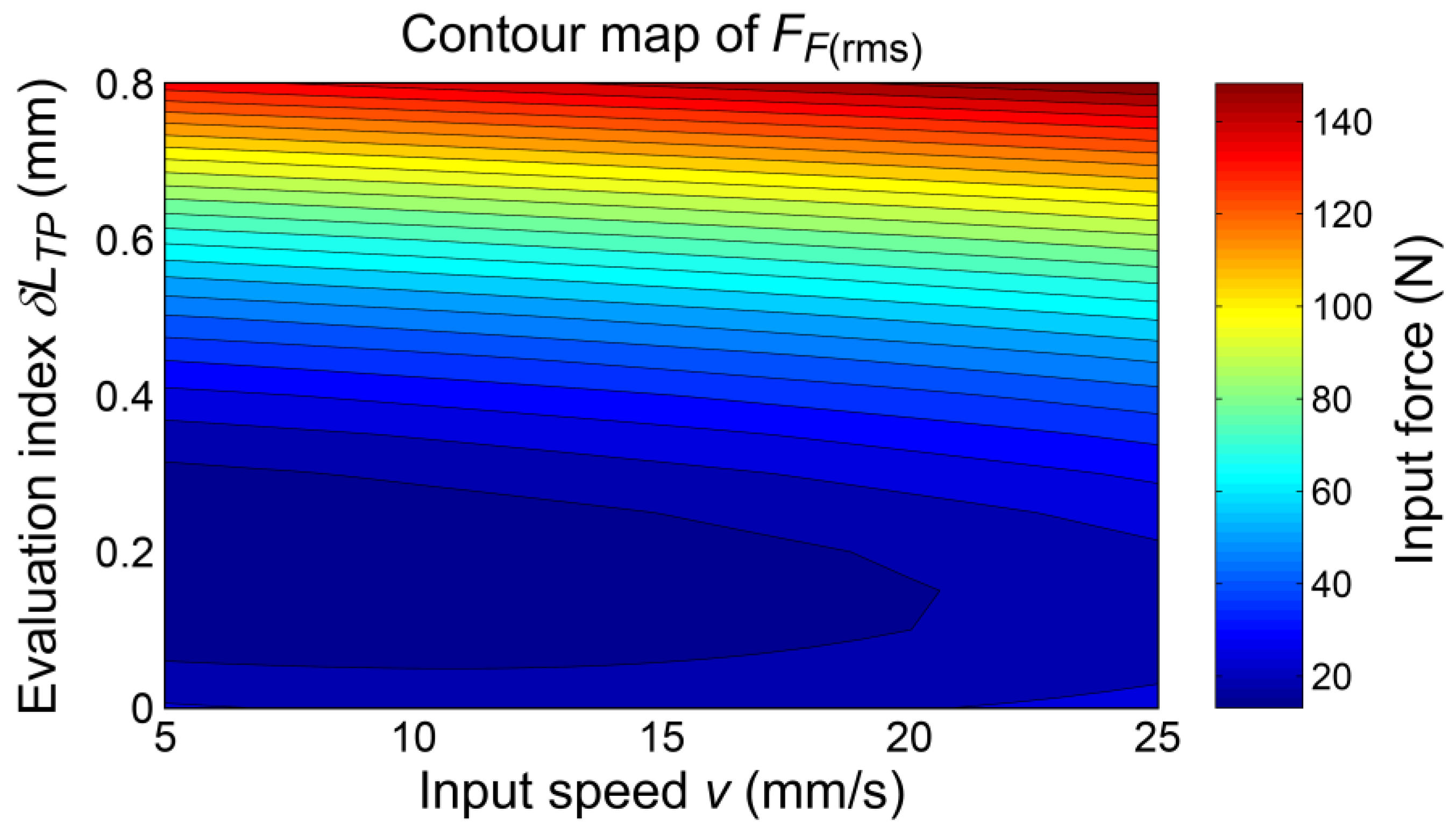
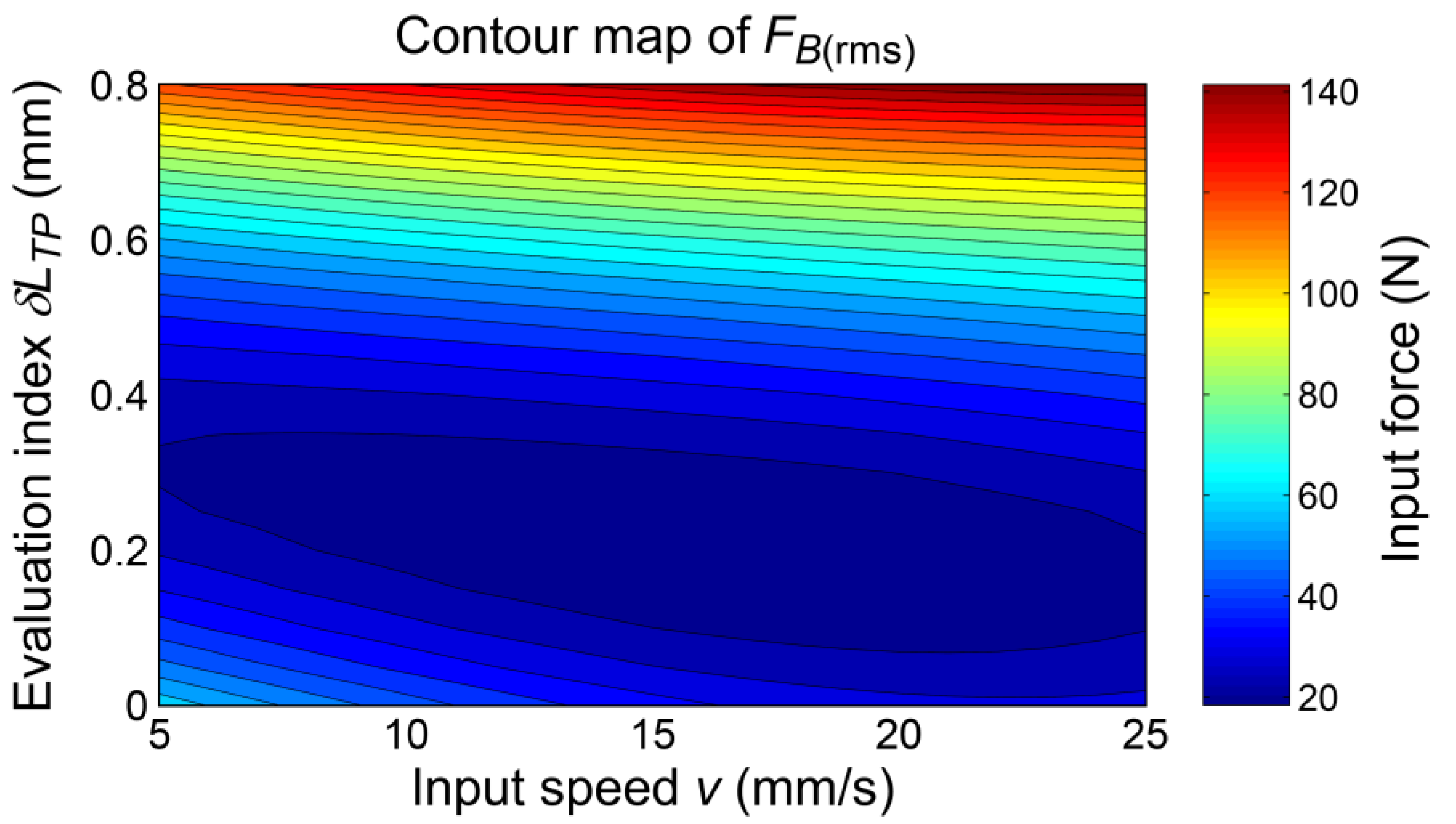
5.2. Response Surface Modelling
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Johannaber, F. Injection Molding Machines—A User’s Guide, 3rd ed.; Hanser/Gardner Publications: Cincinnati, OH, USA, 1994. [Google Scholar]
- Frantz, C.E. Mold-Separating Device. U.S. Patent 1880380, 4 October 1932. [Google Scholar]
- Yan, H.S. Mechanisms—Theory and Applications; McGraw-Hill Education (Asia): Singapore, 2016; pp. 19–30, 50–51, 69–70, 124–125. [Google Scholar]
- Fung, R.F.; Hwang, C.C.; Hwang, C.S.; Chen, W.P. Inverse dynamics of a toggle mechanism. Comput. Struct. 1997, 63, 91–99. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hsiao, K.M. Investigation of the friction effect at pin joints for the five-point double-toggle clamping mechanisms of injection molding machines. Int. J. Mech. Sci. 2003, 45, 1913–1927. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hsiao, K.M. Study on improvements of the five-point double-toggle mould clamping mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 761–774. [Google Scholar] [CrossRef]
- Lin, W.Y.; Shen, C.L.; Hsiao, K.M. A case study of the five-point double-toggle mould clamping mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 527–535. [Google Scholar] [CrossRef]
- Huang, M.S.; Lin, T.Y.; Fung, R.F. Key design parameters and optimal design of a five-point double-toggle clamping mechanism. Appl. Math. Model 2011, 35, 4304–4320. [Google Scholar] [CrossRef]
- Chiang, M.H.; Yang, F.L.; Chen, Y.N.; Yeh, Y.P. Integrated control of clamping force and energy-saving in hydraulic injection moulding machines using decoupling fuzzy sliding-mode control. Int. J. Adv. Manuf. Technol. 2005, 27, 53–62. [Google Scholar] [CrossRef]
- Rao, B.; Zhou, H.; Ouyang, H.; Wan, Y.; Zhang, Y.; Wu, J. Study on the clamping force measurement and partial load regulation technology of injection molding machine. CIRP J. Manuf. Sci. Technol. 2017, 19, 19–24. [Google Scholar] [CrossRef]
- Huang, M.S.; Lin, C.Y. A novel clamping force searching method based on sensing tie-bar elongation for injection molding. Int. J. Heat Mass Tran. 2017, 109, 223–230. [Google Scholar] [CrossRef]
- Huang, M.S.; Nian, S.C.; Chen, J.Y.; Lin, C.Y. Influence of clamping force on tie-bar elongation, mold separation, and part dimensions in injection molding. Precis. Eng. 2018, 51, 647–658. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, P.; Zhang, J.; Huang, J.; Xia, N.; Fu, J. On-line measurement of clamping force for injection molding machine using ultrasonic technology. Ultrasonics 2019, 91, 170–179. [Google Scholar] [CrossRef]
- Hartenberg, R.S.; Denavit, J. Kinematic Synthesis of Linkages; McGraw-Hill: New York, NY, USA, 1964; pp. 315–320. [Google Scholar]
- Garrett, R.E.; Hall, A.S. Effect of tolerance and clearance in linkage design. J. Eng. Ind. 1969, 9, 198–202. [Google Scholar] [CrossRef]
- Dhande, S.G.; Chakraborty, J. Analysis and synthesis of mechanical error in linkages—a stochastic approach. J. Eng. Ind. 1973, 95, 672–676. [Google Scholar] [CrossRef]
- Lakshminarayan, K.; Narayanamurthi, R.G. On the analysis of the effect of tolerances in linkages. J. Mech. 1971, 6, 59–67. [Google Scholar] [CrossRef]
- Choubey, M.; Rao, A.C. Synthesizing linkages with minimal structural and mechanical error based upon tolerance allocation. Mech. Mach. Theory 1982, 17, 91–97. [Google Scholar] [CrossRef]
- Sukhija, R.P.; Rao, A.C. Mechanical error synthesis of path generating mechanism using reliability index. Trans. Can. Soc. Mech. Eng. 1986, 10, 85–90. [Google Scholar] [CrossRef]
- Chatterjee, G.B.; Mallik, A.K. Mechanical error of a four-bar linkage coupler curve. Mech. Mach. Theory 1987, 22, 85–88. [Google Scholar] [CrossRef]
- Mallik, A.K.; Dhande, S.G. Analysis and synthesis of mechanical error in path-generating linkages using a stochastic approach. Mech. Mach. Theory 1987, 22, 115–123. [Google Scholar] [CrossRef]
- Flores, P. A methodology for quantifying the kinematic position errors due to manufacturing and assembly tolerances. J. Mech. Eng. 2011, 57, 457–467. [Google Scholar] [CrossRef]
- Mutawe, S.; Al-Smadi, Y.M.; Sodhi, R.S. Planar Four-bar Path Generation Considering Worst Case Joint Tolerances. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 19–21 October 2011. [Google Scholar]
- Pavlović, N.D. Analysis of Mechanical Error In Quick-Return Shaper Mechanism. In Proceedings of the 12th IFToMM World Congress, Besançon, France, 18–21 June 2007. [Google Scholar]
- Oprisan, C.; Leohchi, D. Methodology for analysis of the influence of the mechanical errors and of the clearances on the precision of Watt and Stephenson mechanisms. Lat. Am. J. Solids Struct. 2007, 4, 1–17. [Google Scholar]
- Ting, K.L.; Long, Y. Performance quality and tolerance sensitivity of mechanisms. Trans. ASME J. Mech. Des. 1996, 118, 144–150. [Google Scholar] [CrossRef]
- Creveling, C.M. Tolerance Design—A Handbook for Developing Optimal Specifications; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Chang, W.T.; Wu, L.I. Tolerance analysis and synthesis of cam-modulated linkages. Math. Comput. Model. 2013, 57, 641–660. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mischke, C.R. Mechanical Engineering Design, 5th ed.; McGraw-Hill: New York, NY, USA, 1989; pp. 157–163. [Google Scholar]
- Beckwith, T.G.; Marangoni, R.D.; Lienhard, J.H. Mechanical Measurements, 5th ed.; Pearson Education Taiwan Ltd.: Taipei, Taiwan, 2004; pp. 45–125. [Google Scholar]
- The MathWorks Inc. MATLAB Statistics Toolbox User’s Guide—Version 2; The MathWorks Inc.: Natick, MA, USA, 1999. [Google Scholar]
- Lee, E.S.; Hwang, S.C.; Lee, J.T.; Won, J.K. A study on the characteristic of parameters by the response surface method in final wafer polishing. Int. J. Precis. Eng. Manuf. 2009, 10, 25–30. [Google Scholar] [CrossRef]
- Yoon, H.S.; Wu, R.; Lee, T.M.; Ahn, S.H. Geometric optimization of micro drills using Taguchi methods and response surface methodology. Int. J. Precis. Eng. Manuf. 2011, 12, 871–875. [Google Scholar] [CrossRef]
- Zębala, W.; Kowalczyk, R. Estimating the effect of cutting data on surface roughness and cutting force during WC-Co turning with PCD tool using Taguchi design and ANOVA analysis. Int. J. Adv. Manuf. Technol. 2015, 77, 2241–2256. [Google Scholar] [CrossRef]
- Aggarwal, V.; Khangura, S.S.; Garg, R.K. Parametric modeling and optimization for wire electrical discharge machining of Inconel 718 using response surface methodology. Int. J. Adv. Manuf. Technol. 2015, 79, 31–47. [Google Scholar] [CrossRef]
- Chang, W.T.; Chen, L.C. Design and experimental evaluation of a circular saw blade with self-clamped cutting inserts. Int. J. Adv. Manuf. Technol. 2016, 83, 365–379. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks—A Comprehensive Foundation, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]



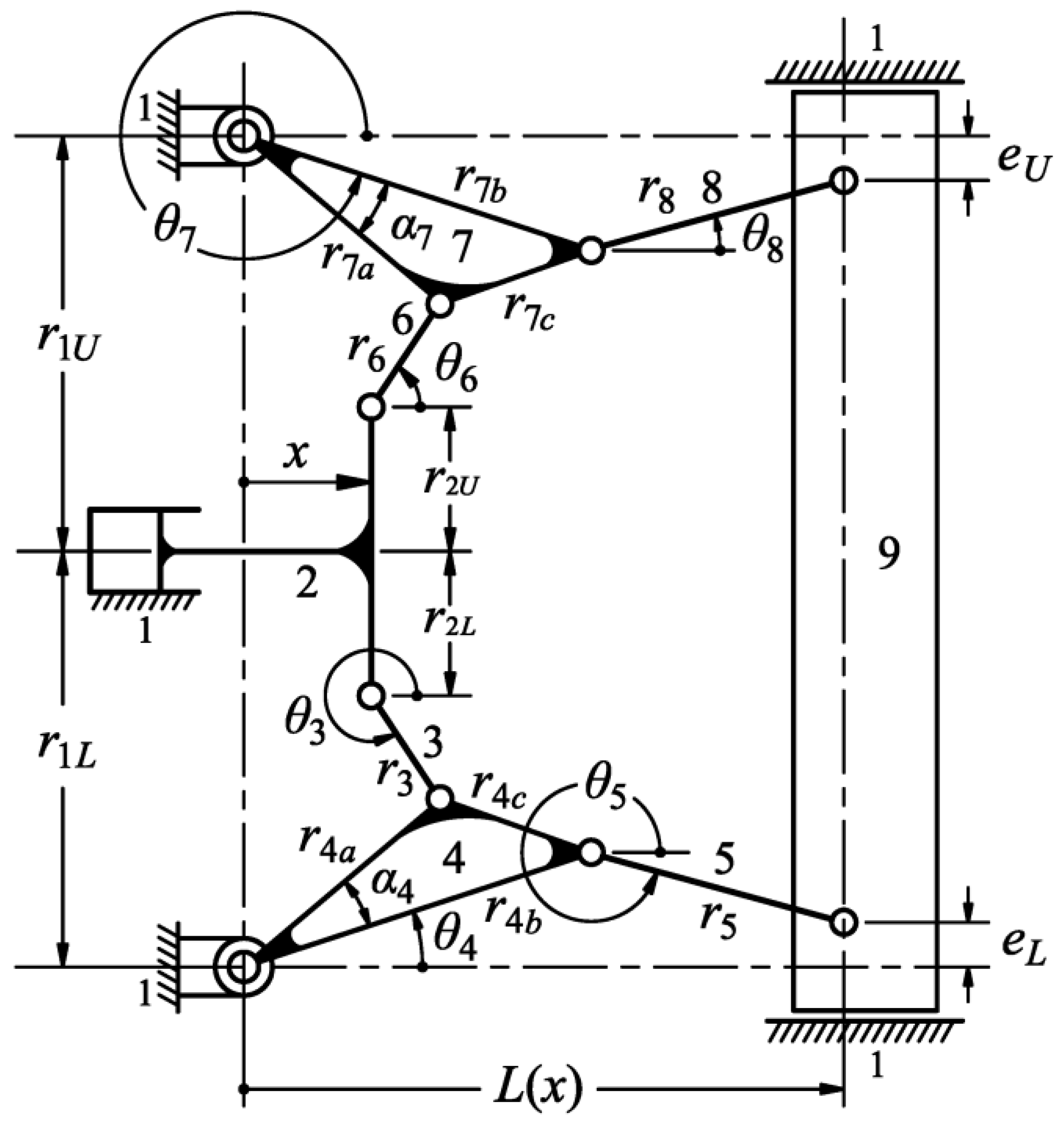
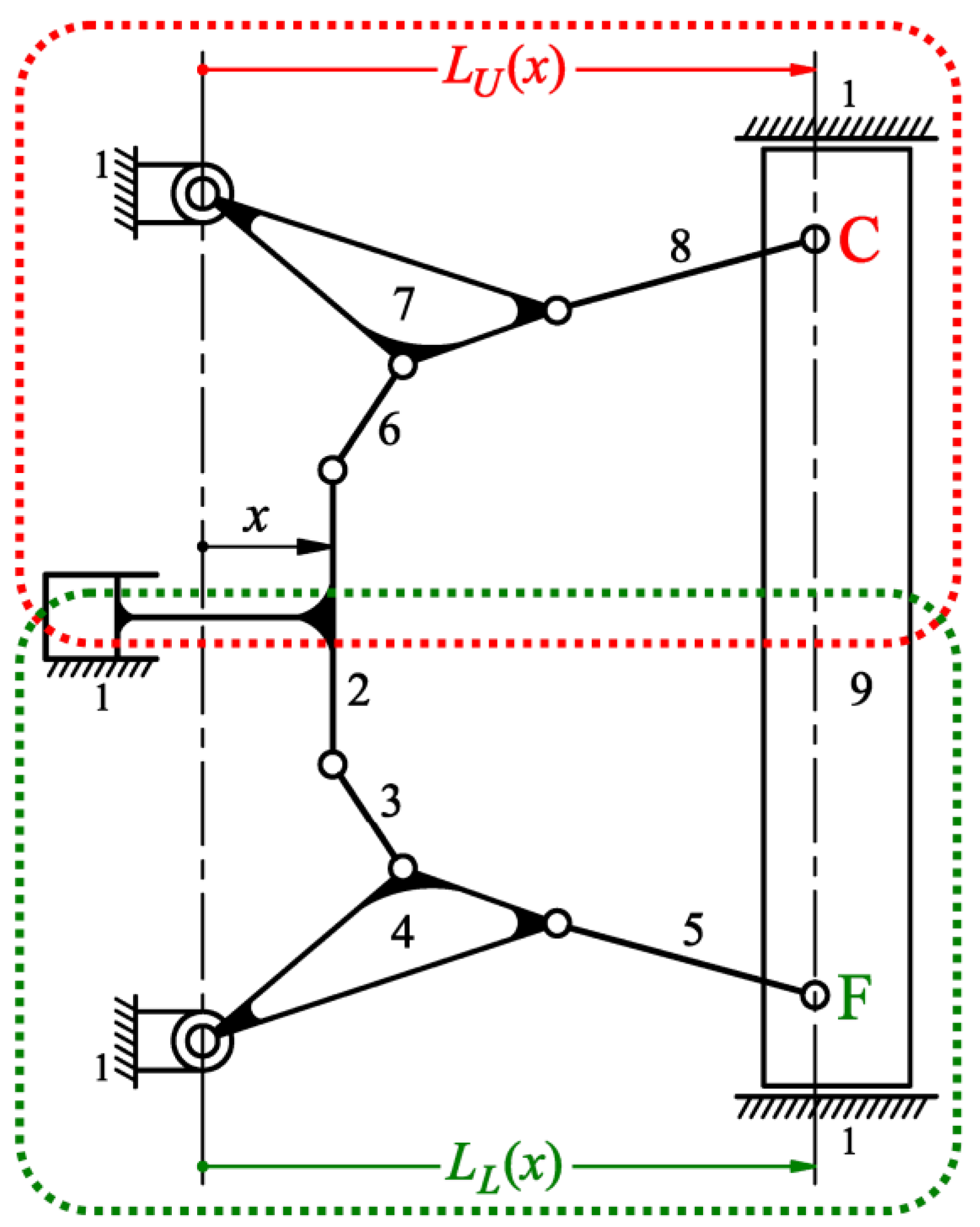
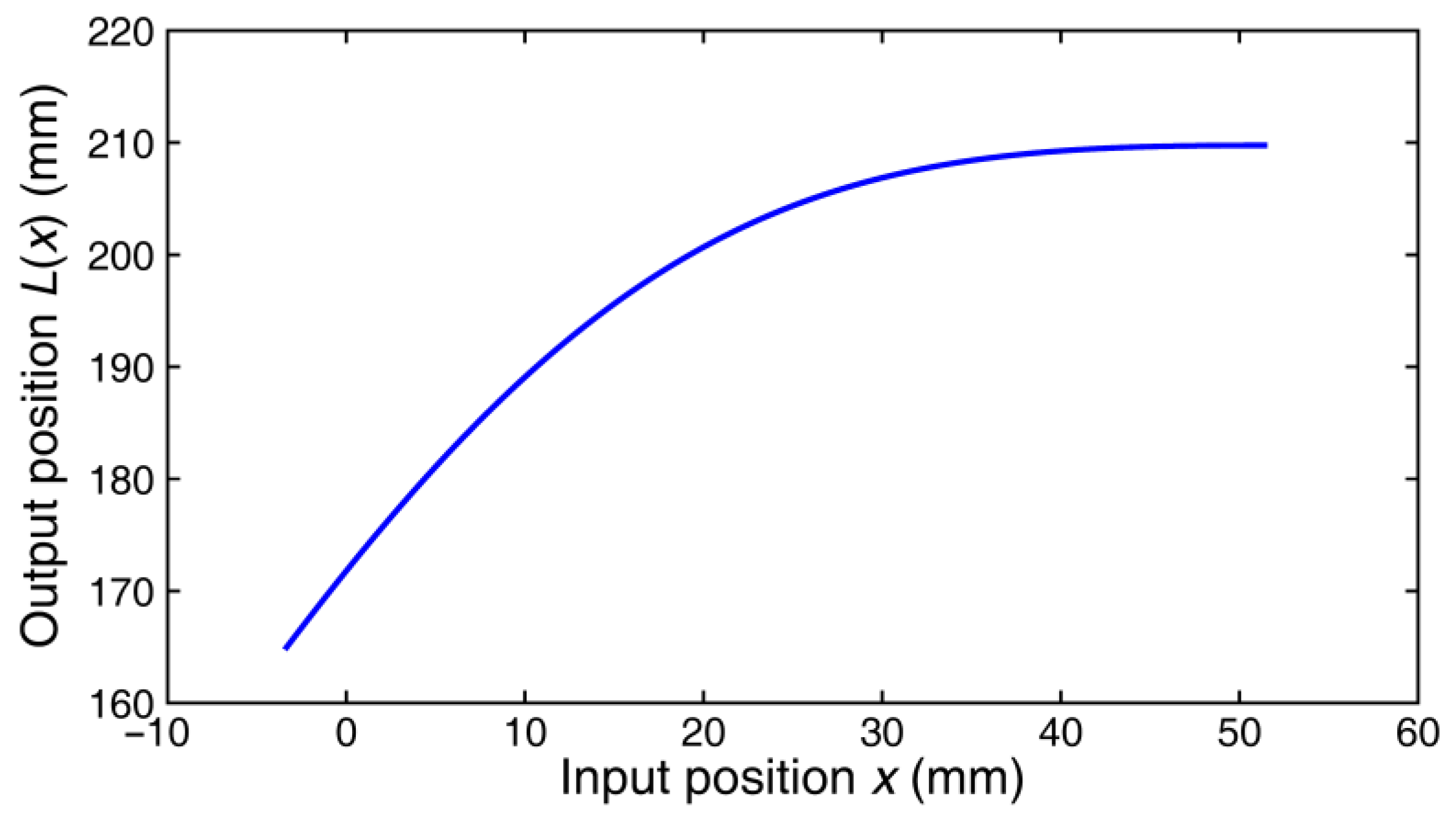
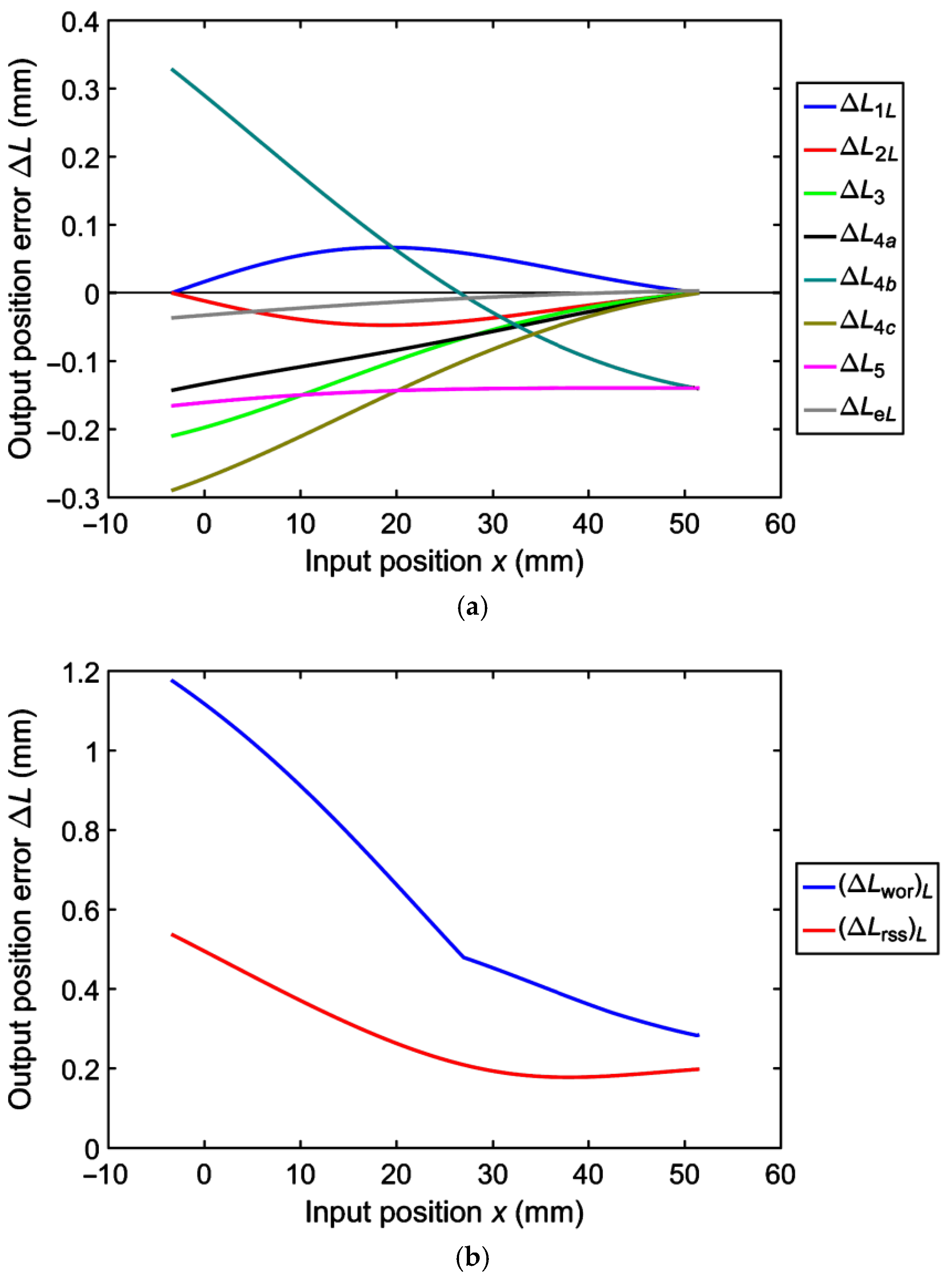





| Term | Value | Term | Value |
|---|---|---|---|
| r1L | 100.000 mm | r1U | 100.000 mm |
| r2L | 45.162 mm | r2U | 45.162 mm |
| r3 | 36.573 mm | r6 | 36.573 mm |
| r4a | 64.071 mm | r7a | 64.071 mm |
| r4b | 100.000 mm | r7b | 100.000 mm |
| r4c | 41.563 mm | r7c | 41.563 mm |
| r5 | 110.000 mm | r8 | 110.000 mm |
| eL | 10.000 mm | eU | 10.000 mm |
| IT Grade | δLwor (mm) | δLrss (mm) |
|---|---|---|
| 6 | 0.089 | 0.062 |
| 7 | 0.142 | 0.099 |
| 8 | 0.218 | 0.153 |
| 9 | 0.352 | 0.246 |
| 10 | 0.566 | 0.396 |
| 11 | 0.890 | 0.623 |
| 12 | 1.416 | 0.991 |
| Term | Stochastic result (mm) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
| Initial stroke position Si | −0.011 ± 0.033 | −0.078 ± 0.016 | −0.051 ± 0.023 | −0.180 ± 0.012 |
| Final stroke position Sf | 45.394 ± 0.009 | 45.309 ± 0.020 | 45.391 ± 0.008 | 45.272 ± 0.006 |
| Stroke S | 45.405 ± 0.030 | 45.387 ± 0.024 | 45.442 ± 0.018 | 45.452 ± 0.011 |
| Stroke error ΔS | 0.402 ± 0.030 | 0.383 ± 0.024 | 0.439 ± 0.018 | 0.449 ± 0.011 |
| Term | Stochastic result (mm) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
| Initial stroke position Si | −0.074 ± 0.028 | −0.017 ± 0.020 | −0.104 ± 0.017 | −0.129 ± 0.017 |
| Final stroke position Sf | 45.378 ± 0.017 | 45.403 ± 0.012 | 45.460 ± 0.003 | 45.425 ± 0.006 |
| Stroke S | 45.452 ± 0.037 | 45.420 ± 0.016 | 45.564 ± 0.017 | 45.555 ± 0.014 |
| Stroke error ΔS | 0.448 ± 0.037 | 0.417 ± 0.016 | 0.561 ± 0.017 | 0.551 ± 0.014 |
| Term | Stochastic result (mm) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
| Initial stroke position Si | −0.049 ± 0.020 | −0.040 ± 0.023 | −0.051 ± 0.014 | −0.126 ± 0.011 |
| Final stroke position Sf | 45.395 ± 0.006 | 45.427 ± 0.010 | 45.469 ± 0.005 | 45.431 ± 0.005 |
| Stroke S | 45.444 ± 0.021 | 45.467 ± 0.023 | 45.520 ± 0.014 | 45.557 ± 0.012 |
| Stroke error ΔS | 0.441 ± 0.021 | 0.464 ± 0.023 | 0.517 ± 0.014 | 0.553 ± 0.012 |
| Term | Stochastic result (N) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
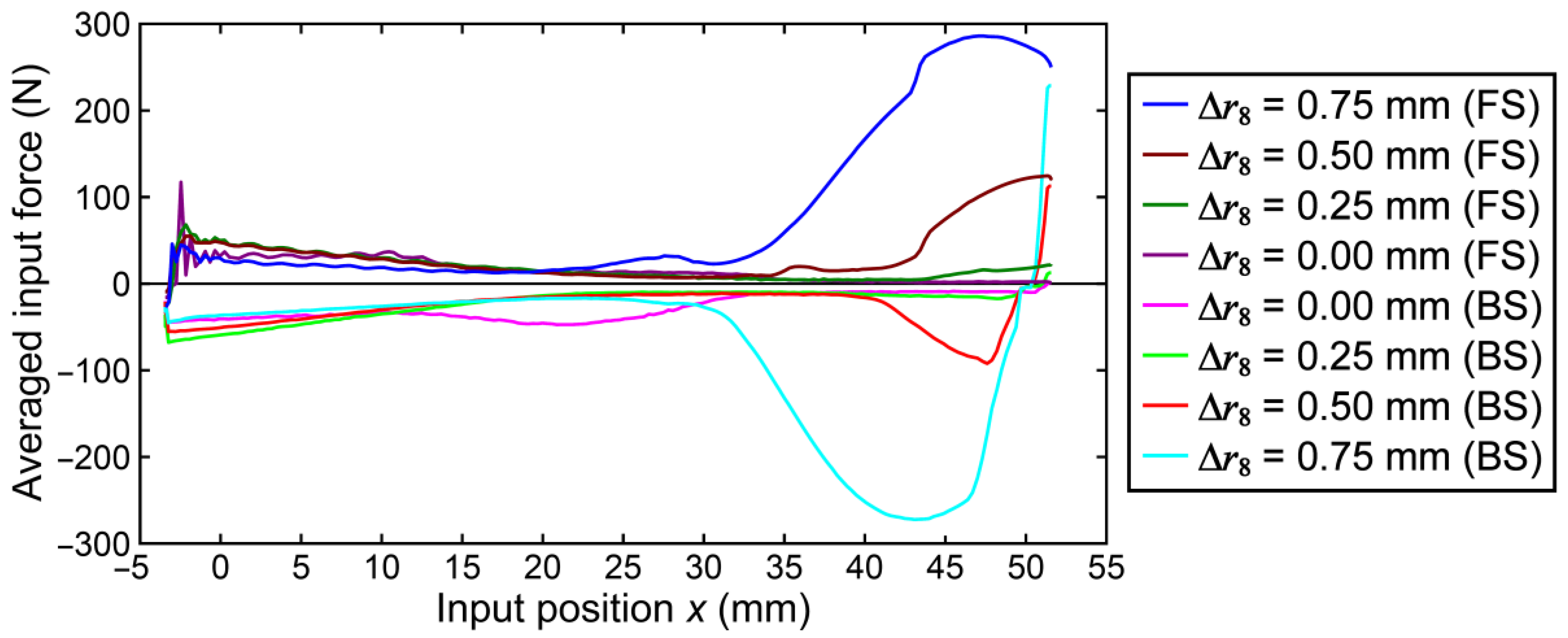
| Extreme value in FS FF(max) | 66.032 ± 17.772 | 48.819 ± 14.692 | 108.367 ± 12.236 | 269.966 ± 36.694 |
| RMS value in FS FF(rms) | 23.045 ± 3.054 | 19.025 ± 1.516 | 40.357 ± 6.898 | 117.941 ± 17.599 |
| Extreme value in BS FB(min) | −147.437 ± 25.544 | −54.892 ± 6.975 | −84.609 ± 10.057 | −246.336 ± 22.966 |
| RMS value in BS FB(rms) | 59.982 ± 5.610 | 28.155 ± 2.013 | 33.094 ± 2.694 | 104.091 ± 10.206 |
| Value at toggle position FTP | 2.877 ± 3.386 | 28.690 ± 9.473 | 106.655 ± 11.971 | 223.383 ± 27.948 |
| Term | Stochastic result (N) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
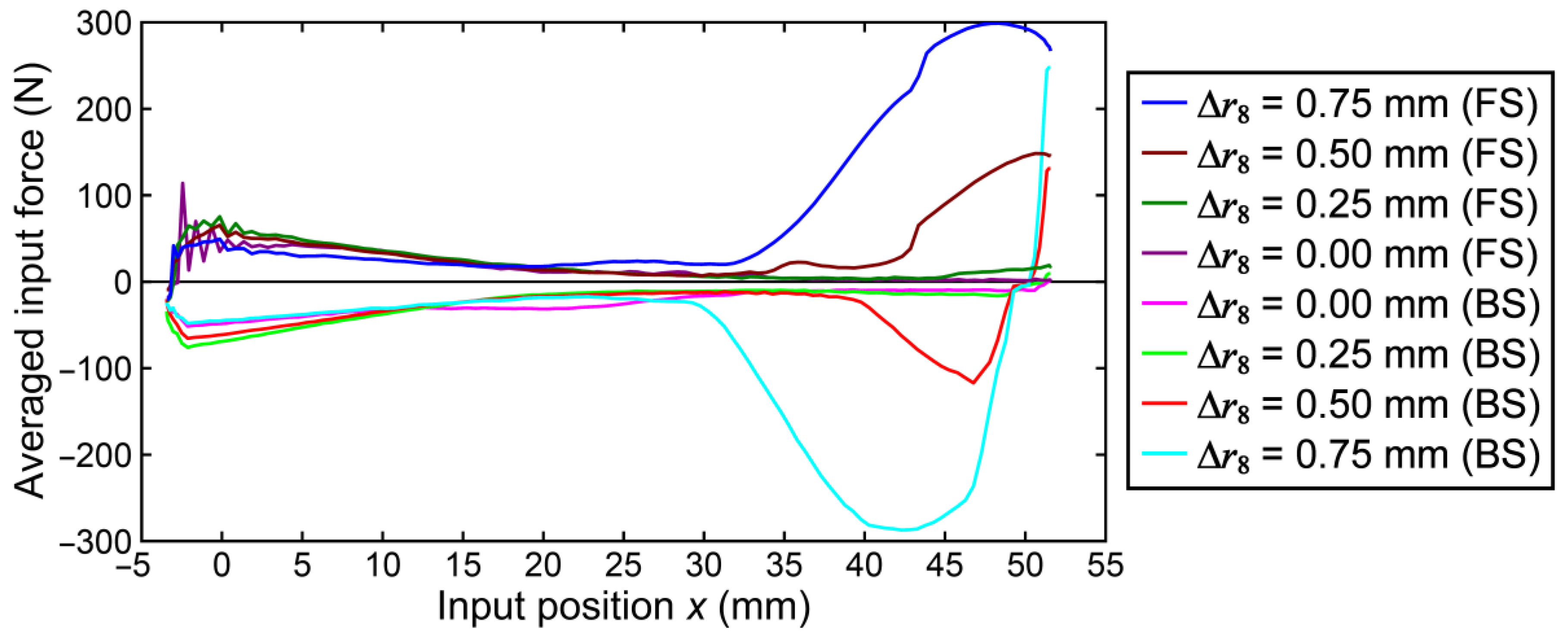
| Extreme value in FS FF(max) | 117.288 ± 4.772 | 68.483 ± 9.201 | 125.169 ± 11.873 | 287.808 ± 33.581 |
| RMS value in FS FF(rms) | 21.071 ± 1.508 | 24.027 ± 3.575 | 47.593 ± 5.863 | 127.264 ± 14.888 |
| Extreme value in BS FB(min) | −48.900 ± 6.391 | −67.925 ± 3.337 | −93.332 ± 21.255 | −276.353 ± 28.698 |
| RMS value in BS FB(rms) | 31.009 ± 1.946 | 29.547 ± 2.065 | 38.483 ± 5.470 | 122.033 ± 10.691 |
| Value at toggle position FTP | 0.788 ± 3.320 | 22.623 ± 5.008 | 122.541 ± 11.237 | 249.794 ± 31.624 |
| Term | Stochastic result (N) | |||
|---|---|---|---|---|
| Δr8 = 0.00 mm | Δr8 = 0.25 mm | Δr8 = 0.50 mm | Δr8 = 0.75 mm | |
| Extreme value in FS FF(max) | 113.887 ± 9.546 | 75.209 ± 4.825 | 149.142 ± 12.193 | 300.124 ± 23.999 |
| RMS value in FS FF(rms) | 24.850 ± 1.917 | 28.582 ± 2.044 | 60.052 ± 5.255 | 135.961 ± 12.514 |
| Extreme value in BS FB(min) | −52.013 ± 3.904 | −76.086 ± 6.657 | −117.523 ± 14.073 | −292.028 ± 21.391 |
| RMS value in BS FB(rms) | 27.452 ± 1.097 | 32.503 ± 2.859 | 48.496 ± 4.294 | 131.139 ± 10.510 |
| Value at toggle position FTP | 0.878 ± 4.076 | 18.186 ± 5.898 | 145.657 ± 11.635 | 266.727 ± 23.079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, W.-T.; Lee, W.-I.; Hsu, K.-L. Analysis and Experimental Verification of Mechanical Errors in Nine-Link Type Double-Toggle Mold/Die Clamping Mechanisms. Appl. Sci. 2021, 11, 832. https://doi.org/10.3390/app11020832
Chang W-T, Lee W-I, Hsu K-L. Analysis and Experimental Verification of Mechanical Errors in Nine-Link Type Double-Toggle Mold/Die Clamping Mechanisms. Applied Sciences. 2021; 11(2):832. https://doi.org/10.3390/app11020832
Chicago/Turabian StyleChang, Wen-Tung, Wei-I Lee, and Kuan-Lun Hsu. 2021. "Analysis and Experimental Verification of Mechanical Errors in Nine-Link Type Double-Toggle Mold/Die Clamping Mechanisms" Applied Sciences 11, no. 2: 832. https://doi.org/10.3390/app11020832
APA StyleChang, W.-T., Lee, W.-I., & Hsu, K.-L. (2021). Analysis and Experimental Verification of Mechanical Errors in Nine-Link Type Double-Toggle Mold/Die Clamping Mechanisms. Applied Sciences, 11(2), 832. https://doi.org/10.3390/app11020832





