Early Robust Design—Its Effect on Parameter and Tolerance Optimization
Abstract
:Featured Application
Abstract
1. Introduction
2. Related Work
2.1. Robust Design in Product Development
2.1.1. Early Robust Design
2.1.2. Late Robust Design
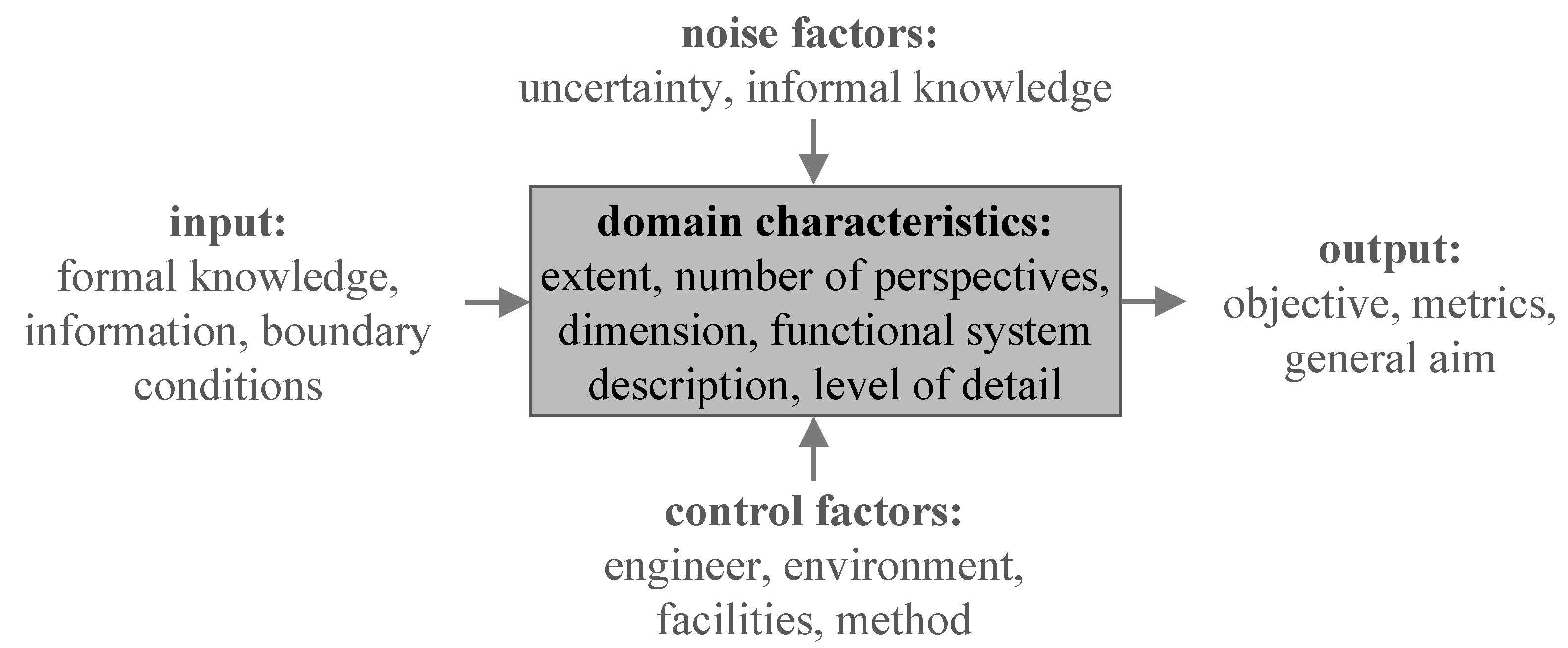
2.2. Interaction between Early and Late Robust Design
2.3. Discussion of the State-of-the-Art and Research Question
3. Linking Early Robust Design and Optimal Parameter and Tolerance Design
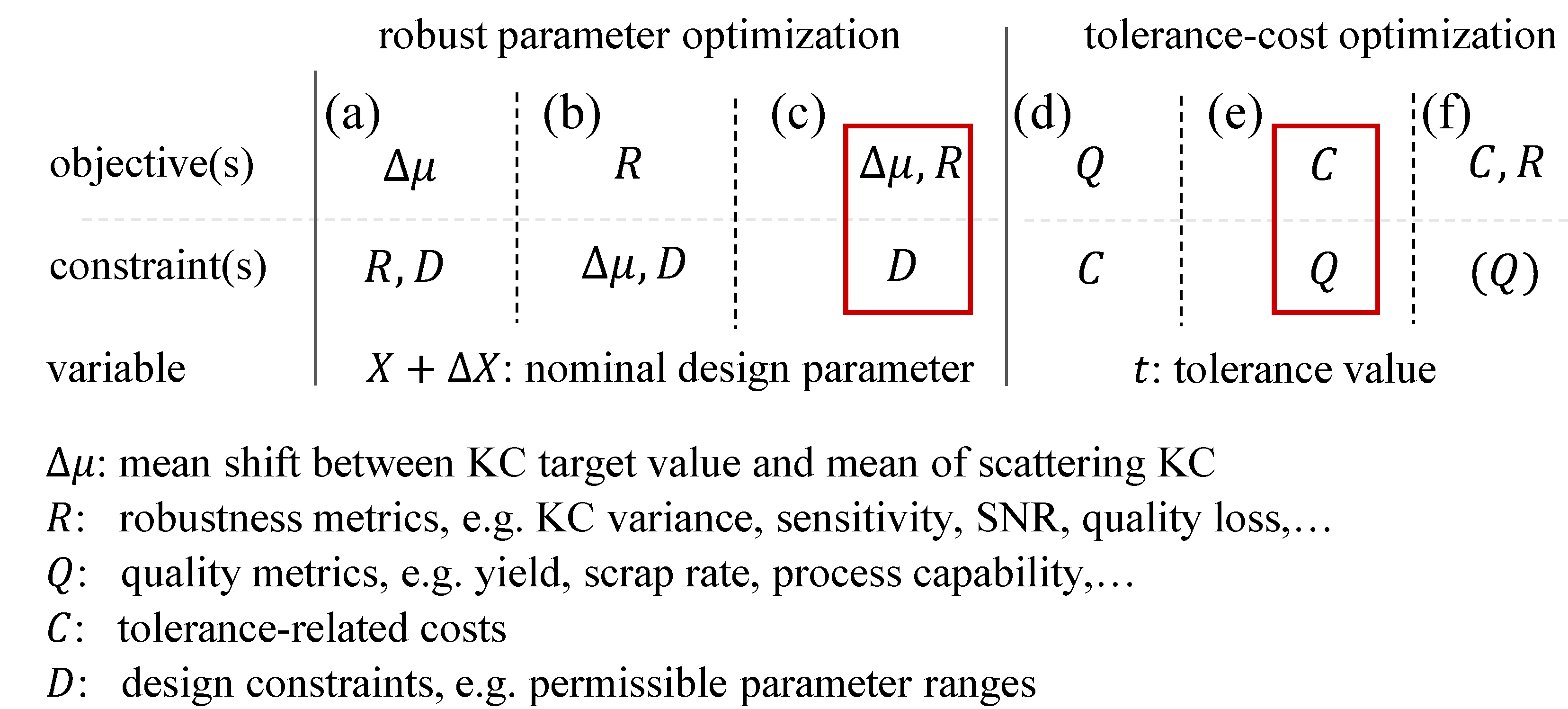
3.1. Comparison of Characteristic Aspects
3.2. Effects of Robust Concept Design on Parameter and Tolerance Optimization
4. Application
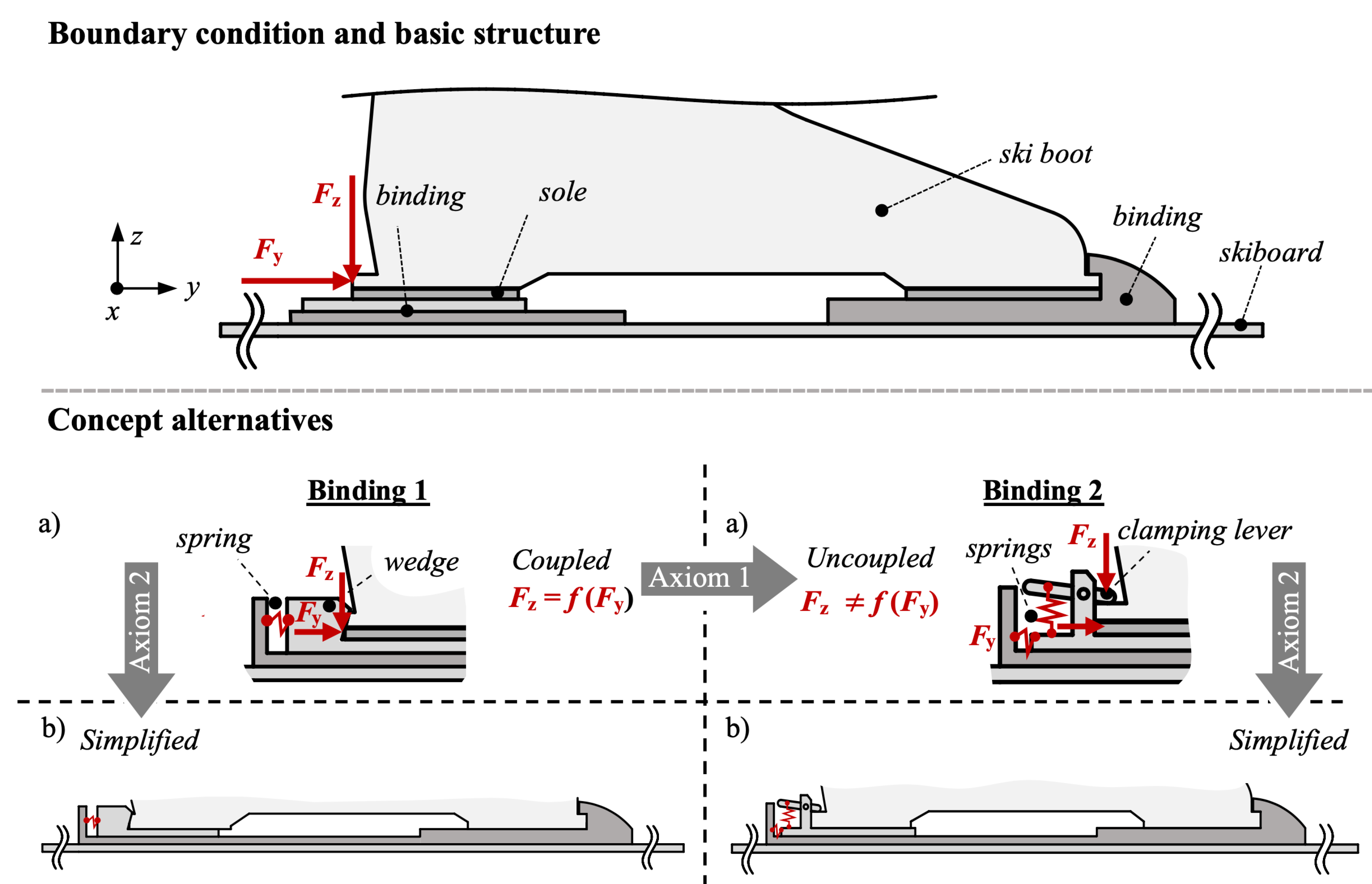
4.1. Presentation of the Case Study
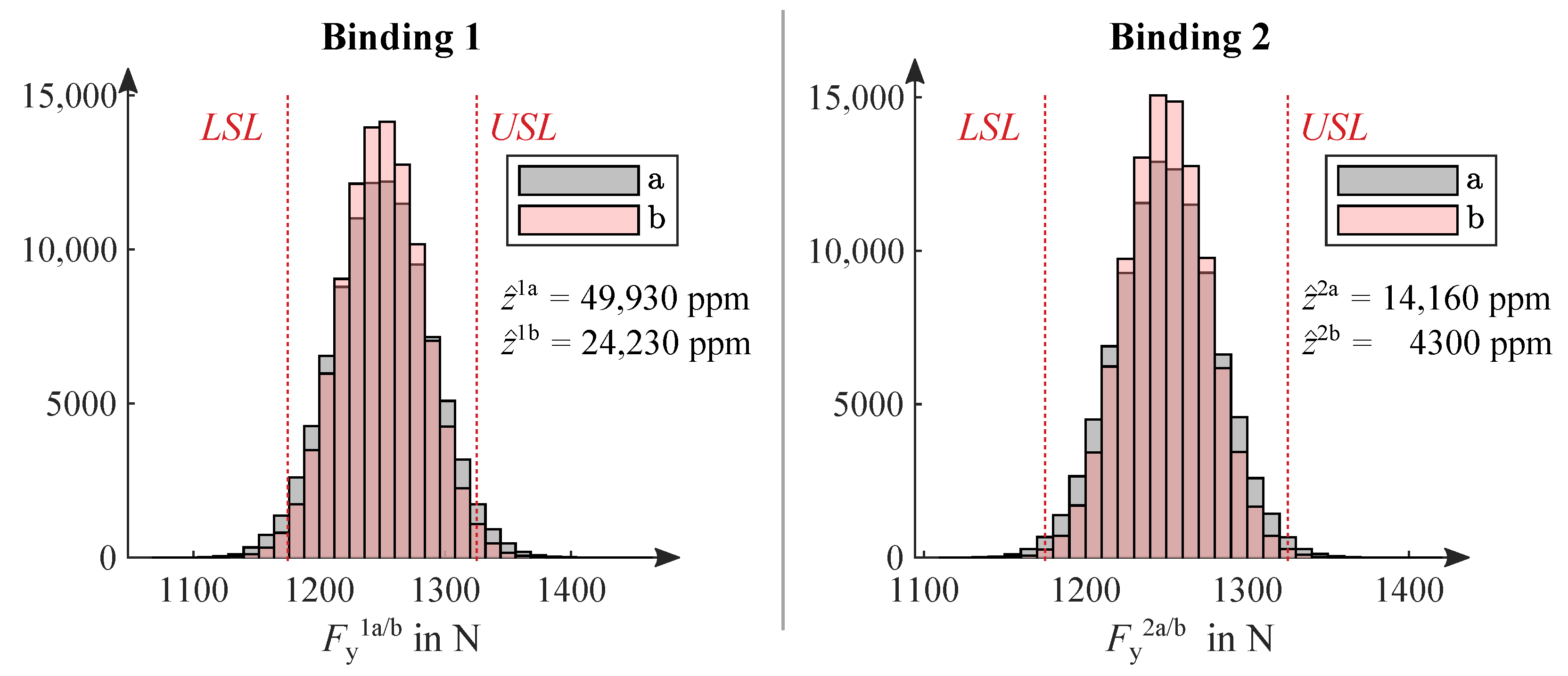
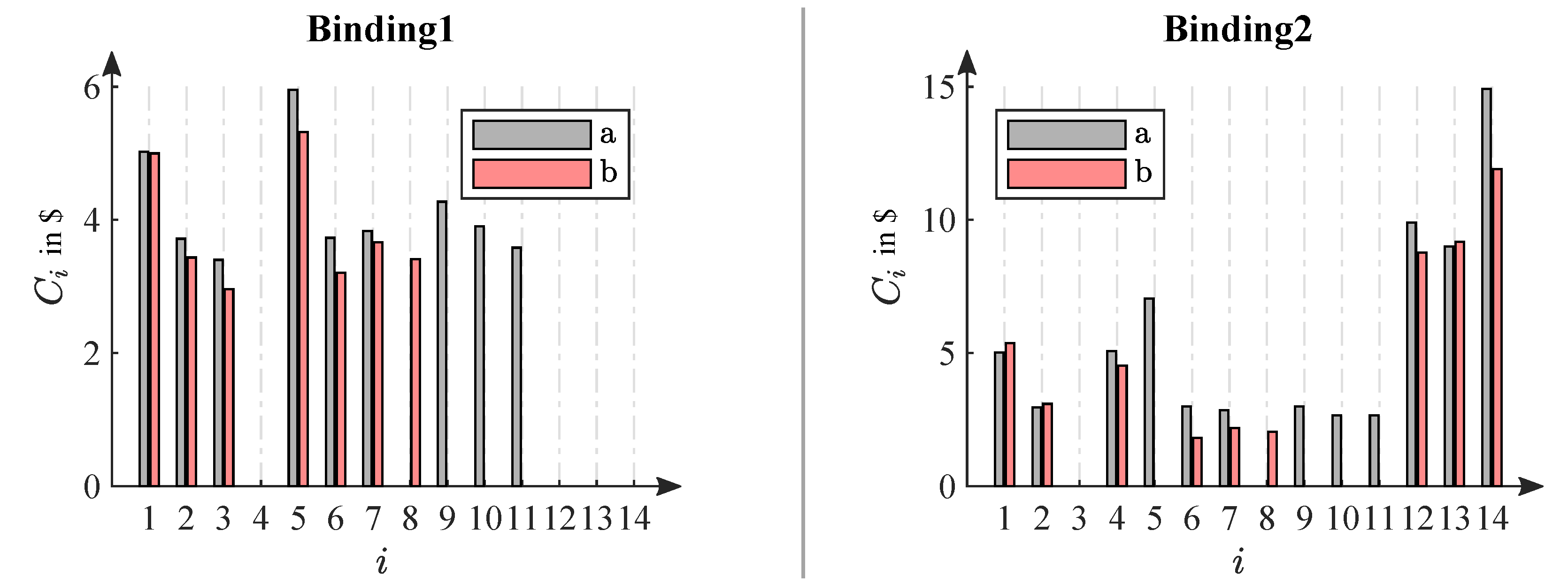
4.2. Parameter and Tolerance–Cost Optimization
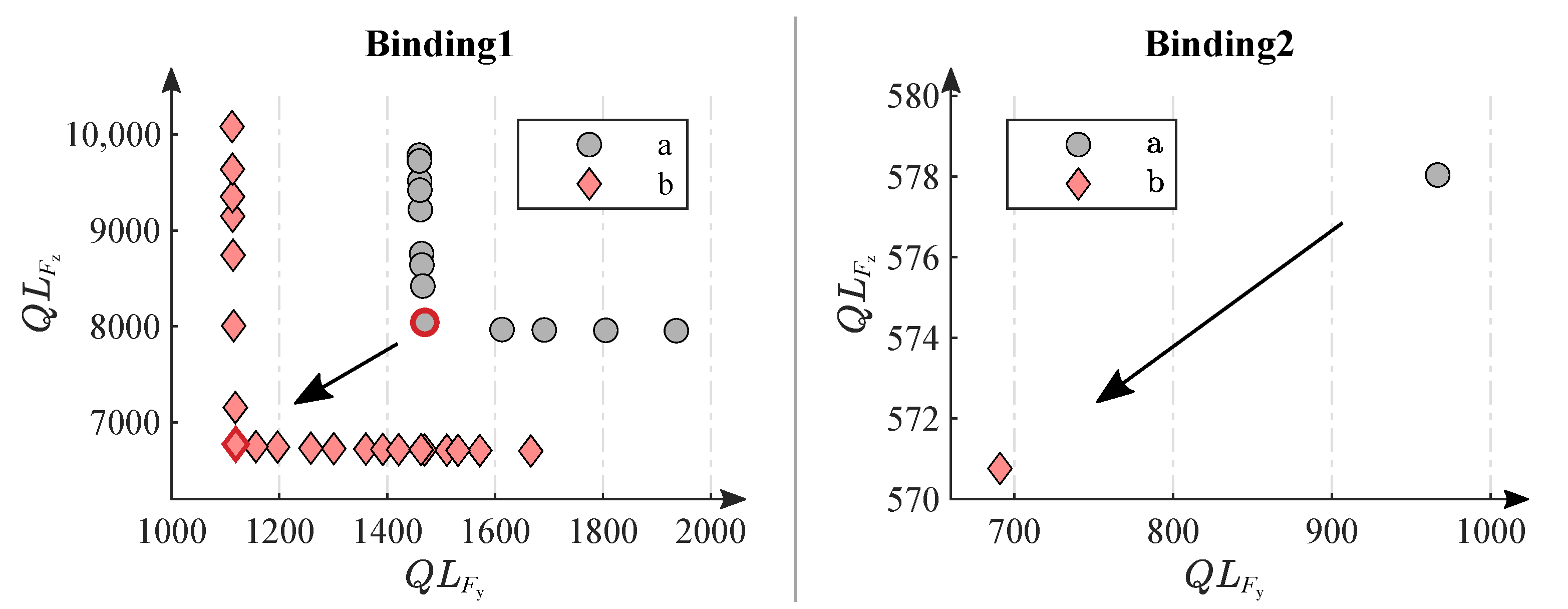
4.3. Discussion of the Results
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAD | Computer-aided design |
| DoE | Design of Experiments |
| KC | Key Characteristic |
| LSL | Lower Specification Limit |
| QL | Quality Loss |
| SNR | Signal-to-Noise Ratio |
| USL | Upper Specification Limit |
Appendix A. Detailed Description of the Case Study
Appendix A.1. Binding 1
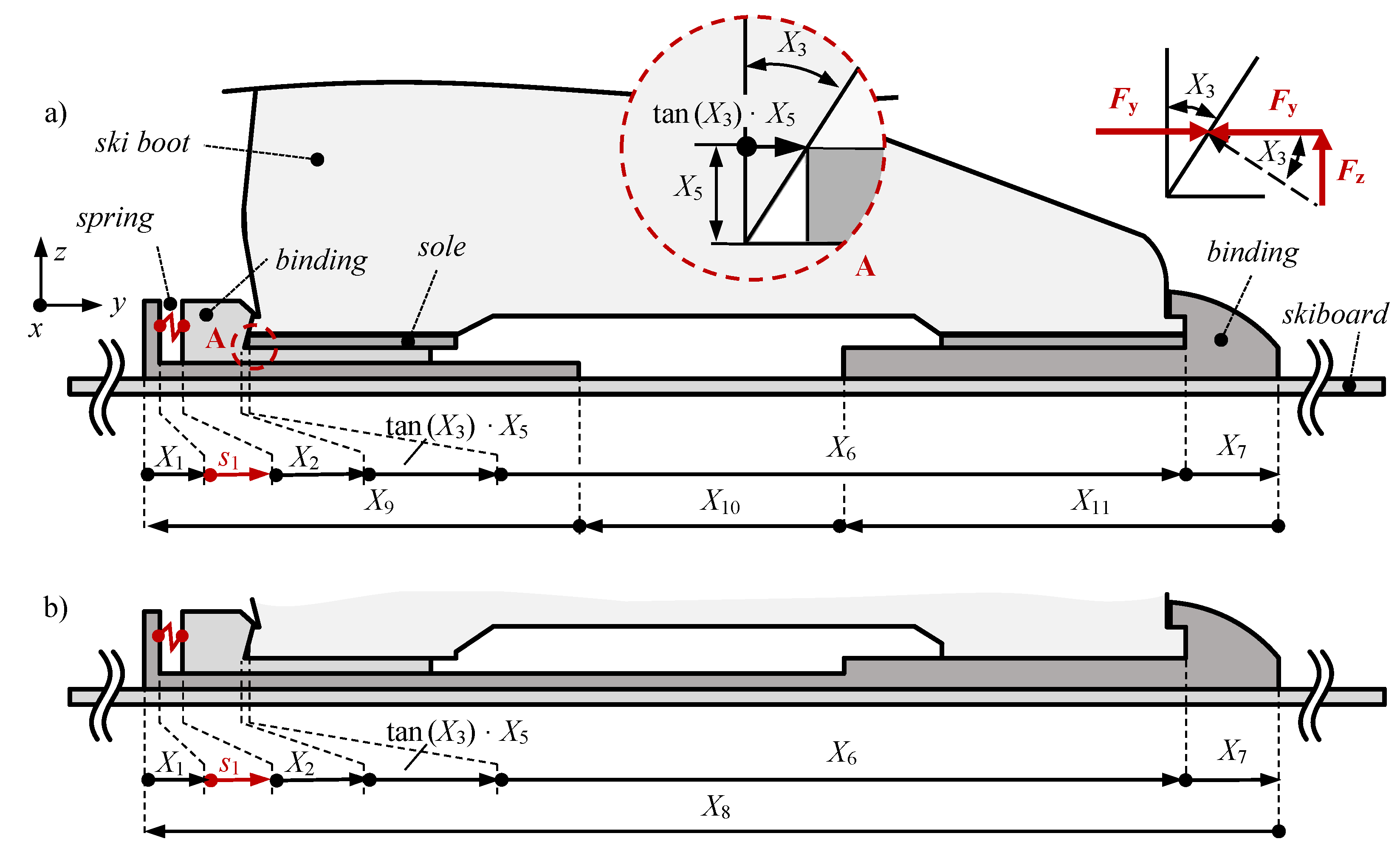
Appendix A.2. Binding 2
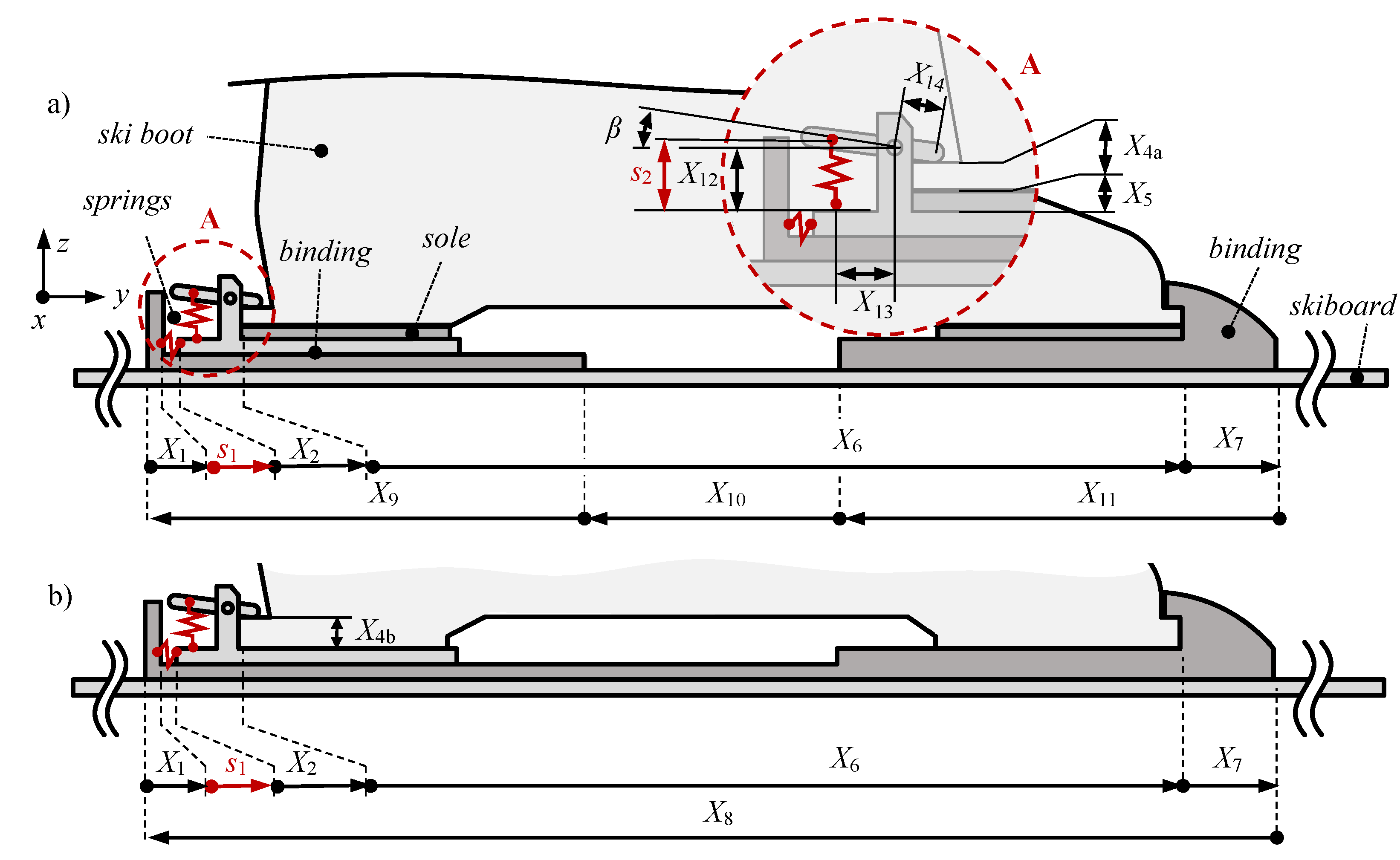
Appendix A.3. Specification
Appendix A.4. Design Parameter
| Parameter | Description | Nominal Value | Tolerance |
|---|---|---|---|
| binding heel length 1 | |||
| binding heel length 2 | |||
| wedge angle | |||
| ski boot heel size | |||
| ski boot heel size | |||
| ski boot sole size | |||
| ski boot length | |||
| binding length 3 | |||
| total binding length | |||
| binding heel length | |||
| distance between binding heel and toe | |||
| binding toe length | |||
| vertical position of pivot lever | |||
| horizontal position of spring 2 | |||
| clamping lever length | |||
| spring rate | |||
| spring rate |
- Nominal values: , ,
- Dimensional and angular tolerances , ,
References
- Pahl, G.; Beitz, W.; Blessing, L.; Feldhusen, J.; Grote, K.-H. Engineering Design: A Systematic Approach, 3rd ed.; Springer: London, UK, 2007. [Google Scholar] [CrossRef]
- Isaksson, O.; Eckert, C. Product Development 2040: Technologies are just as good as the designer’s ability to integrate them. Des. Soc. Rep. DS107 2020. [Google Scholar] [CrossRef]
- Srinivasan, R.S.; Wood, K.L.; McAdams, D.A. Functional tolerancing: A design for manufacturing methodology. Res. Eng. Des. 1996, 8, 99–115. [Google Scholar] [CrossRef]
- Bennett, G.; Gupta, L.C. Least-cost tolerances–I. Int. J. Prod. Res. 1970, 8, 65–74. [Google Scholar] [CrossRef]
- Taguchi, G.; Yano, H.; Chowdhury, S. Taguchi’s Quality Engineering Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 978-047-025-835-4. [Google Scholar]
- Ehrlenspiel, K.; Kiewert, A.; Lindemann, U. Cost-Efficient Design; Springer: Berlin, Germany, 2007. [Google Scholar] [CrossRef]
- Andersson, P. A semi-analytic approach to robust design in the conceptual design phase. Res. Eng. Des. 1996, 8, 229–239. [Google Scholar] [CrossRef]
- Ebro, M.; Howard, T.J.; Rasmussen, J.J. The foundation for robust design: Enabling robustness through kinematic design and design clarity. In DS 70 Proceedings of DESIGN 2012, Proceedings of the 12th International Design Conference, Dubrovnik, Croatia, 21–24 May 2012; The Design Society: Glasgow, UK, 2012; pp. 817–826. [Google Scholar]
- Matthiassen, B. Design for Robustness and Reliability: Improving the Quality Consciousness in Engineering Design. Ph.D. Thesis, Technical University of Denmark, Kgs. Lyngby, Denmark, 1997. [Google Scholar]
- Suh, N.P. The Principles of Design; Oxford University Press: New York, NY, USA, 1990; ISBN 978-019-504-345-7. [Google Scholar]
- Andersson, P. A Process Approach to Robust Design in Early Engineering Design Phases. Ph.D. Thesis, Department of Machine Design, Lund Institute of Technology, Lund, Sweden, 1996. [Google Scholar]
- Pahl, G.; Beitz, W. Konstruktionslehre: Methoden und Anwendung, 4th ed.; Springer: Berlin, Germany, 1997; ISBN 978-3-662-08161-7. [Google Scholar]
- Cross, N. Engineering Design Methods; John Wiley & Sons: Chichester, UK, 2007; ISBN 978-0-471-87250-4. [Google Scholar]
- Fowlkes, W.Y.; Creveling, C.M. Engineering Methods for Robust Product Design: Using Taguchi Methods in Technology and Product Development; Addison-Wesley: Reading, UK, 1995; ISBN 978-013-300-703-9. [Google Scholar]
- Thornton, A.C. Variation Risk Management: Focusing Quality Improvements in Product Development and Production; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 978-047-144-679-8. [Google Scholar]
- Howard, T.J.; Eifler, T.; Pedersen, S.N.; Göhler, S.M.; Boorla, S.M.; Christensen, M.E. The variation management framework (VMF): A unifying graphical representation of robust design. Qual. Eng. 2017, 29, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Göhler, S.M.; Howard, T.J. A Framework for the Application of Robust Design Methods and Tools. In Proceedings of the 1st International Symposium on Robust Design, København, Denmark, 14–15 August 2014; pp. 123–133. [Google Scholar] [CrossRef]
- Eifler, T.; Christensen, M.E.; Howard, T.J. A classification of the industrial relevance of robust design methods. In Proceedings of the 19th International Conference on Engineering Design, Seoul, Korea, 19–22 August 2013; pp. 427–436. [Google Scholar]
- Hasenkamp, T.; Arvidsson, M.; Gremyr, I. A review of practices for robust design methodology. J. Eng. Des. 2009, 20, 645–657. [Google Scholar] [CrossRef]
- Jugulum, R.; Frey, D.D. Toward a taxonomy of concept designs for improved robustness. J. Eng. Des. 2007, 18, 139–156. [Google Scholar] [CrossRef]
- Ebro, M.; Howard, T.J. Robust design principles for reducing variation in functional performance. J. Eng. Des. 2016, 27, 75–92. [Google Scholar] [CrossRef] [Green Version]
- Johansson, P.; Chakhunashvili, A.; Barone, S.; Bergman, B. Variation Mode and Effect Analysis: A Practical Tool for Quality Improvement. Qual. Reliab. Eng. Int. 2006, 22, 865–876. [Google Scholar] [CrossRef]
- Goetz, S.; Schleich, B.; Wartzack, S. A new approach to first tolerance evaluations in the conceptual design stage based on tolerance graphs. Procedia CIRP 2018, 75, 167–172. [Google Scholar] [CrossRef]
- Goetz, S.; Hartung, J.; Schleich, B.; Wartzack, S. Robustness Evaluation of Product Concepts based on Function Structures. Proc. Des. Soc. Int. Conf. Eng. Des. 2019, 1, 3521–3530. [Google Scholar] [CrossRef] [Green Version]
- Park, G.-J.; Lee, T.-H.; Lee, K.H.; Hwang, K.-H. Robust design: An overview. AIAA J. 2006, 44, 181–191. [Google Scholar] [CrossRef]
- Göhler, S.M.; Howard, T.J. The Contradiction Index (CI): A New Metric Combining System Complexity and Robustness for Early Design Stages. In Proceedings of the ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 7: 27th International Conference on Design Theory and Methodology, Boston, MA, USA, 2–5 August 2015; p. V007T06A023. [Google Scholar] [CrossRef]
- Eifler, T.; Howard, T.J. Exact Constraint Design and its Potential for Robust Embodiment. Procedia CIRP 2017, 60, 302–307. [Google Scholar] [CrossRef] [Green Version]
- Andersson, P. On Robust Design in the Conceptual Design Phase: A Qualitative Approach. J. Eng. Des. 1997, 8, 75–89. [Google Scholar] [CrossRef]
- Lindkvist, L.; Söderberg, R. Computer-aided tolerance chain and stability analysis. J. Eng. Des. 2003, 14, 17–39. [Google Scholar] [CrossRef]
- Tsui, K.-L. An Overview of Taguchi Method and Newly Developed Statistical Methods for Robust Design. IIE Trans. 1992, 24, 44–57. [Google Scholar] [CrossRef]
- Ford, R.B. Process for the Conceptual Design of Robust Mechanical Systems: Going Beyond Parameter Design to Achieve World-Class Quality. Ph.D. Thesis, Stanford University, Standford, CA, USA, 1996. [Google Scholar]
- Göhler, S.M.; Husung, S.; Howard, T.J. The Translation between Functional Requirements and Design Parameters for Robust Design. Procedia CIRP 2016, 43, 106–111. [Google Scholar] [CrossRef] [Green Version]
- Thornton, A.C. Variation Risk Management Using Modeling and Simulation. J. Mech. Des. 1999, 121, 297–304. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Wartzack, S. From tolerance allocation to tolerance-cost optimization: A comprehensive literature review. Int. J. Adv. Manuf. Technol. 2020, 107, 4859–4912. [Google Scholar] [CrossRef]
- Creveling, C.M. Tolerance Design: A Handbook for Developing Optimal Specifications, 1st ed.; Addison-Wesley: Berkeley, CA, USA, 1997; ISBN 978-020-163-473-0. [Google Scholar]
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; ISBN 978-013-745-167-8. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 978-047-005-997-5. [Google Scholar]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Göhler, S.M.; Eifler, T.; Howard, T.J. Robustness Metrics: Consolidating the Multiple Approaches to Quantify Robustness. J. Mech. Des. 2016, 138, 111407. [Google Scholar] [CrossRef] [Green Version]
- Eifler, T.; Johannes, M.; Roland, E.; Marion, W.; Hermann, K.; Herbert, B.; Bohn, A. Evaluation of Solution Variants in Conceptual Design by Means of Adequate Sensitivity Indices. In Proceedings of the DS 68-9: 18th International Conference on Engineering Design (ICED 11), Copenhagen, Denmark, 15–19 August 2011; pp. 314–323. [Google Scholar]
- Ostwald, P.F.; Huang, J. A Method for Optimal Tolerance Selection. J. Eng. Ind. 1977, 99, 558–565. [Google Scholar] [CrossRef]
- Patel, A.M. Computer-Aided Assignment of Manufacturing Tolerances. In Proceedings of the DAC ’80: 17th Design Automation Conference, Minneapolis, MN, USA, 23–25 June 1980; pp. 129–1330. [Google Scholar] [CrossRef]
- Dong, Z.; Hu, W.; Xue, D. New Production Cost-Tolerance Models for Tolerance Synthesis. J. Eng. Ind. 1994, 116, 199–206. [Google Scholar] [CrossRef]
- Iannuzzi, M.P.; Sandgren, E. Tolerance Optimization Using Genetic Algorithms: Benchmarking with Manual Analysis. In Computer-Aided Tolerancing; Kimura, F., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 219–234. [Google Scholar] [CrossRef]
- Haq, A.N.; Sivakumar, K.; Saravanan, R.; Muthiah, V. Tolerance design optimization of machine elements using genetic algorithm. Int. J. Adv. Manuf. Technol. 2005, 25, 385–391. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Panek, D.; Orosz, T.; Karban, P. Artap: Robust Design Optimization Framework for Engineering Applications. In Proceedings of the Third International Conference on Intelligent Computing in Data Sciences, Marrakech, Morocco, 28–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kunath, S. Master of Design—CAE-based Robust Design Optimization with Optislang. RDO-J. 2014, 1, 2–5. [Google Scholar]
- Lee, K.-H.; Park, G.-J. Robust Optimization in Discrete Design Space for Constrained Problems. AIAA J. 2002, 40, 774–780. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-111-945-481-6. [Google Scholar]
- Hong, Y.S.; Chang, T.C. A comprehensive review of tolerancing research. Int. J. Prod. Res. 2002, 40, 2425–2459. [Google Scholar] [CrossRef]
- Singh, P.K.; Jain, P.K.; Jain, S.C. Important issues in tolerance design of mechanical assemblies. Part 2: Tolerance synthesis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 1249–1287. [Google Scholar] [CrossRef]
- Hu, J.; Peng, Y. Tolerance modelling and robust design for concurrent engineering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 455–465. [Google Scholar] [CrossRef]
- Han, M.; Yong Tan, M.H. Integrated parameter and tolerance design with computer experiments. IIE Trans. 2016, 48, 1004–1015. [Google Scholar] [CrossRef]
- Hazrati-Marangaloo, H.; Shahriari, H. A Novel Approach to Simultaneous Robust Design of Product Parameters and Tolerances Using Quality Loss and Multivariate ANOVA Concepts. Qual. Reliab. Eng. Int. 2017, 33, 71–85. [Google Scholar] [CrossRef]
- Engelhardt, F. Improving Systems by Combining Axiomatic Design, Quality Control Tools and Designed Experiments. Res. Eng. Des. 2000, 12, 204–219. [Google Scholar] [CrossRef]
- Söderberg, R.; Johannesson, H. Tolerance Chain Detection by Geometrical Constraint Based Coupling Analysis. J. Eng. Des. 1999, 10, 5–24. [Google Scholar] [CrossRef]
- Campatelli, G. Tolerance synthesis using axiomatic design. In Proceedings of the Sixth International Conference on Axiomatic Design, Daedeok Innopolis, Daejeon, Korea, 30–31 March 2011; pp. 152–157, ISBN 978-898-969-330-7. [Google Scholar]
- Fradinho, J.; Mourão, A.; Gabriel-Santos, A.; Gonçalves-Coelho, A. An Axiomatic Design Interpretation for the Synthesis of Dimensional Tolerances. Procedia CIRP 2016, 53, 89–94. [Google Scholar] [CrossRef] [Green Version]
- Hwang, K.H.; Park, G.J. Development of a Robust Design Process Using a New Robustness Index. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Volume 2: 31st Design Automation Conference, Parts A and B, Long Beach, CA, USA, 24–28 September 2005; pp. 231–241. [Google Scholar] [CrossRef]
- Henriques, D.; Requeijo, J.G.; Gonçalves-Coelho, A.; Mourão, A. Adaptive tolerance allocation to adjust the sigma level through minimization of the information content. In Proceedings of the 8th International Conference on Axiomatic Design, Lisbon, Portugal, 24–26 September 2014; pp. 87–92, ISBN 978-098-946-582-3. [Google Scholar]
- Sigurdarson, N.S.; Eifler, T.; Ebro, M. Functional Trade-offs in the Mechanical Design of Integrated Products-Impact on Robustness and Optimisability. Proc. Des. Soc. Int. Conf. Eng. Des. 2019, 1, 3491–3500. [Google Scholar] [CrossRef] [Green Version]
- Thornton, A.C.; Donnelly, S.; Ertan, B. More than Just Robust Design: Why Product Development Organizations Still Contend with Variation and its Impact on Quality. Res. Eng. Des. 2000, 12, 127–143. [Google Scholar] [CrossRef]
- Ishikawa, K. Introduction to Quality Control, 1st ed.; Chapman-Hall: London, UK, 1989; ISBN 978-94-011-7690-3. [Google Scholar]
- Liliana, L. A new model of Ishikawa diagram for quality assessment. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 012099. [Google Scholar] [CrossRef] [Green Version]
- Reich, Y.; Subrahmanian, E. Designing PSI: An Introduction to the PSI Framework. In Proceedings of the DS 80-11, 20th International Conference on Engineering Design (ICED 15), Vol 2: Design Theory and Research Methodology, Design Processes, Design Theory and Research Methodology, Milan, Italy, 27–30 July 2015; pp. 137–146. [Google Scholar]
- Morse, E.; Dantan, J.-Y.; Anwer, N.; Söderberg, R.; Moroni, G.; Qureshi, A.; Jiang, X.; Mathieu, L. Tolerancing: Managing uncertainty from conceptual design to final product. CIRP Ann. 2018, 67, 695–717. [Google Scholar] [CrossRef] [Green Version]
- Frey, D.; Palladino, J.; Sullivan, J.; Atherton, M. Part count and design of robust systems. Syst. Eng. 2007, 10, 203–221. [Google Scholar] [CrossRef]
- Heling, B.; Schleich, B.; Wartzack, S. Robust-Design-Optimization of mechanisms based on kinematic requirements considering uncertainties. Procedia CIRP 2018, 75, 27–32. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Heling, B.; Aschenbrenner, A.; Wartzack, S. Comparison of different methods for scrap rate estimation in sampling-based tolerance-cost-optimization. Procedia CIRP 2018, 75, 51–56. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Wartzack, S. Sampling-based Tolerance-Cost Optimization of Systems with Interrelated Key Characteristics. Procedia CIRP 2020, 91, 87–92. [Google Scholar] [CrossRef]
- Posch, M.; Ruedl, G.; Eberle, R.; Burtscher, M. Self-Release of Ski Bindings: A Sex Comparison. In Snow Sports Trauma and Safety; Scher, I.S., Greenwald, R.M., Petrone, N., Eds.; Springer: Cham, Switzerland, 2017; pp. 109–117. [Google Scholar] [CrossRef] [Green Version]
- DIN ISO 11088:2018. Alpine Ski/Binding/Boot (S-B-B) System–Assembly, Adjustment and Inspection; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- DIN ISO 8061:2019. Alpine Ski-Bindings–Selection of Release Torques Values; ISO: Geneva, Switzerland, 2019. [Google Scholar]
- Göhler, S.M.; Frey, D.D.; Howard, T.J. A model-based approach to associate complexity and robustness in engineering systems. Res. Eng. Des. 2017, 28, 223–234. [Google Scholar] [CrossRef] [Green Version]
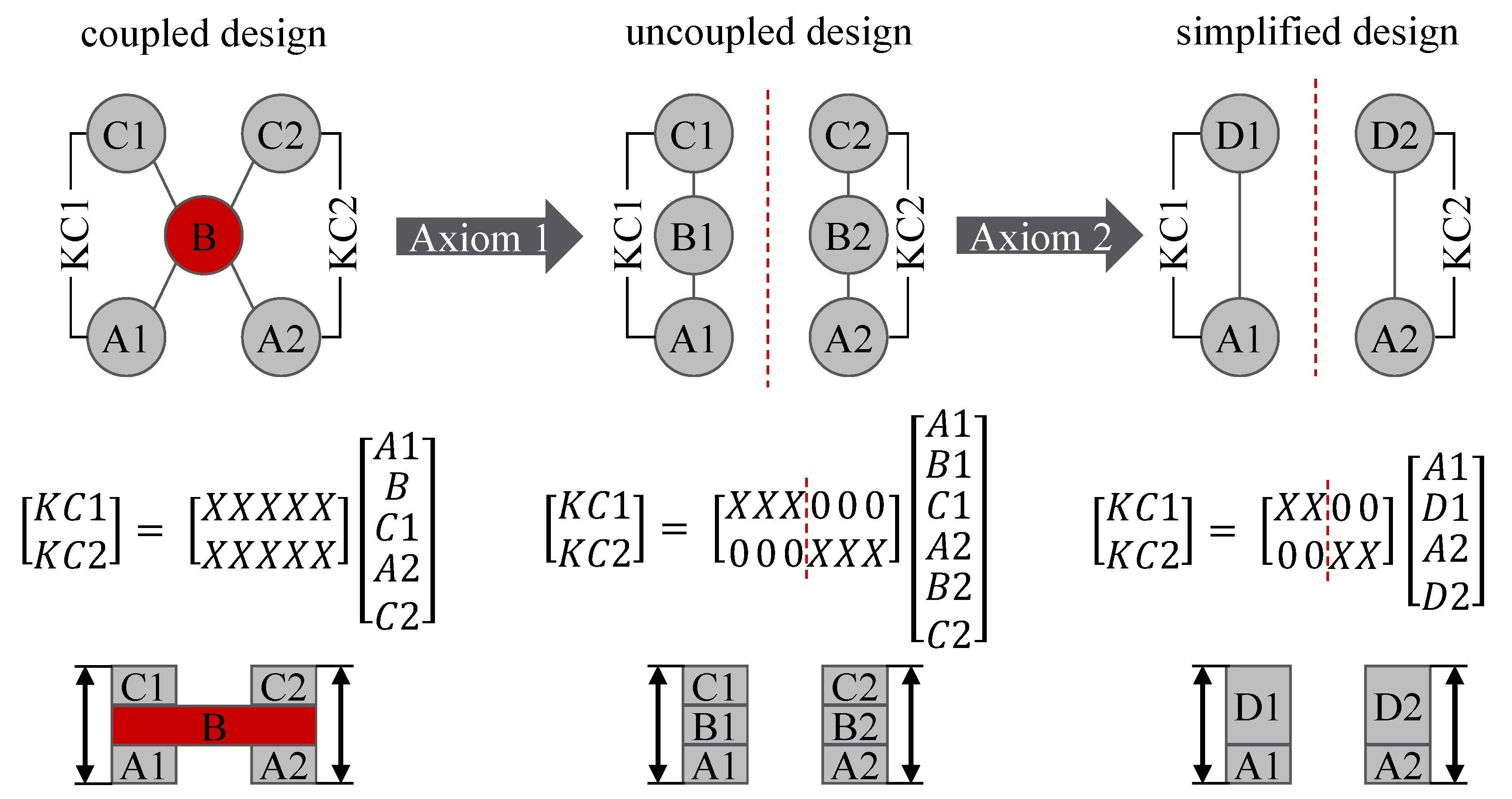
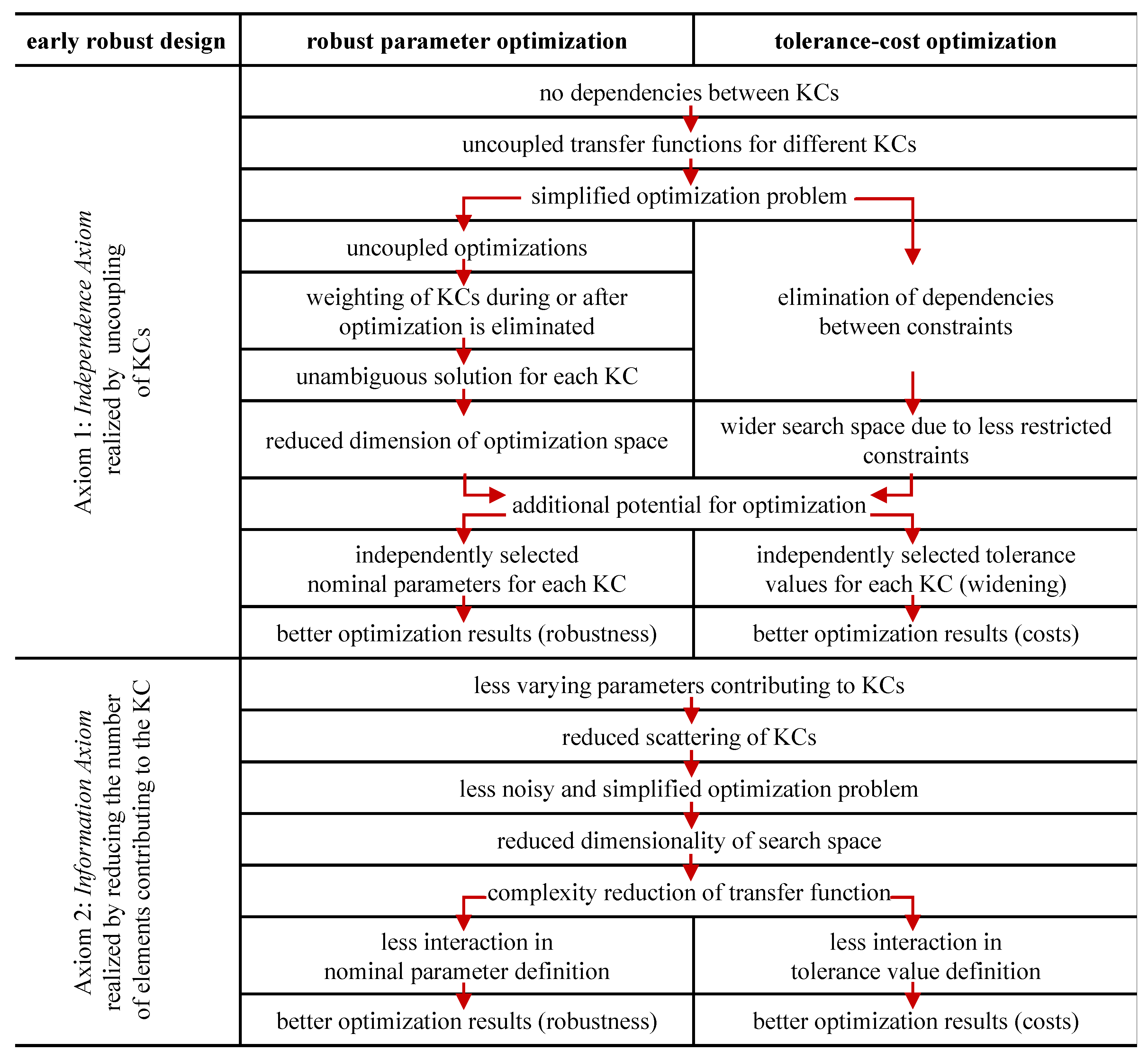
| Suh’s Axiom | Robust Design Principle | Classification |
|---|---|---|
| Axiom 1 | prevention of overconstrained systems by proper definition of constraints and degree of freedom [27] | kinematic design |
| unambiguous design of interfaces, e.g., by sufficient clearance to avoid unintended contact [8] | kinematic design | |
| division of tasks [28] | complexity control | |
| decoupling and uncoupling [29] | complexity control | |
| Axiom 2 | shortening of force-transmission paths [28] | kinematic design |
| minimizing the number of design parameters [21] | complexity control | |
| shielding from the cause of variation (e.g., heat) [21] | complexity control |
| Aspect | Early Robust Design | Robust Parameter Optimization | Tolerance-Cost Optimization |
|---|---|---|---|
| domain characteristics | |||
| extent | entire system | specific aspects | specific aspects |
| number of perspectives | high (design, parameter, variation) | medium (parameter, variation) | medium (variation, manufacturing) |
| dimension | primarily 2D | 2D/3D | 2D/3D |
| functional system description | qualitative | quant. transfer function (implicit/explicit) | quant. transfer function (implicit/explicit), quant. tolerance-cost function, (quality loss function) |
| level of detail | low | medium | high |
| control factors | |||
| engineer | design engineer | product simulation engineer, design engineer | tolerance engineer, design engineer |
| environment / department | design, concept development | design | tolerance management |
| facilities | paper, visualization tools | computer-aided tools | computer-aided tools |
| specific method | n.a. (workflow) | optimization | optimization |
| noise factors | |||
| uncertainty | epistemic uncertainty in designer decision | reduced ambiguity, aleatory uncertainty | primarily aleatory uncertainty |
| informal knowledge | epistemic design knowledge | n.a. | n.a. |
| input | |||
| formal knowledge availability | low | high | high |
| information—data | requirements, initial concept and product structure | embodiment design | nominal design, manufacturing information |
| information—documents | sketch, graph | product model, (CAD/drawing) | product model, (CAD/drawing) |
| boundary conditions | requirements | design constraints, parameter ranges, noise | quality requirements, tolerance ranges, KC |
| output | |||
| quantitative objective | n.a. | KC (mean shift and robustness) | tolerance-related costs |
| objective metrics | n.a. | robustness metrics | tangible and intangible costs |
| general aim | robust concept design | robust nominal design parameters | cost-optimal tolerance values |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goetz, S.; Roth, M.; Schleich, B. Early Robust Design—Its Effect on Parameter and Tolerance Optimization. Appl. Sci. 2021, 11, 9407. https://doi.org/10.3390/app11209407
Goetz S, Roth M, Schleich B. Early Robust Design—Its Effect on Parameter and Tolerance Optimization. Applied Sciences. 2021; 11(20):9407. https://doi.org/10.3390/app11209407
Chicago/Turabian StyleGoetz, Stefan, Martin Roth, and Benjamin Schleich. 2021. "Early Robust Design—Its Effect on Parameter and Tolerance Optimization" Applied Sciences 11, no. 20: 9407. https://doi.org/10.3390/app11209407
APA StyleGoetz, S., Roth, M., & Schleich, B. (2021). Early Robust Design—Its Effect on Parameter and Tolerance Optimization. Applied Sciences, 11(20), 9407. https://doi.org/10.3390/app11209407






