A Study on Sputtering of Copper Seed Layer for Interconnect Metallization via Molecular Dynamics Simulation
Abstract
:1. Introduction
2. Simulation Method and Model
2.1. Molecular Dynamics
2.2. Interatomic Potential
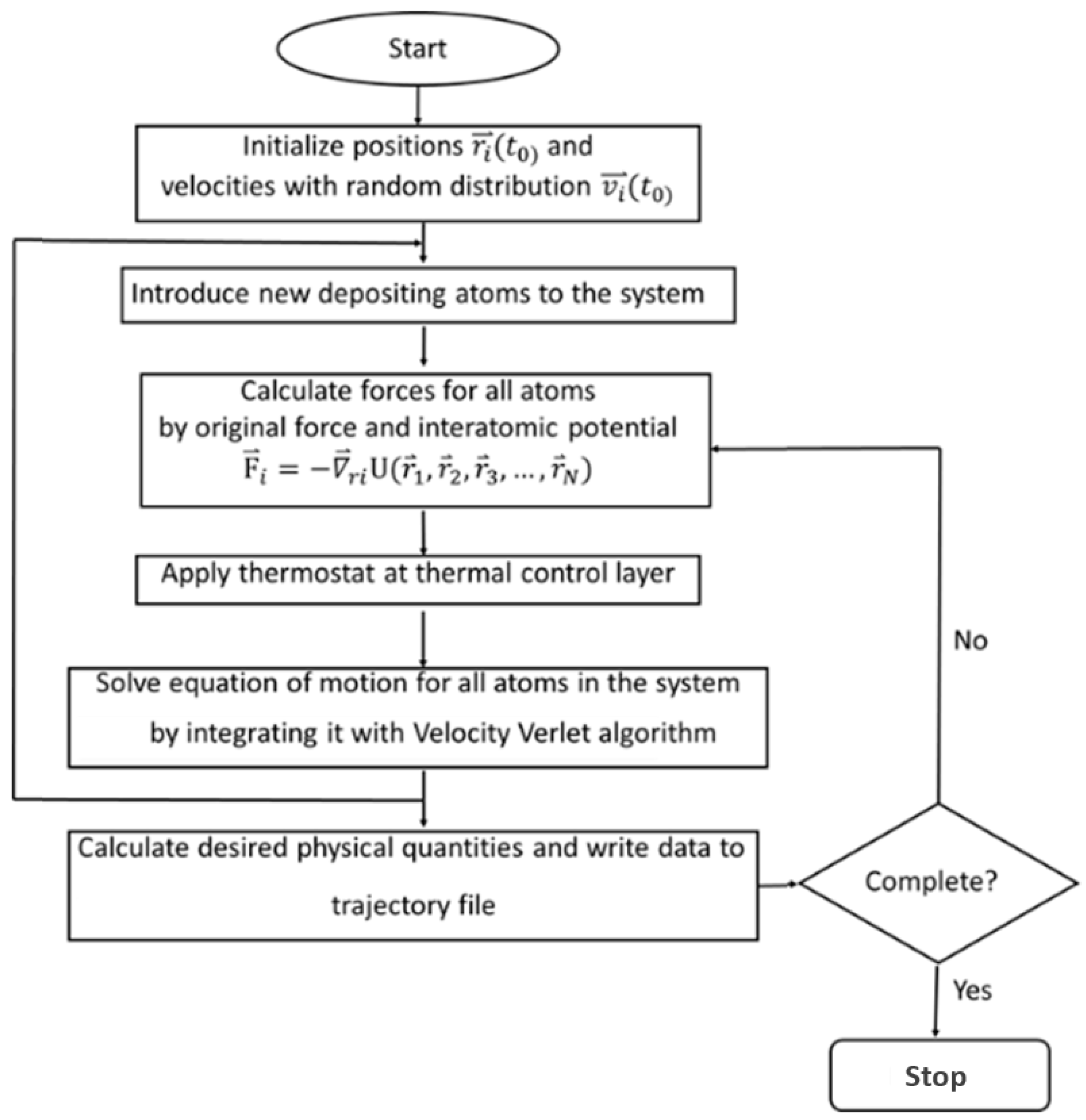
2.3. Computation Method
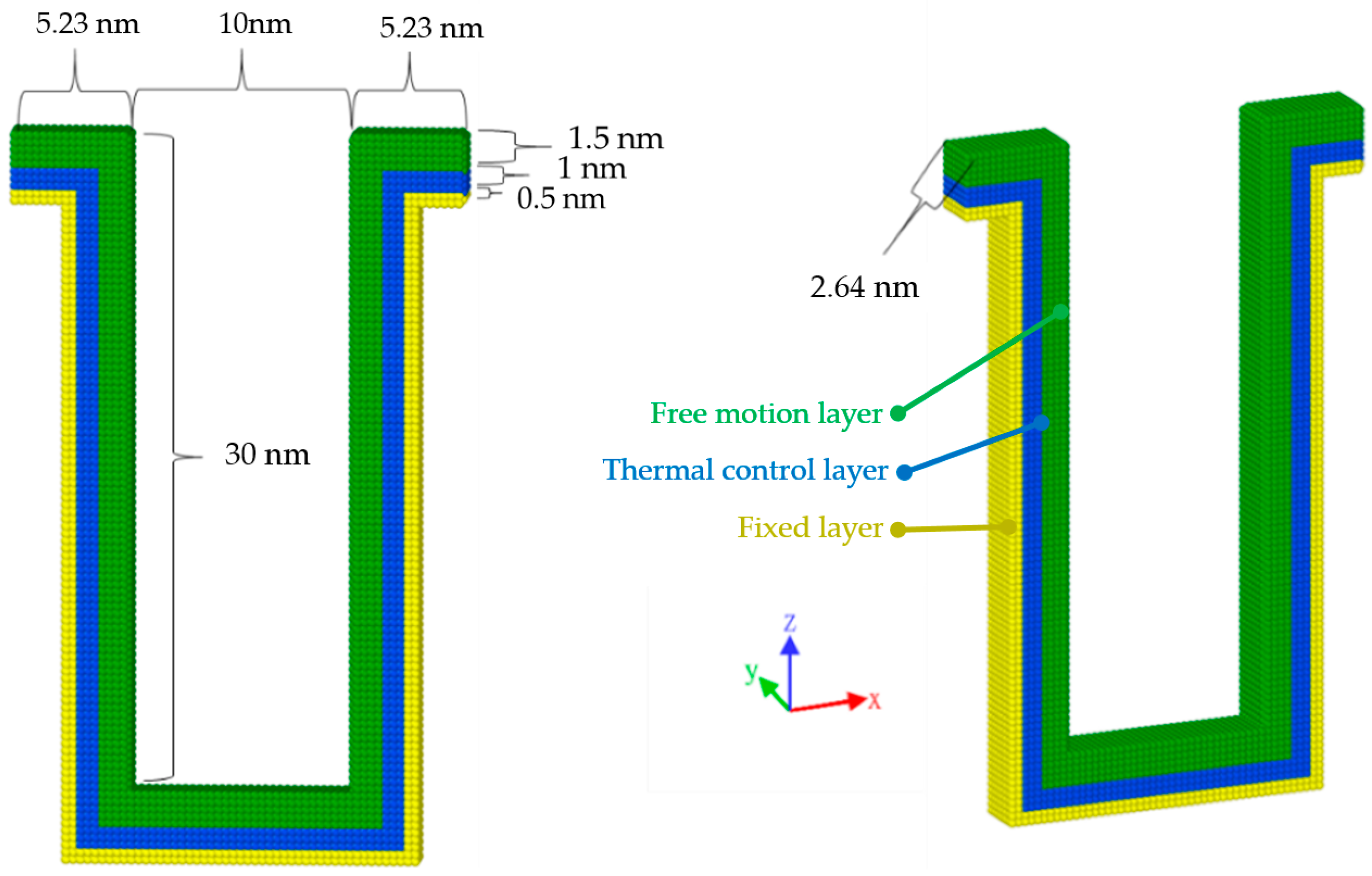
2.4. Substrate Model
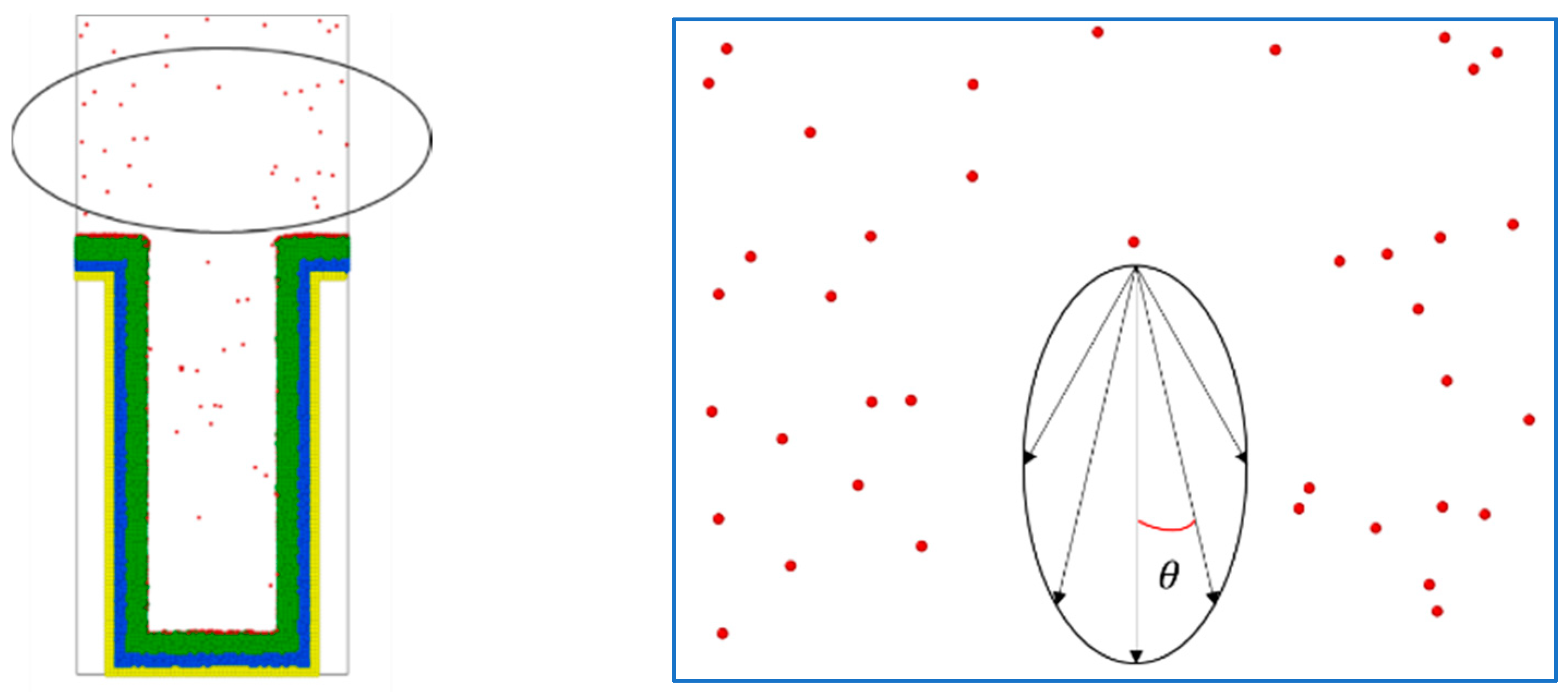
2.5. Deposition Model
3. Results and Discussion
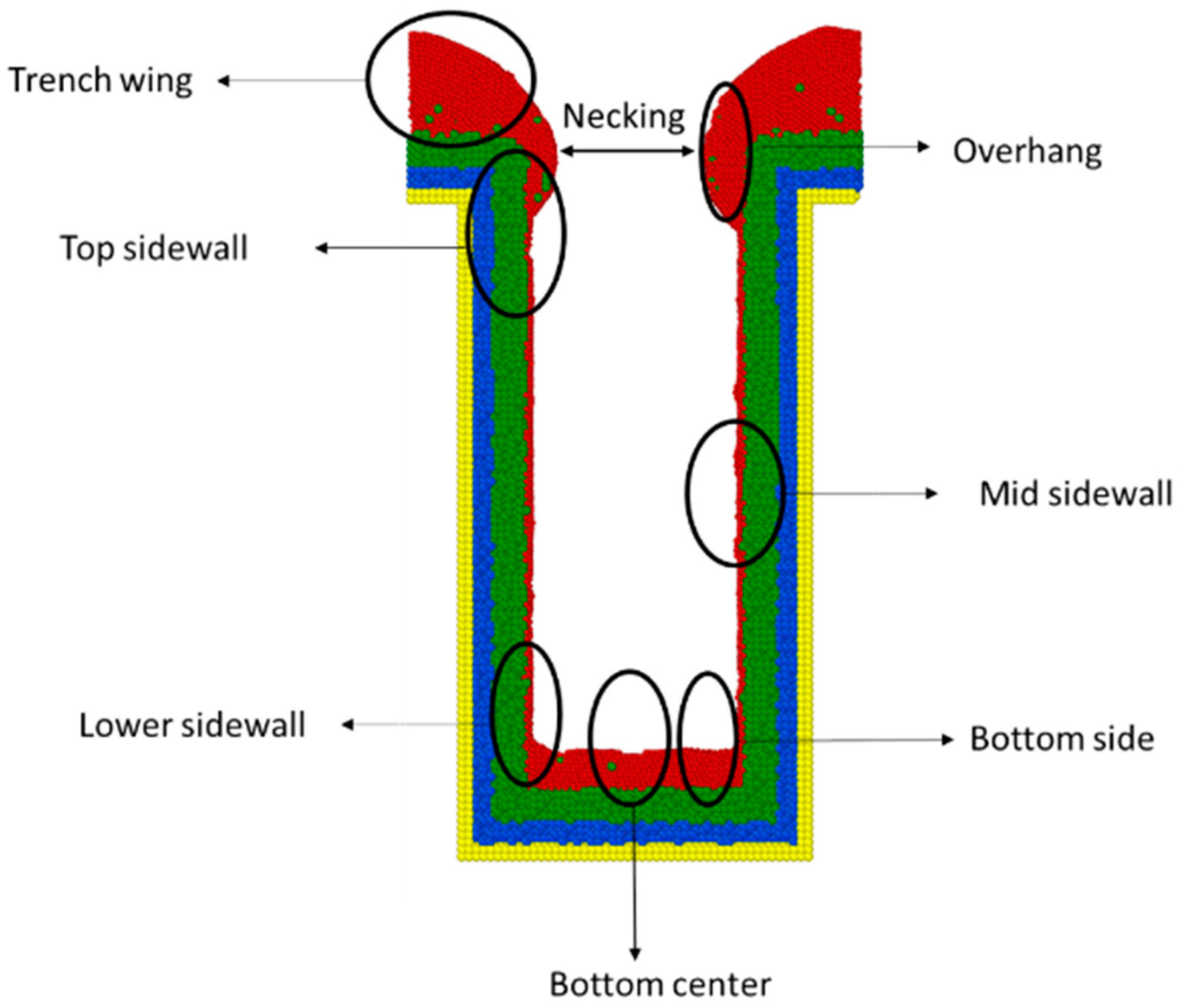
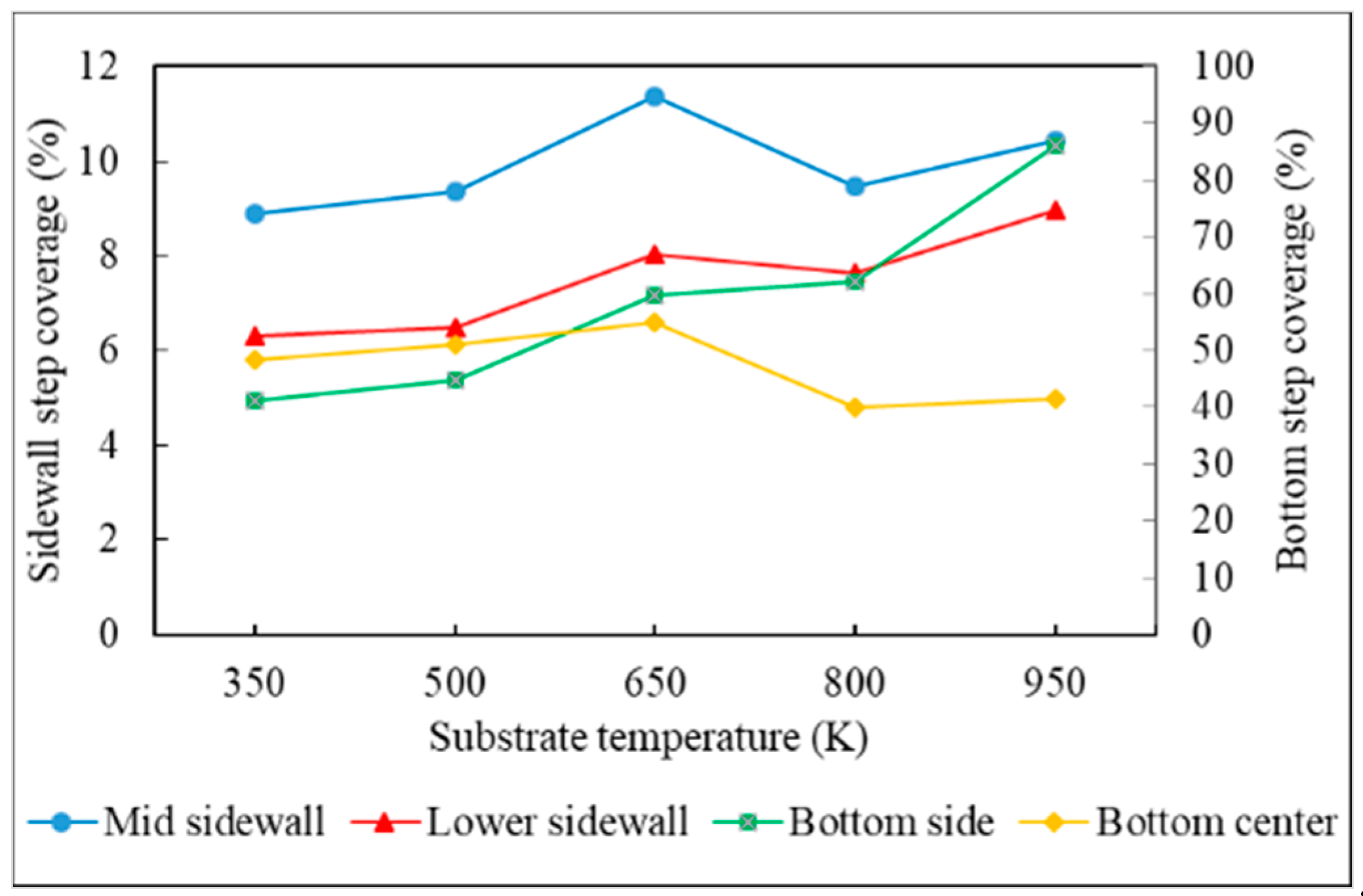
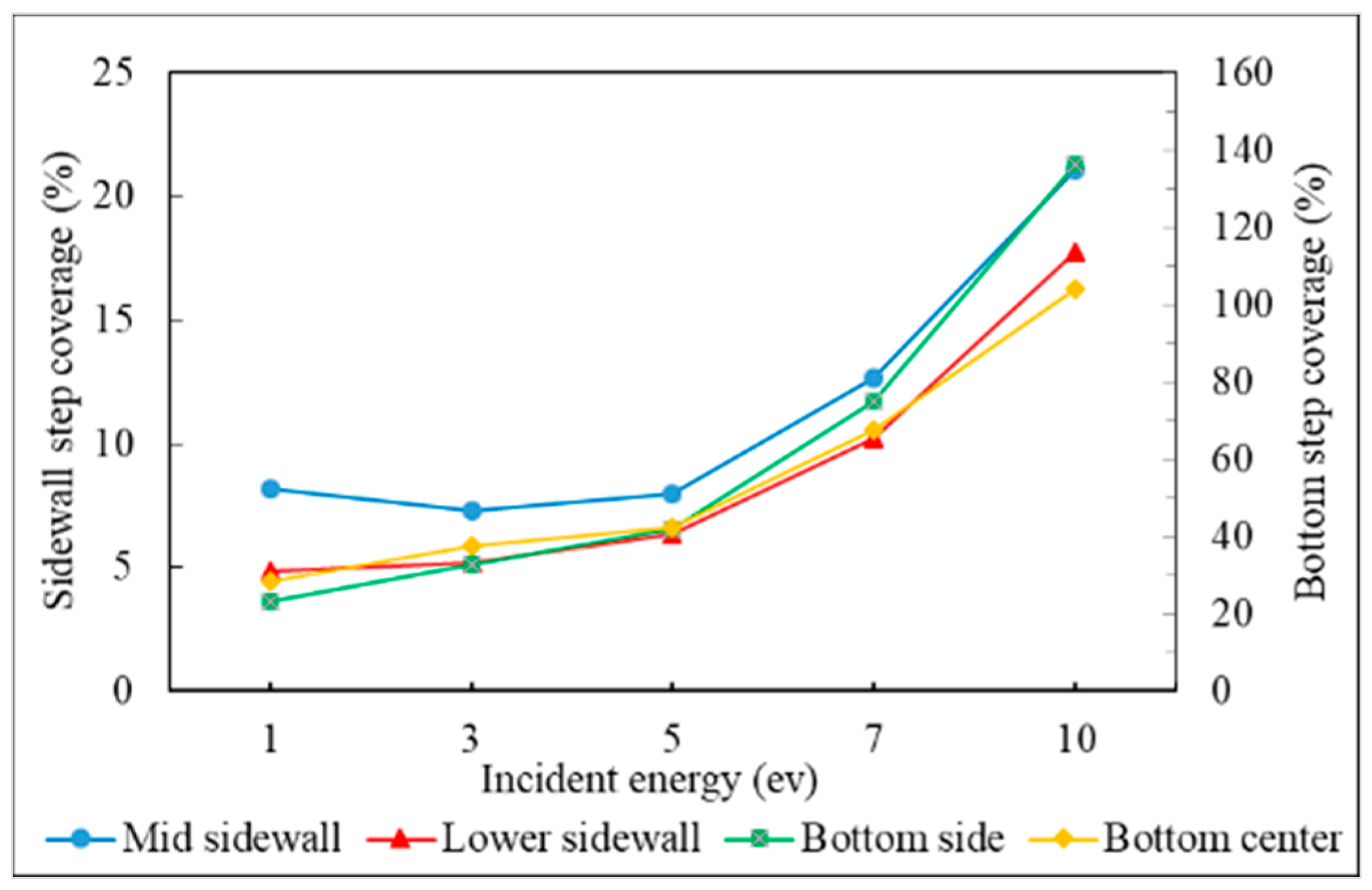
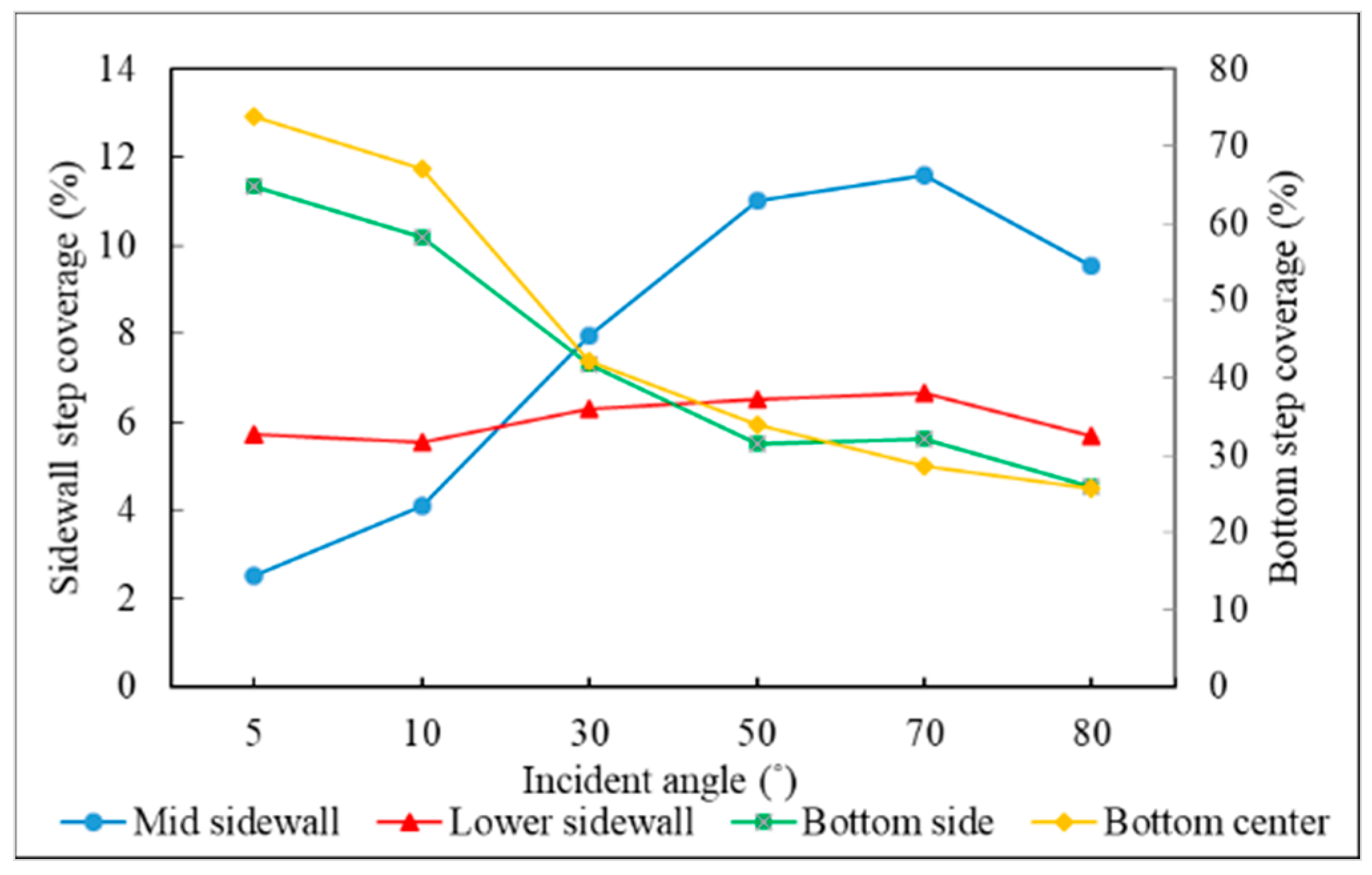
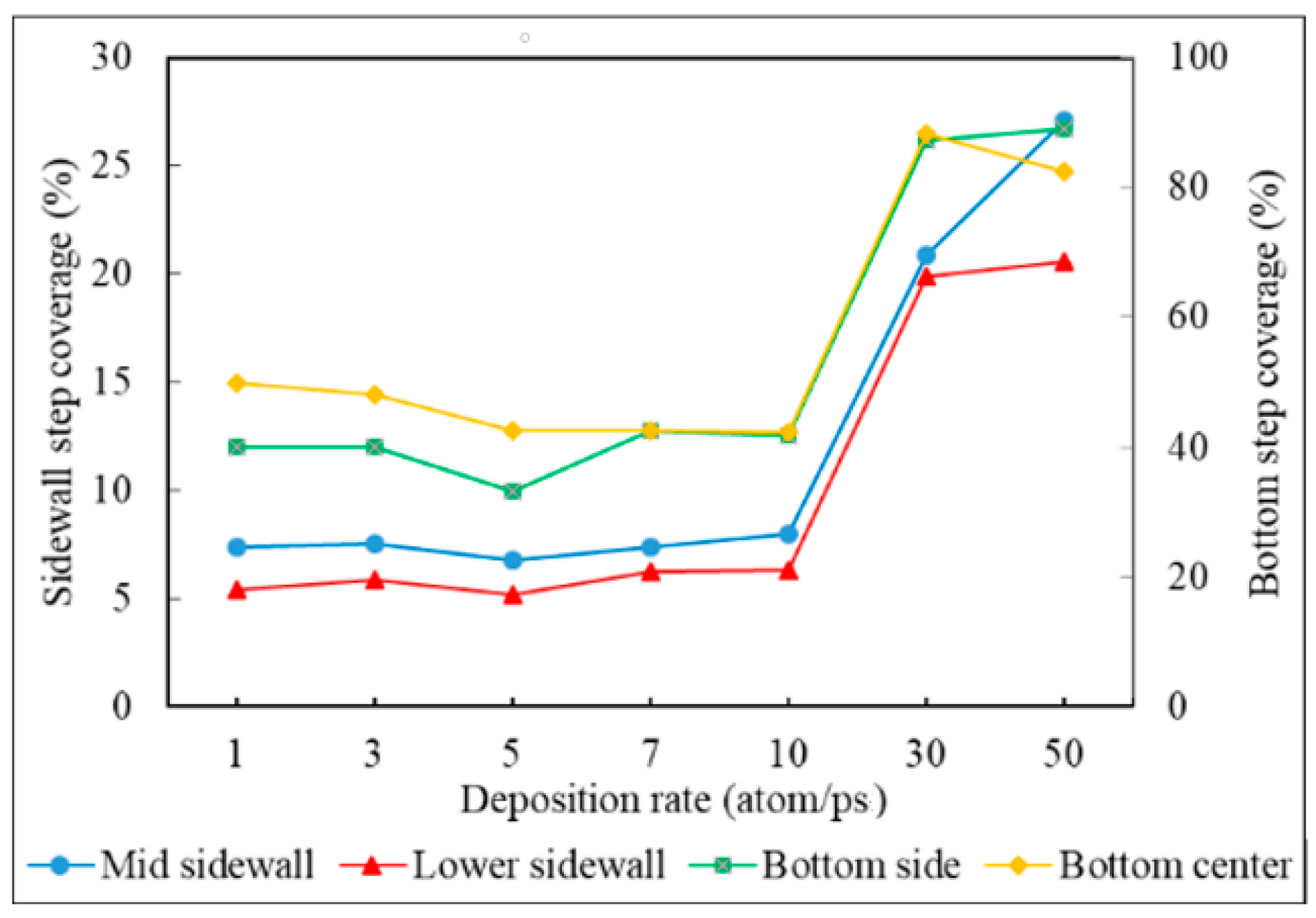
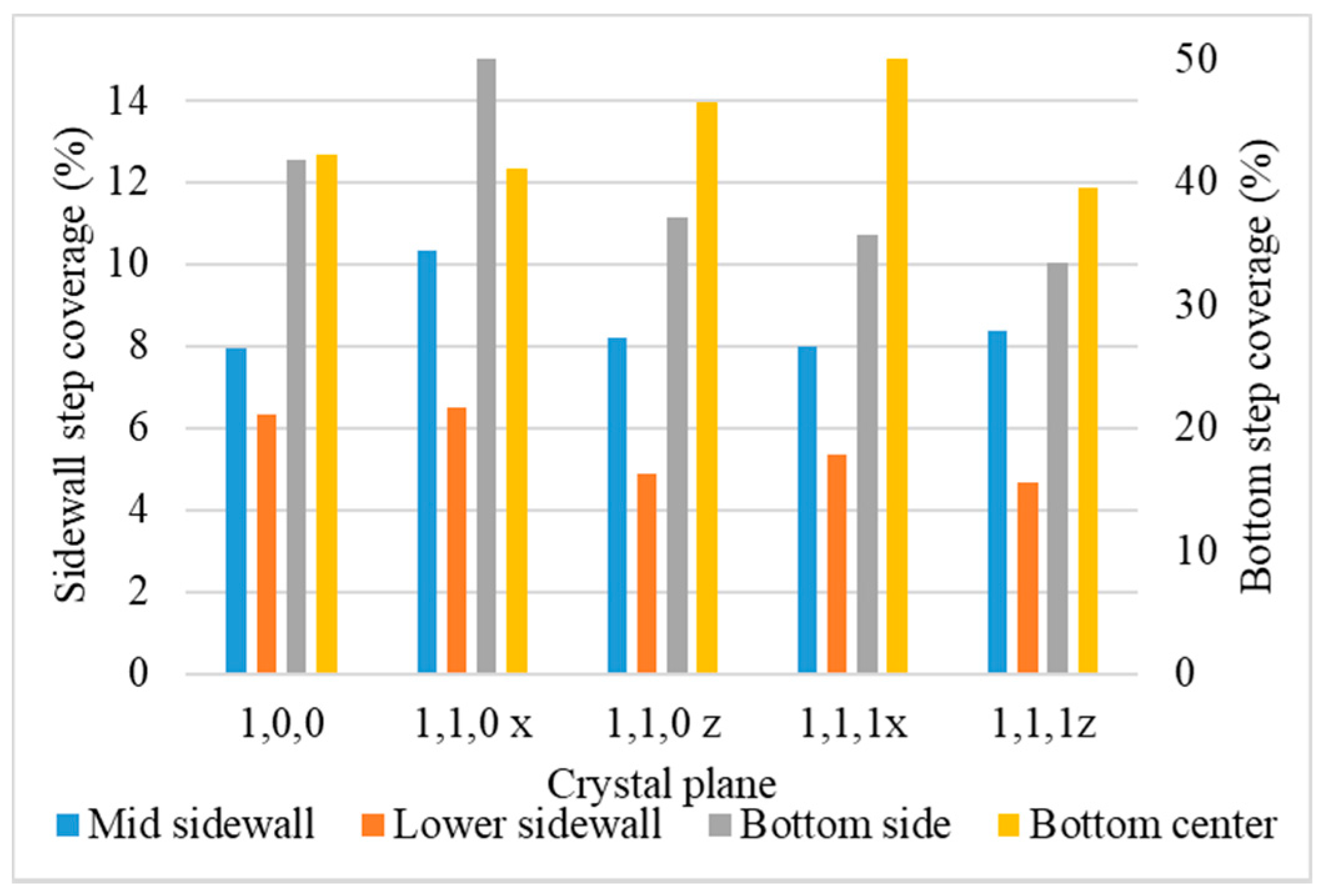
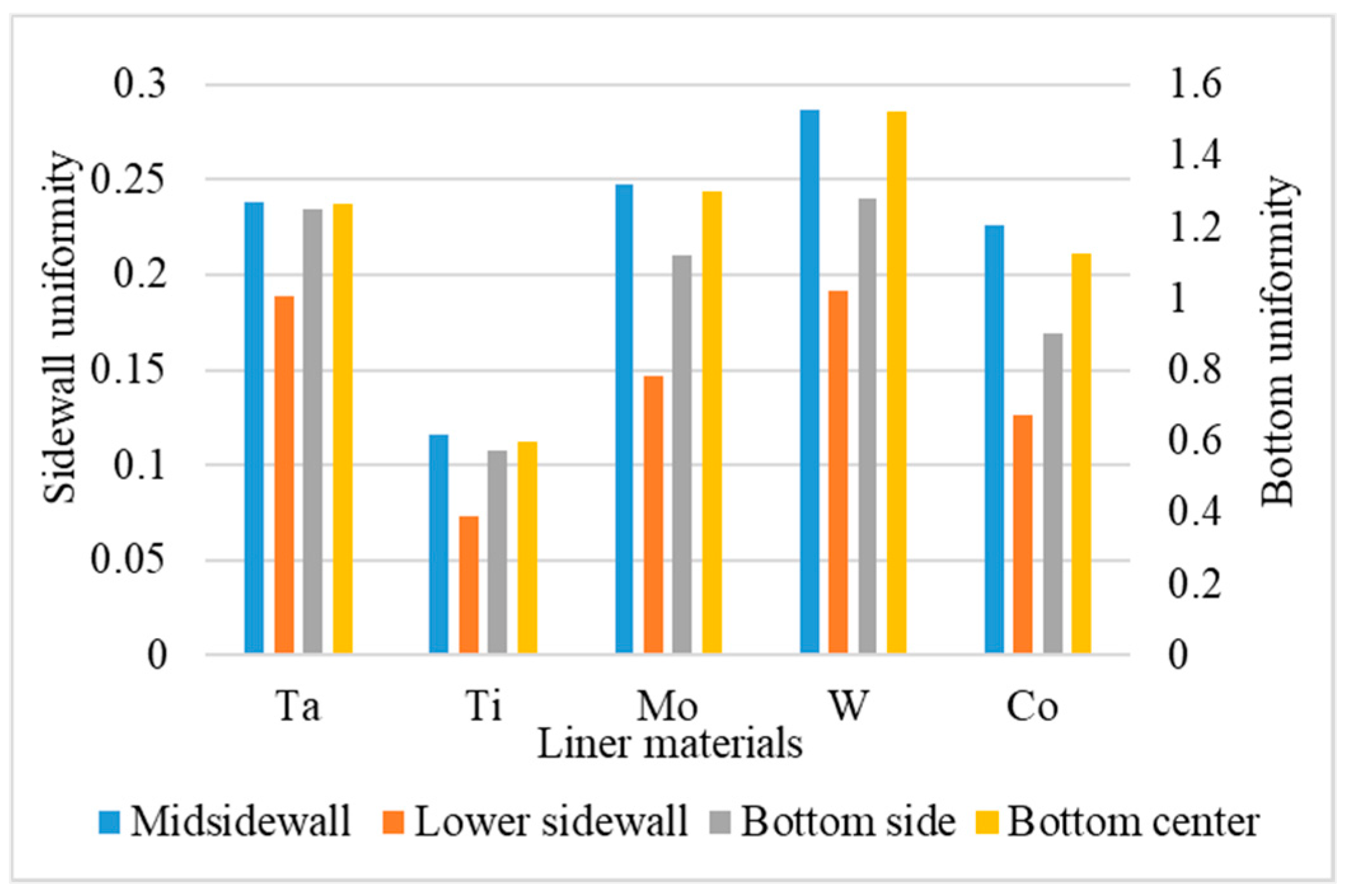
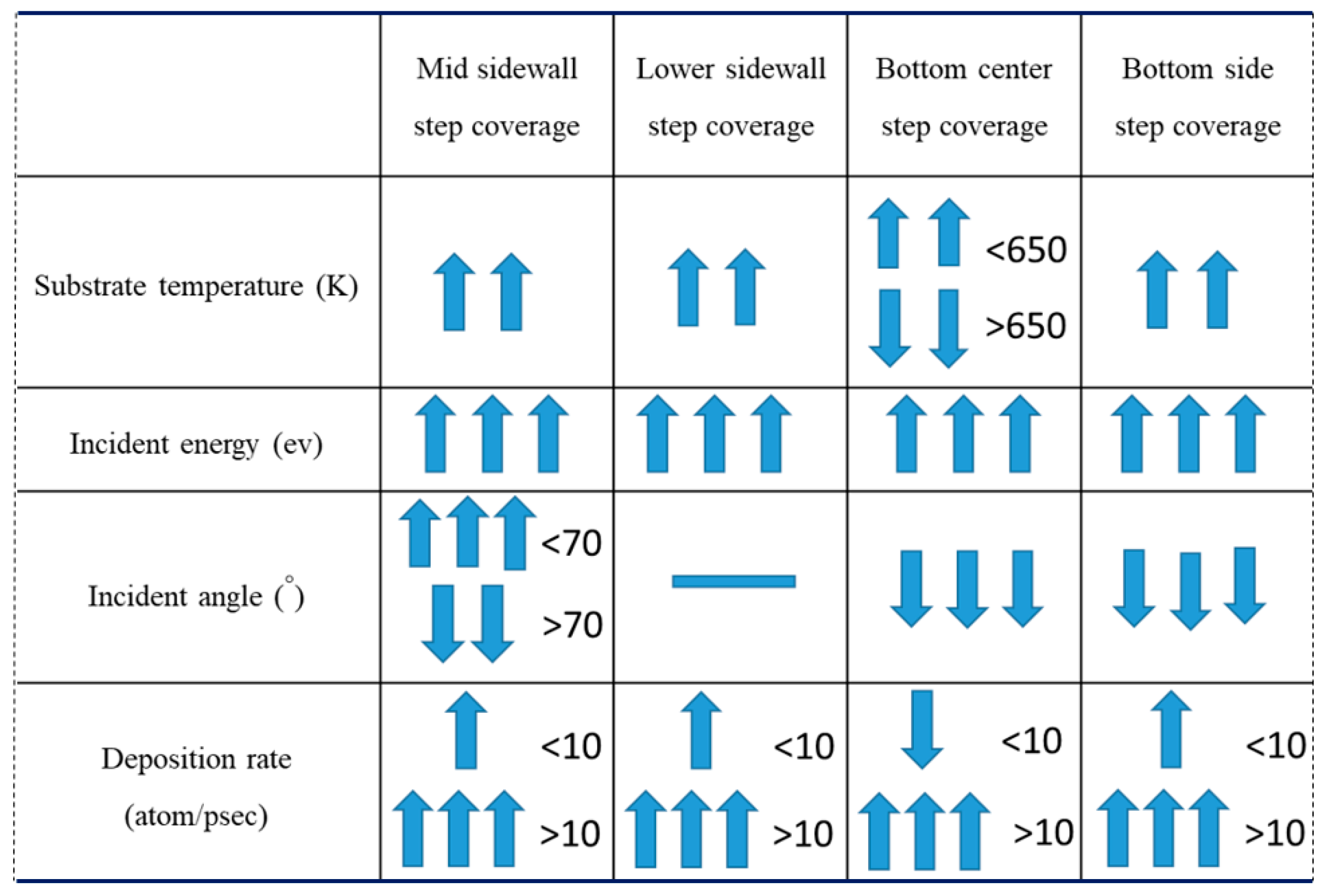
- Step coverage is defined as the average number of atoms deposited on the target region over the average number of atoms deposited on wing of the trench.
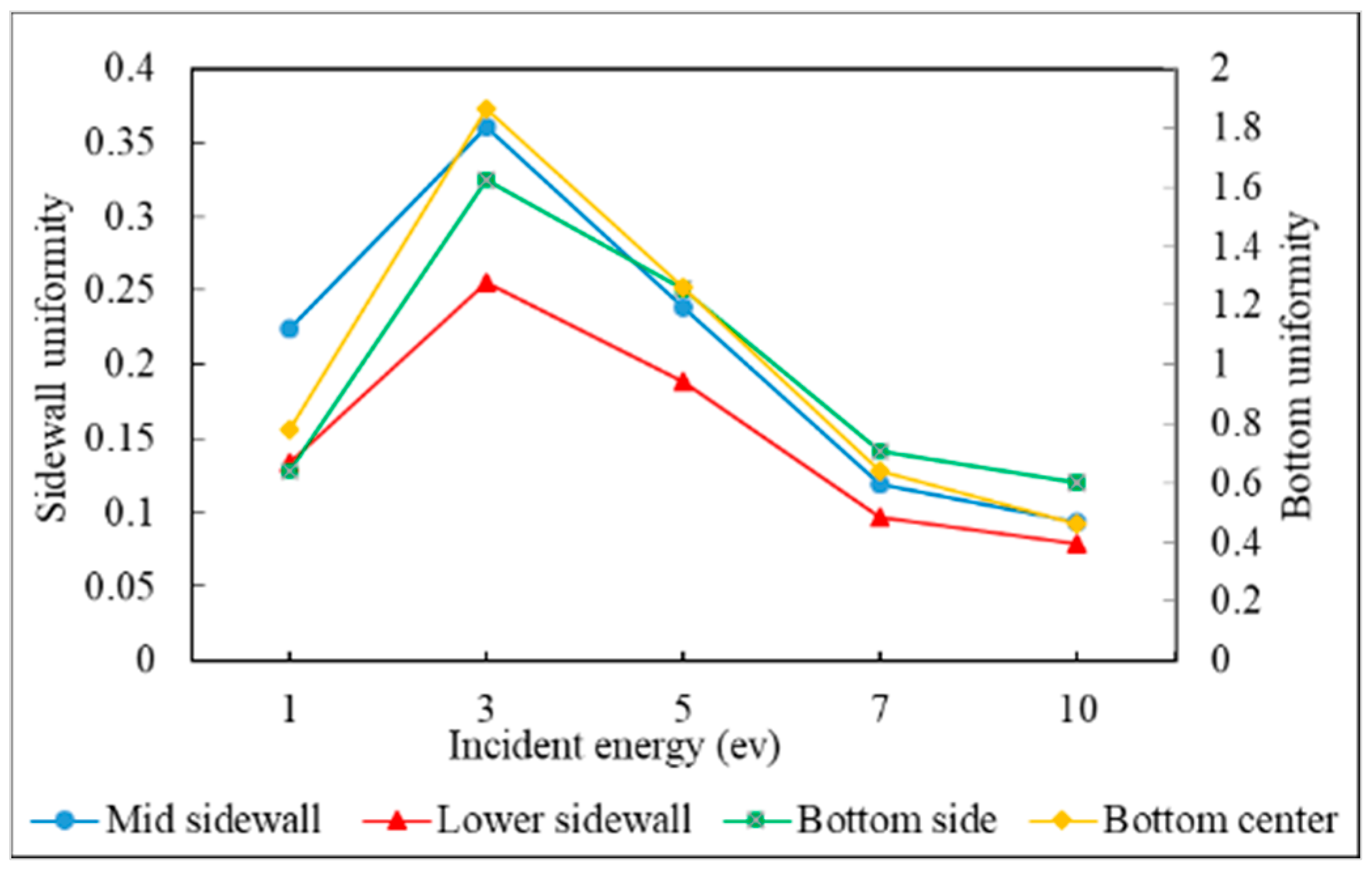
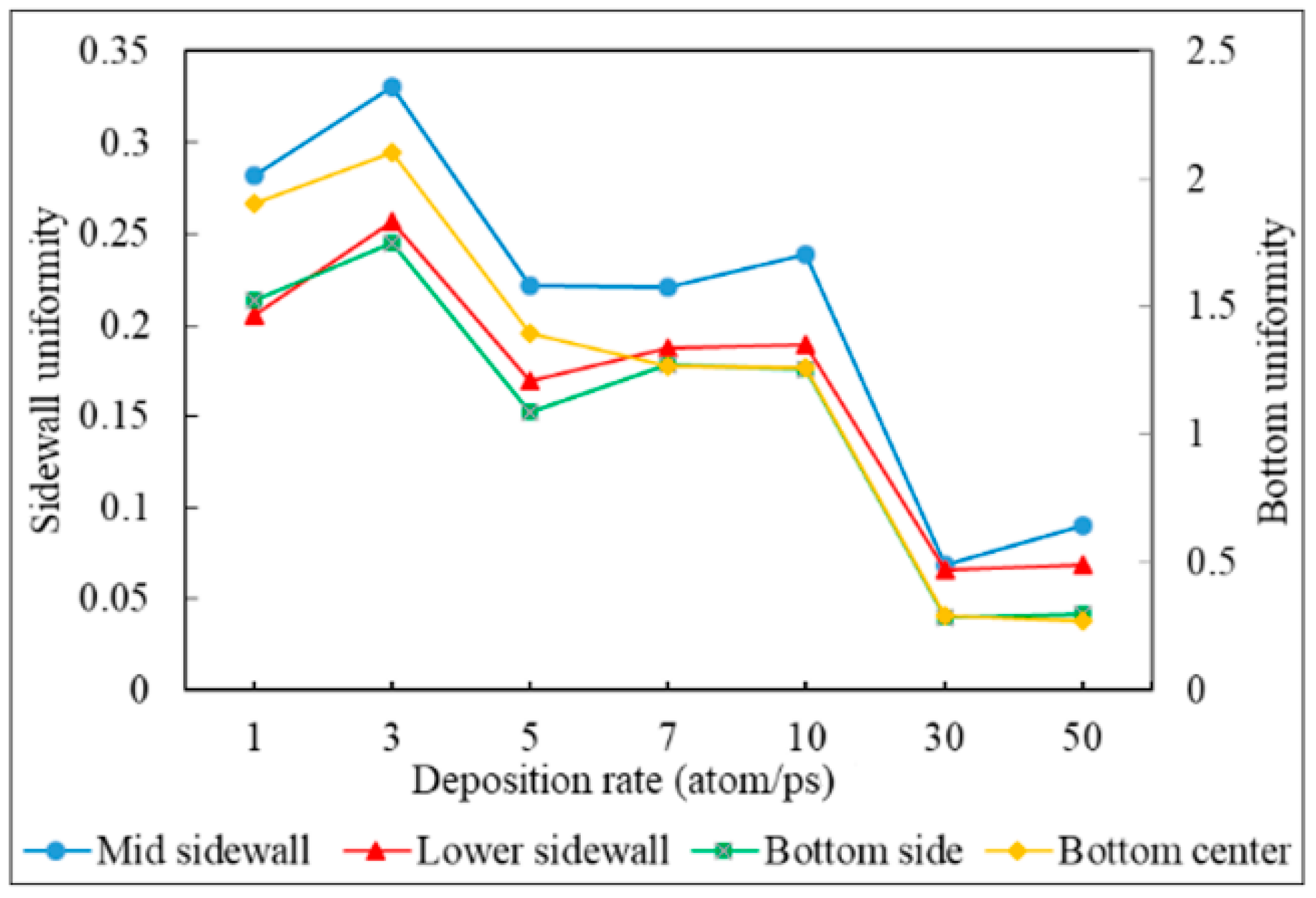
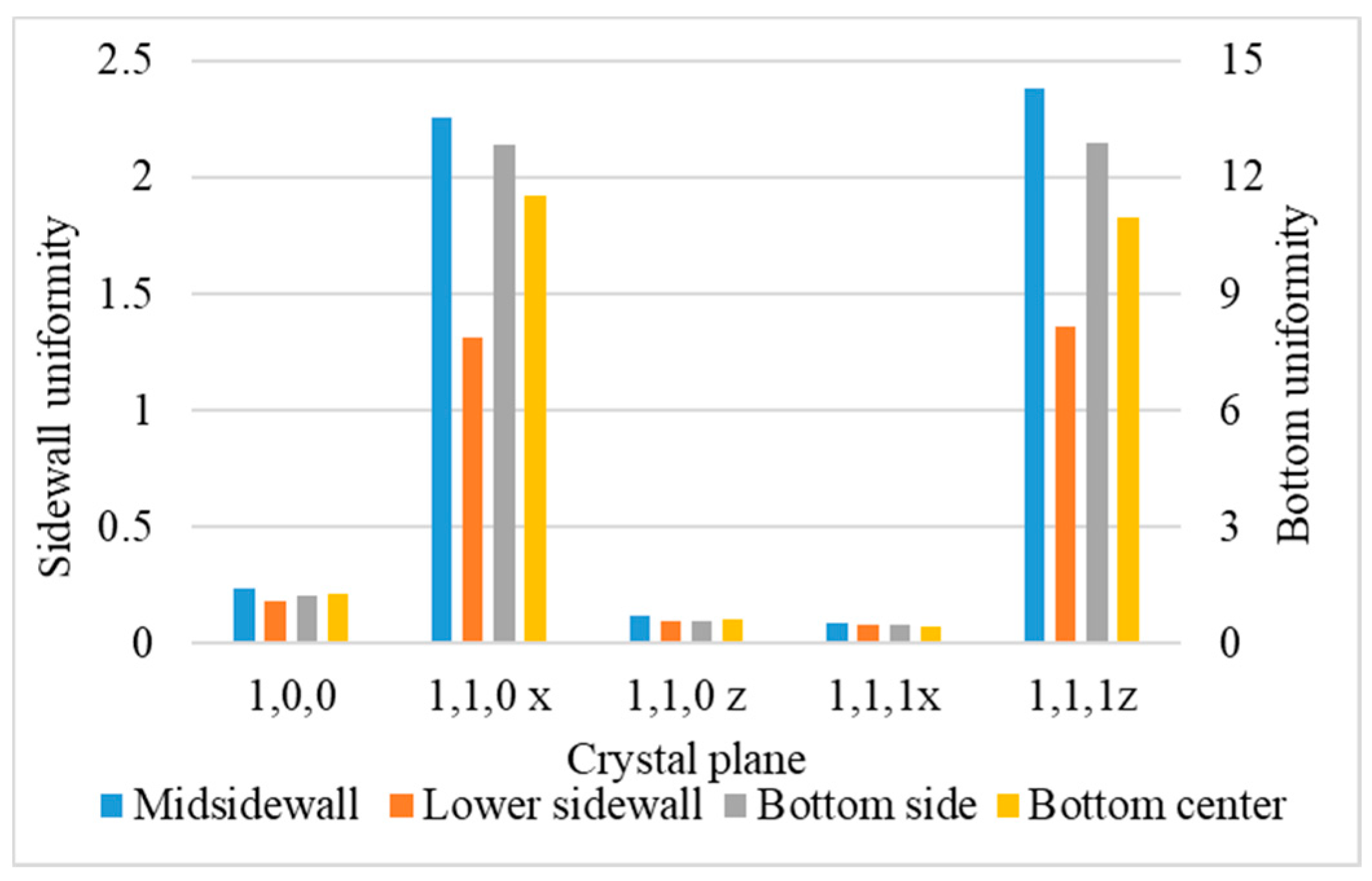
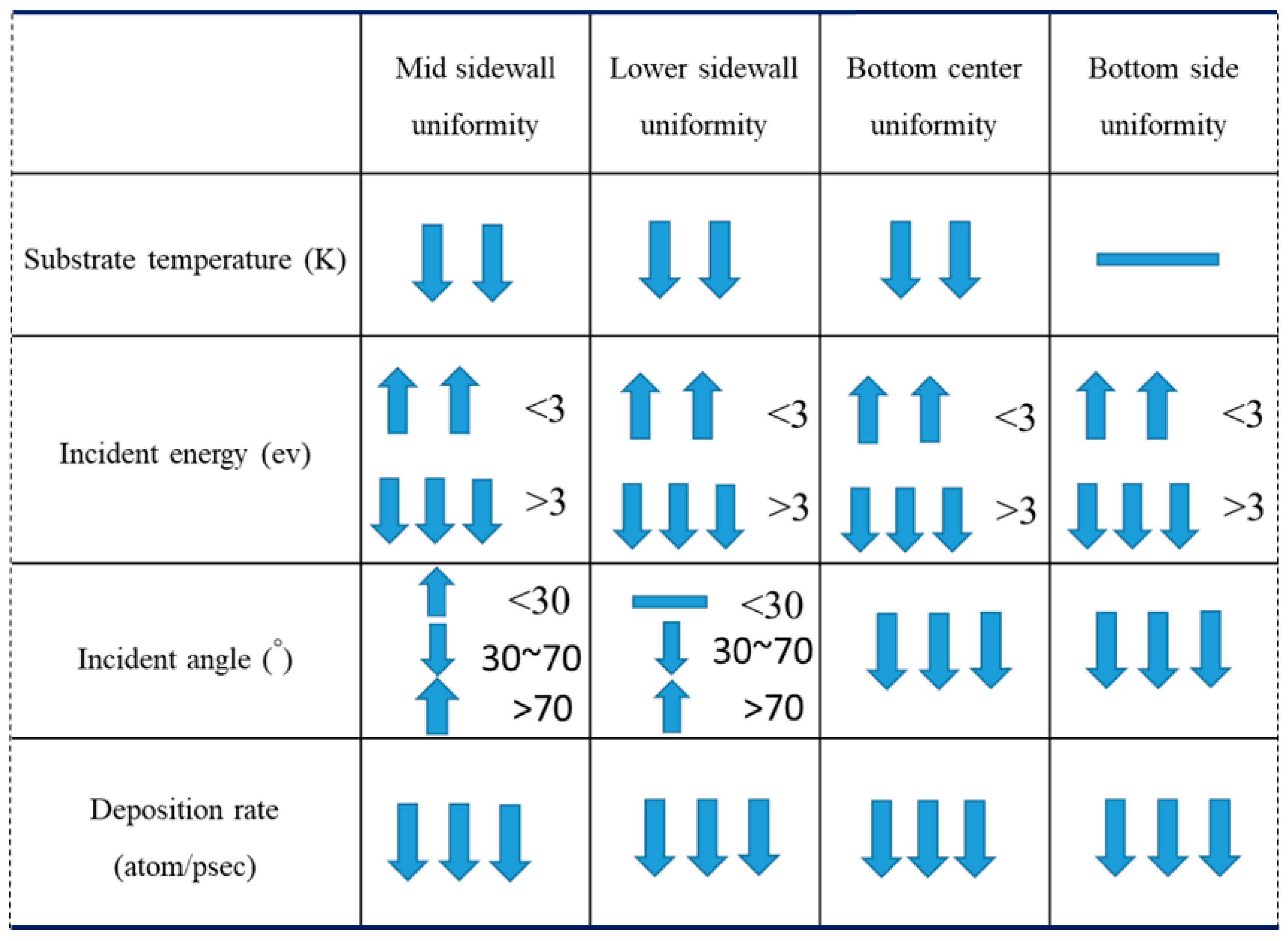
- Uniformity is defined as the average number of atoms deposited on the top sidewall over the average number of atoms of the overhang.
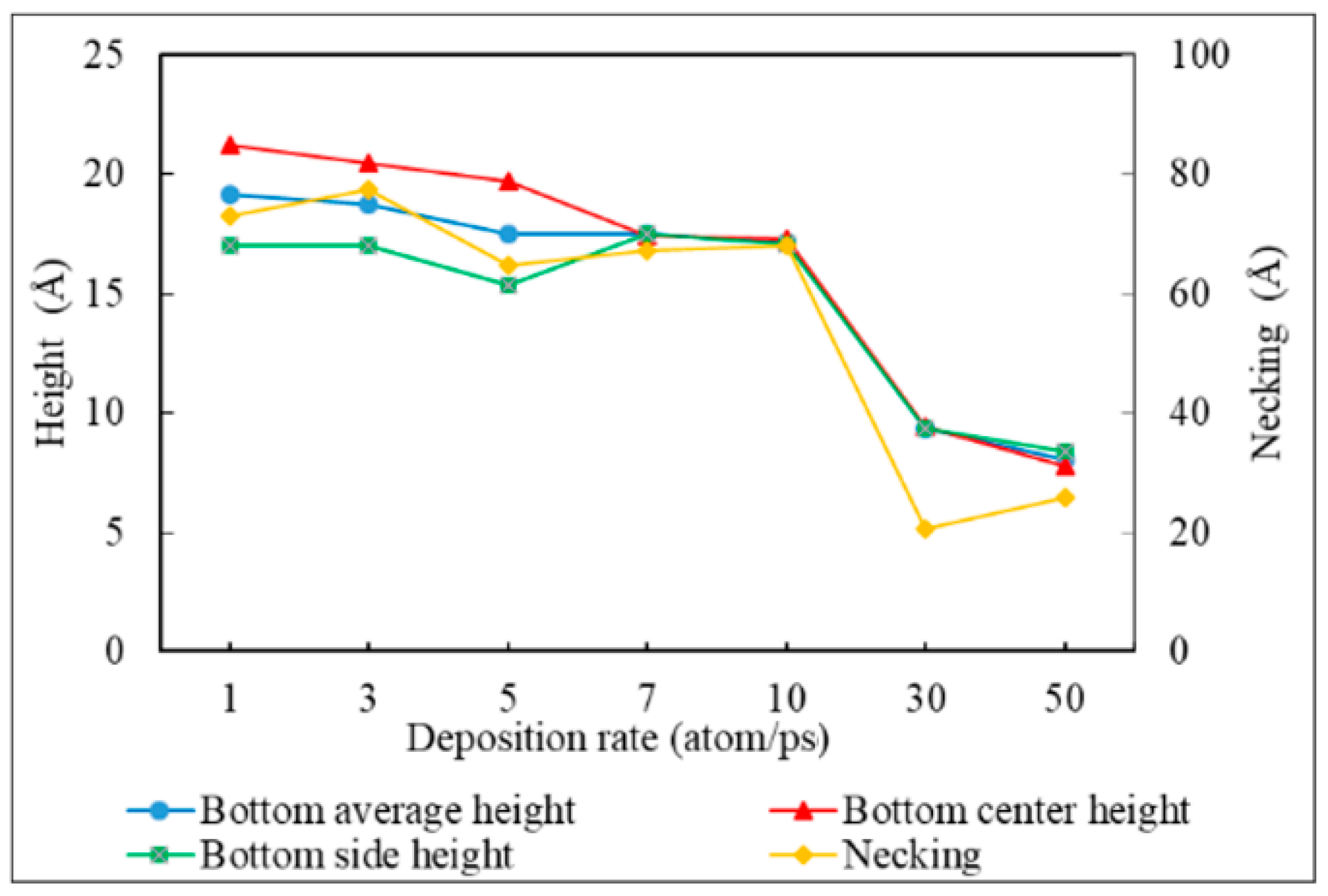
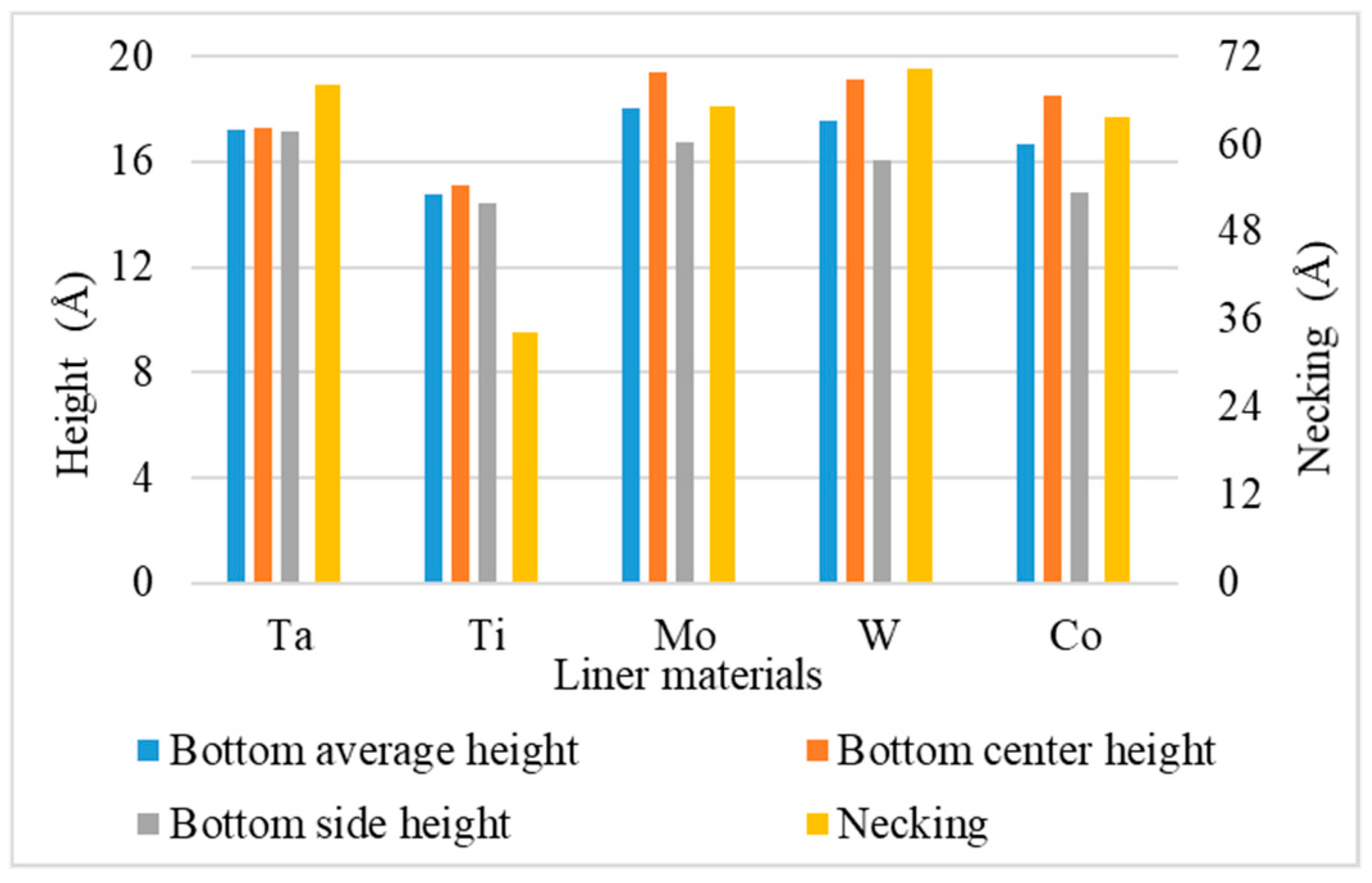
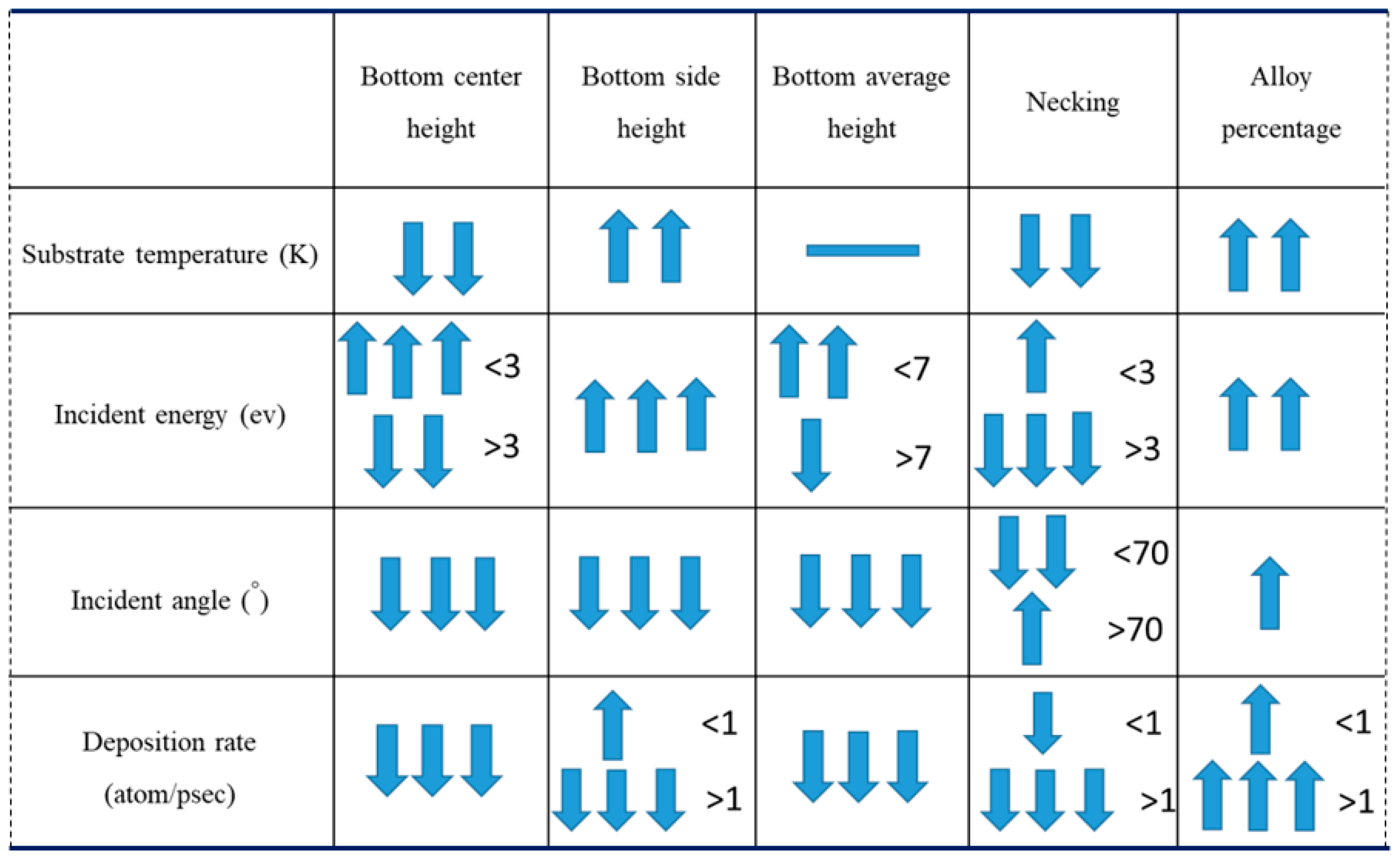
- Bottom height is defined as the average height of atoms accumulated at the bottom of the trench.
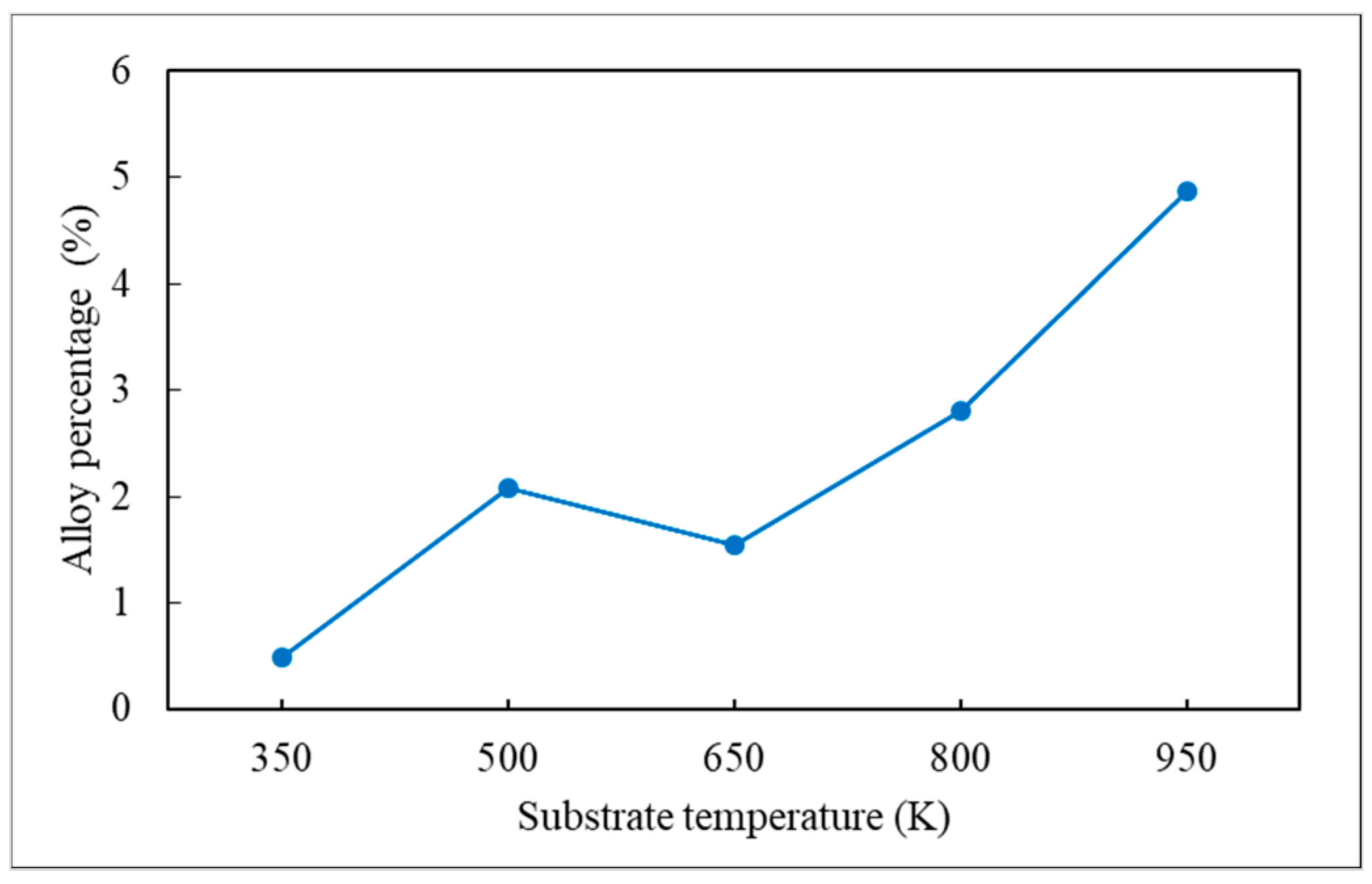
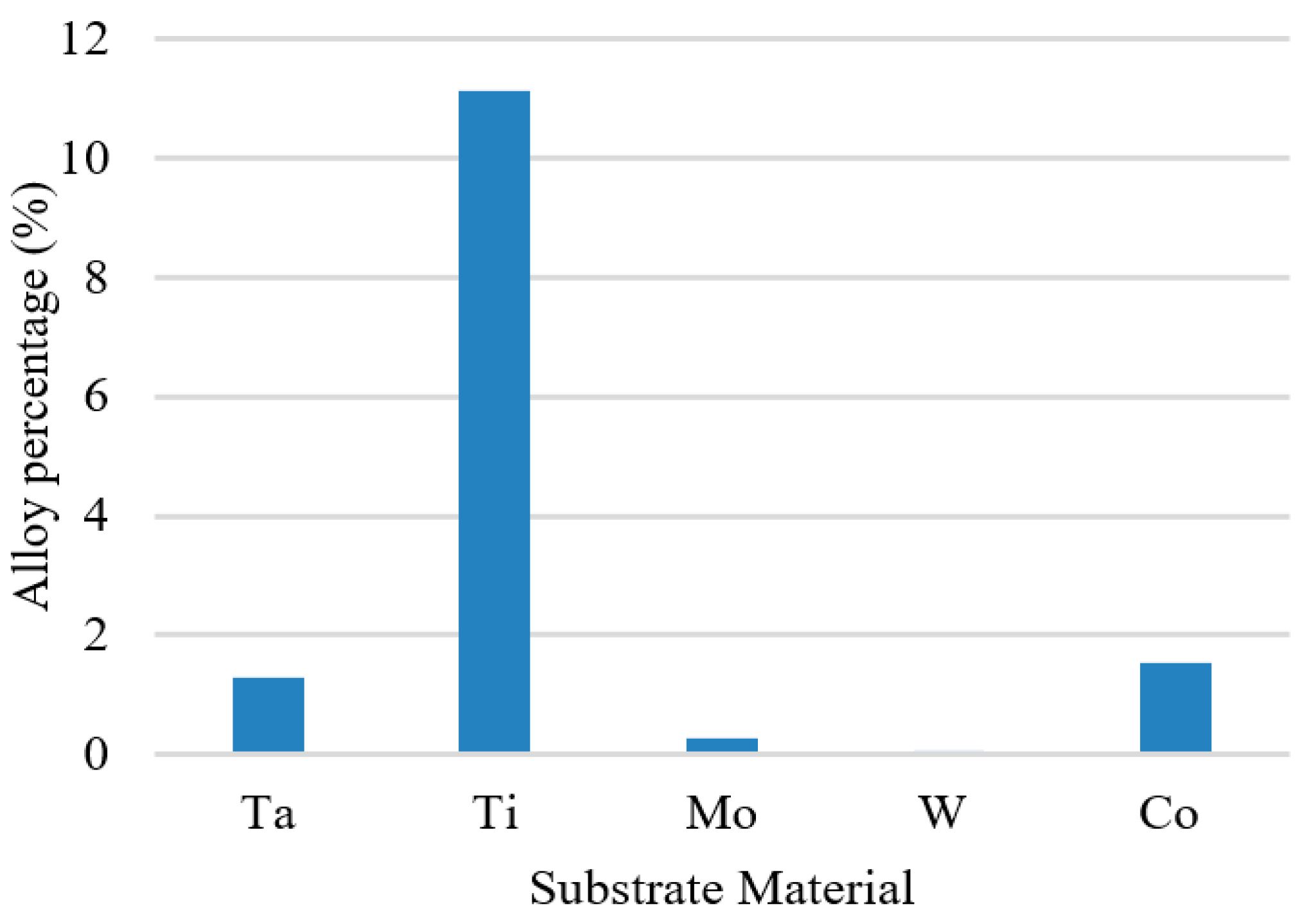
- Alloy percentage is defined as the percentage of substrate atoms in the copper seed layer.
- Necking is defined as the distance between the atoms at the two trench necks.
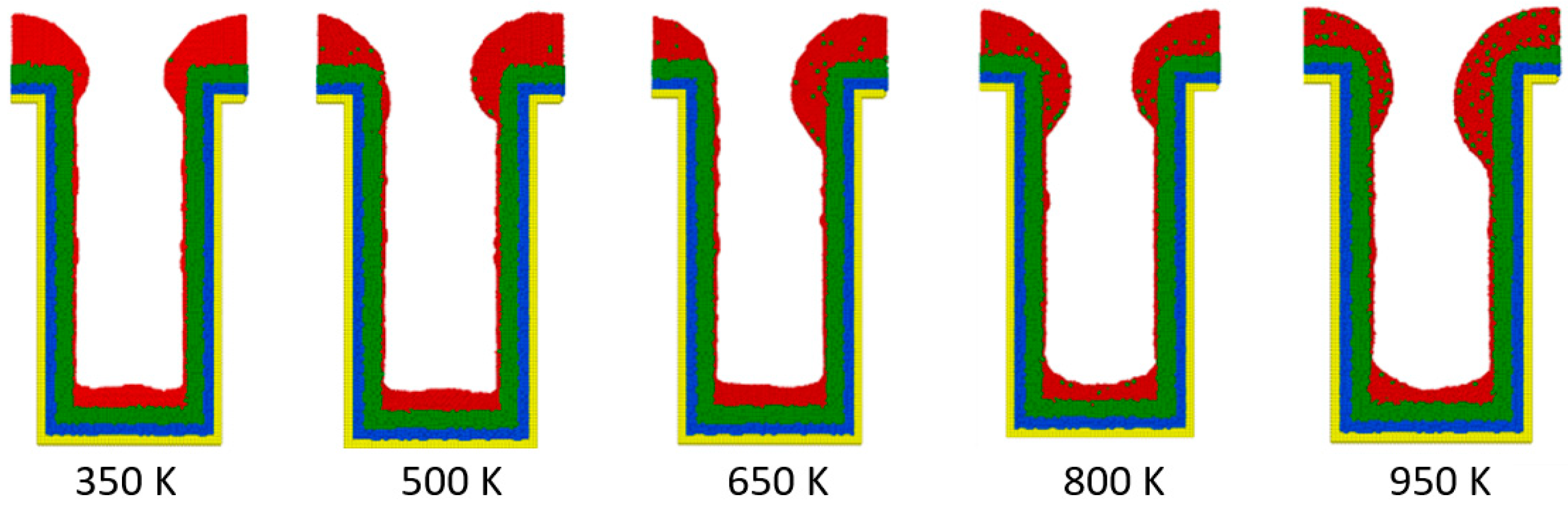
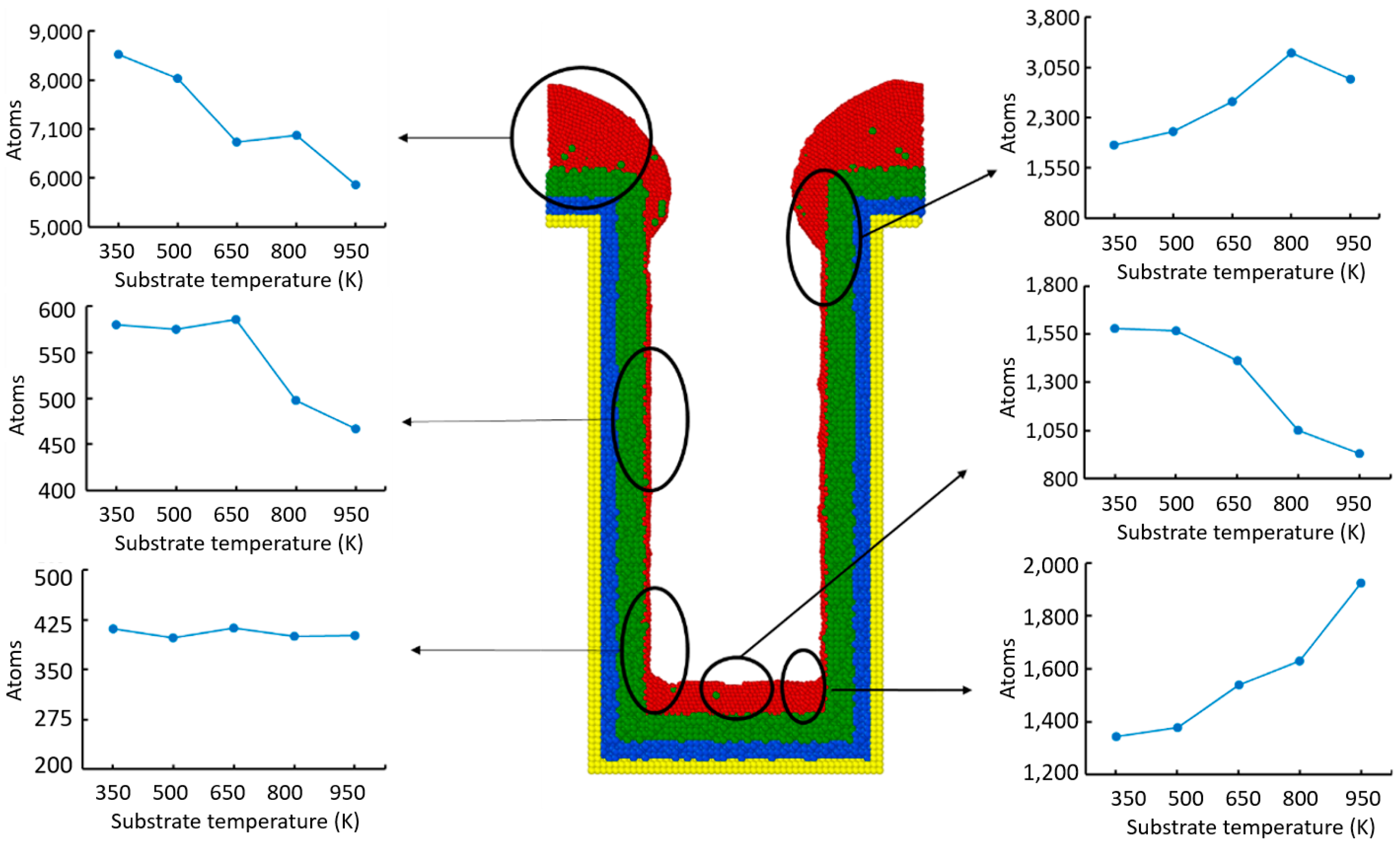
3.1. Substrate Temperature
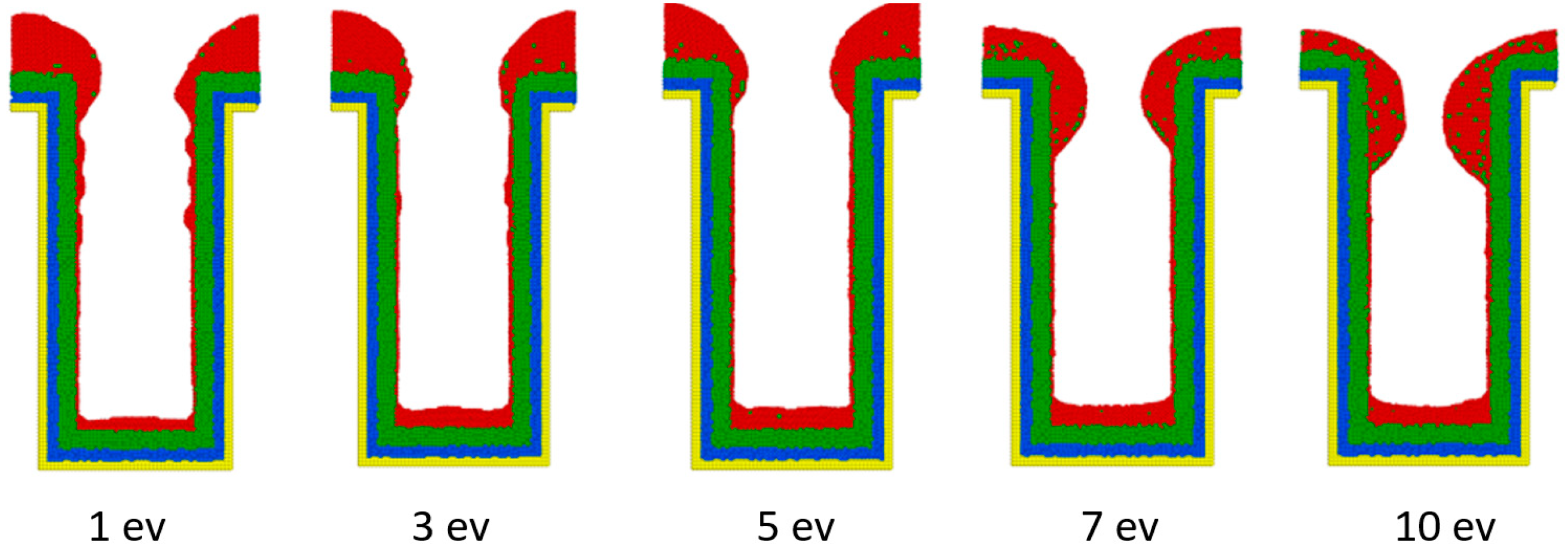
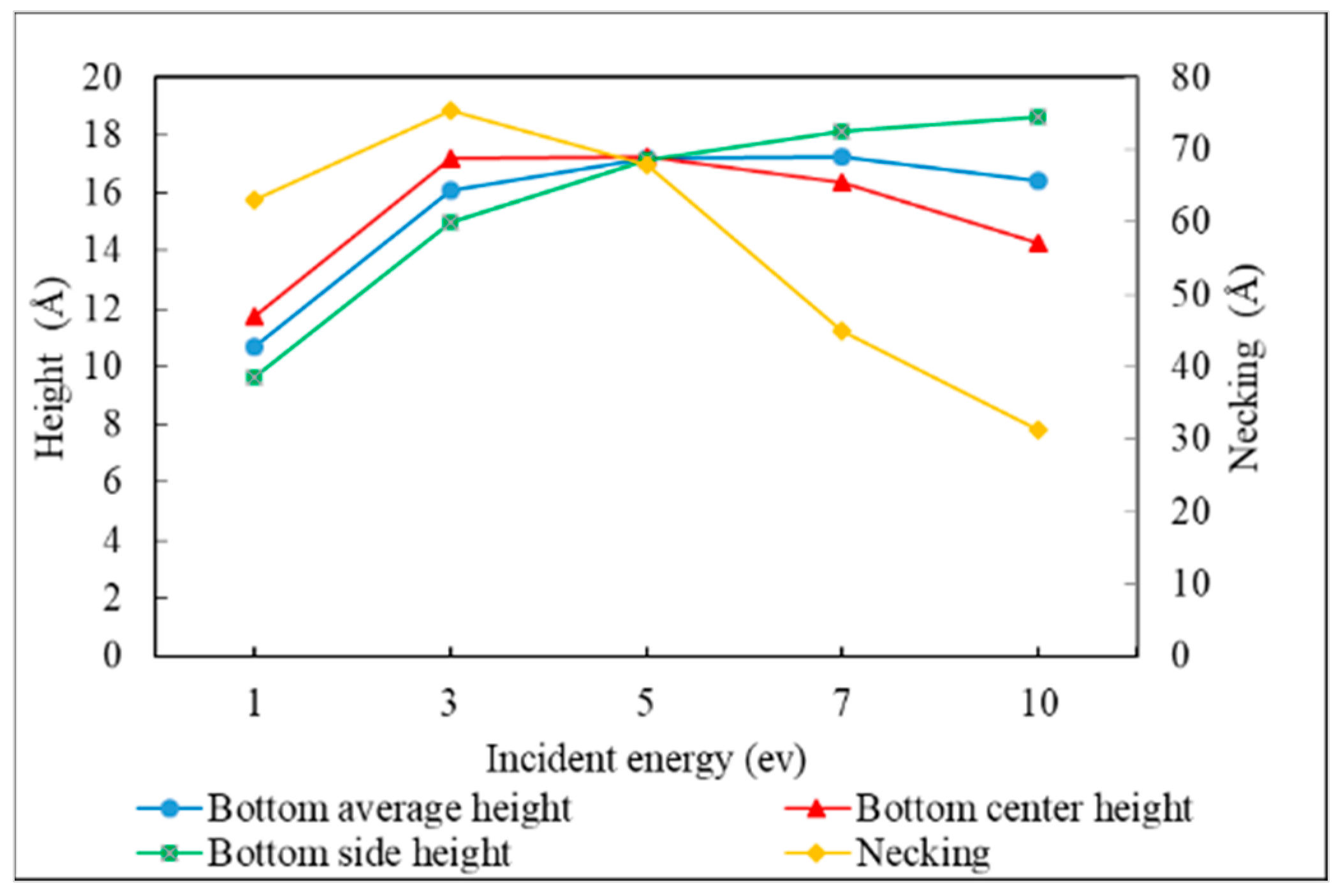
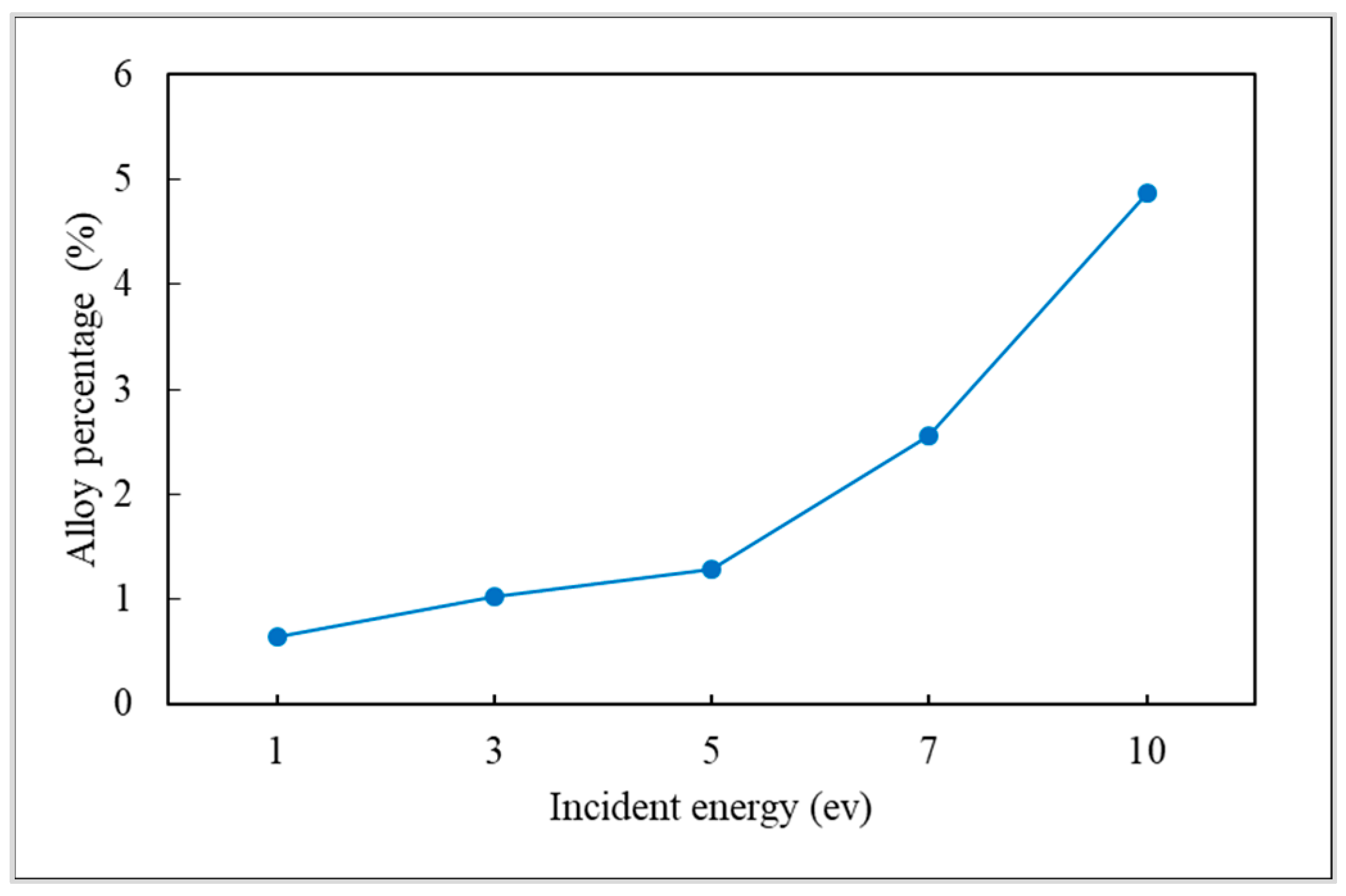
3.2. Incident Energy
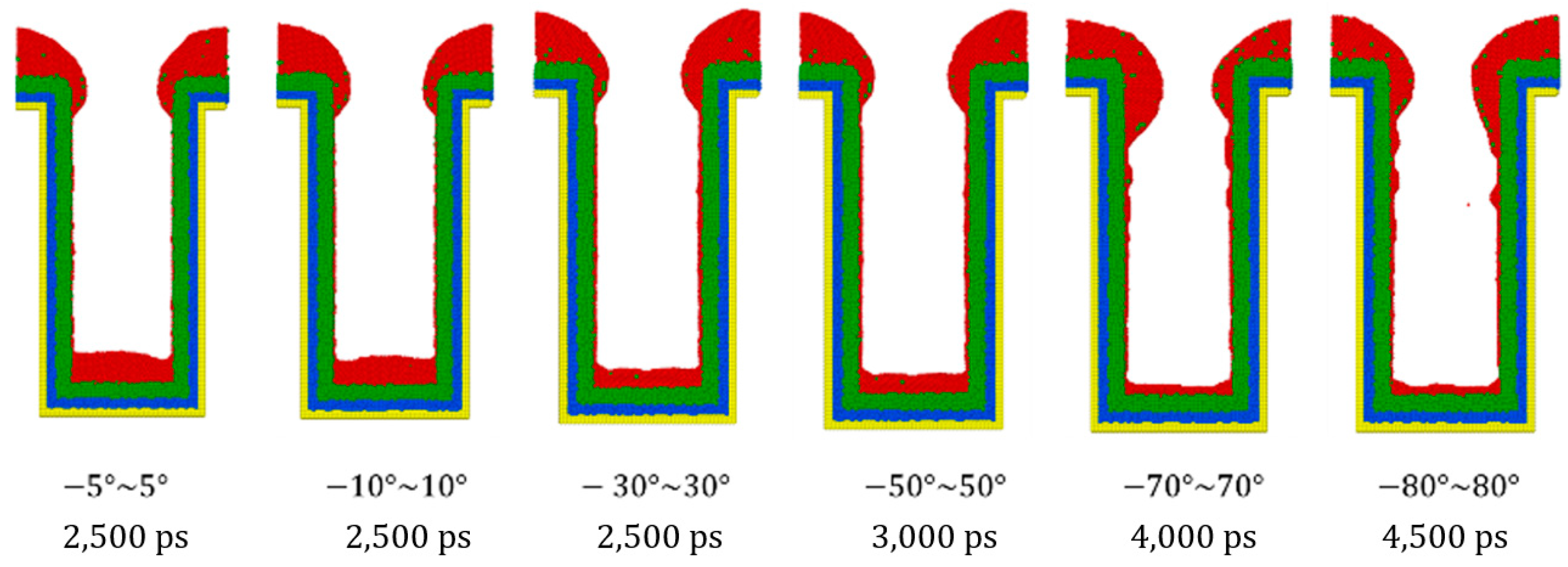
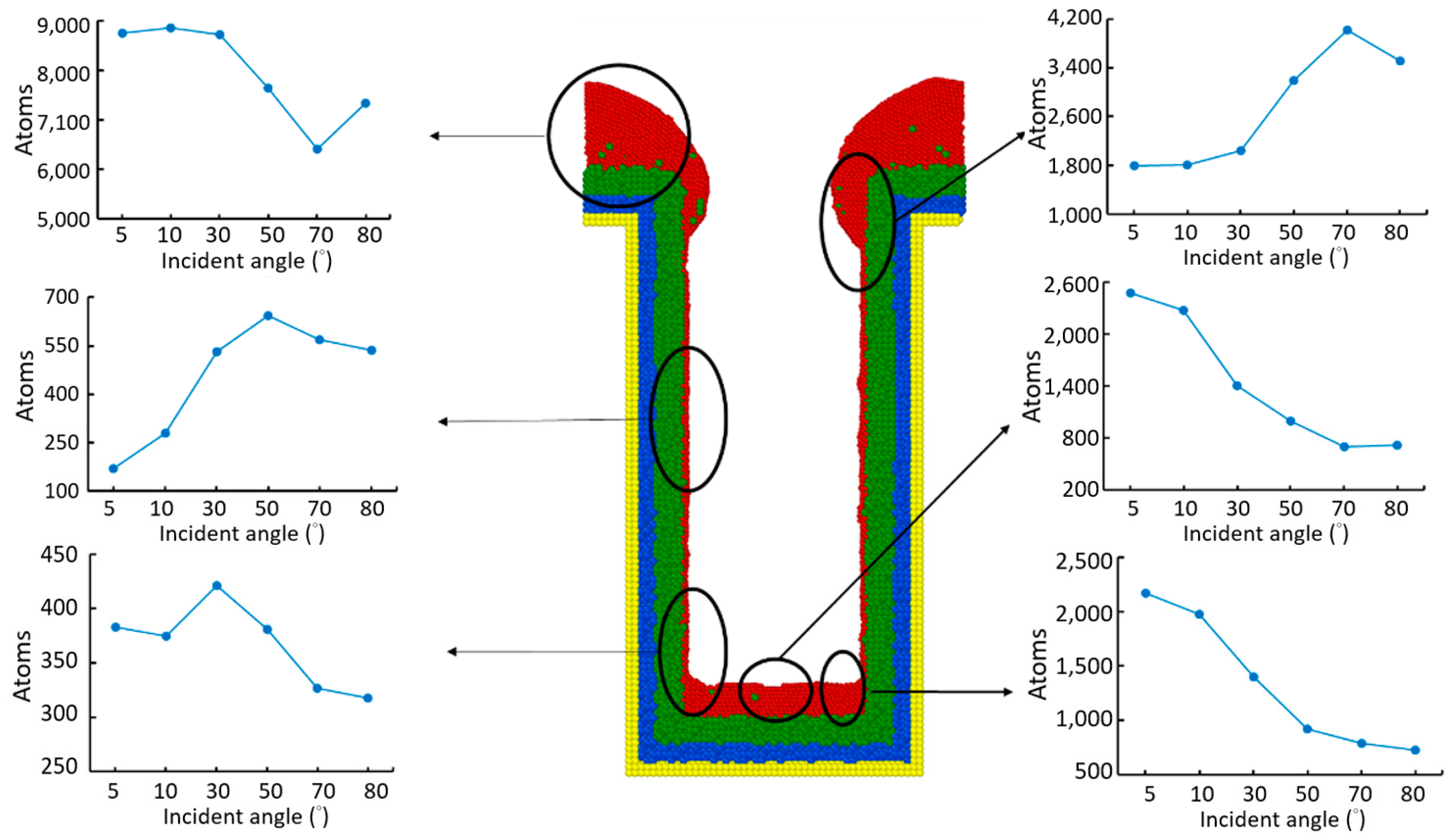
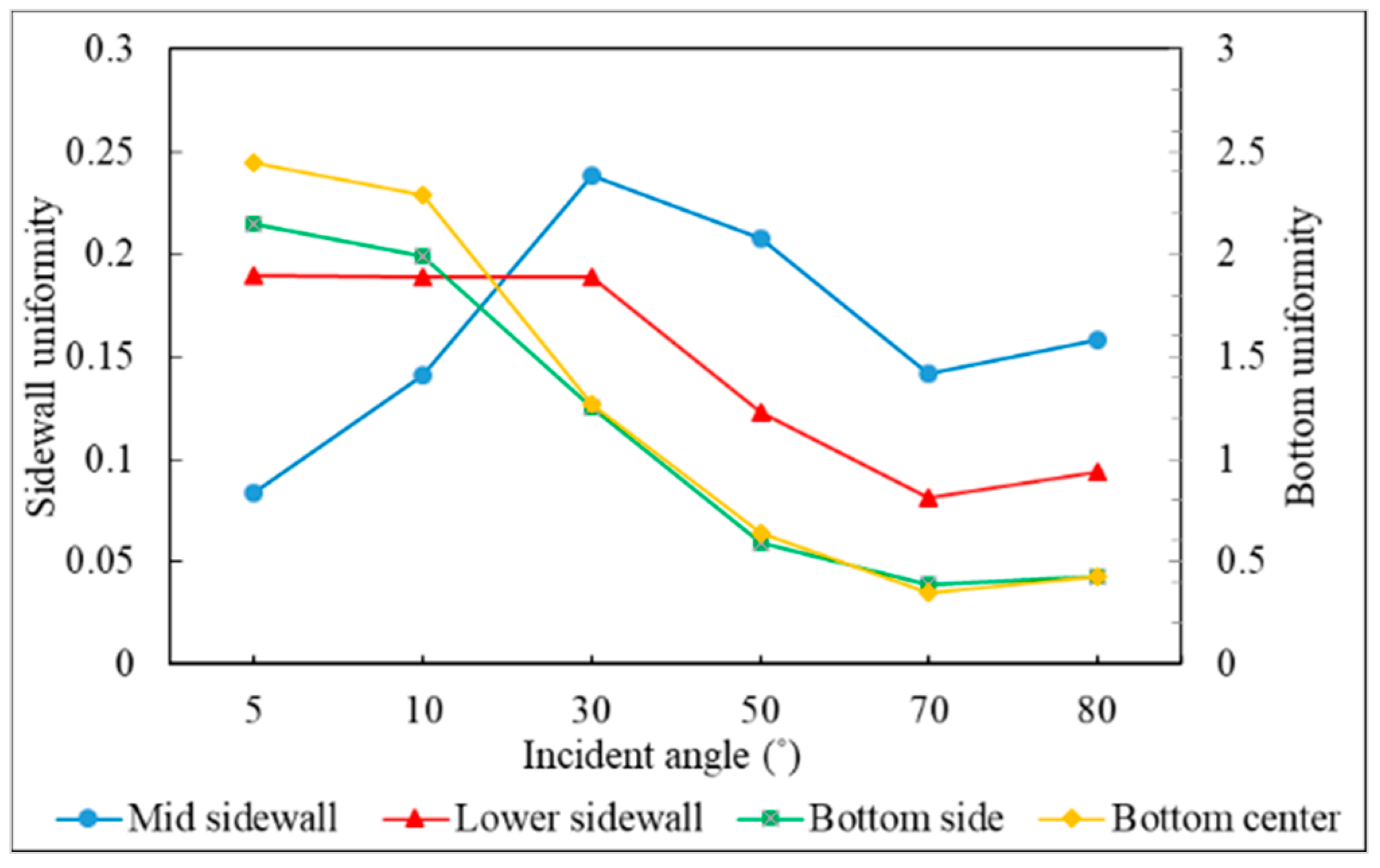
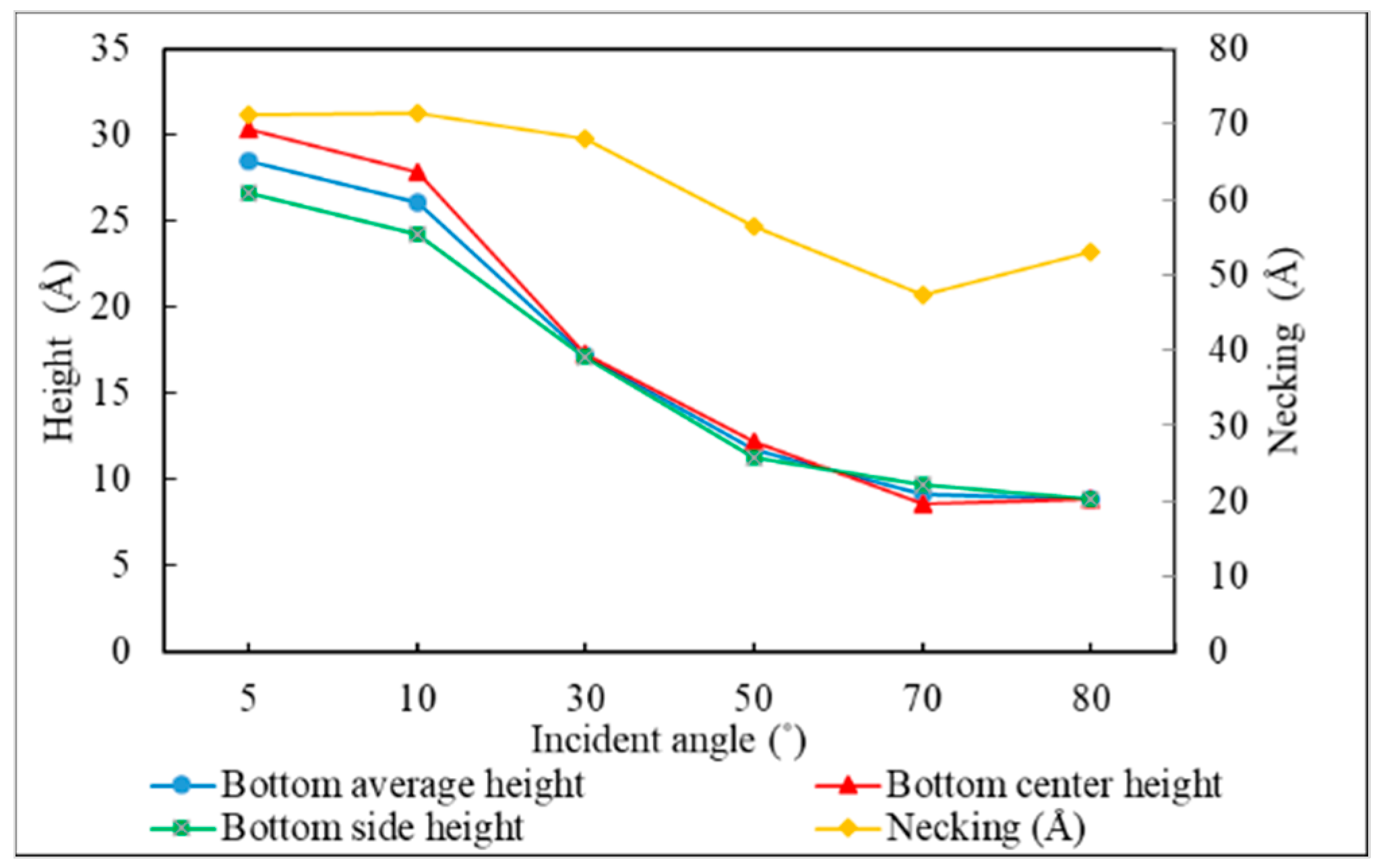
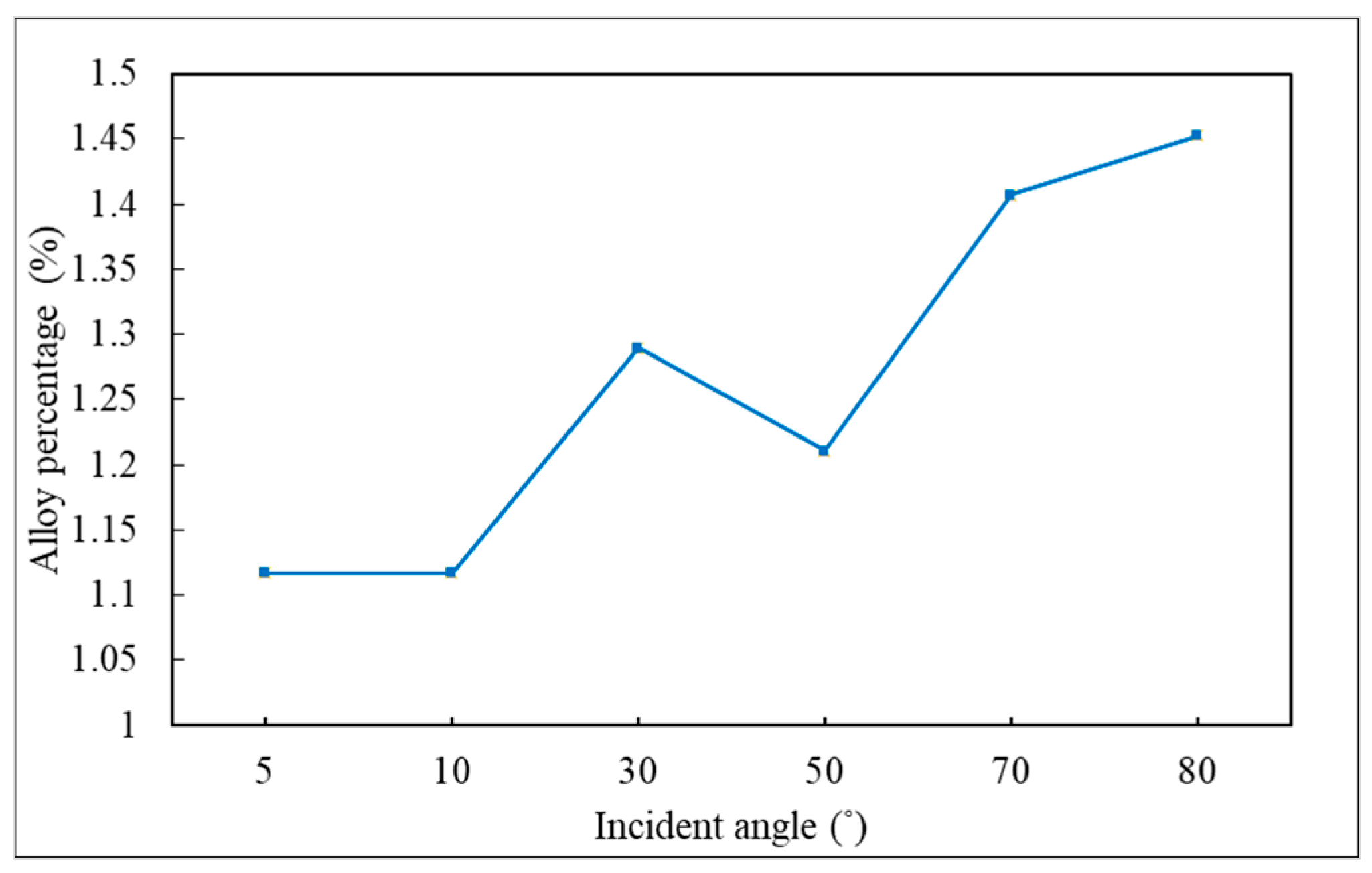
3.3. Incident Angle
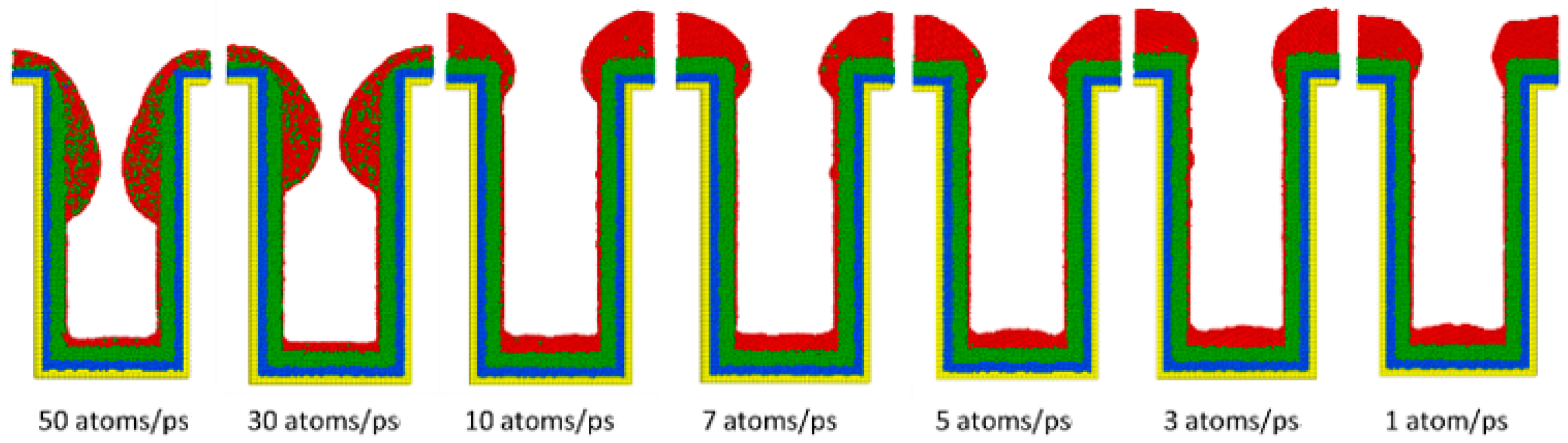
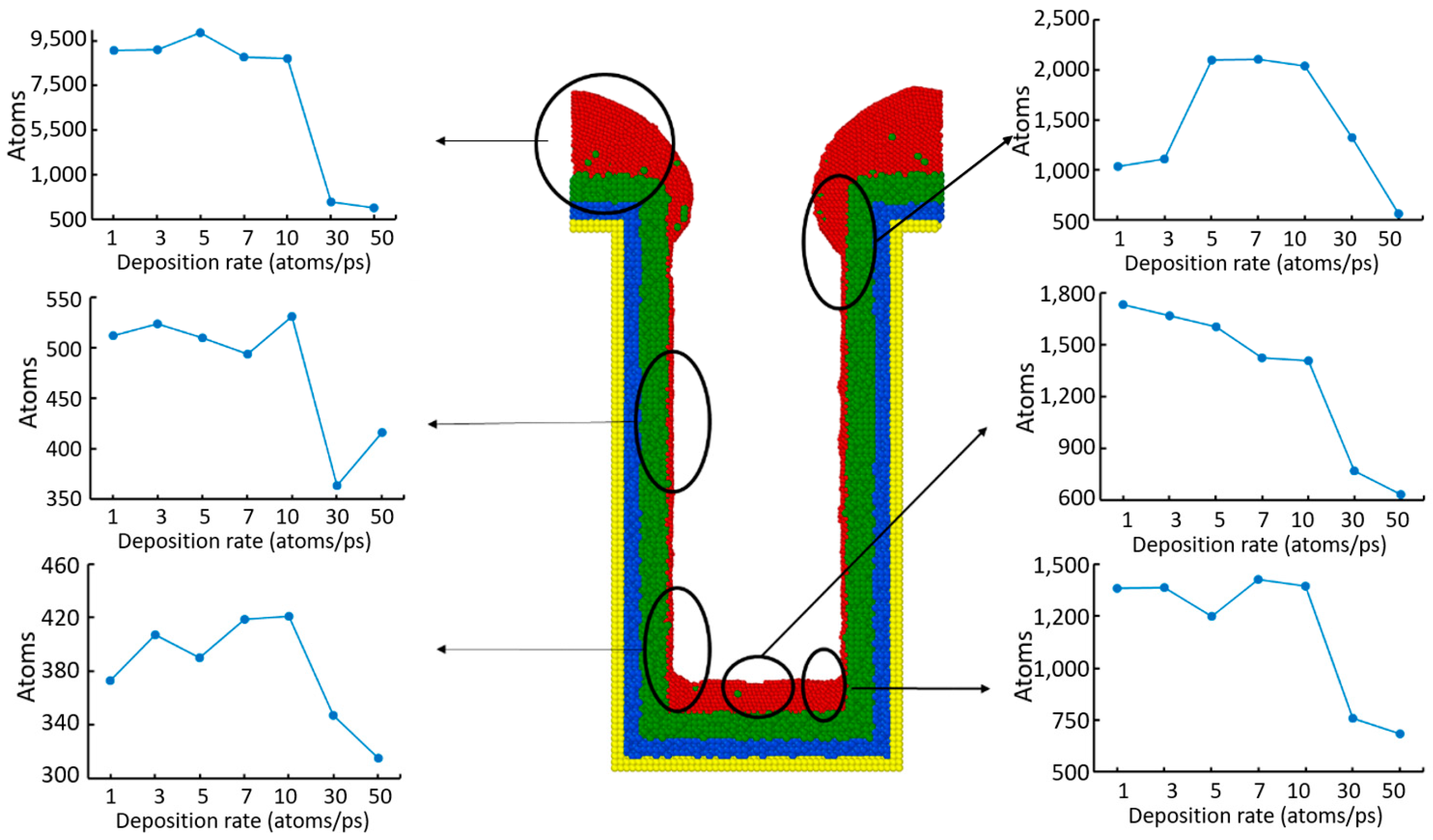
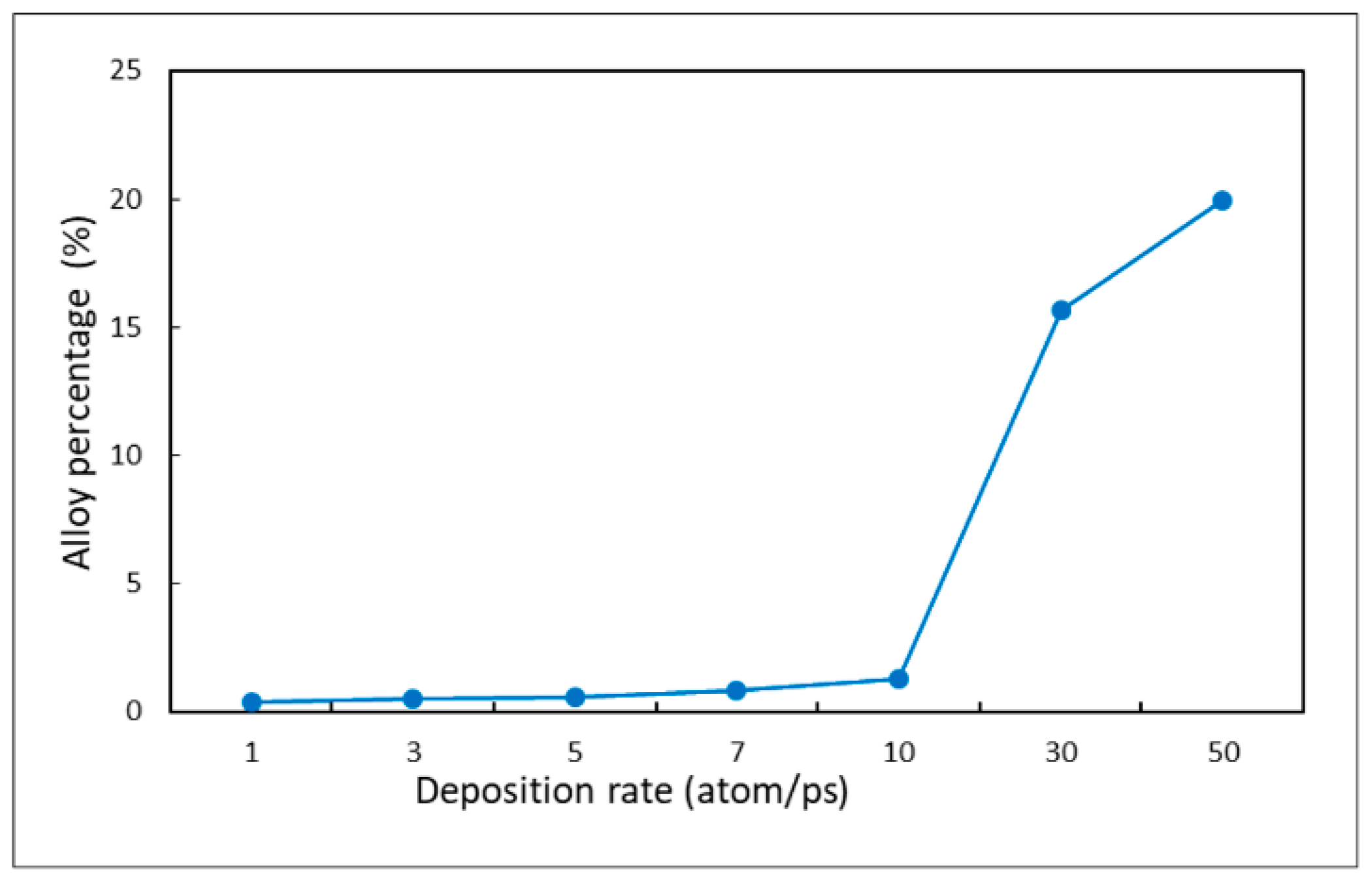
3.4. Deposition Rate
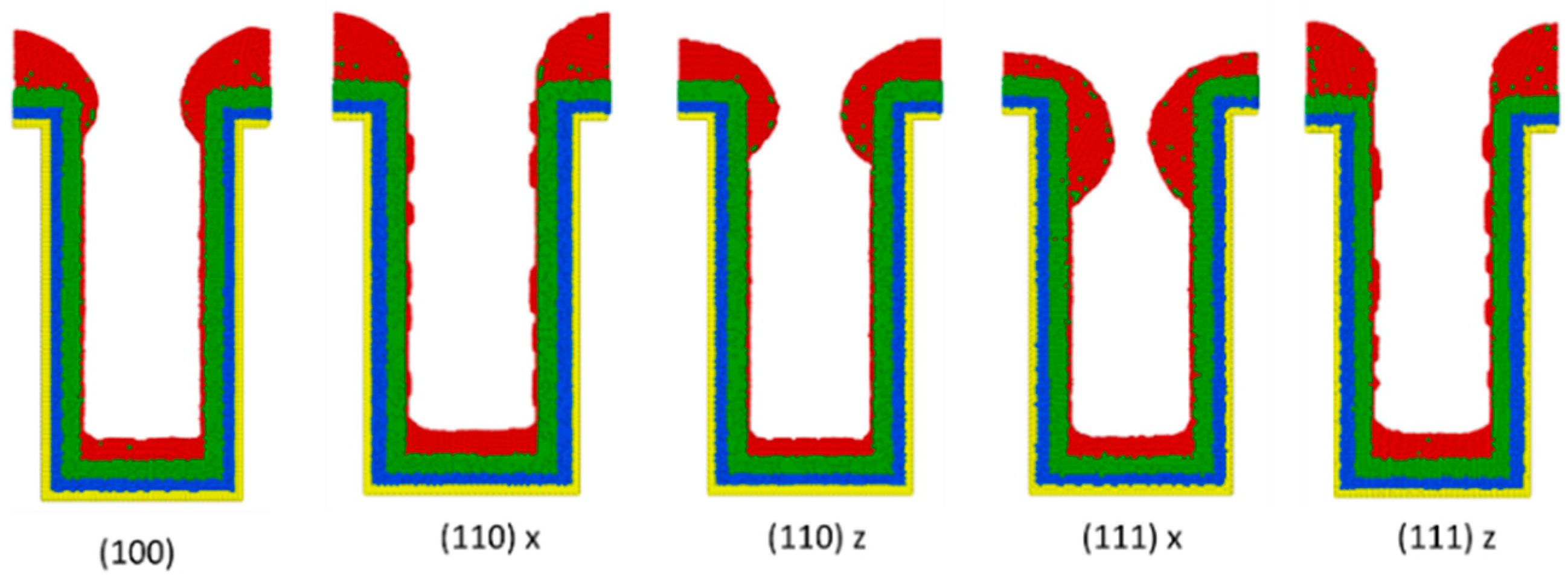
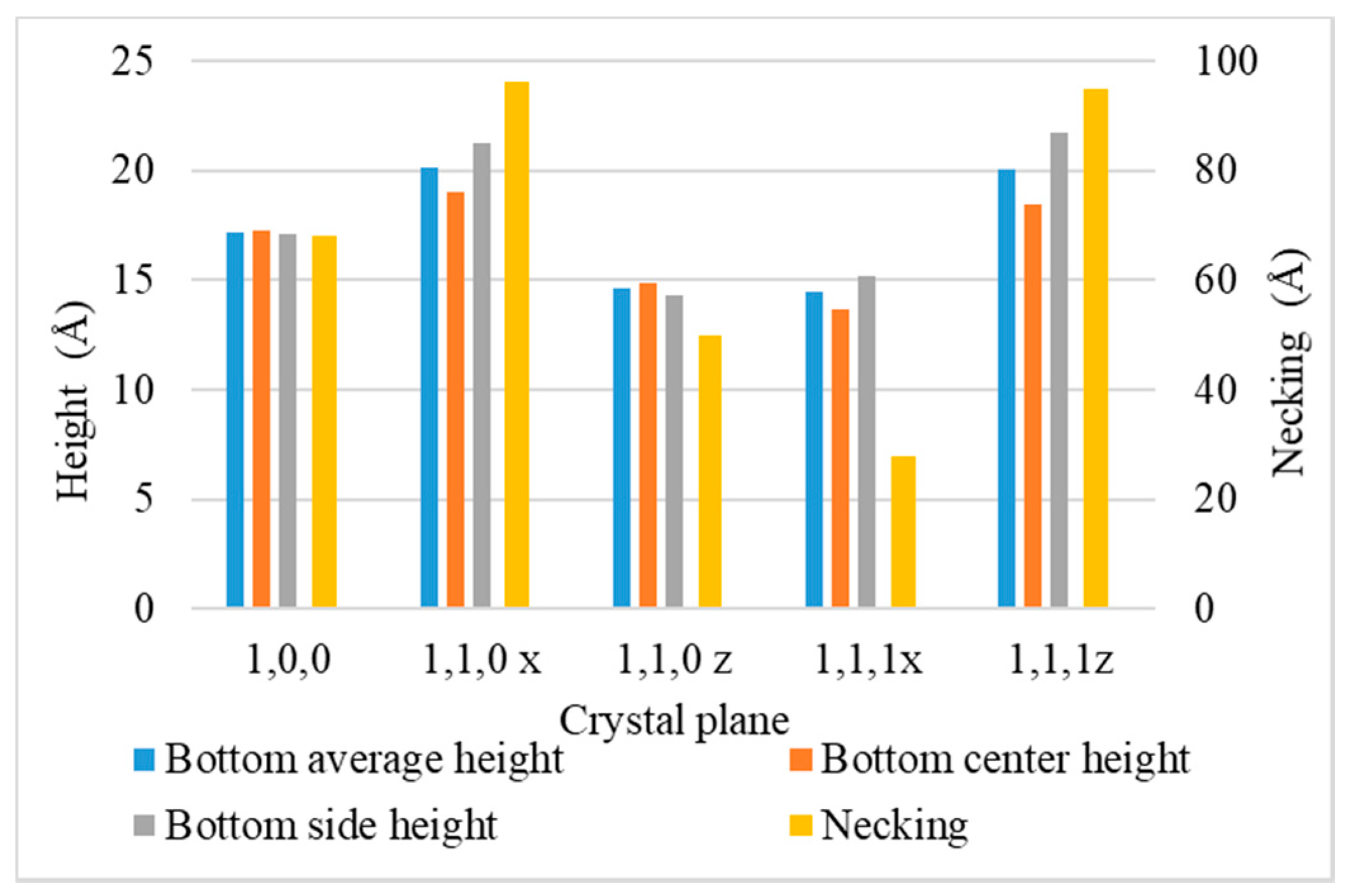
3.5. Crystal Plane
- (100): (100) at X direction, (010) at Y direction, (001) at Z direction.
- (110) x: (110) at X direction, (10) at Y direction, (001) at Z direction.
- (110) z: (001) at X direction, (1,0) at Y direction, (110) at Z direction.
- (111) x: (111) at X direction, (11) at Y direction, (01) at Z direction.
- (111) z: (01) at X direction, (2) at Y direction, (111) at Z direction.
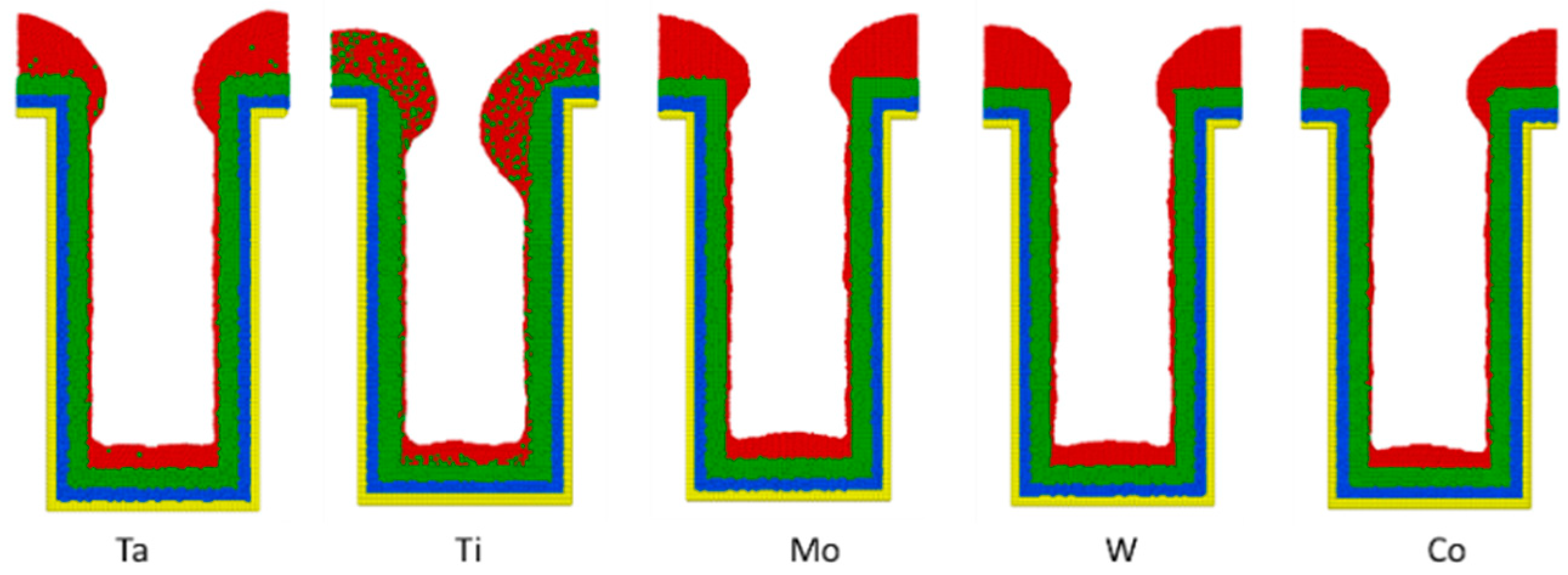
3.6. Liner Materials
4. Conclusions
- The additional energy of atoms, such as increasing substrate temperature and increasing incident energy, leads the atoms at the wing to flow into the trench and mainly accumulate at the top sidewall. This increases the step coverage but decreases the uniformity.
- Decreasing the deposition rate results in a better diffusion of deposited atoms to the substrate, thus increasing the effect of Ostwald ripening, which leads to better uniformity.
- Different sections of the trench have optimal incident angles for receiving atoms, which are dependent on the size and features of the trench.
- The necking of the copper seed layer can be increased by decreasing the substrate temperature, incident energy, incident angle, and deposition rate.
- The overall bottom height of the copper seed layer can be increased by increasing the incident energy and decreasing the substrate temperature, incident angle, and deposition rate.
- The alloy percentage can be decreased by decreasing the substrate temperature, incident energy, and deposition rate.
- Surface diffusion barrier energy caused by the potential energy and lattice structure is the dominant factor of different crystal planes. A lower diffusion barrier energy at the sidewall direction of the trench with a larger diffusion barrier energy at the wing direction of the trench allows the atoms at the top sidewall to flow to the wing, while stopping atoms from flowing the other way. This increases the necking and leads to better uniformity.
- For different liner materials, the alloy percentage of the copper seed layer is the dominant factor. With greater cohesive energy, the alloy percentage decreases and thus decreases the additional diffusion barrier energy from the alloy atoms, which results in atoms at the top sidewall flowing towards the wing. Consequently, the necking and uniformity are increased.
- The wing and top sidewall are the dominant areas of the copper seed layer. If the atoms tend to flow from the top sidewall to the wing rather than the other way around, necking would increase. Atoms depositing into the trench would thus increase and result in better uniformity.
- Among the parameters discussed in this study, the diffusion barrier of different crystal planes is the most decisive factor, which leads to good uniformity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Motegi, N.; Kashimoto, Y.; Nagatani, K.; Takahashi, S.; Kondo, T.; Mizusawa, Y.; Nakayama, I. Long-throw low-pressure sputtering technology for very large-scale integrated devices. J. Vac. Sci. Technol. B 1995, 13, 1906–1909. [Google Scholar] [CrossRef]
- Rossnagel, S.M.; Mikalsen, D.; Kinoshita, H.; Cuomo, J.J. Collimated magnetron sputter deposition. J. Vac. Sci. Technol. A 1991, 9, 261–265. [Google Scholar] [CrossRef]
- Rossnagel, S.M.; Hopwood, J. Metal ion deposition from ionized magnetron sputtering discharge. J. Vac. Sci. Technol. B 1994, 12, 449–453. [Google Scholar] [CrossRef]
- Hopwood, J. Ionized physical vapor deposition of integrated circuit interconnects. Phys. Plasmas 1998, 5, 1624–1631. [Google Scholar] [CrossRef] [Green Version]
- Edelstein, D.; Uzoh, C.; Cabral, C., Jr.; DeHaven, P.; Buchwalter, P.; Simon, A. An optimal liner for copper damascene interconnects. In Proceedings of the Advanced Metallization Conference, Montreal, QC, Canada, 7–10 October 2001; pp. 541–547. [Google Scholar]
- Wu, W.; Wu, H.J.; Dixit, G.; Shaviv, R.; Gao, M.; Mountsier, T. Ti-based barrier for Cu interconnect applications. In Proceedings of the IEEE International Interconnect Technology Conference, Burlingame, CA, USA, 1–4 June 2008; pp. 202–204. [Google Scholar]
- Lanzillo, N.A.; Yang, C.C.; Motoyama, K.; Huang, H.; Cheng, K.; Maniscalco, J.; Van Der Straten, O.; Penny, C.; Standaert, T.; Choi, K. Exploring the Limits of Cobalt Liner Thickness in Advanced Copper Interconnects. IEEE Electron Device Lett. 2019, 40, 1804–1807. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, K.; Song, Z.; Yang, J. Ultrathin Mo/MoN bilayer nanostructure for diffusion barrier application of advanced Cu metallization. Appl. Surf. Sci. 2010, 256, 6003–6006. [Google Scholar] [CrossRef]
- Ono, H.; Nakano, T.; Ohta, T. Diffusion Barrier Effects Against Cu of W-N Layer Formed by Electron Cyclotron Resonance Plasma Nitridation on W Layer. Jpn. J. Appl. Phys. 1995, 34, 1827–1830. [Google Scholar] [CrossRef]
- Yang, Y.G.; Zhou, X.W.; Johnson, R.A.; Wadley, H.G. Atomistic Simulations of Deep Submicron Interconnect Metallization. J. Vac. Sci. Technol. B 2002, 20, 622–630. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Kushnerb, M.J. Trench filling by ionized metal physical vapor deposition. J. Vac. Sci. Technol. A 2001, 19, 2652–2663. [Google Scholar] [CrossRef] [Green Version]
- Ju, S.P.; Weng, C.I.; Hwang, C.C. Damascene process simulation using molecular dynamics. J. Appl. Phys. 2002, 92, 7062–7069. [Google Scholar] [CrossRef]
- Hong, R.T.; Yang, J.Y. Molecular Dynamics Study on Enhanced Cu Coverage of Trench Filling with Low-Index Ta Surfaces. Jpn. J. Appl. Phys. 2012, 51, 06FF14-1–06FF14-6. [Google Scholar] [CrossRef]
- Chan, K.Y.; Teo, B.-S. Sputtering power and deposition pressure effects on the electrical and structural properties of copper thin films. J. Mater. Sci. 2005, 40, 5971–5981. [Google Scholar] [CrossRef]
- Adrien Chauvin, A.; Horak, L.; Duverger-Nédellec, E.; Dopita, M.; Tessier, P.-Y.; El Mel, A.-A. Effect of the substrate temperature during gold-copper alloys thin film deposition by magnetron co-sputtering on the dealloying process. Surf. Coat. Technol. 2020, 383, 125220. [Google Scholar] [CrossRef]
- Li, Z.; Tian, Y.; Teng, C.; Cao, H. Recent Advances in Barrier Layer of Cu Interconnects. Materials 2020, 13, 5049. [Google Scholar] [CrossRef] [PubMed]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef] [Green Version]
- Johnson, R.A. Alloy Models with the Embedded-Atom Method. Phys. Rev. B 1989, 39, 12554–12559. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef] [Green Version]
- Langevin, P. On the theory of Brownian motion. C. R. Acad. Sci. 1908, 146, 530–533. [Google Scholar]





| Materials | Crystal Structure | Lattice Parameters (Angstroms) |
|---|---|---|
| Tantalum (Ta) | BCC | 3.3, 3.3, 3.3 |
| Titanium (Ti) | HCP | 2.95, 2.95, 4.68 |
| Molybdenum (Mo) | BCC | 3.147, 3.147, 3.147 |
| Cobalt (Co) | HCP | 2.51, 2.51, 4.07 |
| Tungsten (W) | BCC | 3.17, 3.17, 3.17 |
| Surface | Layers | Surface Diffusion Barrier Energy (ev) |
|---|---|---|
| Ta (100) | 16 | 0.883 |
| Ta (110) | 14 | 0.543 |
| Ta (111) | 14 | 2.076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, C.-H.; Chen, C.-K.; Chen, C.-L. A Study on Sputtering of Copper Seed Layer for Interconnect Metallization via Molecular Dynamics Simulation. Appl. Sci. 2021, 11, 9702. https://doi.org/10.3390/app11209702
Ho C-H, Chen C-K, Chen C-L. A Study on Sputtering of Copper Seed Layer for Interconnect Metallization via Molecular Dynamics Simulation. Applied Sciences. 2021; 11(20):9702. https://doi.org/10.3390/app11209702
Chicago/Turabian StyleHo, Cheng-Hsuan, Cha’o-Kuang Chen, and Chieh-Li Chen. 2021. "A Study on Sputtering of Copper Seed Layer for Interconnect Metallization via Molecular Dynamics Simulation" Applied Sciences 11, no. 20: 9702. https://doi.org/10.3390/app11209702
APA StyleHo, C.-H., Chen, C.-K., & Chen, C.-L. (2021). A Study on Sputtering of Copper Seed Layer for Interconnect Metallization via Molecular Dynamics Simulation. Applied Sciences, 11(20), 9702. https://doi.org/10.3390/app11209702






