Experimental Investigation of the Fatigue Lifespan of Anchor Bolts with Consideration of Loading History
Abstract
:1. Introduction
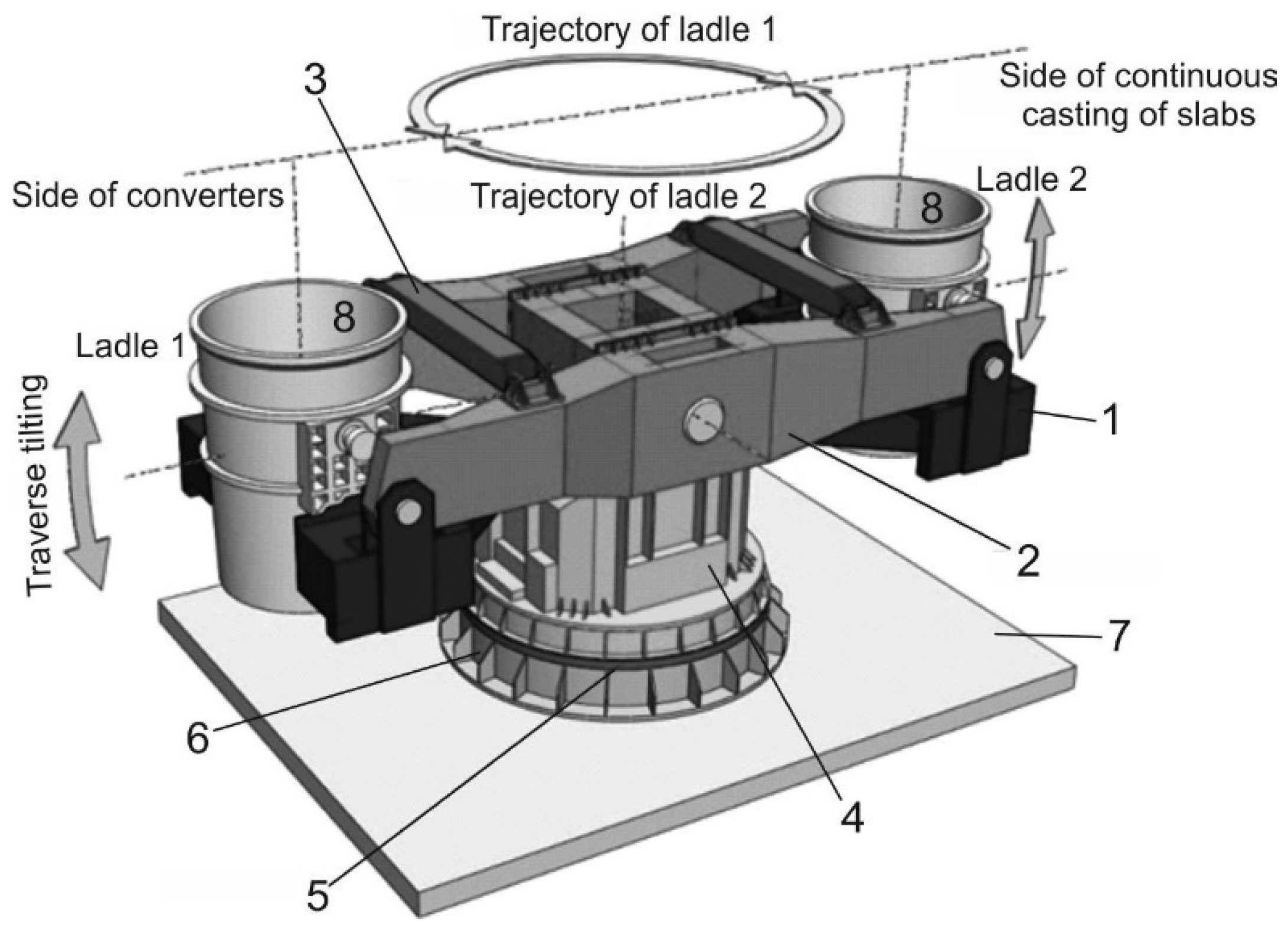
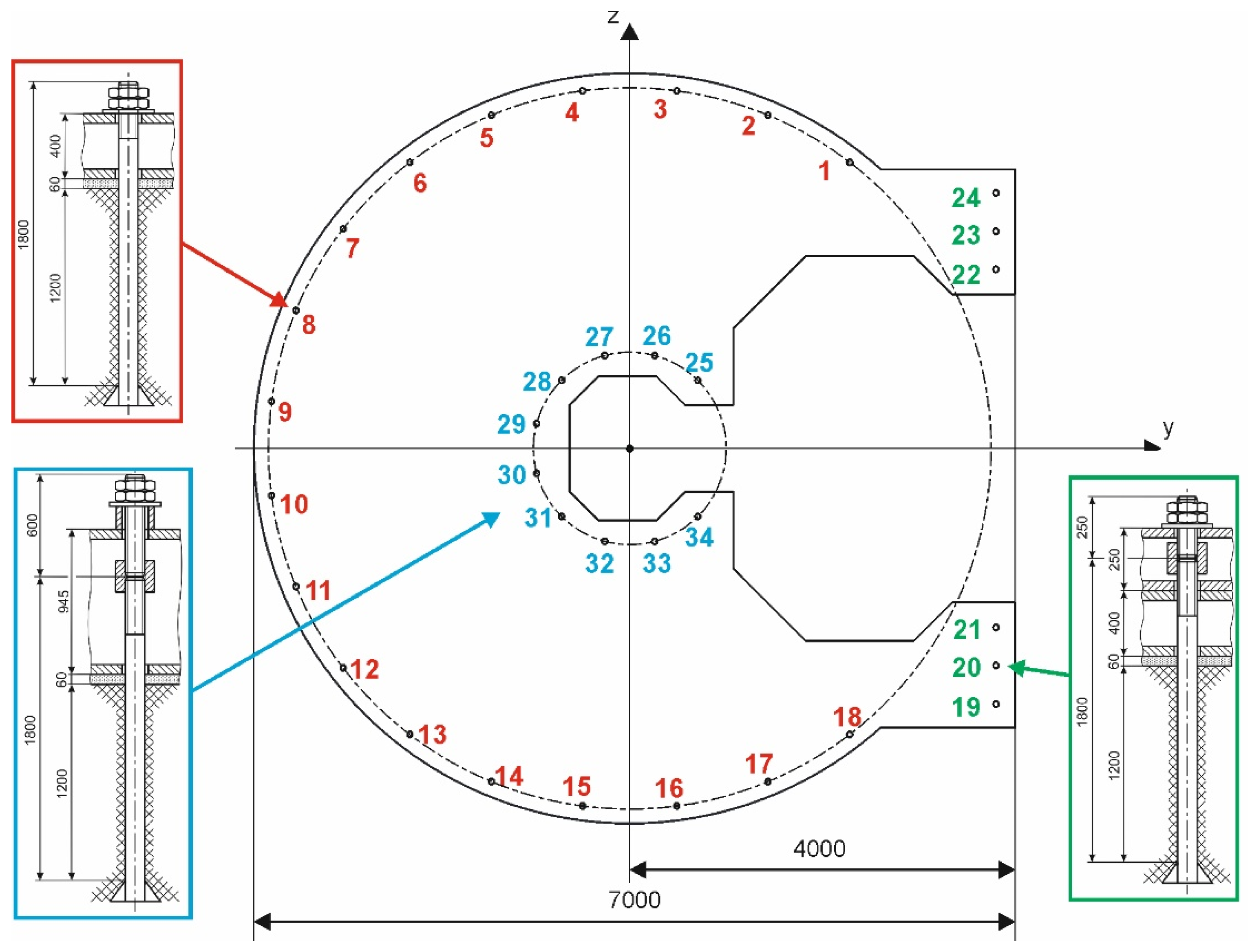
2. Introduction to the Anchoring of the Casting Pedestal
| Maximum weight of the casting ladle with metal (steel) | 260,000 kg |
| Weight of empty ladle | 70,000 kg |
| Ladle lift height | 800 mm |
| Pedestal angular velocity | 1 rpm |
| Maximum angle of rotation | 230° |
| Roller track mean diameter | 6400 mm |
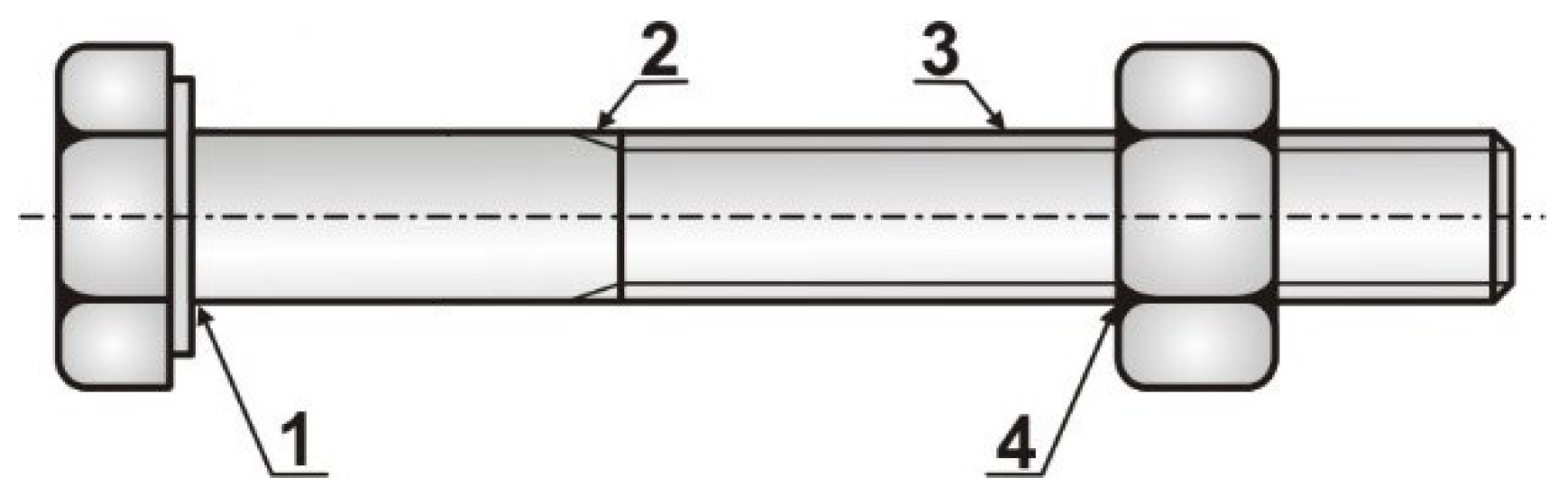
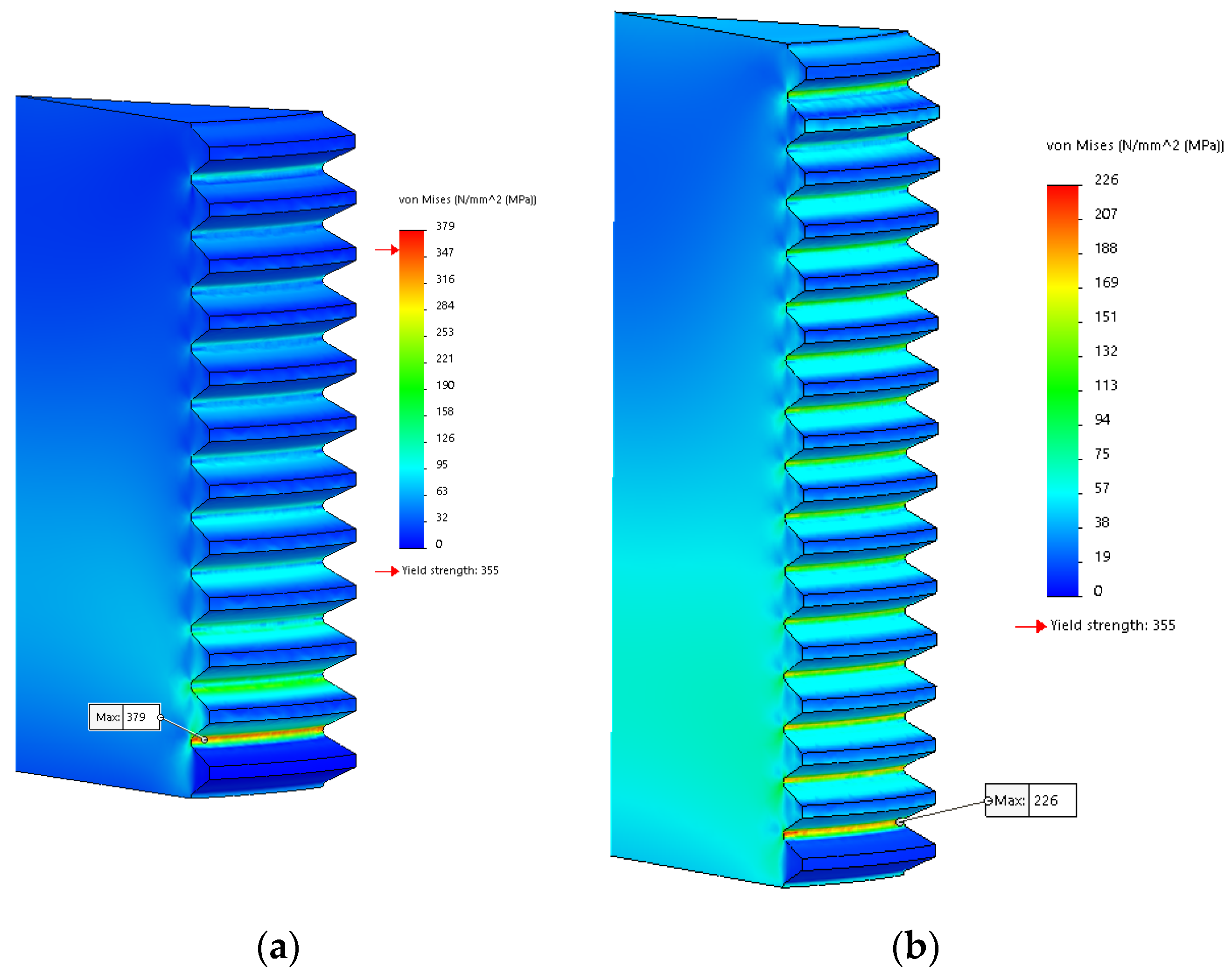
- Location 1—passage of the cylindrical part of the bolt to the head—this location is absent from the anchor bolts;
- Location 2—thread runout;
- Location 3—thread;
- Location 4—bolt thread at the first nut’s support thread (the most common cause of failure).
3. Materials and Methods
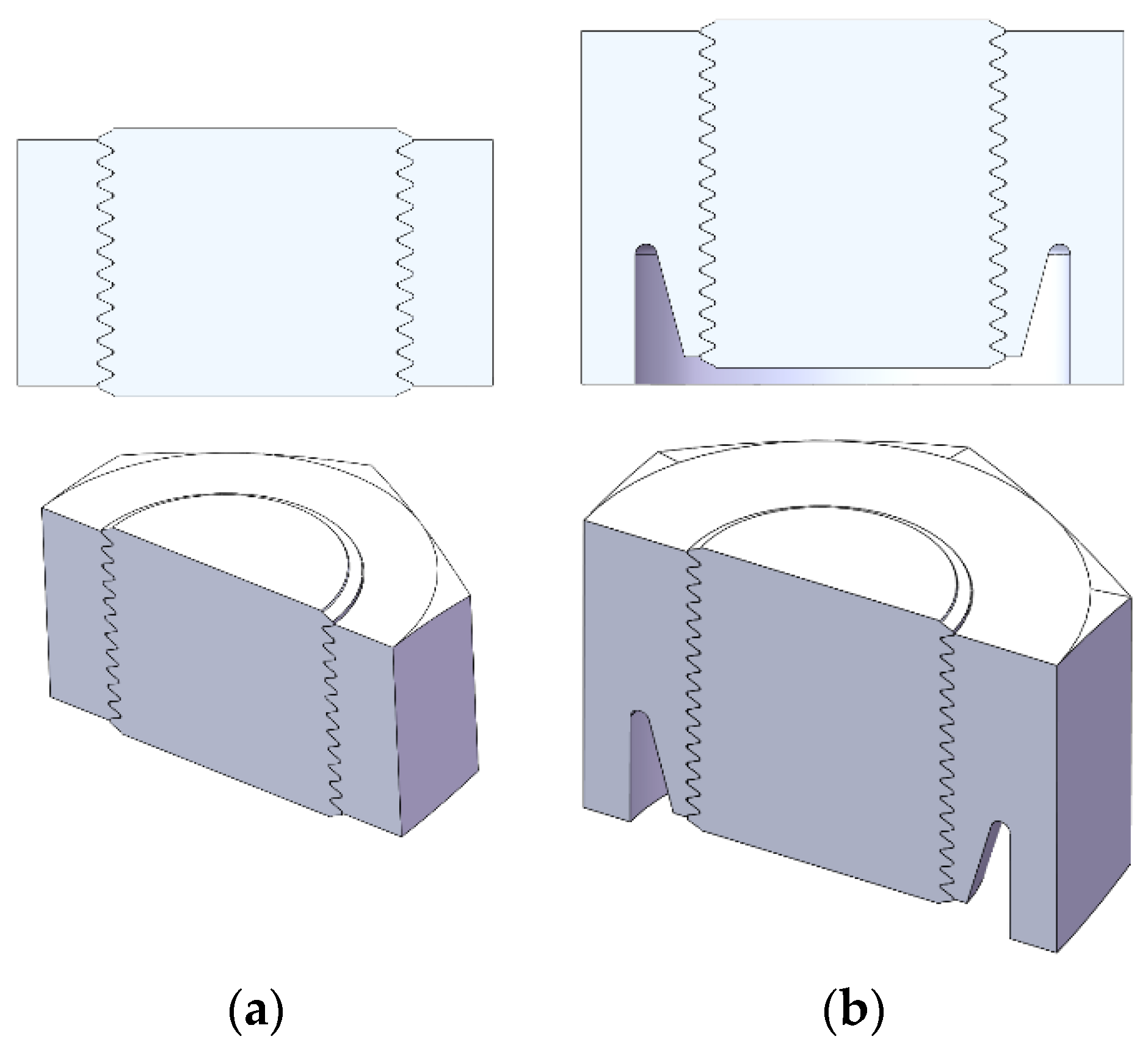
4. Proposal of Nuts Modification Using Finite Element Method (FEM)
5. Experimental Analysis of the Interaction of Anchor Bolts and Concrete Foundation
5.1. Measurement under Static Loading
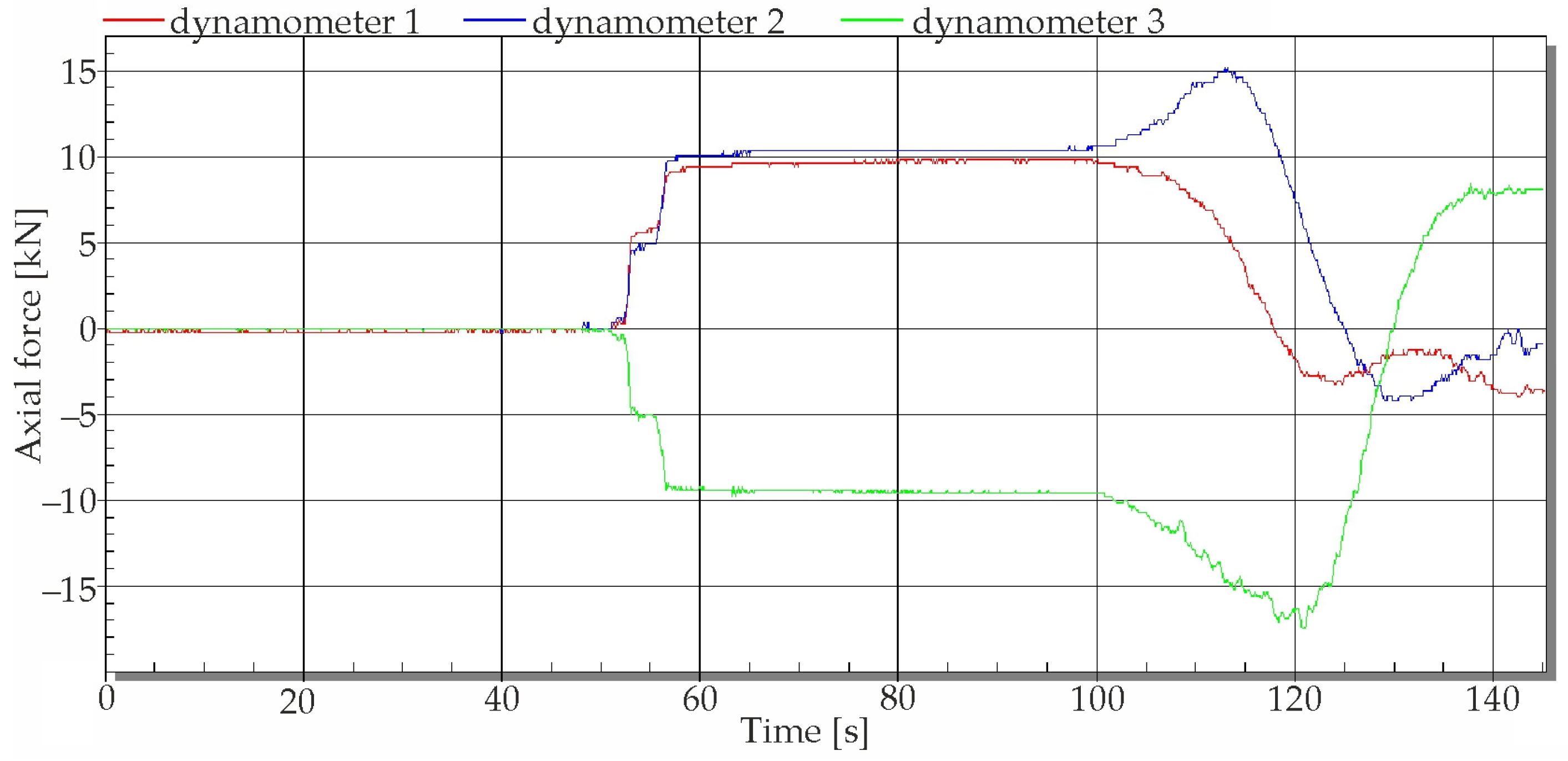
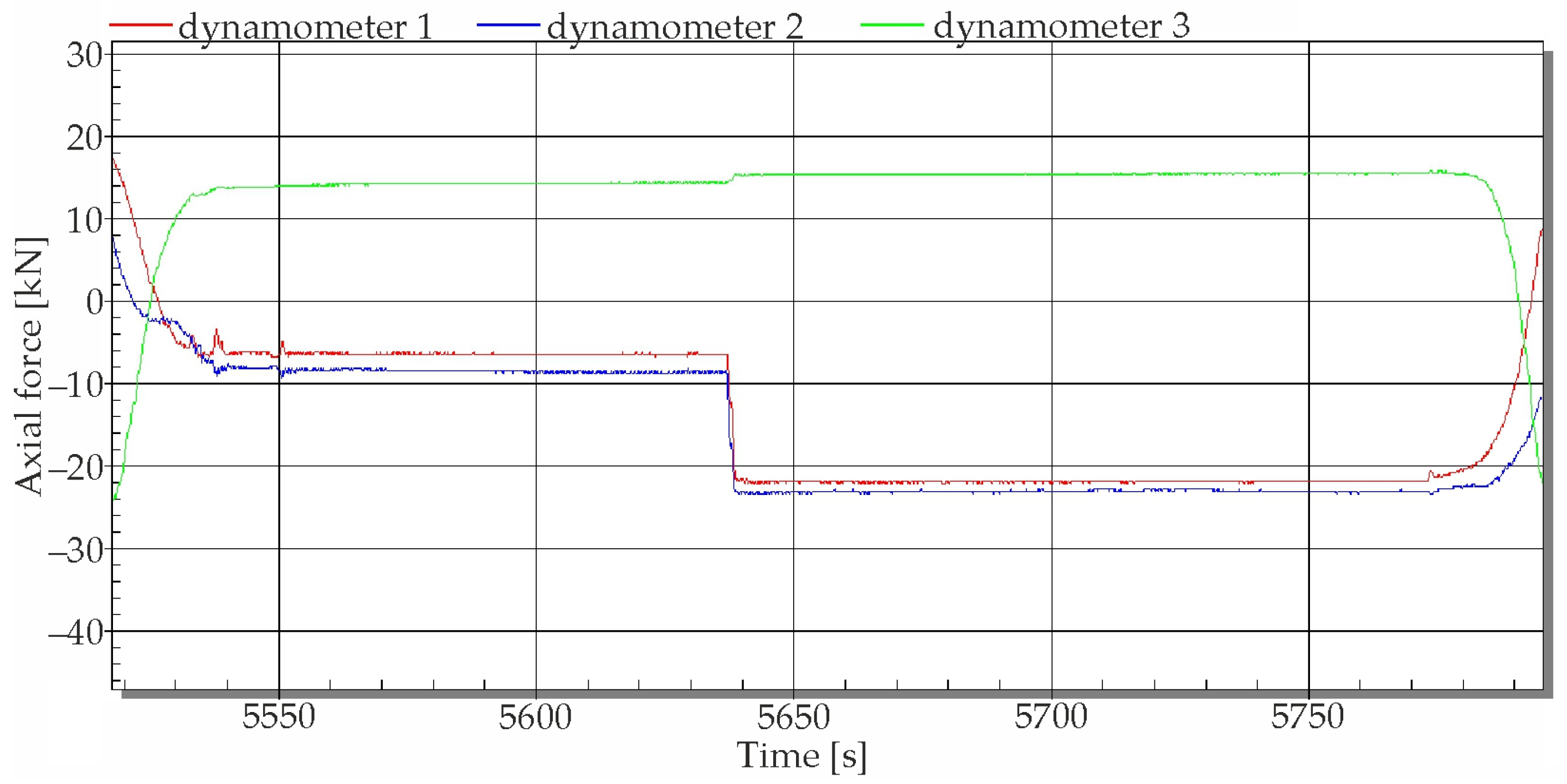
5.2. Measurement at Operational Loading
- Anchor Bolts No. 1 to No. 24 should be preloaded to an axial force corresponding to 200 kN, which corresponds to a given state of bolts, nuts, and washers when defining a pressure value of 120 bar;
- Anchor Bolts No. 25 to No. 34 should have a preload with regard to the passage of the thread into the shank as well as the flexibility of the supporting structure, and a lower range of operational axial forces of 180 kN, i.e., approximately 110 bar.
- Rotation of the pedestal without a ladle in Baskets 1 and 2;
- Loading the empty ladle with subsequent rotation, and lifting of the ladle in the casting position in Basket 1 and subsequently in Basket 2;
- Loading a full ladle weighing 241,600 kg into Basket 1 and subsequently into Basket 2, rotating the pedestal, and lifting and launching the basket with the ladle;
- Loading the empty and full ladle and handling the pedestal, including the replaced ladles in baskets.
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
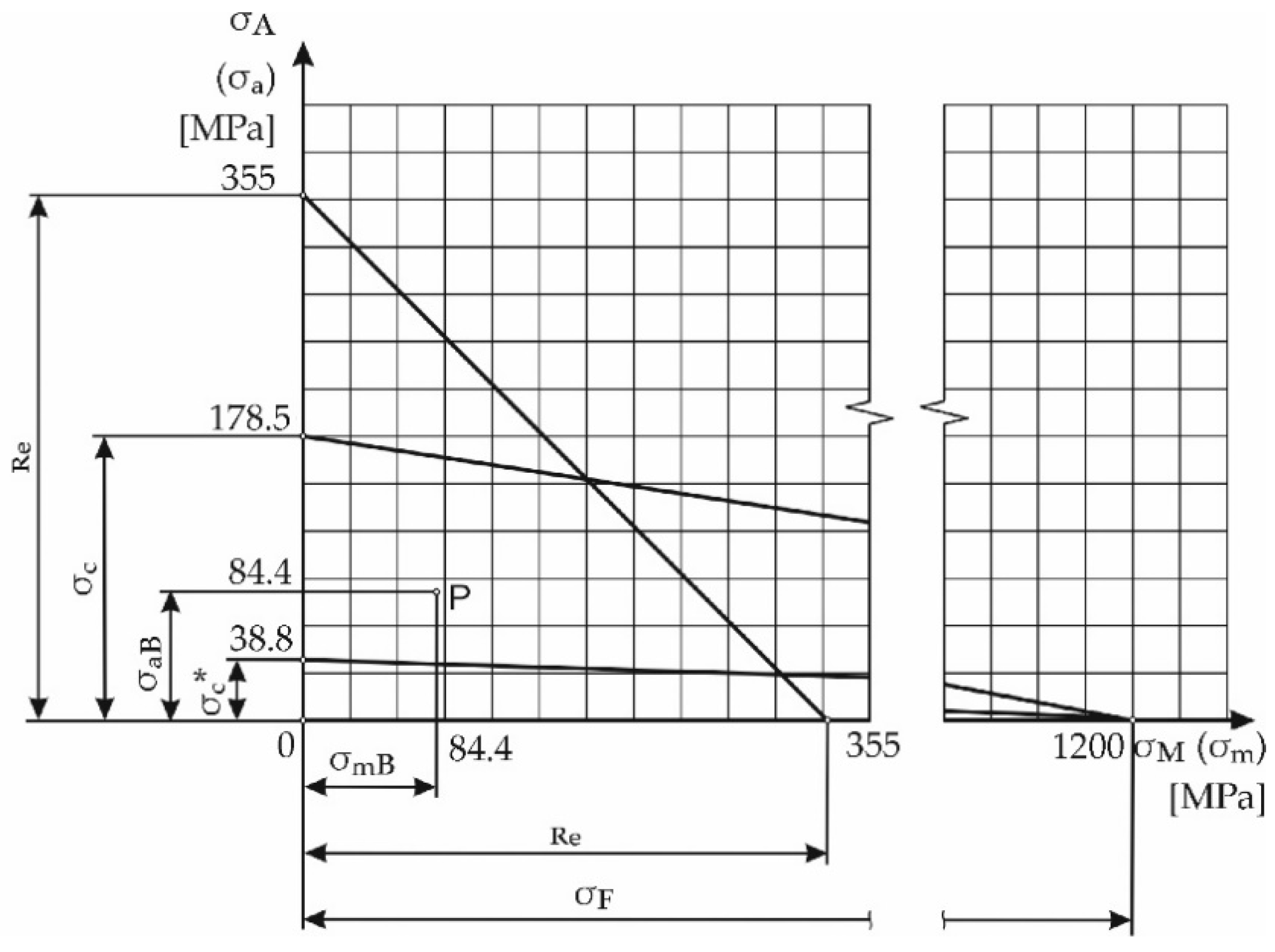
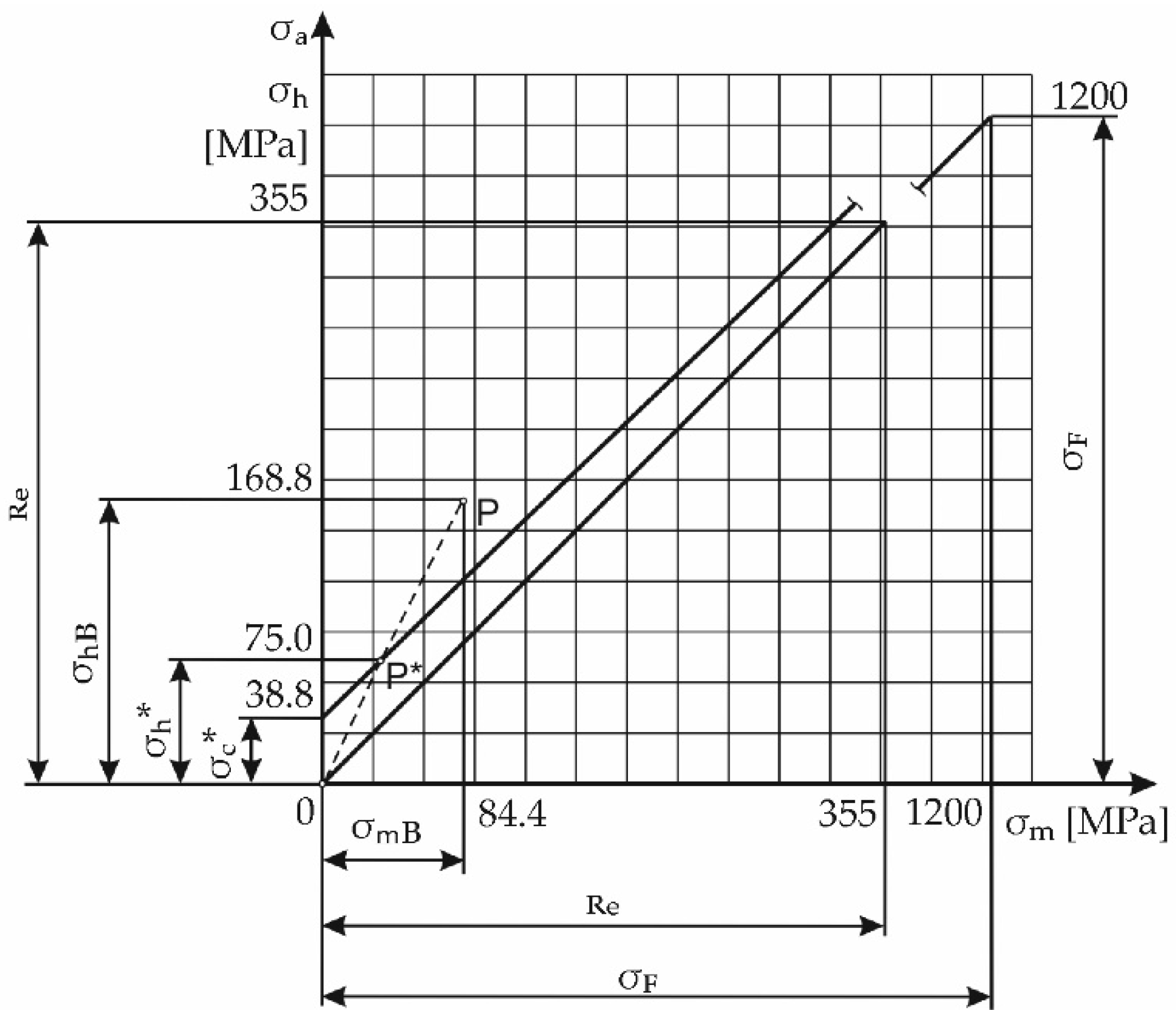
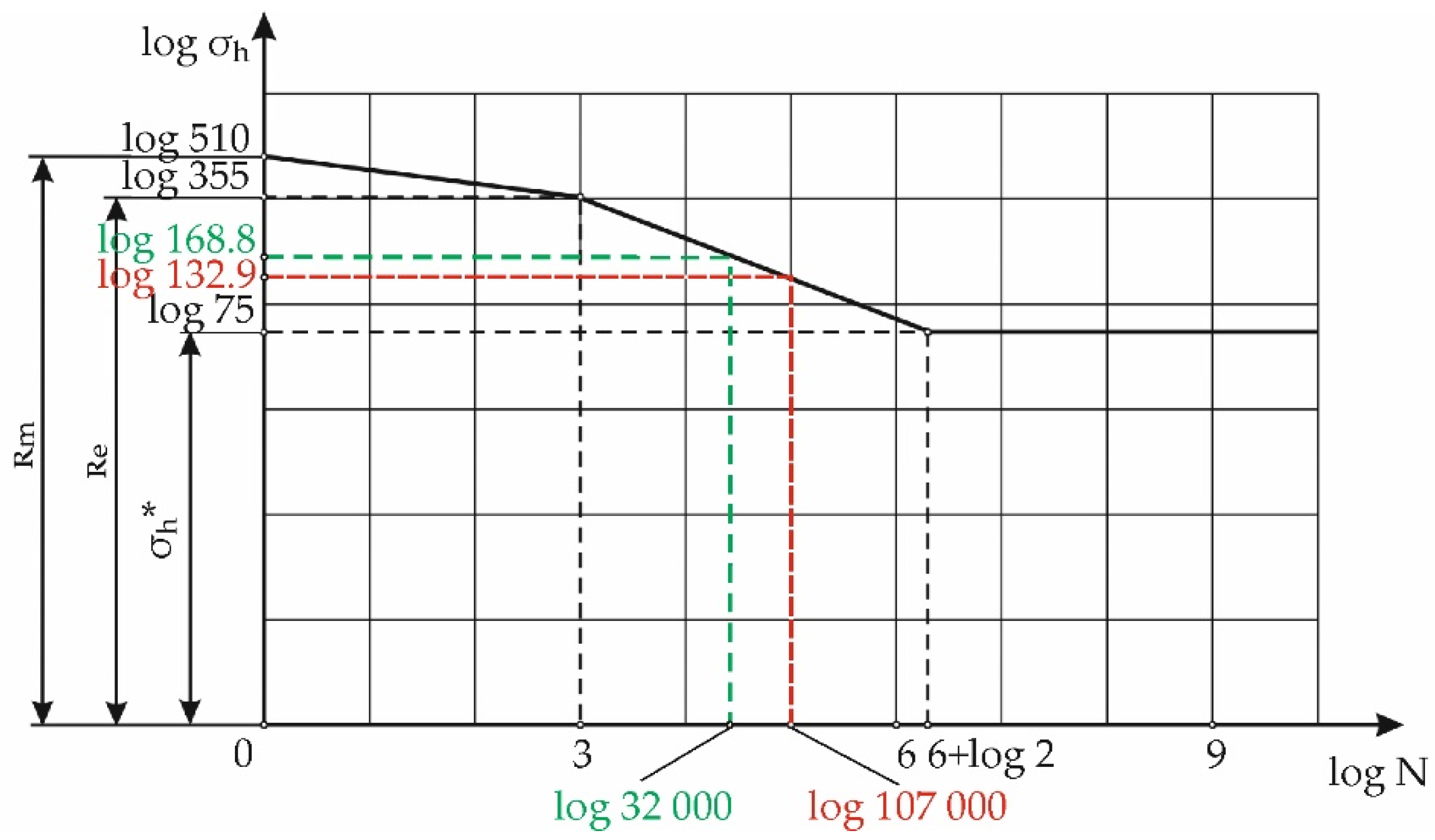
Appendix A
| Yield strength | |
| Tensile strength | |
| Fatigue limit | |
| Fatigue limit for the disappearing cycle | |
| Surface quality factor | |
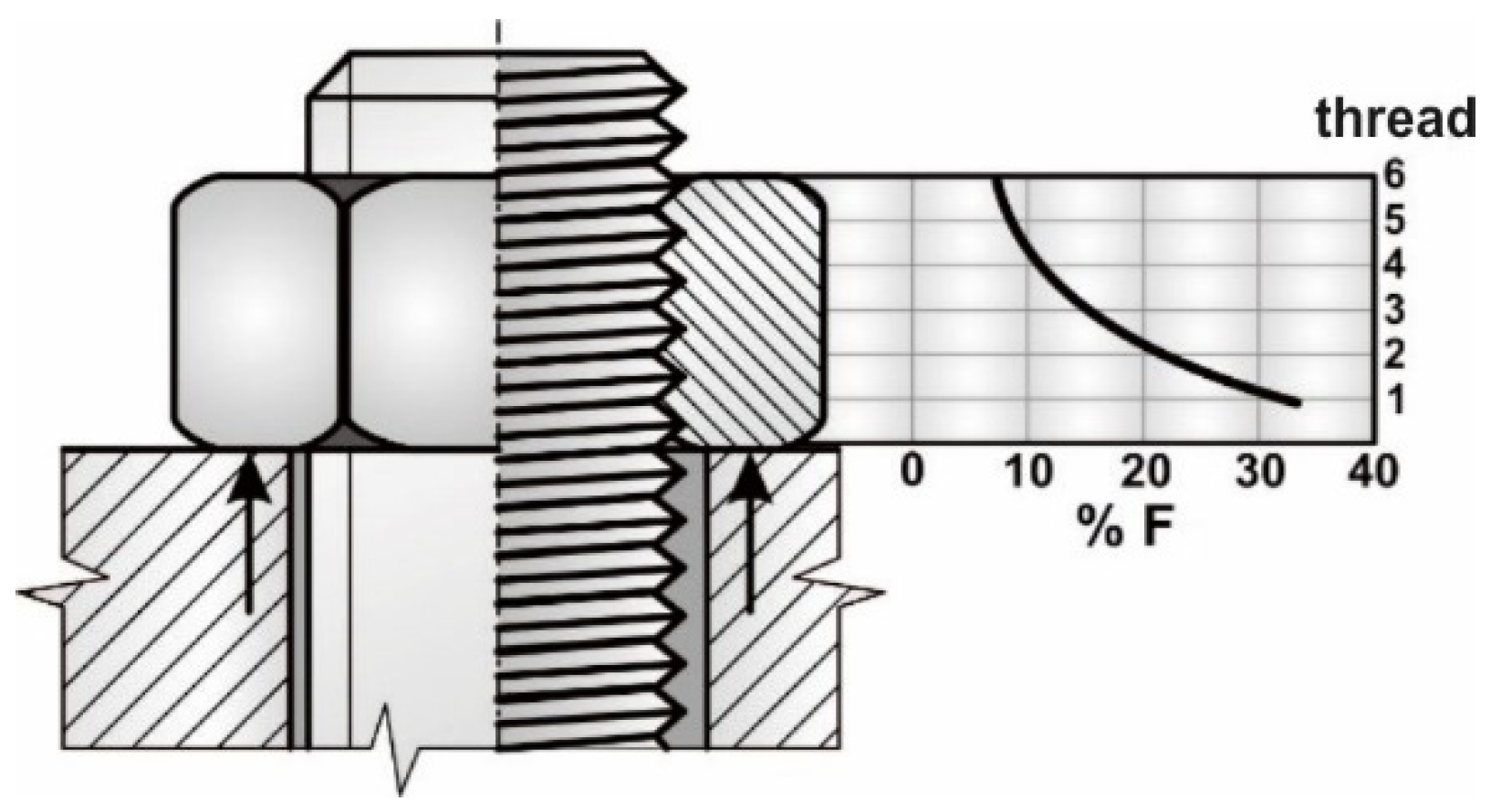
| Fatigue notch factor of Notch 4 was set to |
References
- Design Guide 1: Base Plate and Anchor Rod Design, 2nd ed.; American Institute of Steel Construction: Chicago, IL, USA, 2006; Available online: https://www.aisc.org/Design-Guide-1-Base-Plate-and-Anchor-Rod-Design-Second-Edition (accessed on 21 June 2021).
- Design of Fastenings in Concrete—Design Guide—Parts 1 to 3; Part 1; 1997; ISBN 978-0-7277-2558-5. Available online: https://www.fib-international.org/publications/ceb-bulletins/design-of-fastenings-in-concrete-pdf-detail.html (accessed on 21 November 2021).
- EN 1993-1-8:2005—Eurocode 3: Design of Steel Structures Part 1–8: Design of Joints. Available online: https://standards.iteh.ai/catalog/standards/cen/312c51d1-0813-4e29-b1dd-5db5f15e2497/en-1993-1-8-2005 (accessed on 21 June 2021).
- Delhomme, F.; Debicki, G.; Chaib, Z. Experimental Behaviour of Anchor Bolts under Pullout and Relaxation Tests. Constr. Build. Mater. 2010, 24, 266–274. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C. Experimental Study on the Shear Behavior of Fully Grouted Bolts. Constr. Build. Mater. 2019, 223, 1123–1134. [Google Scholar] [CrossRef]
- Gong, Y.; Ding, Q.; Yang, Z.-G. Failure Analysis on Premature Fracture of Anchor Bolts in Seawater Booster Pump of Nuclear Power Plant. Eng. Fail. Anal. 2019, 97, 10–19. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, N.; Yang, S.; He, F. Mechanical Response of Fully Bonded Bolts under Cyclic Load. Int. J. Rock Mech. Min. Sci. 2018, 109, 138–154. [Google Scholar] [CrossRef]
- Gabáni, Ľ.; Trebuňa, F.; Šimčák, F.; Bocko, J.; Pástor, M. Using Experimental Methods of Mechanics for Failure Prediction of Casting Pedestal. Acta Mech. Slovaca 2015, 19, 42–50. [Google Scholar] [CrossRef]
- Pástor, M.; Trebuňa, F.; Šimčák, F.; Buršák, M.; Šarga, P.; Gabáni, Ľ. Proposal of Methodology and Calibration of Dynamometers for Quantification of Forces in Anchor Bolts. Acta Mech. Slovaca 2014, 18, 14–19. [Google Scholar] [CrossRef]
- Wang, D.S.; Liu, A.Q. Study on the Performance of Full-Length Pre-Stressed Anchor Bolts. Adv. Mater. Res. 2013, 639–640, 765–769. [Google Scholar] [CrossRef]
- Liu, Q.; Chai, J.; Chen, S.; Zhang, D.; Yuan, Q.; Wang, S. Monitoring and Correction of the Stress in an Anchor Bolt Based on Pulse Pre-Pumped Brillouin Optical Time Domain Analysis. Energy Sci. Eng. 2020, 8, 2011–2023. [Google Scholar] [CrossRef]
- Huang, M.H.; Zhao, M.H.; Chen, C.F. Influence of anchorage length on stress in bolt and its critical value calculation. Rock Soil Mech. 2018, 39, 4033–4041. [Google Scholar]
- Yang, S.S.; Cao, J.P. Evolution mechanism of anchoring stress and its correlation with anchoring length. J. Min. Saf. Eng. 2010, 27, 1–7. [Google Scholar]
- Wen, Z.; Shi, Y.; Cui, Z.-D.; Wang, R.-C. Study of Stress Features of Fully Grouted Prestressed Anchors. Rock Soil Mech. 2010, 31, 177–181. [Google Scholar]
- Sapieta, M.; Sapietova, A.; Gajdos, L. Determine the Fatigue Life of Flange of Bearings Test Station. Procedia Eng. 2017, 177, 548–553. [Google Scholar] [CrossRef]
- Trebuňa, F.; Šimčák, F.; Bocko, J. Decreasing of Vibration Amplitudes of the Converter Pedestal by Design Changes and Changes in Prestress of the Bolted Joints. Eng. Fail. Anal. 2009, 16, 262–272. [Google Scholar] [CrossRef]
- Tizani, W.; Rahman, N.A.; Pitrakkos, T. Fatigue Life of an Anchored Blind-Bolt Loaded in Tension. J. Constr. Steel Res. 2014, 93, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.; Lu, L.; Zeng, D. Fatigue Failure Analysis of High Strength Bolts Used for High-Speed Railway Vehicle Braking Discs. Eng. Fail. Anal. 2020, 115, 104661. [Google Scholar] [CrossRef]
- Choi, J.; Kim, B. Failure Analysis of Anchor Bolt of Rail Fastening System for Direct Fixation Track. Eng. Fail. Anal. 2020, 112, 104513. [Google Scholar] [CrossRef]
- Miao, R.; Shen, R.; Zhang, S.; Xue, S. A Review of Bolt Tightening Force Measurement and Loosening Detection. Sensors 2020, 20, 3165. [Google Scholar] [CrossRef]
- Bocko, J.; Čarák, P.; Čajka, M. Analysis of Stress and Deformation States in Bolted Joints with Prestress. Am. J. Mech. Eng. 2016, 4, 241–246. [Google Scholar] [CrossRef]
- Lin, S.-R.; Wu, W.-F. Estimation of Maximum Axial Force of Anchor Bolts in Consideration of Random Bolt Failures. Int. J. Press. Vessel. Pip. 2015, 131, 52–59. [Google Scholar] [CrossRef]
- Zheng, X.G.; Zhang, N.; Xue, F. Study on stress distribution law in anchoring section of prestressed bolt. J. Min. Saf. Eng. 2012, 29, 365–370. [Google Scholar]
- Konstrukce Strojů a Zařízení I: Spojovací Části Strojů: Návrh, Výpočet, Konstrukce/Zdeněk Dejl Portaro Katalog Knihovny. Available online: https://katalog.vsb.cz/documents/46509 (accessed on 21 June 2021).



| Tightening Device Pressure [bar] | Axial Force in Bolt [kN] |
|---|---|
| 60 | 93 |
| 110 | 178 |
| 160 | 266 |
| 200 | 345 |
| Anchor Bolt | Dynamometer |
|---|---|
| 19 | 1 |
| 24 | 2 |
| 8 | 3 |
| 11 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pástor, M.; Lengvarský, P.; Hagara, M.; Sapietová, A.; Šarga, P. Experimental Investigation of the Fatigue Lifespan of Anchor Bolts with Consideration of Loading History. Appl. Sci. 2021, 11, 11399. https://doi.org/10.3390/app112311399
Pástor M, Lengvarský P, Hagara M, Sapietová A, Šarga P. Experimental Investigation of the Fatigue Lifespan of Anchor Bolts with Consideration of Loading History. Applied Sciences. 2021; 11(23):11399. https://doi.org/10.3390/app112311399
Chicago/Turabian StylePástor, Miroslav, Pavol Lengvarský, Martin Hagara, Alžbeta Sapietová, and Patrik Šarga. 2021. "Experimental Investigation of the Fatigue Lifespan of Anchor Bolts with Consideration of Loading History" Applied Sciences 11, no. 23: 11399. https://doi.org/10.3390/app112311399
APA StylePástor, M., Lengvarský, P., Hagara, M., Sapietová, A., & Šarga, P. (2021). Experimental Investigation of the Fatigue Lifespan of Anchor Bolts with Consideration of Loading History. Applied Sciences, 11(23), 11399. https://doi.org/10.3390/app112311399






