Influence of the Final Ratio on the Consumption of an Electric Vehicle under Conditions of Standardized Driving Cycles
Abstract
:1. Introduction
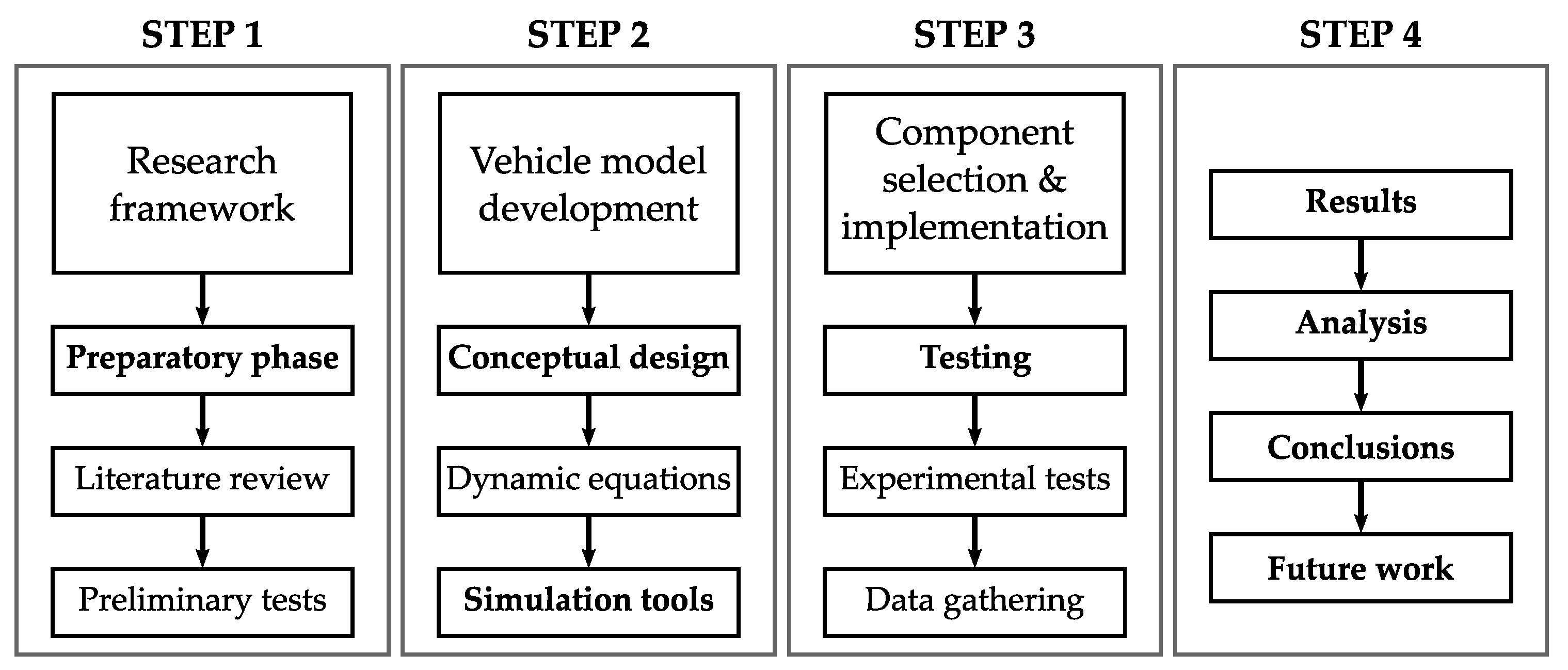
2. Proposed Methodology
2.1. Test Setup
2.2. Physical Implementation
2.3. Data Acquisition
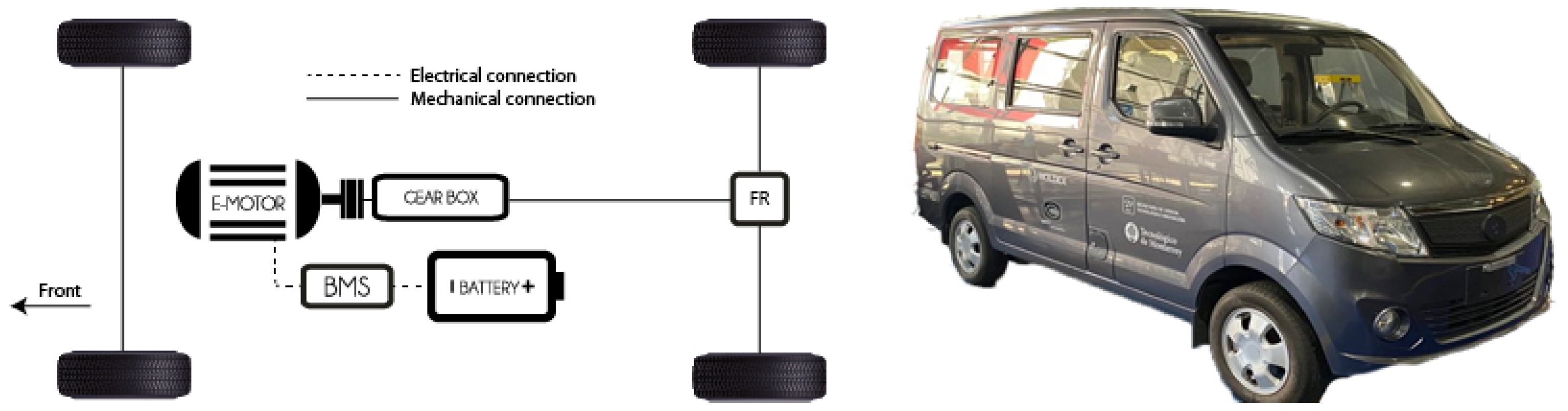
3. Experimental Test Vehicle
Physical Implementation of the New Differential Final Ratio
4. Modeling
4.1. Vehicle Dynamics
- Rolling resistance
- Aerodynamic drag
- Vehicle weight when running through a graded road
- Inertial forces whenever a change in velocity is required
4.1.1. Rolling Resistance Force
4.1.2. Aerodynamic Drag
4.1.3. Hill Climbing Force
4.1.4. Net Force
4.1.5. Tractive Force
4.1.6. Gradability
4.2. Battery Model
5. Simulations
- The vehicle moves only in the longitudinal direction.
- The system is considered as ideally rigid; no vibration or damping effects are accounted for.
- The tire radius is assumed to be constant.
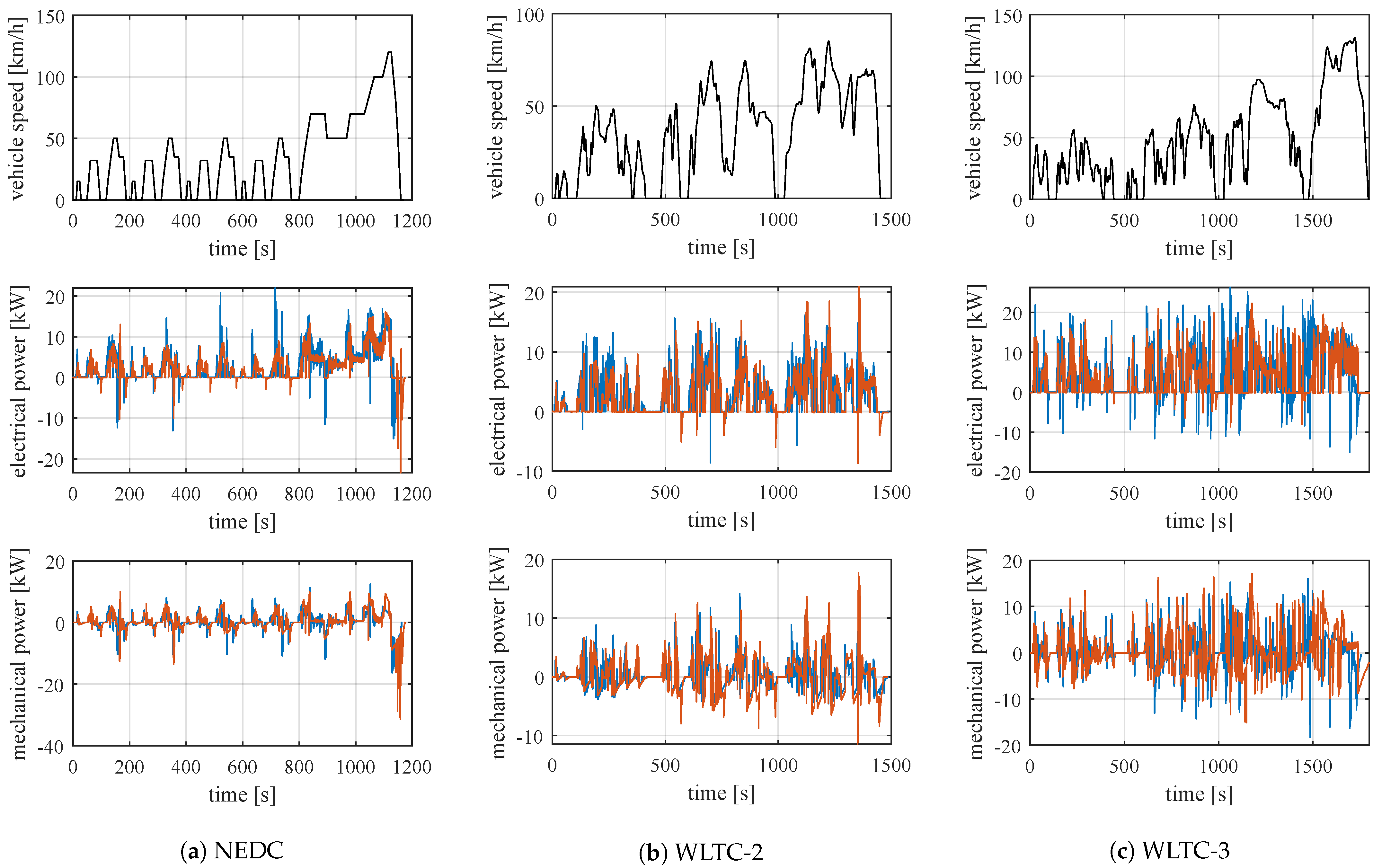
5.1. Driving Cycles
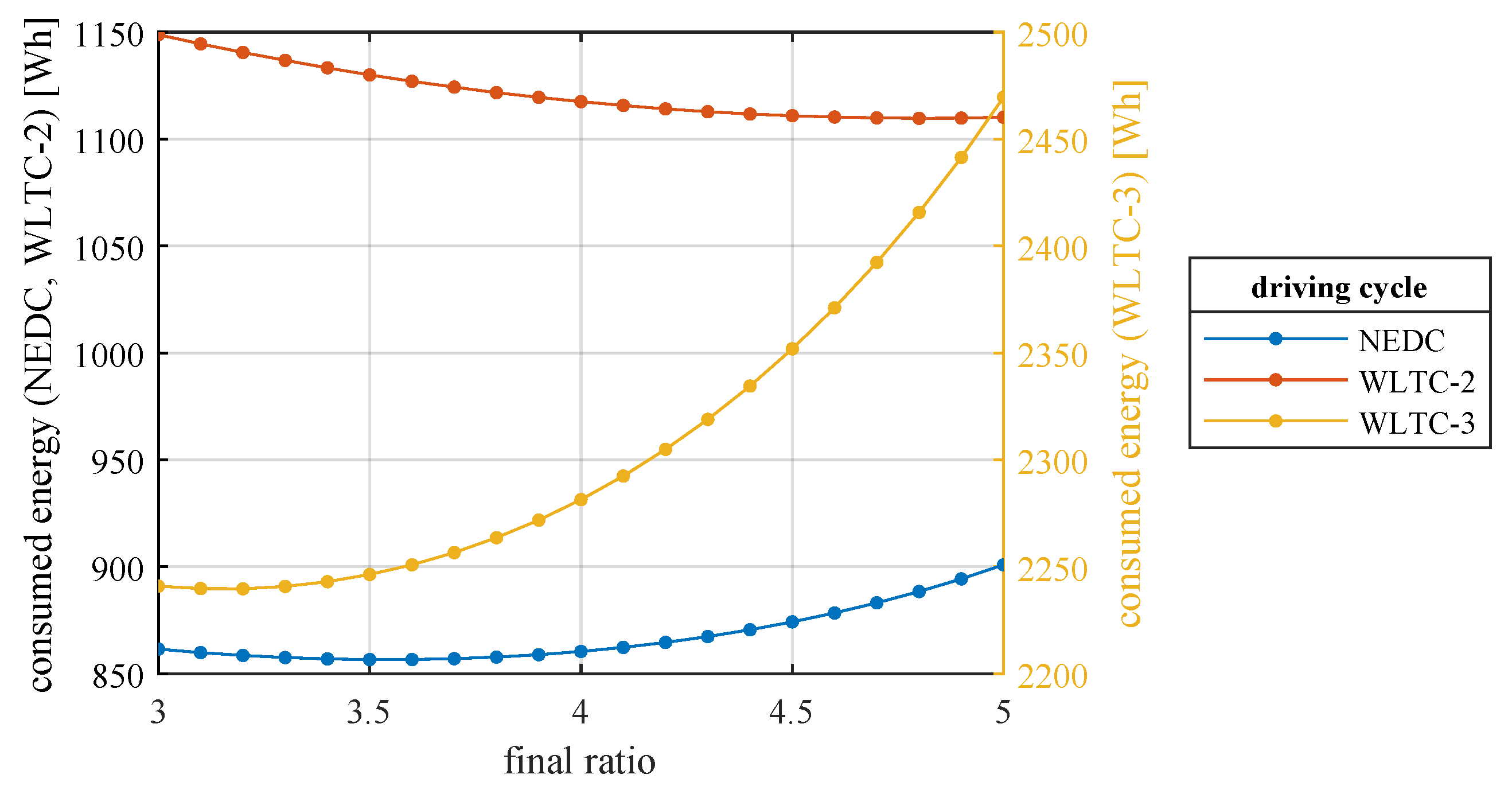
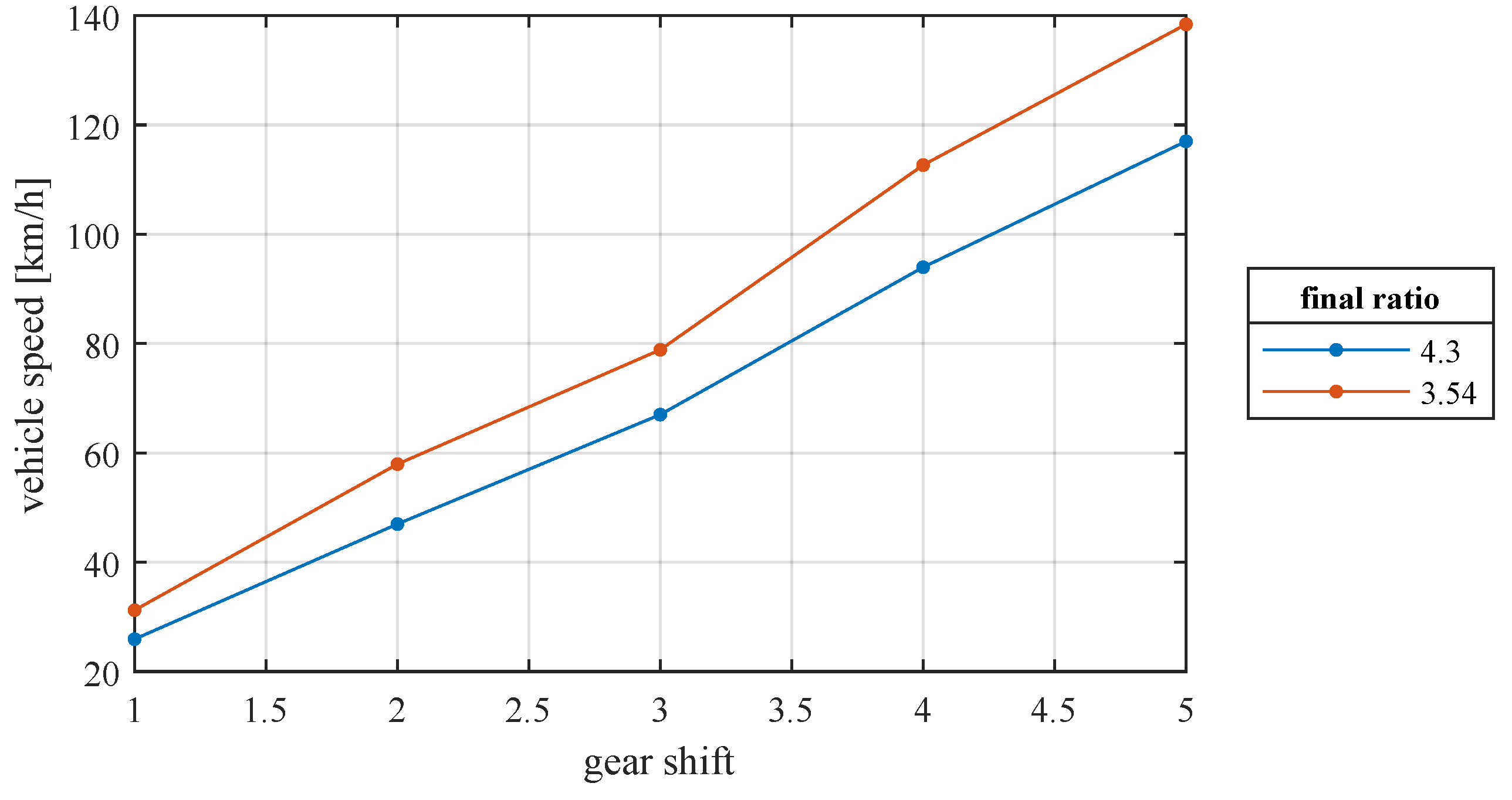
5.2. Final Ratio Influence
6. Experimental Validation
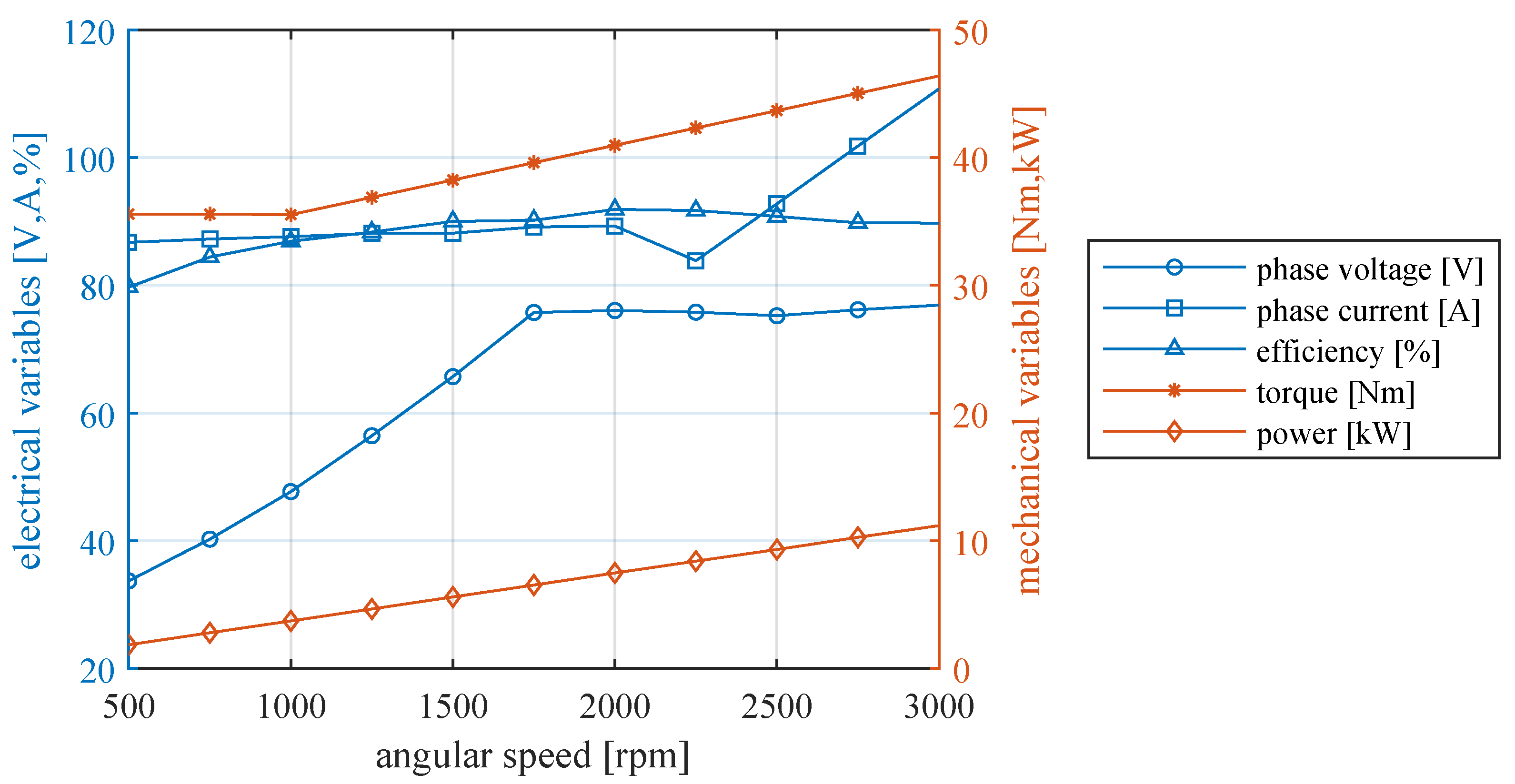
6.1. Electric and Mechanical Power Delivered by the Vehicle
6.2. Energy Management Test Simulation
7. Results and Discussion
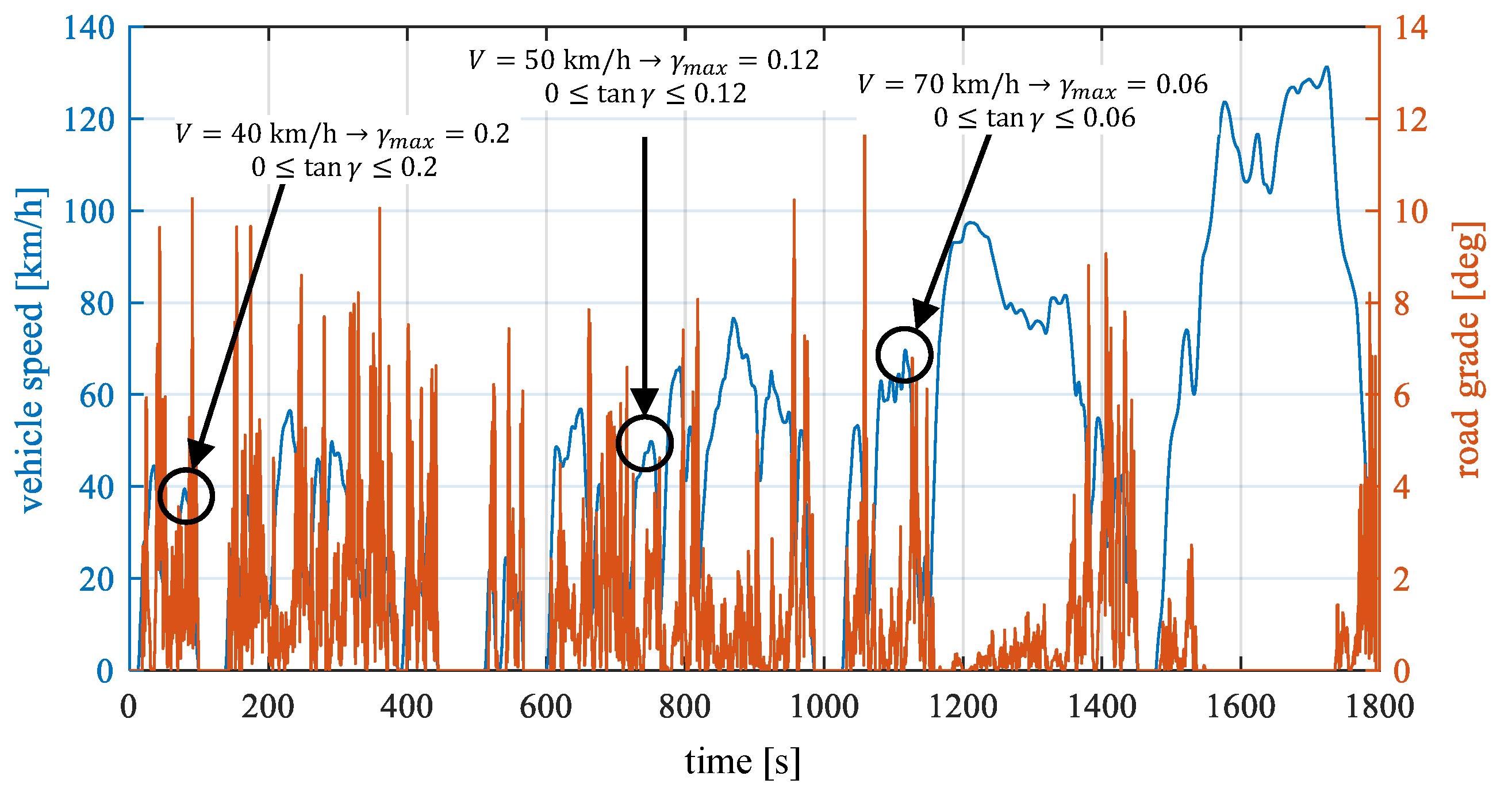
7.1. Road Grade Influence
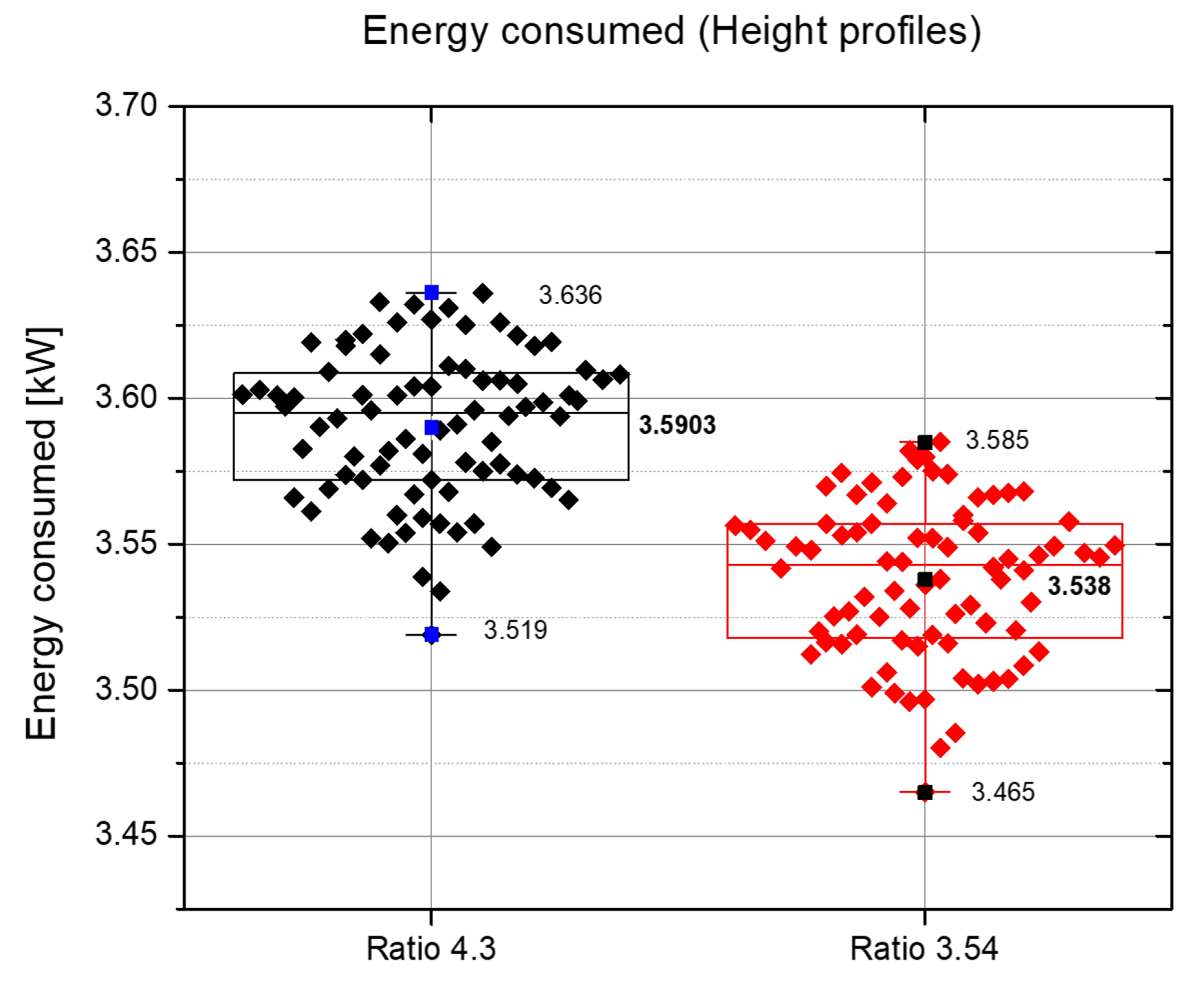
7.2. Energy Consumed Simulated with Height Profiles
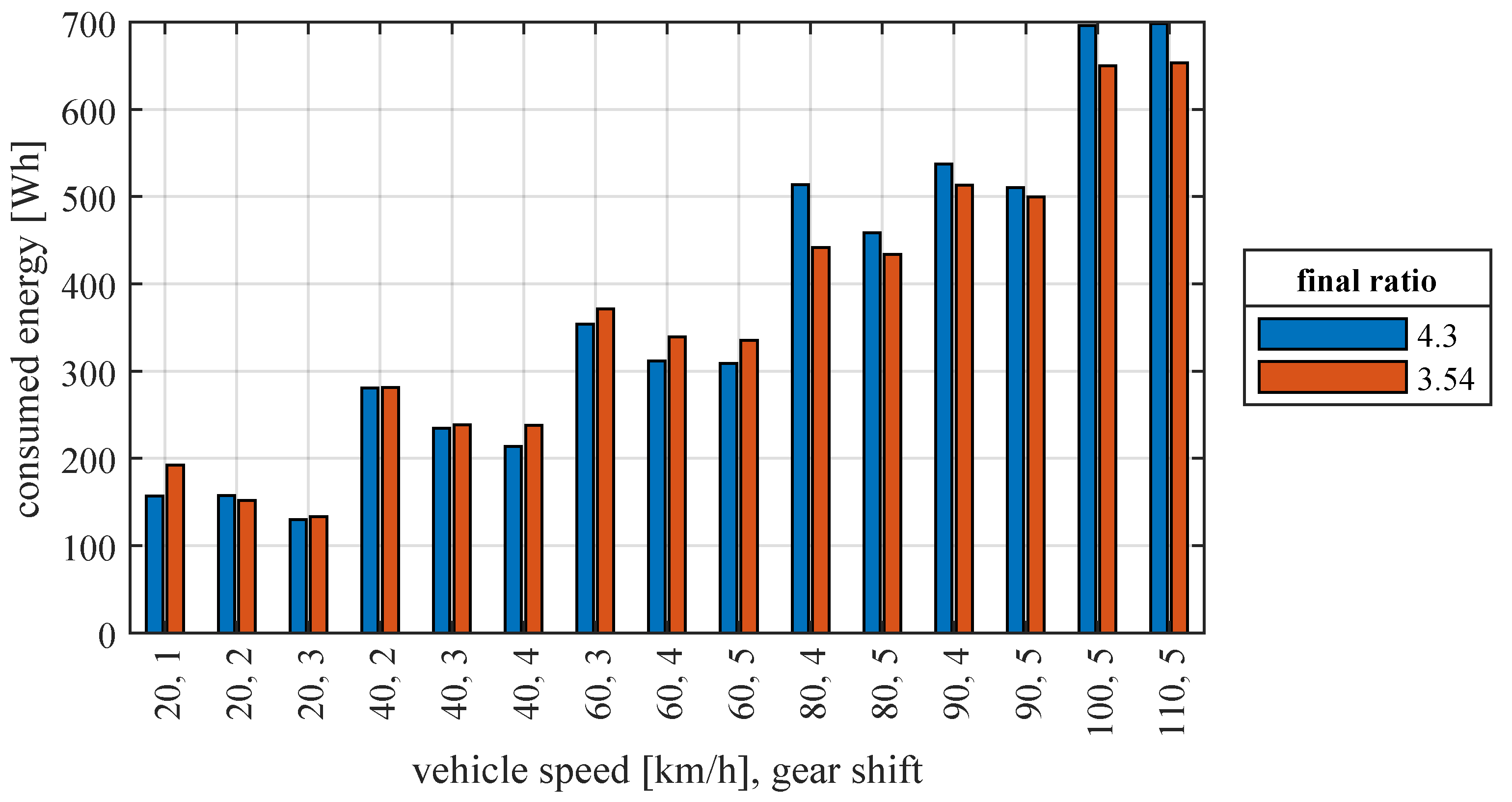
7.3. Energy Consumed at a Constant Speed
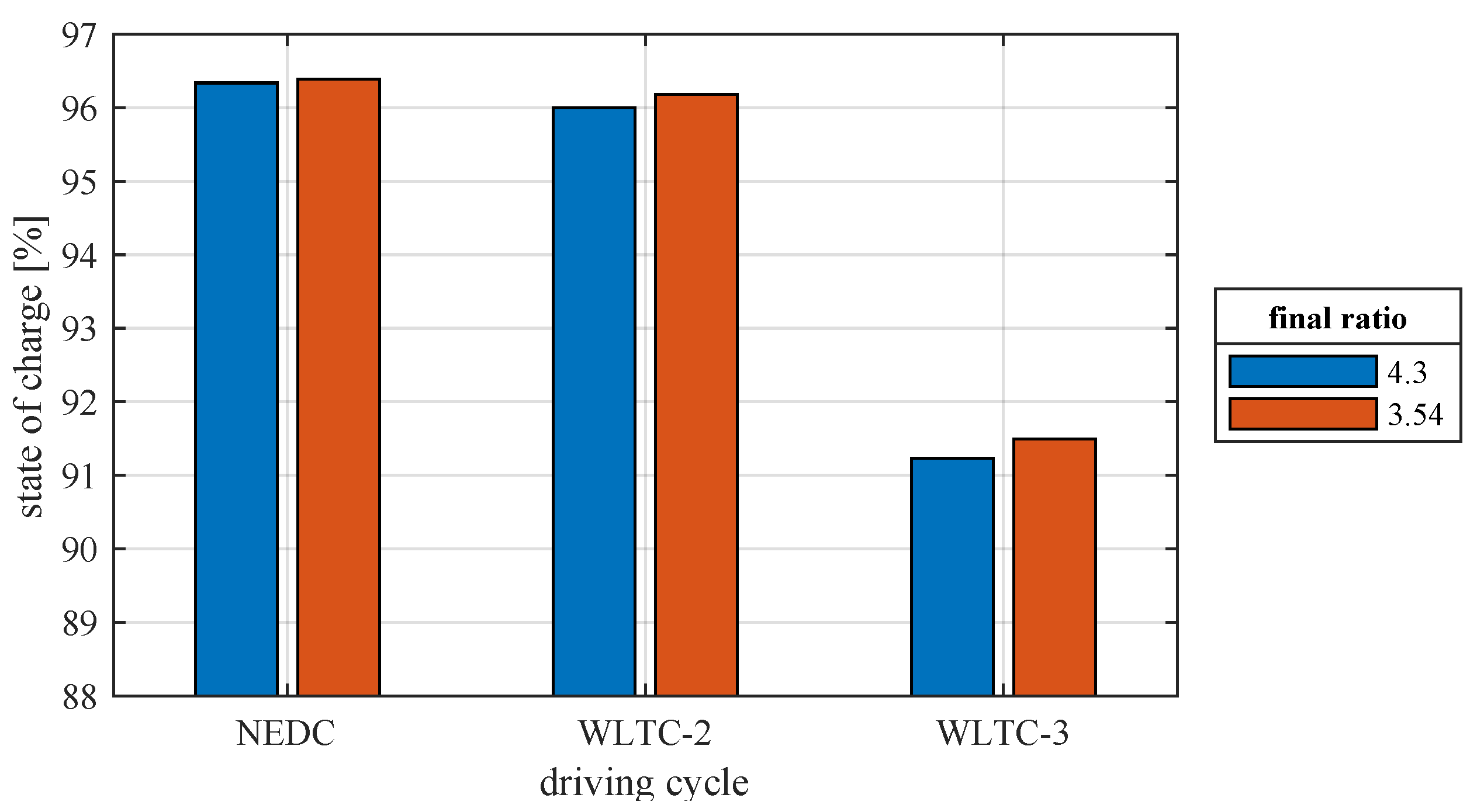
7.4. Energy Consumed in Driving Cycles
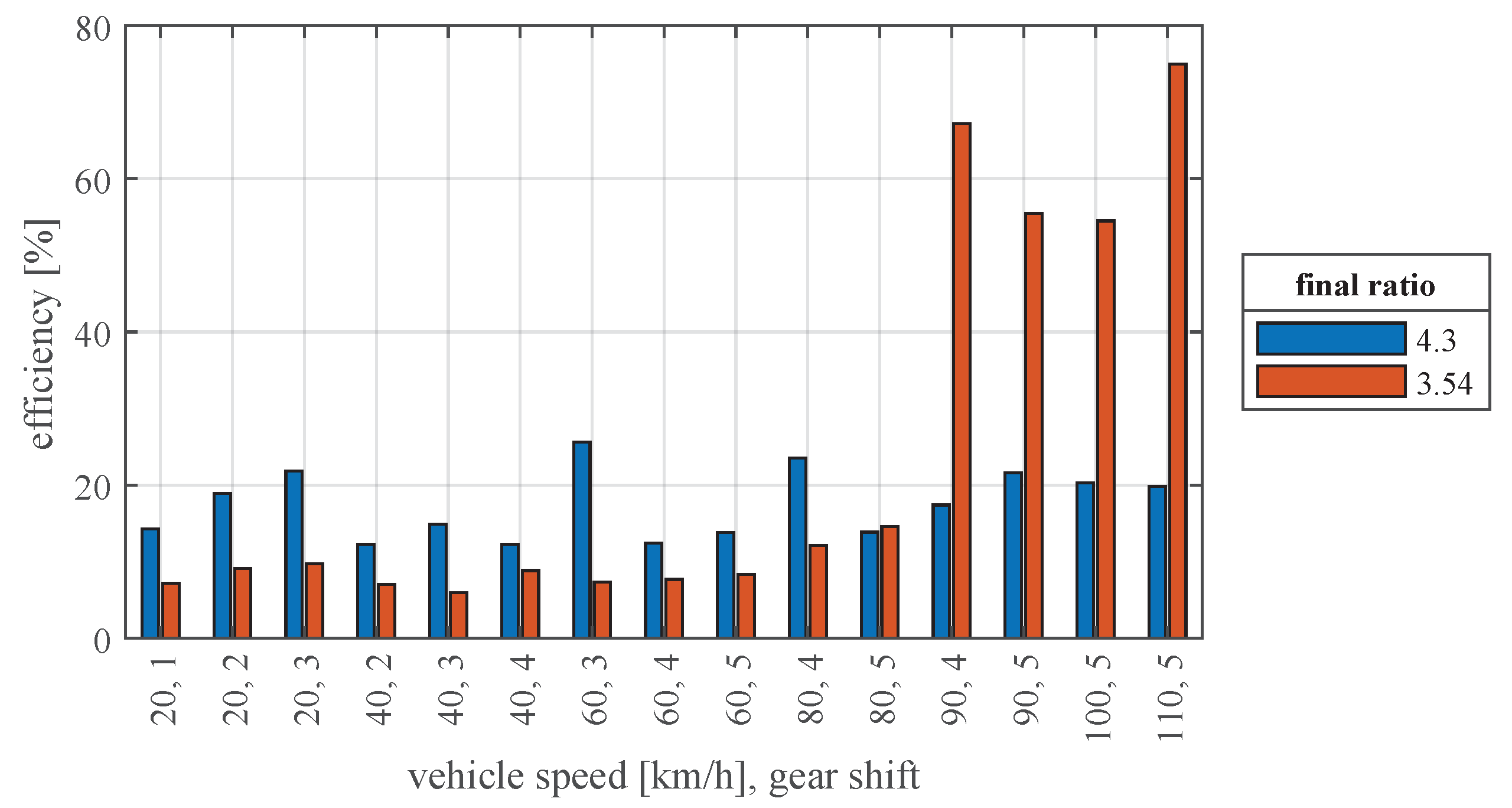
7.5. Efficiency
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.S.; Chong, Z. Smart city projects against COVID-19: Quantitative evidence from China. Sustain. Cities Soc. 2021, 70, 102897. [Google Scholar] [CrossRef]
- Thornbush, M.; Golubchikov, O. Smart energy cities: The evolution of the city-energy-sustainability nexus. Environ. Dev. 2021, 39, 100626. [Google Scholar] [CrossRef]
- Puma-Benavides, D.S.; Izquierdo-reyes, J.; Calderon-najera, J.D.D.; Ramirez-mendoza, R.A. A Systematic Review of Technologies, Control Methods, and Optimization for Extended-Range Electric Vehicles. Appl. Sci. 2021, 11, 7095. [Google Scholar] [CrossRef]
- Chan, C.C. The state of the art of electric and hybrid vehicles. Proc. IEEE 2002, 90, 247–275. [Google Scholar] [CrossRef] [Green Version]
- Tesla Company. Model S Owner’s Manual; Tesla Company: Palo Alto, CA, USA, 2019. [Google Scholar]
- Tesla Company. Model X Owner’s Manual; Tesla Company: Palo Alto, CA, USA, 2018. [Google Scholar]
- General Motors. 2019 Chevrolet Volt Brochure; General Motors: Detroit, MI, USA, 2018. [Google Scholar]
- Krasopoulos, C.T.; Beniakar, M.E.; Kladas, A.G. Velocity and torque limit profile optimization of electric vehicle including limited overload. IEEE Trans. Ind. Appl. 2017, 53, 3907–3916. [Google Scholar]
- Wu, G.; Zhang, X.; Dong, Z. Impacts of Two-Speed Gearbox on Electric Vehicle’S Fuel Economy and Performance; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Hofstetter, M.; Lechleitner, D.; Hirz, M.; Gintzel, M.; Schmidhofer, A. Multi-objective gearbox design optimization for xEV-axle drives under consideration of package restrictions. Forsch. Ingenieurwesen 2018, 82, 361–370. [Google Scholar]
- Nemeth, T.; Bubert, A.; Becker, J.N.; De Doncker, R.W.; Sauer, D.U. A simulation platform for optimization of electric vehicles with modular drivetrain topologies. IEEE Trans. Transp. Electrif. 2018, 4, 888–900. [Google Scholar]
- Kabalan, B.; Vinot, E.; Trigui, R.; Dumand, C. Systematic methodology for architecture generation and design optimization of hybrid powertrains. IEEE Trans. Veh. Technol. 2020, 69, 14846–14857. [Google Scholar]
- Schiffer, S.; Kain, A.; Wilde, P.; Haber, J.; Helbing, M.; Baeker, B. Influence of the final drive ratio on the consumption of passenger cars under real driving conditions. In Proceedings of the 2017 12th International Conference on Ecological Vehicles and Renewable Energies (EVER 2017), Monte Carlo, Monaco, 11–13 April 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Miller, J.M. Hybrid electric vehicle propulsion system architectures of the e-CVT type. IEEE Trans. Power Electron. 2006, 21, 756–767. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.; Cha, S.W.; Peng, H. Optimal Equivalent Fuel Consumption for Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 817–825. [Google Scholar] [CrossRef]
- Tang, X.; Yang, W.; Hu, X.; Zhang, D. A novel simplified model for torsional vibration analysis of a series-parallel hybrid electric vehicle. Mech. Syst. Signal Process. 2017, 85, 329–338. [Google Scholar] [CrossRef]
- Prajwal, C.P.; Rao, K.U.; Hegde, K.R.; Nagaraj, S. A simple novel algorithm to optimize final gear ratio in electric and hybrid formula racing cars. In Proceedings of the 2013 IEEE International Multi Conference on Automation, Computing, Control, Communication and Compressed Sensing (iMac4s 2013), Kottayam, India, 22–23 March 2013; pp. 415–419. [Google Scholar] [CrossRef]
- Naunheimer, H.; Bertsche, B.; Ryborz, J.; Novak, W. Automotive Transmissions; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Hofman, T.; Dai, C.H. Energy efficiency analysis and comparison of transmission technologies for an electric vehicle. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference (VPPC 2010), Lille, France, 1–3 September 2010. [Google Scholar] [CrossRef]
- Ding, X.; Guo, H.; Xiong, R.; Chen, F.; Zhang, D.; Gerada, C. A new strategy of efficiency enhancement for traction systems in electric vehicles. Appl. Energy 2017, 205, 880–891. [Google Scholar] [CrossRef]
- Julio-Rodríguez, J.D.C.; Santana-Díaz, A.; Ramirez-Mendoza, R.A. Individual Drive-Wheel Energy Management for Rear-Traction Electric Vehicles with In-Wheel Motors. Appl. Sci. 2021, 11, 4679. [Google Scholar] [CrossRef]
- Liu, K.; Yamamoto, T.; Morikawa, T. Impact of road gradient on energy consumption of electric vehicles. Transp. Res. Part D Transp. Environ. 2017, 54, 74–81. [Google Scholar] [CrossRef]
- Birkhofer, H. The Future of Design Methodology; Springer: New York, NY, USA, 2011. [Google Scholar]
- ISO. Passenger Car, Truck and Bus Tyre Rolling Resistance Measurement Method—Single Point Test and Correlation of Measurement Results; ISO 28580:2018; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; Wiley-Interscience: Hoboken, NJ, USA, 2001; p. 528. [Google Scholar]
- Mohan, G.; Assadian, F.; Longo, S. Comparative analysis of forward-facing models vs. backwardfacing models in powertrain component sizing. In Proceedings of the IET Hybrid and Electric Vehicles Conference 2013 (HEVC 2013), London, UK, 6–7 November 2013; IET: London, UK, 2013; pp. 1–6. [Google Scholar]
- Analysis, U.E.; Learning, M.; Sizing, B. Applied Energy Energy Storage Sizing in Plug-in Electric Vehicles: Driving Cycle Uncertainty Effect Analysis and Machine Learning Based Sizing Framework. J. Energy Storage 2021, 41, 102864. [Google Scholar] [CrossRef]
- Huzayyin, O.A.; Salem, H.; Hassan, M.A. A representative urban driving cycle for passenger vehicles to estimate fuel consumption and emission rates under real-world driving conditions. Urban Clim. 2021, 36, 100810. [Google Scholar] [CrossRef]
- Kammuang-lue, N.; Boonjun, J. Energy consumption of battery electric bus simulated from international driving cycles compared to real-world driving cycle in Chiang Mai. Energy Rep. 2021, 7, 3267–3272. [Google Scholar] [CrossRef]



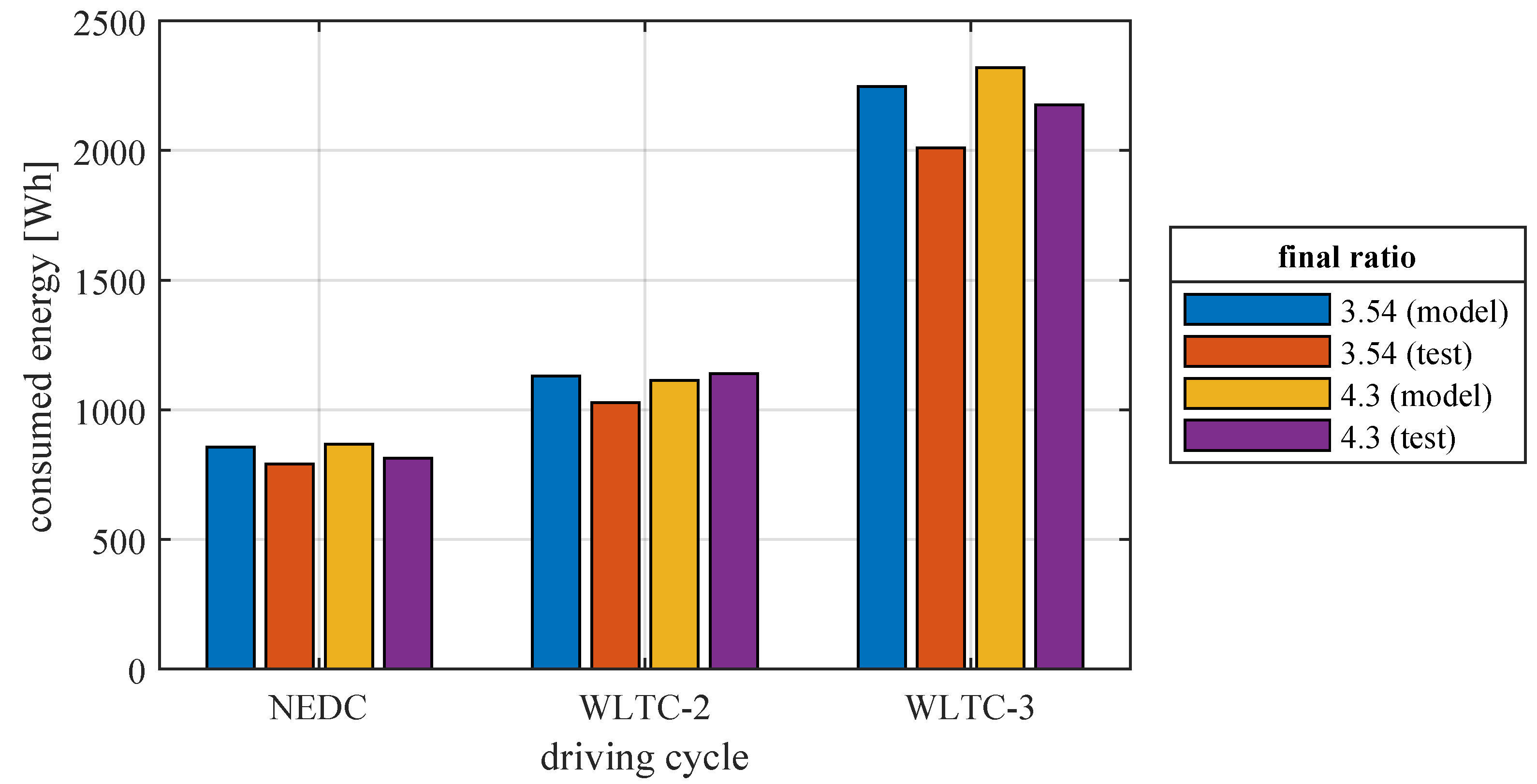
| Description | Symbol | Unit | Value |
|---|---|---|---|
| Powertrain | − | − | Central electric motor with five-speed gearbox and final ratio |
| Vehicle mass | m | 1370 | |
| Battery pack capacity | − | 32 (Li-ion cells) | |
| Nominal voltage | 105 | ||
| Maximum capacity | Q | 304 | |
| Initial state-of-charge | − | % | 100 |
| Internal resistance | 0.07 | ||
| Nominal current discharge | i | 160 | |
| Exponential voltage | 106 | ||
| Exponential capacity | 260 | ||
| Frontal area | A | 2.15 | |
| Drag coefficient | − | 0.436 | |
| Rolling resistance coefficient | − | ||
| Gearbox efficiency | − | 0.95 | |
| First shift ratio | − | 3.636 | |
| Second shift ratio | − | 1.9641 | |
| Third shift ratio | − | 1.428 | |
| Fourth shift ratio | − | 1 | |
| Fifth shift ratio | − | 0.801 | |
| Final ratio efficiency | − | 0.95 | |
| Final ratio | − | 4.3 | |
| Maximum torque | − | 691.51 | |
| Maximum power | − | 25.92 | |
| Maximum speed | − | 117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puma-Benavides, D.S.; Izquierdo-Reyes, J.; Galluzzi, R.; Calderon-Najera, J.d.D. Influence of the Final Ratio on the Consumption of an Electric Vehicle under Conditions of Standardized Driving Cycles. Appl. Sci. 2021, 11, 11474. https://doi.org/10.3390/app112311474
Puma-Benavides DS, Izquierdo-Reyes J, Galluzzi R, Calderon-Najera JdD. Influence of the Final Ratio on the Consumption of an Electric Vehicle under Conditions of Standardized Driving Cycles. Applied Sciences. 2021; 11(23):11474. https://doi.org/10.3390/app112311474
Chicago/Turabian StylePuma-Benavides, David Sebastian, Javier Izquierdo-Reyes, Renato Galluzzi, and Juan de Dios Calderon-Najera. 2021. "Influence of the Final Ratio on the Consumption of an Electric Vehicle under Conditions of Standardized Driving Cycles" Applied Sciences 11, no. 23: 11474. https://doi.org/10.3390/app112311474
APA StylePuma-Benavides, D. S., Izquierdo-Reyes, J., Galluzzi, R., & Calderon-Najera, J. d. D. (2021). Influence of the Final Ratio on the Consumption of an Electric Vehicle under Conditions of Standardized Driving Cycles. Applied Sciences, 11(23), 11474. https://doi.org/10.3390/app112311474







