Experimental Study on Out-of-Plane Seismic Performance of New Type Masonry System
Abstract
:1. Introduction
2. Proposed Block Systems and Material Characteristics
2.1. Proposed Block Systems
2.2. Material Characteristics
3. Shaking Table Tests
3.1. Test Specimens
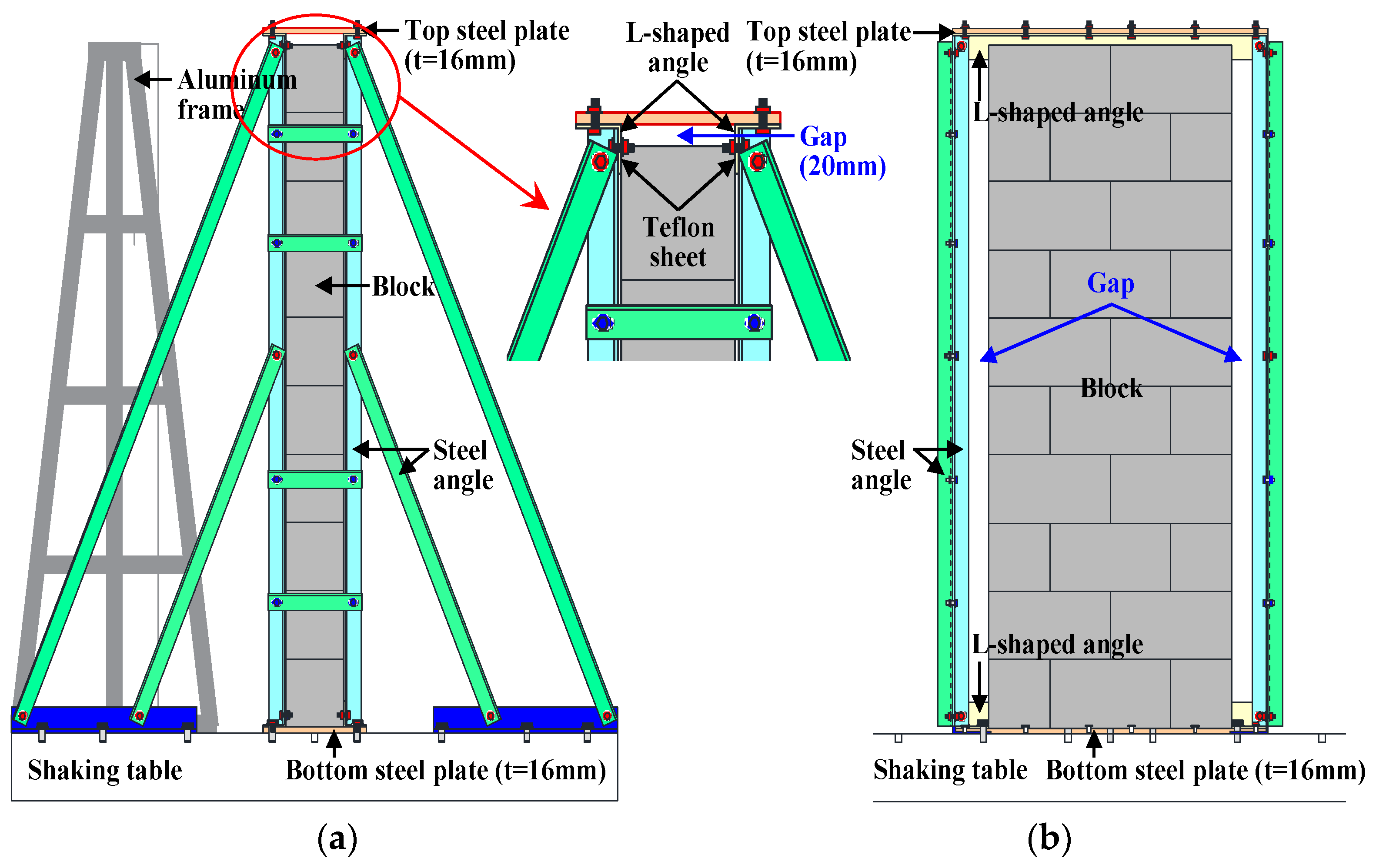
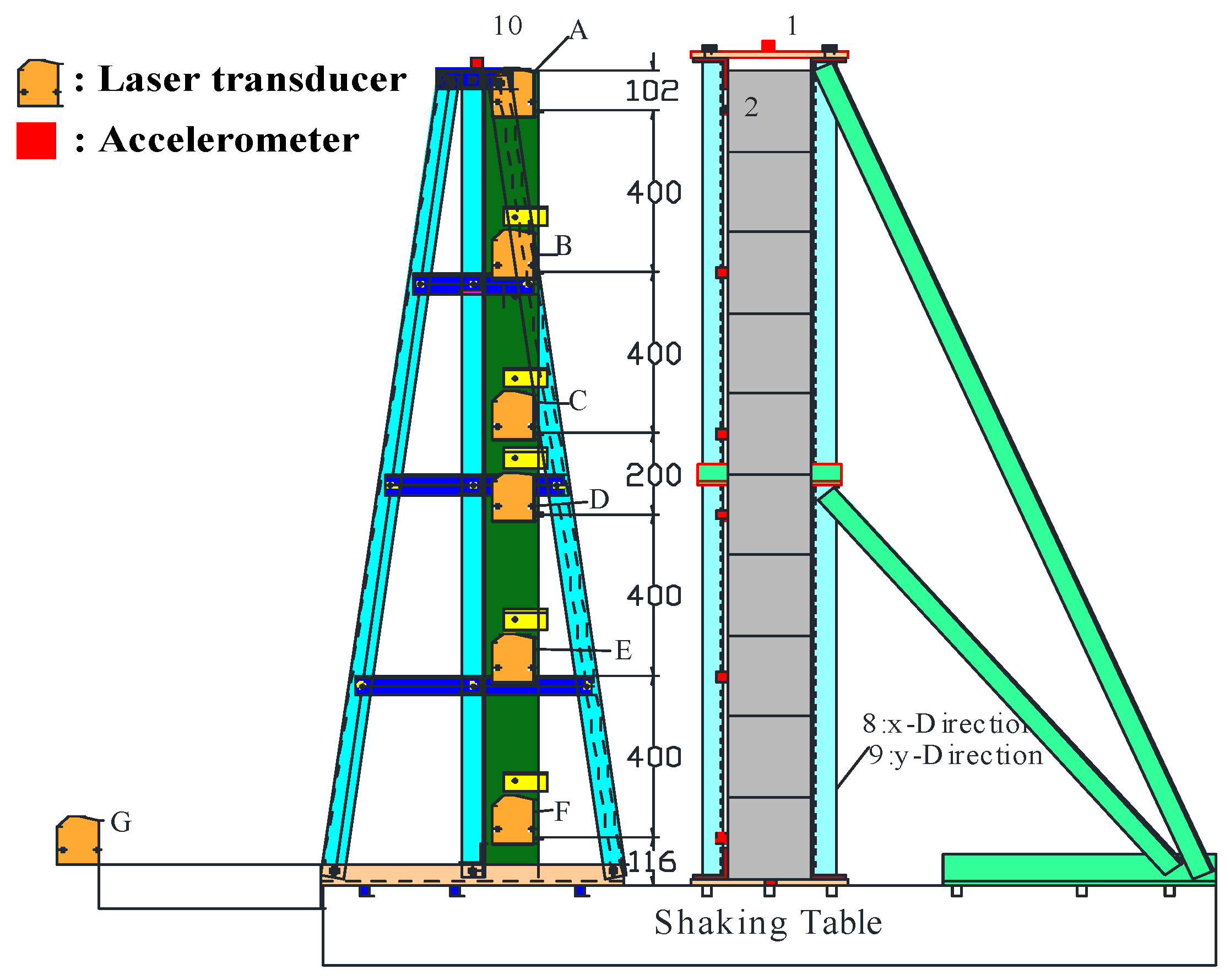
3.2. Test Setup and Measurement System
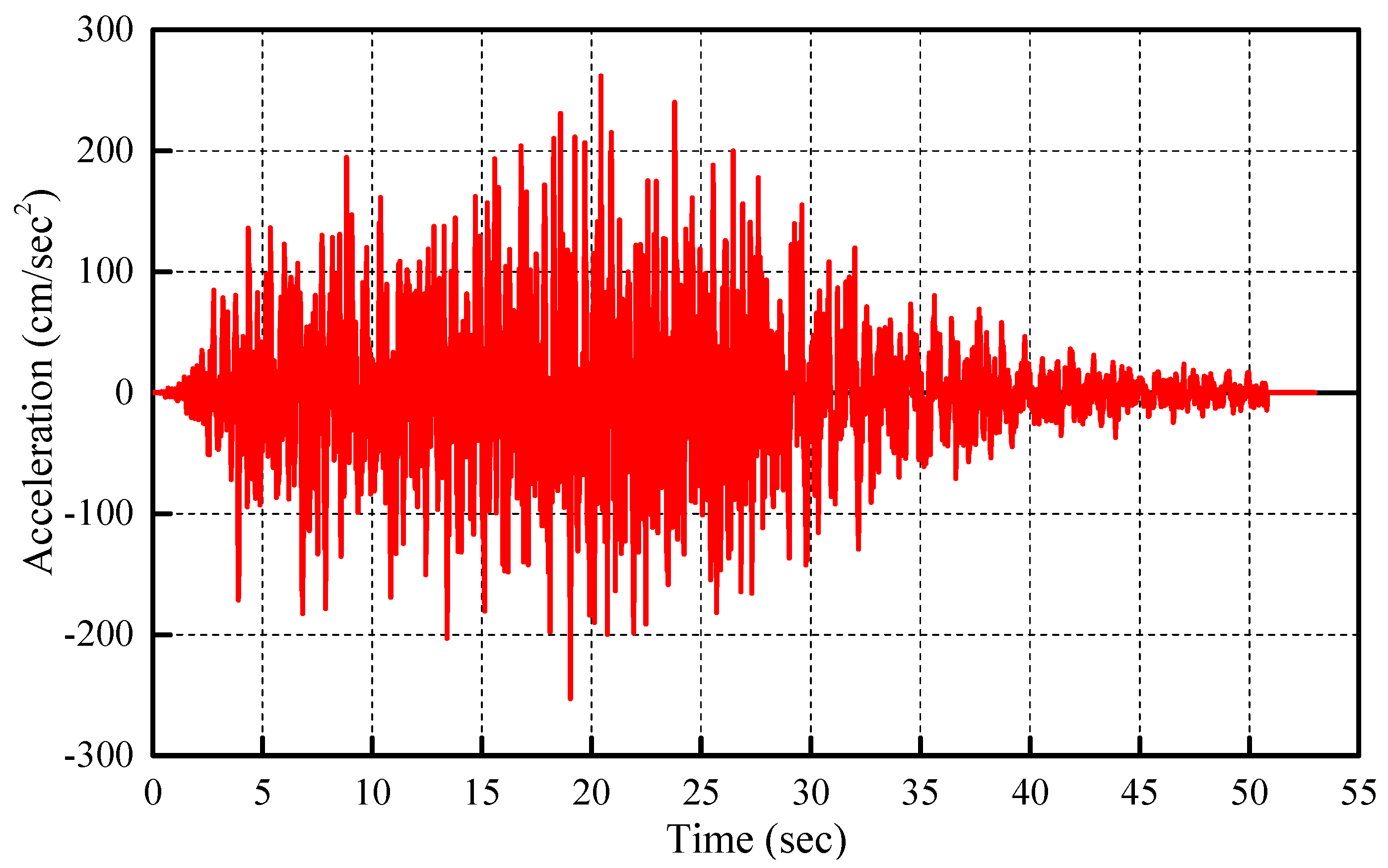
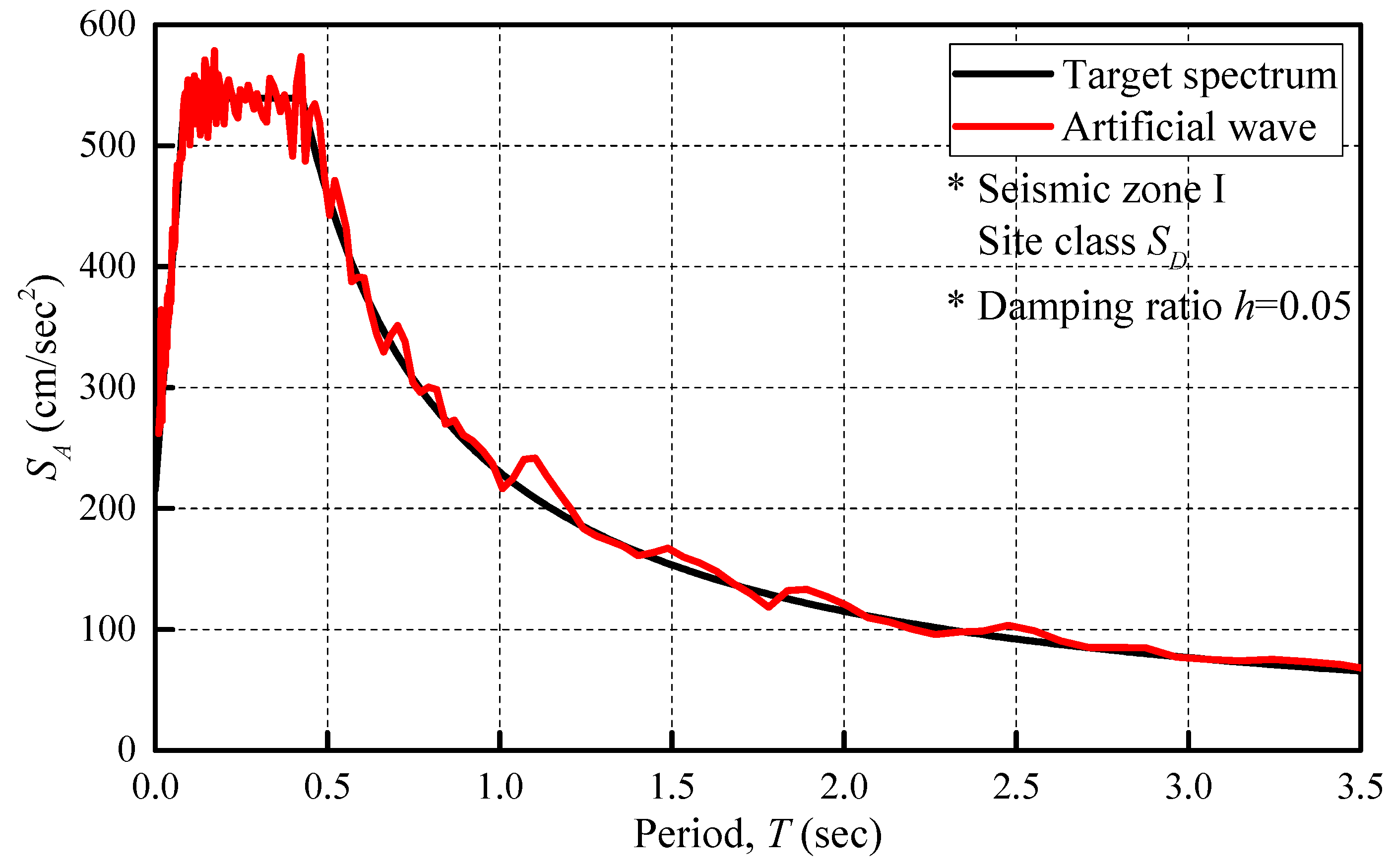
3.3. Test Program
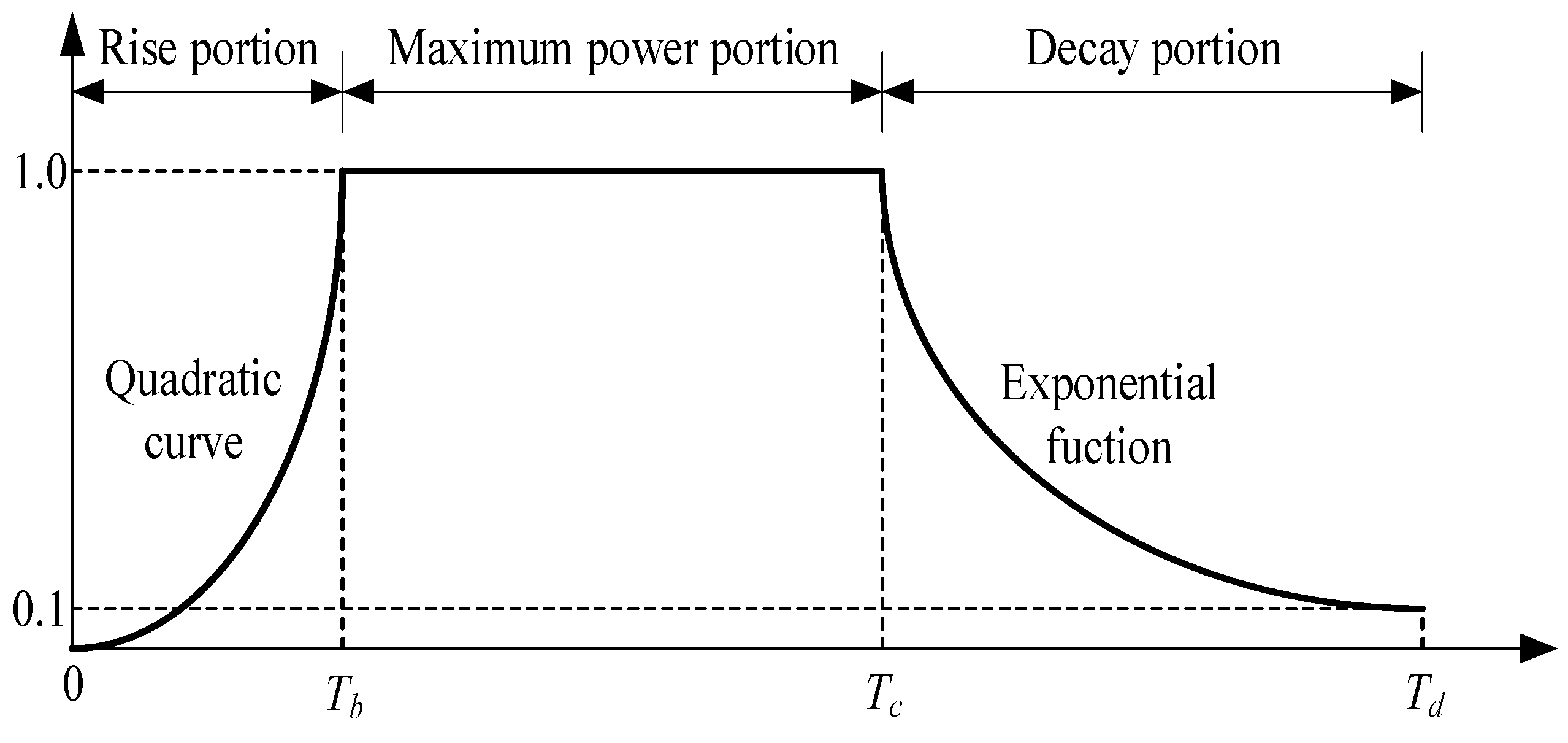
- Td: Excitation duration of an earthquake (s);
- M: Magnitude of an earthquake (M = 8.0, herein).
3.4. Experimental Results of Shaking Table Tests
3.4.1. Failure Patterns
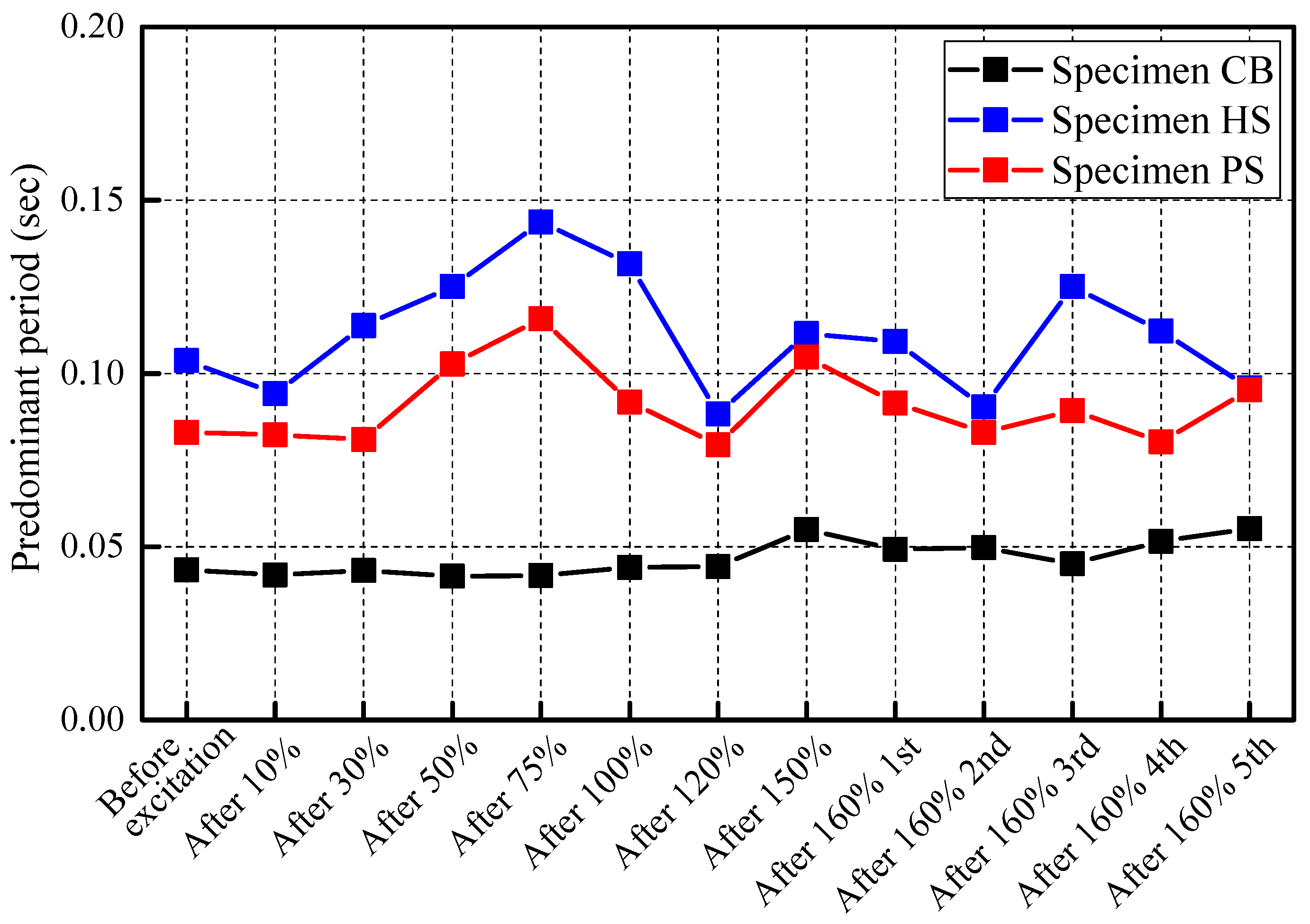
3.4.2. Development of Predominant Periods
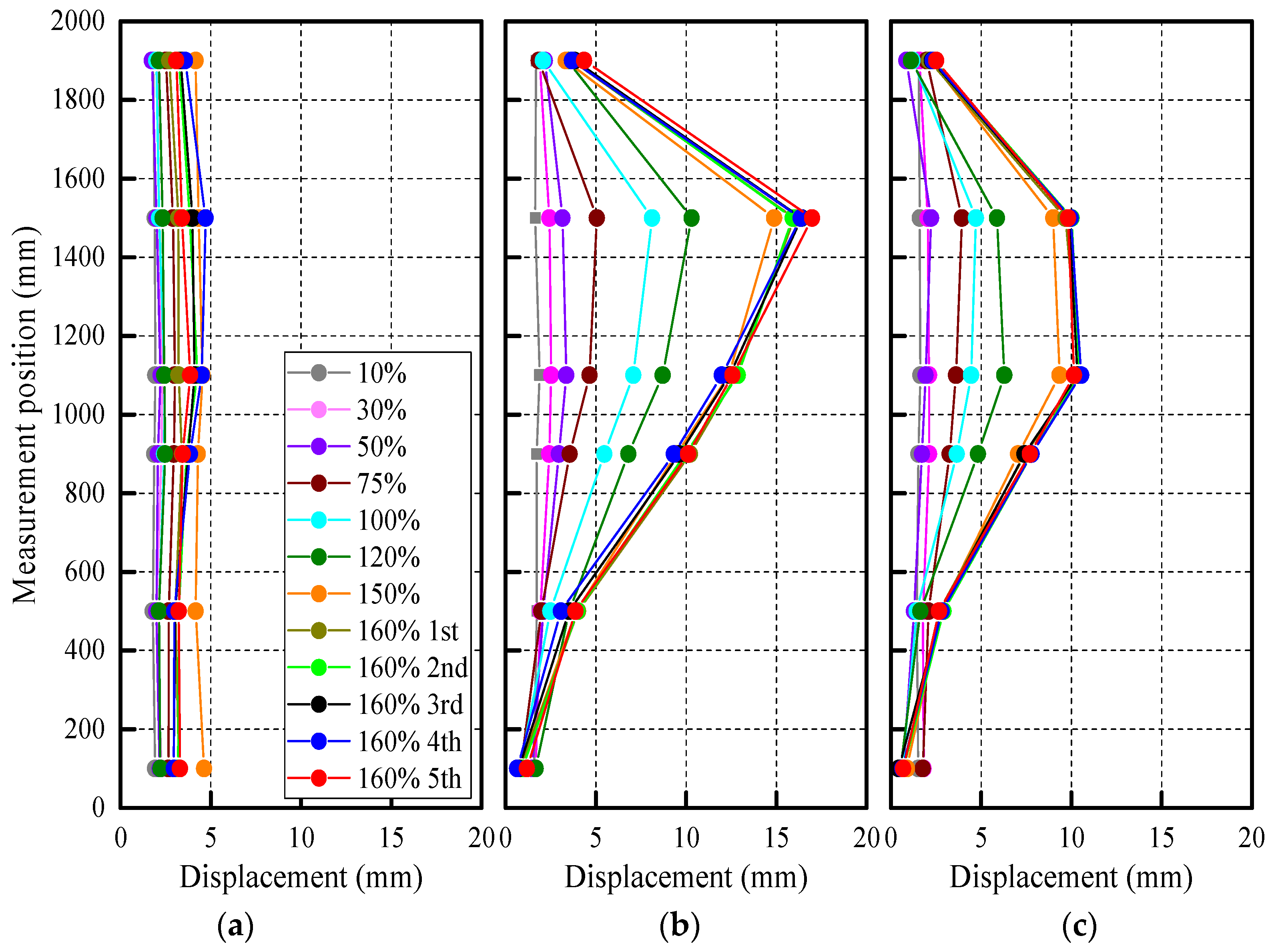
3.4.3. Acceleration and Displacement Profiles
4. Four-Point Bending Tests
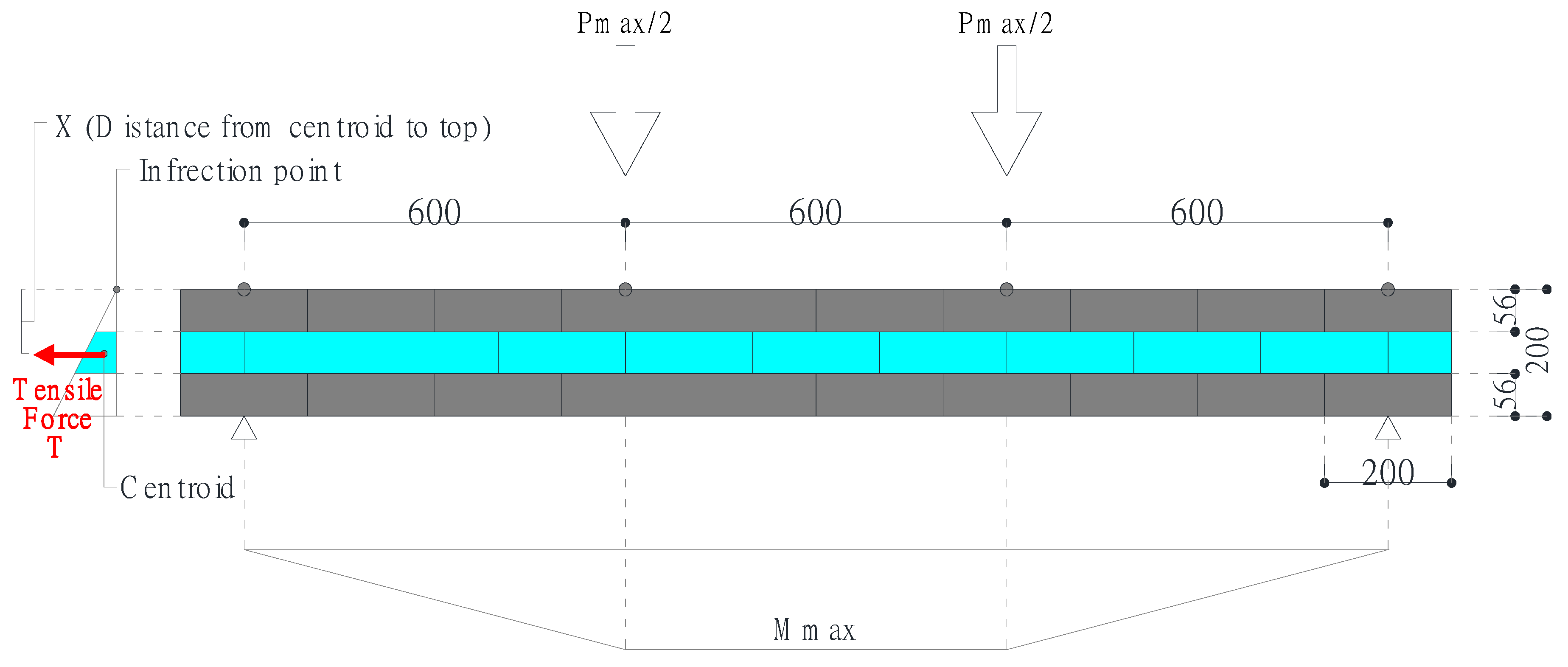
4.1. Test Specimens and Test Setup
- m: Wall weight of Specimen CB (=377 kg, herein);
- g: Gravitational acceleration (=9.8 m/s2);
- α: collapsed inclination angle (=21°).
4.2. Maximum Tensile Strength of Specimens HS and PS
5. Conclusions
- (1)
- From the shaking table test results, no extension of the predominant period was observed in all specimens, and this result was consistent with the fact that there was no noticeable damage to each specimen, until the final excitation. Since there was a gap between the main and key blocks in the proposed block system, the periods of Specimen HS and PS were longer than that of Specimen CS in all stages. The acceleration and displacement values were the largest on the upper side than the center in all specimens. This result is consistent with the wall constraints, which, at the bottom and top of the wall, were the fixed roller supports, respectively. In addition, due to the gap in the proposed block system, Specimens HS and PS had smaller acceleration and larger displacement than Specimen CS.
- (2)
- During the laying works, Specimen CB collapsed when the inclination angle was 21°, and the force that cause the out-of-plane failure was 3.4 kN.
- (3)
- From the four-point bending test results, the tensile stresses of the key block were almost the same, regardless of rectangular cross-section replacement methods of the key block. The tensile stresses of Specimen HS and PS were 0.87 to 0.89 N/mm2, which were almost the same results. Furthermore, the maximum load of Specimen CS was about 1/4 to 1/3 of that of Specimens HS and PS. This result means that the proposed block system has significantly improved seismic performance in the out-of-plane direction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abrams, D.P.; Shah, N. Cyclic Load Testing of Unreinforced Masonry Walls; Advanced Construction Technology Centre Report No. 92-26-10; University of Illinois at Urbana Champaign: Champaign, IL, USA, 1992. [Google Scholar]
- Magenes, G.; Calvi, G.M. Shaking Table Tests on Brick Masonry Walls. In Proceedings of the 10th European Conference on Earthquake Engineering 1995, Vienna, Austria, 28 August–2 September 1994; Volume 3, pp. 2419–2424. [Google Scholar]
- Doherty, K.T. An Investigation of the Weak Links in the Seismic Load Path of Unreinforced Masonry Buildings. Ph.D. Thesis, Faculty of Engineering, University of Adelaide, Adelaide, Australia, 2000. [Google Scholar]
- Griffith, M.C.; Vaculik, J.; Lam, T.K.; Wilson, J.; Lumntarna, E. Cyclic Testing of Unreinforced Walls in Two-way Bending. Earthq. Eng. Struct. Dyn. 2006, 36, 801–821. [Google Scholar] [CrossRef]
- Simsir, C.; Aschheim, M.; Abrams, D. Influence of Diaphragm Flexibility on the Out-of-plane Response of Unreinforced Masonry Bearing Walls. In Proceedings of the 9th North American Masonry Conference 2002, Clemson, SC, USA, 1–4 June 2003. [Google Scholar]
- Tomazevic, M. Dynamic Modelling of Masonry Buildings: Storey Mechanism as a Simple Alternative. Earthq. Eng. Struct. Dyn. 1987, 15, 731–749. [Google Scholar] [CrossRef]
- Qamaruddin, M.; Chandra, B. Behaviour of Unreinforced Masonry Buildings Subjected to Earthquakes. Prof. J. Mason. Soc. USA 1991, 9, 47–55. [Google Scholar]
- Calvi, G.M.; Pavese, A. Application of Dynamic Identification Techniques to a Brick Masonry Building Prototype. In Proceedings of the 10th European Conference on Earthquake Engineering 1995, Vienna, Austria, 28 August–2 September 1994; Volume 3, pp. 2413–2418. [Google Scholar]
- Tomazevic, M. Seismic Upgrading of Old Brick-Masonry Urban Houses: Tying of Walls with Steel Ties. Earthq. Spectra 1996, 12, 599–622. [Google Scholar] [CrossRef]
- Costley, A.C.; Abrams, S.P. Dynamic Response of Unreinforced Masonry Buildings with Flexible Diaphragm; Technical Report No. MCEER-96-0001; MCEER: Buffalo, NY, USA, 1996; p. 22. [Google Scholar]
- Benedetti, D.; Carydis, P.; Pezzoli, P. Shaking Table Test on 24 Masonry Buildings. Earthq. Eng. Struct. Dyn. 1998, 27, 67–90. [Google Scholar] [CrossRef]
- Yi, T.; Moon, F.L.; Leon, R.T.; Kahn, L.F. Lateral Load Tests on a Two-story Unreinforced Masonry Building. ASCE J. Struct. Eng. 2006, 132, 643–652. [Google Scholar] [CrossRef]
- Architectural Institute of Japan (AIJ). Report on the Damage Investigation of the 1999 Chi-Chi Earthquake; AIJ: Tokyo, Japan, 2000. [Google Scholar]
- Architectural Institute of Japan (AIJ). Report on the Damage Investigation of the 2006 Central Java Earthquake; AIJ: Tokyo, Japan, 2007. [Google Scholar]
- Manafpour, A.R. Bam Earthquake, Iran: Lessons on the Seismic Behavior of Building Structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Sanada, Y.; Kishimoto, I.; Kuroki, M.; Sakashita, M.; Choi, H.; Tani, M.; Hosono, Y.; Fauzan, M.S.; Farida, F. Preliminary Report on Damage to Buildings due to the September 2 and 30, 2009 Earthquakes in Indonesia. In Proceedings of the Eleventh Taiwan-Korea-Japan Joint Seminar on Earthquake Engineering for Building Structures, Kyoto, Japan, 2–3 November 2009; pp. 297–306. [Google Scholar]
- Choi, H.; Sanada, Y.; Kuroki, M.; Sakashita, M.; Tani, M.; Hosono, Y.; Musalamah, S.; Farida, F. Comparing Damage to Building Structures Due to the 2009 West Java Earthquake in Indonesia. In Proceedings of the 2nd International Conference on Earthquake Engineering and Disaster Mitigation, Surabaya, Indonesia, 19 July 2011; pp. E-9–E-18. [Google Scholar]
- Architectural Institute of Japan (AIJ). Reconnaissance Report on the 2015 Nepal Gorkha Earthquake; AIJ: Tokyo, Japan, 2016. [Google Scholar]
- Akhoundi, F.; Vasconcelos, G.; Lourenco, P.; Silva, L.C. Out-of-Plane Response of Masonry Infilled RC Frames: Effect of Workmanship and Opening. In Proceedings of the 16th International Brick and Block Masonry Conference, Padova, Italy, 23 June 2016. [Google Scholar]
- Angel, R.; Abrams, D.P.; Shapiro, D.; Uzarski, J.; Webster, M. Behavior of Reinforced Concrete Frames with Masonry Infills; Department of Civil Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1994. [Google Scholar]
- Dizhur, D.; Walsh, K.; Giongo, I.; Derakhshan, H.; Ingham, J. Out-of-Plane Proof Testing of Masonry Infill Walls. Structures 2018, 15, 244–258. [Google Scholar] [CrossRef]
- Hashemi, A.; Mosalam, K.M. Shake-Table Experiment on Reinforced Concrete Structure Containing Masonry Infill Wall. Earthq. Eng. Struct. Dyn. 2006, 35, 1827–1852. [Google Scholar] [CrossRef]
- Petrone, C.; Magliulo, G.; Manfredi, G. Shake Table Tests for the Seismic Assessment of Hollow Brick Internal Partitions. Eng. Struct. 2014, 72, 203–214. [Google Scholar] [CrossRef]
- Derakhshan, H.; Dizhur, D.; Griffith, M.C.; Ingham, J.M. In Situ Out-of-Plane Testing of As-Built and Retrofitted Unreinforced Masonry Walls. J. Struct. Eng. 2014, 140, 04014022. [Google Scholar] [CrossRef] [Green Version]
- Giaretton, M.; Dizhur, D.; da Porto, F.; Ingham, J.M. Construction Details and Observed Earthquake Performance of Unreinforced Clay Brick Masonry Cavity-Walls. Structures 2016, 6, 159–169. [Google Scholar] [CrossRef]
- Damiola, M.; Esposito, R.; Messali, F.; Rots, J.G. Quasi-Static Cyclic Two-Way out-of-Plane Bending Tests and Analytical Models Comparison for URMWalls. In Proceedings of the 10th International Masonry Conference, Milan, Italy, 9–11 July 2018. [Google Scholar]
- Drysdale, R.G.; Essawy, A.S. Out-of-Plane Bending of Concrete Block Walls. J. Struct. Eng. 1988, 114, 121–133. [Google Scholar] [CrossRef]
- Gattesco, N.; Boem, I. Out-of-Plane Behavior of Reinforced MasonryWalls: Experimental and Numerical Study. Compos. Part B Eng. 2017, 128, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Graziotti, F.; Tomassetti, U.; Sharma, S.; Grottoli, L.; Magenes, G. Experimental Response of URM Single Leaf and Cavity Walls in Out-of-Plane Two-Way Bending Generated by Seismic Excitation. Constr. Build. Mater. 2019, 195, 650–670. [Google Scholar] [CrossRef]
- Amin, A.; Bashar, S.M.; Fadhil, N.; Ehsan, N. Development of Interlocking Masonry Bricks and its’ Structural Behaviour: A Review Paper. IOP Conf. Ser. Earth Environ. Sci. 2018, 140, 012127. [Google Scholar]
- Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. Experimental assessment of large displacement cyclic in-plane shear behaviour of semi-interlocking masonry panels. Int. J. Mason. Res. Innov. 2019, 4, 378–399. [Google Scholar] [CrossRef]
- Liu, H.; Liu, P.; Lin, K.; Zhao, S. Cyclic Behavior of Mortarless Brick Joints with Different Interlocking Shapes. Materials 2016, 3, 166. [Google Scholar] [CrossRef]
- Majid, A.; Romain, B.; Nawawi, C. Dynamic response of mortar-free interlocking structures. Constr. Build. Mater. 2013, 42, 168–189. [Google Scholar]
- Choi, H.; Lee, K.S. Experimental Study on the In-Plane Seismic Performance of a New Type of Masonry Wall System. Appl. Sci. 2020, 10, 9102. [Google Scholar] [CrossRef]
- Choi, H.; Jin, K.W.; Jeong, J.C.; Kim, B.S.; Hwang, E.J.; Jin, C. Feasibility Study on Seismic Block without Joint Mortar, Part1 Shape Determination Using Finite Element Analysis. Summaries of Technical Papers of Annual Meeting; Architectural Institute of Japan: Tokyo, Japan, 2019; Volume 4, pp. 977–978. (In Japanese) [Google Scholar]
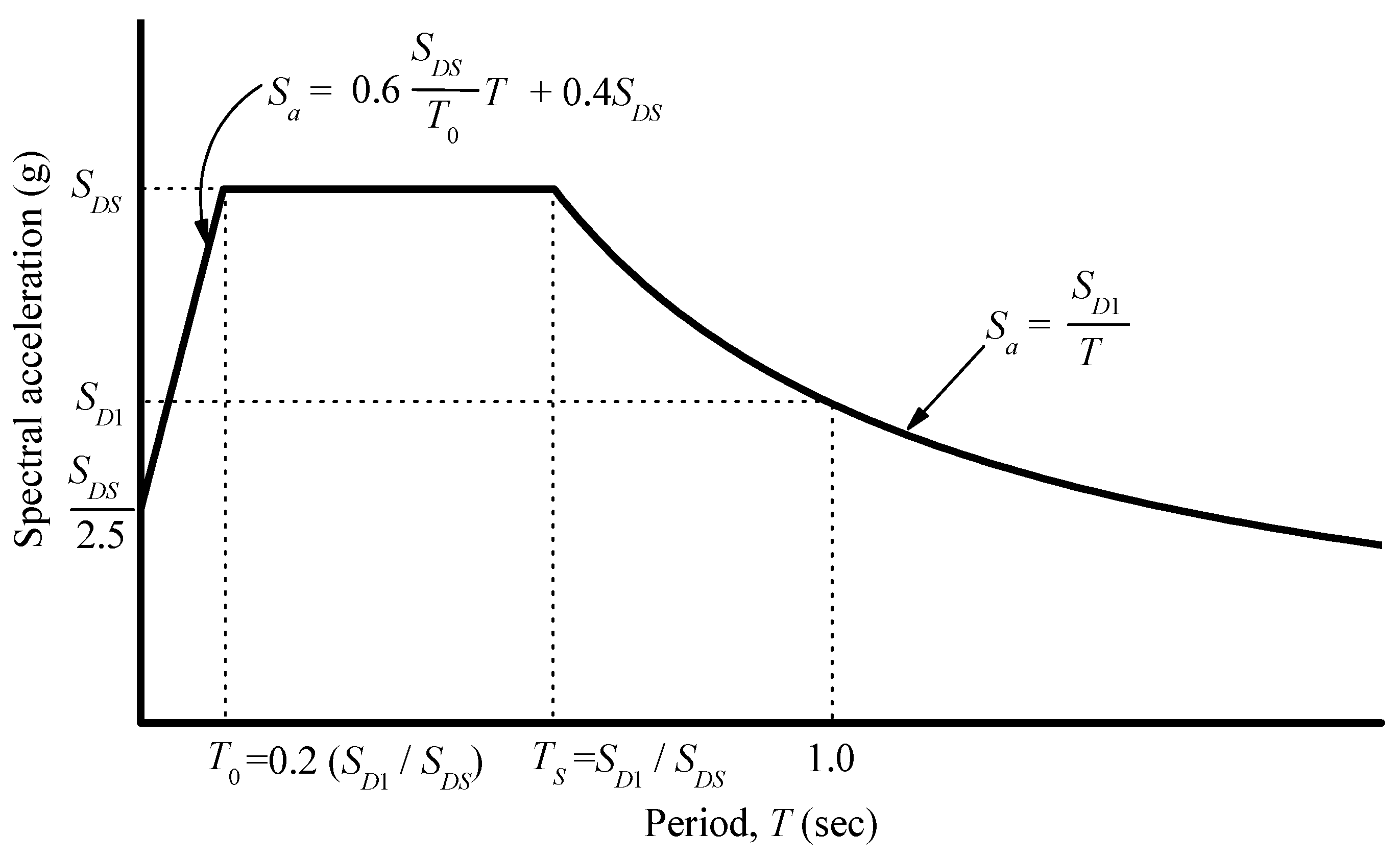
- Architectural Institute of Korea (AIK). 2016 Korean Building Code; AIK: Seoul, Korea, 2016. (In Korean) [Google Scholar]
- Ohsaki, Y. New Introduction of Sepctral Analysis of Earthquake Ground Motion; Kajima Institute Publishing: Tokyo, Japan, 1994; pp. 81–109. (In Japanese) [Google Scholar]



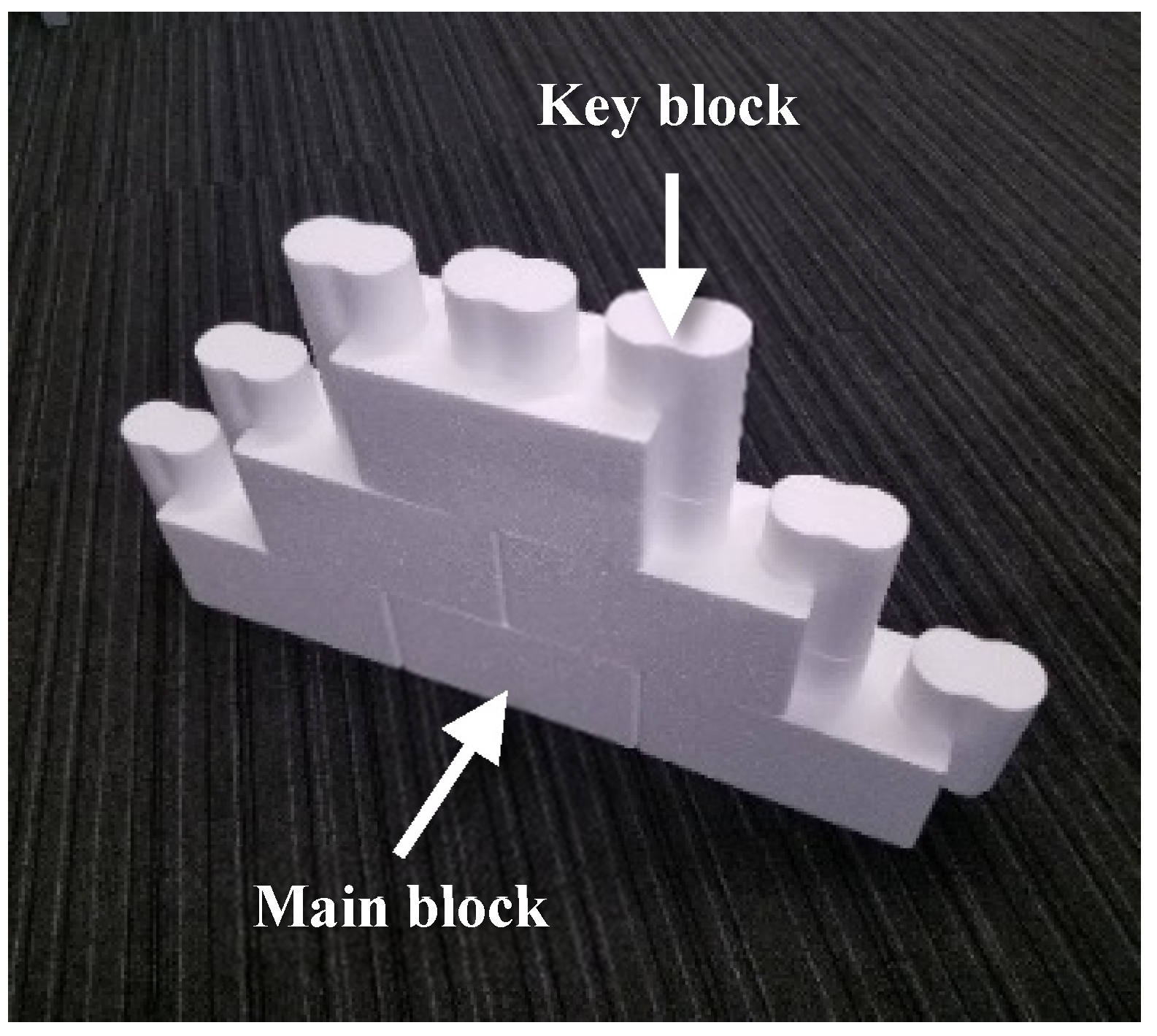
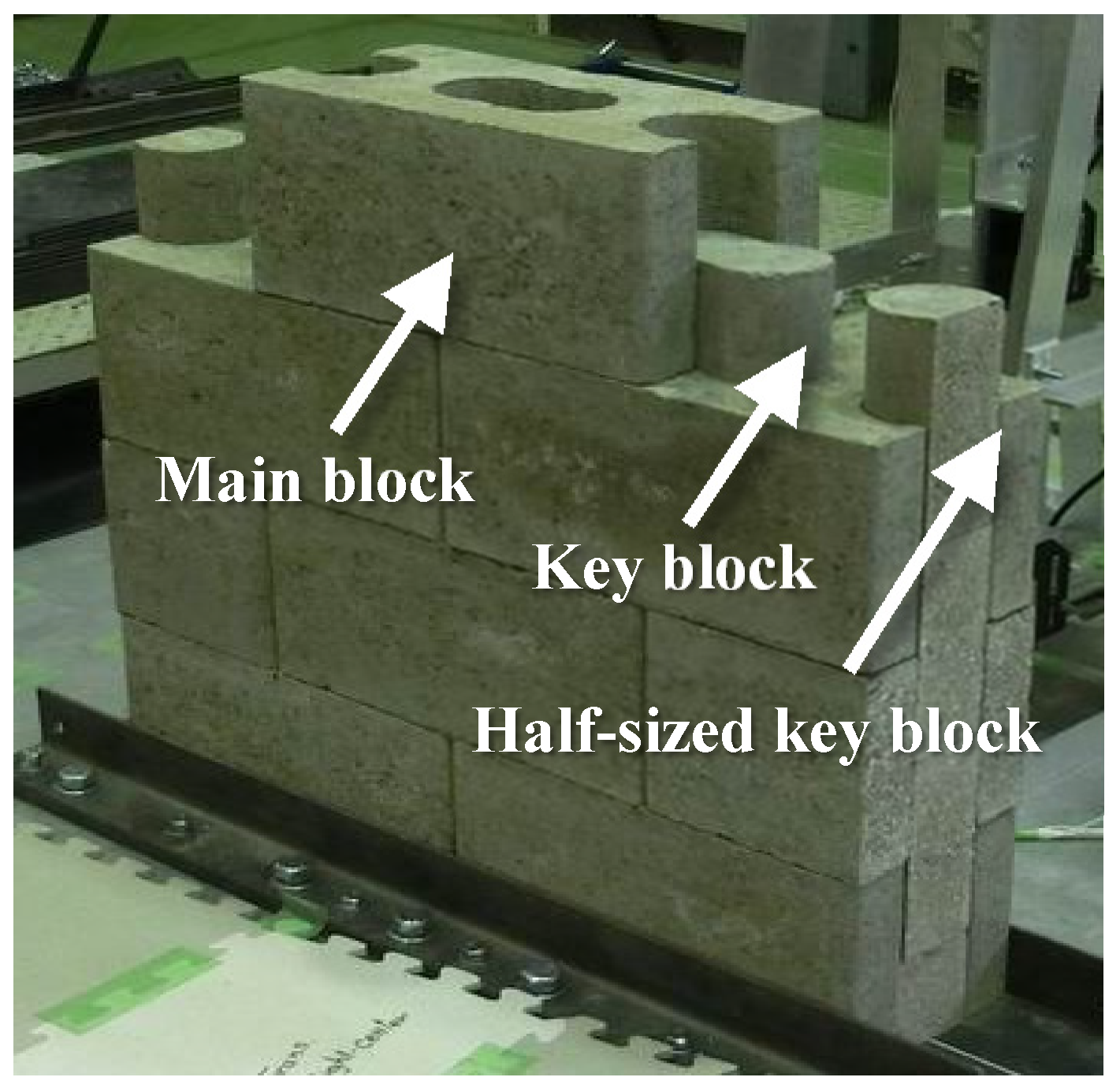






| Compressive Strength (N/mm2) 1 | |||
|---|---|---|---|
| Typical Concrete Block | Peanut-Shaped Concrete Block 2 | H-Shaped Concrete Block 2 | |
| Block unit | 8.8 | 14.9 | 22.0 |
| Block prism 3 | 5.8 | 7.7 | 18.1 |
| Site Class | Seismic Zone | |||
|---|---|---|---|---|
| SS ≤ 0.25 | SS = 0.50 | SS = 0.75 | ||
| SA | 0.8 | 0.8 | 0.8 | |
| SB | 1.0 | 1.0 | 1.0 | |
| SC | Depth to bedrock: not less than 20 m | 1.2 | 1.2 | 1.1 |
| Depth to bedrock: less than 20 m | 1.4 | 1.4 | 1.3 | |
| SD | Depth to bedrock: not less than 20 m | 1.6 | 1.4 | 1.2 |
| Depth to bedrock: less than 20 m | 1.7 | 1.5 | 1.3 | |
| SE | 2.5 | 1.9 | 1.3 | |
| Site Class | Seismic Zone | |||
|---|---|---|---|---|
| S ≤ 0.1 | S = 0.2 | S = 0.3 | ||
| SA | 0.8 | 0.8 | 0.8 | |
| SB | 1.0 | 1.0 | 1.0 | |
| SC | 1.7 | 1.6 | 1.5 | 1.1 |
| 1.5 | 1.4 | 1.3 | 1.3 | |
| SD | 2.4 | 2.0 | 1.8 | 1.2 |
| 1.7 | 1.6 | 1.5 | 1.3 | |
| SE | 3.5 | 3.2 | 2.8 | |
| Site Class | Soil Class | Shear Wave Velocity Vs (m/s) | Standard Penetration Test Blow Count N (/300 mm) | Undrained Shear Strength Su (×10−3 N/mm2) |
|---|---|---|---|---|
| SA | Hard rock | >1500 | - | - |
| SB | Rock | 760–1500 | - | - |
| SC | Very dense soil, soft rock | 360–760 | >50 | >100 |
| SD | Stiff soil | 180–360 | 15–50 | 50–100 |
| SE | Soft clay | <180 | <15 | <50 |
| Seismic Zone | Zone | Seismic Zone Factor, S | Remarks |
|---|---|---|---|
| I | All of zone, except seismic zone II | 0.22 g |  |
| II | North Gangwon pref., South Jeollanam pref., Jeju pref. | 0.14 g |
| Original Wall Cross Section | Simplified Cross Section |
|---|---|
 | 1. Same horizontal length of key block |
2. Average vertical length of key block |
| Specimen | Simplification Method | Maximum Load Pmax (kN) | Maximum Bending Moment (kN·m) | Distance from Centroid to Top X (mm) | Tensile Strength of Key Block (kN) | Tensile Stress (N/mm2) |
|---|---|---|---|---|---|---|
| Specimen HS | 1 | 14.8 | 4.44 | 106.5 | 41.7 | 0.89 |
| 2 | 106.3 | 41.7 | 0.89 | |||
| Specimen PS | 1 | 12.6 | 3.78 | 99.7 | 37.9 | 0.88 |
| 2 | 100.8 | 37.5 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Lee, K.-S. Experimental Study on Out-of-Plane Seismic Performance of New Type Masonry System. Appl. Sci. 2021, 11, 11736. https://doi.org/10.3390/app112411736
Choi H, Lee K-S. Experimental Study on Out-of-Plane Seismic Performance of New Type Masonry System. Applied Sciences. 2021; 11(24):11736. https://doi.org/10.3390/app112411736
Chicago/Turabian StyleChoi, Ho, and Kang-Seok Lee. 2021. "Experimental Study on Out-of-Plane Seismic Performance of New Type Masonry System" Applied Sciences 11, no. 24: 11736. https://doi.org/10.3390/app112411736
APA StyleChoi, H., & Lee, K. -S. (2021). Experimental Study on Out-of-Plane Seismic Performance of New Type Masonry System. Applied Sciences, 11(24), 11736. https://doi.org/10.3390/app112411736







