CDL-GAN: Contrastive Distance Learning Generative Adversarial Network for Image Generation

Abstract

While Generative Adversarial Networks (GANs) have shown promising performance in image generation, they suffer from numerous issues such as mode collapse and training instability. To stabilize GAN training and improve image synthesis quality with diversity, we propose a simple yet effective approach as Contrastive Distance Learning GAN (CDL-GAN) in this paper. Specifically, we add Consistent Contrastive Distance (CoCD) and Characteristic Contrastive Distance (ChCD) into a principled framework to improve GAN performance. The CoCD explicitly maximizes the ratio of the distance between generated images and the increment between noise vectors to strengthen image feature learning for the generator. The ChCD measures the sampling distance of the encoded images in Euler space to boost feature representations for the discriminator. We model the framework by employing Siamese Network as a module into GANs without any modification on the backbone. Both qualitative and quantitative experiments conducted on three public datasets demonstrate the effectiveness of our method.

1. Introduction

Generative Adversarial Networks (GANs) [1] have shown incredible success as effective data-driven models for image synthesis, but have become exposed to inevitable training obstacles. To find the theoretic Nash equilibrium with non-convex objective functions, GAN needs to exploit image information from a continuous and high-dimensional parameter space. Because GAN training is substantially more complicated than a standard neural network, it is challenging to keep the training stable. As a result, the outputs of a generative model frequently become uncontrollable and are of poor quality. To handle these challenges, many solutions have been introduced to improve GANs’ performance.

In recent times, numerous proposals for better designs and optimization of basic GANs have been reported. Mirza and Osindero [2], Huang et al. [3], Odena et al. [4] proposed a re-engineered network architecture based on conditional generation. Conditional GANs (cGANs) learn a conditional probability distribution from auxiliary information about real data. Wang et al. [5], Hoang, Quan et al. [6], and Nguyen Tu et al. [7] modeled generative–discriminative network pairs to increase the generation capacity of the generator. With multiple generators or discriminators, GANs can get more constructive gradient signals to learn intermediate representation. Larsen et al. [8], Makhzani et al. [9], Dumoulin et al. [10], Wang, Xiaoqing [11], and Kwak, Jeong gi et al. [12] use the most common encoder–decoder architecture to learn image features from latent space. These hybrid models are useful for addressing mode collapse. In the face of the oscillation in model parameters, previous work by Martin Arjovsky et al. [13], Takeru Miyato et al. [14], Salimans et al. [15], and Chunliang Li et al. [16] utilized appropriate loss functions to tackle stability issues. Some added interventions such as normalization [13,14] and regularization [17,18] to the discriminator [19], the generator [20] or both together [21]. Others found new probability distance metric [15,16,22] to replace JS divergence. Concerning the optimization algorithm, several researchers proposed the use of another gradient descent optimization technique [23,24], or modified the training technique [25,26]. Within the solutions mentioned above, diverse characteristic GANs variants have made a difference to some extent in the GANs literature, but some issues still remain unsolved. In practice, these methods more or less result in poor image quality due to training instability or mode collapse.

In this work, we undertake a comprehensive and effective approach using Contrastive Distance Learning (CDL) to make GANs perform better. Motivated by Improved Consistency Regularized GAN (ICR-GAN) [21] and Mode Seeking GAN (MS-GAN) [20], we present Consistent Contrastive Distance (CoCD) to modulate the sensitivity of the generator with prior changes in the noise. In light of the work of Ansari [22] and Miyato [27], we establish additional Characteristic Contrastive Distance (ChCD) to capture more informative image features for the discriminator. The CoCD is aimed at mitigating mode collapse to improve the training stability, while the ChCD forces the discriminator to remember more useful high-level semantics to further improve image synthesis quality. In particular, to alleviate computational cost with two additional auxiliary losses, we design our framework with the Siamese modules.

In our experiments, we conduct comparisons on CDL-GAN across the existing optimized GAN models for three public datasets. CDL-GAN yields state-of-the-art image synthesis results among the existing models. In extensive qualitative and quantitative studies, we show that our work offers multi-faceted improvements. It achieves lower Fréchet Inception Distance (FID) [28] scores under the same training and evaluation conditions with different datasets. Meanwhile, it works well across a large range of GAN models with different hyperparameter sets of the Adam optimizer. Furthermore, our proposed approach further mitigates mode collapse and training instability issues in both the generator and discriminator.

In brief, the main contributions of this work can be summarised as follows in three fold:

• We propose a comprehensive and effective approach as Contrastive Distance Learning (CDL) to train GAN. This method can be easily extended into different GAN models without any other modification of the backbone.
• We subtly integrate the Siamese modules into the GAN framework with a low computational cost. With its superiority, we alleviate the antagonism between the generator and the discriminator.
• We conduct extensive experiments on three public datasets and demonstrate the versatility of our approach. The results show that CDL can not only address some existing issues in both the generator and discriminator, but also boost the visual quality of the generated images.

2. Preliminaries and Related Works

A GAN is composed of two components: a generator, G, which converts random noise vectors into images, and a discriminator, D, which tries to distinguish between generated and real images. With adversarial training, the generator G is trained to take a latent vector $z\sim P\left(z\right)$ and generated target samples $G\left(z\right)$ that encourage the capture of the distribution of real images and reduce the discrepancy with the real distribution. The discriminator D as a critic makes a decision score over possible observation sources (either from $G\left(z\right)$ or from the empirical data distribution $P_{real}\left(x\right)$). Both components have respective loss functions written as follows:

$$\begin{array}{cc}\hfill {\mathit{L}}_{\mathit{D}}=& -{\mathbb{E}}_{x\sim p_{real}}[log\left(D\left(x\right)\right)]\hfill \\ \hfill & -{\mathbb{E}}_{z\sim p\left(z\right)}[log(1-D\left(G\left(z\right)\right))]\hfill \end{array}$$

(1)

$${\mathit{L}}_{\mathit{G}}=-{\mathbb{E}}_{z\sim p\left(z\right)}[logD\left(G\left(z\right)\right)]$$

(2)

The losses defined above originate from the vanilla GAN [1] and are known as the non-saturating constraint. Abundant works have proved that a suitable objective function plays a key role in generation quality and training stability. For example, the hinge loss proposed by Jae Hyun Lim [29], is a very popular redesign loss on GANs and can be written as follows:

$$\begin{array}{cc}\hfill {\mathit{L}}_{\mathit{D}}=& -{\mathbb{E}}_{x\sim p_{real}}[min(0,D\left(x\right)-1)]\hfill \\ \hfill & -{\mathbb{E}}_{z\sim p\left(z\right)}[min(0,-D\left(G\left(z\right)\right)-1)]\hfill \end{array}$$

(3)

$${\mathit{L}}_{\mathit{G}}=-{\mathbb{E}}_{z\sim p\left(z\right)}\left[D\left(G\left(z\right)\right)\right]$$

(4)

With 1-Lipschitz constrained Wasserstein distance [30], Martin Arjovsky [13] proposes the Wasserstein GAN (W-GAN) to measure distributions, which are fed to the discriminator. Subsequent work has refined this technique in several ways [31,32]. In particular, Takeru Miyato [14] proposed spectral normalization to stabilize the training, which is widely used in many GAN frameworks.

2.1. Regularizations for GANs

Regularization applied in the GANs literature, which encodes some prior knowledge into model training and keeps the predictions consistent, has emerged in recent years. Zhao et al. [21] proposed ICR-GAN and introduced two new techniques, which are abbreviated as bCR and zCR, to improve consistent regularization for GANs. The bCR adds two consistency terms to the discriminator: one is applied in real images, the other is applied in the corresponding sampling from the generator. The zCR augments noise vectors z by a slightly perturbing $\Delta z\sim N(0,{\delta }_{noise})$ for the generator. Meanwhile, zCR changes the loss function with an additional constraint by maximizing the distance between $G\left(z\right)$ and $G\left(T\right(z\left)\right)$ for the discriminator, and motivates the generator to create images with diversity. ICR-GAN improves the quality of generated images indeed compared with CR-GAN [19]; however, it needs some prior knowledge such as image transformations in real data space or noise augmentations in latent space. On the one hand, the discriminator is too sensitive to balance the generator in the bCR and this easily results in training instability and over-fitting. On the other hand, the noise enhancement $\Delta z$ is fixed when fed to the generator and the augmentation cannot make a difference directly to the consistent constraint. It is difficult to guarantee generations with diversity.

To the best of our knowledge, mode seeking regularization (MSR), as presented by Mao et al. [20], has been applied to cGANs for various tasks to alleviate the mode collapse problem. This regularization term encourages generators to generate dissimilar images during training and provide gradients from minor modes to fool the discriminator. MS-GAN can be applied to different conditional image generation tasks for image diversity without sacrificing visual quality. It is a pity that MSR requires labels or extra data as auxiliary information to improve the diversity of synthesized images.

2.2. Characteristic Function Distance for GANs

More recently, characteristic function distance (CFD) [22] reduced to the Integral Probability Metric (IPM) has been reported in the GANs literature and proposes the use of CFD-GAN to improve GANs’ performance. Characteristic functions have been widespread in probability theory and successful in two-sample testing [33,34,35]. The CFD formulates the problem of learning an Implicit Generative Model (IGM) as minimizing the expected distance between characteristic functions. The approximate distance between empirical characteristic functions is seen as a mixture of degenerate distributions with the same weights. The CFD-GAN replaces the Jensen–Shannon (JS) divergence with the CFD and uses the discrepancy expectation between the sampled distribution on real images and generations as an optimizable function. The CFD exhibits desirable mathematical properties such as continuity, differentiability, and weak topology; however, IPM is time-consuming compared to other distance metrics and CFD-GAN has little improvement in the quality of image synthesis.

2.3. Siamese Network

The Siamese Network proposed by Jane Bromley [36] is a type of metric learning. It is composed of two identical neural networks with sharing weights. The network’s map inputs to another space and forms new representations as outputs. In the initial Siamese Network, the loss function is a contrastive loss, which is effective to determine the relationship between paired data. With the rise of deep learning, the Siamese Network has been gradually applied to face detection [37] and object tracking [38,39] in computer vision. In the GANs literature, [40] proposes TraVeLGAN to achieve an image-to-image translation task, which employs the Siamese Network to balance the relationship between the generator and the discriminator by a transformation vector.

Within these optimized approaches mentioned above, GANs has shown its potential for generating natural images, but they are still associated with some problems. Due to mode collapse, samples produced by CFD-GAN often lack diversity and introduce artificial flaws. MS-GAN effectively deals with mode collapse, but it only applies in supervised learning. With augmentations based on the exiting data, ICR-GAN sometimes suffers from unstable training and generates poor-quality images. To alleviate these problems, we introduce MS-GAN into unsupervised learning and propose novel regularizations to the objective function.

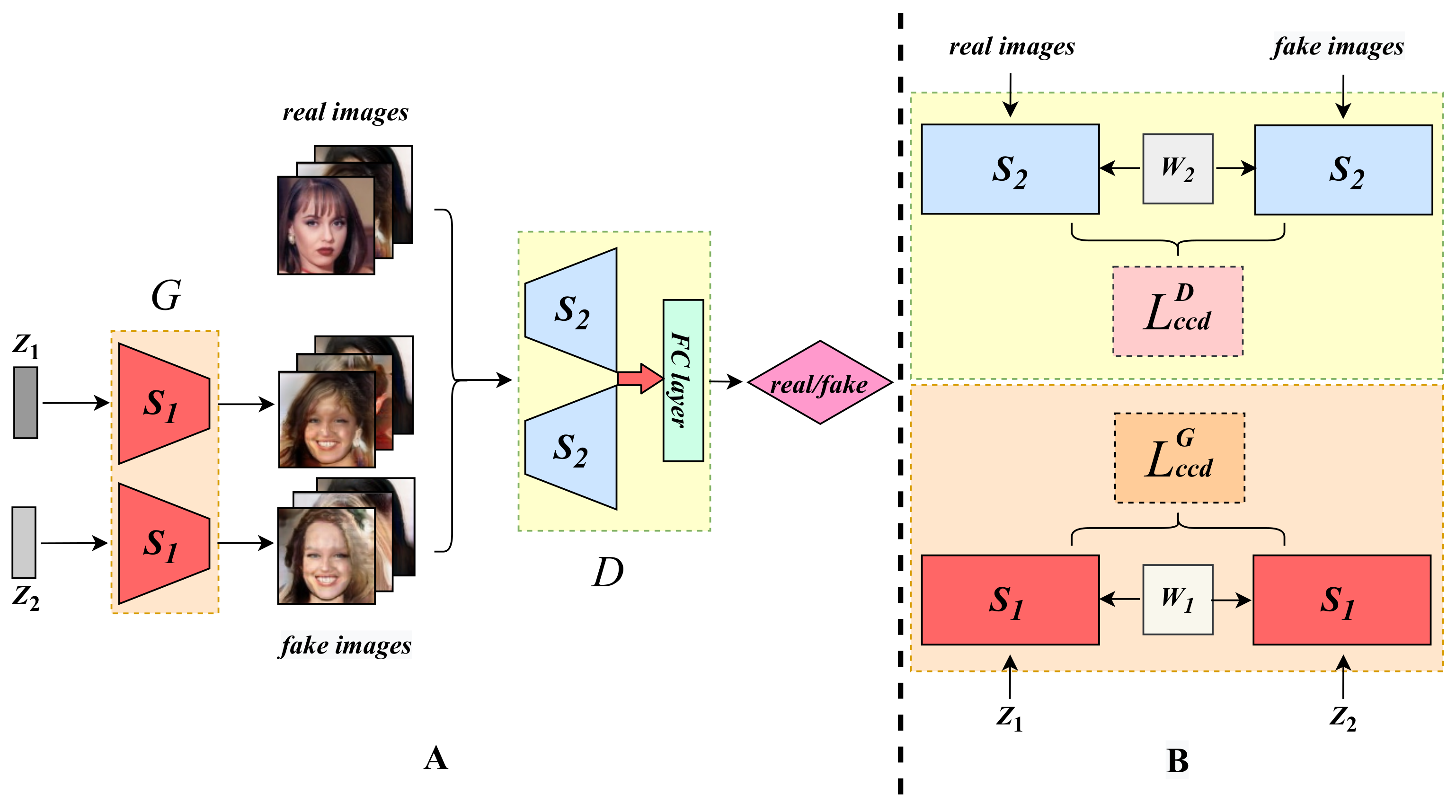
3. Methodology: Contrastive Distance Learning

In this section, we present two novel regularizers, Consistent Contrastive Distance (CoCD) and characteristic contrastive distance (ChCD), which are combined and denoted as Contrastive Distance Learning (CDL). To integrate CoCD and ChCD into a GAN architecture perfectly, we utilized the Siamese Network [41] to build the generator and the discriminator. In the training, the Siamese module shares the weights and parameters passing through the model, and we can alleviate the antagonism between the generator and the discriminator by contrastive learning. Our CDL-GAN framework is illustrated in Figure 1. $z_1$ and $z_2$ stand for noise vectors. G is composed by two of the same modules $S_1$, D is built by two of the same modules $S_2$ and a Fully Connected (FC) layer. $L_{ccd}^G$ means Characteristic Contrastive Distance (CoCD). $S_1$ is used to generate two fake images and optimize the $L_{ccd}^G$. $L_{ccd}^D$ means Characteristic Contrastive Distance (CoCD), the decision layer of $S_2$ means a projection operation [27] which maps fake or real images into characteristic vectors and gets the metric $L_{ccd}^D$. $S_1$ and $S_2$ both share the weights in the training. The whole framework is used to balance the generative model and discriminative model with CDL.

3.1. Consistent Contrastive Distance

Inspired by ICR-GAN [21] and MS-GAN [20], we focus on the difference between latent consistency regularization (zCR) and mode seeking regularization (MSR). The zCR augments noise vector z to the generator with $T\left(z\right)$ by slightly perturbing $\Delta z\sim N(0,{\delta }_{noise})$, while MSR uses random noise which is variable without controlling parameters. Both regularizations expect to maximize the distance between fake images generated by corresponding noise. To alleviate mode collapse, zCR requires an additional constraint on the discriminator, while MSR just adds a noise coefficient to images’ distance. Given the generator with a prior noise input, it is reasonable to explore the effect of the augmentation $\Delta z$ on the outputs. Considering $\Delta z$ as a conditional constraint, it is possible for us to make MSR work in unsupervised learning.

To integrate MSR into unconditional GANs, we propose Consistent Contrastive Distance (CoCD). We augment noise z to the generator by setting a hyperparameter $\gamma$ and yield $A\left(z\right)=(1+\gamma )\ast z,\gamma \in (0,1)$. To this end, $\Delta z=\gamma \ast z$. What we need to emphasize here is that we only augment the amplitude of noise vector z to keep them consistent. In the training processing, z and $A\left(z\right)$ learn feature distribution from the same image. When the augment $\Delta z$ is small enough, we expect that the distance between $G\left(z\right)$ and $G\left(A\right(z\left)\right)$ is large enough to encourage generations to be discrepant. Taking $\Delta z$ into consideration, the distance metric can be written as follows:

$${\mathit{L}}_{ccd}^G=\underset{G}{argmax}\left(\frac{L_2\left(G\left(A\right(z\left)\right)-G\left(z\right)\right)}{L_2(\Delta z)}\right)$$

(5)

where $L_2$ means the second-norm. With the adversarial mechanism, consistent contrastive distance as a regularization term can be appended into the original objective function. Here, we take Equation (4) for example and the generator’s loss can be written as follows:

$${\mathit{L}}_G^{\prime }={\mathit{L}}_G-{\lambda }_{gen}{\mathit{L}}_{ccd}^G$$

(6)

where ${\lambda }_{gen}$ denotes the control of the weights and highlights the importance of the regularizer. In the training process, $\Delta z$ is controlled by $\gamma$ after a noise vector is generated randomly. We can modulate the parameter $\gamma$ to achieve the effectiveness of CoCD.

3.2. Characteristic Contrastive Distance

To stabilize training, we utilize Characteristic Function Distance (CFD) introduced in CFD-GAN [22] as a regularization for the discriminator. Meanwhile, the transformation vector introduced in TraVeLGAN [40], which uses a function to represent high-level semantics in some latent space, is aimed at mapping images to some space with the same relationship between the original and generated versions. TraVeLGAN gives us a feasible scheme to add the CFD regularization to the discriminator. We extract semantic information by a characteristic function and utilize a transformation vector to achieve Characteristic Contrastive Distance (ChCD). To elaborate, we firstly extract the output of the second-to-last layer as high-level semantic information when a real image or generated image is encoded by the discriminator. Then, we take a characteristic function as the transformation mode and utilize the transformation vector to learn characteristic semantic information. Next, we turn characteristic semantic information into characteristic vectors with a finite-dimensional approximation in Euler space. Finally, we compute the distance between real characteristic vectors and generated characteristic vectors.

Unlike the density function, the Euler space always exists with uniform continuity, differentiability, and boundedness. From the perspective of manifold learning, a characteristic vector is regarded as an essential element of images, and we could get the discrepancy between images by contrasting the distance between characteristic vectors. For GAN, ChCD can keep the parameters of the discriminator continuous and differentiable almost everywhere and provide a more informative signal to the discriminator for feature representations. The proofs of CFD properties are stated in CFD-GAN [21], which the reader is highly encouraged to read.

Letting t be the input argument of the characteristic vector $V:\left\{v_1,\dots ,v_n\right\}$, the characteristic function $\widehat{\psi }$ is a weighted sum of characteristic vectors transformed in Euler space:

$$\widehat{\psi }\left(t\right)=\frac{1}{n}\sum _{j=1}^n{e}^{i(t⨀v_j)}$$

(7)

where $i=\sqrt{(-1)}$, $\left|e^{ix}\right|\le 1$, $t\in R^d$, ⨀ means vector dot product, and t is a random variable of a degenerated sampling distribution ${\delta }_V$. Given $X:=\left\{x_1,\dots ,x_n\right\}$ and $Y:=\left\{y_1,\dots ,y_n\right\}$ with $x_i,y_i\in R^d$ are samples from the distributions $\mathbb{P}$ and $\mathbb{Q}$, respectively, and let $t_1,\dots ,t_k$ be samples from ${\delta }_V$. We define the characteristic contrastive distance between ${\mathit{V}}_{\mathbb{P}}$ and ${\mathit{V}}_{\mathbb{Q}}$ as

$${\mathit{L}}_{ccd}^D({\mathit{V}}_{\mathbb{P}},{\mathit{V}}_{\mathbb{Q}})=\frac{1}{k}\sum _{i=1}^k{\parallel {\widehat{\psi }}_{\mathbb{P}}\left(t_i\right)-{\widehat{\psi }}_{\mathbb{Q}}\left(t_i\right)\parallel }^2$$

(8)

where ${\widehat{\psi }}_{\mathbb{P}}$ and ${\widehat{\psi }}_{\mathbb{Q}}$ are the characteristic functions of characteristic vectors, computed by X and Y, respectively. With the characteristic contrastive distance, the new objective function of the discriminator can be written as follows:

$${\mathit{L}}_D^{\prime }={\mathit{L}}_D+{\lambda }_{dis}{\mathit{L}}_{ccd}^D$$

(9)

where ${\lambda }_{dis}$ denotes the control of the importance of the ${\mathit{L}}_{ccd}^D$ and ${\mathit{L}}_D$ denotes the original loss.

3.3. Enhancement with the Siamese Modules

Combining Contrastive Distance Learning (CDL) with the Siamese modules, we can make use of the same structure to share the weights and handle the relationship between paired data effectively. The method is shown in greater detail in Algorithm 1. On the one hand, Consistent Contrastive Distance (CoCD) offers a virtuous cycle for the generator exploiting more modes. On the other hand, Characteristic Contrastive Distance (ChCD) forces the discriminator to focus on meaningful visual information. The goal of the Siamese module, $S_1$, is cooperative with the generator, G. Meanwhile, the discriminator, D, is constrained by the module $S_2$, to make training more bidirectionally stable. In the training process, the generator creates two parts of fake data, while the discriminator needs to consider the difference of each real image with the two corresponding generated images. CDL can be balanced by adjusting the parameters of ${\lambda }_{gen}$ and ${\lambda }_{dis}$.

Algorithm 1 Contrastive Distance Learning (CDL)

Input: parameters of generator ${\theta }_G$ and discriminator ${\theta }_D$, consistent contrastive distance coefficient ${\lambda }_{gen}$ and characteristic contrastive distance coefficient ${\lambda }_{dis}$, noise z and noise augment parameter $\gamma$.  1: for number of training iterations do  2:       for $t=1$ to $N_D$ do  3:          sample batch $Z\sim P\left(z\right)$, $X\sim P_{real}\left(x\right)$  4:          sample augment noise $\Delta z=\gamma \ast z$  5:          augment latent vector $A\left(z\right)=z+\Delta z$  6:          $L_D\leftarrow \left(G\left(z\right)\right)-D\left(x\right)+D\left(G\left(A\left(z\right)\right)\right)-D\left(x\right)$  7:          $L_{dis}\leftarrow L_{ccd}^D(V_{G\left(z\right)},V_x)+L_{ccd}^D(V_{G\left(A\right(Z\left)\right)},V_x)$  8:          ${\theta }_D\leftarrow$ AdamOptimizer $(L_D+{\lambda }_{dis}{L}_{dis})$  9:       end for  10:     sample batch $Z\sim P\left(z\right)$  11:     sample augment noise $\Delta z=\gamma \ast z$  12:     augment latent vector $A\left(z\right)=z+\Delta z$  13:     $L_G\leftarrow -D\left(G\left(z\right)\right)-D\left(G\left(A\left(z\right)\right)\right)$  14:     $L_{gen}\leftarrow -L_{ccd}^G$  15:     ${\theta }_G\leftarrow AdamOptimizer(L_G-{\lambda }_{gen}{L}_{gen})$  16: end for

4. Experiments

To validate our proposed CDL-GAN method, we conducted extensive quantitative and qualitative experiments to evaluate different aspects. First, we compare CDL-GAN to several existing optimized works, ICR-GAN [21], CFD-GAN [22], and WGAN-GP [31], with the same GAN backbone for three public datasets. We highlight here that CDL-GAN is motivated by ICR-GAN and CFD-GAN, while WGAN-GP is effective for stabilizing GAN training with 1-Lipschitz; therefore, it is necessary for us to conduct comparisons with them. Then, we applied CoCD, ChCD, and CDL, respectively, to a recent state-of-the-art baseline SNGAN [14] with two different hyperparameter sets of the Adam optimizer [42]. Next, we re-implemented SNGAN with our approach to analyze the training time for different datasets. Finally, we conducted studies based on DCGAN [43] and ICR-GAN to evaluate CDL-GAN’s mode recovery ability. For fairness, we emphasize that all GAN models as discussed are unconditional and our operational procedures were under the same training conditions with a uniform code base. In the same experiment, we chose the same GAN backbone. We reproduced the existing models using the description in the corresponding works.

4.1. Settings and Evaluation Metrics

We evaluate our models against the above existing models for three public datasets: MNIST [44], CIFAR-10 [45], and CelebA [46]. For preprocessing of data sets, we follow the detailed settings in [47]. MNIST contains 70 K $28\times 28$ handwritten digits with 10 labels; 60 K for training and 10 K for testing. We use all unlabeled training images in our experiments, resized to $32\times 32$. CIFAR-10 consists of 60 K $32\times 32$ natural images in 10 classes, out of which 50 K for training and 10 K for testing. We use all the training images without labels. For CelebA, we use the aligned face version in two resolutions: about 200 K images at a resolution of $64\times 64$ and $30K$ images reshaped to size $128\times 128$. In this paper, we regard the higher resolution images of CelebA as CelebA-HD.

To assess the quality of generated images against corresponding real images, we adopted the Fréchet Inception Distance (FID) [28] as a standard metric, which is used to measure the distance between generated and real image features and proved to correlate well with human evaluation. In our experiments, we calculated FID scores on different datasets with different image numbers: we used 10 K generated images vs. 10 K real images on CIFAR-10, 50 K vs. 50 K face images on CelebA in the size of $64\times 64$, and 3 K vs. 3 K on the high-resolution CelebA. Lower FID scores indicate better quality of the synthetic images.

For all experiments, we use a single Tesla V100 GPU with our implementation in PyTorch. Meanwhile, we chose the Adam optimizer [42] with the learning rate of $0.0002$ and set the batch size of images as 64. For iterations, the number of discriminator steps was 5 per generator step. For hyperparameters, we initialized $\gamma =0.05$, ${\lambda }_{dis}=10$, and ${\lambda }_{gen}=10$. For objective function, we used hinge loss as a basic criterion except for CFD-GAN, because CFD-GAN utilizes a characteristic function distance as its objective function.

To integrate CDL into GAN architecture perfectly, we updated the DCGAN and SNGAN backbone with Siamese modules, allowing the generator to transform the global structure of an input image by ChCD regularization. We further enhanced the training stability and applyied ChCD regularization and switched the depth-wise concatenation to adaptive instance normalization in the discriminator. Our generator consists of four downsampling blocks, four intermediate blocks, and four upsampling blocks, all of which inherit preactivation residual units. Our discriminator is a projection discriminator [27], which contains multiple linear output branches. The discriminator contains six pre-activation residual blocks with leaky ReLU.

4.2. Results

For improved image synthesis, we achieved a coincident and remarkable improvement in FID scores across three public datasets over the existing models mentioned above. All the models use the DCGAN as the backbone. As seen in

Table 1. Fréchet Inception Distance (FID) scores for CDL-GAN and the existing models.

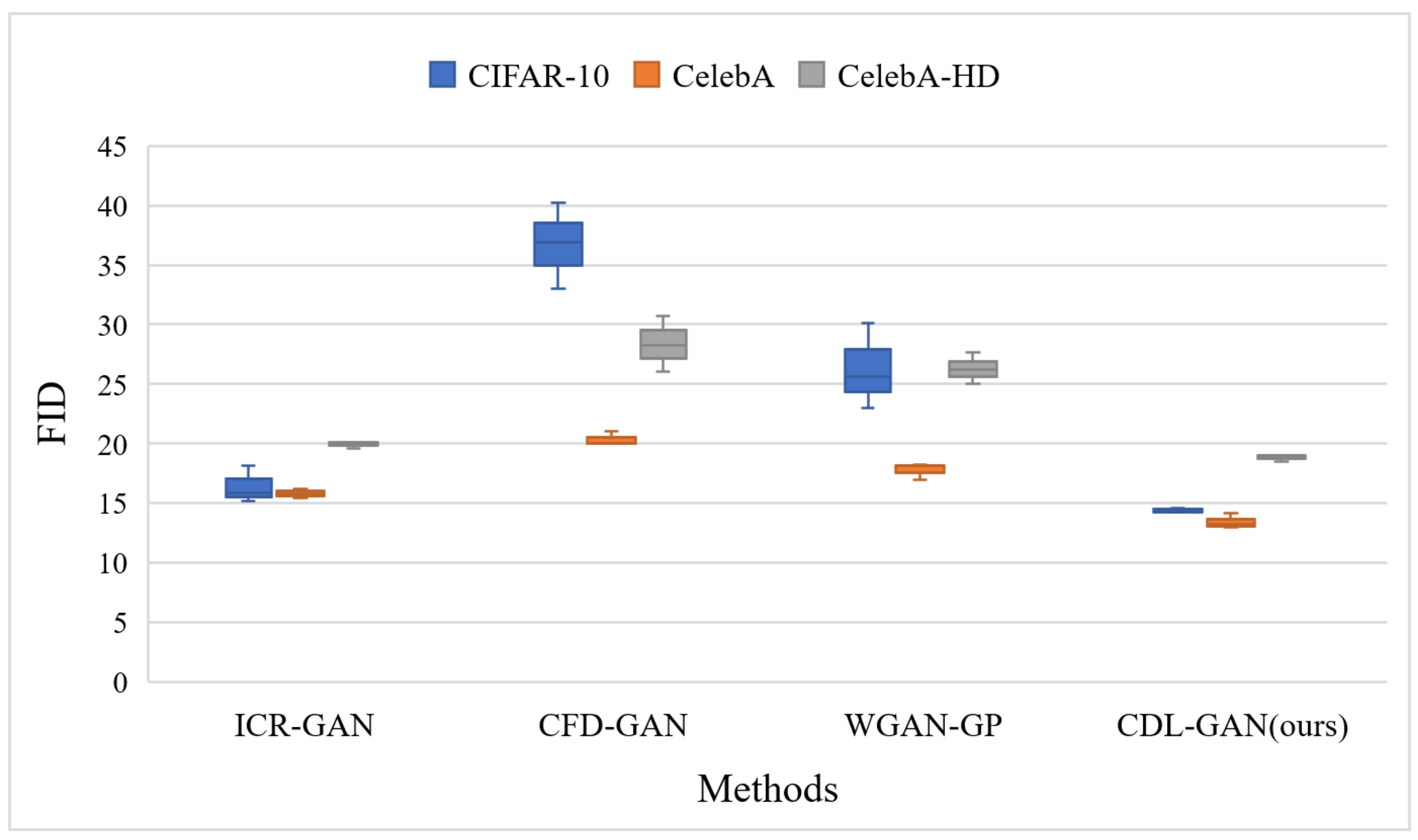
Models	MNIST (32*32)	CIFAR-10 (32*32)	CelebA (64*64)	CelebA-HD (128*128)
ICR-GAN	0.55	15.87	15.43	19.56
CFD-GAN	0.53	33.08	20.48	25.73
WGAN-GP	0.69	22.29	17.85	23.98
CDL-GAN (ours)	0.48	14.33	13.18	16.53

, CDL-GAN improves FID scores on CIFAR-10 by $1.54$ points over ICR-GAN, $18.75$ points over CFD-GAN, and $7.96$ points over WGAN-GP. On CelebA dataset, CDL-GAN achieved an improvement of $2.25$ points over ICR-GAN, $7.30$ points over CFD-GAN, and $4.67$ points over WGAN-GP at a resolution of $64\times 64$. On the high-resolution of CelebA, CDL-GAN improved by $3.03$ points over ICR-GAN, $9.20$ points over CFD-GAN, and $6.55$ points over WGAN-GP. The results in Figure 2 show that CDL-GAN significantly outperforms all other models in terms of FID scores. We determined the FID scores in each dataset with five validations for different models. The improvement is still significant compared to the measurement variance. The height difference of each rectangle suggests that our method is more reliable than the existing models in terms of the quality of image synthesis.

For improved training stability, we verified it in two aspects: using the Adam parameters $({\beta }_1,{\beta }_2)$ to evaluate the sensitivity of model performance based on the SNGAN [14] backbone and observing the convergence rate of GAN training without any hyperparameter tuning. As seen in

Table 2. FID scores (lower is better) among SNGAN, SNGAN + CoCD, SNGAN + ChCD, and SNGAN + CDL on CelebA-HD. “SNGAN + CoCD” means combining SNGAN with the consistent contrastive distance, “SNGAN + ChCD” means combining SNGAN with the characteristic contrastive distance, and “SNGAN + CDL” means combing SNGAN with contrastive distance learning.

$({\mathit{\beta }}_1,{\mathit{\beta }}_2)$	SNGAN	SNGAN + CoCD	SNGAN + ChCD	SNGAN + CDL
(0.0, 0.9)	12.97	12.12	11.35	10.08
(0.5, 0.999)	14.88	13.33	12.98	10.27

, in comparison to the baseline SNGAN, SNGAN + CDL achieves lower FID scores than SNGAN. When the Adam optimizer hyperparameter set was $(0.0,0.9)$, SNGAN + CDL improved by $2.89$ points over SNGAN. Meanwhile, SNGAN + CDL achieved an improvement of $4.31$ points over SNGAN with the Adam parameters $(0.5,0.999)$. Furthermore, the variability in FID scores for SNGAN + CDL on different Adam parameters was $0.49$ points, which is smaller than SNGAN with $1.97$ points. In Figure 3, we show the relationship between FID scores and training iterations on the baseline SNGAN. It is obvious that SNGAN + CDL converges faster in the early training period and achieves better FID scores in the end. Thereby, our method possesses better robustness in all of these settings.

For a lower computational cost, we profile CDL-GAN’s training time with SNGAN backbone for 100 generator update steps, which is similar to [14]. From Figure 4, we can see that our approach takes up minimal time at less than $0.1\%$ of training time per update for all datasets. GANs training with less time taken means decreasing computational costs, and we can easily integrate CDL into the existing GAN frameworks without worrying about extra burden.

For mitigating mode collapse, we followed the procedure in [43,48] evaluated mode recovery with DCGAN [43] and ICR-GAN [21]. We utilized a pre-trained MNIST classifier and the Stacked MNIST [48] dataset with 1000 possible modes to conduct a comparative analysis. As seen in

Table 3. Number of modes (higher is better) recovered by the generator on the Stacked MNIST dataset.

Metric	K	DCGAN	ICR-GAN	CDL-GAN
Modes	$1/4$	30.64	48.47	50.50
Modes	$1/2$	605.17	703.25	725.88
${\mathit{D}}_{KL}(p\parallel q)$	$1/4$	5.48	4.96	4.55
${\mathit{D}}_{KL}(p\parallel q)$	$1/2$	1.97	1.64	1.45

, K indicates the size of the discriminator relative to the generator, $D_{KL}(p\parallel q)$ means the $KL$ divergence between the generated mode distribution p and optimal uniform distribution of the mode q. The results show that CDL-GAN recovers more modes for all K and has a lower KL divergence with the ideal uniform distribution than both DCGAN and ICR-GAN. More modes recovery from CDL-GAN means that our method possesses better generation diversity.

To support our improvements directly in the observation, we also provide image samples randomly generated by CDL-GAN and the existing models for all datasets in Figure 5, Figure 6, Figure 7 and Figure 8. It can be seen from these results that the generations yielded by CDL-GAN are more explicit and more authentic.

4.3. Ablation Study

To verify the effectiveness of our proposed CoCD and ChCD, we further analyzed the training stability results. As seen in Table 2, we also added CoCD and ChCD into SNGAN [14], respectively, and the effect is cogent. When the Adam parameter set was $(0.0,0.9)$, SNGAN + CoCD improved FID scores by $0.85$ points over SNGAN, SNGAN + ChCD improved by $1.62$ points over SNGAN. Meanwhile, SNGAN + CoCD improved by $1.55$ points over SNGAN with the Adam parameters $(0.5,0.999)$, while an improvement of $2.60$ was found for SNGAN + ChCD. With two different ranges of the Adam parameter, the FID score discrepancies were $1.21$ points for SNGAN + CoCD, $0.93$ points for SNGAN + ChCD, which are lower than SNGAN with $1.97$ points. The results in Figure 3 also present a faster convergence in the early training period for CoCD and ChCD applied to SNGAN. The best FID scores achieved by SNGAN + CDL suggest that CoCD and ChCD can cooperate with each other to improve GANs’ performance. From Figure 9, we can see the visualization results of the generated samples. When CoCD and ChCD are respectively attached to the SNGAN model, the generated images have better quality. In particular, when CDL is attached to SNGAN, the generated face images are more authentic and recognizable.

5. Conclusions and Discussion

In this work, we presented Contrastive Distance Learning (CDL) as a novel optimized approach for GANs. For clarity, CDL includes two regularizations: Consistent Contrastive Distance (CoCD) and Characteristic Contrastive Distance (ChCD). Furthermore, we added the Siamese modules to the GAN backbone to balance the relationship between the generator and discriminator.

Extensive experiments have shown that our approach is practical and versatile. With the DCGAN backbone, CDL-GAN not only achieved lower FID scores than the existing optimized methods, but also effectively alleviated the mode collapse problem. With the SNGAN backbone, CDL-GAN also achieved better FID scores and improved training stability compared to SNGAN. Meanwhile, all the experiments show that CDL can be integrated into different GAN backbones, such as DCGAN and SNGAN, which indicates that CDL has universality in the GANs literature. All the results prove that CDL leads to significant improvements in the image synthesis task and provides an effective and alternative means for GAN training.

As for future work, we hope to explore CDL for other image tasks such as image-to-image translation and try to integrate mutual information into ChCD to improve GAN performance.