Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach
Abstract
:1. Introduction
2. Methods
2.1. Original Proposal of Motion Equations for a Primary System with Attached MTMDs, Reduced to an SDOF System through the Modal Approach
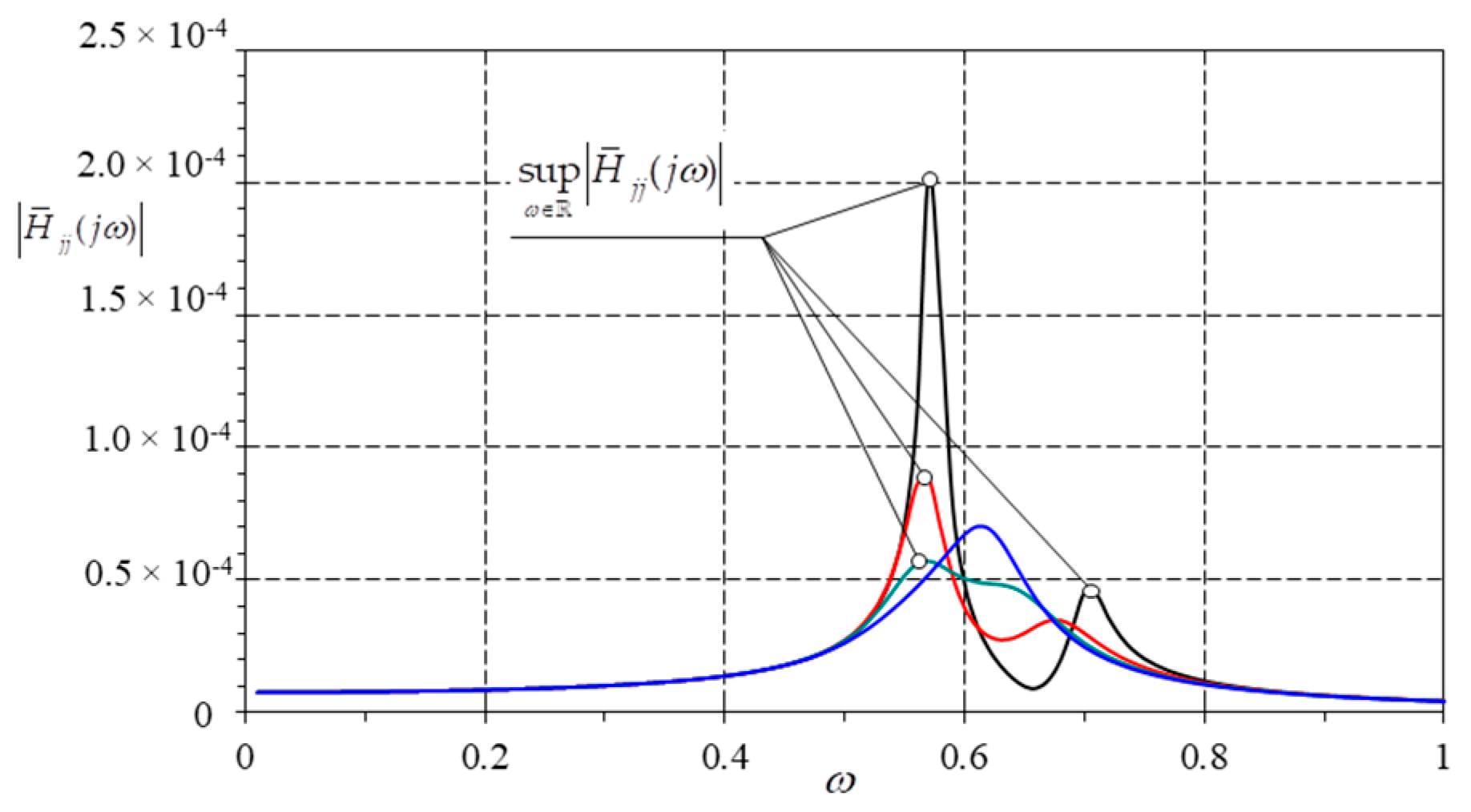
2.2. Determination of a Transfer Matrix Used to Determine the Objective Function in Optimization Issues
2.3. The Issue of Optimization
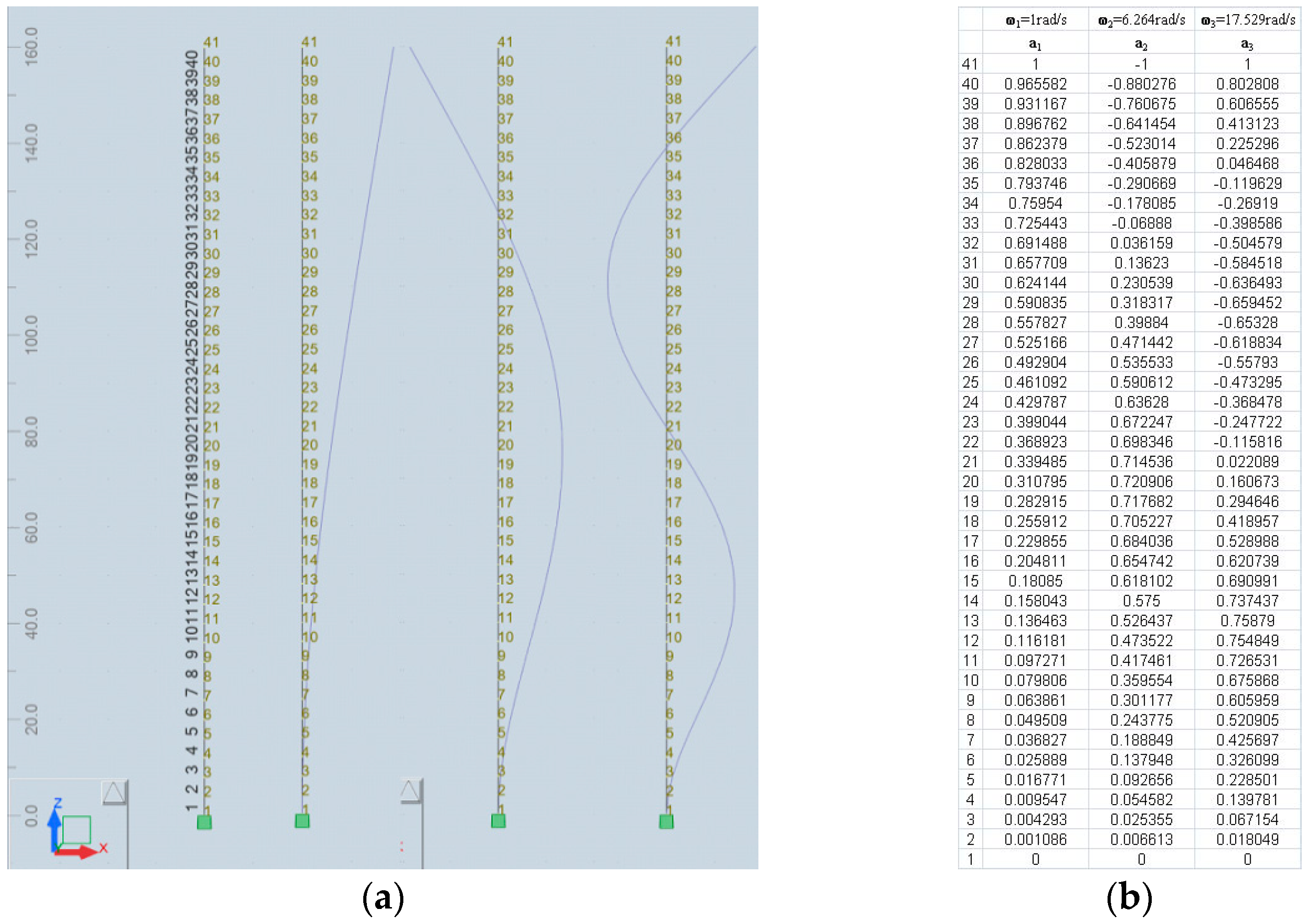
- Calculations of the eigenvalues and eigenvectors in Finite Element (FEM) software, adopting baseline frequency , to which MTMDs will be tuned;
- Adopting a point for reducing a system to an equivalent SDOF system, normalization of eigenvectors and determination of the parameters for the Equation (7);
- Adopting a TMD number and initial parameters for the TMDs;
- Adopting variables, which will be subject to the optimization process, e.g., for a constant value of (different constant parameter options possible);
- Selection of the optimization method (GA or SA) and the optimization issue, calculations of the equivalent system FRF , and the determination of values using the Equations (61) or (62) at each optimization step;
- After reaching the desired calculation accuracy (change of the J1 or J2) value, saving the obtained MTMD parameters, and calculations of the equivalent system FRF associated with the j degree of freedom, which was adopted as the equivalent system reduction point.
3. Numerical Example 1
3.1. Input Data
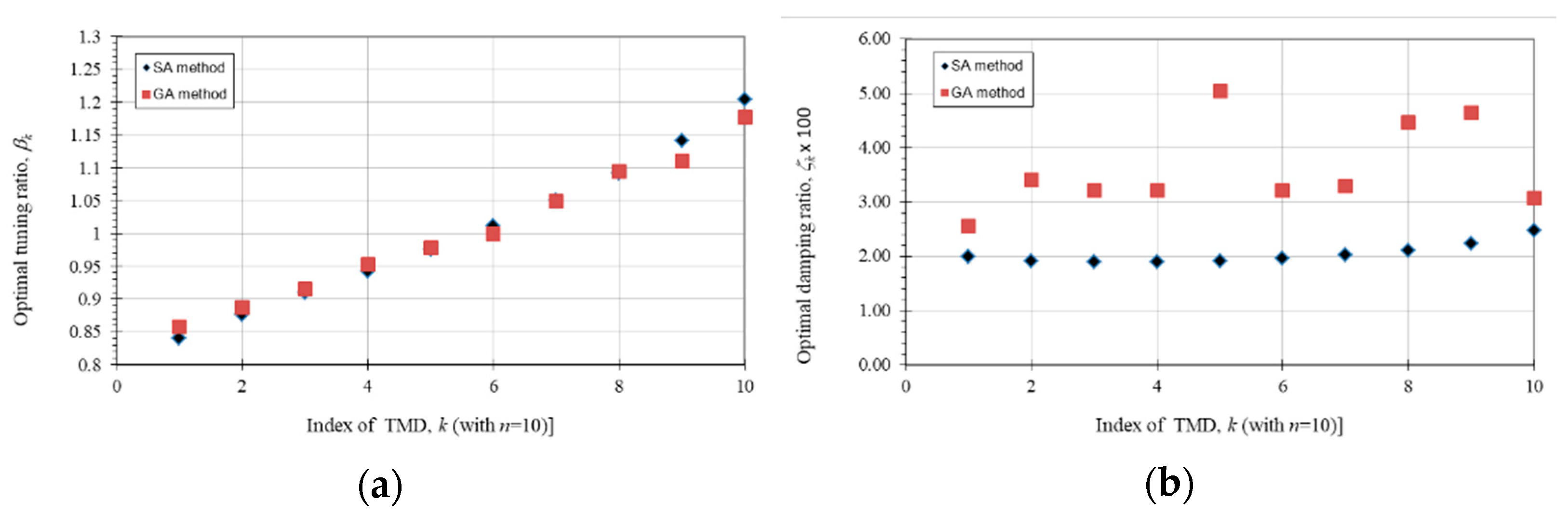
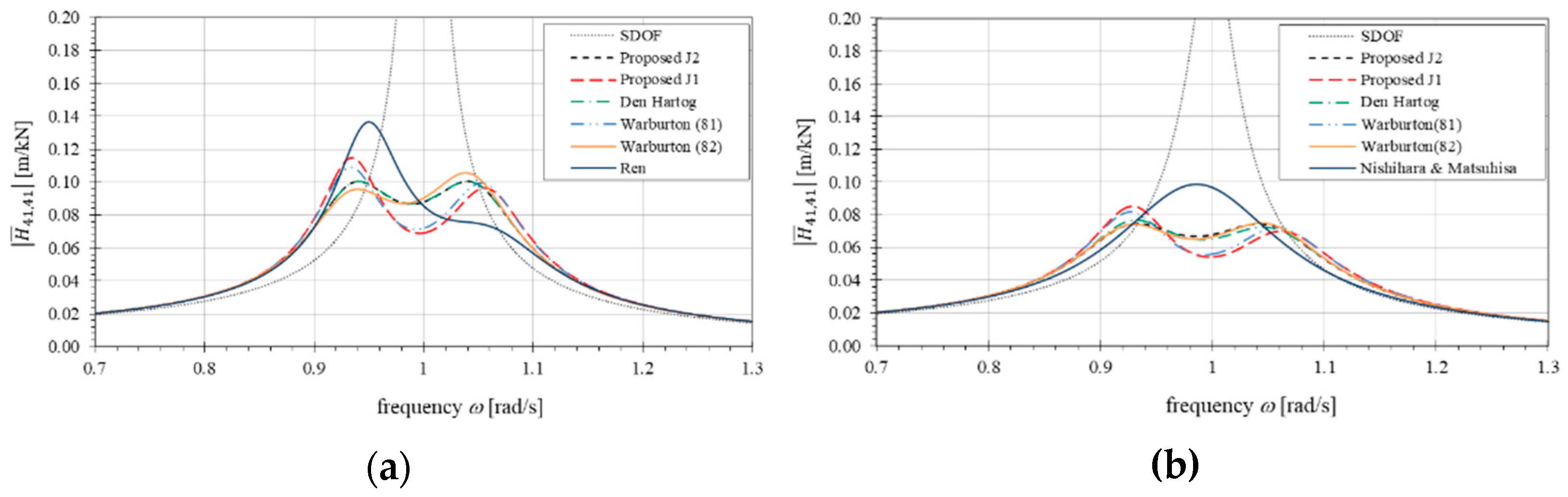
3.2. Numerical Optimization Results—Comparison of the GA and SA Heuristic Methods
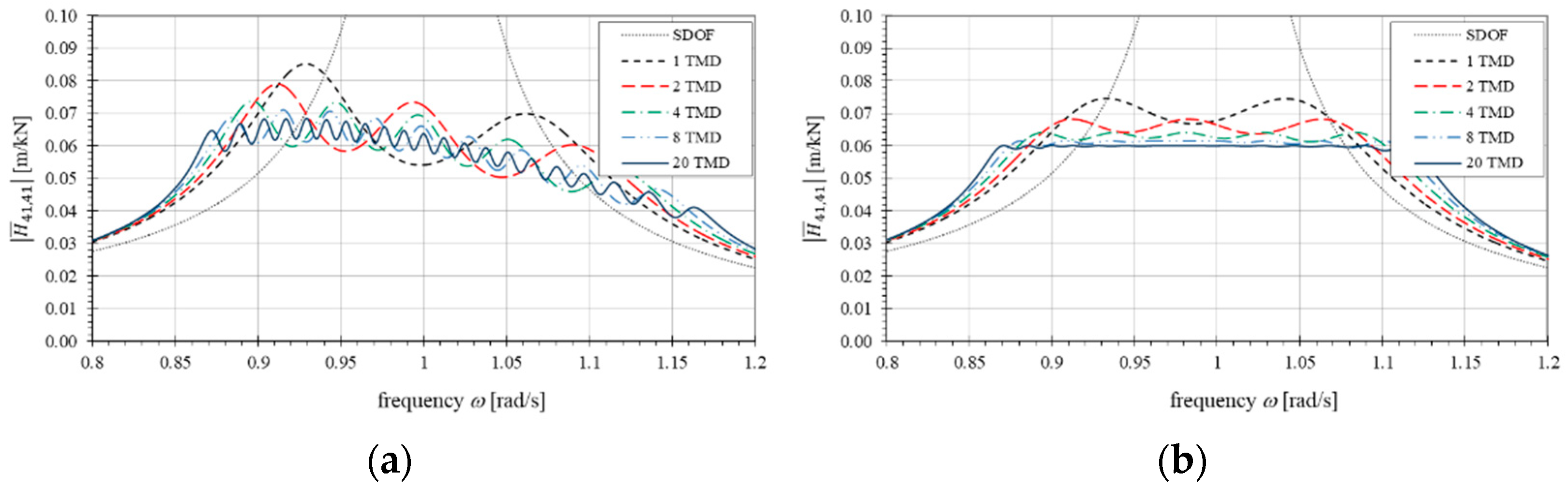
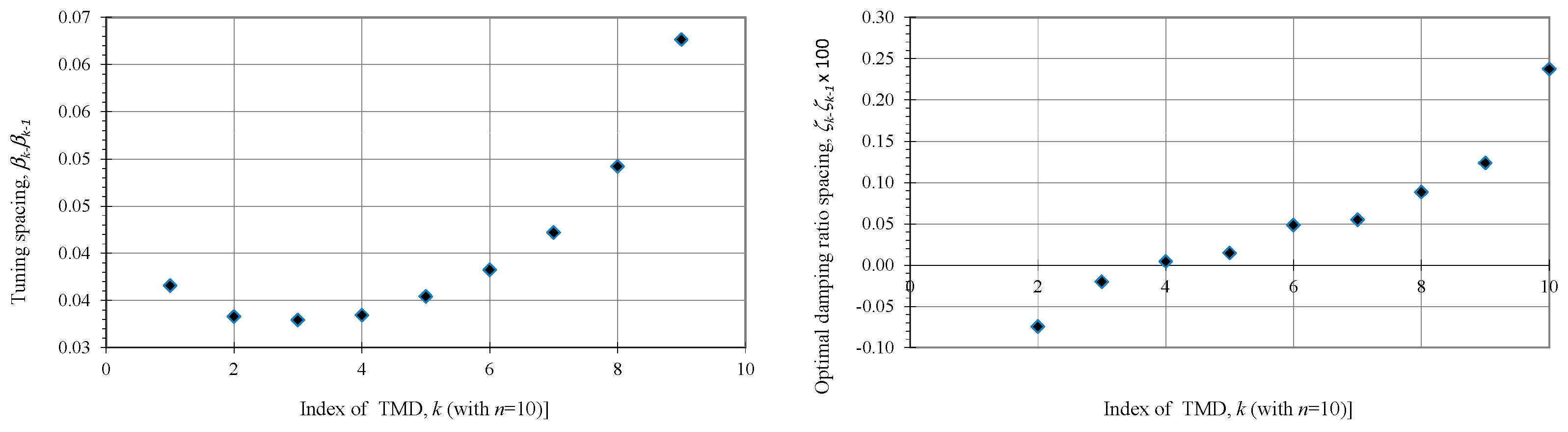
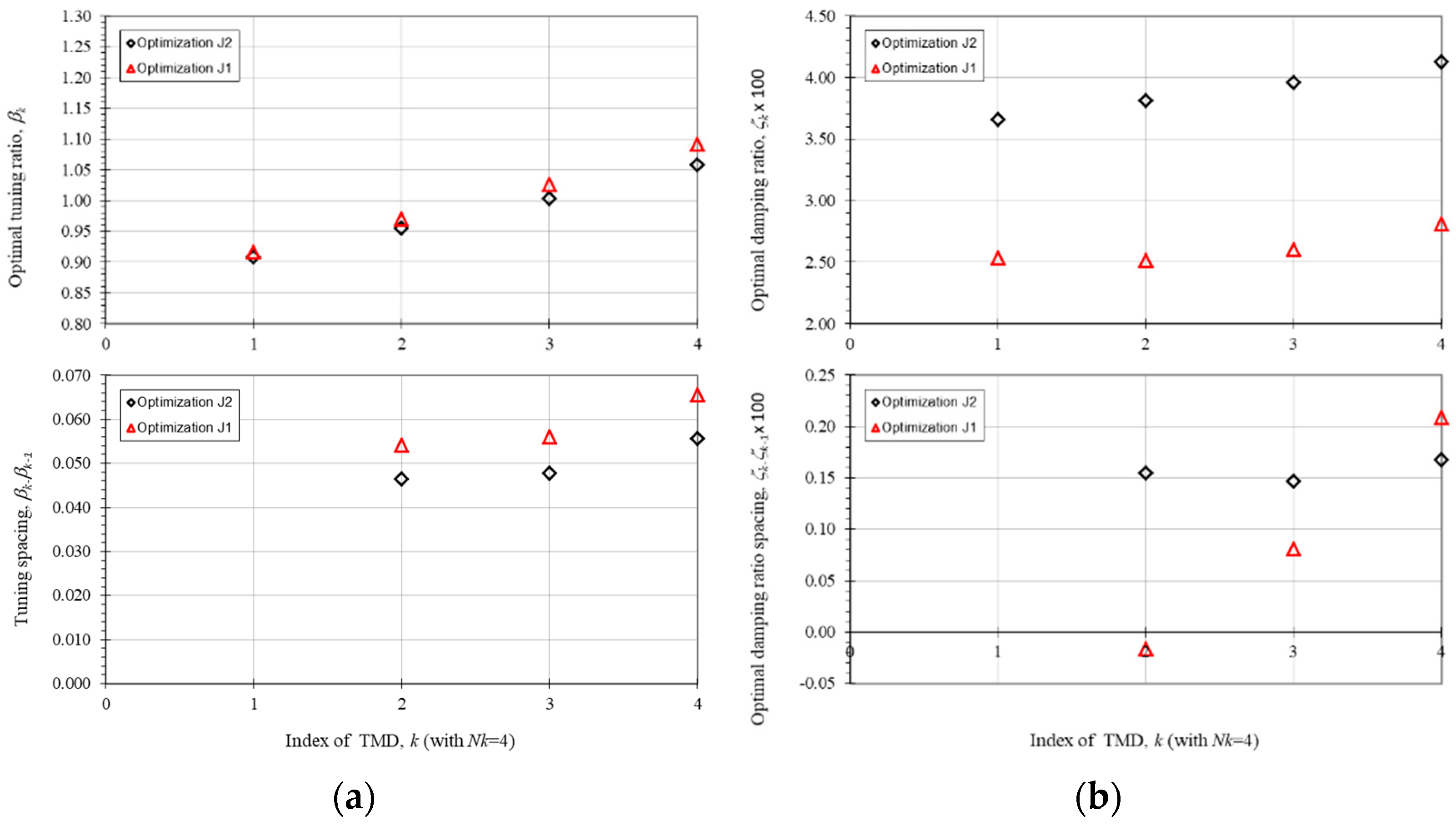
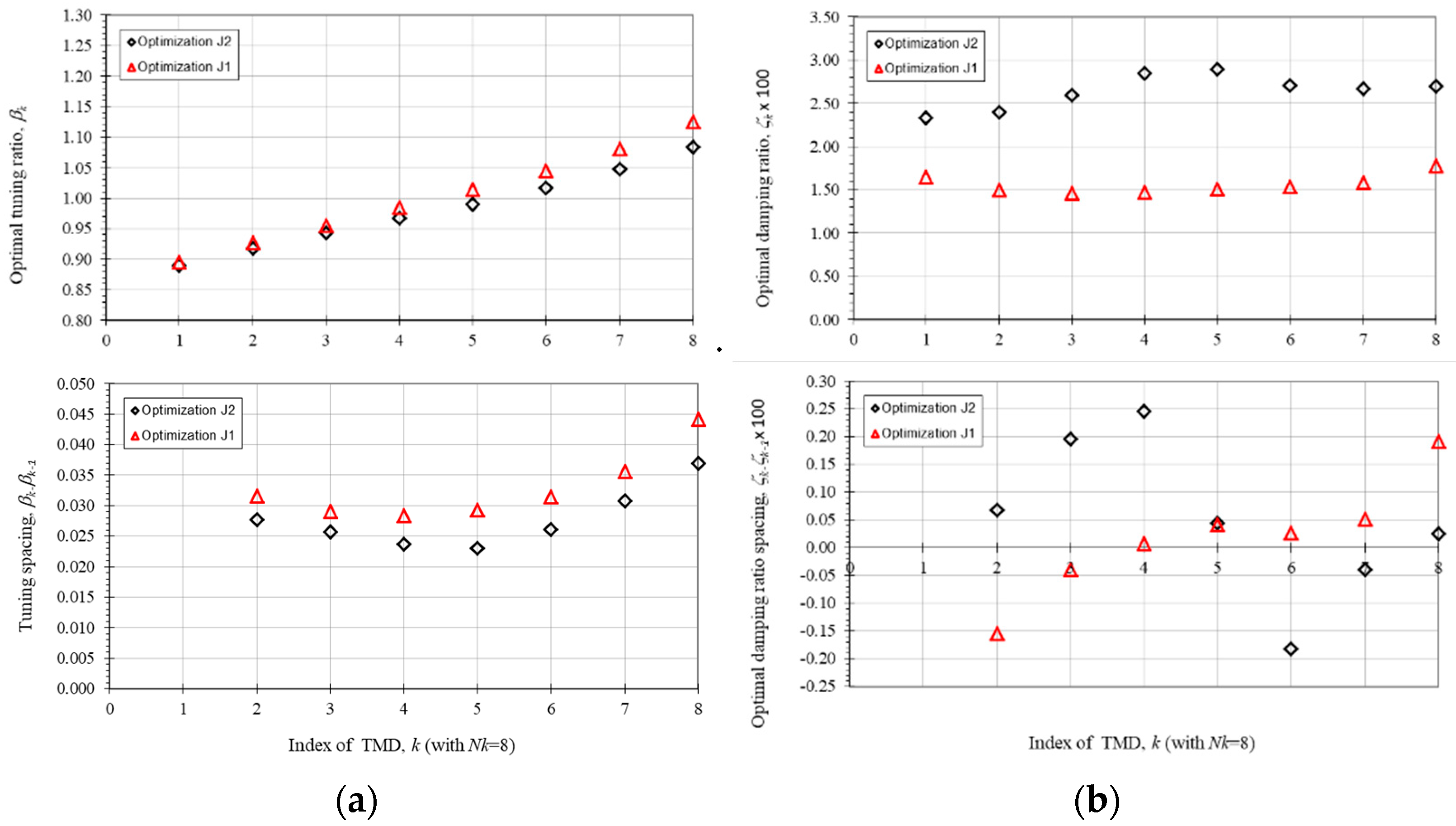
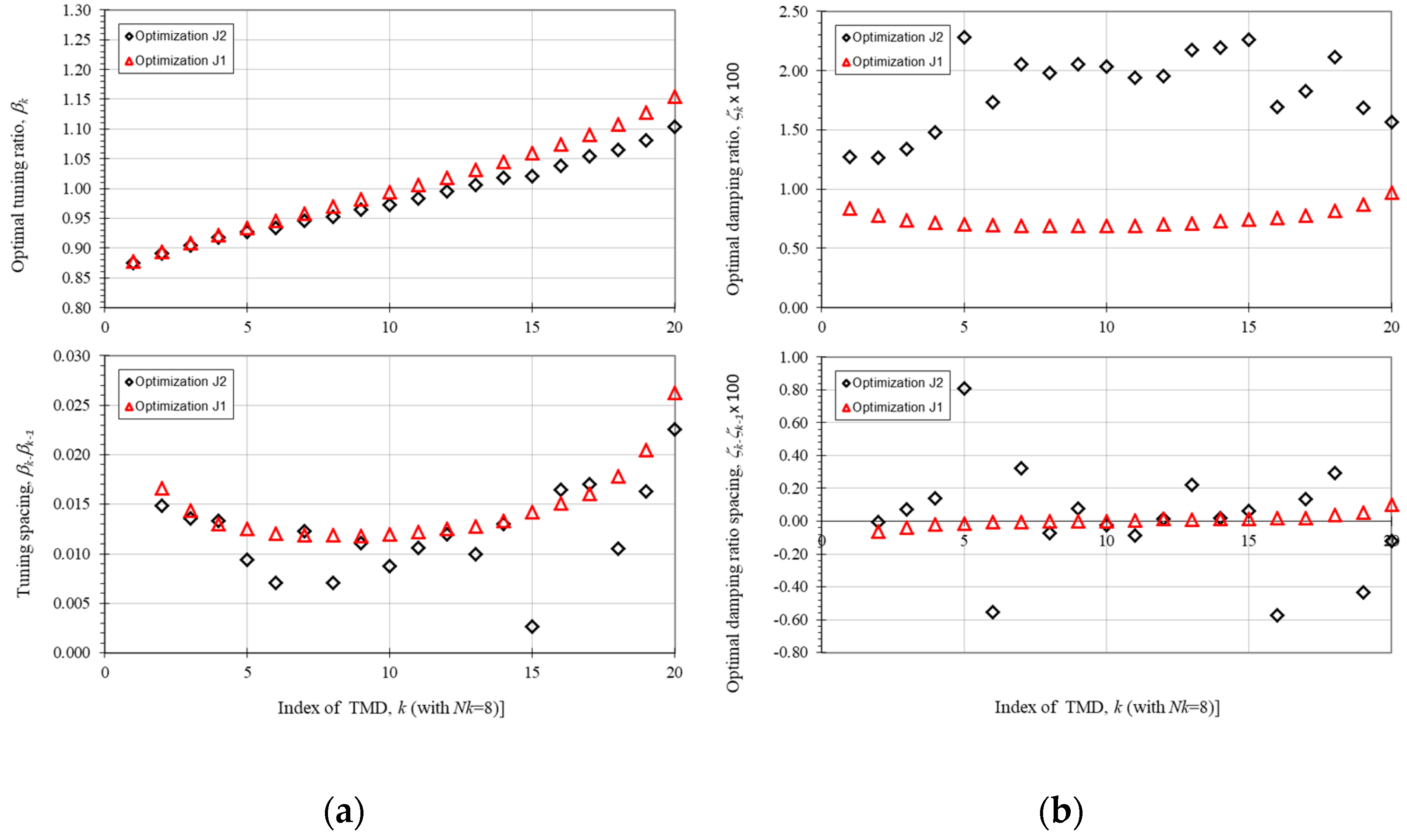
3.3. Numerical Optimization Results—SA Method
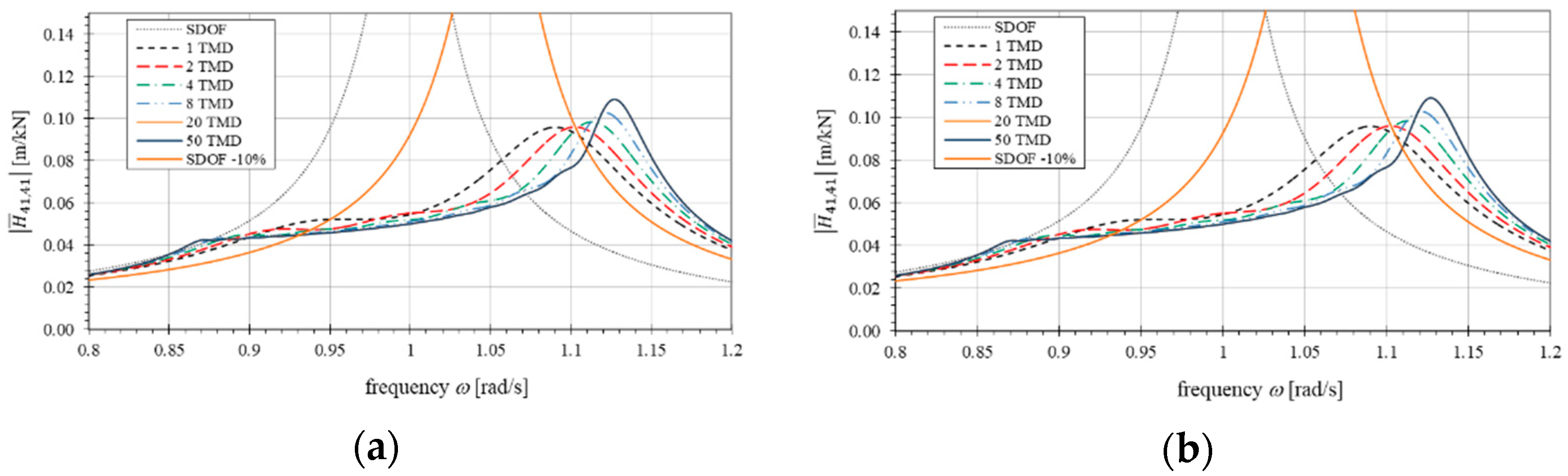
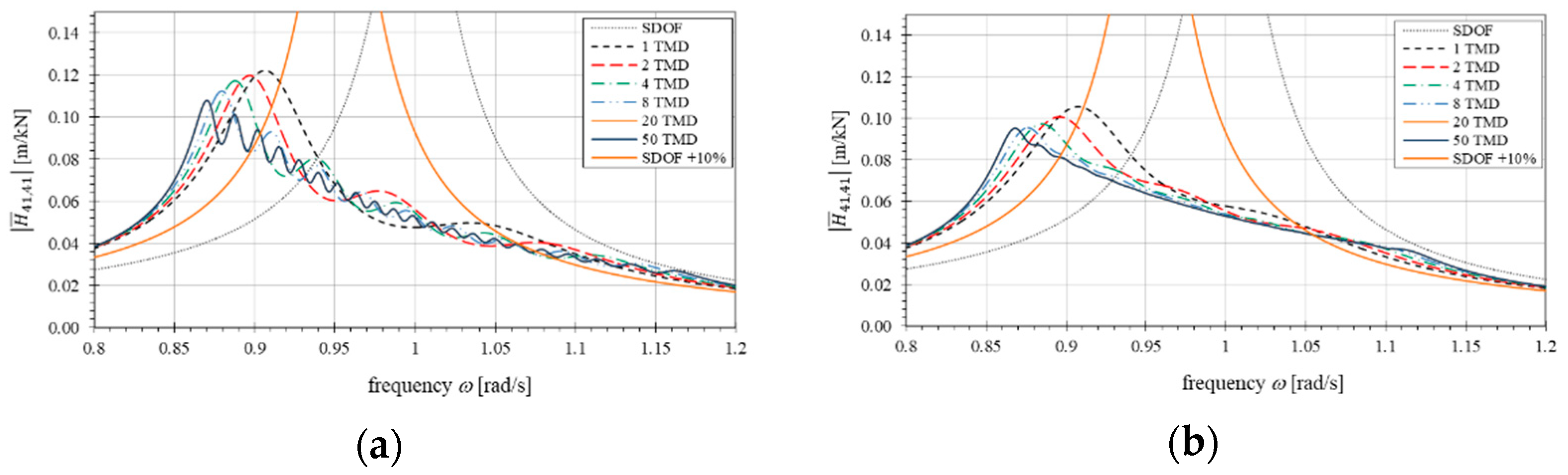
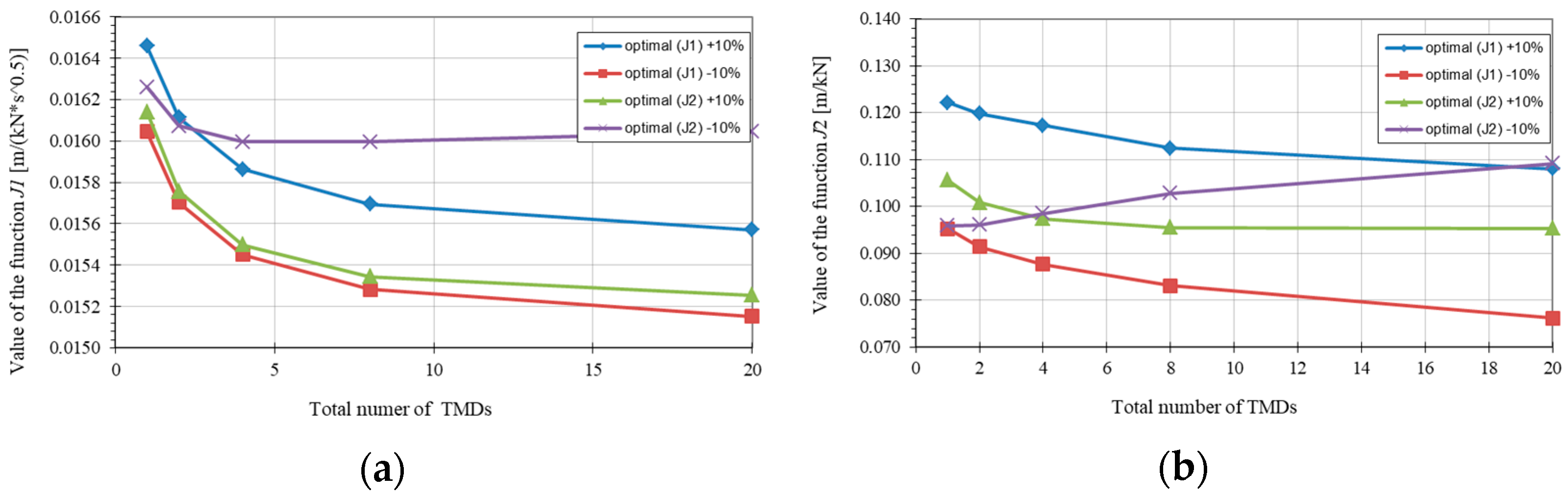
3.4. Impact of Primary System Mistuning
3.5. Discussion
4. Numerical Example 2
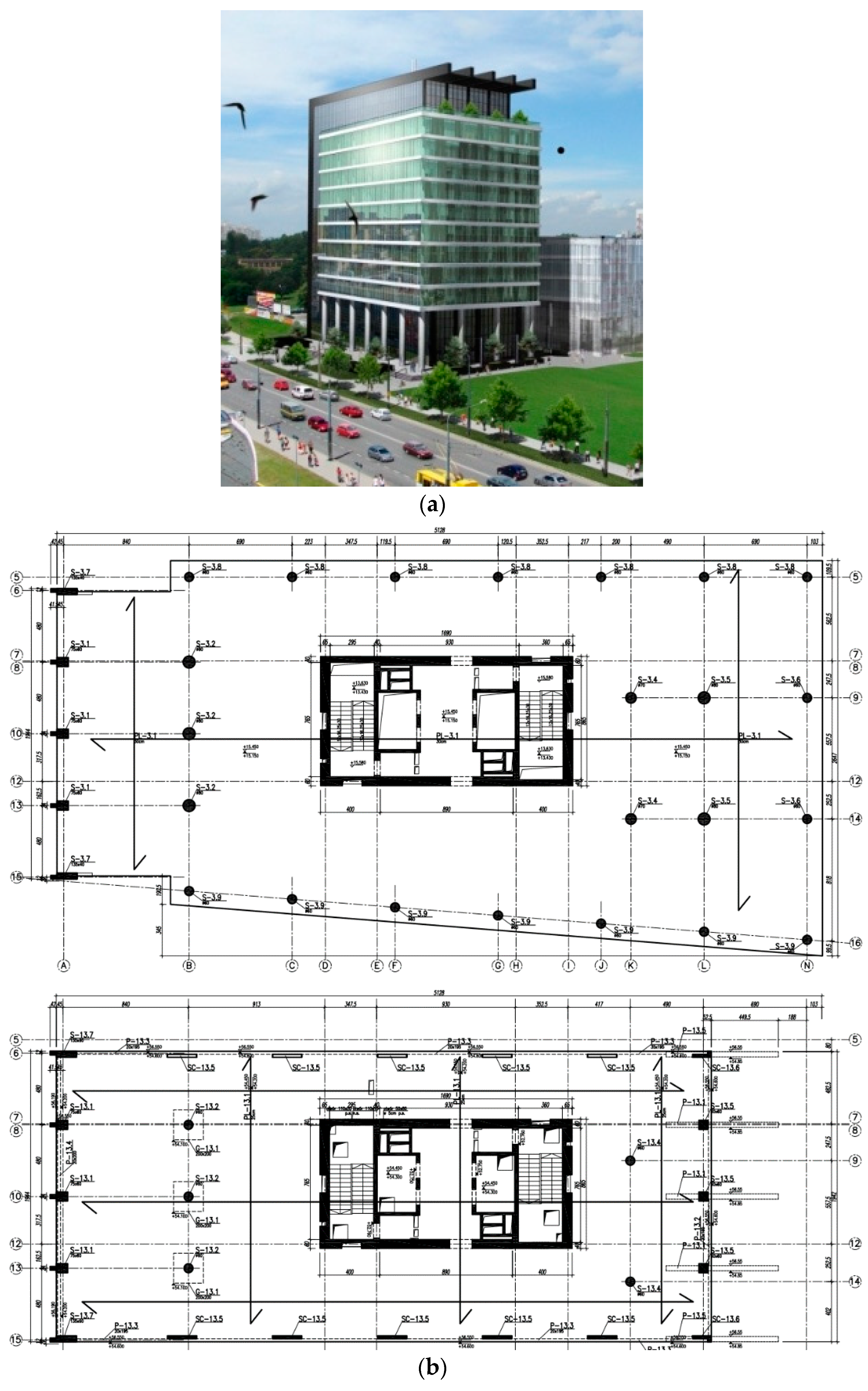
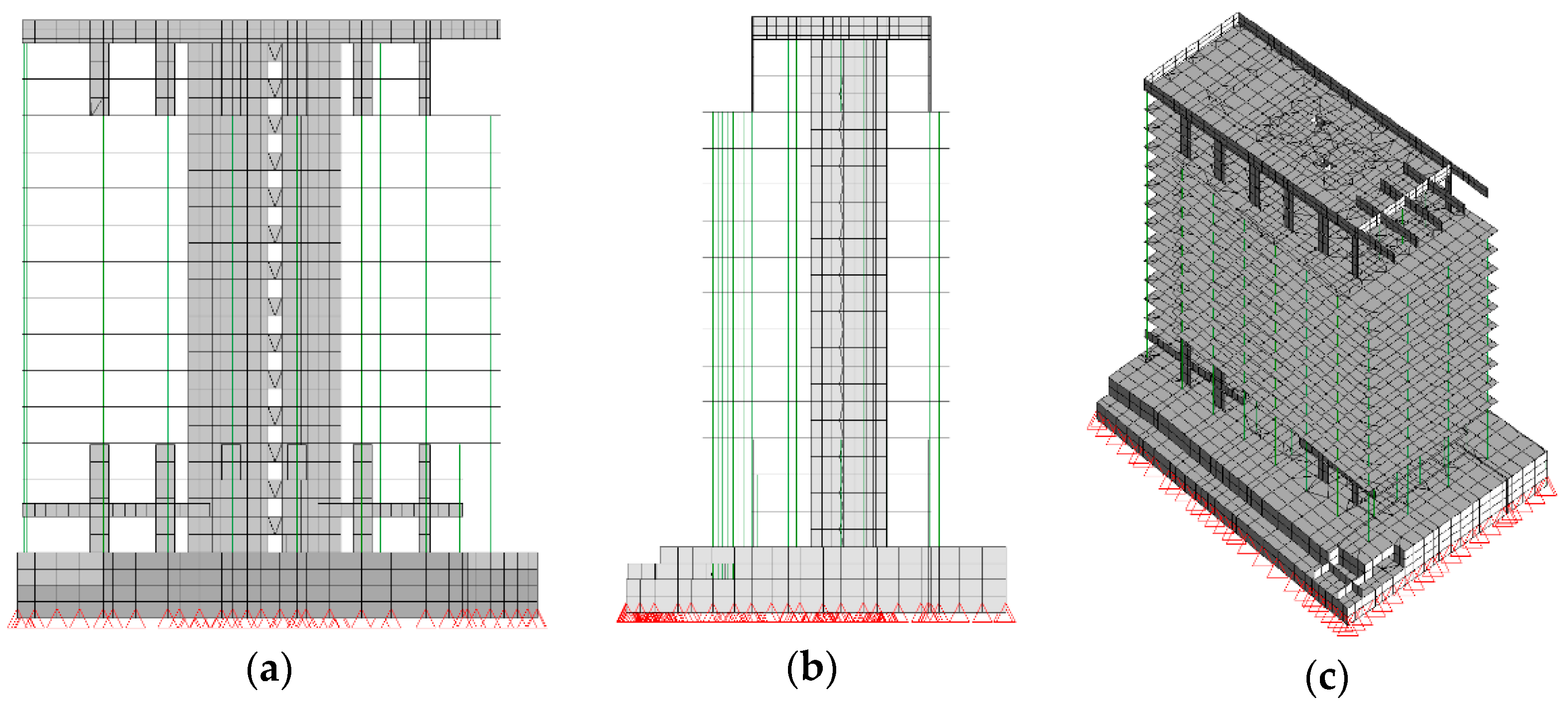
4.1. Input Data
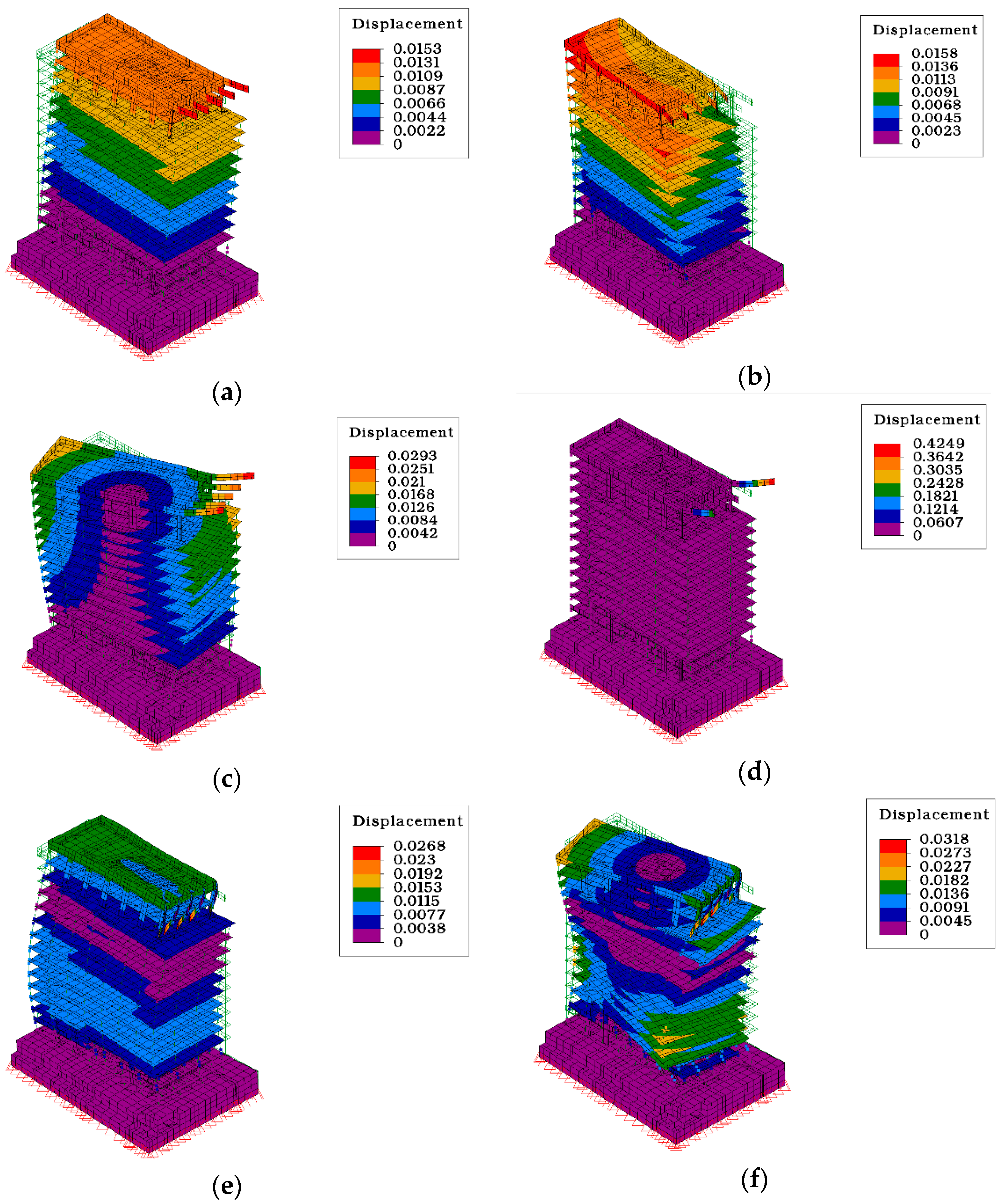
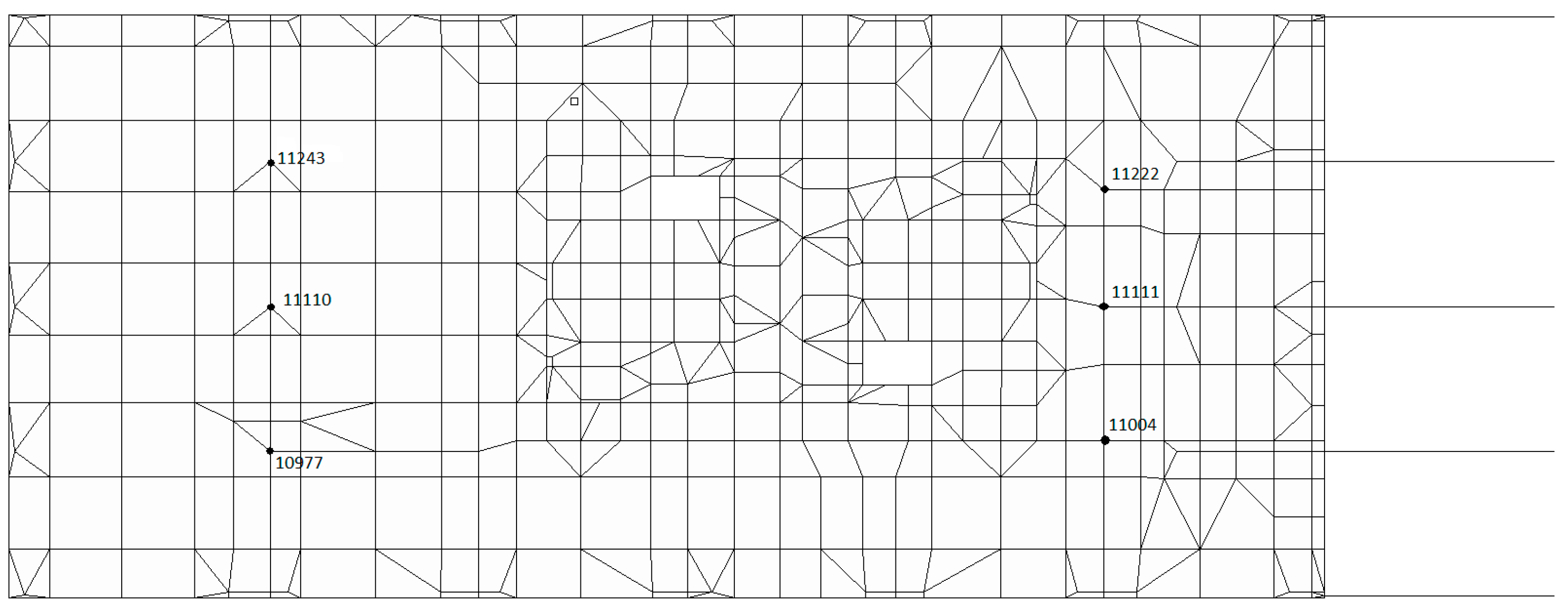
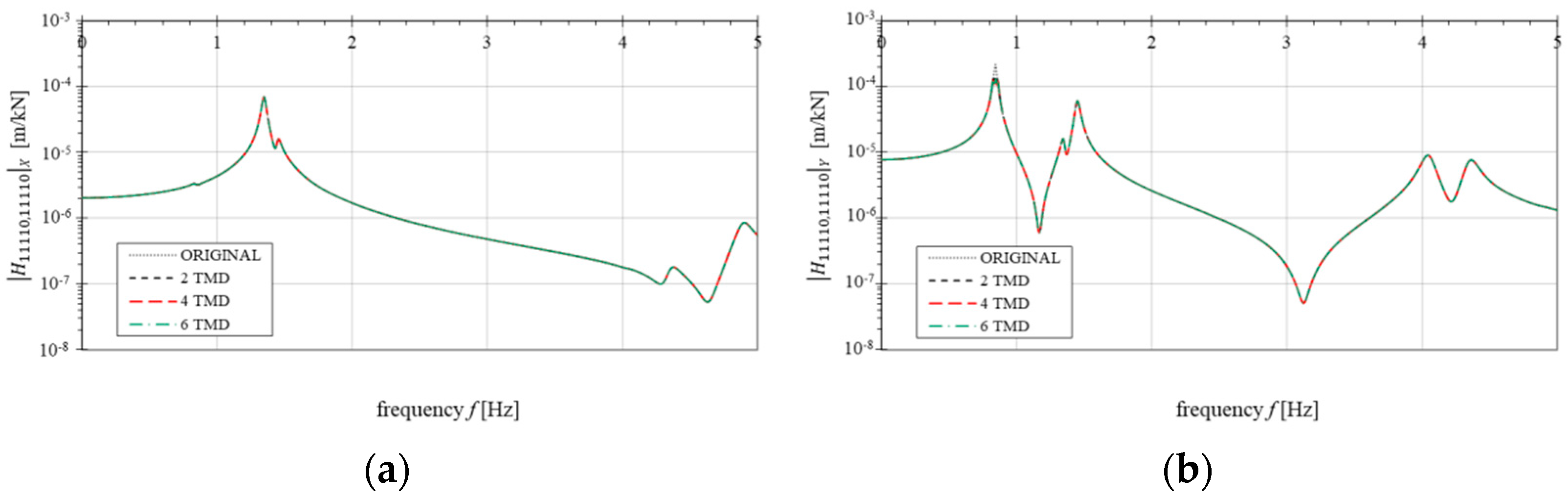
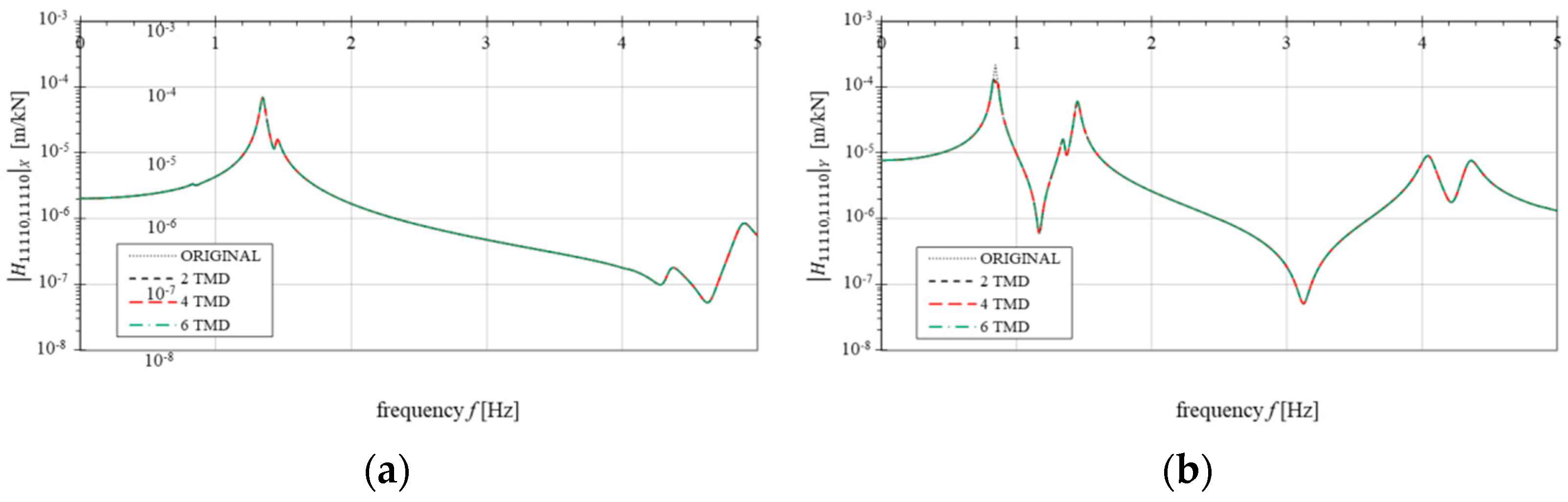
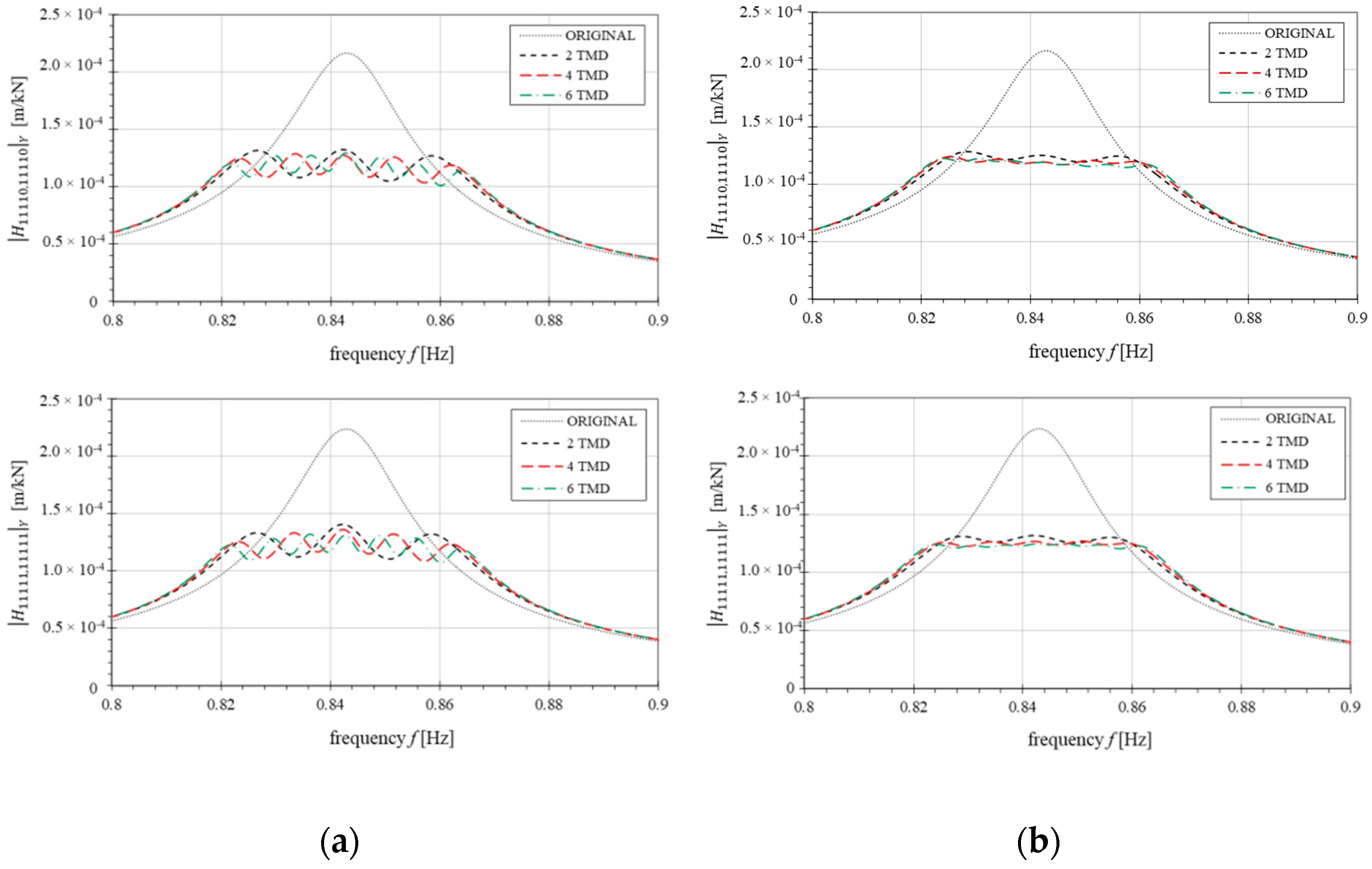
4.2. Numerical Optimization Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Den Hartog, J.P.D. Mechanical Vibration; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Warburton, G.B. Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Warburton, G.B. Optimum absorber parameters for minimizing vibration response. Earthq. Eng. Struct. Dyn. 1981, 9, 251–262. [Google Scholar] [CrossRef]
- Bakre, S.V.; Jangid, R.S. Optimum parameters of tuned mass damper for damped main system. Struct. Control Health Monit. 2007, 14, 448–470. [Google Scholar] [CrossRef]
- Bakre, S.V.; Jangid, R.S. Optimum multiple tuned mass dampers for base-excited damped main system. Int. J. Struct. Stab. Dyn. 2004, 4, 527–542. [Google Scholar] [CrossRef]
- Krenk, S. Frequency analysis of the tuned mass damper. J. Appl. Mech. Trans. ASME 2005, 72, 936–942. [Google Scholar] [CrossRef]
- Batou, A.; Adhikari, S. Optimal parameters of viscoelastic tuned-mass dampers. J. Sound Vib. 2019, 445, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Marian, L.; Giaralis, A. The tuned mass-damper-inerter for harmonic vibrations suppression, attached mass reduction, and energy harvesting. Smart Struct. Syst. 2017, 19, 665–678. [Google Scholar] [CrossRef]
- Sentyakov, K.; Peterka, J.; Smirnov, V.; Bozek, P.; Sviatskii, V. Modeling of boring mandrel working process with vibration damper. Materials 2020, 13, 1931. [Google Scholar] [CrossRef] [Green Version]
- Bergman, L.A.; McFarland, D.M.; Hall, J.K.; Johnson, E.A.; Kareem, A. Optimal distribution of tuned mass dampers in wind-sensitive structures. In Proceedings of the ICOSSAR ’89, the 5th International Conference on Structural Safety and Reliability, Part I, San Francisco, CA, USA, 7–11 August 1989; ASCE: New York, NY, USA, 1989; pp. 95–102. [Google Scholar]
- Kareem, A.; Kline, S. Performance of Multiple Mass Dampers under Random Loading. J. Struct. Eng. 1995, 121, 348–361. [Google Scholar] [CrossRef]
- Igusa, T.; Xu, K. Vibration Control Using Multiple Tuned Mass Dampers. J. Sound Vib. 1994, 175, 491–503. [Google Scholar] [CrossRef]
- Joshi, A.S.; Jangid, R.S. Optimum parameters of multiple tuned mass dampers for base-excited damped systems. J. Sound Vib. 1997, 202, 657–667. [Google Scholar] [CrossRef]
- Jangid, R.S. Optimum Multiple Tuned Mass Dampers for base-excited undamped system. Earthq. Eng. Struct. Dyn. 1999, 28, 1041–1049. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Harnpornchai, N. Fundamental characteristics of Multiple Tuned Mass Dampers for suppressing harmonically forced oscillations. Earthq. Eng. Struct. Dyn. 1993, 22, 51–62. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. The two-degree-of-freedom tuned-mass damper for suppression of single-mode vibration under random and harmonic excitation. J. Vib. Acoust. Trans. ASME 2006, 128, 56–65. [Google Scholar] [CrossRef]
- Zhao, G.; Raze, G.; Paknejad, A.; Deraemaeker, A.; Kerschen, G.; Collette, C. Active tuned inerter-damper for smart structures and its ∞ optimisation. Mech. Syst. Signal Process. 2019, 129, 470–478. [Google Scholar] [CrossRef] [Green Version]
- Aggumus, H.; Guclu, R. Robust H∞ control of STMDs used in structural systems by hardware in the loop simulation method. Actuators 2020, 9, 55. [Google Scholar] [CrossRef]
- Asami, T. Optimal Design of Double-Mass Dynamic Vibration Absorbers Arranged in Series or in Parallel. J. Vib. Acoust. 2017, 139. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. Optimization of the individual stiffness and damping parameters in multiple-tuned-mass-damper systems. J. Vib. Acoust. Trans. ASME 2005, 127, 77–83. [Google Scholar] [CrossRef]
- Li, H.N.; Ni, X.L. Optimization of non-uniformly distributed multiple tuned mass damper. J. Sound Vib. 2007. [Google Scholar] [CrossRef]
- Zuo, L.; Nayfeh, S.A. Minimax optimization of multi-degree-of-freedom tuned-mass dampers. J. Sound Vib. 2004, 272, 893–908. [Google Scholar] [CrossRef]
- Ok, S.Y.; Song, J.; Park, K.S. Optimal design of hysteretic dampers connecting adjacent structures using multi-objective genetic algorithm and stochastic linearization method. Eng. Struct. 2008, 30, 1240–1249. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Zhang, H. Particle swarm optimization of tuned mass dampers. Eng. Struct. 2009, 31, 715–728. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Zheng, Z.; Mo, L.; Wu, C. Parametrical optimization of particle dampers based on particle swarm algorithm. Appl. Acoust. 2020, 160, 107083. [Google Scholar] [CrossRef]
- Aydin, E.; Öztürk, B.; Dutkiewicz, M. Analysis of efficiency of passive dampers in multistorey buildings. J. Sound Vib. 2019, 439, 17–28. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lee, C.H. Optimum design of linear multiple tuned mass dampers subjected to white-noise base acceleration considering practical configurations. Eng. Struct. 2018. [Google Scholar] [CrossRef]
- Stanikzai, M.H.; Elias, S.; Matsagar, V.A.; Jain, A.K. Seismic response control of base-isolated buildings using tuned mass damper. Aust. J. Struct. Eng. 2019. [Google Scholar] [CrossRef]
- Yin, X.; Song, G.; Liu, Y. Vibration Suppression of Wind/Traffic/Bridge Coupled System Using Multiple Pounding Tuned Mass Dampers (MPTMD). Sensors 2019, 19, 1133. [Google Scholar] [CrossRef] [Green Version]
- Bendat, J.S.; Piersol, A.G. Random Data; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; ISBN 9781118032428. [Google Scholar]
- Ren, M.Z. A variant design of the dynamic vibration absorber. J. Sound Vib. 2001, 245, 762–770. [Google Scholar] [CrossRef]
- Nishihara, O.; Matsuhisa, H. Design of a dynamic vibration absorber for minimization of maximum amplitude magnification factor (Derivation of algebraic exact solution). Jpn. Soc. Mech. Eng. 1997, 63, 3438–3445. [Google Scholar] [CrossRef] [Green Version]




| TMD Number | |||
|---|---|---|---|
| [kg] | [kN/m] | [–] | |
| 1 TMD | 2000 | 2.00 | 0.05 |
| 2 TMDs | 1000 | 1.00 | 0.05 |
| 4 TMDs | 500 | 0.50 | 0.05 |
| 8 TMDs | 250 | 0.25 | 0.05 |
| 20 TMDs | 100 | 0.10 | 0.05 |
| TMD Number | J1 Value | J1 Change | J2 Value | J2 Change |
|---|---|---|---|---|
| [m/(kN*s^0.5)] | [%] | [m/kN] | [%] | |
| SDOF | 2.4910 × 10−2 | 2.5005 × 10−1 | ||
| 1 TMD | 1.5515 × 10−2 | 0.00% | 7.4579 × 10−2 | 0.00% |
| 2 TMDs | 1.5203 × 10−2 | −2.01% | 6.8248 × 10−2 | −8.49% |
| 4 TMDs | 1.5001 × 10−2 | −3.31% | 6.4091 × 10−2 | −14.06% |
| 8 TMDs | 1.4875 × 10−2 | −4.12% | 6.1620 × 10−2 | −17.38% |
| 20 TMDs | 1.4783 × 10−2 | −4.72% | 6.0202 × 10−2 | −19.28% |
| MTMD | No. | ||||
|---|---|---|---|---|---|
| [kg] | [kN/m] | [–] | [–] | ||
| 1 TMD | 1 | 2000 | 1.960905 | 0.068462 | 0.990178 |
| 2 TMDs | 1 | 1000 | 0.895498 | 0.041605 | 0.946307 |
| 2 | 1000 | 1.096614 | 0.044381 | 1.047193 | |
| 4 TMDs | 1 | 500 | 0.419478 | 0.025349 | 0.915945 |
| 2 | 500 | 0.470454 | 0.025186 | 0.970004 | |
| 3 | 500 | 0.526416 | 0.025998 | 1.026076 | |
| 4 | 500 | 0.595890 | 0.028082 | 1.091687 | |
| 8 TMDs | 1 | 250 | 0.200353 | 0.016536 | 0.895215 |
| 2 | 250 | 0.214738 | 0.014990 | 0.926796 | |
| 3 | 250 | 0.228431 | 0.014593 | 0.955889 | |
| 4 | 250 | 0.242203 | 0.014669 | 0.984282 | |
| 5 | 250 | 0.256858 | 0.015086 | 1.013624 | |
| 6 | 250 | 0.273079 | 0.015356 | 1.045139 | |
| 7 | 250 | 0.291974 | 0.015877 | 1.080691 | |
| 8 | 250 | 0.316299 | 0.017789 | 1.124809 |
| MTMD | No. | ||||
|---|---|---|---|---|---|
| [kg] | [kN/m] | [–] | [–] | ||
| 1 TMD | 1 | 2000 | 1.905820 | 0.089169 | 0.976171 |
| 2 TMDs | 1 | 1000 | 0.878697 | 0.056278 | 0.937388 |
| 2 | 1000 | 1.046257 | 0.062921 | 1.022867 | |
| 4 TMDs | 1 | 500 | 0.413107 | 0.036608 | 0.908964 |
| 2 | 500 | 0.456409 | 0.038155 | 0.955415 | |
| 3 | 500 | 0.503223 | 0.039621 | 1.003218 | |
| 4 | 500 | 0.560626 | 0.041295 | 1.058892 | |
| 8 TMDs | 1 | 250 | 0.198173 | 0.023339 | 0.890332 |
| 2 | 250 | 0.210676 | 0.024023 | 0.917988 | |
| 3 | 250 | 0.222606 | 0.025988 | 0.943624 | |
| 4 | 250 | 0.233932 | 0.028452 | 0.967329 | |
| 5 | 250 | 0.245215 | 0.028899 | 0.990383 | |
| 6 | 250 | 0.258339 | 0.027081 | 1.016542 | |
| 7 | 250 | 0.274253 | 0.026689 | 1.047383 | |
| 8 | 250 | 0.293970 | 0.026947 | 1.084380 |
| J1 Value | J2 Value | J1 Value | J2 Value | |||
|---|---|---|---|---|---|---|
| [m/(kN*s0.5] | [m/kN] | [m/(kN*s0.5] | [m/kN] | |||
| Den Hartog | 0.9803922 | 0.0870388 | 1.886 × 10−2 | 1.005 × 10−1 | 1.559 × 10−2 | 7.676 × 10−2 |
| Warburton (1981) | 0.9852819 | 0.0701871 | 1.866 × 10−2 | 1.091 × 10−1 | 1.550 × 10−2 | 8.176 × 10−2 |
| Warburton (1982) | 0.9754779 | 0.0861813 | 1.891 × 10−2 | 1.057 × 10−1 | 1.560 × 10−2 | 7.497 × 10−2 |
| Ren | 1.0101525 | 0.0870388 | 1.941 × 10−2 | 1.366 × 10−1 | - | - |
| Nishihara and Matsuhisa | 0.9776460 | 0.1596084 | - | - | 1.677 × 10−2 | 9.865 × 10−2 |
| Proposed J1 | - 0.9890635 | - 0.0682140 | 1.885 × 10−2 | 1.148 × 10−2 | - | - |
| Proposed J2 | - 0.9803647 | - 0.0853719 | 1.868 × 10−2 | 1.006 × 10−2 | - | - |
| Proposed J1 | - 0.9901779 | - 0.0684623 | - | - | 1.563 × 10−2 | 8.521 × 10−2 |
| Proposed J2 | - 0.9761710 | - 0.0891687 | - | - | 1.552 × 10−2 | 7.458 × 10−2 |
| Item No. | Frequency [Hz] | Period of Vibrations [s] | Form of Vibration |
|---|---|---|---|
| 1 | 0.8431 | 1.18607 | flexural in the Y direction |
| 2 | 1.3476 | 0.74207 | torsional |
| 3 | 1.4488 | 0.69022 | torsional |
| 4 | 2.5197 | 0.39688 | local flexural form of cantilevers |
| 5 | 2.5222 | 0.39647 | local flexural form of cantilevers |
| 6 | 2.9290 | 0.34141 | local flexural form of cantilevers |
| 7 | 2.9361 | 0.34059 | local flexural form of cantilevers |
| 8 | 2.9372 | 0.34046 | local flexural form of cantilevers |
| 9 | 4.0457 | 0.24717 | flexural in the Y direction |
| 10 | 4.3516 | 0.22980 | torsional |
| 11 | 4.8888 | 0.20455 | flexural in the Z direction |
| MTMD | No. | ||||
|---|---|---|---|---|---|
| [103 kg] | [kN/m] | [–] | [–] | ||
| 2 TMDs | 1 | 2.09840 | 60 | 0.007908 | 1.009423 |
| 2 | 2.18777 | 60 | 0.007888 | 0.988589 | |
| 4 TMDs | 1 | 1.03307 | 30 | 0.004949 | 1.017274 |
| 2 | 1.05885 | 30 | 0.004739 | 1.004811 | |
| 3 | 1.08320 | 30 | 0.004698 | 0.993454 | |
| 4 | 1.11004 | 30 | 0.005010 | 0.981369 | |
| 6 TMDs | 1 | 0.68397 | 20 | 0.003796 | 1.020795 |
| 2 | 0.69665 | 20 | 0.003459 | 1.011457 | |
| 3 | 0.70786 | 20 | 0.003420 | 1.003420 | |
| 4 | 0.71903 | 20 | 0.003489 | 0.995597 | |
| 5 | 0.73084 | 20 | 0.003547 | 0.987518 | |
| 6 | 0.74467 | 20 | 0.003926 | 0.978307 |
| MTMD | No. | ||||
|---|---|---|---|---|---|
| [103 kg] | [kN/m] | [–] | [–] | ||
| 2 TMDs | 1 | 2.10516 | 60 | 0.011970 | 1.007800 |
| 2 | 2.18180 | 60 | 0.011816 | 0.989942 | |
| 4 TMDs | 1 | 1.03823 | 30 | 0.008284 | 1.014739 |
| 2 | 1.06098 | 30 | 0.007508 | 1.003804 | |
| 3 | 1.08231 | 30 | 0.007402 | 0.993861 | |
| 4 | 1.10542 | 30 | 0.007627 | 0.983416 | |
| 6 TMDs | 1 | 0.68809 | 20 | 0.006004 | 1.017729 |
| 2 | 0.69927 | 20 | 0.005902 | 1.009561 | |
| 3 | 0.70923 | 20 | 0.005837 | 1.002452 | |
| 4 | 0.71897 | 20 | 0.005787 | 0.995633 | |
| 5 | 0.72918 | 20 | 0.005922 | 0.988639 | |
| 6 | 0.74093 | 20 | 0.006122 | 0.980767 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wielgos, P.; Geryło, R. Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach. Appl. Sci. 2021, 11, 1389. https://doi.org/10.3390/app11041389
Wielgos P, Geryło R. Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach. Applied Sciences. 2021; 11(4):1389. https://doi.org/10.3390/app11041389
Chicago/Turabian StyleWielgos, Piotr, and Robert Geryło. 2021. "Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach" Applied Sciences 11, no. 4: 1389. https://doi.org/10.3390/app11041389
APA StyleWielgos, P., & Geryło, R. (2021). Optimization of Multiple Tuned Mass Damper (MTMD) Parameters for a Primary System Reduced to a Single Degree of Freedom (SDOF) through the Modal Approach. Applied Sciences, 11(4), 1389. https://doi.org/10.3390/app11041389





