Figure 1.
The four digitised historical maps of Trento (1851, 1887, 1908, and 1936). Please note the different levels of detail of building footprints, e.g., between 1851 and 1887: in the latter case, footprints are bigger and include multiple buildings with regard to the other maps.
Figure 1.
The four digitised historical maps of Trento (1851, 1887, 1908, and 1936). Please note the different levels of detail of building footprints, e.g., between 1851 and 1887: in the latter case, footprints are bigger and include multiple buildings with regard to the other maps.
Figure 2.
A view of the level of detail 1 (LoD1) buildings in Trento generated from the actual (2016) topographic data available as open data. Height values are referred to as the mean level of the pitched roofs.
Figure 2.
A view of the level of detail 1 (LoD1) buildings in Trento generated from the actual (2016) topographic data available as open data. Height values are referred to as the mean level of the pitched roofs.
Figure 3.
The two digitised historical maps of Bologna (1884 and 1945).
Figure 3.
The two digitised historical maps of Bologna (1884 and 1945).
Figure 4.
A view of the LoD1 buildings in Bologna generated from the actual (2017) topographic data available as open data.
Figure 4.
A view of the LoD1 buildings in Bologna generated from the actual (2017) topographic data available as open data.
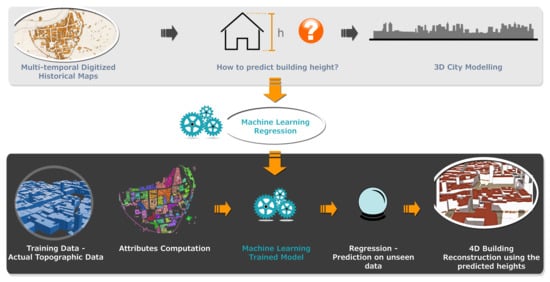
Figure 5.
The general workflow based on machine learning regression to learn building heights.
Figure 5.
The general workflow based on machine learning regression to learn building heights.
Figure 6.
Examples of attributes (predictors) computed for the Trento 1851 dataset: number of vertices (a); the distance of the polygon centroids from the nearest centroids (b); kernel density value—radius 100 m (c); groups (d). In (a) and (d) each colour corresponds to the computed (a) or assigned (d) numerical value. In (b) and (c), classes are colourised with a graduated scale.
Figure 6.
Examples of attributes (predictors) computed for the Trento 1851 dataset: number of vertices (a); the distance of the polygon centroids from the nearest centroids (b); kernel density value—radius 100 m (c); groups (d). In (a) and (d) each colour corresponds to the computed (a) or assigned (d) numerical value. In (b) and (c), classes are colourised with a graduated scale.
Figure 7.
Alignment of four points defining a cross-ratio invariant in image and object space (top). An example of height computation, deriving first the three vanishing points and then the unknown distance HU from the known H (bottom).
Figure 7.
Alignment of four points defining a cross-ratio invariant in image and object space (top). An example of height computation, deriving first the three vanishing points and then the unknown distance HU from the known H (bottom).
Figure 8.
3D view of the inferred building heights (orange) with respect to the ground truth data (white) for Trento. Despite metrics indicating acceptable accuracy (
Table 5), a visual check highlights gross errors mainly on towers.
Figure 8.
3D view of the inferred building heights (orange) with respect to the ground truth data (white) for Trento. Despite metrics indicating acceptable accuracy (
Table 5), a visual check highlights gross errors mainly on towers.
Figure 9.
Data distribution before (left) and after (right) adding synthetic data for the under-represented classes in the Trento dataset.
Figure 9.
Data distribution before (left) and after (right) adding synthetic data for the under-represented classes in the Trento dataset.
Figure 10.
3D view of the inferred building heights (orange) in Trento with respect to the ground truth data (white) after data augmentation. The visual inspection shows a relevant reduction of the errors on towers and churches.
Figure 10.
3D view of the inferred building heights (orange) in Trento with respect to the ground truth data (white) after data augmentation. The visual inspection shows a relevant reduction of the errors on towers and churches.
Figure 11.
Two examples of single-view-metrology applied to historical photos in Trento to determine heights of buildings not present anymore in the actual topographic database.
Figure 11.
Two examples of single-view-metrology applied to historical photos in Trento to determine heights of buildings not present anymore in the actual topographic database.
Figure 12.
Overviews of the generated multi-temporal 3D buildings (LoD1) using machine learning and historical maps for the Trento case study.
Figure 12.
Overviews of the generated multi-temporal 3D buildings (LoD1) using machine learning and historical maps for the Trento case study.
Figure 13.
Closer views of inferred 3D buildings in Trento in 1851 and 1936.
Figure 13.
Closer views of inferred 3D buildings in Trento in 1851 and 1936.
Figure 14.
An example of an historical photo used to texture a 3D building in Trento in 1887.
Figure 14.
An example of an historical photo used to texture a 3D building in Trento in 1887.
Figure 15.
Multi-temporal 3D reconstruction of Bologna with building heights inferred using machine learning and historical maps (1884 and 1945).
Figure 15.
Multi-temporal 3D reconstruction of Bologna with building heights inferred using machine learning and historical maps (1884 and 1945).
Figure 16.
Predictors importance of the Random Forest method in the Trento dataset. The most relevant are function (e.g., civil or religious), class (e.g., churches, palaces, castle), and distance (from a polygon’s centroid from the nearest centroid). On the y-axis, the features importance score is given, i.e., the normalised average scores indicating the weighted variance decrease in a decision tree.
Figure 16.
Predictors importance of the Random Forest method in the Trento dataset. The most relevant are function (e.g., civil or religious), class (e.g., churches, palaces, castle), and distance (from a polygon’s centroid from the nearest centroid). On the y-axis, the features importance score is given, i.e., the normalised average scores indicating the weighted variance decrease in a decision tree.
Figure 17.
Feature importance of the Random Forest method and RFE in the Trento dataset.
Figure 17.
Feature importance of the Random Forest method and RFE in the Trento dataset.
Figure 18.
3D view of the inferred building heights (pink) in Trento with respect to the ground truth data (white), using the actual Bologna dataset as training. Training contains augmented data.
Figure 18.
3D view of the inferred building heights (pink) in Trento with respect to the ground truth data (white), using the actual Bologna dataset as training. Training contains augmented data.
Figure 19.
3D view of the inferred building heights (pink) in Trento with respect to the ground truth data (white), using the actual Bologna dataset as training. Data augmentation was removed from the training set.
Figure 19.
3D view of the inferred building heights (pink) in Trento with respect to the ground truth data (white), using the actual Bologna dataset as training. Data augmentation was removed from the training set.
Table 1.
The number of polygons and their average area in the four digitised historical maps and in the actual topographic data (2016).
Table 1.
The number of polygons and their average area in the four digitised historical maps and in the actual topographic data (2016).
| Dataset | Total n. of Polygons | Average Polygons Area (m2) |
|---|
| 1851 | 1274 | 197.18 |
| 1887 | 632 | 499.97 |
| 1908 | 1685 | 238.24 |
| 1936 | 3112 | 236.62 |
| Actual | 4537 | 149.87 |
Table 2.
The actual (2016) topographic data of man-made structures available for Trento.
Table 2.
The actual (2016) topographic data of man-made structures available for Trento.
| Dataset | Total n. of Polygons | Average Polygons Area (m2) | Average Height (m) | Median Height (m) | St. Deviation (m) |
|---|
| Actual | 4537 | 149.87 | 12.26 | 12.41 | 5.36 |
Table 3.
The number of polygons and their average area in the two digitised maps and in the actual topographic data (2017).
Table 3.
The number of polygons and their average area in the two digitised maps and in the actual topographic data (2017).
| Dataset | Total n. of Polygons | Average Polygons Area (m2) |
|---|
| 1884 | 482 | 1750.35 |
| 1945 | 1174 | 738.62 |
| Actual | 3241 | 215.04 |
Table 4.
The actual topographic data (2017) for Bologna, used as training data and ground-truth.
Table 4.
The actual topographic data (2017) for Bologna, used as training data and ground-truth.
| Dataset | Total n. of Polygons | Average Polygons Area (m2) | Average Height (m) | Median Height (m) | St. Deviation (m) |
|---|
| Actual | 3241 | 215.04 | 14.71 | 14.00 | 6.43 |
Table 5.
Accuracy evaluation of the compared regressors for the Trento dataset.
Table 5.
Accuracy evaluation of the compared regressors for the Trento dataset.
| Regressor | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Linear | 5.56 | 4.38 | −0.08 | 0.68 | 6.13 |
| Random Forest | 3.79 | 2.88 | 0.49 | −0.05 | 2.41 |
| CatBoost | 4.03 | 3.05 | 0.43 | −0.02 | 3.05 |
| Support Vector | 4.88 | 3.81 | 0.16 | 0.00 | 4.69 |
| Multilayer Perceptron | 4.26 | 3.20 | 0.36 | −0.09 | 3.64 |
Table 6.
Accuracy evaluation of the compared regressors for the Bologna dataset.
Table 6.
Accuracy evaluation of the compared regressors for the Bologna dataset.
| Regressor | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Linear | 7.64 | 6.06 | −0.36 | −0.87 | 7.57 |
| Random Forest | 4.67 | 3.64 | 0.49 | −0.06 | 2.95 |
| CatBoost | 4.76 | 3.69 | 0.47 | 0.00 | 2.70 |
| Support Vector | 4.88 | 4.10 | 0.33 | 0.05 | 5.03 |
| Multilayer Perceptron | 4.94 | 3.18 | 0.43 | 0.07 | 4.31 |
Table 7.
Data distribution for the Trento and Bologna dataset.
Table 7.
Data distribution for the Trento and Bologna dataset.
| Dataset | Total n. of Polygons | Towers | Churches | Civil Buildings |
|---|
| Trento | 4537 | 30 (~1%) | 53 (~1%) | 4454 (~98%) |
| Bologna | 3241 | 30 (~1%) | 21 (~1%) | 3190 (~98%) |
Table 8.
Data distribution after the inclusion of synthetic data for the under-represented classes.
Table 8.
Data distribution after the inclusion of synthetic data for the under-represented classes.
Dataset
Data Augmentation | Total n. of Polygons | Towers | Churches | Civil Buildings |
|---|
| Trento | 5369 | 379 (~7%) | 531 (~10%) | 4454 (~83%) |
| Bologna | 3553 | 176 (~5%) | 136 (~4%) | 3241 (~91%) |
Table 9.
Accuracy evaluation of the regressor methods on the Trento dataset after data augmentation.
Table 9.
Accuracy evaluation of the regressor methods on the Trento dataset after data augmentation.
| Regressor | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Linear | 5.90 | 4.69 | −0.15 | 1.15 | 6.66 |
| Random Forest | 3.59 | 2.83 | 0.57 | 0.00 | 2.07 |
| CatBoost | 3.76 | 2.95 | 0.53 | 0.00 | 2.61 |
| Support Vector | 5.30 | 4.24 | 0.07 | −0.06 | 5.44 |
| Multilayer Perceptron | 4.17 | 3.20 | 0.43 | −0.05 | 3.57 |
Table 10.
Accuracy evaluation of the regressor methods on the Bologna dataset after data augmentation.
Table 10.
Accuracy evaluation of the regressor methods on the Bologna dataset after data augmentation.
| Regressor | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Linear | 8.52 | 6.81 | 0.04 | −0.75 | 8.51 |
| Random Forest | 4.52 | 3.54 | 0.49 | 0.00 | 2.72 |
| CatBoost | 4.64 | 3.66 | 0.52 | 0.00 | 2.49 |
| Support Vector | 5.15 | 3.49 | 0.41 | 0.00 | 4.78 |
| Multilayer Perceptron | 4.83 | 3.79 | 0.48 | −0.02 | 3.91 |
Table 11.
Metrics evaluation of the Random Forest performance on the four historical datasets of Trento, considering twenty unaltered buildings digitised in all the maps as the test set.
Table 11.
Metrics evaluation of the Random Forest performance on the four historical datasets of Trento, considering twenty unaltered buildings digitised in all the maps as the test set.
| Historical Map-Year | RMSE (m) | MAE (m) | R2 | Min Error (m) | Max Error (m) | Median (m) | St. Dev. (m) |
|---|
| 1851 | 0.96 | 1.13 | 0.97 | 2.95 | 1.75 | 1.09 | 0.74 |
| 1887 | 2.86 | 2.25 | 0.92 | 0.07 | 6.35 | 1.52 | 1.77 |
| 1908 | 1.80 | 1.50 | 0.96 | −2.78 | 3.91 | 1.18 | 0.99 |
| 1936 | 1.67 | 1.40 | 0.97 | −2.62 | 3.20 | 1.14 | 0.90 |
Table 12.
Metrics evaluation of the Catboost performance on the four historical datasets of Trento, considering twenty unaltered buildings as the test set.
Table 12.
Metrics evaluation of the Catboost performance on the four historical datasets of Trento, considering twenty unaltered buildings as the test set.
| Historical Map-Year | RMSE (m) | MAE (m) | R2 | Min Error (m) | Max Error (m) | Median (m) | St. Dev. (m) |
|---|
| 1851 | 4.91 | 3.22 | 0.83 | −2.93 | 13.87 | 2.02 | 3.71 |
| 1887 | 6.09 | 3.93 | 0.67 | 0.24 | 17.15 | 2.31 | 4.65 |
| 1908 | 4.66 | 3.08 | 0.81 | −3.12 | 14.38 | 2.11 | 3.49 |
| 1936 | 5.80 | 3.31 | 0.70 | −2.72 | 19.02 | 1.38 | 4.76 |
Table 13.
Evaluation on eight disappeared buildings visible in historical photos: heights predicted with Random Forest were compared with single-view-metrology heights and metrics derived.
Table 13.
Evaluation on eight disappeared buildings visible in historical photos: heights predicted with Random Forest were compared with single-view-metrology heights and metrics derived.
| Dataset | RMSE (m) | MAE (m) | Median (m) | St. Dev. (m) |
|---|
| Trento | 1.41 | 1.28 | −0.83 | 1.29 |
Table 14.
Metric evaluation of the Random Forest prediction on the two historical datasets of Bologna, considering as a test set ten unaltered buildings digitised in both maps.
Table 14.
Metric evaluation of the Random Forest prediction on the two historical datasets of Bologna, considering as a test set ten unaltered buildings digitised in both maps.
| Historical Map-Year | RMSE (m) | MAE (m) | R2 | Min Error (m) | Max Error (m) | Median (m) | St. Dev. (m) |
|---|
| 1884 | 2.67 | 2.35 | 0.97 | 2.10 | 1.09 | 0.73 | 0.54 |
| 1945 | 1.71 | 1.63 | 0.99 | −1.66 | 6.35 | 1.52 | 1.89 |
Table 15.
Metric evaluation of the Catboost prediction on the two historical datasets and ten unaltered buildings as the test set.
Table 15.
Metric evaluation of the Catboost prediction on the two historical datasets and ten unaltered buildings as the test set.
| Historical Map-Year | RMSE (m) | MAE (m) | R2 | Min Error (m) | Max Error (m) | Median (m) | St. Dev. (m) |
|---|
| 1884 | 7.56 | 6.81 | 0.88 | −2.30 | 10.92 | 8.39 | 3.28 |
| 1945 | 7.98 | 7.05 | 0.83 | −1.98 | 12.38 | 7.76 | 3.70 |
Table 16.
Evaluation metrics for the Trento dataset with and without a recursive feature elimination (RFE) approach.
Table 16.
Evaluation metrics for the Trento dataset with and without a recursive feature elimination (RFE) approach.
| Regressor | N. of Features | RMSE TEST (m) | MAE TEST (m) | R2 TEST | St. Dev. (m) |
|---|
| Random Forest—without RFE | 20 | 3.59 | 2.83 | 0.57 | 2.07 |
| Random Forest—with RFE | 10 | 3.83 | 2.99 | 0.51 | 2.18 |
Table 17.
Evaluation metrics for the Bologna dataset with and without an RFE approach.
Table 17.
Evaluation metrics for the Bologna dataset with and without an RFE approach.
| Regressor | N. of Features | RMSE TEST (m) | MAE TEST (m) | R2 TEST | St. Dev. (m) |
|---|
| Random Forest—without RFE | 20 | 4.52 | 3.54 | 0.49 | 2.72 |
| Random Forest—with RFE | 10 | 4.59 | 3.54 | 0.53 | 2.76 |
Table 18.
Accuracy evaluation with the Random Forest regressor, training on Bologna data, and predicting on Trento dataset, and vice-versa. In this test, positional attributes were removed, and augmented data were employed for both cases.
Table 18.
Accuracy evaluation with the Random Forest regressor, training on Bologna data, and predicting on Trento dataset, and vice-versa. In this test, positional attributes were removed, and augmented data were employed for both cases.
| Dataset Prediction | Dataset Training | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Trento | Bologna | 4.60 | 3.57 | 0.53 | 0.00 | 2.77 |
| Bologna | Trento | 3.73 | 2.95 | 0.54 | 0.00 | 2.15 |
Table 19.
Accuracy evaluation with the Random Forest regressor and inverted training data. In this case, augmented data were removed from the training.
Table 19.
Accuracy evaluation with the Random Forest regressor and inverted training data. In this case, augmented data were removed from the training.
| Dataset Prediction | Dataset Training | RMSE TEST (m) | MAE TEST (m) | R2 TEST | Median (m) | St. Dev. (m) |
|---|
| Trento | Bologna | 3.90 | 2.98 | 0.47 | −0.03 | 2.49 |
| Bologna | Trento | 4.75 | 3.70 | 0.47 | −0.09 | 2.99 |