Integrated Tolerance and Fixture Layout Design for Compliant Sheet Metal Assemblies
Abstract
:Featured Application
Abstract
1. Introduction
1.1. Tolerance-Cost Optimization
1.2. Assembly Fixture Layout Optimization
1.3. Compliant Variation Simulations
1.4. Scope of the Paper
2. Problem Description
2.1. Design Parameters
2.1.1. Design Parameters of Tolerances
2.1.2. Design Parameters of Fixture Layouts
2.2. Objectives
2.3. Constraints
3. Optimization Method
3.1. Optimization Problem
3.2. Optimization Algorithm
| Algorithm 1: The utilized GA |
Input: The number of parts and candidate node numbers of each part. Output: The optimal solution including: the optimal production strategy and fixture layout.
|
4. Case Study and Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FE | Finit Element |
| KCC | Key Control Characteristic |
| KPC | Key Product Characteristic |
| MIC | Method of Influence Coefficients |
| GA | Genetic Algorithm |
| RMS | Root Mean Square |
References
- Taguchi, G.; Elsayed, E.A.; Hsiang, T.C. Quality Engineering in Production Systems; McGraw-Hill Series in Industrial Engineering and Management Science; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Söderberg, R. Tolerance allocation considering customer and manufacturing objectives. Adv. Des. Autom. 1993, 2, 149–157. [Google Scholar]
- Rezaei Aderiani, A.; Wärmefjord, K.; Söderberg, R. Evaluating Different Strategies to Achieve the Highest Geometric Quality in Self-adjusting Smart Assembly Lines. In Robotics and Computer-Integrated Manufacturing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–15. [Google Scholar]
- Morse, E.; Dantan, J.Y.; Anwer, N.; Söderberg, R.; Moroni, G.; Qureshi, A.; Jiang, X.; Mathieu, L. Tolerancing: Managing Uncertainty from Conceptual Design to Final Product. CIRP Ann. 2018, 67, 695–717. [Google Scholar] [CrossRef] [Green Version]
- Dantan, J.; Qureshi, A.; Antoine, J.; Eisenbart, B.; Blessing, L. Management of Product Characteristics Uncertainty Based on Formal Logic and Characteristics Properties Model. CIRP Ann. 2013, 62, 147–150. [Google Scholar] [CrossRef] [Green Version]
- Marziale, M.; Polini, W. A review of two models for tolerance analysis of an assembly: Jacobian and torsor. Int. J. Comput. Integr. Manuf. 2011, 24, 74–86. [Google Scholar] [CrossRef] [Green Version]
- Armillotta, A. A Method for Computer-Aided Specification of Geometric Tolerances. Comput. Aided Des. 2013, 45, 1604–1616. [Google Scholar] [CrossRef]
- Sfantsikopoulos, M.M. A Cost-Tolerance Analytical Approach for Design and Manufacturing. Int. J. Adv. Manuf. Technol. 1990, 5, 126–134. [Google Scholar] [CrossRef]
- Chase, K.W.; Parkinson, A.R. A Survey of Research in the Application of Tolerance Analysis to the Design of Mechanical Assemblies. Res. Eng. Des. 1991, 3, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Bjørke, Ø. Computer-Aided Tolerancing, 2nd ed.; ASME Press: New York, NY, USA, 1989. [Google Scholar]
- Iannuzzi, M.P.; Sandgren, E. Tolerance Optimization Using Genetic Algorithms: Benchmarking with Manual Analysis. In Computer-Aided Tolerancing; Kimura, F., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 219–234. [Google Scholar] [CrossRef]
- Hallmann, M.; Schleich, B.; Wartzack, S. From Tolerance Allocation to Tolerance-Cost Optimization: A Comprehensive Literature Review. Int. J. Adv. Manuf. Technol. 2020, 107, 4859–4912. [Google Scholar] [CrossRef]
- Singh, P.K.; Jain, P.K.; Jain, S.C. Important Issues in Tolerance Design of Mechanical Assemblies. Part 2: Tolerance Synthesis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 1249–1287. [Google Scholar] [CrossRef]
- Karmakar, S.; Maiti, J. A Review on Dimensional Tolerance Synthesis: Paradigm Shift from Product to Process. Assem. Autom. 2012, 32, 18. [Google Scholar] [CrossRef]
- Ding, Y.; Jin, J.; Ceglarek, D.; Shi, J. Process-Oriented Tolerancing for Multi-Station Assembly Systems. IIE Trans. 2005, 37, 493–508. [Google Scholar] [CrossRef]
- Mantripragada, R.; Whitney, D. Modeling and Controlling Variation Propagation in Mechanical Assemblies Using State Transition Models. IEEE Trans. Robot. Autom. 1999, 15, 124–140. [Google Scholar] [CrossRef]
- Cui, A.; Zhang, H.P. Tolerance Allocation and Maintenance Optimal Design for Fixture in Multi-Station Panel Assembly Process. Appl. Mech. Mater. 2010, 34–35, 1039–1045. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Jin, J.; Ceglarek, D. Integration of Process-Oriented Tolerancing and Maintenance Planning in Design of Multistation Manufacturing Processes. IEEE Trans. Autom. Sci. Eng. 2006, 3, 440–453. [Google Scholar] [CrossRef]
- Hoffenson, S.; Dagman, A.; Söderberg, R. Tolerance Optimisation Considering Economic and Environmental Sustainability. J. Eng. Des. 2014, 25, 367–390. [Google Scholar] [CrossRef]
- Pehlivan, S.; Summers, J.D. A review of computer-aided fixture design with respect to information support requirements. Int. J. Prod. Res. 2008, 46, 929–947. [Google Scholar] [CrossRef]
- Ceglarek, D.; Shi, J. Dimensional variation reduction for automotive body assembly. Manuf. Rev. 1995, 8, 139–154. [Google Scholar]
- Aderiani, A.R. Individualizing Assembly Processes for Geometric Quality Improvement. Ph.D. Thesis, Chalmers Tekniska Hogskola, Gothenburg, Sweden, 2019. [Google Scholar]
- Söderberg, R.; Lindkvist, L. Computer aided assembly robustness evaluation. J. Eng. Des. 1999, 10, 165–181. [Google Scholar] [CrossRef]
- Jin, J.; Shi, J. State Space Modeling of Sheet Metal Assembly for Dimensional Control. J. Manuf. Sci. Eng. 1999, 121, 756–762. [Google Scholar] [CrossRef]
- Kim, P.; Ding, Y. Optimal design of fixture layout in multistation assembly processes. IEEE Trans. Autom. Sci. Eng. 2004, 1, 133–145. [Google Scholar] [CrossRef]
- Phoomboplab, T.; Ceglarek, D. Process yield improvement through optimum design of fixture layouts in 3D multistation assembly systems. J. Manuf. Sci. Eng. Trans. ASME 2008, 130, 0610051–06100517. [Google Scholar] [CrossRef]
- Zhaoqing, T.; Xinmin, L.; Zhongqin, L. Robust fixture layout design for multi-station sheet metal assembly processes using a genetic algorithm. Int. J. Prod. Res. 2009, 47, 6159–6176. [Google Scholar] [CrossRef]
- Xie, W.; Deng, Z.; Ding, B.; Kuang, H. Fixture layout optimization in multi-station assembly processes using augmented ant colony algorithm. J. Manuf. Syst. 2015, 37, 277–289. [Google Scholar] [CrossRef]
- Tyagi, S.; Shukla, N.; Kulkarni, S. Optimal design of fixture layout in a multi-station assembly using highly optimized tolerance inspired heuristic. Appl. Math. Model. 2016, 40, 6134–6147. [Google Scholar] [CrossRef] [Green Version]
- Masoumi, A.; Shahi, V.J. Fixture layout optimization in multi-station sheet metal assembly considering assembly sequence and datum scheme. Int. J. Adv. Manuf. Technol. 2018, 95, 4629–4643. [Google Scholar] [CrossRef]
- Camelio, J.A.; Hu, S.J.; Marin, S.P. Compliant Assembly Variation Analysis Using Component Geometric Covariance. J. Manuf. Sci. Eng. 2004, 126, 355–360. [Google Scholar] [CrossRef]
- Liao, X.; Wang, G.G. Simultaneous optimization of fixture and joint positions for non-rigid sheet metal assembly. Int. J. Adv. Manuf. Technol. 2008, 36, 386–394. [Google Scholar] [CrossRef]
- Das, A.; Franciosa, P.; Ceglarek, D. Fixture Design Optimisation Considering Production Batch of Compliant Non-Ideal Sheet Metal Parts. Procedia Manuf. 2015, 1, 157–168. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Zhao, H.W. Fixture layout optimization for deformable sheet metal workpiece. Int. J. Adv. Manuf. Technol. 2015, 78, 85–98. [Google Scholar] [CrossRef]
- Franciosa, P.; Gerbino, S.; Ceglarek, D. Fixture Capability Optimisation for Early-stage Design of Assembly System with Compliant Parts Using Nested Polynomial Chaos Expansion. Procedia CIRP 2016, 41, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Yu, K. Robust fixture design of compliant assembly process based on a support vector regression model. Int. J. Adv. Manuf. Technol. 2019, 103, 111–126. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, Y. Minimizing assembly variation in selective assembly for auto-body parts based on IGAOT. Int. J. Intell. Comput. Cybern. 2018, 11, 254–268. [Google Scholar] [CrossRef]
- Rezaei Aderiani, A.; Wärmefjord, K.; Söderberg, R.; Lindkvist, L.; Lindau, B. Optimal design of fixture layouts for compliant sheet metal assemblies. Int. J. Adv. Manuf. Technol. 2020, 110, 2181–2201. [Google Scholar] [CrossRef]
- Liu, S.C.; Hu, S.J. Sheet metal joint configurations and their variation characteristics. J. Manuf. Sci. Eng. 1998, 120, 461–467. [Google Scholar] [CrossRef]
- Dahlström, S.; Lindkvist, L. Variation simulation of sheet metal assemblies using the method of influence coefficients with contact modeling. J. Manuf. Sci. Eng. 2007, 129, 615–622. [Google Scholar] [CrossRef]
- Wärmefjord, K.; Lindkvist, L.; Söderberg, R. Tolerance simulation of compliant sheet metal assemblies using automatic node-based contact detection. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; pp. 35–44. [Google Scholar] [CrossRef]
- Lindau, B.; Lindkvist, L.; Andersson, A.; Söderberg, R. Statistical shape modeling in virtual assembly using PCA-technique. J. Manuf. Syst. 2013, 32, 456–463. [Google Scholar] [CrossRef]
- Lorin, S.; Lindkvist, L.; Söderberg, R.; Sandboge, R. Combining Variation Simulation with Thermal Expansion Simulation for Geometry Assurance. J. Comput. Inf. Sci. Eng. 2013, 13, 031007. [Google Scholar] [CrossRef]
- Camuz, S.; Lorin, S.; Wärmefjord, K.; Söderberg, R. Nonlinear Material Model in Part Variation Simulations of Sheet Metals. J. Comput. Inf. Sci. Eng. 2019, 19, 021012. [Google Scholar] [CrossRef]
- Wärmefjord, K.; Söderberg, R.; Lindkvist, L. Variation Simulation of Spot Welding Sequence for Sheet Metal Assemblies. In Proceedings of the Norddesign 2010 International Conference on Methods and Tools for Product and Production Development, Gothenburg, Sweden, 25–27 August 2010; pp. 519–528. [Google Scholar]
- Sadeghi Tabar, R.; Wärmefjord, K.; Söderberg, R.; Lindkvist, L. A Novel Rule-Based Method for Individualized Spot Welding Sequence Optimization with Respect to Geometrical Quality. J. Manuf. Sci. Eng. 2019, 141. [Google Scholar] [CrossRef]
- Clements, J.A. Process capability calculations, for non-normal distributions. Qual. Prog. 1989, 22, 95–100. [Google Scholar]
- Asada, H.; By, A. Kinematic analysis of workpart fixturing for flexible assembly with automatically reconfigurable fixtures. IEEE J. Robot. Autom. 1985, 1, 86–94. [Google Scholar] [CrossRef]
- Bäck, T. Evolutionary Algorithms in Theory and Practice; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Lorin, S.; Lindkvist, L.; Söderberg, R.; Sandboge, R. Combining Variation Simulation with Thermal Expansion for Geometry Assurance. In Proceedings of the 17th Design for Manufacturing and the Life Cycle Conference, Chicago, IL, USA, 12–15 August 2012; Volume 5, pp. 477–485. [Google Scholar] [CrossRef]

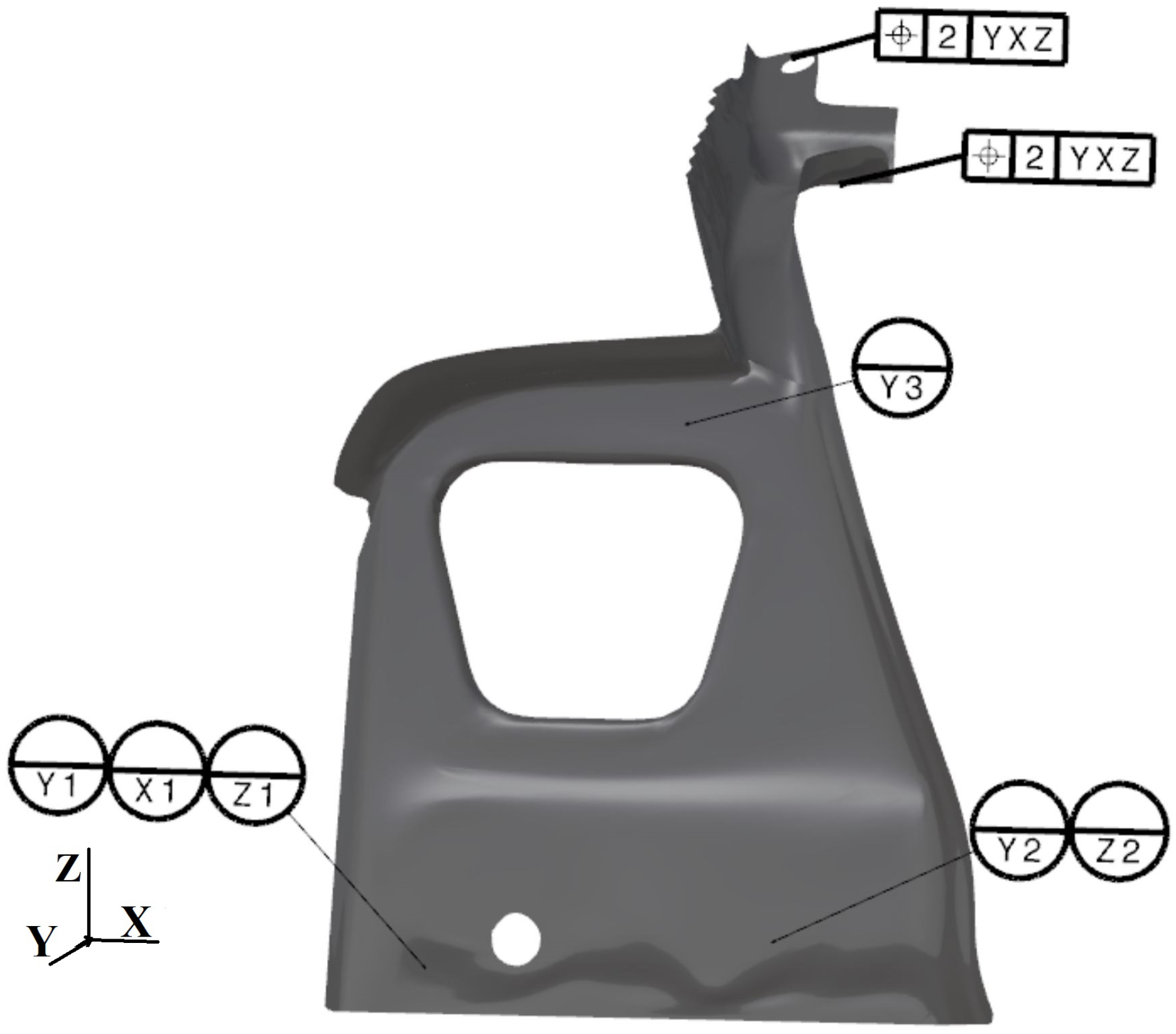
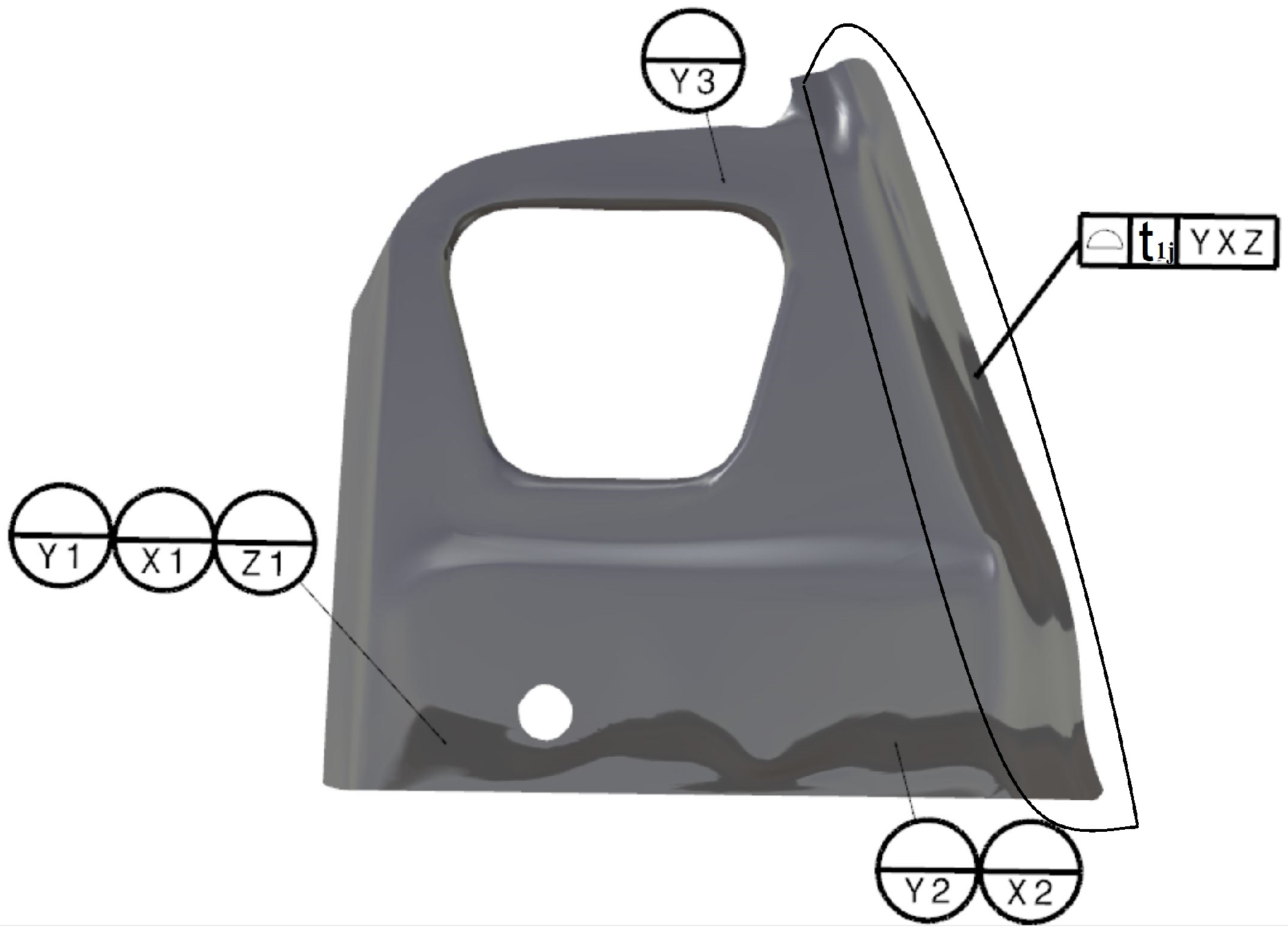

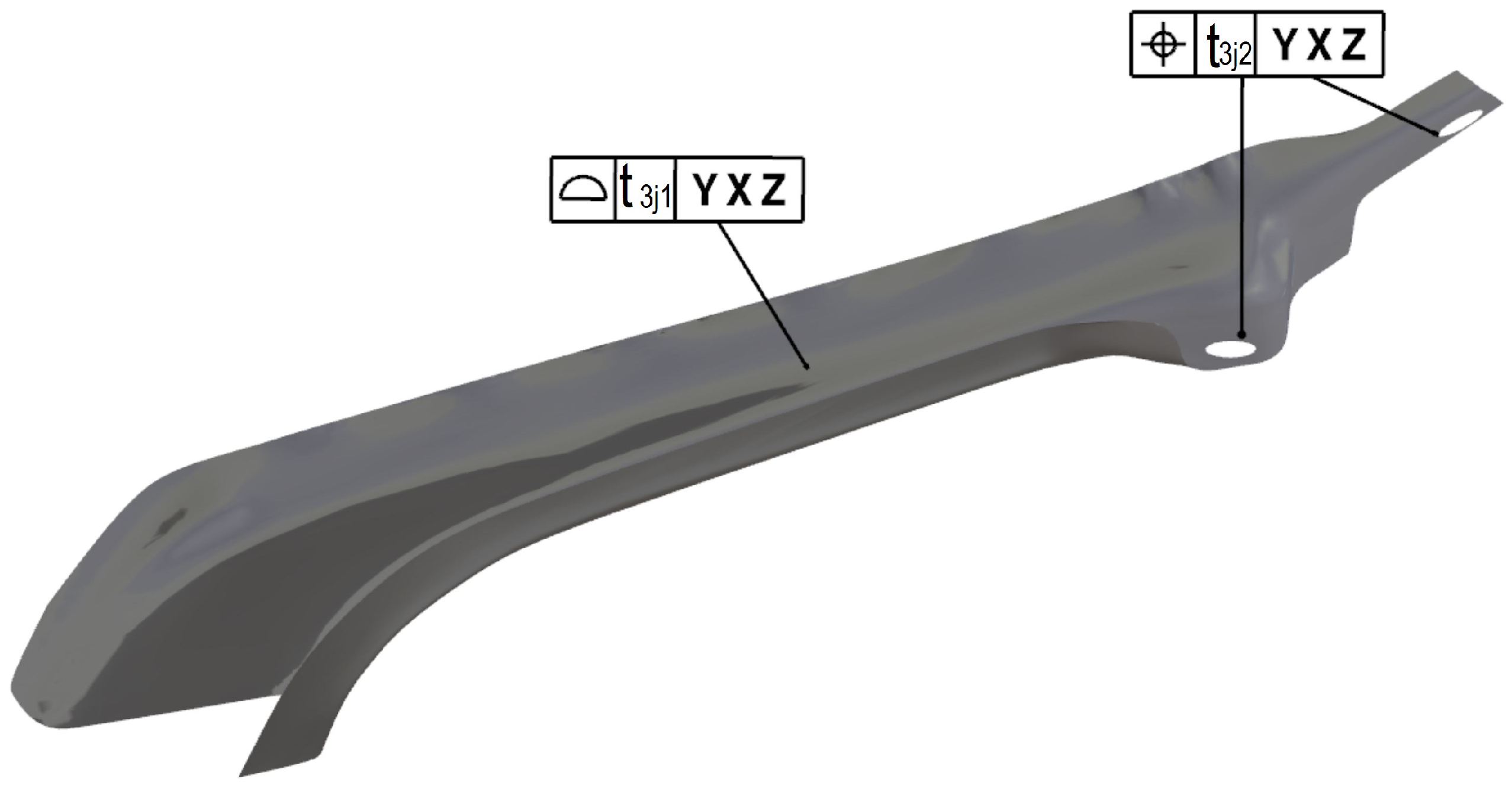


| … | |||||
|---|---|---|---|---|---|
| … | |||||
| … | |||||
| … | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| … |
| Parameter | Variable | Feasible Values |
|---|---|---|
| Production scenario of part i | 0, 1 | |
| Being clamped or not for the node k of part i | 0, 1 | |
| Assigned node to the hole | 1, 2, …, n. | |
| Assigned node to the slot | 1, 2, …, n. | |
| Slot direction | [0 180] |
| Production Strategy (j) | Part 1 () | Part 2 () | Part 3 () | Part 3 () |
|---|---|---|---|---|
| 1 | 0.5 | 0.5 | 0.5 | 0.4 |
| 2 | 0.75 | 0.75 | 0.75 | 0.8 |
| 3 | 1 | 1 | 1 | 1.2 |
| 4 | 1.5 | 1.5 | 1.5 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaei Aderiani, A.; Hallmann, M.; Wärmefjord, K.; Schleich, B.; Söderberg, R.; Wartzack, S. Integrated Tolerance and Fixture Layout Design for Compliant Sheet Metal Assemblies. Appl. Sci. 2021, 11, 1646. https://doi.org/10.3390/app11041646
Rezaei Aderiani A, Hallmann M, Wärmefjord K, Schleich B, Söderberg R, Wartzack S. Integrated Tolerance and Fixture Layout Design for Compliant Sheet Metal Assemblies. Applied Sciences. 2021; 11(4):1646. https://doi.org/10.3390/app11041646
Chicago/Turabian StyleRezaei Aderiani, Abolfazl, Martin Hallmann, Kristina Wärmefjord, Benjamin Schleich, Rikard Söderberg, and Sandro Wartzack. 2021. "Integrated Tolerance and Fixture Layout Design for Compliant Sheet Metal Assemblies" Applied Sciences 11, no. 4: 1646. https://doi.org/10.3390/app11041646
APA StyleRezaei Aderiani, A., Hallmann, M., Wärmefjord, K., Schleich, B., Söderberg, R., & Wartzack, S. (2021). Integrated Tolerance and Fixture Layout Design for Compliant Sheet Metal Assemblies. Applied Sciences, 11(4), 1646. https://doi.org/10.3390/app11041646








