Hydrothermal and Entropy Investigation of Ag/MgO/H2O Hybrid Nanofluid Natural Convection in a Novel Shape of Porous Cavity
Abstract
:1. Introduction
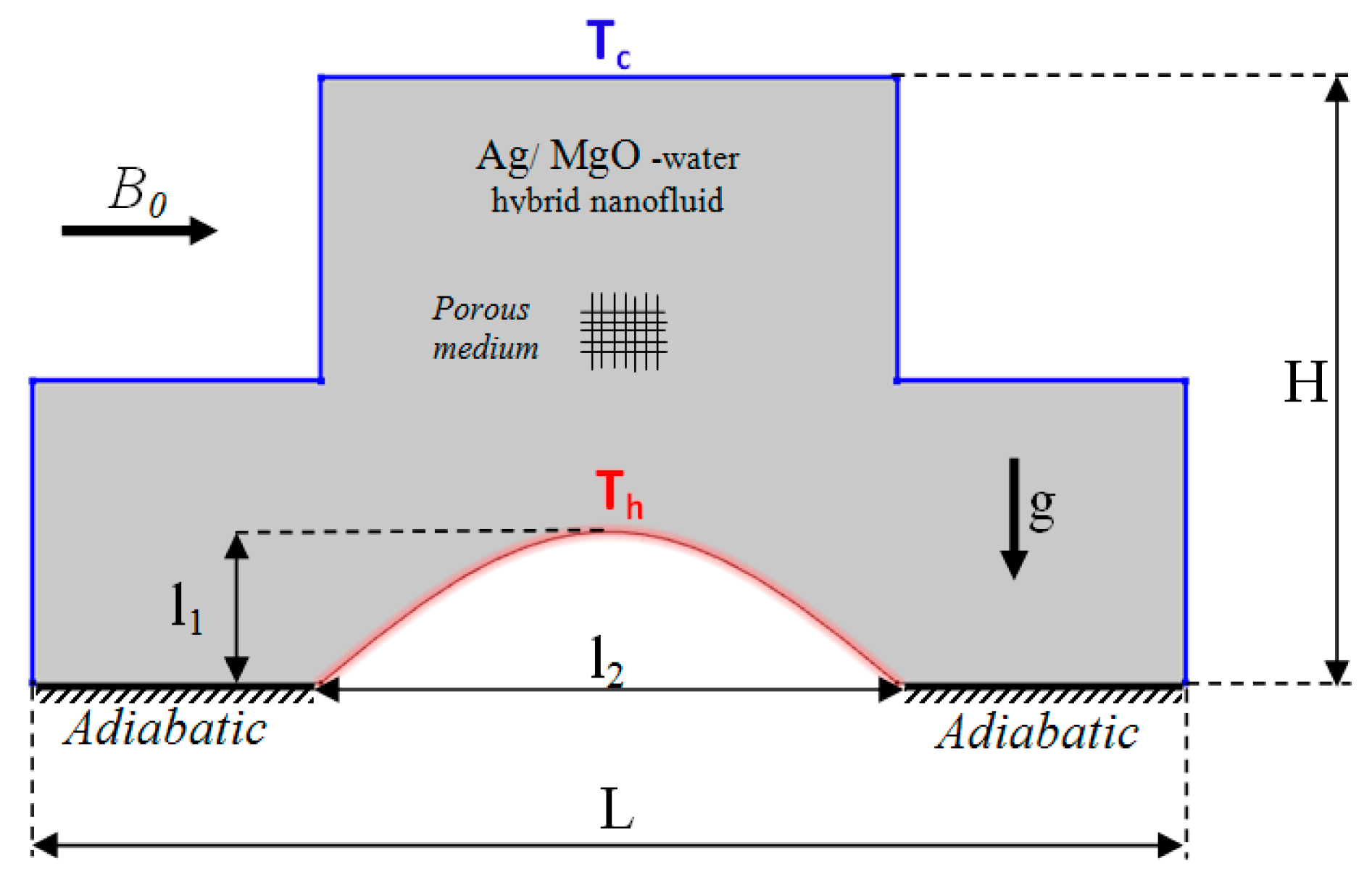
2. Problem Description
3. Formulation of the Mathematical Model
3.1. Governing Equations and Boundary Conditions
- The outer wall
- The mi sphere wall
- The down walls
3.2. Thermophysical Propertiesofthe Nanofluid
3.3. Nondimensional Entropy Generation
3.4. Numerical Procedure
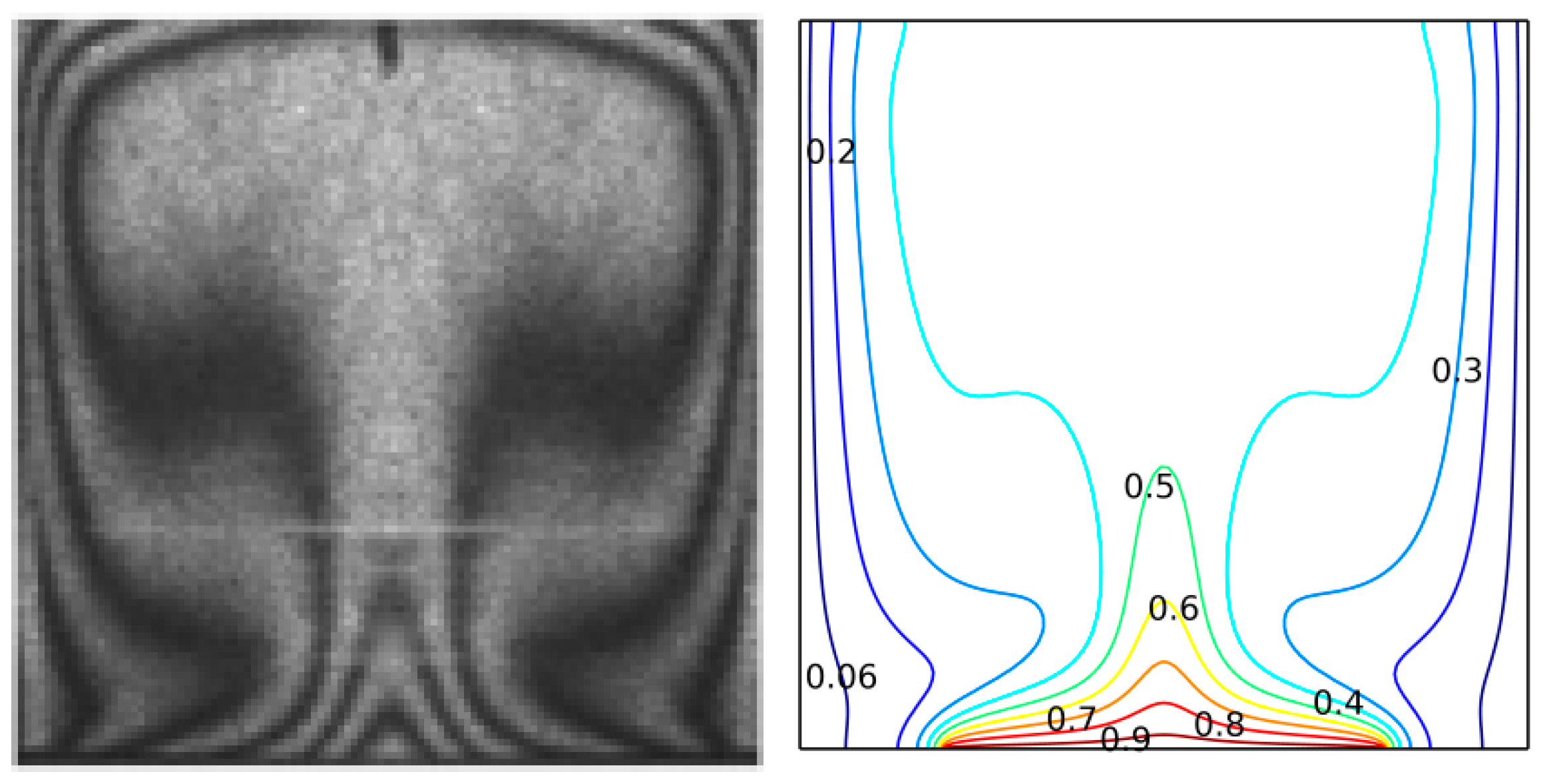
4. Validation and Grid Independency Analysis
5. Results Discussion
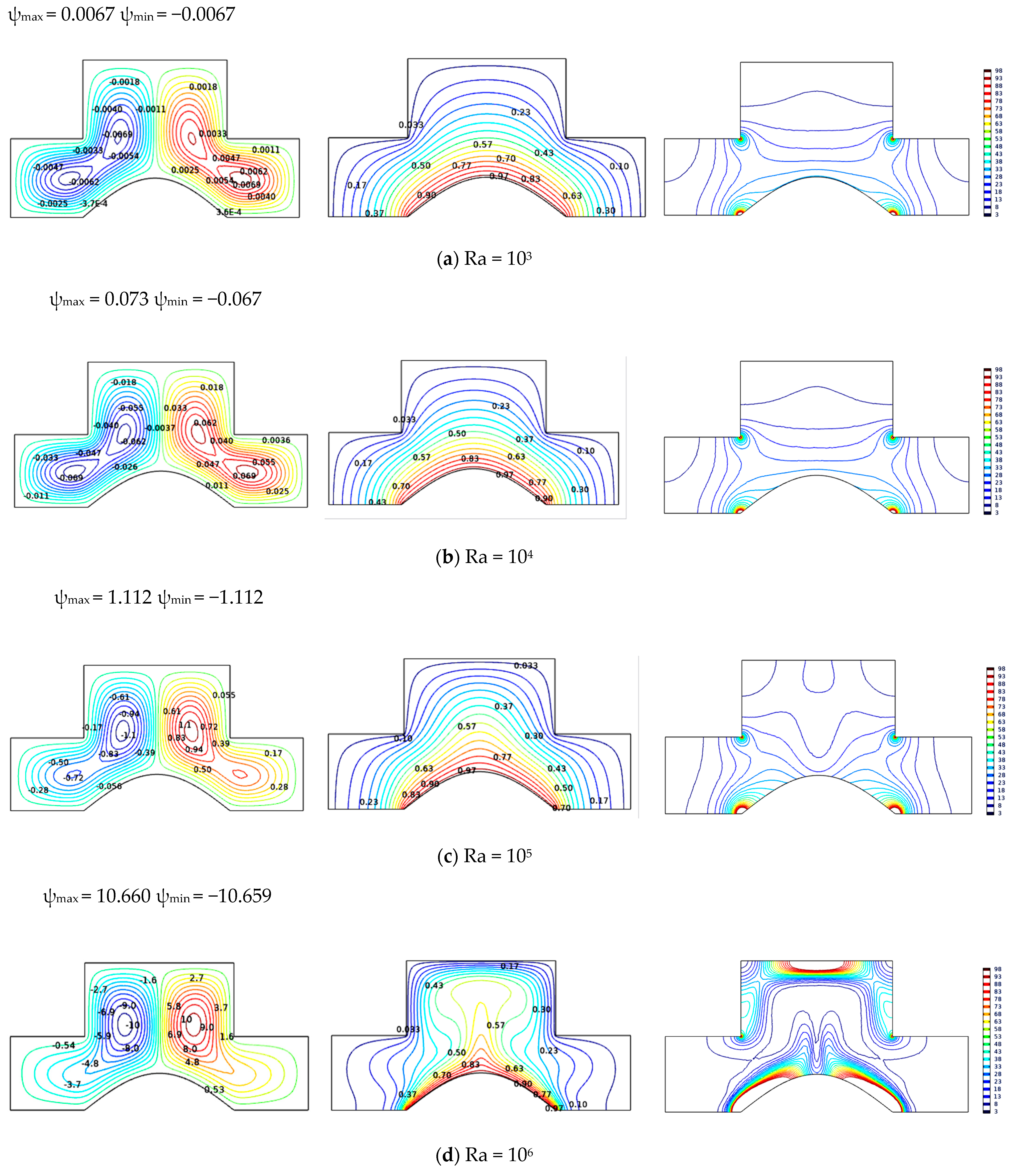
5.1. Effect of Rayleigh Number
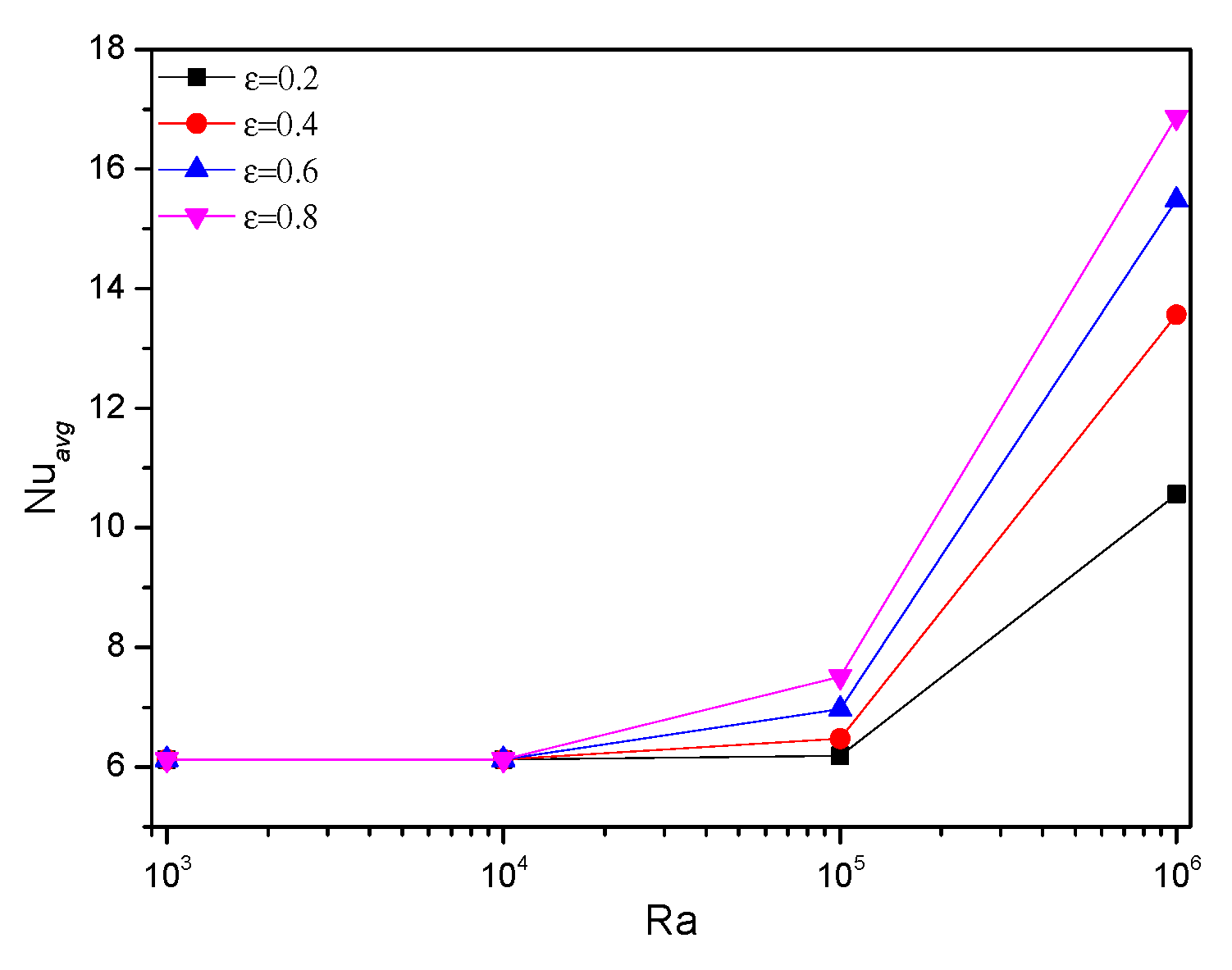
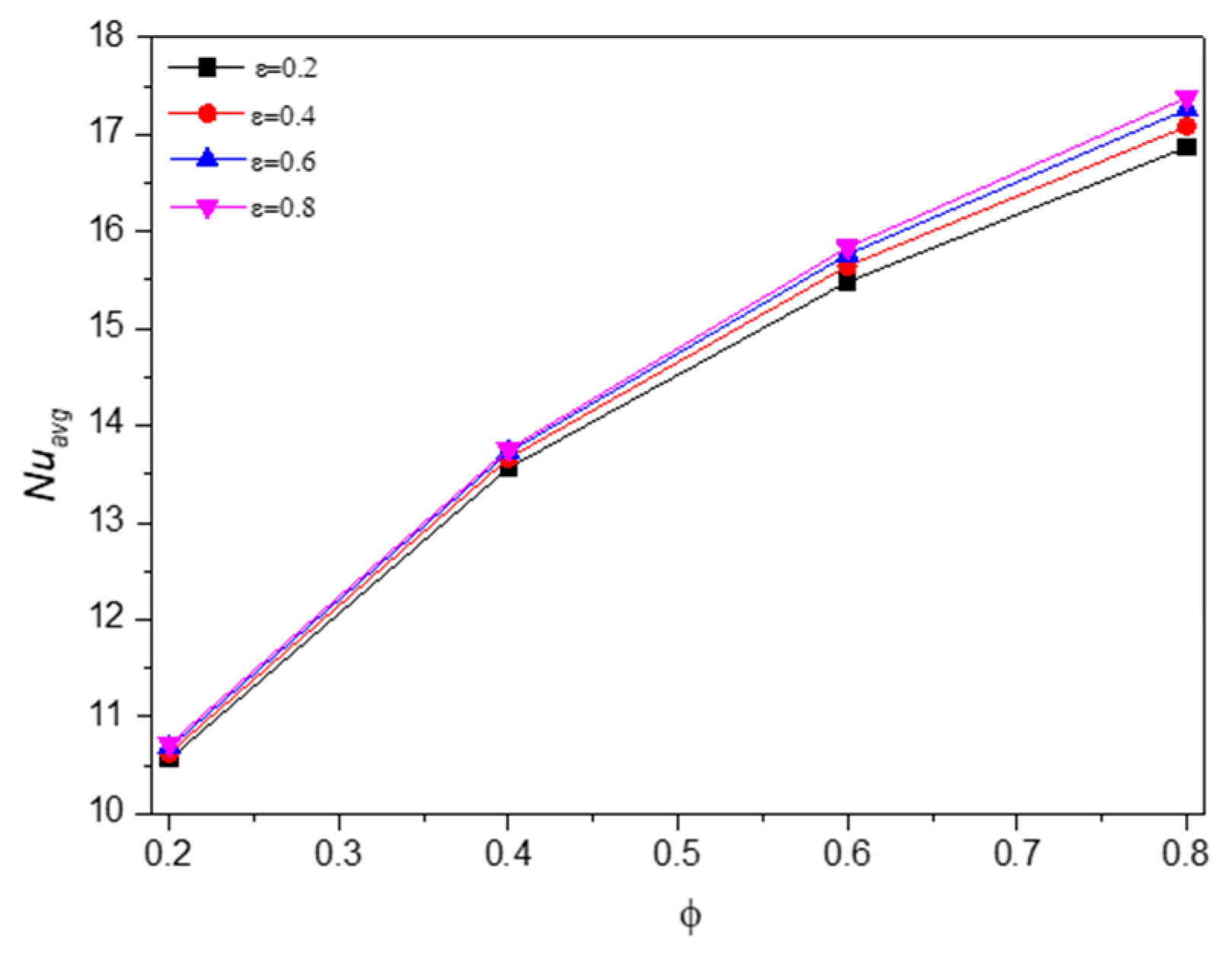
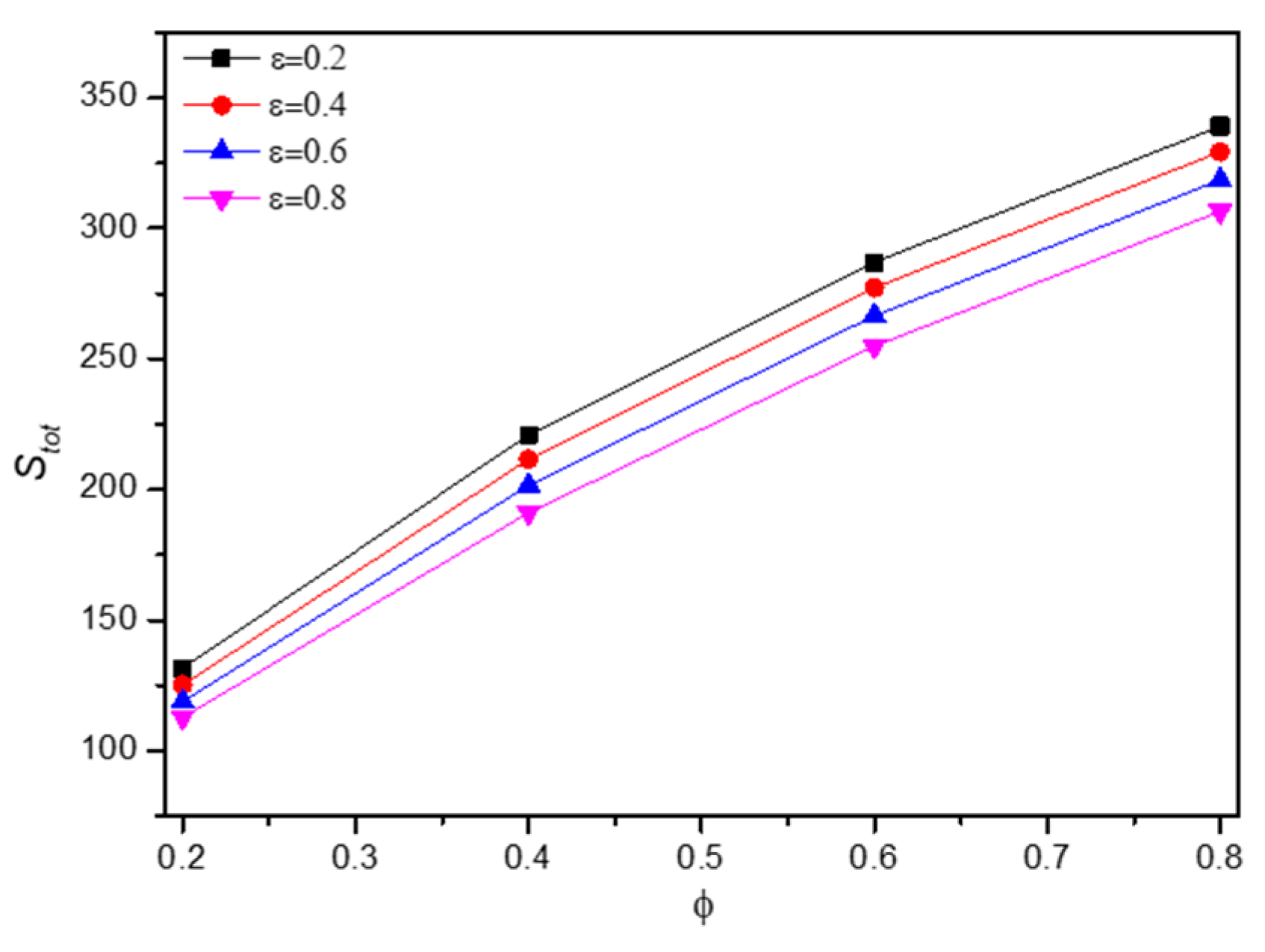
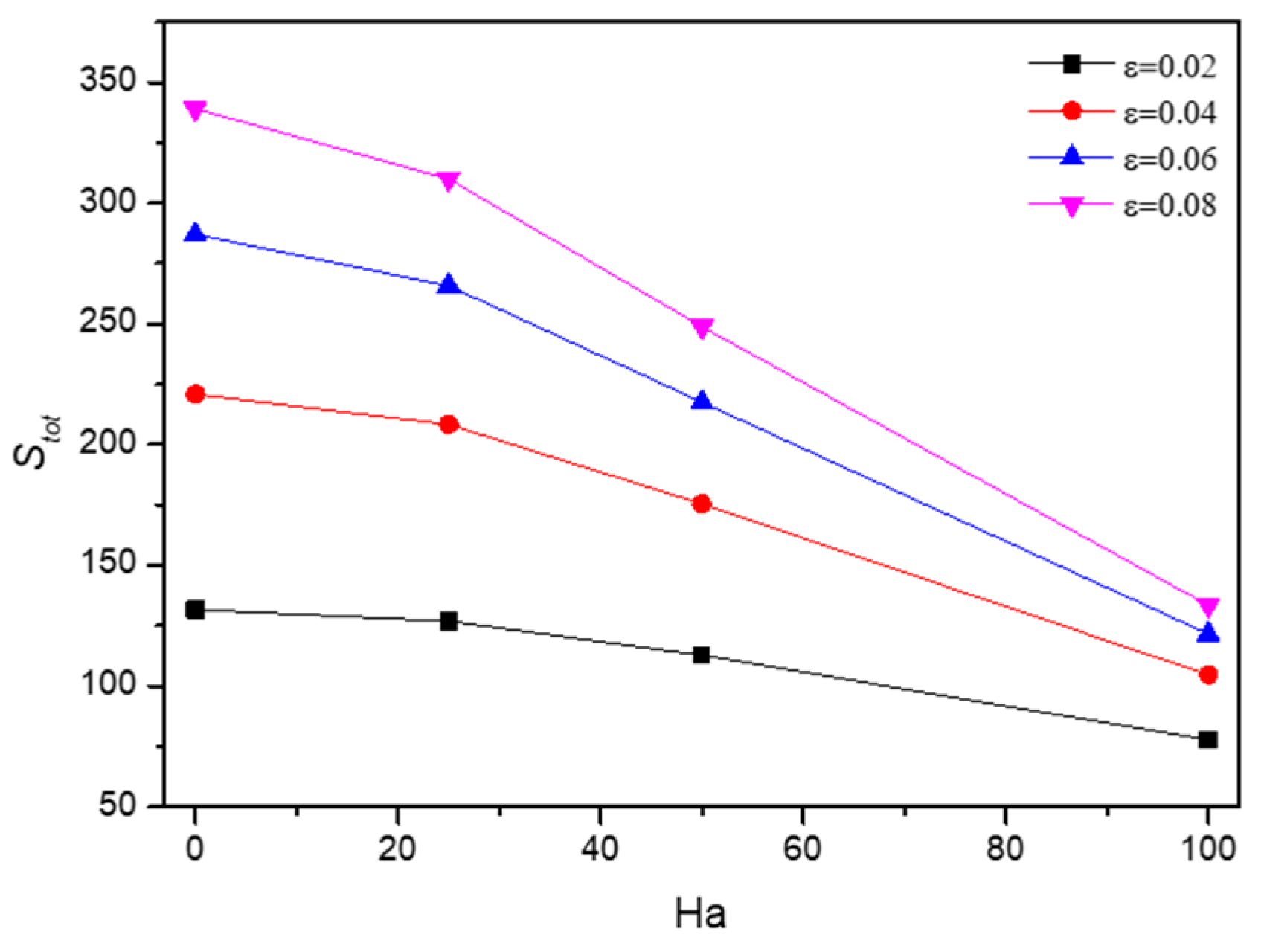
5.2. Effect of Nanofluid Loading
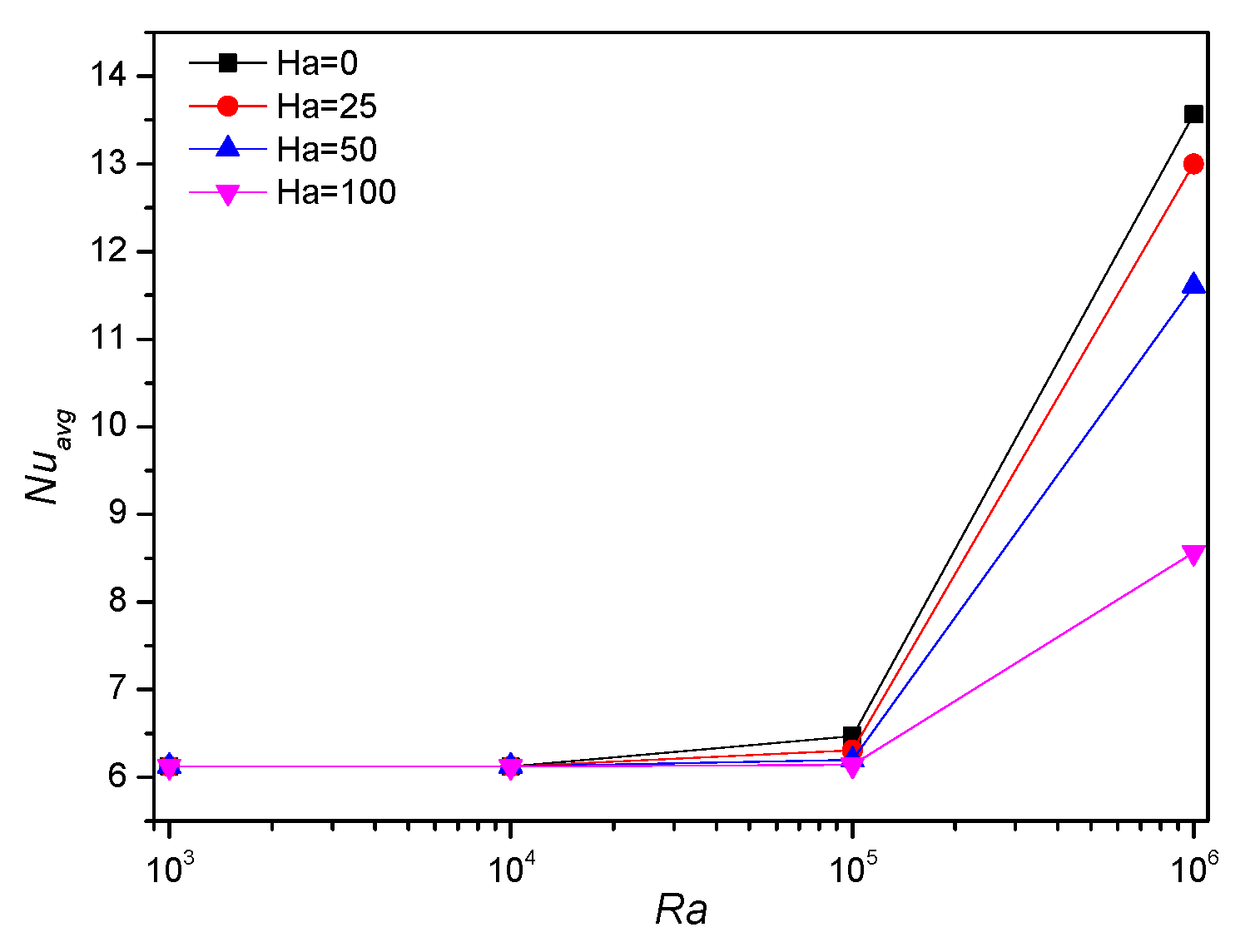
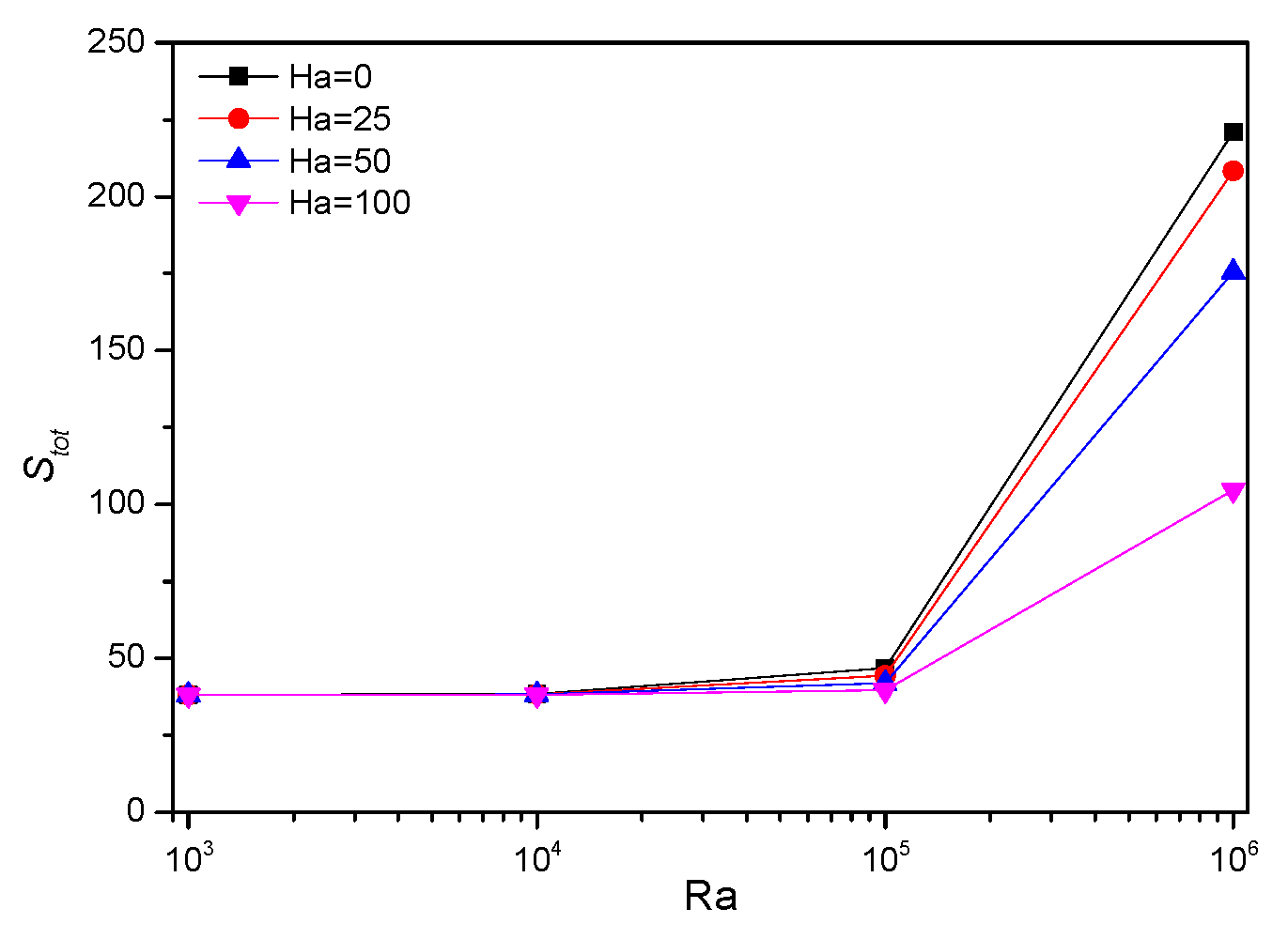
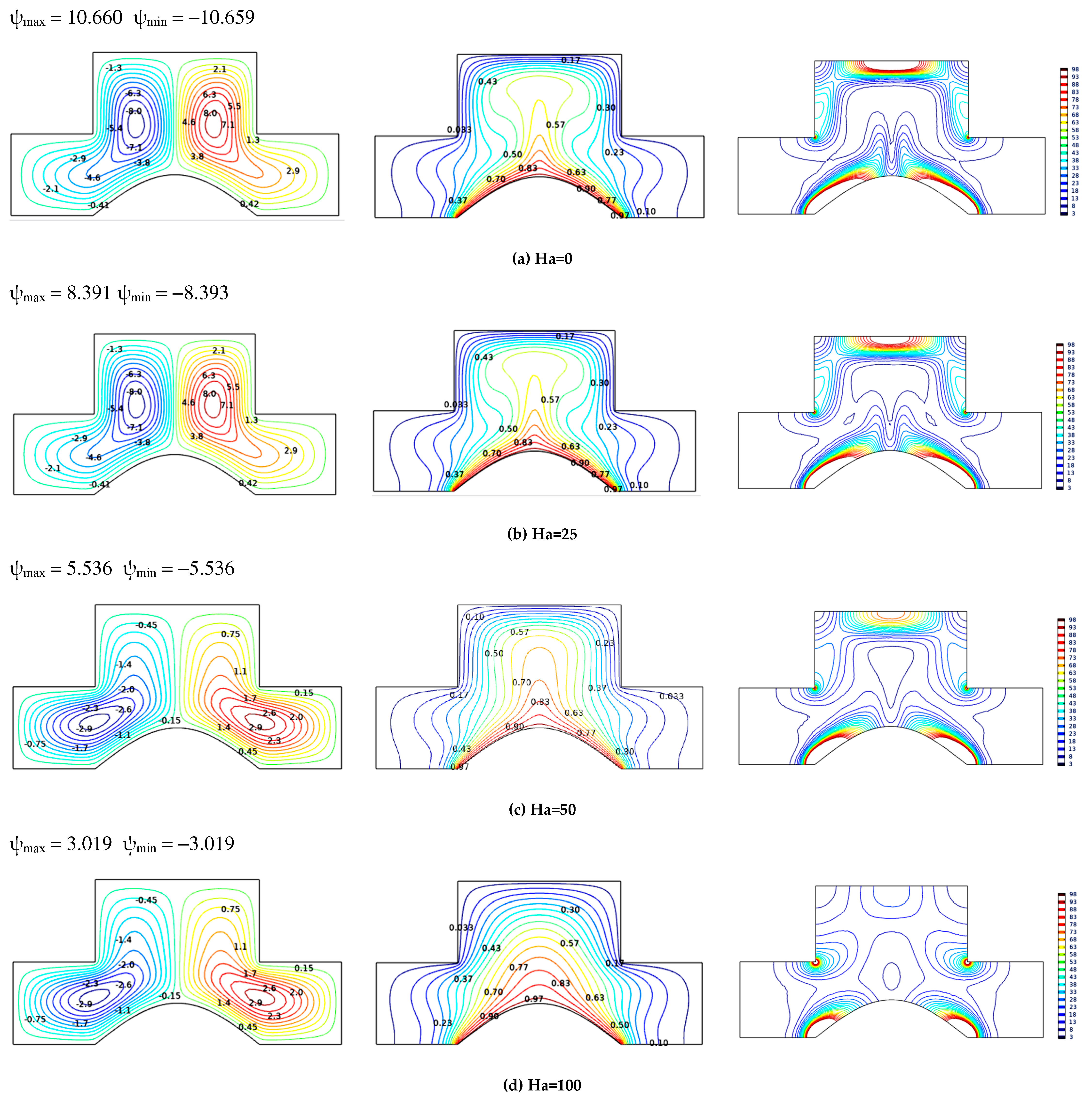
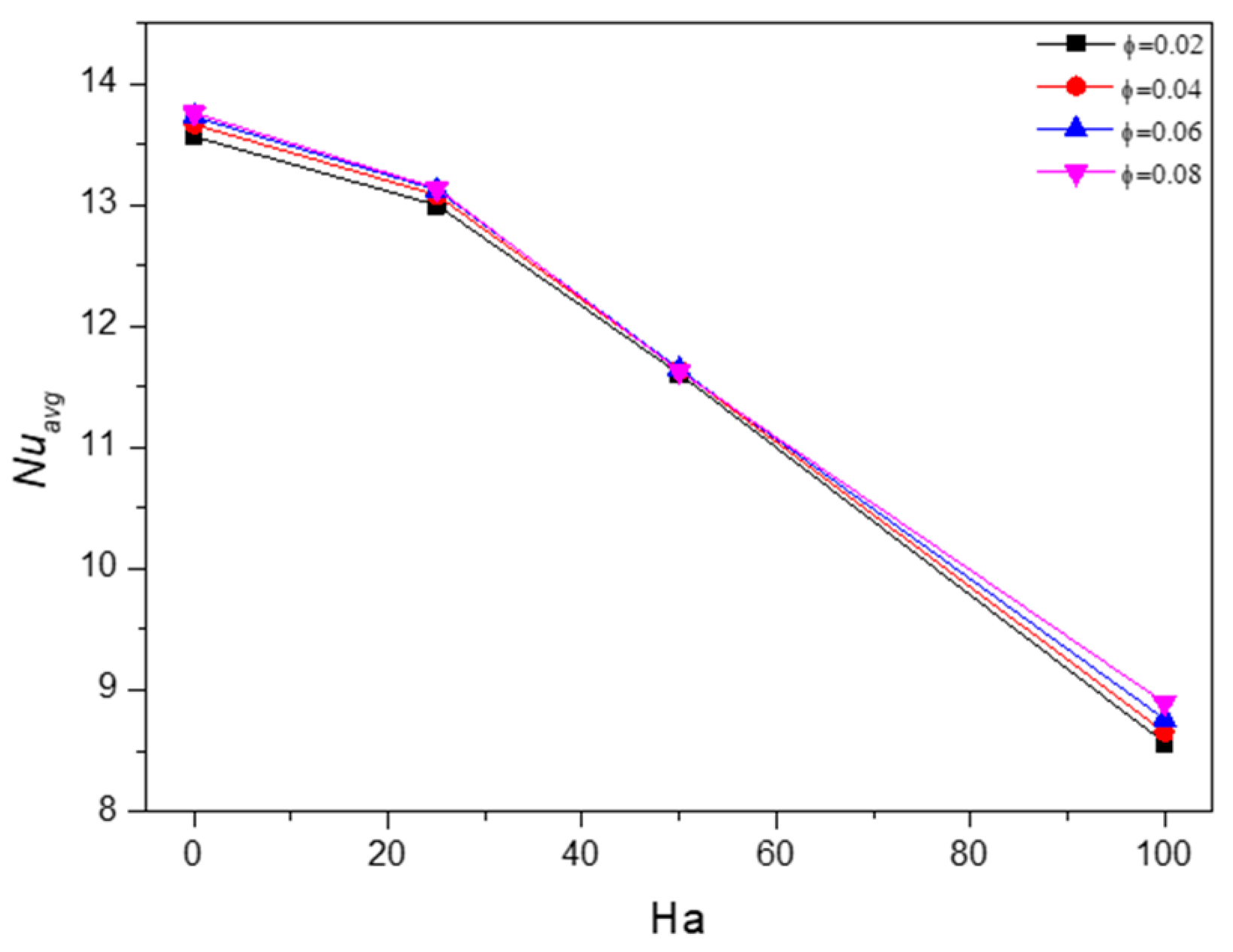
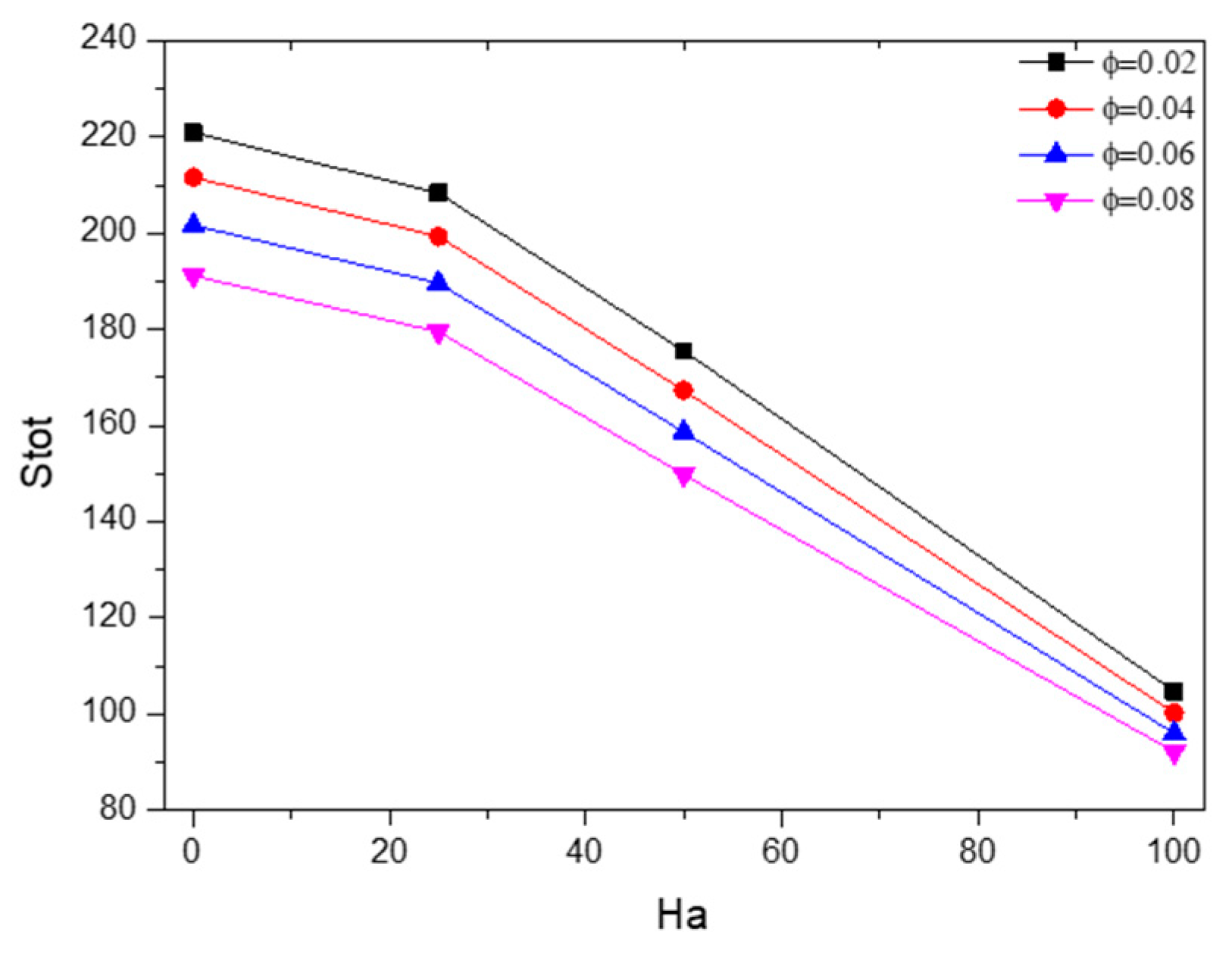
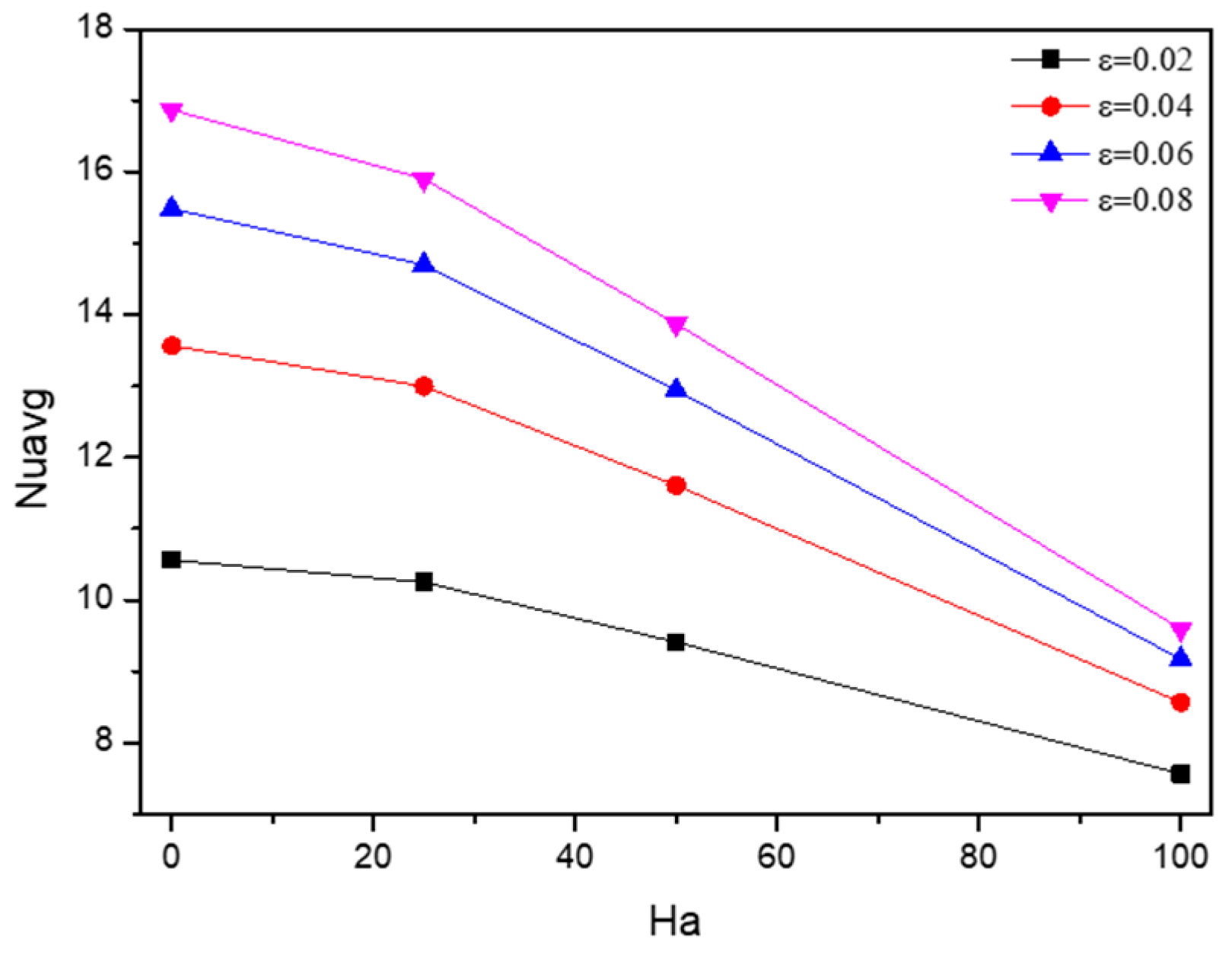
5.3. Effect of Hartmann Number
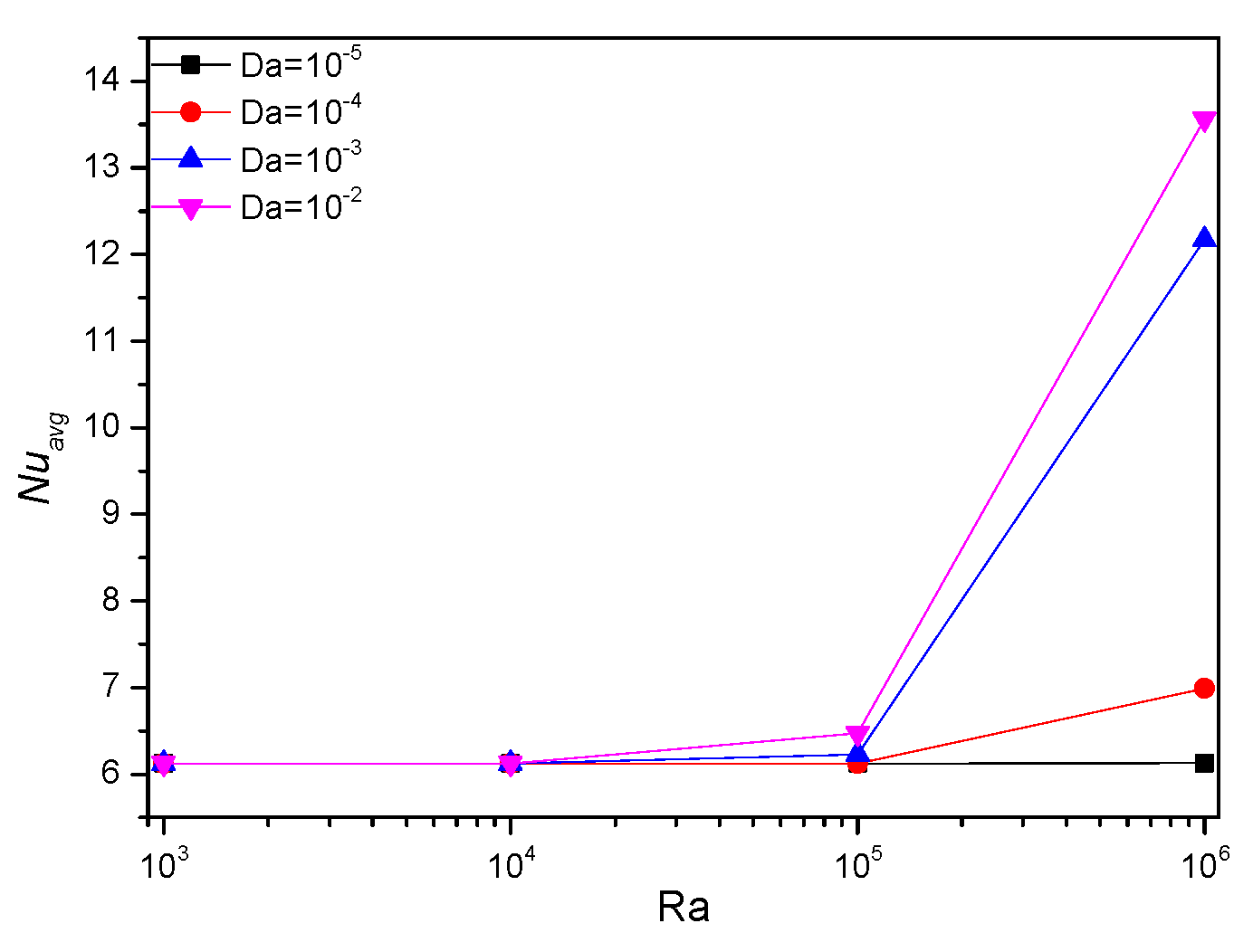
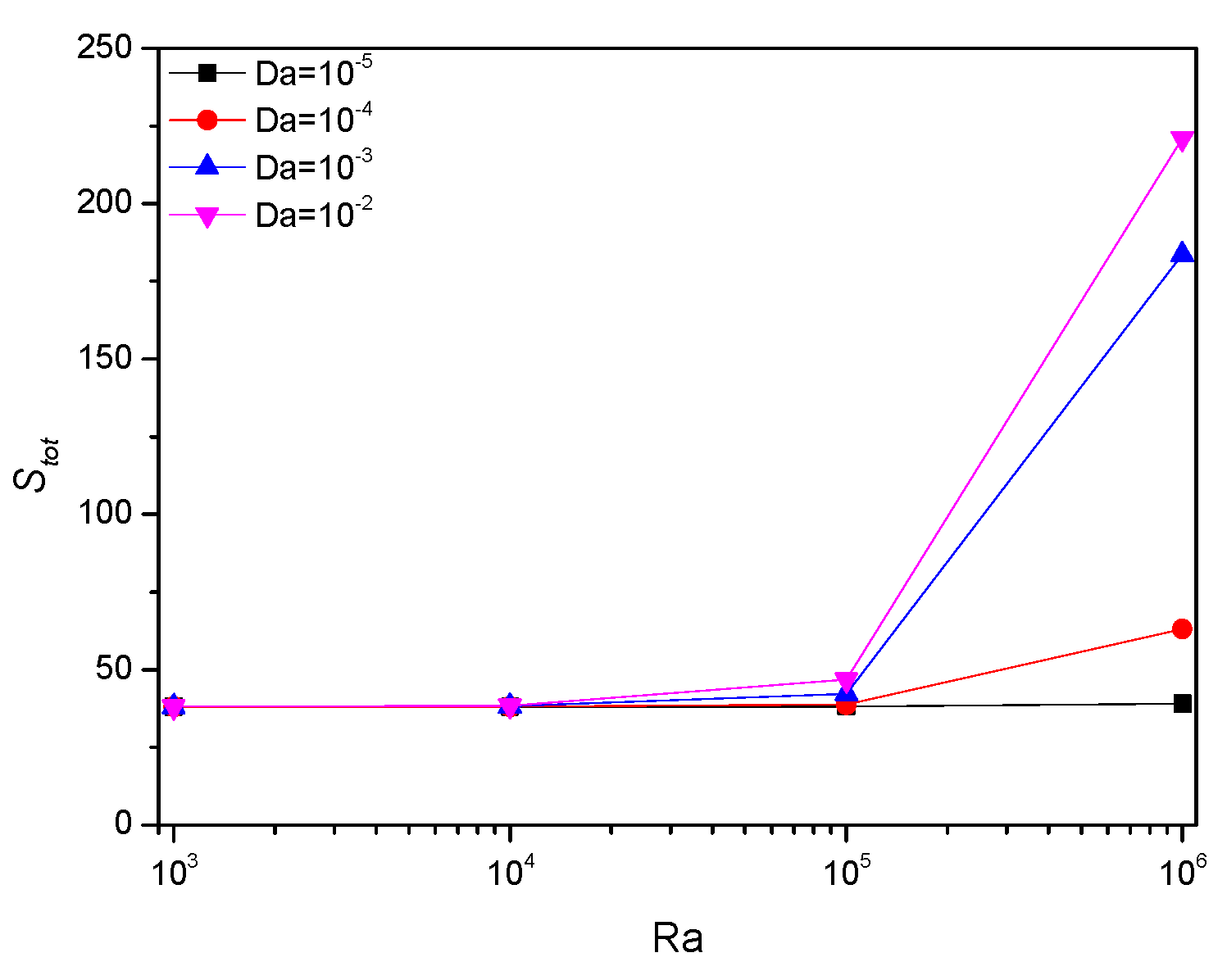
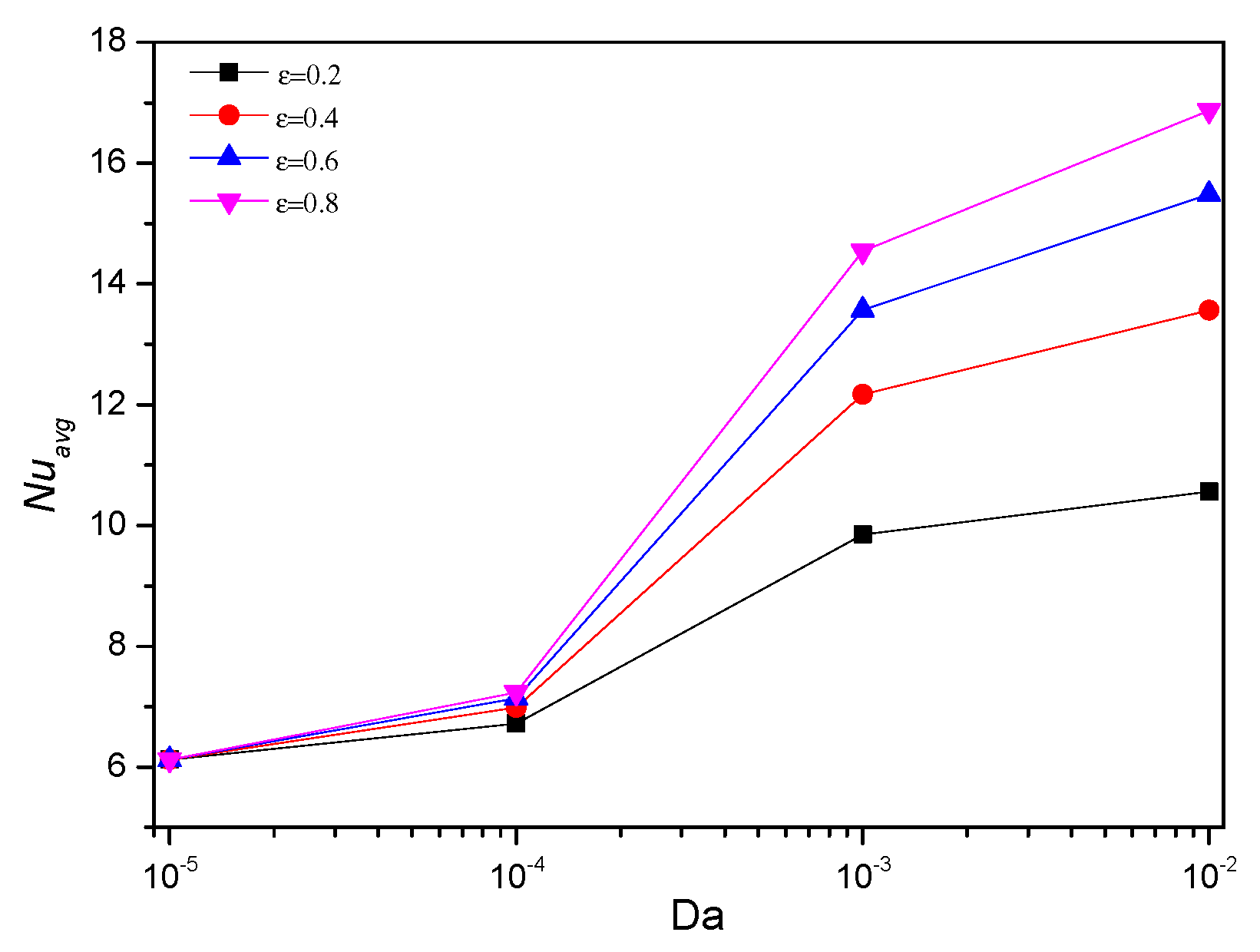
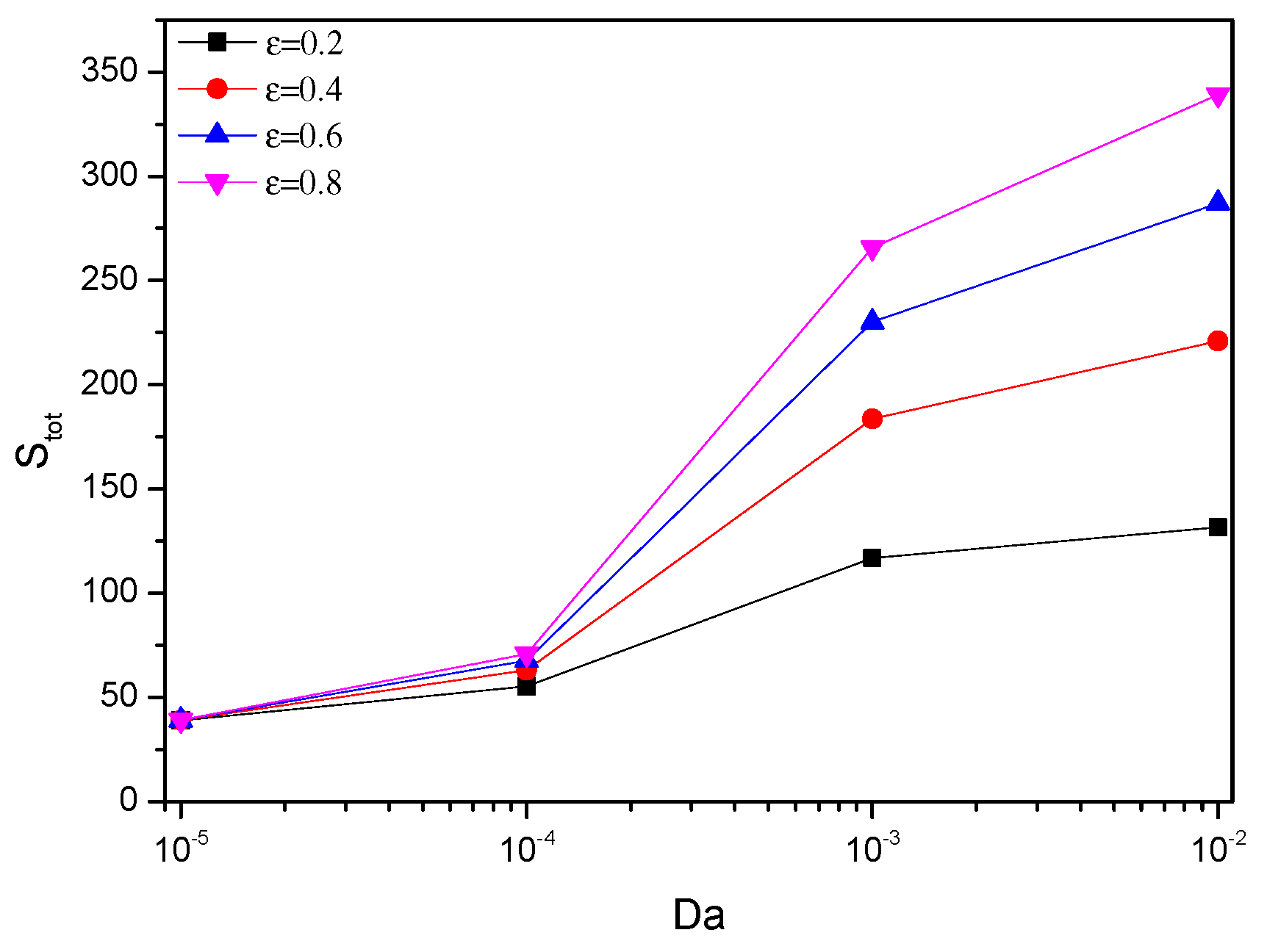
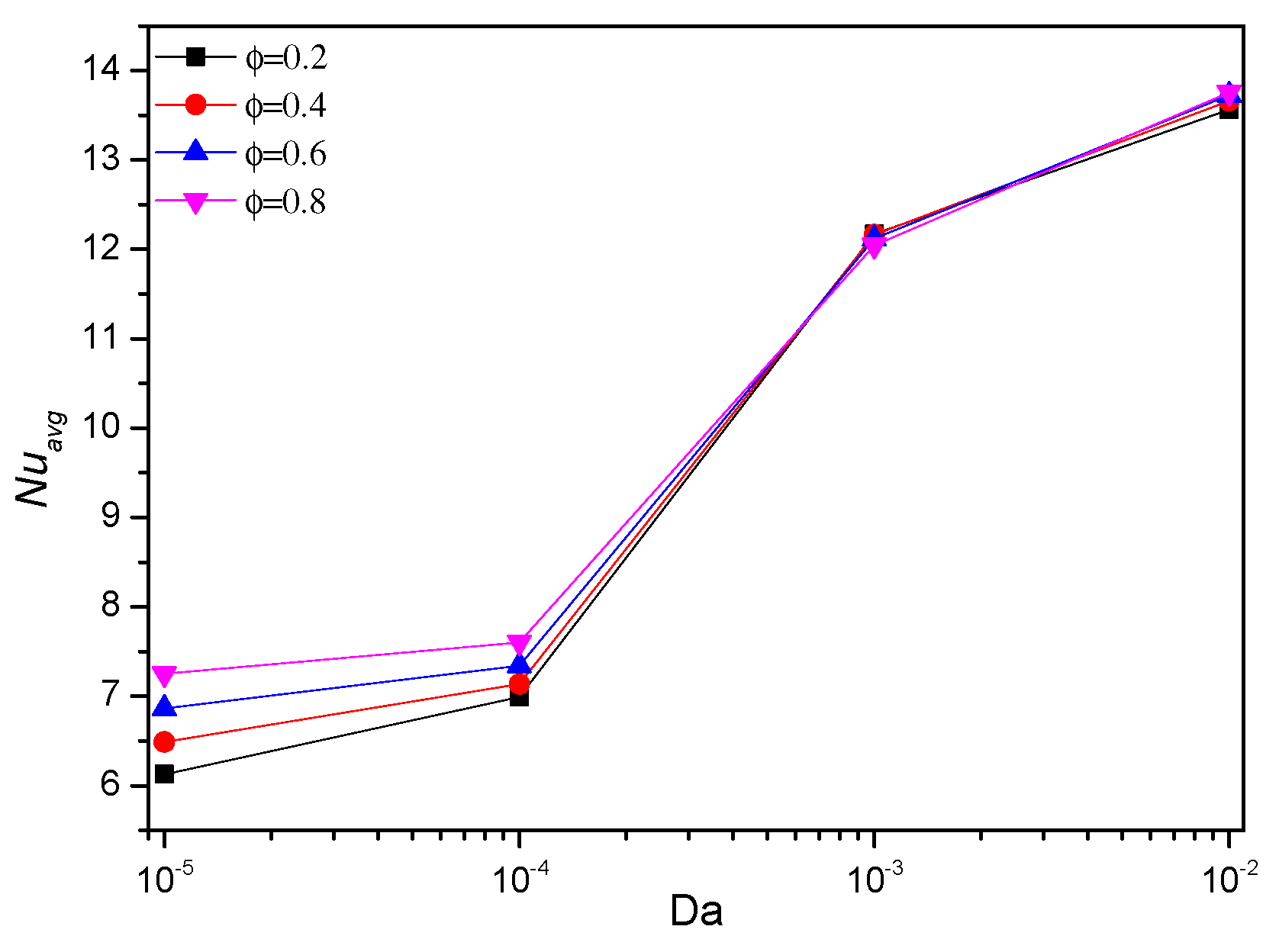
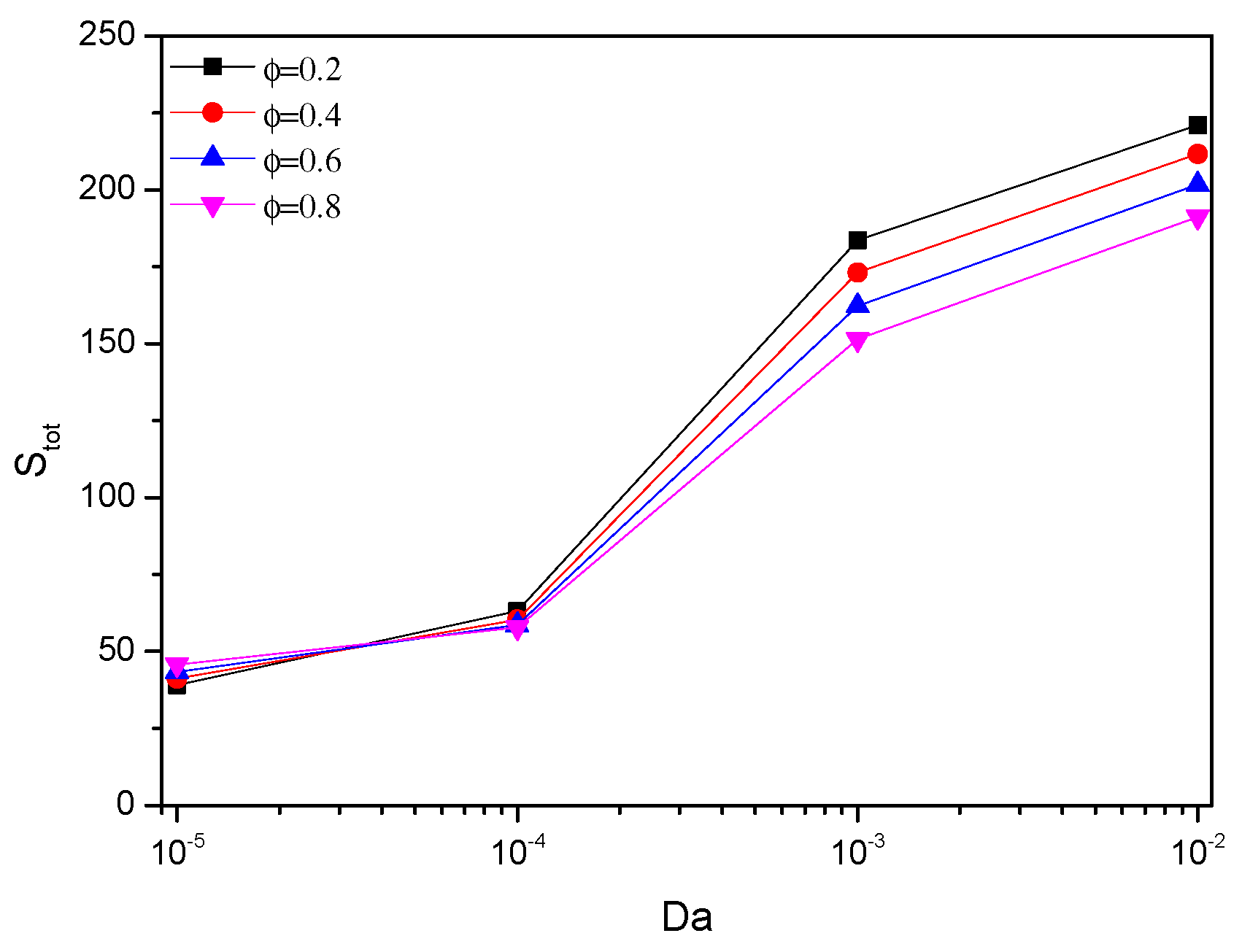
5.4. Effect of Darcy Number
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of symbols | |
| Thermal conductivity | |
| L,H | Long and height of the cavity (m) |
| Long and height of heat wall (m) | |
| Rayleigh number | |
| Hartmann number | |
| Nusselt number | |
| Average Nusselt number | |
| Local Nusselt number | |
| Prandtl number | |
| Da | Darcy number |
| Coordinate(m) | |
| X,Y | Dimensionless coordinate |
| Velocity components(m/s) | |
| Nondimensional velocity components | |
| Temperature (°C) | |
| p | Pressure (N/m2) |
| P | Dimensionless pressure |
| Permeability | |
| g | Gravitational acceleration vector (m/s2) |
| Forchheimer coefficient | |
| Intensity of magnetic field | |
| Total dimensionless entropy generation | |
| Greeks symbols | |
| Dimensionless temperature | |
| Porosity | |
| Thermal diffusivity (m2/s) | |
| Kinematic viscosity (m2/s) | |
| Volume fraction | |
| Thermal expansion coefficient (1/K) | |
| Dynamic viscosity (kg/m∙s) | |
| Density (kg/m3) | |
| Electrical conductivity | |
| Nondimensional stream function | |
| Subscripts | |
| Base fluid | |
| Hybrid-nanofluid | |
| Nanoparticles | |
| Average | |
| Local | |
| Hot | |
| Cold |
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Maxwell, J.C. Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Diglio, G.; Roselli, C.; Sasso, M.; Channabasappa, U.J. Borehole heat exchanger with nanofluids as heat carrier. Geothermics 2018, 72, 112–123. [Google Scholar] [CrossRef]
- Zaim, A.; Aissa, A.; Mebarek-Oudina, F.; Mahanthesh, B.; Lorenzini, G.; Sahnoun, M.; El Ganaoui, M. Galerkin finite element analysis of magneto-hydrodynamic natural convection of Cu-water nanoliquid in a baffled U-shaped enclosure. Propuls. Power Res. 2020, 9, 383–393. [Google Scholar] [CrossRef]
- Fares, R.; Mebarek-Oudina, F.; Aissa, A.; Bilal, S.M.; Öztop, H.F. Optimal Entropy Generation in Darcy-Forchheimer Magnetized Flow in a Square Enclosure Filled with Silver Based Water Nanoliquid. J. Therm. Anal. Calorim. 2021, 1–11. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Redouane, F.; Rajashekhar, C. Convection Heat Transfer of MgO-Ag/Water Magneto-Hybrid Nanoliquid Flow into a Special Porous Enclosure. Alger. J. Renew. Energy Sustain. Dev. 2020, 2, 84–95. [Google Scholar] [CrossRef]
- Molana, M. A Comprehensive Review on the Nanofluids Application in the Tubular Heat Exchangers. Am. J. Heat Mass Transf. 2016, 3, 352–381. [Google Scholar] [CrossRef] [Green Version]
- Sui, D.; Langåker, V.H.; Yu, Z. Investigation of Thermophysical Properties of Nanofluids for Application in Geothermal Energy. Energy Procedia 2017, 105, 5055–5060. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Molana, M.; Rahnama, A.; Ghadami, F. On the nanofluids applications in microchannels: A comprehensive review. Powder Technol. 2018, 332, 287–322. [Google Scholar]
- Patterson, J.; Imberger, J. Unsteady natural convection in a rectangular cavity. J. Fluid Mech. 1980, 100, 65–86. [Google Scholar] [CrossRef]
- Armaghani, T.; Kasaeipoor, A.; Alavi, N.; Rashidi, M.M. Numerical investigation of water-alumina nanofluid natural convection heat transfer and entropy generation in a baffled L.-shaped cavity. J. Mol. Liq. 2016, 223, 243–251. [Google Scholar] [CrossRef]
- Malekpour, A.; Karimi, N.; Mehdizadeh, A. Magnetohydrodynamics, natural convection and entropy generation of CuO-water nanofluid in an I-shape enclosure. J. Therm. Sci. Eng. Appl. 2018, 10, 061016. [Google Scholar] [CrossRef] [Green Version]
- Mamourian, M.; Shirvan, K.M.; Pop, I. Sensitivity analysis for MHD effects and inclination angles on natural convection heat transfer and entropy generation of Al2O3-water nanofluid in square cavity by Response Surface Methodology. Int. Commun. Heat Mass Transf. 2016, 79, 46–57. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Heatline visualization of MHD natural convection in an inclined wavy open porous cavity filled with a nanofluid with a local heater. Int. J. Heat Mass Transf. 2016, 99, 872–881. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Armaghani, T.; Chamkha, A.J.; Ganji, D.D. Natural Convection Analysis in a Cavity with an Inclined Elliptical Heater Subject to Shape Factor of Nanoparticles and Magnetic Field. Arab. J. Sci. Eng. 2019, 44, 7919–7931. [Google Scholar] [CrossRef]
- Rashad, A.M.; Armaghani, T.; Chamkha, A.J.; Mansour, M.A. Entropy generation and MHD natural convection of a nanofluid in an inclined square porous cavity: Effects of a heat sink and source size and location. Chin. J. Phys. 2018, 56, 193–211. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Izadi, M.; Mohebbi, R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT–Fe3O4/water hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 132, 1087–1104. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Chamkha, A.J.; Ganji, D.D. Investigation of natural convection of magnetic nanofluid in an enclosure with a porous medium considering Brownian motion. Case Stud. Therm. Eng. 2019, 14, 100502. [Google Scholar]
- Mebarek-Oudina, F.; Aissa, A.; Mahanthesh, B.; Öztop, H.F. Heat Transport of Magnetized Newtonian Nanoliquids in an Annular Space between Porous Vertical Cylinders with Discrete Heat Source. Int. Commun. Heat Mass Transf. 2020, 117, 104737. [Google Scholar] [CrossRef]
- Zahri, M.; Al-Kouz, W.; Rehman, K.U.; Malik, M. Thermally magnetized rectangular chamber optimization (TMRCO) of partially heated continuous stream: Hybrid meshed case study. Case Stud. Therm. Eng. 2020, 22, 100770. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Mackolil, J.; Radhika, M.; Al-Kouz, W. Significance of quadratic thermal radiation and quadratic convection on boundary layer two-phase flow of a dusty nanoliquid past a vertical plate. Int. Commun. Heat Mass Transf. 2021, 120, 105029. [Google Scholar] [CrossRef]
- Mukhtar, T.; Jamshed, W.; Aziz, A.; Al-Kouz, W. Computationalinvestigation of heat transfer in a flow subjected to magnetohydrodynamic of Maxwellnanofluid over a stretched flat sheet with thermal radiation. Numer. Methods Partial. Differ. Equ. 2020, 1–21. [Google Scholar] [CrossRef]
- Alshare, A.; Al-Kouz, W.; Alkhalidi, A.; Kiwan, S.; Chamkha, A. Periodically fully developed nanofluid transport through a wavy module. J. Therm. Anal. Calorim. 2020, 1–13. [Google Scholar] [CrossRef]
- Xiong, Q.; Abohamzeh, E.; Ali, J.A.; Hamad, S.M.; Tlili, I.; Shafee, A.; Habibeh, H.; Nguyen, T.K. Influences of nanoparticles with various shapes on MHD flow inside wavy porous space in appearance of radiation. J. Mol. Liq. 2019, 292, 111386. [Google Scholar] [CrossRef]
- Radouane, F.; Abderrahmane, A.; Mebarek-Oudina, F.; Ahmed, W.; Rashad, A.M.; Sahnoun, M.; Ali, H.M. Magneto-Free Convectiveof Hybrid Nanofluid inside Non-Darcy Porous Enclosure Containing an Adiabatic Rotating Cylinder. Energy Sources Part A Recovery Util. Environ. Eff. 2020. [Google Scholar] [CrossRef]
- Marzougui, S.; Bouabid, M.; Mebarek-Oudina, F.; Abu-Hamdeh, N.; Magherbi, M.; Ramesh, K. A computational analysis of heat transport irreversibility phenomenon in a magnetized porous channel. Int. J. Numer. Methods Heat Fluid Flow 2020. ahead of print. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abdelhafez, M.A.; Mebarek-Oudina, F.; Bilal, S.M. MHD Cassonnanofluid flow over nonlinearly heated porous medium in presence of extending surface effect with suction/injection. Indian J. Phys. 2021, 1–15. [Google Scholar] [CrossRef]
- Swain, K.; Mebarek-Oudina, F.; Abo-Dahab, S.M. Influence of MWCNT/Fe3O4 hybrid nanoparticles on an exponentially porous shrinking sheet with chemical reaction and slip boundary conditions. J. Therm. Anal. Calorim. 2021, 1–10. [Google Scholar] [CrossRef]
- Fares, R.; Abderrahmane, A.; Meddeber, A.; Abdelkrim, A. Numerical investigation of hydrodynamic nanofluid convective flow in a porous enclosure. Nat. Technol. 2018, 18, 54–57. [Google Scholar]
- Fares, R.; Naim, H.; Abderrahmane, A.; Bouadi, A. Mixed Convection of Nanofluid Flow in a Vented Cavity Under The Influence Of Magnetic Field. J. Mater. Struct. 2020, 4, 1–11. [Google Scholar]
- Al-Kouz, W.; Saleem, K.B.; Chamkha, A. Numerical investigation of rarefied gaseous flows in an oblique wavy sided walls square cavity. Int. Commun. Heat Mass Transfer 2020, 116, 104719. [Google Scholar] [CrossRef]
- Hussien, A.A.; Abdullah, M.Z.; Yusop, N.M.; Al-Kouz, W.; Mahmoudi, E.; Mehrali, M. Heat transfer and entropy generation abilities of MWCNTs/GNPs hybrid nanofluids in microtubes. Entropy 2019, 21, 480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Kouz, W.G.; Kiwan, S.; Alkhalidi, A.; Sari, M.E.; Alshare, A. Numerical study of heat transfer enhancement for low-pressure flows in a square cavity with two fins attached to the hot wall using AL2O3-air nanofluid. Strojniški Vestnik J. Mech. Eng. 2018, 64, 26–36. [Google Scholar]
- Al-Kouz, W.; Al-Muhtady, A.; Owhaib, W.; Al-Dahidi, S.; Hader, M.; Abu-Alghanam, R. Entropy generation optimization for rarified nanofluid flows in a square cavity with two fins at the hot wall. Entropy 2019, 21, 103. [Google Scholar] [CrossRef] [Green Version]
- Hussien, A.A.; Al-Kouz, W.; Yusop, N.M.; Abdullah, M.Z.; Janvekar, A.A. A Brief Survey of Preparation and Heat Transfer Enhancement of Hybrid Nanofluids. Stroj. Vestn. J. Mech. Eng. 2019, 65, 441–453. [Google Scholar] [CrossRef] [Green Version]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2017. [Google Scholar]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Mehryan, S.A.; Kashkooli, F.M.; Ghalambaz, M.; Chamkha, A.J. Free convection of hybrid MgO-Ag water nanofluid in a differentially heated porous cavity. Adv. Powder Technol. 2017, 28, 2295–2305. [Google Scholar] [CrossRef]
- Woods, L.C. Thermodynamics of Fluid Systems; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Calcagni, B.; Marsili, F.; Paroncini, M. Natural convective heat transfer in square enclosures heated from below. Appl. Therm. Eng. 2005, 25, 2522–2531. [Google Scholar]
- Ghasemi, B.; Aminossadati, S.M.; Raisi, A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]






| Physical Properties | ||||||
|---|---|---|---|---|---|---|
| Water | 4179 | 0.613 | 997.1 | 21 | 5.5×10−6 | 1.47 ×10−7 |
| Ag | 235 | 429 | 10500 | 5.4 | 8.1× 10−4 | 147 ×10−3 |
| MgO | 879 | 30 | 3580 | 3.36 | 8 ×10−4 | 95.3 ×10−7 |
| Mesh size | 2988 | 4740 | 2442 | 29912 | 41728 |
| Nuavg | 7.2360 | 7.2876 | 7.4241 | 7.4959 | 7.4969 |
| 1.3074 | 1.3181 | 1.3244 | 1.3279 | 1.3306 |
| Ra | 103 | 104 | 105 | 106 |
|---|---|---|---|---|
| Present work | 1.1803 | 2.2745 | 4.8759 | 9.6335 |
| Ghassemi et al. | 1.17612 | 2.2679 | 4.8608 | 9.5918 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Libdeh, N.; Redouane, F.; Aissa, A.; Mebarek-Oudina, F.; Almuhtady, A.; Jamshed, W.; Al-Kouz, W. Hydrothermal and Entropy Investigation of Ag/MgO/H2O Hybrid Nanofluid Natural Convection in a Novel Shape of Porous Cavity. Appl. Sci. 2021, 11, 1722. https://doi.org/10.3390/app11041722
Abu-Libdeh N, Redouane F, Aissa A, Mebarek-Oudina F, Almuhtady A, Jamshed W, Al-Kouz W. Hydrothermal and Entropy Investigation of Ag/MgO/H2O Hybrid Nanofluid Natural Convection in a Novel Shape of Porous Cavity. Applied Sciences. 2021; 11(4):1722. https://doi.org/10.3390/app11041722
Chicago/Turabian StyleAbu-Libdeh, Nidal, Fares Redouane, Abderrahmane Aissa, Fateh Mebarek-Oudina, Ahmad Almuhtady, Wasim Jamshed, and Wael Al-Kouz. 2021. "Hydrothermal and Entropy Investigation of Ag/MgO/H2O Hybrid Nanofluid Natural Convection in a Novel Shape of Porous Cavity" Applied Sciences 11, no. 4: 1722. https://doi.org/10.3390/app11041722






