A New Switching Adaptive Fuzzy Controller with an Application to Vibration Control of a Vehicle Seat Suspension Subjected to Disturbances
Abstract
:1. Introduction
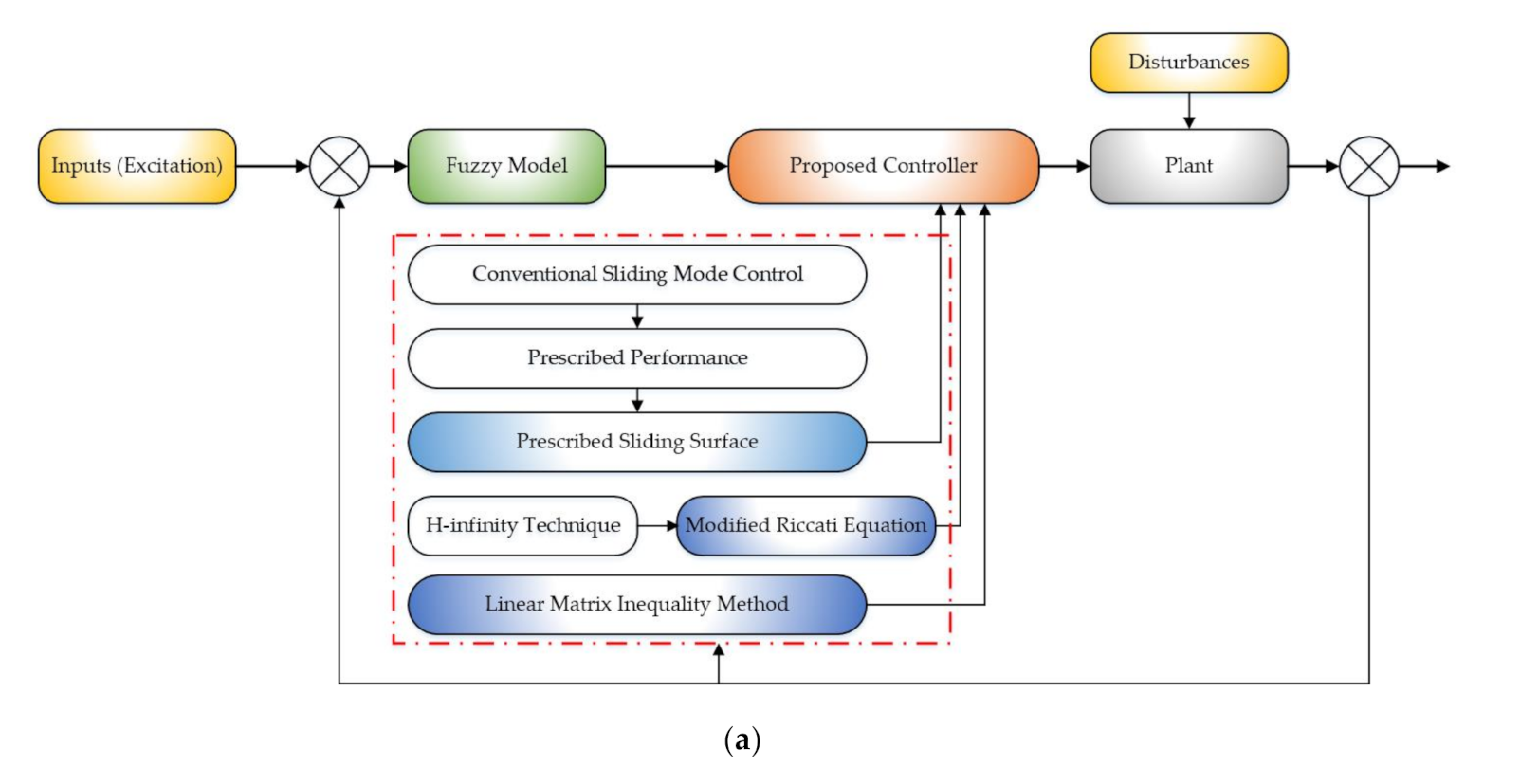
2. Design of a New Adaptive Fuzzy Controller
2.1. Robustness of Input Controls
2.2. Formulation of Control Strategy
2.2.1. Proposed Switching Control: High Disturbance Condition
2.2.2. Proposed Switching Control: Small Disturbance Condition
2.2.3. Switching Condition
3. Simulations for Control Performances
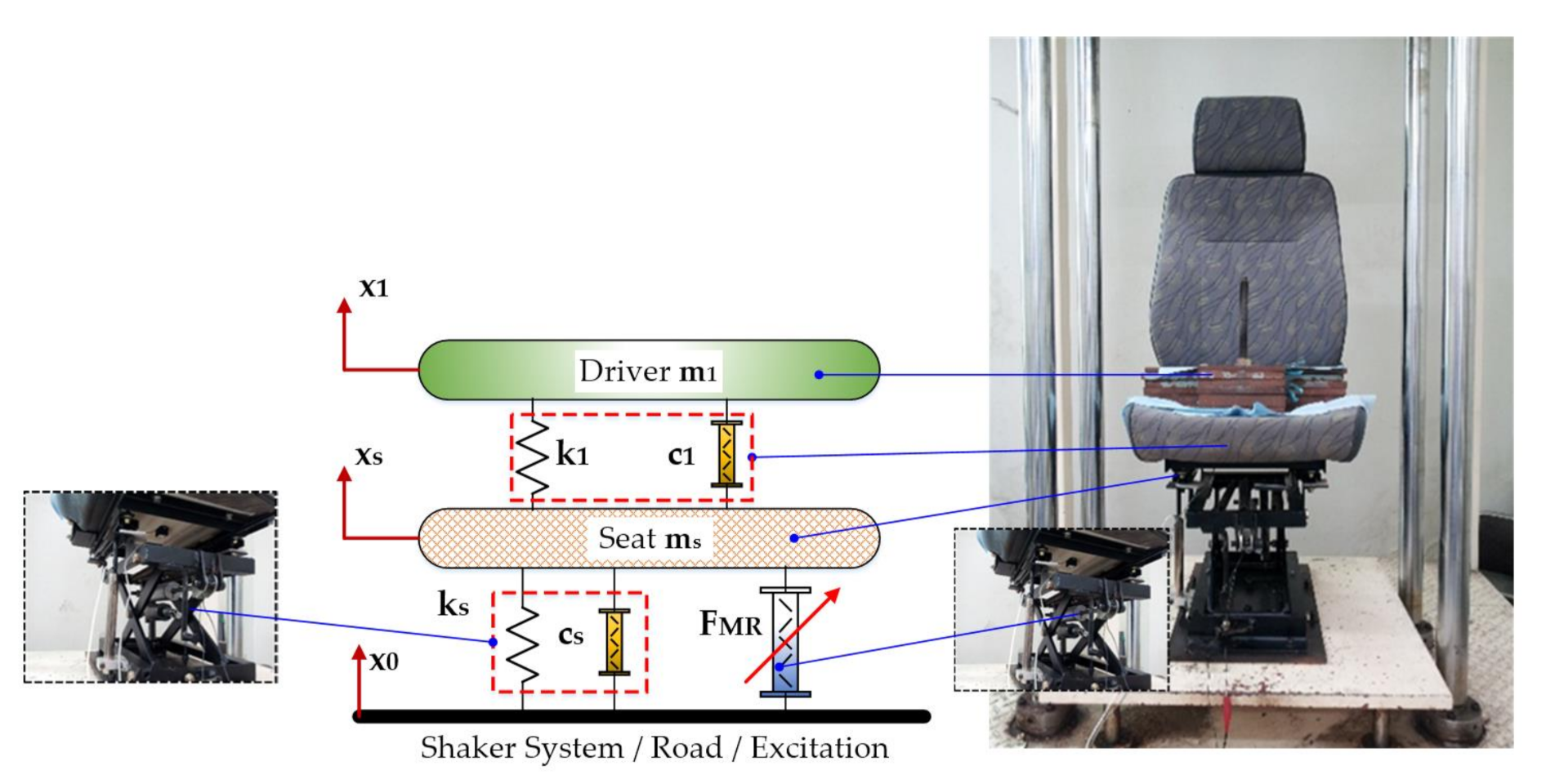
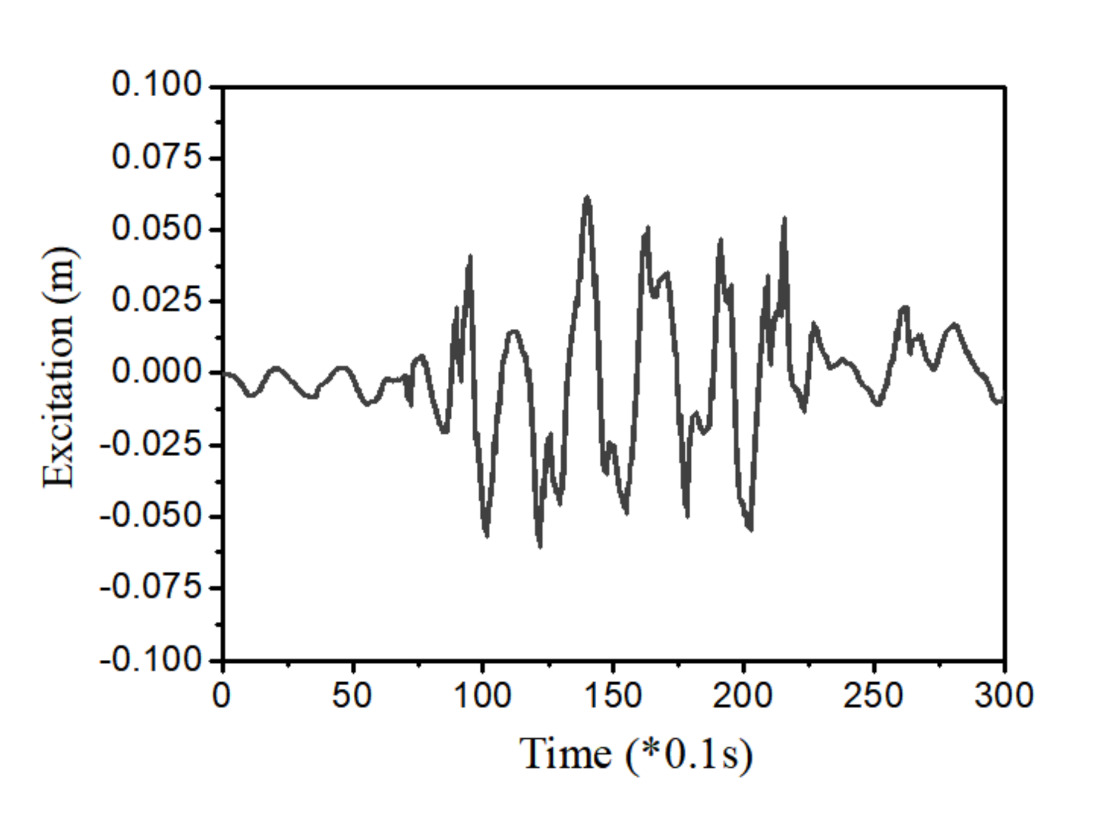
3.1. Dynamic Model and Parameters
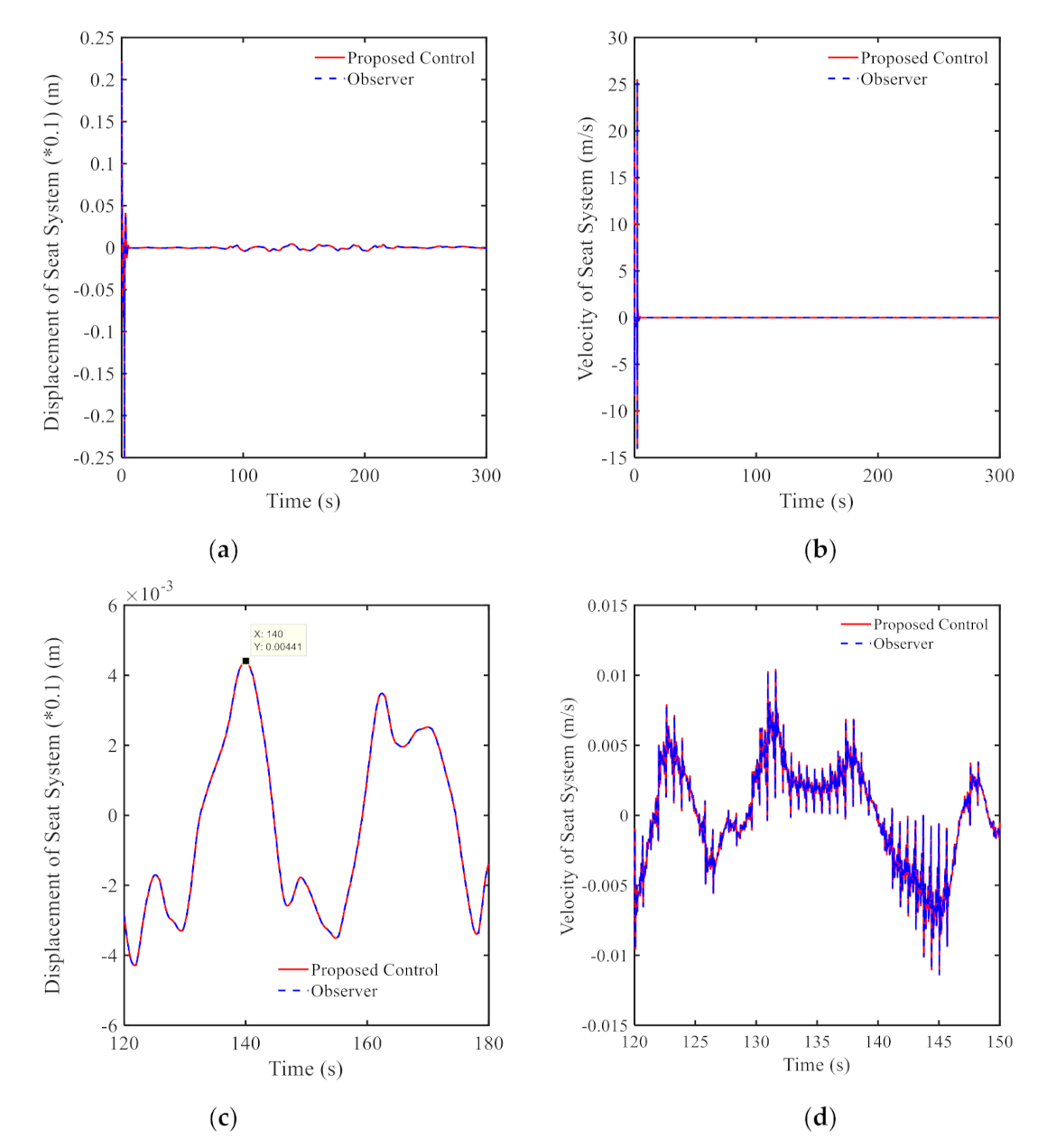
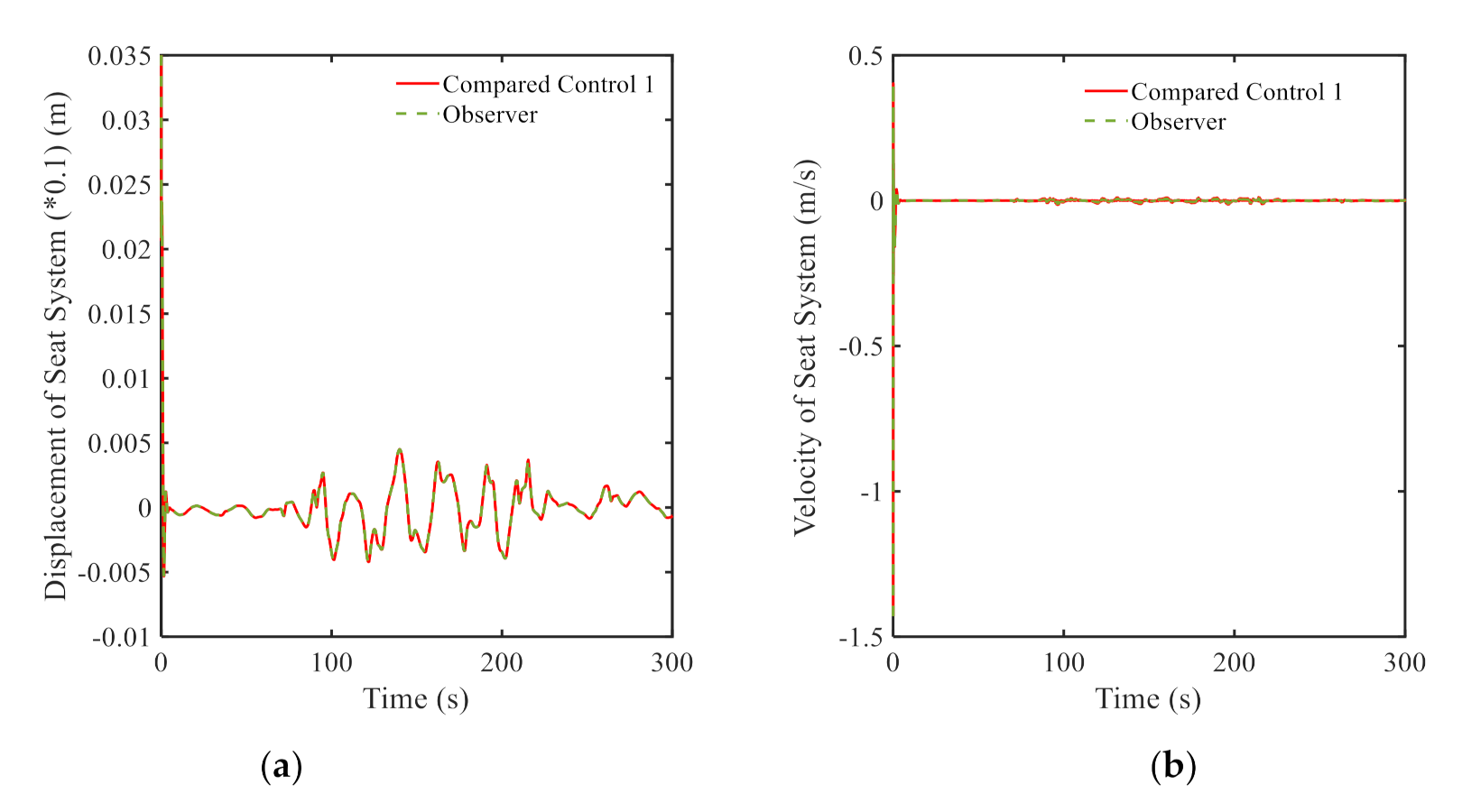
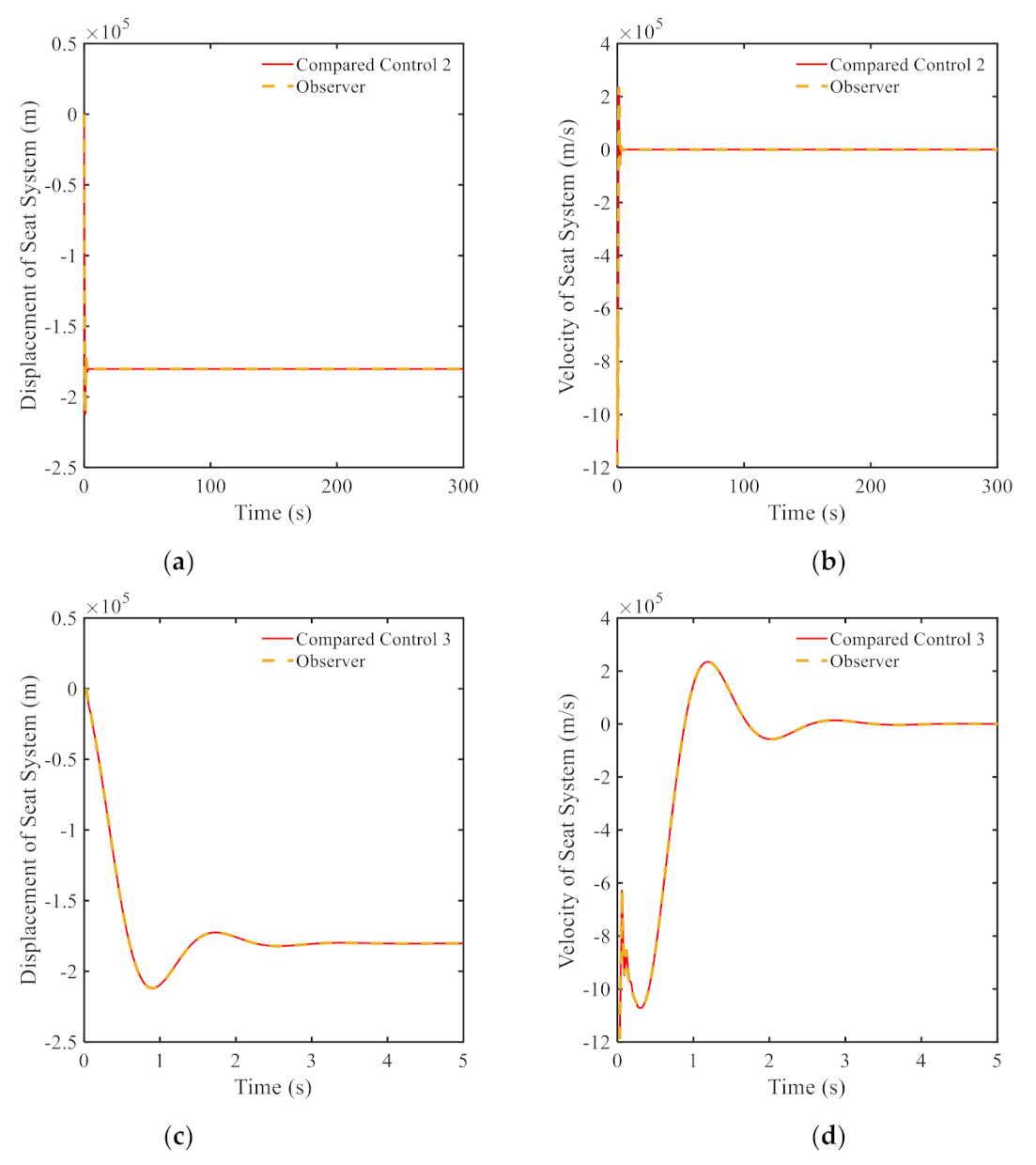
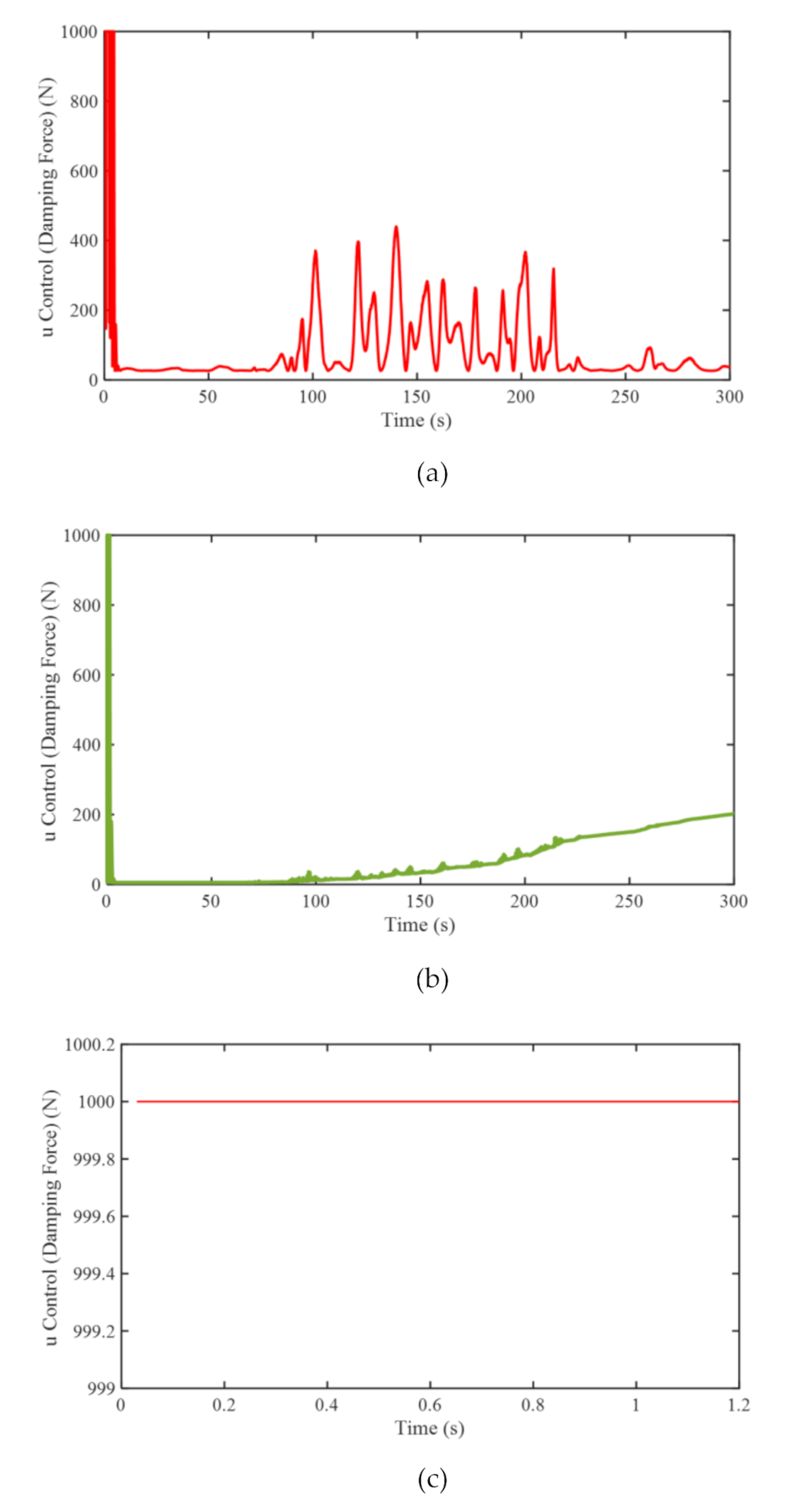
3.2. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, Y.; Yin, Y.; Zhang, S.; Dong, J.; Johansson, R. Composite adaptive control for bilateral teleoperation systems without persistency of excitation. J. Frankl. Inst. 2020, 357, 773–795. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wu, Y. Adaptive Fuzzy Tracking Control of Autonomous Underwater Vehicles with Output Constraints. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef]
- Sun, W.; Wu, Y.-Q.; Sun, Z.-Y. Command Filter-Based Finite-Time Adaptive Fuzzy Control for Uncertain Nonlinear Systems With Prescribed Performance. IEEE Trans. Fuzzy Syst. 2020, 28, 3161–3170. [Google Scholar] [CrossRef]
- Shi, W. Adaptive Fuzzy Output Feedback Control for Non-Affine MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S. Adaptive Fuzzy Integral Sliding Mode Control for Robust Fault Tolerant Control of Robot Manipulators with Disturbance Observer. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Lin, J.-W.; Su, S.-F.; Wang, N.; Er, M.J. Reduced Adaptive Fuzzy Decoupling Control for Lower Limb Exoskeleton. IEEE Trans. Cybern. 2021, 51, 1099–1109. [Google Scholar] [CrossRef] [PubMed]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Hybrid design of PID controller for four DoF lower limb exoskeleton. Appl. Math. Model. 2019, 72, 17–27. [Google Scholar] [CrossRef]
- Gaidhane, P.J.; Nigam, M.J.; Kumar, A.; Pradhan, P.M. Design of interval type-2 fuzzy precompensated PID controller applied to two-dof robotic manipulator with variable payload. ISA Trans. 2019, 89, 169–185. [Google Scholar] [CrossRef]
- Yu, W.; Rosen, J. Neural PID Control of Robot Manipulators with Application to an Upper Limb Exoskeleton. IEEE Trans. Cybern. 2013, 43, 673–684. [Google Scholar] [CrossRef]
- Sangpet, T.; Kuntanapreeda, S.; Schmidt, R. An adaptive PID-like controller for vibration suppression of piezo-actuated flexible beams. J. Vib. Control. 2017, 24, 2656–2670. [Google Scholar] [CrossRef]
- Shojaei, K. Neural adaptive PID formation control of car-like mobile robots without velocity measurements. Adv. Robot. 2017, 31, 947–964. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C. PID control for global finite-time regulation of robotic manipulators. Int. J. Syst. Sci. 2016, 48, 547–558. [Google Scholar] [CrossRef]
- Van, M.; Do, X.P.; Mavrovouniotis, M. Self-tuning fuzzy PID-nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators. ISA Trans. 2020, 96, 60–68. [Google Scholar] [CrossRef]
- Raaja, G.S.; Vinodh, K.E.; Selvakumar, K.; Vamsi, K.C. Uniform ultimate bounded robust model reference adaptive PID control scheme for visual servoing. J. Frankl. Inst. 2017, 354, 1741–1758. [Google Scholar]
- Phu, D.X.; An, J.-H.; Choi, S.-B. A Novel Adaptive PID Controller with Application to Vibration Control of a Semi-Active Vehicle Seat Suspension. Appl. Sci. 2017, 7, 1055. [Google Scholar] [CrossRef]
- Phu, D.X.; Huy, T.D.; Mien, V.; Choi, S.-B. A new composite adaptive controller featuring the neural network and prescribed sliding surface with application to vibration control. Mech. Syst. Signal Process. 2018, 107, 409–428. [Google Scholar] [CrossRef]
- Do, X.P.; Nguyen, Q.H.; Choi, S.-B. New hybrid optimal controller applied to a vibration control system subjected to severe disturbances. Mech. Syst. Signal Process. 2019, 124, 408–423. [Google Scholar] [CrossRef]
- Phu, D.X.; Choi, S.-M.; Choi, S.-B. A new adaptive hybrid controller for vibration control of a vehicle seat suspension featuring MR damper. J. Vib. Control. 2016, 23, 3392–3413. [Google Scholar] [CrossRef]
- Ciccarella, G.; Mora, M.D.; Germani, A. A Luenberger-like observer for nonlinear systems. Int. J. Control. 1993, 57, 537–556. [Google Scholar] [CrossRef]
- Jiao, T.; Zheng, W.X.; Xu, S. On stability of a class of switched nonlinear systems subject to random disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 2278–2289. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Sadati, N.; Zamani, I. H∞ disturbance attenuation of fuzzy large scale system. In Proceedings of the IEEE International Conference on Fuzzy Systems 2011, Taipei, Taiwan, 27–30 June 2011. [Google Scholar]
- Aguiar, C.; Leite, D.; Pereira, D.; Andonovski, G.; Škrjanc, I. Nonlinear modeling and robust LMI fuzzy control of overhead crane systems. J. Frankl. Inst. 2021, 358, 1376–1402. [Google Scholar] [CrossRef]
- Do, X.P.; Seung, B.C. A new adaptive fuzzy PID controller based on Riccati-like equation with application to vibration control of vehicle seat suspension. Appl. Sci. 2019, 9, 4540. [Google Scholar]
- Zimenko, K.; Polyakov, A.; Efimov, D.; Perruquetti, W. Robust Feedback Stabilization of Linear MIMO Systems Using Generalized Homogenization. IEEE Trans. Autom. Control. 2020, 65, 5429–5436. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Initial value of prescribed performance | 0.5 |
| Infinity value of prescribed performance | 0.001 |
| Exponential value of prescribed performance | 0.00047 |
| Maximum damping force | 1000 N |
| Parameters of sliding surface | |
| Constant of prescribed surface | 5000 |
| Riccati’s parameter | 10 |
| Riccati’s matrix | |
| Observer matrix | |
| Observer matrix | |
| Constants of adaptation laws | 10 |
| Initial state for proposed control | |
| Initial state for observer | |
| Robustness parameter | 0.00001 |
| Robustness parameter | 1 |
| Robustness parameter | 1 |
| Robustness parameter | 0.5 |
| Disturbance matrix | |
| Robustness matrix | |
| Constant of switching condition | 0.001 m |
| Constant of switching condition | 0.8 |
| Acceleration maximum value | 0.01 m/s2 |
| Parameter | Value |
|---|---|
| Parameters of sliding surface | |
| Constant of PID | 10 |
| Constant of PID | 150 |
| Constant of PID | 50 |
| Maximum damping force | 1000 N |
| Riccati’s parameter | 0.01 |
| Riccati’s matrix | |
| Observer matrix | |
| Observer matrix | |
| Constants of adaptation laws | 700 |
| Initial state for proposed control | |
| Initial state for observer |
| Parameter | Value |
|---|---|
| Maximum damping force | 1000 N |
| Observer matrix | |
| Observer matrix | |
| Robustness parameter | 0.00001 |
| Robustness parameter | 1 |
| Robustness parameter | 1 |
| Robustness parameter | 0.1 |
| Robustness vector | |
| Robustness matrix | |
| Robustness matrix | |
| Initial state for control | |
| Initial state for observer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phu, D.X.; Mien, V.; Choi, S.-B. A New Switching Adaptive Fuzzy Controller with an Application to Vibration Control of a Vehicle Seat Suspension Subjected to Disturbances. Appl. Sci. 2021, 11, 2244. https://doi.org/10.3390/app11052244
Phu DX, Mien V, Choi S-B. A New Switching Adaptive Fuzzy Controller with an Application to Vibration Control of a Vehicle Seat Suspension Subjected to Disturbances. Applied Sciences. 2021; 11(5):2244. https://doi.org/10.3390/app11052244
Chicago/Turabian StylePhu, Do Xuan, Van Mien, and Seung-Bok Choi. 2021. "A New Switching Adaptive Fuzzy Controller with an Application to Vibration Control of a Vehicle Seat Suspension Subjected to Disturbances" Applied Sciences 11, no. 5: 2244. https://doi.org/10.3390/app11052244
APA StylePhu, D. X., Mien, V., & Choi, S. -B. (2021). A New Switching Adaptive Fuzzy Controller with an Application to Vibration Control of a Vehicle Seat Suspension Subjected to Disturbances. Applied Sciences, 11(5), 2244. https://doi.org/10.3390/app11052244







