1. Introduction
The assessment of the condition of existing bridges and their appropriate and optimal maintenance plan is certainly an issue that will take priority over the design of new transport infrastructure in the near future. To be more precise, the construction of much of today’s European transport infrastructure began in the 1960s and more and more European bridges are approaching their planned lifetime [
1,
2]. This hot topic is further accentuated by exceptional events and the increasing failure of bridges in recent years, which, in addition to material damage [
3,
4], also has tragic consequences.
It is also worth mentioning that these structures are often located in areas of extreme seismicity. The current design approach for new structures implies that it is uneconomic to design structures that provide a fully elastic response to the design value of seismic actions. An alternative is the widely accepted structural design approach for smaller seismic design loads, while at the same time detailing them according to the rules of ductile behavior so that they can withstand significant seismic loads due to inelastic deformation. There are many existing bridges that were designed according to now outdated norms which did not contain guidelines for the design of elements for ductile behavior. Some even older bridges do not even take earthquake loads into account. The degree of ductility of these bridges is unknown. Therefore, the question of the correct seismic assessment of bridges is still open for research.
Several previous studies [
5,
6,
7,
8,
9] indicate that structures that are not designed and detailed for seismic actions may still have some degree of seismic resistance. The loss of bond strength between concrete and smooth reinforcement, but also the better ductility of such reinforcement allows for greater deformability of the elements. In general, previous research on structural elements has focused on elements typical of high-rise buildings (beams, columns), which are produced with ribbed reinforcement [
10,
11,
12,
13,
14] while a smaller number of studies evaluate the seismic resistance of bridges, especially girders [
15,
16,
17] and arches [
18,
19,
20,
21]. By analyzing the main parameters of the seismic resistance indicators [
22,
23,
24], selecting a suitable evaluation method [
25], and using the currently available guidelines for the evaluation of structures [
26] and recent research in this field [
10,
11,
12,
13,
14], it is possible to determine seismic resistance reserves of bridges that have not been previously designed and detailed for such actions.
Nonlinear methods are mainly used to assess the seismic load-bearing capacity of existing bridges [
25,
26,
27]. The application of such methods requires the knowledge of the actual behavior of the structure, either the actual rotational capacity of the elements under static load, if non-linear static analyses are used, or under cyclic load, if non-linear dynamic analyses are used.
The ductility of reinforced concrete elements in the cracked state is estimated based on of the effective stiffness when the yield strength is reached. A review of the literature shows two approaches in defining effective stiffness [
11]. First approach is the theoretical effective stiffness obtained from the relationship between the bending moment M
y and the chord rotation θ
y when the yield point is reached. This approach is more suitable for assessing the state of existing structures. The second approach is empirical formulation which is more suitable for designing new structures. The chord rotation at the yield point depends on the sum of the rotations of all cross-sections along the height of the element. The rotation of the end section is dominant. The end section of columns fixed to the foundation, arch, or superstructure is the key component in assessing the seismic resistance of bridges.
The ratio of moment and cross-section rotation is the basis for deriving the value of the cross-section rotation parameter φ
y when the yield point is reached. Several expressions [
14,
28,
29] can be found in the literature to calculate the approximate value of cross-sectional rotation during yielding. These expressions can be used to estimate the value of rotation when the yield point is reached for rectangular and circular sections. In bridge structures, we often use cross-sections of columns that differ from these two typical shapes, i.e., cross-sections for which a detailed M/φ analysis is required to obtain information about their rotational capacity.
Accurate data input (shape and dimensions of the cross-section, arrangement, and quantity of longitudinal and transverse reinforcement) and the properties of the materials used (stress and strain ratio) are crucial to obtain the most accurate ratio of moment to rotation of the cross-section. This refers primarily to the ratio between stress and strain, which should be considered as close as possible to the actual behavior of the material (non-linear diagrams). The accurate determination of the bending moment to rotation diagram of reinforced concrete sections is a reliable indicator of the bearing capacity of elements under seismic loads [
30,
31].
In simplified calculations of reinforced concrete elements, the connection between the reinforcement and the concrete is considered completely fixed. This assumption can be applied in areas where very low stresses occur between concrete and reinforcement. In areas with high shear stresses, such as in sections around cracks, relative deformations between concrete and reinforcement occur. For this reason, the slip effect must be used as a parameter when analyzing the behavior of the structural element [
32].
The low bond strength between reinforcement and concrete directly affects three main deformation mechanisms: Bending, shear, and end section rotation. The results of experimental research show an average 35% higher deformation capacity of elements made with smooth reinforcement compared to elements made with ribbed reinforcement [
7]. While the deformability of elements with smooth reinforcement is increased due to their better ductility properties, it simultaneously decreases due to the nonseismic detailing of such elements. Unconfined concrete has significantly lover properties in the region of plastic hinges than confined concrete. Tests have shown that the level of the rotational capacity is significantly affected by the amount of axial force applied and that the deformability of the elements decreases almost linearly under the influence of such a force [
33]. An insufficient number of tests on elements with such properties suggests caution in assessing their deformability.
In addition to rectangular, square, and circular cross-sections, which are all typical for columns in buildings, bridge columns often have cross-sections whose seismic resistance indicators cannot be analyzed using the previously mentioned expressions developed by individual researchers.
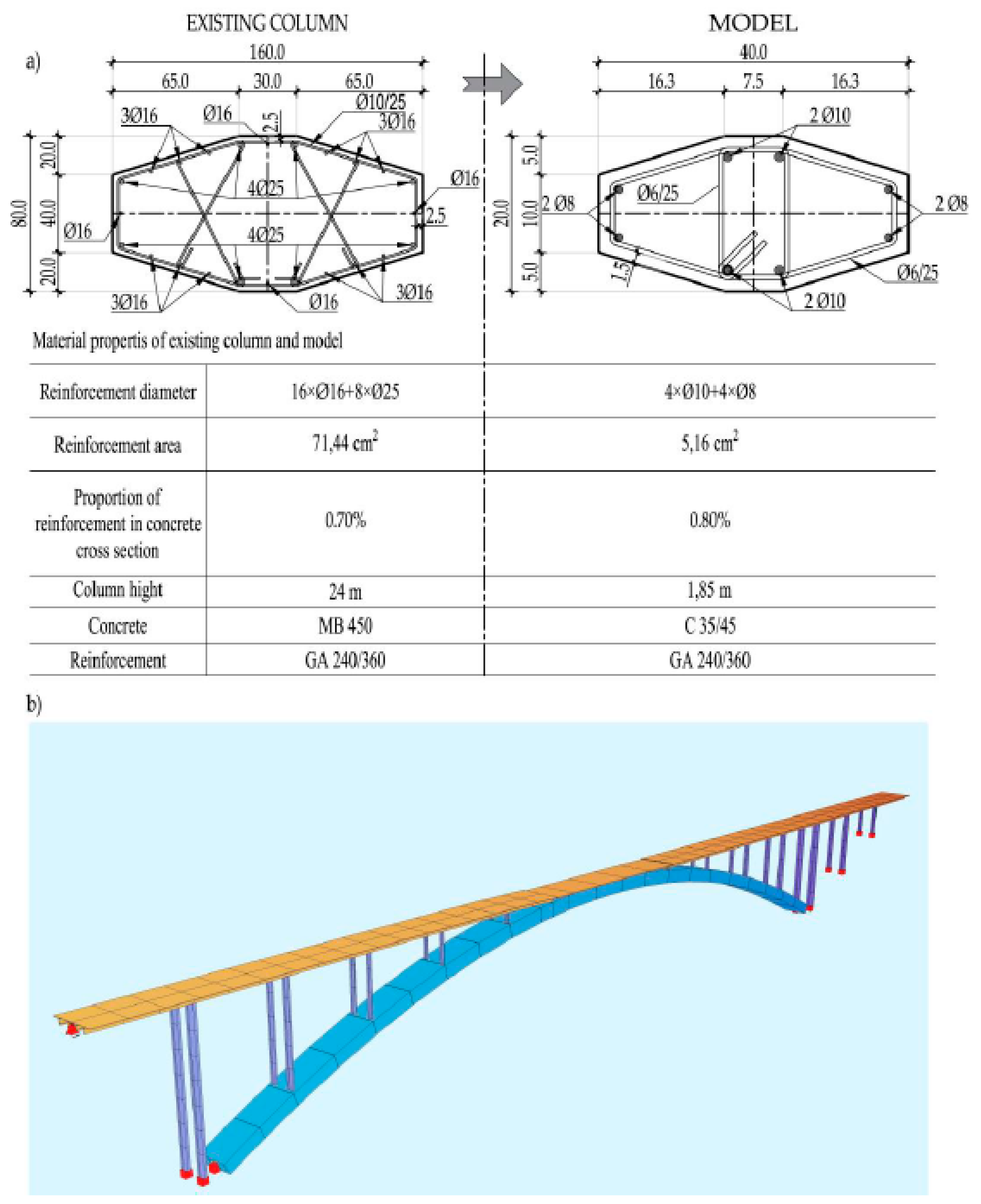
The purpose of the research presented in this paper is to define the seismic resistance indicators of the columns of the existing bridge, which have an atypical cross-section with smooth reinforcement and without seismic details. The experimental part of this research extends the current base of the tested column thus providing the improvement and development of the standards for the seismic assessment of structures.
3. Numerical and Analytical Analysis
In order to compare the experimentally obtained results, a numerical and analytical analysis of the ratio of moment and rotation of the end section was carried out. To obtain the best possible comparison, the properties of the material obtained experimentally on the samples taken during the erection of the columns were used.
The numerical analysis was performed with a commercial software professionally used for bridge structures using FEM. A non-linear numerical analysis was used, which included material and geometric non-linearity. The material properties were taken as material working law diagrams (stress/deformation ratio) for concrete (Equation (2)) and for reinforcement (Equations (3)–(5)). These expressions resulted in a good match of the constitutive laws with the experimentally obtained ones. The quantities and the position of the reinforcement in each cross-section of the column were taken in the same way as in the experimentally tested specimens. Numerical column models comprise cantilever 3D beam finite elements (mesh size 2 cm) with 6 degrees of freedom which are fixed for all translations and rotations at the point corresponding to the connection of the column and the anchor block. The beam axis was assigned the column cross-section in its center of gravity. Model of the column was then loaded horizontally in steps corresponding to those performed in the experimental tests. The load increase was carried out until the load-bearing capacity of the element was reached. The vertical axial load was entered immediately at the beginning of the calculation and remained unchanged until the end of the calculation. The amount of the axial load changes for different columns (
Table 1). Due to the properties of the software package used, it was possible to perform the calculation until the maximum concrete stress value and the corresponding relative deformation was reached. Then the ratio of moment and rotation of the final cross-section was observed. Points of interest, such as the yield strength, are marked to compare the results. Only the monotonic load was applied in the numerical analysis and the results obtained were processed for comparison with experimental and analytical results.
The analytically obtained ratio of moment and rotation of the end section is presented. This ratio is described by three characteristic points in the curve, which represent the cross-sectional state due to the load increase. The first domain is up to the point where the first crack occurs, followed by the domain until the yield strength of the reinforcement is reached (or concrete compressive failure), and finally the domain until the load bearing capacity of the cross-section is reached (concrete tensile strength or compression zone failure). The domain between the characteristic points was achieved by gradually increasing the load. Non-linear material properties were used. The non-linear stress-strain ratio specified in [
46] was used for concrete, while the ratio specified in [
47] was used for reinforcement.
where
σc and
εc are compressive stress and strain respectively. The coefficients
η and
k are given in [
32].
In Equations (3)–(5), εs and fs are the reinforcement steel strain and stress, Es is the elasticity module, fu and εsu are the stress and strain at the ultimate stress, fy and εy are the stress and strain at the yielding.
As the cross-section was not seismically designed, the influence of the concrete reinforcement confinement was not considered, i.e., the stress–strain ratio of unconfined concrete was used. The method itself includes the analysis of the equilibrium of internal and external forces acting on the cross-section. The internal forces resulted from the tension and compression part of the concrete cross-section and the force in the tension and compression reinforcement, while the external forces were the axial compression force and the bending moment. The irregular shape of the cross-section was divided into a sufficient number of strips with the corresponding values of stresses and strains, which were then integrated into the resultant of the compression and tension zone of the concrete. The analytically obtained ratio agreed well with the numerically obtained results, as shown in chapter 4.4. Due to the large number of parameters that have different influences on the cross-sectional behavior, the analysis of the influence of each parameter on the ratio of moment and cross-section rotation helped in understanding the results of the experimental analysis. The method of analysis used is presented in [
48].
4. Experimental Results and Discussion
The results of the monotonically and cyclically tested specimens are given below. The results are presented in the form of the ratio of moment and rotation of the cross-section at several points in the area of the plastic joint (
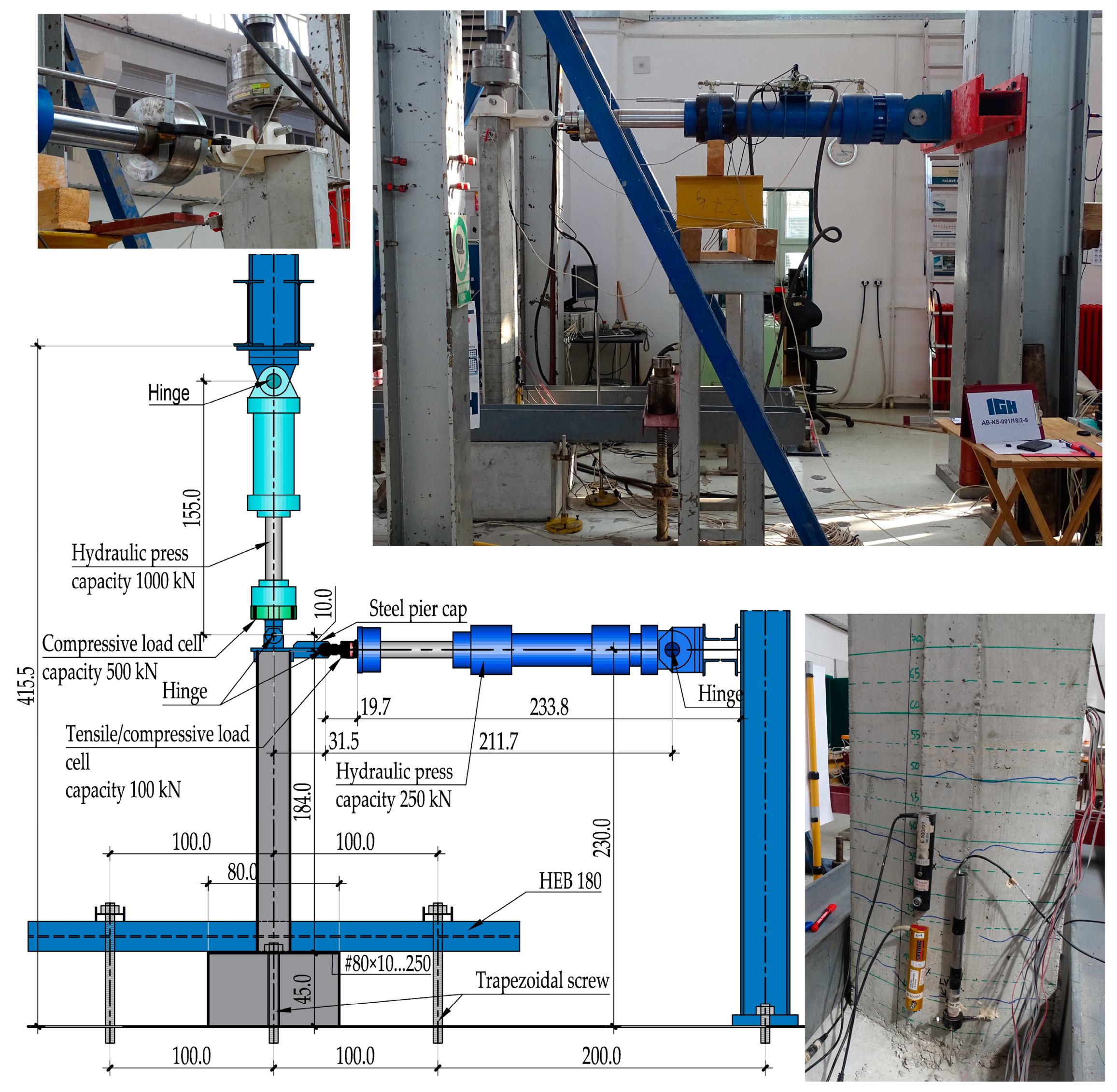
Figure 9 and Figure 13). The width and distribution of the cracks along the height of the element is shown in Figure 11. The rotation of the cross-section was measured at three points along the height of the element, starting at the bottom of the column. The first point is located directly at the connection of column and anchor block, the second point is located at a height of 150 mm from the bottom of the column, while the third point is 350 mm from the bottom of the column.
Knowing the level of the horizontal and vertical force and the displacement and rotation of the top of the column, the bending moment in each section was determined. The bending moment of a single section includes the influence of the horizontal force component, the influence of the vertical force due to the rotation of the vertical press, and the influence of the vertical force due to the displacement of the column top (P-Δ effect).
There are many parameters that influence the result of the relationship between bending moment and section rotation. The interaction of the individual parameters makes it difficult to define the degree of influence of each parameter on the indicators of seismic resistance of the element. Therefore, in the next chapter separate results for monotonically and cyclically loaded specimens are presented and commented on in detail in order to draw final conclusions.
4.1. Monotonously Tested Specimens
In total, seven column specimens were tested with a monotonic load. The specimens AB-NS-001-1, AB-NS-001-2, AB-NS-001-5 and AB-NS-001-6 are made with smooth reinforcement and have the same cross-sectional properties (same amount of reinforcement-central reinforcement 4 × Ø10 and corner reinforcement 4 × Ø8). The first two specimens were loaded with a force of 100 kN, while the other two specimens were loaded with a force of 150 kN. The specimens AB -NS-002-1 and AB -NS-003-1 were loaded with the same force of 125 kN, but had different diameters of the longitudinal reinforcement bars. The central cross-sectional reinforcement (4 × Ø12) is the same for both specimens. The corner reinforcement is different, it is 4 × Ø10 in the first specimen, while it is 4 × Ø8 in the second specimen. The last monotonically tested specimen with the designation AB-NS-004-1 was produced with ribbed reinforcement, 4Ø10 as central reinforcement and 4Ø8 as corner reinforcement. This specimen was loaded with an axial force of 100 kN. The geometrical properties and the type of longitudinal reinforcement of each column are given in
Table 1, while the mechanical properties of each type of reinforcement are shown in
Table 3.
For monotonically tested specimens, the analyzed results of the moment and the rotation ratio showed a clear correlation. The main characteristic of all tested specimens is a high ductility due to the plastic deformation of the smooth reinforcement around the plastic joint resulting in a large displacement at the top of the column. The behavior of the column in three characteristic cross-sections of the monotonically tested column specimens is shown as the M/φ relationship in
Figure 9.
Experimentally obtained curves show three characteristic domains of the ratio of moment and rotation of the cross-section: the domain until the occurrence of the first crack (the initial part of the diagram where the curve of the ratio of moment and rotation for all samples coincides), the linear elastic domain until the occurrence of the cross-section yield (the part of the diagram from the beginning of the separation of the curves up to the beginning of the horizontal part of each curve) and the plastic domain up to the limit state of the bearing capacity of the cross-section (the horizontal part of the diagram).
After the first crack has appeared, there is a significant separation of results for each sample. The reasons for this are differences in cross-section properties, material properties, and changes in axial force.
When the yield strength of the reinforcement is reached, we move to the third domain of the diagram, which shows a small slope of the curve tangent for all monotonically examined samples. This relationship between moment and cross-section rotation is then continued until the specimen fails.
From the ratio of moment and cross-section rotation it is clear that in the end cross-section and cross-section at a height of 150 mm there is a yield area, whereas in a cross-section at a height of 350 mm the yield area only occurred in two tested specimens (in one specimen AB-NS-004-1 with ribbed reinforcement and in one specimen AB-NS-001-2, which showed a different crack pattern). All tested specimens manufactured with smooth reinforcement have a pronounced plastic area that is five times or more larger than the elastic area. The influence of the axial force on the bearing capacity is also visible, as well as the influence on the rotation of the cross-section around the plastic joint. A higher axial force leads to a higher bending resistance of the cross-section, but also to a slightly lower rotation of the cross-section when reaching the final limit state. This can be seen from a comparison of monotonically tested columns loaded with an axial force of 100 kN (AB-NS-001-1) and columns loaded with a force of 150 kN (AB-NS-001-5). These specimens have the same cross-sectional properties but different axial force levels.
Besides the influence of the axial force, the influence of the amount of the longitudinal reinforcement is also clearly visible. The samples AB-NS-002-1 and AB-NS-003-1 were produced with different diameters in the corners of the column (AB-NS-002-1: 4 × Φ10, AB-NS-003-1: 4 × Φ8), whereby a larger amount of reinforcement is expected to increase the load-bearing capacity of the column. These two specimens were tested with the same axial force (125 kN) and were erected in the same series so that their concrete properties are the same. It should be noted that in addition to the amount of horizontal force and the amount of reinforcement (diameter), there are also differences in the mechanical properties of the installed reinforcement.
In order to compare the influence of the different types of reinforcement, the results of the experimental testing of three specimens, which were carried out with the same amount of reinforcement, are compared. Specimens AB-NS-001-1 and AB-NS-001-2 were made with smooth reinforcement, while specimen AB-NS-004-1 was made with ribbed reinforcement. The same axial force (100 kN) was applied to all three specimens by experimental testing. When examining the moment to rotation ratio of the end cross-section, we can see that the specimen made with ribbed reinforcement can reach a limit moment almost 40% higher than the specimen with smooth reinforcement with the same properties. The same can be concluded by observing the other two cross-sections in which the relative deformations have been measured, thus determining the ratio of moment and rotation of the cross-section. From this it can be concluded that the specimen made with ribbed reinforcement has a higher load bearing capacity than the specimens made with smooth reinforcement. It should be emphasized that by testing the compressive strength of the concrete on cubes of specimens made with ribbed reinforcement, the mean compressive strength was determined to be 36.2 MPa, while the same was determined for specimens with smooth reinforcement at 47.3 MPa. From this it can be concluded that the load-bearing capacity of the specimen would have been even higher if it had been made from the concrete with the same properties as those of the two specimens made with smooth reinforcement. If we compare the end cross-sectional rotations of these specimens, we can see that a specimen made with ribbed reinforcement has a significantly lower value of cross-sectional rotation on failure than specimens made with smooth reinforcement with the same geometrical properties and the same level of applied axial force. However, if we look at the rotation of other measured cross-sections along the height of the ribbed reinforced specimen, we can see that a slightly higher value of rotation was measured at failure than for smooth reinforced specimens. From this we can conclude that the cross-sectional rotation is more evenly distributed over the height of the member in the ribbed reinforcement specimen than in the specimens made with smooth reinforcement where the dominant rotation occurs in the end cross-section and in the cross-section where the first crack occurs.
Most of the monotonically examined specimens made with smooth reinforcement do not show a clear boundary between the areas in the diagram. If one considers bending moment and section rotation ratio for all tested specimens, it is not possible to determine the beginning of the reinforcement yield clearly. The reason for this is the loss of bond strength between the concrete and the reinforcement, which significantly influences the cross-sectional rotation. The gradual reduction in the stiffness of the element makes it difficult to detect the appearance of the first crack. For specimens with ribbed reinforcement, these limits are somewhat more pronounced.
The effect of gradual loss of bond strength and its influence on stiffness is visible in a constant change of the tangent slope almost from the beginning of load introduction (the ratio M-φ does not show a constant tangent slope until the first crack). This is particularly evident in the diagram of the ratio M/φ of the end section. In the two other observed cross-sections, the characteristic points in the diagram are more clearly visible (sudden jumps in the slope of the tangent of the diagram). The tested column specimen AB-NS-001-6 shows a sudden loss of stiffness immediately at the beginning of the test, followed by a strong increase in stiffness with the ratio M/φ almost vertical. This is considered to be caused by a slippage between concrete and reinforcement at the beginning of the test due to a larger unanchored part of the bar as a result of the column erection method, which then causes a decrease in stiffness. As the process progresses, the effects of slipping become less pronounced and lead to a significant increase in stiffness.
4.2. Specimens Cracking
The pattern of crack development of all monotonically tested specimens made with smooth reinforcement is characterized by the occurrence of two dominant cracks. The first crack is a crack of the previously mentioned end cross-section. The second crack occurs in most specimens near the first stirrup (125 mm from the bottom of the column).
A monotonically tested specimens showed a crack at a height of 200 mm, which differs significantly from all other specimens (the ratio of moment and cross-sectional rotation of this specimen also showed differences compared to other tested specimens). These two cracks at the bottom of the column have a constant change in width as the displacement of the top of the column increases and have a significant effect on the amount of element rotation around the plastic joint. Other cracks along the height of the column do not show significant width growth during the test (in some cases it even decreases). The crack width measurements of each specimen are shown in
Figure 10. The results given apply to monotonic (designation M) and cyclic (designation C) specimens.
The cracks shown are located on the plastic joint itself, but also in the immediate vicinity. The crack designations contain the distance of the observed crack from the bottom of the column. The figure shows the dominance of the crack at the end cross-section and the smaller but still significant influence of the first crack from the bottom of the column of all monotonically tested specimens. For monotonically tested specimens (AB-NS-004-1) made with ribbed reinforcement, the crack width at the end section is almost half of the crack width of specimens made with smooth reinforcement. The crack in the end cross-section is also significantly less pronounced compared to the first crack from the bottom of the column. The occurrence of cracks in the sample with ribbed reinforcement was observed up to a height of 1.2 m from the bottom of the column, whereas in the samples with smooth reinforcement the height of the crack reached only 0.65 m. In total, two specimens made with a larger amount of longitudinal reinforcement (AB-NS-002-1 and AB-NS-003-1) also show a smaller crack width in the end section and thus a lower dominance of the crack in relation to the adjacent crack. It should be noted that a larger amount of reinforcement was achieved by increasing the reinforcement diameter, while the position and distribution of the reinforcement over the cross-section remained almost the same (the only difference is the position of the center of gravity due to a larger bar diameter).
Figure 11 shows the width and distribution of cracks at the location of the plastic joint and in its vicinity for cyclically tested specimens. For almost all cyclically tested specimens, the dominance of the crack is visible at the end cross-section. In contrast to the monotonous tests, these tests show that the second crack from the bottom of the column is significantly less dominant and does not deviate much from the other cracks above. According to the measured crack sizes at the location of the plastic joint and in its immediate vicinity, the specimens with ribbed reinforcement behave in the same way as specimens with smooth reinforcement. The difference is only visible in the height at which cracks occur. In the case of the cyclically tested specimen with ribbed reinforcement, cracks appear up to a height of 1 m, whereas in the case of specimens with smooth reinforcement the crack height is the same as in the monotonously tested specimens and is about 0.65 m.
4.3. Cyclically Tested Specimens
Cyclic load tests were carried out on eight column specimens.
Figure 12 shows the hysteresis loop for one test column obtained through the ratio of the transverse load and the displacement of the column upper end. A gradual increase in the area of the hysteresis loop with an increase in the displacement cycle is visible, which results in greater energy dissipation. The low bond strength between reinforcement and concrete affects pinching effect. The gradual reduction in stiffness in each cycle is favorable in term of the seismic resistance of the columns. For cyclically tested specimens, the results were prepared in such a way that envelope curves were derived from the hysteresis curves, which connect the extreme values of the curves and thus define the relationship between moment and cross-sectional rotation, which can be analyzed further.
As with monotonically loaded specimens, the diagram of the ratio of moment to rotation obtained here can be divided into three characteristic areas. In the second area, the results for each specimen differ due to the geometrical and material properties of the individual specimen and the amount of axial load.
Figure 13 shows the behavior of a single column specimen in three characteristic cross-sections around the plastic joint area. Their analysis shows the influence of each parameter on the load bearing capacity and deformability of the column.
The specimens AB-NS-001-3, AB-NS-001-4, AB-NS-001-7, AB-NS-001-8, and AB-NS-001-9 are made with smooth reinforcement and have the same cross-sectional properties. The longitudinal reinforcement in the central part of the cross-section is 4 × Ø10, while the reinforcement in the corners is 4 × Ø8. The differences are only in the applied axial load and the concrete properties, as they are not all from the same series. The first two specimens were loaded with an axial force of 100 kN, the other two with a force of 150 kN, while the last specimen was loaded with a force of 125 kN. For the first two specimens, the mean compressive strength of the concrete tested on cubes was 47.5 MPa, while the other three specimens were loaded with 36.0 MPa. The specimens AB-NS-002-2 and AB-NS-003-2 were loaded with the same axial force of 125 kN, but their geometrical and material properties of the cross-sections are different, as they are made with smooth reinforcement. As with the monotonically tested specimens of the same series, the differences are in the amount of the reinforcement. The longitudinal reinforcement in the middle of the cross-section is Ø12 mm. In the first specimen, the corner bars are Ø10 mm, in the second specimen these bars are Ø8 mm. The concrete compressive strength test showed a small difference in the average compressive strength for both specimens, as they were not erected in the same series. The average compressive strength of 40.8 MPa was measured in the specimen AB-NS-002-2, while the compressive strength of 36.2 MPa was measured in the specimen AB-NS-003-2. The specimen AB-NS-004-2 is made with ribbed reinforcement. The reinforcement around the center of the cross-section is Ø10 mm, while the corner reinforcement is Ø8 mm. The average compressive strength of the concrete cube is 36.2 MPa. The specimen was loaded with an axial force of 150 kN.
A characteristic failure of all specimens occurs as crushing of the concrete in the compression area around the end section after large deformations of the tensile area due to the loss of bond strength between reinforcement and concrete and the yielding of the reinforcement.
As with the monotonically tested specimens, no clear boundaries are visible between the individual areas of the M/φ ratio of the end section diagram, while in the other two sections these boundaries are more pronounced. The reason for this is again the loss of bond strength between the reinforcement and the concrete, where there is no sudden change in the slope of the diagram due to the loss of stiffness after crack formation. In cyclically tested specimens, the effect of the loss of bond strength between reinforcement and concrete on the decrease in stiffness during loading with horizontal force is not visible, as was the case with a monotonically tested specimen.
The influence of the axial force on the displacement–force ratio is visible in the first four cyclically tested specimens. During the test, the specimens AB-NS-001-3 and AB-NS-001-4 were loaded with a lower axial force than the specimens AB-NS-001-7 and AB-NS-001-8, resulting in a lower cross-sectional load capacity. It should be noted that the compressive strength test showed that the first two sets of specimens had a concrete compressive strength one class higher than the other two (47.5/36.0 MPa). It can therefore be assumed that the differences would be even greater for the same concrete properties. Looking at the rotation of the cross-section when the failure is reached on the same specimens, it can be seen that for both specimens with a smaller value of the axial force, the rotation of the cross-section is higher. Specimen AB-NS-001-9 was tested with an axial force of 125 kN. The load bearing capacity of this specimen is between the specimens tested with forces of 100 and 150 kN, while its rotation is lower than that of the other specimens tested in this series, which is also due to the lower compressive strength of the concrete.
The specimens AB-NS-002-2 and AB-NS-003-2 were made with different amounts of reinforcement in the corners. The column AB -NS-002-2 column has a larger amount of reinforcement (4Φ10) than the column AB-NS-003-2 (4Φ8), so the load-bearing capacity is higher as expected.
If we compare columns AB-NS-001-7, AB-NS-001-8, and AB-NS-004-2, we can see differences in the load-bearing capacity of smooth and ribbed reinforcement of cyclically loaded columns. These columns are made with the same amount of reinforcement, have approximately the same concrete properties and are loaded with the same axial force, but the column made with ribbed reinforcement AB-NS-004-2 showed a 30% higher load bearing capacity than the column made with smooth reinforcement. If we observe the rotation of the end cross-section of specimens with the same geometric properties and the same amount of axial force applied, we see that the specimen tested with ribbed reinforcement has a slightly lower rotation on failure than the specimens produced with smooth reinforcement. The difference here is not as pronounced as in the case of monotonically tested specimens.
The results of measuring the relative deformations of the cross-section at a height of 150 and 350 mm from the bottom of the column and the corresponding values of cross-section rotation show the behavior of the column at the plastic joint. For the cross-section at a height of 150 mm from the bottom, we can see that in most of the tested specimens a third area, i.e., the area of plasticization, was present. At a height of 350 mm from the bottom, the two specimens reached the values where plastification takes place.
4.4. Comparison between Results of Analytical and Numerical Analysis
By measuring the relative deformations at the location of the extremely loaded cross-section (at the bottom of the column), the amount of cross-section rotation at which the yield strength of the reinforcement was reached was determined. The results obtained were compared with the values of the cross-section rotation when the yield strength obtained by analytical and numerical methods was reached. As the analytical and numerical results do not include the effect of slippage of the smooth reinforcement, a significant difference of the experimentally obtained cross-section rotation when reaching the yield strength is visible.
Figure 14 (above) shows the moment and rotation ratios for the end cross-section of the two monotonically tested specimens. Experimentally, analytically, and numerically obtained curves are compared in the diagram. The first specimen was made with smooth reinforcement (
Figure 14 top left) and the second with ribbed reinforcement (
Figure 14 top right).
The point of reaching the yield strength obtained by experimental tests is shown by a rhombus marking, while the point of reaching the analytically and numerically obtained yield strength is shown by cross and triangle markings. The cross-sectional rotation at the point of reaching the analytically and numerically obtained yield strength almost coincides, while the difference of the experimentally obtained rotation angle in comparison with the two previous analyzes is marked with the notation Δφ. The given diagrams clearly show the differences in the angle of rotation of the cross-section when reaching the yield strength of the specimen made with smooth reinforcement and the specimen made with ribbed reinforcement. Specimens with smooth reinforcement show a significantly greater deviation of the experiment results from the numerical or analytical analysis.
The values of the angle of rotation angle when reaching the yield strength of other monotonically tested columns are shown in
Figure 15. A comparison of the results for the end section and two sections where relative deformations were measured in relation to the results obtained analytically and numerically is given. The results of the tested specimens with smooth reinforcement show on average a five-times higher rotation of the experimentally obtained end section when reaching the yield point compared to the results obtained with analytical and numerical methods which do not take into account the effect of slippage from the anchoring area (
Figure 15). For specimens with ribbed reinforcement (AB-NS-004), the rotation angles of the end cross-section when reaching the yield point in the experiment have a significantly smaller difference from the results obtained by analytical and numerical analysis (two-times the rotation of the experimental result).
After opening the first crack, specimens made with smooth reinforcement also show a greater deviation of the experimentally obtained moment to rotation curves compared to specimens with ribbed reinforcement. The effect of slipping of the smooth reinforcement from the anchorage area on the side of the anchor block and the column body itself influences the rotation of the cross-section as soon as the first crack occurs.
The greater distance between the anchoring points of the smooth reinforcement leads to a greater relative deformation of the bar and thus to a greater rotation of the cross-section, which then accumulates at the end cross-section. From this it can be concluded that the ribbed reinforcement bars are better anchored in the concrete, which leads to a shorter length where relative deformation occurs, and thus to a smaller angle of rotation of the end cross-section.
To compare the ratio of moment and cross-sectional rotation of smooth and ribbed reinforcement under cyclic loading, comparative M/φ diagrams of two specimens with smooth and one specimen with ribbed reinforcement are shown in
Figure 14 (below). In addition, the locations where the yield strength of the reinforcement is reached are marked according to different analysis methods. For cyclically tested specimens, the difference between the angle of rotation when the yield point is reached, which was determined by experimental analysis, and those determined numerically and analytically for smooth and ribbed reinforcement is significantly smaller than for monotonously tested specimens. This leads to the conclusion that these two types of reinforcement around the plastic joint behave similarly with regard to bond strength under cyclic loading. Alternating load cycles with a compression–tension effect causes the concrete to be crushed near the reinforcement ribs, which causes the non-anchored part of the ribbed bar to increase in size and thus behave like smooth reinforcement, so that the results for both smooth and ribbed reinforcement are closer together.
The results of measurements on cyclically tested specimens made with smooth reinforcement show similar behavior near the end cross-section as monotonically tested specimens. The rotations of the end section and the section where the first crack occurs are dominant. For cyclically tested specimens, the difference between the experimental results of the end section rotation when the yield strength is reached, and the analytical and numerical results is somewhat smaller compared to monotonically tested specimens. On average, the difference is four-and-a-half-times higher than the difference between the rotation of the experimental measurements compared to the analytical and numerical results. As with monotonically tested specimens, the reason for this discrepancy is the loss of bond strength between concrete and reinforcement in the anchorage area of the smooth reinforcement.
Differences between the cyclically tested specimens and the monotonically tested specimens can be seen in the specimens made with ribbed reinforcement. A 50% larger rotation of the end cross-section of the cyclically tested specimens can be seen in comparison to the monotonically tested specimens made with ribbed reinforcement. Since the influence of a higher axial force reduces the rotatability of the cross-section, it can be assumed that the difference would be even greater since the cyclically tested specimen was loaded with a 50% higher force. This proves that ribbed reinforcement with high ductility properties (B500 B) behaves much better under cyclic loading in terms of element ductility than under monotonic loading.
5. Final Remarks
This research defines important indicators that influence the behavior of a column with an atypical cross-section, loaded by seismic action, erected without the guidelines for anti-seismic reinforcement placement, and made with smooth reinforcement in the area of plastic joint formation. From the analytical and experimental analysis results, a great influence on the properties of the material and therefore the importance of modeling them accurately in order to define more realistically the indicators of seismic resistance was achieved. Using non-linear material properties in analytical and numerical analysis, results have been obtained that are approximately equal to those obtained in experimental analysis, with deviations due to slippage of reinforcement from the anchorage area.
For most of the specimens tested, all three methods used showed a good agreement of results in the linear range. Small deviations of the results occurred immediately after the opening of the first crack and significant deviations are visible when the yield strength is reached. The main reason for the discrepancy between the results was the slippage of the reinforcement from the anchorage area. In addition, there were deviations due to a mismatch of the stress-strain curve (material properties) after the beginning of hardening of the reinforcement steel-difference between the working law diagrams of the experimentally obtained reinforcement and the theoretical diagrams used in analytical and numerical analysis. Another reason are the deviations that occurred during the erection, such as deviations in the dimensions of the cross-section and thickness of the protective layer of the reinforcement.
Comparing monotonically and cyclically tested specimens, significant deviations of the end section rotation when reaching the yield strength are visible in relation to the analytical and numerical analysis. For all monotonically tested specimens, the rotation of the experimentally obtained end section is about five times greater than that obtained by analytical and numerical analysis. For cyclically tested samples, this deviation is somewhat smaller and is on average four-and-a-half-times greater. In the case of monotonous testing of spacemen made with ribbed reinforcement, the difference obtained is much smaller and is twice the rotation in the experimental results. When comparing the results of the specimens made with ribbed reinforcement, a 50% higher rotation of the end cross-section of the cyclically tested spacemen compared to the monotonously tested spacemen can be seen. From this it can be concluded that significant deviations of the end section rotation when reaching the yield point are due to the loss of bond strength between concrete and reinforcement.
When the final limit state is reached, the deviation of the experimental results in relation to the analytical results is much smaller than when the yield point is reached. This proves that the influence of reinforcement slippage from the anchorage area decreases as we approach the final limit state.
Depending on the arrangement and width of the cracks around the plastic joint formation area in columns with smooth reinforcement, the following can be concluded:
First cracks appear in the early phase of loading for most of the tested specimens (up to 20 mm displacement at the top of the column).
Discrete cracks generally developed around the area of the transverse reinforcement.
For all specimens, cracks appear first at the location of the initiated crack (end section).
The first crack was formed mainly at a height of 120–140 mm from the bottom of the column and, together with the crack at the bottom, represents the place of plastification of the element.
Other cracks stop expanding after some time (when the displacement at the top of the column is 40–50 mm) and remain within the limits allowed for reinforced concrete elements.
From the above it can be concluded that the total plastic deformation is reduced to a rotation around the crack of the end section and the first crack from the bottom of the element. The same can be concluded by analyzing the rotation of three characteristic cross-sections. It can be observed that most of the plastic rotation is concentrated in the end section, while in the cross-section of the first crack the amount of plastic rotation is much smaller, and in the cross-section of the second crack (the third cross-section observed) plastification is almost non-existent in most of the specimens tested. From all the above, a conclusion is drawn about the height of the plastic joint for monotonically and cyclically tested specimens, which mainly develops to about the height of the first crack and is 0.7 h, where h is the height of the cross-section in the load direction.
For specimens with ribbed reinforcement (monotonically tested), the plastification height extends up to a height of 1.2 h, which corresponds approximately to the values given in [
11]. From this it can be concluded that the given expression is calibrated to elements with ribbed reinforcement and its application to elements with smooth reinforcement is questionable. The experiment has shown that for specimens with ribbed reinforcement, the crack widths are evenly distributed over the height of the column, the larger ones at the bottom, and the smaller ones because the distance from the bottom is greater. The same applies to the distribution of rotations along the height. This explains why the plasticizing zone in specimens with ribbed reinforcement is distributed at a higher column height than in specimens with smooth reinforcement.
For specimens with ribbed reinforcement, the differences in the results of the cyclic and monotonic tests should be emphasized. The specimen subjected to the cyclic test showed a similar behavior in the area of the plastic joint as the specimen with smooth reinforcement (two cracks dominating at the bottom of the element), in contrast to the monotonically tested specimen where the results are significantly different. Alternating load cycles cause the concrete to be crushed in the vicinity of the reinforcement ribs, resulting in a larger area of the non-anchored part of the reinforcement and therefore greater relative deformation. From all the above it can be concluded that this behavior in the vicinity of the ribbed reinforcement further contributes to the ductility of elements made with highly ductile ribbed reinforcement (B 500 B).
The behavior of the elements in the vicinity of the formation of plastic joints under the influence of seismic loads has not yet been sufficiently investigated. This refers primarily to structural elements that were erected before the adoption of regulations and guidelines for the seismic calculation and design of earthquake-resistant elements, to elements that do not have adequate quantities of transverse reinforcement and reinforcement for the concrete core enclosure according to modern design guidelines. Due to the special characteristics of their structural elements, but also the way they react to seismic actions, bridge structures must be included in future guidelines for the assessment of existing structures. These guidelines will certainly become increasingly applicable due to the large number of structures that require a more detailed analysis of the load-bearing elements to determine their actual seismic resistance.
The results of this research are applicable to the analysis of the basic indicator (Diagram M/φ) of the seismic resistance of atypical cross-sections. It will allow for the application of an analytical or numerical method with realistic properties of the materials and elements and the derivation of correction factors due to the effect of slippage of the smooth reinforcement from the anchorage area.