Assessment of Structural Dynamic Response and Vehicle-Track Interaction of Precast Slab Track Systems
Abstract
:Featured Application
Abstract
1. Introduction
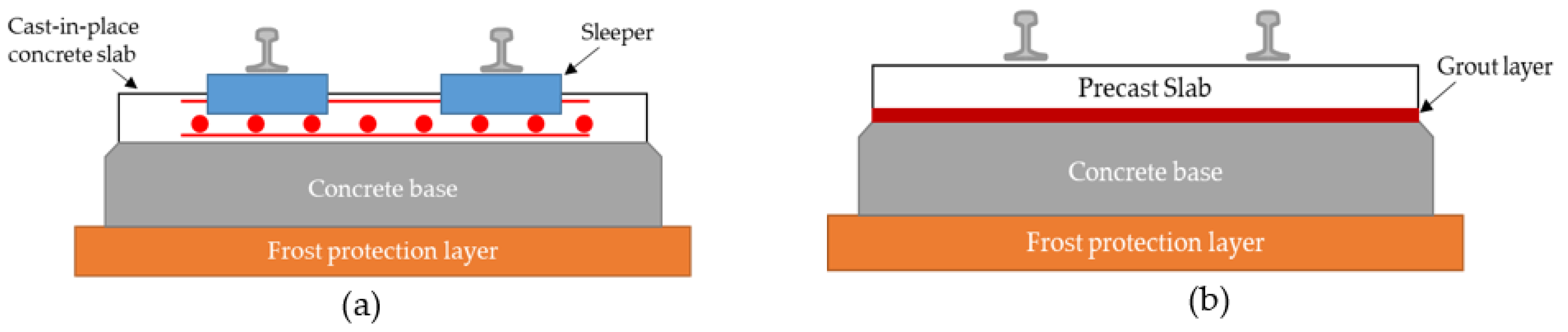
2. Precast Slab Panels
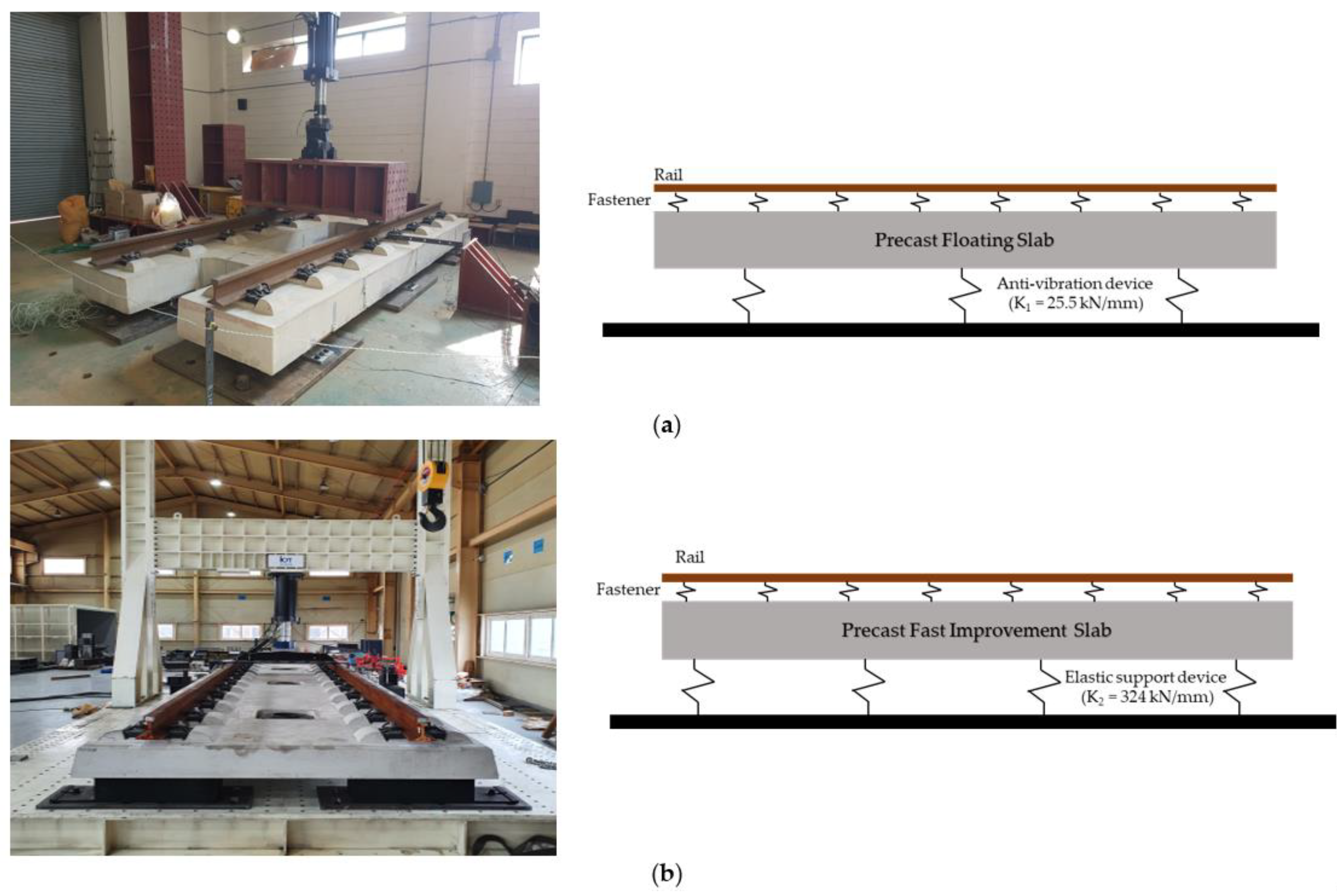
2.1. Precast Slab Track Type I
2.2. Precast Slab Track Type II
3. Numerical Analysis
4. Results and Discussion
4.1. Wheel Load Variation
- KQ/P: Derailment ratio.
- Q: Lateral force.
- P: Dynamic wheel weight due to track distortion.
- αh, αv: Horizontal and vertical accelerations of the vehicle body, respectively.
- η: Wheel reduction rate.
- P0, ΔP: Static wheel load and variation in the wheel weight.
4.2. Rail Uplift Force and Rail Stress
4.3. Rail Relative Displacement
4.4. Load Transfer Efficiency
- δ1: is the rail displacement at loaded panel (mm).
- δ2: is the rail displacement at adjacent panel (mm).
5. Conclusions
- The wheel force variation of both types of tracks was almost similar and met the requirement (smaller than the limitation is 0.372). However, when the train runs from the ballasted track to the Precast Floating slab track (Type I), there was a sudden change of wheel load. The reason is the huge difference in elasticity between the ballast layer and the anti-vibration device attached at the bottom of this type of track. Thus, it will be needed to increase the rigidity at the transition zone when designing this section.
- To ensure comfort when the train running, the rail uplift force of precast slab track systems should not exceed 11.83 kN (which is 70% of the clamping force of fastening systems Vossloh 300-1 system-16.9 kN). The results showed that the maximum rail uplift force of Type II was slightly larger than Type I. In general, these results of both types of tracks satisfied the acceptance criteria and guarantee the riding comfort of the train.
- Both types of tracks used the same kind of rail (KR 60 type). When applied to the conventional trainset, the rail bottom stress of Type I is 1.24 times larger than Type II, especially at the transition zone between the ballasted track and slab track. The main cause was that Type II had the stiffer elastic devices, and the distance of these devices was closer than Type I. However, the result of stress in both types of the track was smaller than the allowable stress (90 MPa).
- According to the Japanese standard for displacement limit of structure in railway application, the rail displacement must be smaller than 3 mm. From the results, the maximum rail relative displacement of Type I was 3 times higher than Type II. When the train was operating at the connection zone between ballasted track and slab track, the rail deflection of Type I rose 4.2 times higher than Type II. This means the elasticity of the supporting device has a huge effect on rail displacement.
- Finally, instead of using steel bars to connect the slab panels, the trainload was transmitted by the KR-60 rail. The step and inclination as well as the load transfer efficiency (LTE) between 20 slab panels were evaluated. As can be seen from the results, the step was smaller than the standard (2 mm), and the maximum inclination of the rail at the 75 mm distance of slabs was 1.07‰ for Type I and 0.53‰ for Type II, which met the requirement of the standard for riding comfort (2.5‰) and running safety (2.0‰) in Japan. The average LTE of Type I and Type II was 98.80% and 97.28%, respectively. Thus, these types of tracks can perfectly transmit the wheel load when the train passes by.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vu, L.; Kang, Y.S. Load transfer efficiency based on structural deflection assessment of the precast floating track. Appl. Sci. 2021, 11, 120. [Google Scholar] [CrossRef]
- Birhane, F.N.; Choi, Y.T.; Lee, S.J. Development of GPR device and analysis method to detect thickness of ballast layer. J. Korean Soc. Railw. 2020, 23, 269–278. [Google Scholar] [CrossRef]
- Koh, T.H.; Shin, M.C. Field tests on Eco-friendly railway precast concrete slab. Appl. Sci. 2020, 10, 4140. [Google Scholar] [CrossRef]
- Cho, Y.K.; Kim, S.M. Evaluation of grouting layer vibration of railway precast concrete slab track system. Constr. Build. Mater. 2018, 193, 244–254. [Google Scholar] [CrossRef]
- Kang, Y.S.; Lee, C.Y.; Jang, D.D.; Kwon, S.G.; Han, W.J.; Vu, L. Study on structural performance of precast track of discrete panel supporting type for rapid ballast improvement. J. Korean Soc. Hazard Mitig. 2020, 20, 233–244. [Google Scholar] [CrossRef]
- Bastin, R. Development of German non-ballasted track forms. Proc. Inst. Civ. Eng. 2006, 159, 25–39. [Google Scholar] [CrossRef]
- Mass, G.; Rickes, T.M.; Winter, T. Productivity in rail construction lessons learned from the development of the RHEDA 2000 track construction system. In Proceedings of the Conference: 23rd International Symposium on Automation and Robotics in Construction, Tokyo, Japan, 3–5 October 2006; pp. 246–251. [Google Scholar]
- Tsoukantas, S.; Giannakos, K.; Topintzis, T.; Zois, H. System Rheda 2000 from the point of view of a structural engineer–The most modern evolution of superstructure technology in railway projects. In Proceedings of the Conference of Greek Department of Concrete, Alexandroupolis, Greece, 25–27 October 2006. [Google Scholar]
- Freudenstein. S. RHEDA 2000®: Ballastless track systems for high-speed rail applications. Int. J. Pavament Eng. 2010, 11, 293–300. [Google Scholar] [CrossRef]
- Cho, Y.K.; Kim, S.M.; Chung, W.; Kim, J.C.; Oh, H.J. Effect of steel ratio on behavior of continuously reinforcement concrete railway track under environmental loads. J. Korean Soc. Civ. Eng. 2014, 18, 1688–1695. [Google Scholar]
- Jang, S.Y.; Kang, Y.S.; Lee, H.S.; Kim, Y.B.; Lee, J.S. Trial installation and performance evaluation of prefabricated concrete slab track on revenue line. Korean Soc. Railw J. Korean Soc. Railw. 2008 Fall Conf. 2008, 840–845. Available online: https://www.dbpia.co.kr/Journal/articleDetail?nodeId=NODE01084168 (accessed on 1 April 2021).
- Ando, K.; Sunaga, M.; Aoki, H.; Haga, O. Development of slab tracks for Hokuriku Shinkansen line. Q. Rep. Railw. Tech. Res. Inst. 2001, 42, 35–41. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, B. Analysis of dynamic behavior for slab track of high-speed railway based on vehicle and track elements. J. Transp. Eng. 2011, 137, 227–240. [Google Scholar] [CrossRef]
- Sun, L.; Duan, Y.F.; Yang, X. Static response analysis of CRTS III ballastless track structure. J. Railw. Eng. Soc. 2013, 30, 32–39. [Google Scholar]
- Dai, F.; Xu, G.; Yang, J.; Liu, X. Dynamic performance of unbonded prestressed steel bar in CRTS I ballastless slab track under train load. In Proceedings of the 4th International Conference on Transportation Engineering, Chengdu, China, 19–20 October 2013; pp. 1765–1770. [Google Scholar]
- Ren, J.; Zhao, H.; Li, X.; Deng, S.; Xu, K. Dynamic performances of CRTS III prefabricated slab track with anti-vibration structure in subgrade-tunnel transition section. J. Southwest Jiaotong Univ. 2016, 51, 1047–1054. [Google Scholar]
- Ren, J.J.; Zhao, H.W.; Li, X.; Xu, K. Analysis of harmonic response of CRTS III prefabricated slab track with anti-vibration structure. J. Railw. Eng. Soc. 2016, 33, 44–50. [Google Scholar]
- Leykauf, G. Prefabricated slabs and frames for non-ballasted track. J. Railw. Transp. 1999, 123, 221–228. [Google Scholar]
- 19. Yu. Z.; Xie. Y.; Tian. X. Research on mechanical performance of CRTS III plate-type ballastless track structure under temperature load based on probability statistics. Adv. Civ. Eng. 2019. [CrossRef]
- Antlauf, W. Bögl system slab track: Installation on the new Nuremberg–Ingolstadt line. Eisenbahningernieur 2004, 55, 64–67. [Google Scholar]
- Antlauf, W. Slab track system FF bögl on the new Nuremberg-Ingolstadt line. ZEV Rail Glassers Ann. 2004, 128, 360–364. [Google Scholar]
- Chung, W.S.; Kwon, K.S.; Yang, S.Y. Deflection-based load transfer efficiency of floating slab track. KSCE J. Civ. Eng. 2014, 18, 616–624. [Google Scholar] [CrossRef]
- Yang, S.C. Enhancement of the finite-element method for the analysis of vertical train-track interactions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 609–620. [Google Scholar] [CrossRef]
- Yang, S.C.; Kim, E. Effect on vehicle and track interaction of installation faults in the concrete bearing surface of a direct-fixation track. J. Sound Vib. 2012, 331, 192–212. [Google Scholar] [CrossRef]
- Yang, S.C.; Hwang, S.H. Train-track-bridge interaction by coupling direct stiffness method and mode superposition method. ASCE J. Bridge Eng. 2016, 21. [Google Scholar] [CrossRef]
- Jang, S.Y.; Yang, S.C. Assessment of train running safety, ride comfort, and track serviceability at transition between floating slab track and conventional concrete track. J. Korean Soc. Railw. 2012, 15, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Namura, A.; Matsuo, K.; Miura, S. Introduction of buffers into a transitional track stiffness region. RTRI Rep. 1997, 11, 39–42. (In Japanese) [Google Scholar]
- Railway Technology Research Institute (RTRI). Design Standards for Railway Structures and Commentary–Limit for Displacement; Maruzen: Tokyo, Japan, 2012. [Google Scholar]
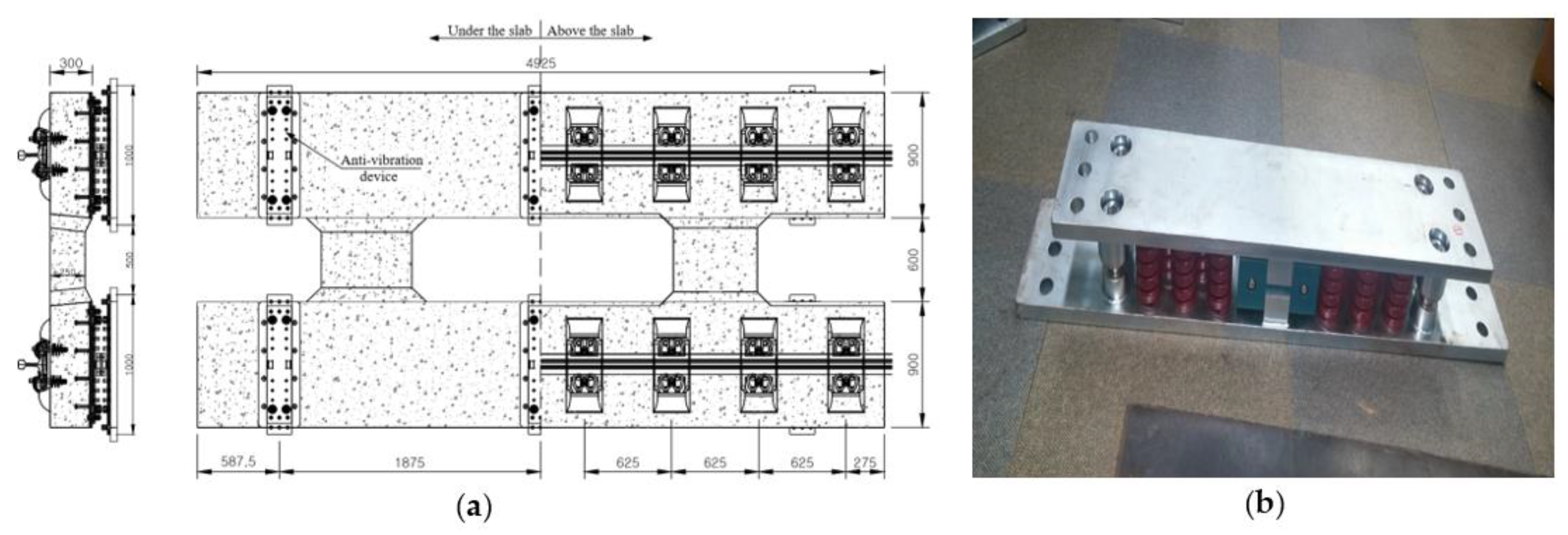
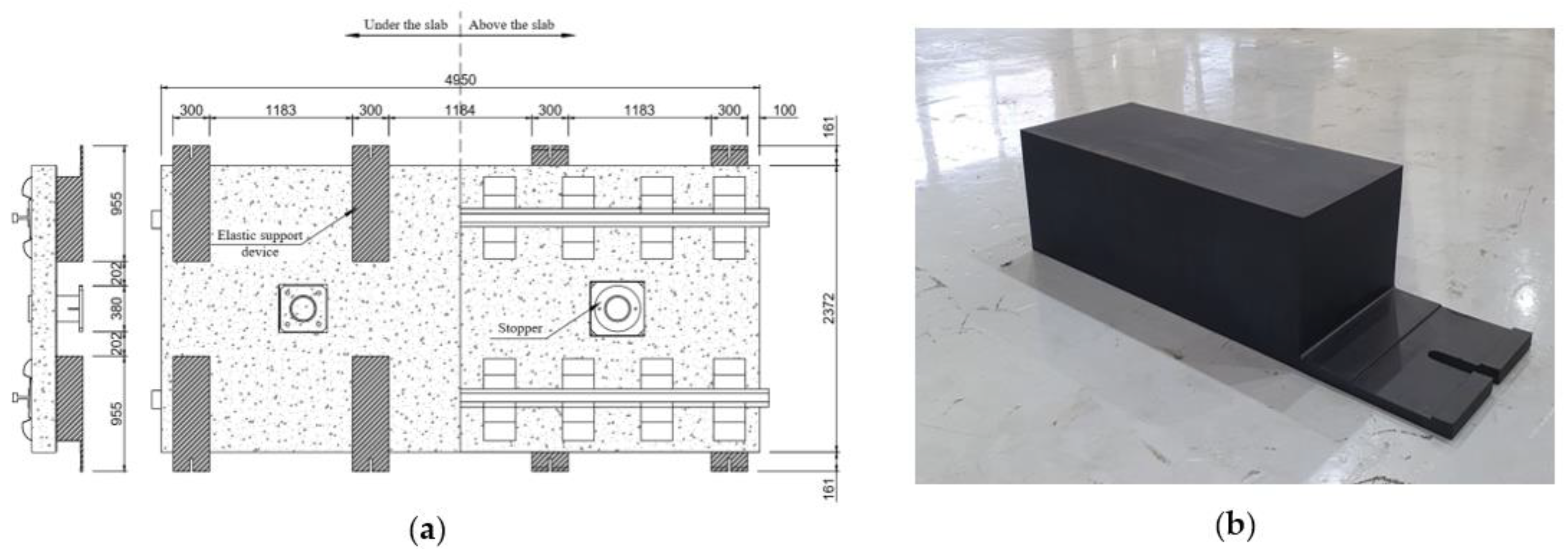
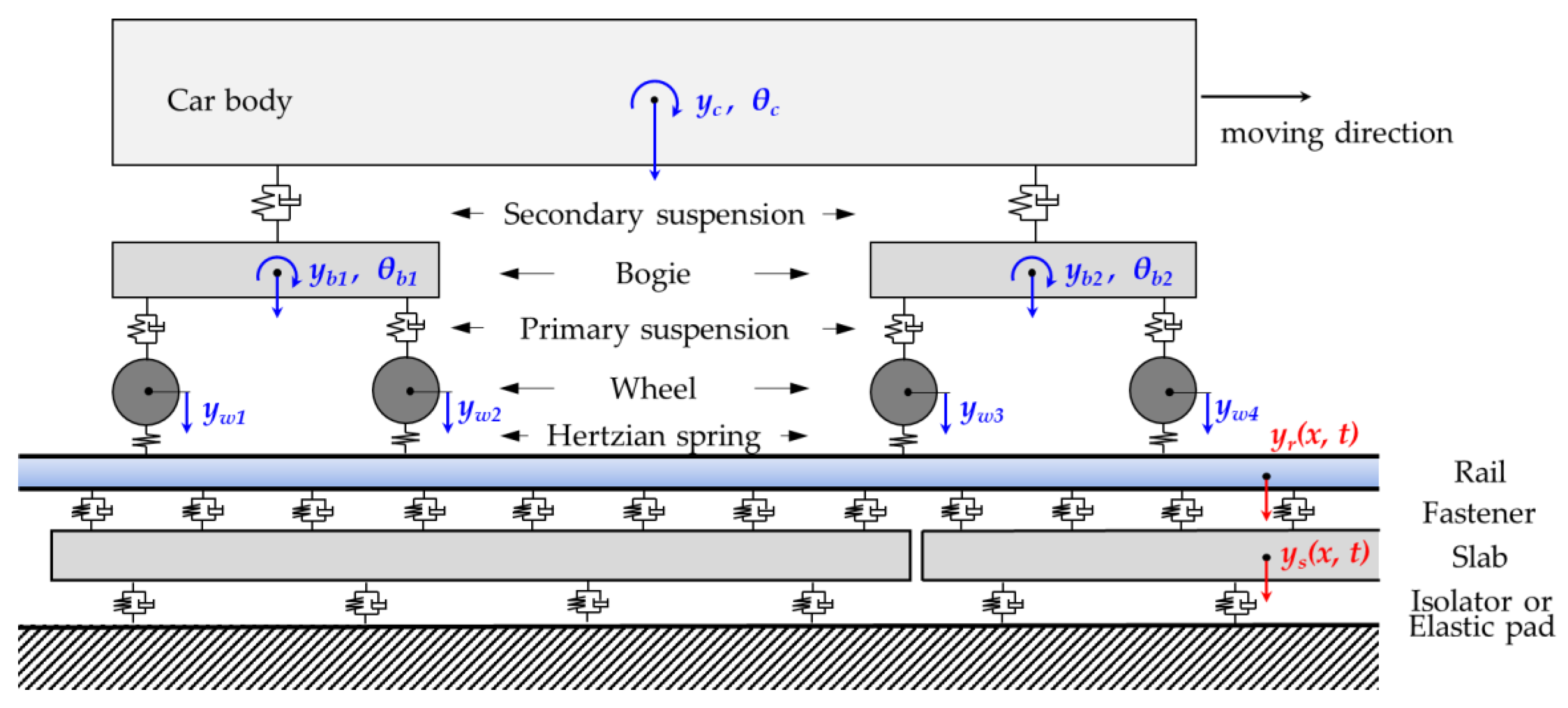


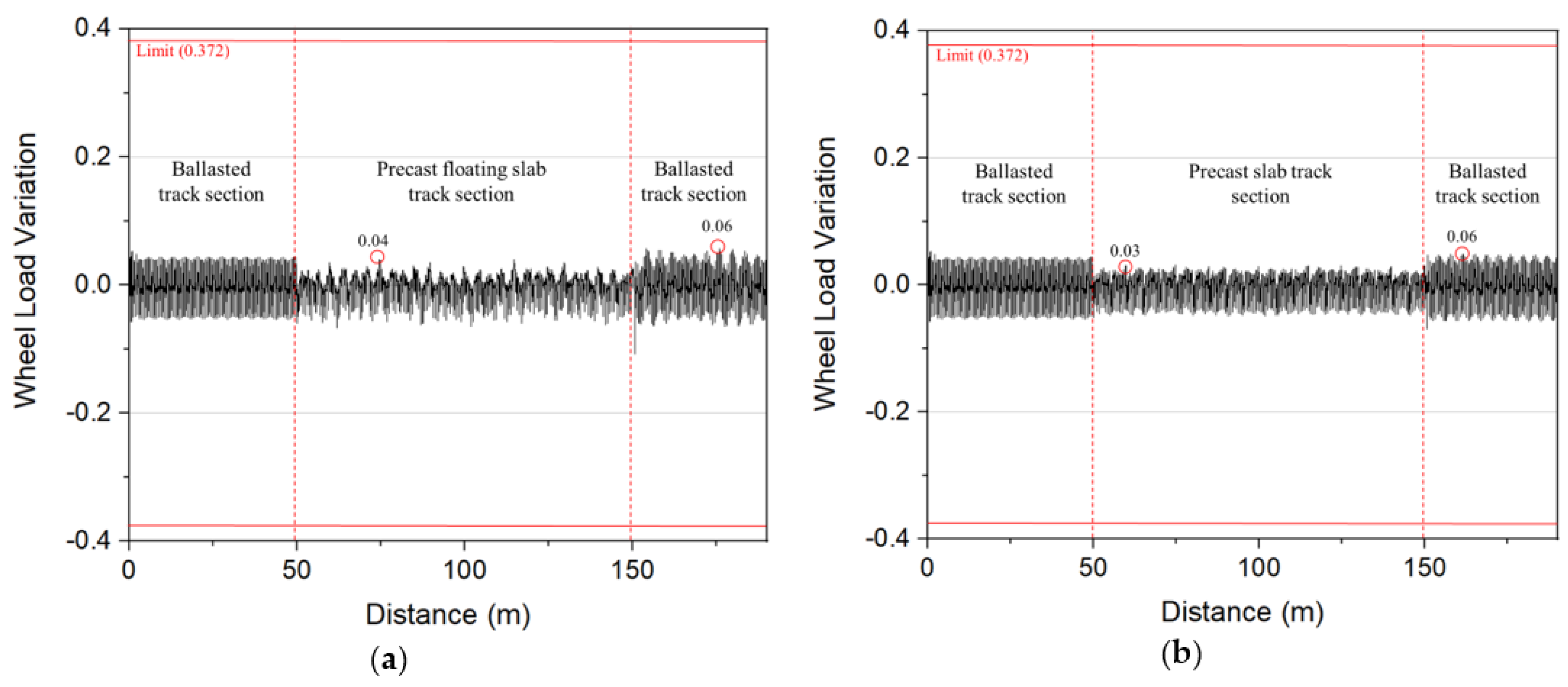
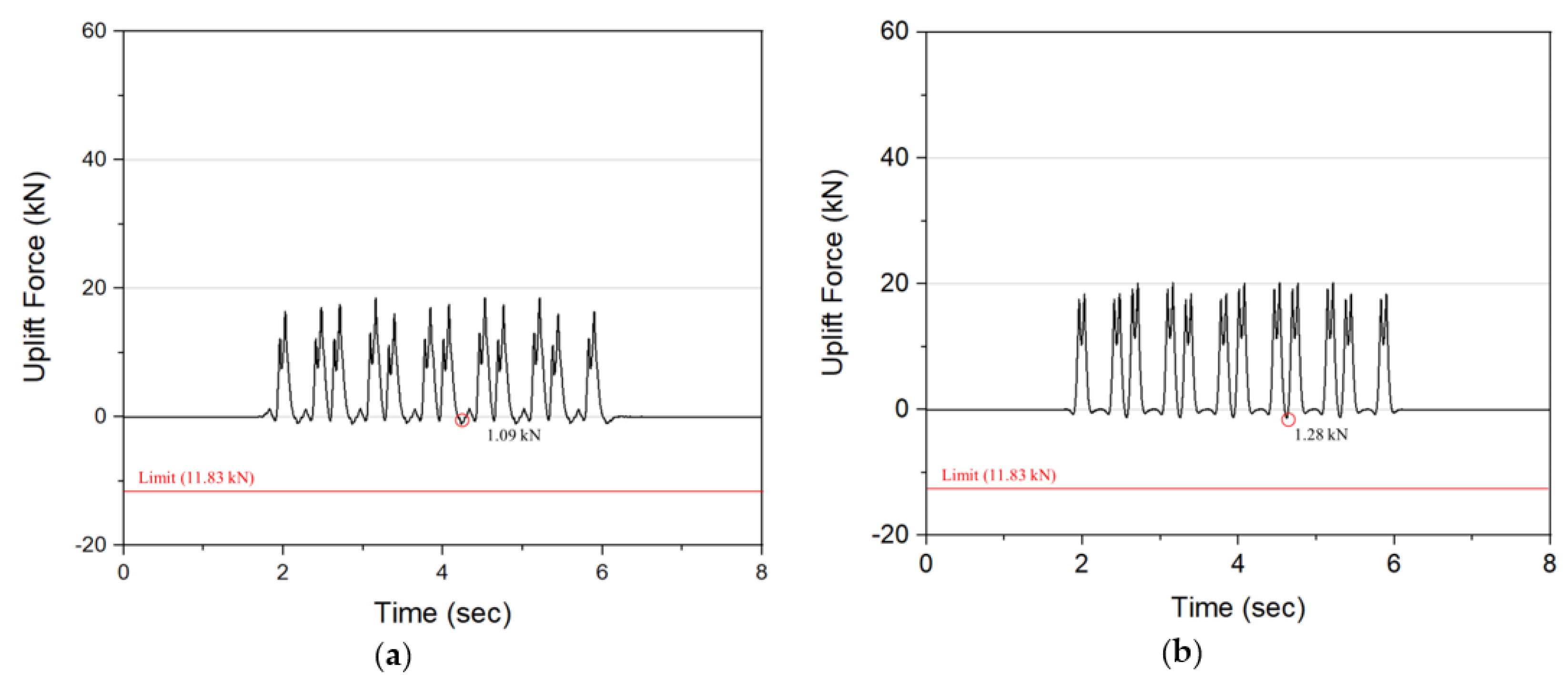

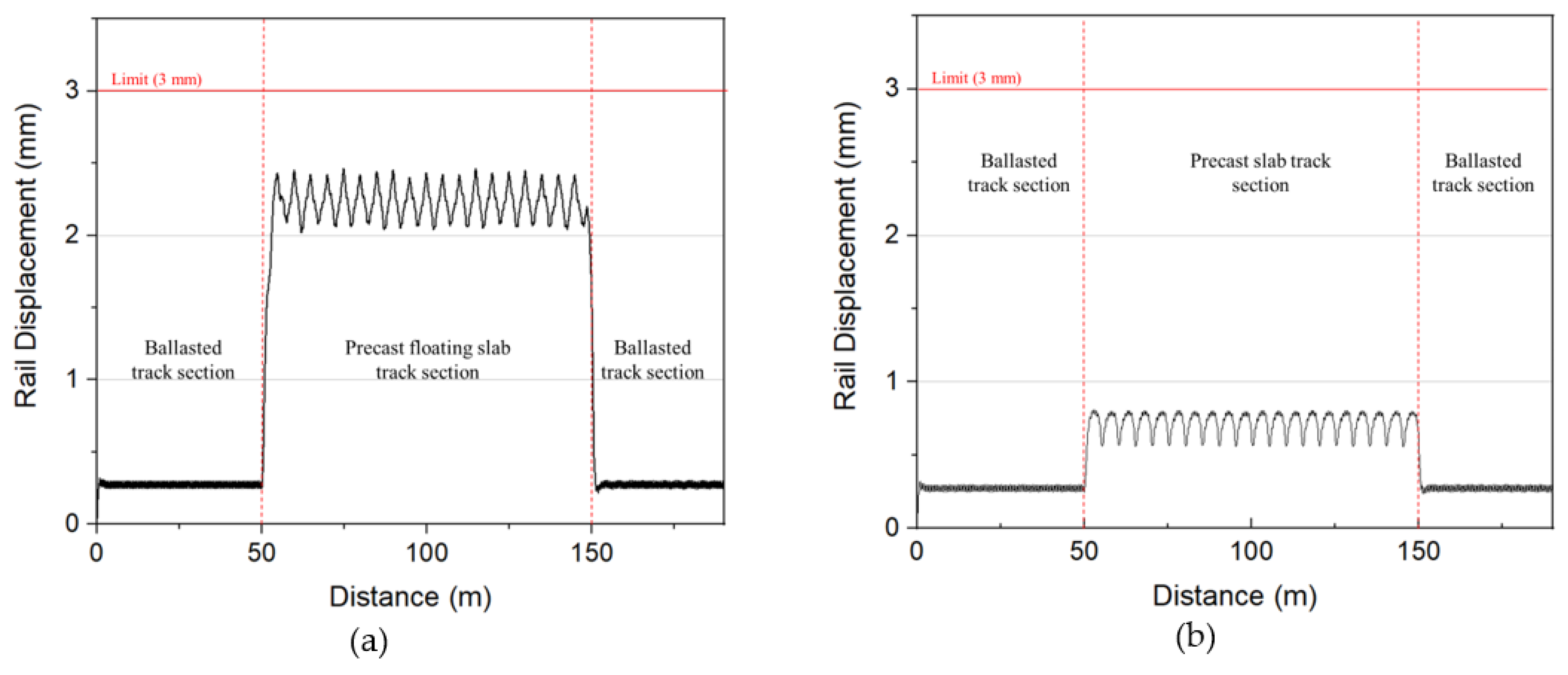
| Specifications | Type I | Type II |
|---|---|---|
| Dimensions (m) | 4.925 (L) × 2.4 (W) × 0.3 (H) | 4.950 (L) × 2.38 (W) × 0.23 (H) |
| Concrete Strength (MPa) | 45 | 45 |
| Panel Weight (ton) | 7.6 | 7.6 |
| Support Stiffness of Elastic Device (kN/mm) | 22.5 | 324 |
| Item | Unit | Motor Car (M) | Passenger Car (P) | |
|---|---|---|---|---|
| Car Body specifications | Car Body Weight | ton | 21 | 19 |
| Car Body Mass Moment of Inertia | ton-m2 | 791 | 856.5 | |
| Weight of Bogie | ton | 0.600 | 0.585 | |
| Bogie Mass Moment of Inertia | ton-m2 | 0.750 | 0.400 | |
| Weight of Wheel | ton | 0.860 | 0.795 | |
| Primary Suspension | Spring Coefficient | MN/m | 1043 | 0.511 |
| Damping Coefficient | MN·s/m | - | - | |
| Secondary Suspension | Spring Coefficient | MN/m | 0.191 | 0.176 |
| Damping Coefficient | MN·s/m | - | - | |
| Length | Balance Interval | m | 13.8 | 13.8 |
| Distance between Wheels | m | 2.1 | 2.1 | |
| Radius of Wheel | m | 0.43 | 0.43 | |
| Parameter | Unit | Type I | Type II | ||
|---|---|---|---|---|---|
| Rail | Modulus of Elasticity | kPa | 2.1 × 108 | ||
| Poisson’s Ratio | 0.3 | ||||
| Mass | ton/m | 6.08 × 10−3 | |||
| Cross Section | m2 | 7.75 × 10−3 | |||
| 2nd moment of cross-section | m4 | 3.06 × 10−5 | |||
| Fastener | Ballasted track section | Stiffness Coefficient | kN/mm | 196 | 196 |
| Damping Coefficient | kN.sec/m | 300 | 300 | ||
| Precast slab track section | Stiffness Coefficient | kN/m | 32,800 (System 300-1) | 32,800 (System 300-1) | |
| Damping Coefficient | kN-sec/m | 200 | 200 | ||
| Slab panel | Modulus of Elasticity | kPa | 356.8 × 105 | 356.8 × 105 | |
| Poisson’s Ratio | 0.18 | 0.18 | |||
| Mass per unit length | ton/m | 0.772 | 0.677 | ||
| Cross Section | m2 | 0.27 | 0.273 | ||
| Second Moment of section | m4 | 2.025 × 10−3 | 1.203 × 10−3 | ||
| Elastic Device | kN/mm | 22.5 (6ea) | 324 (8ea) | ||
| Ballast | Stiffness Coefficient | kN/mm | 314 | 314 | |
| Damping Coefficient | kN·s/m | 300 | 300 | ||
| Panels | Type I | Type II | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Loaded Panel (δ1) | Adjacent Panel (δ2) | Step (mm) | Incli-Nation (‰) | LTE (%) | Loaded Panel (δ1) | Adjacent Panel (δ2) | Step (mm) | Incli-Nation (‰) | LTE (%) | |
| 1st–2nd | 2.62 | 2.57 | 0.05 | 0.67 | 99.04 | 0.689 | 0.657 | 0.03 | 0.43 | 97.623 |
| 2nd–3rd | 2.64 | 2.58 | 0.06 | 0.80 | 98.85 | 0.690 | 0.656 | 0.03 | 0.45 | 97.474 |
| 3rd–4th | 2.64 | 2.58 | 0.06 | 0.80 | 98.85 | 0.690 | 0.656 | 0.03 | 0.45 | 97.474 |
| 4th–5th | 2.65 | 2.59 | 0.06 | 0.80 | 98.85 | 0.691 | 0.657 | 0.03 | 0.45 | 97.478 |
| 5th–6th | 2.66 | 2.60 | 0.06 | 0.80 | 98.86 | 0.692 | 0.659 | 0.03 | 0.44 | 97.557 |
| 6th–7th | 2.67 | 2.61 | 0.06 | 0.80 | 98.86 | 0.693 | 0.658 | 0.03 | 0.47 | 97.409 |
| 7th–8th | 2.67 | 2.61 | 0.06 | 0.80 | 98.86 | 0.693 | 0.658 | 0.03 | 0.47 | 97.409 |
| 8th–9th | 2.67 | 2.60 | 0.07 | 0.93 | 98.67 | 0.693 | 0.658 | 0.03 | 0.47 | 97.409 |
| 9th–10th | 2.67 | 2.61 | 0.06 | 0.80 | 98.86 | 0.694 | 0.657 | 0.04 | 0.49 | 97.261 |
| 10th–11th | 2.68 | 2.62 | 0.06 | 0.80 | 98.87 | 0.694 | 0.657 | 0.04 | 0.49 | 97.261 |
| 11th–12th | 2.69 | 2.63 | 0.06 | 0.80 | 98.87 | 0.694 | 0.656 | 0.04 | 0.51 | 97.185 |
| 12th–13th | 2.70 | 2.63 | 0.07 | 0.93 | 98.69 | 0.693 | 0.656 | 0.04 | 0.49 | 97.257 |
| 13th–14th | 2.70 | 2.63 | 0.07 | 0.93 | 98.69 | 0.693 | 0.655 | 0.04 | 0.51 | 97.181 |
| 14th–15th | 2.70 | 2.63 | 0.07 | 0.93 | 98.69 | 0.693 | 0.654 | 0.04 | 0.52 | 97.105 |
| 15th–16th | 2.69 | 2.62 | 0.07 | 0.93 | 98.68 | 0.692 | 0.653 | 0.04 | 0.52 | 97.100 |
| 16th–17th | 2.69 | 2.63 | 0.06 | 0.80 | 98.87 | 0.690 | 0.651 | 0.04 | 0.52 | 97.092 |
| 17th–18th | 2.70 | 2.62 | 0.08 | 1.07 | 98.50 | 0.690 | 0.650 | 0.04 | 0.53 | 97.015 |
| 18th–19th | 2.71 | 2.66 | 0.05 | 0.67 | 99.07 | 0.688 | 0.648 | 0.04 | 0.53 | 97.006 |
| 19th–20th | 2.70 | 2.62 | 0.08 | 1.07 | 98.50 | 0.688 | 0.648 | 0.04 | 0.53 | 97.006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, L.; Jang, D.-D.; Kang, Y.-S. Assessment of Structural Dynamic Response and Vehicle-Track Interaction of Precast Slab Track Systems. Appl. Sci. 2021, 11, 3558. https://doi.org/10.3390/app11083558
Vu L, Jang D-D, Kang Y-S. Assessment of Structural Dynamic Response and Vehicle-Track Interaction of Precast Slab Track Systems. Applied Sciences. 2021; 11(8):3558. https://doi.org/10.3390/app11083558
Chicago/Turabian StyleVu, Linh, Dong-Doo Jang, and Yun-Suk Kang. 2021. "Assessment of Structural Dynamic Response and Vehicle-Track Interaction of Precast Slab Track Systems" Applied Sciences 11, no. 8: 3558. https://doi.org/10.3390/app11083558








