Theoretical Study on the Flexural Behavior of Structural Elements Strengthened with External Pre-Stressing Methods
Abstract
:1. Introduction
- -
- Higher utilization of small sectional areas.
- -
- Easy inspection and replacement of the tendon corrosion protection.
- -
- Friction losses are significantly reduced because external tendons are linked to the structure only at the deviation and anchorage zones.
- -
- The possibility of controlling and adjusting the tendon forces.
- -
- There is no weakening of the compression area due to ducts, so a minimum web thickness is achievable.
2. Methodology and Programming
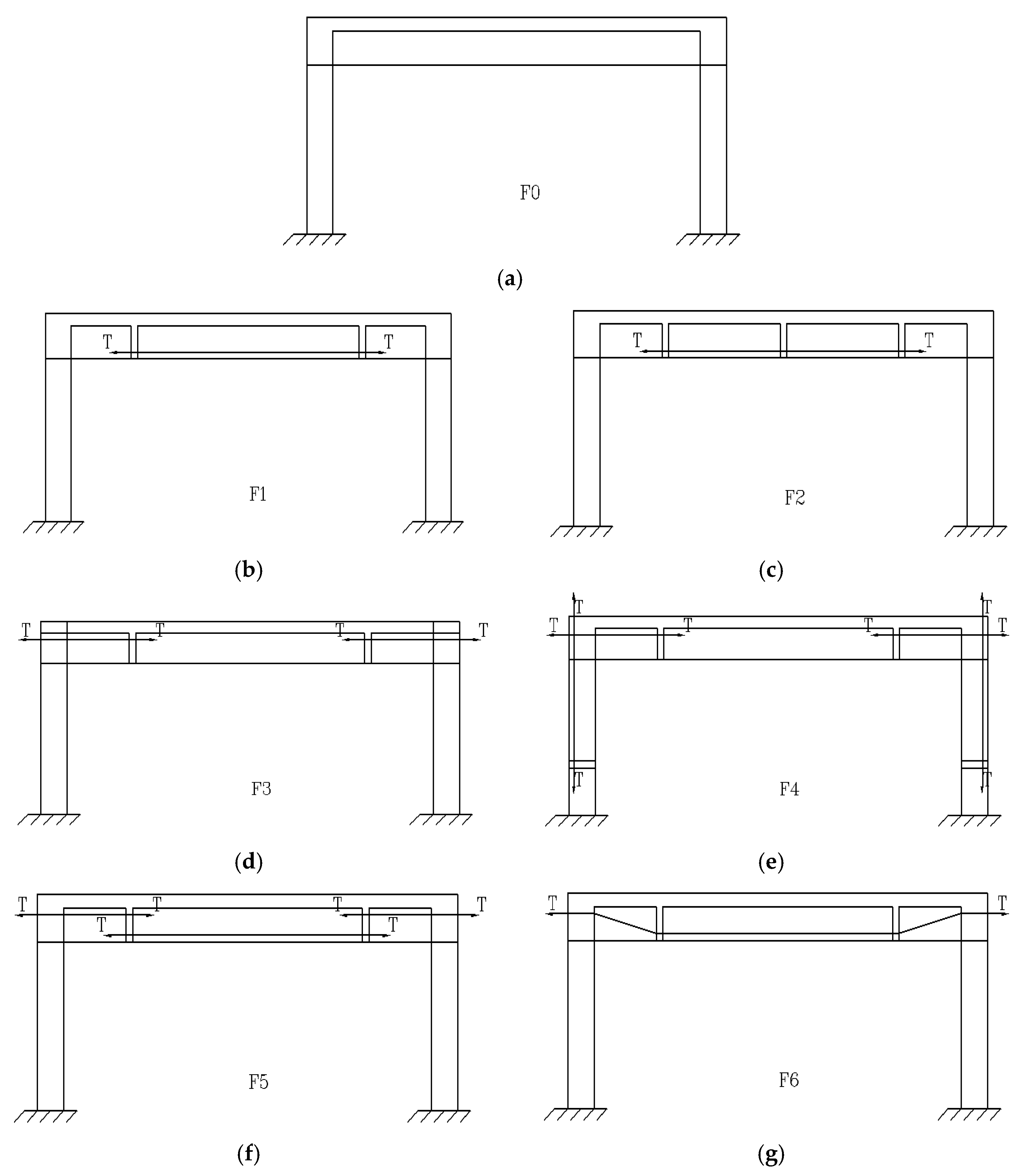
2.1. Methods of External Pre-Stressing Strengthening
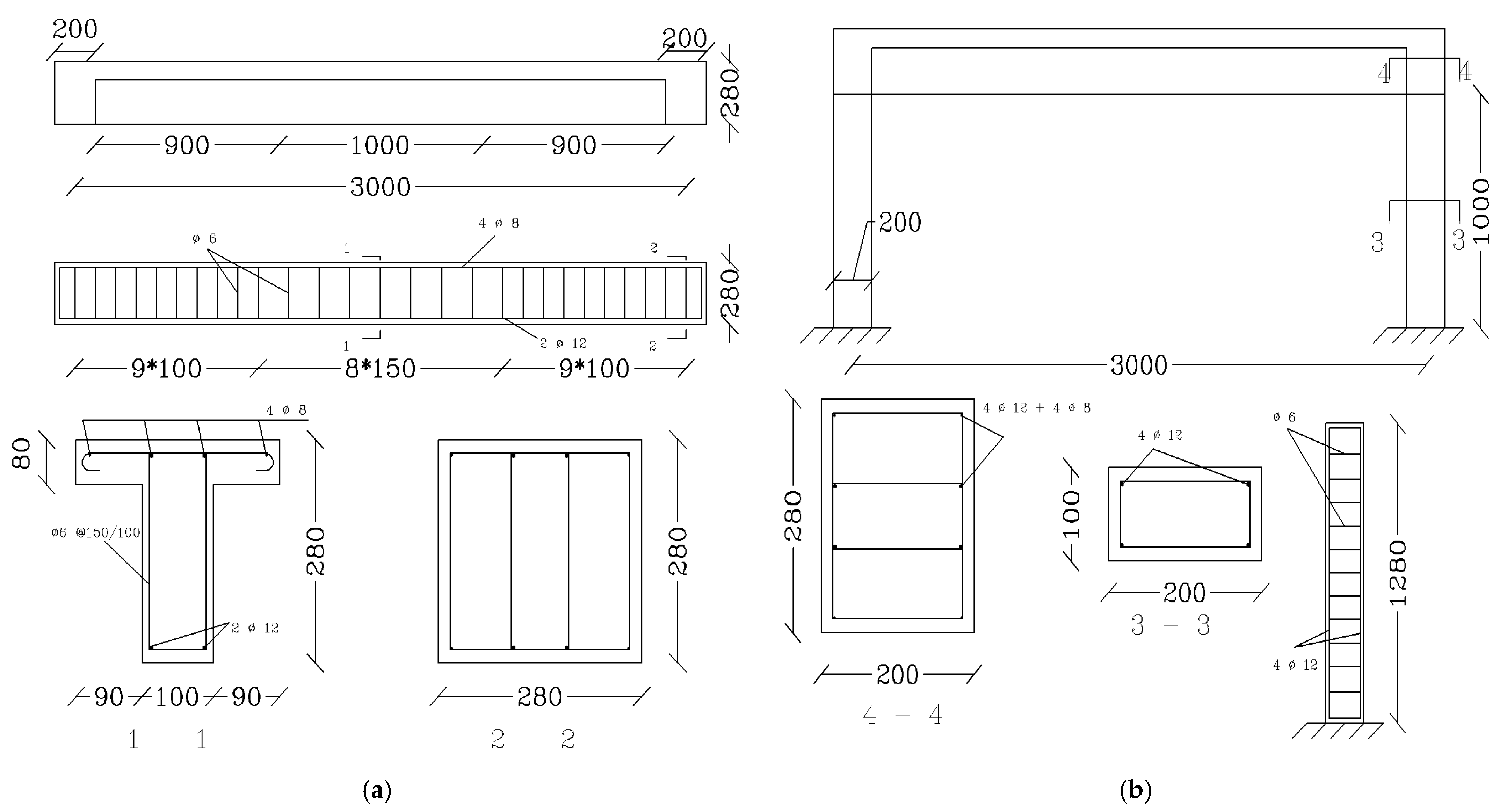
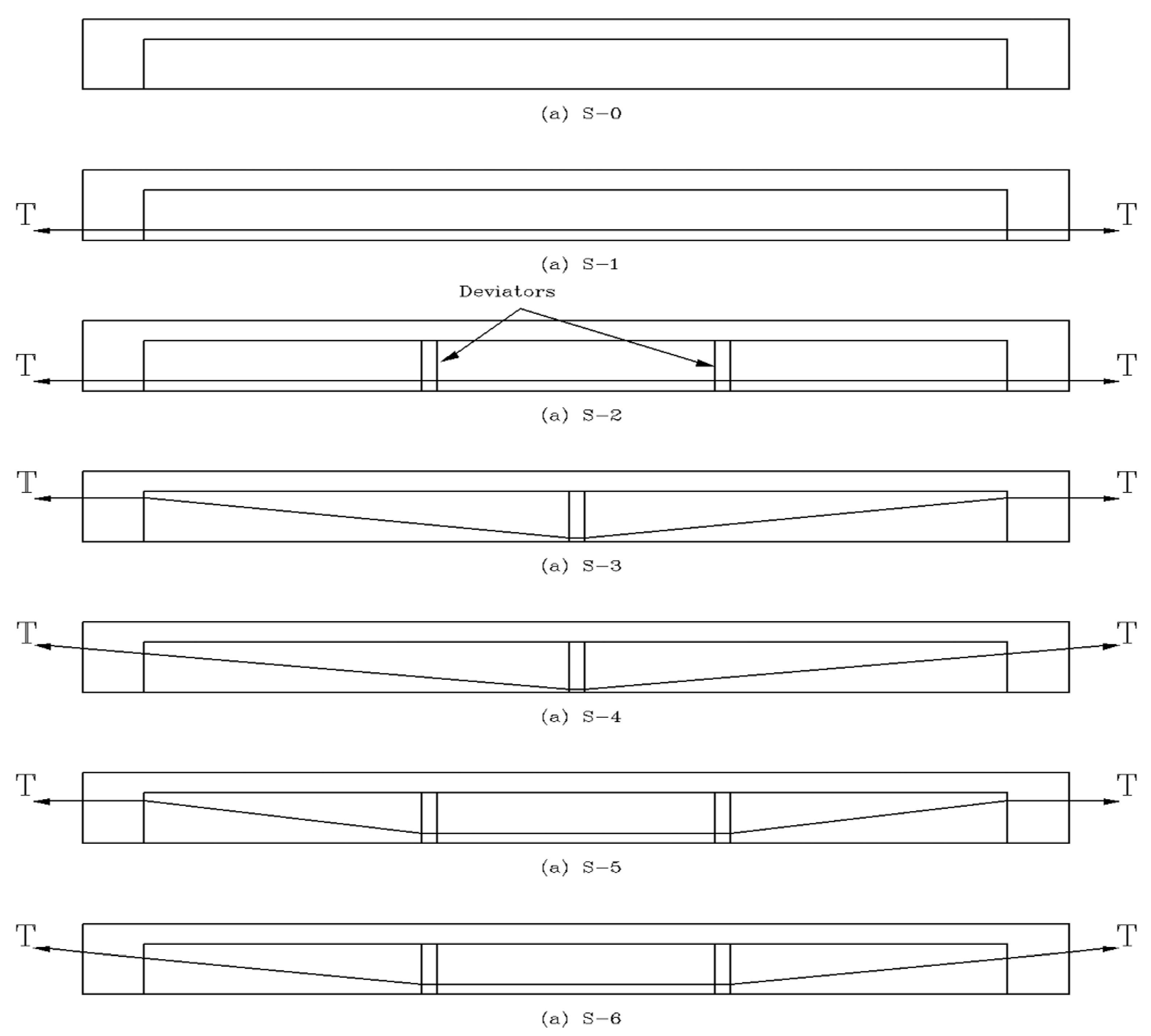
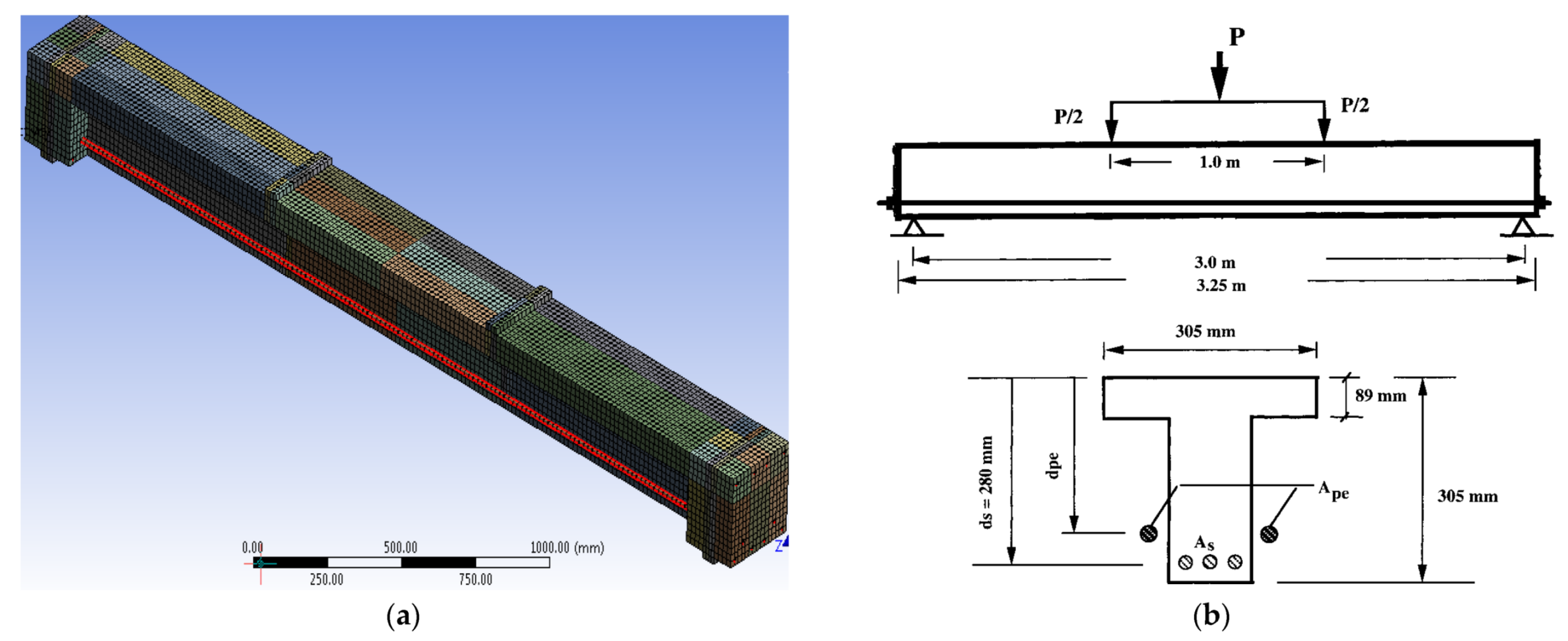
2.2. Sample Design
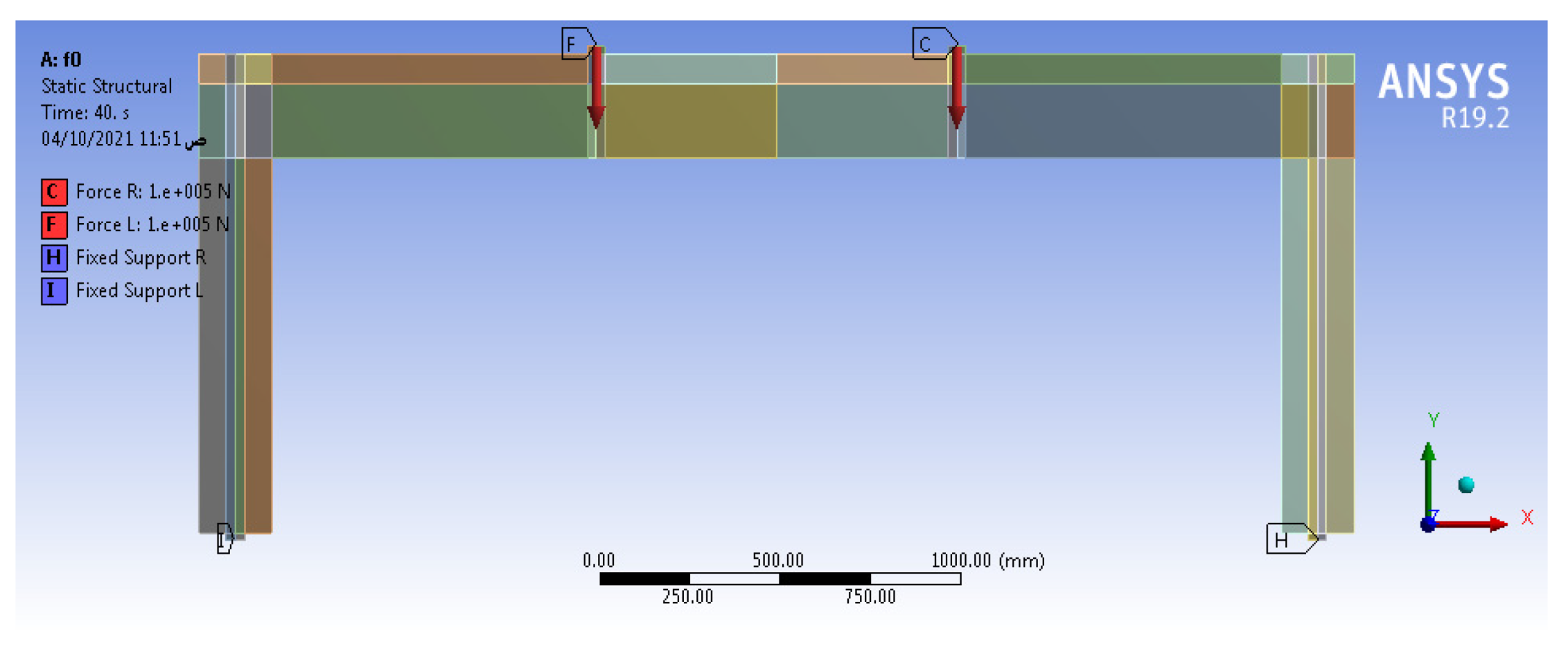
2.3. Loading Method and Pre-Stressing of Tendons
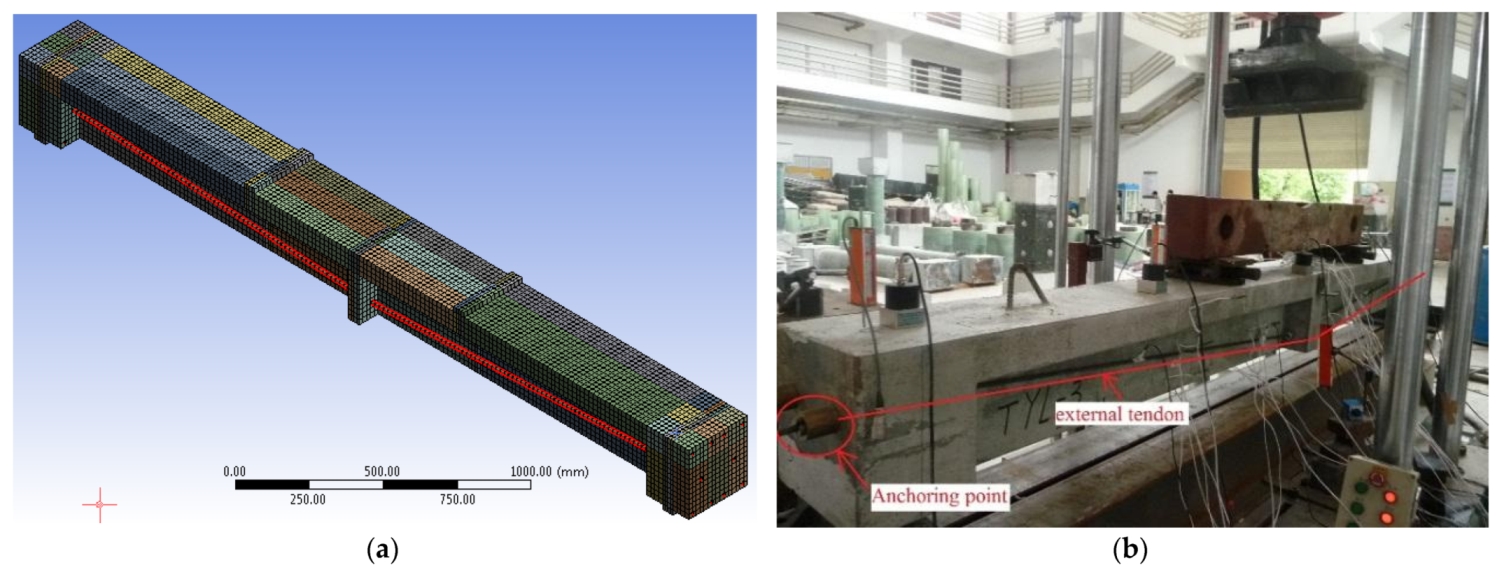
2.4. Programming Models
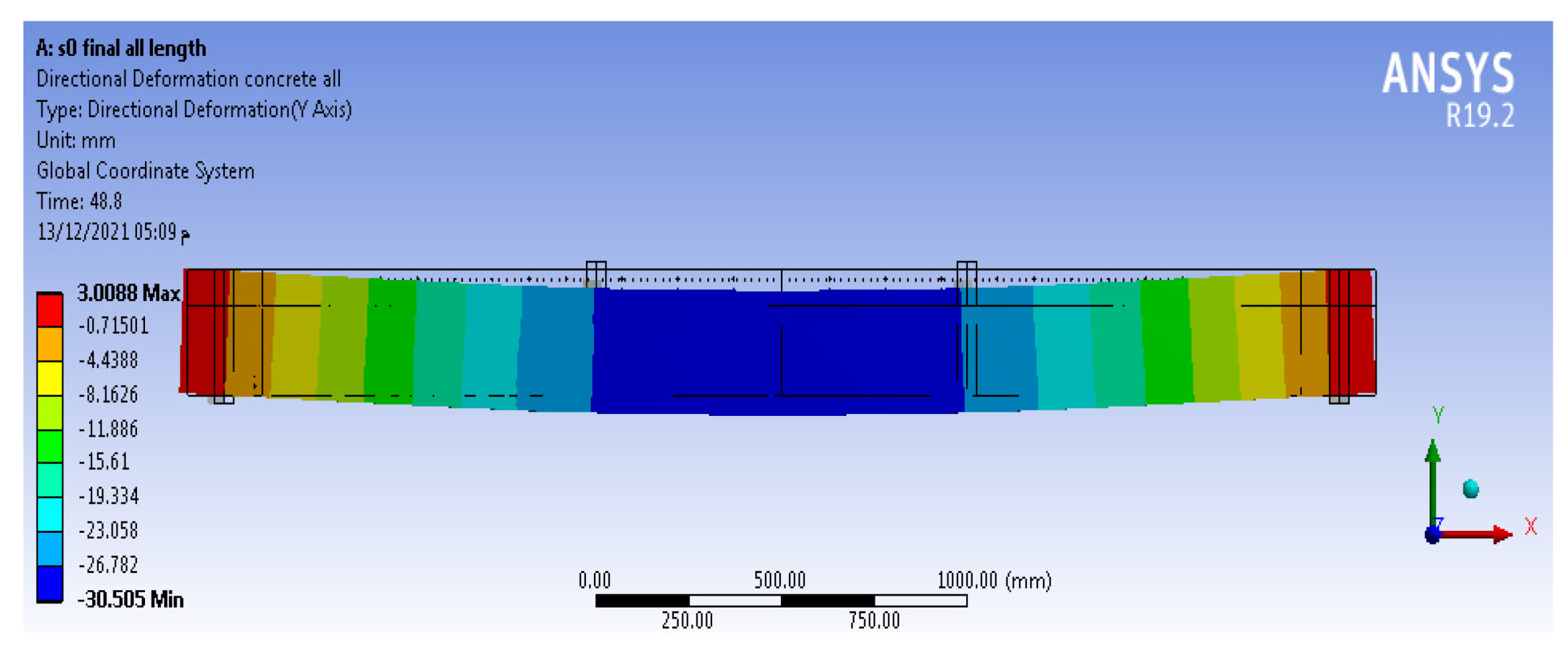
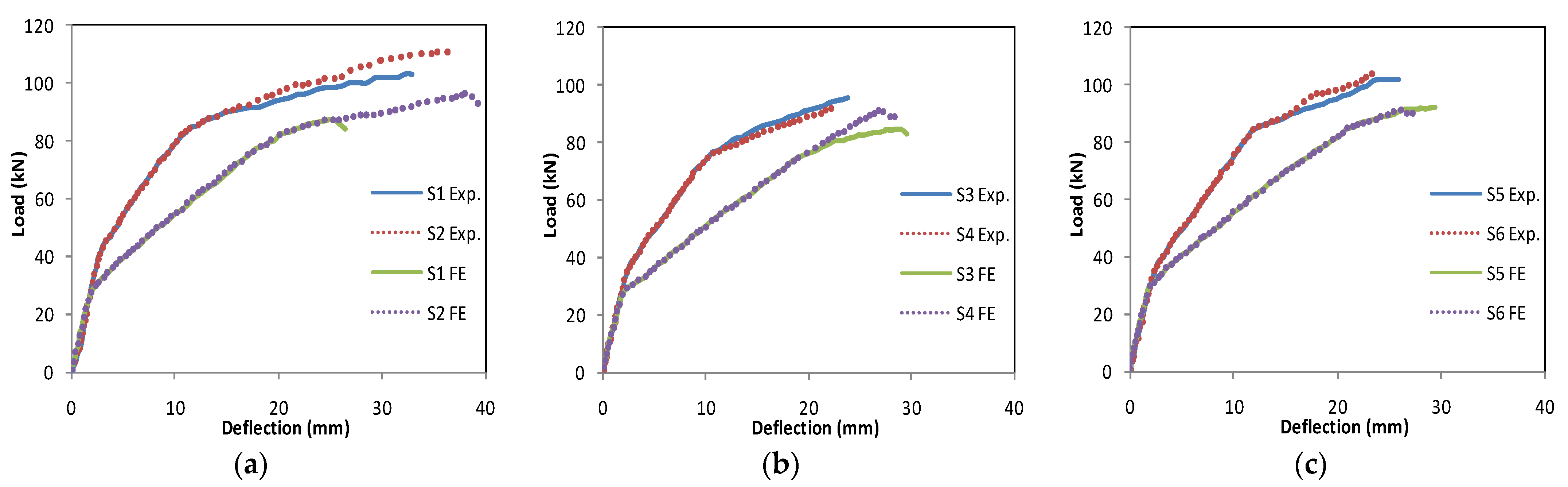
3. Verifications of the Models
3.1. Verification with Zou J. et al.
3.2. Verification with Harajli M. et al.
4. Strengthening Frames with External Tendons
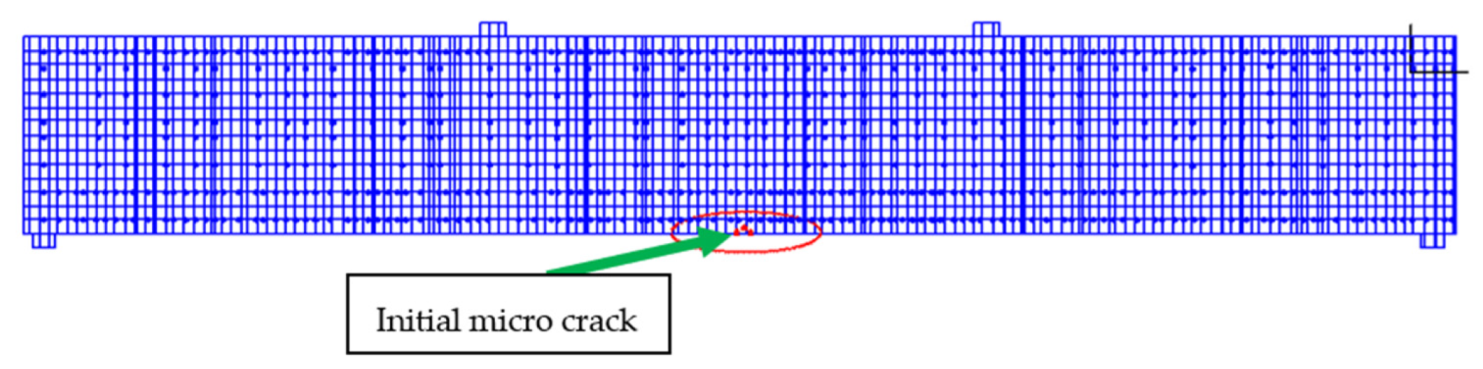
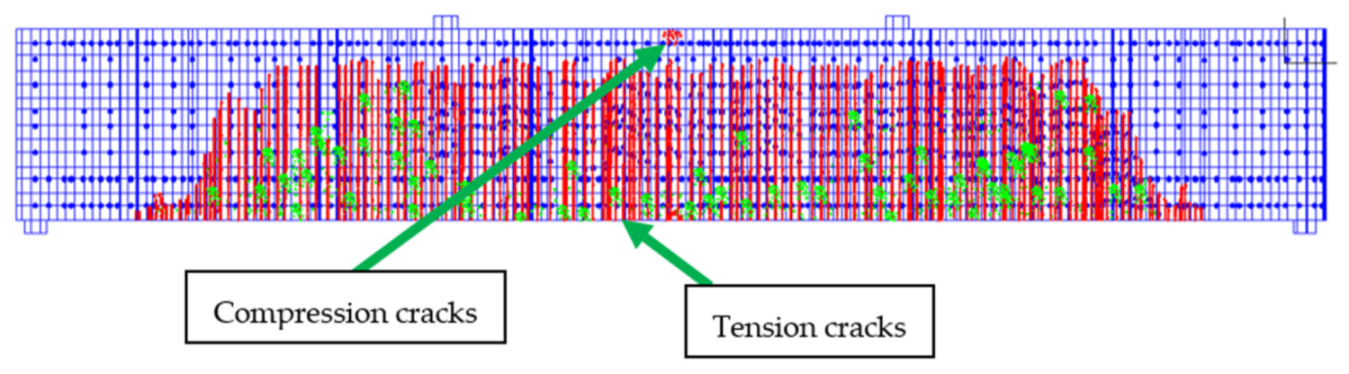
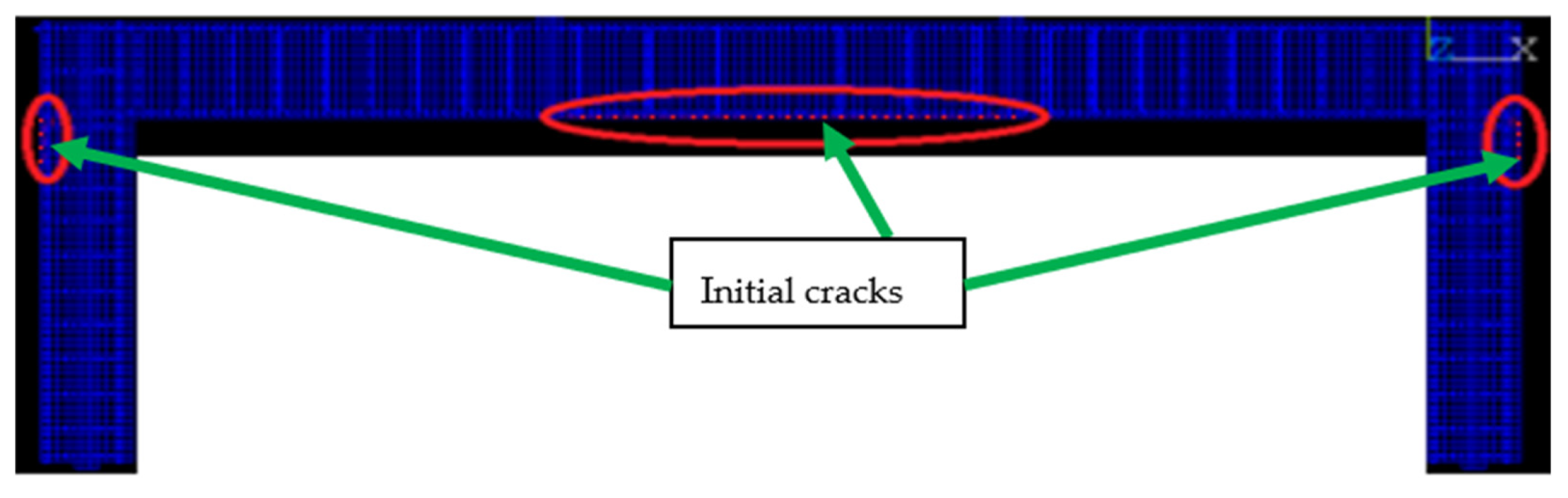
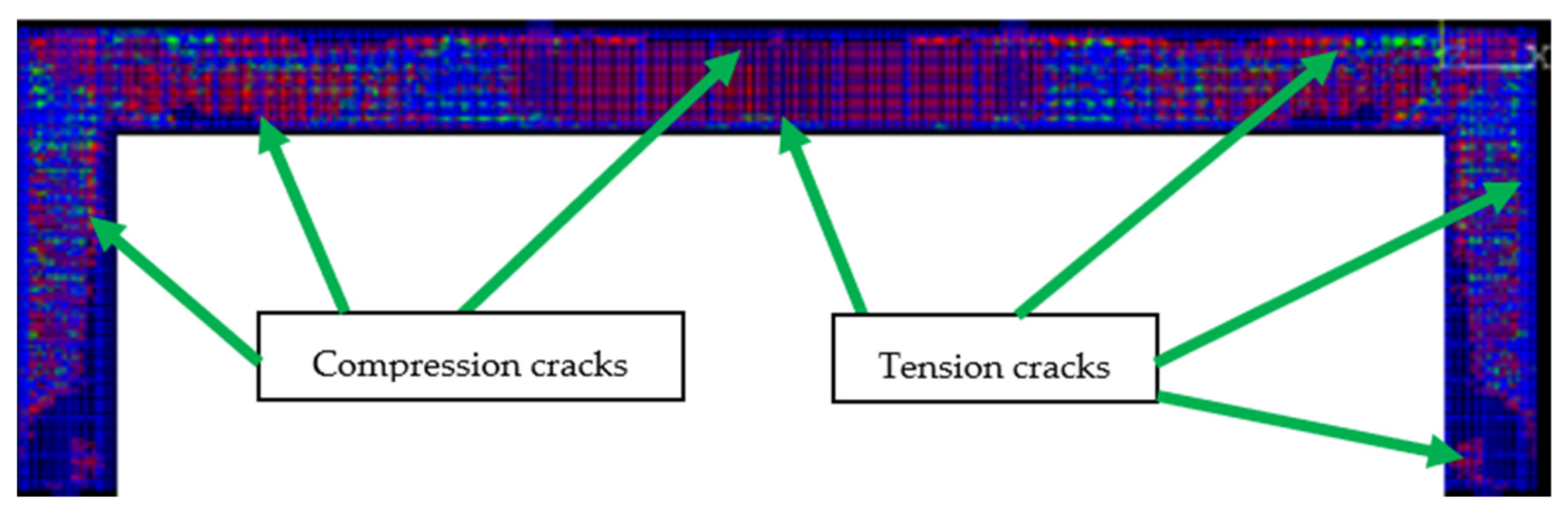
4.1. Failure Stages
- (1)
- Appearance of a micro-bending crack (cracking stage).
- (2)
- Yield of tensile steel reinforcement and rapid deflection (yielding stage).
- (3)
- Sample failure and submission due to large flexural deflections (ultimate stage).
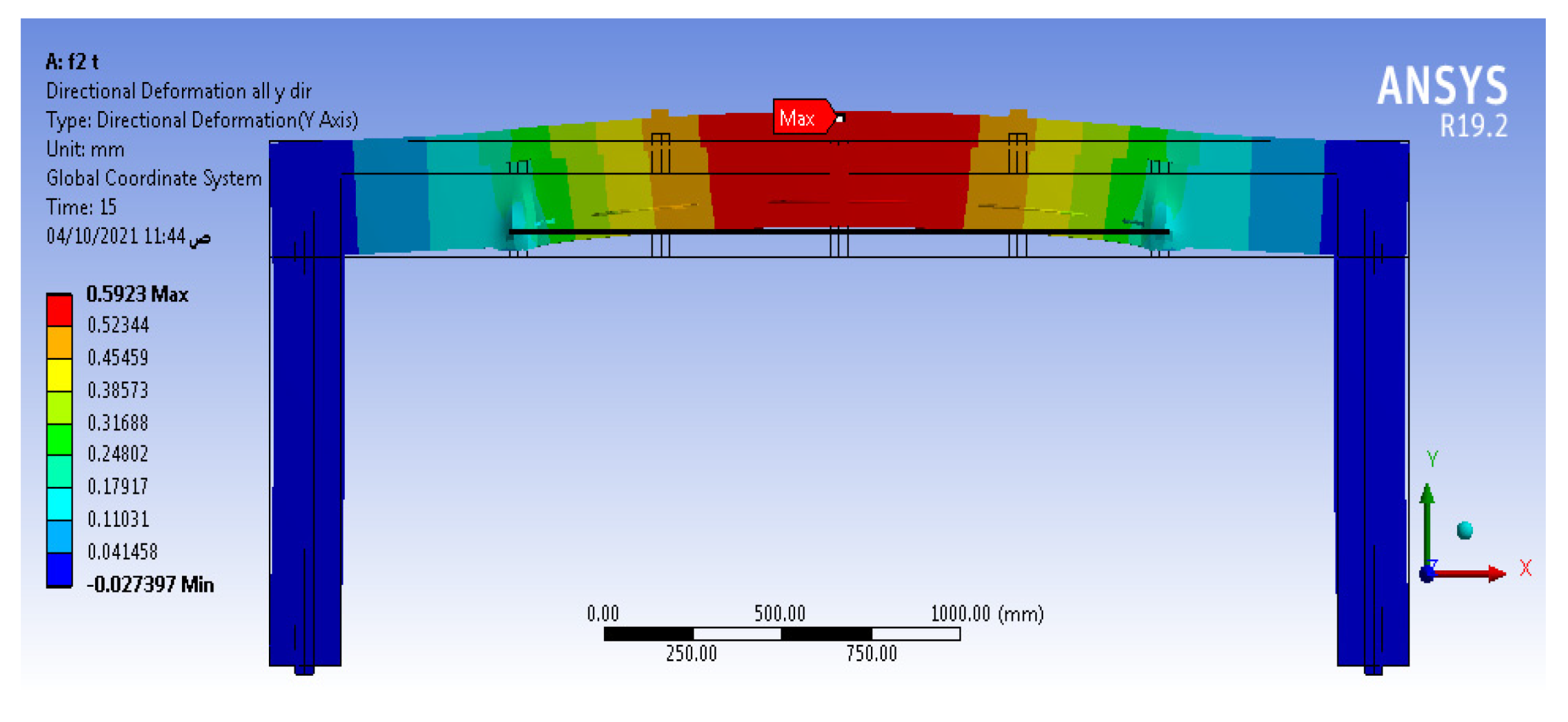
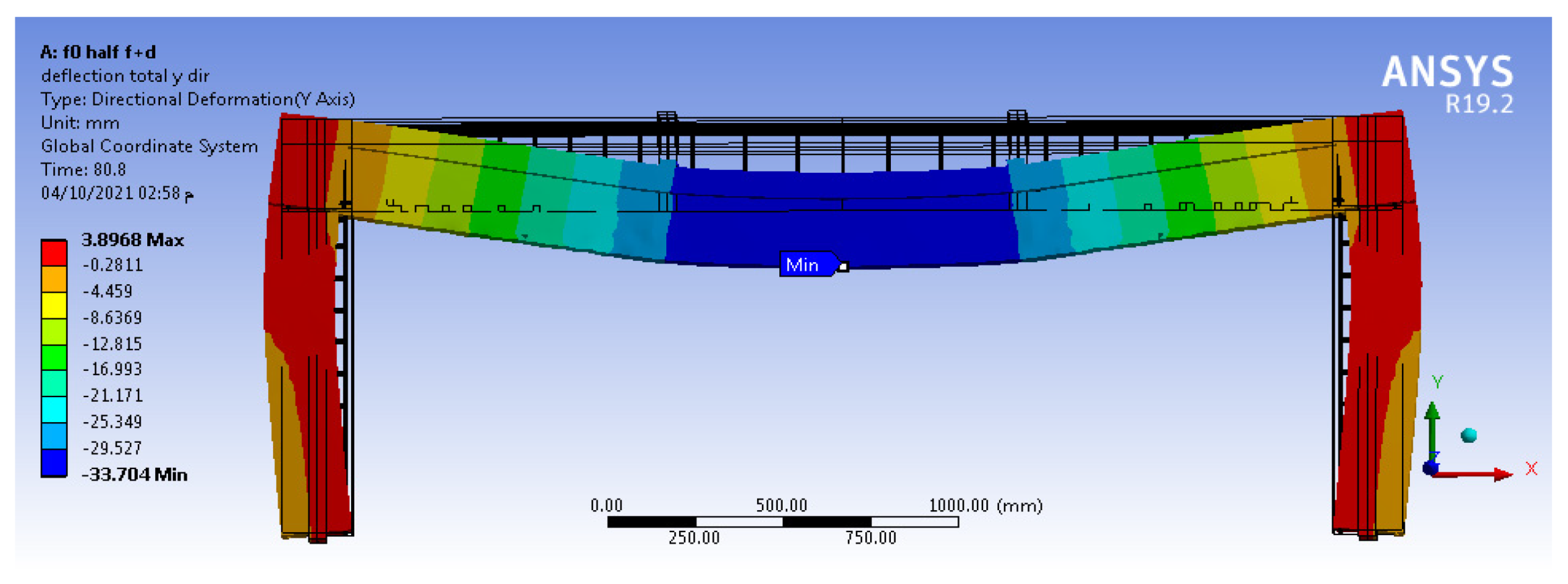
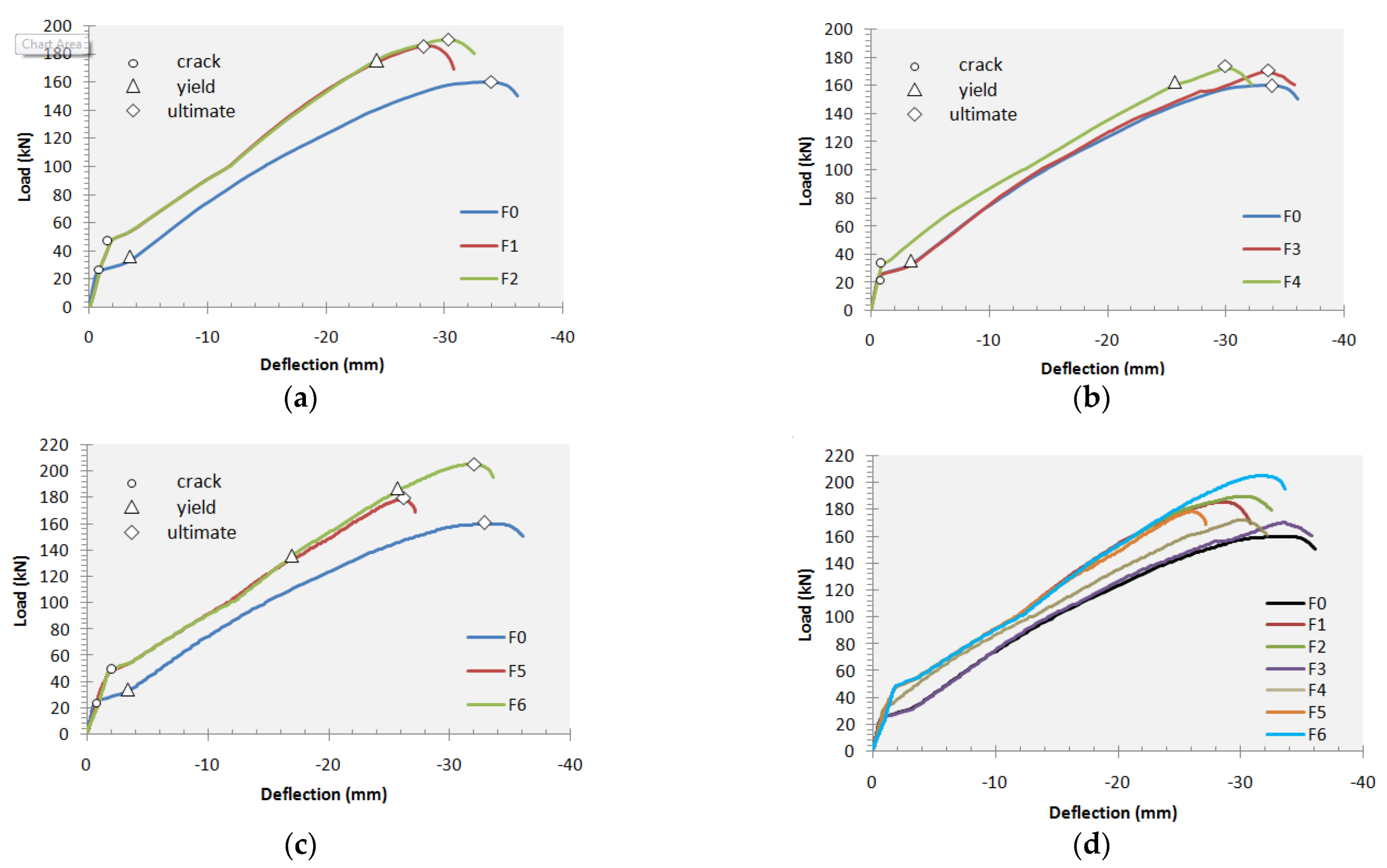
4.2. Load–Deflection Relation
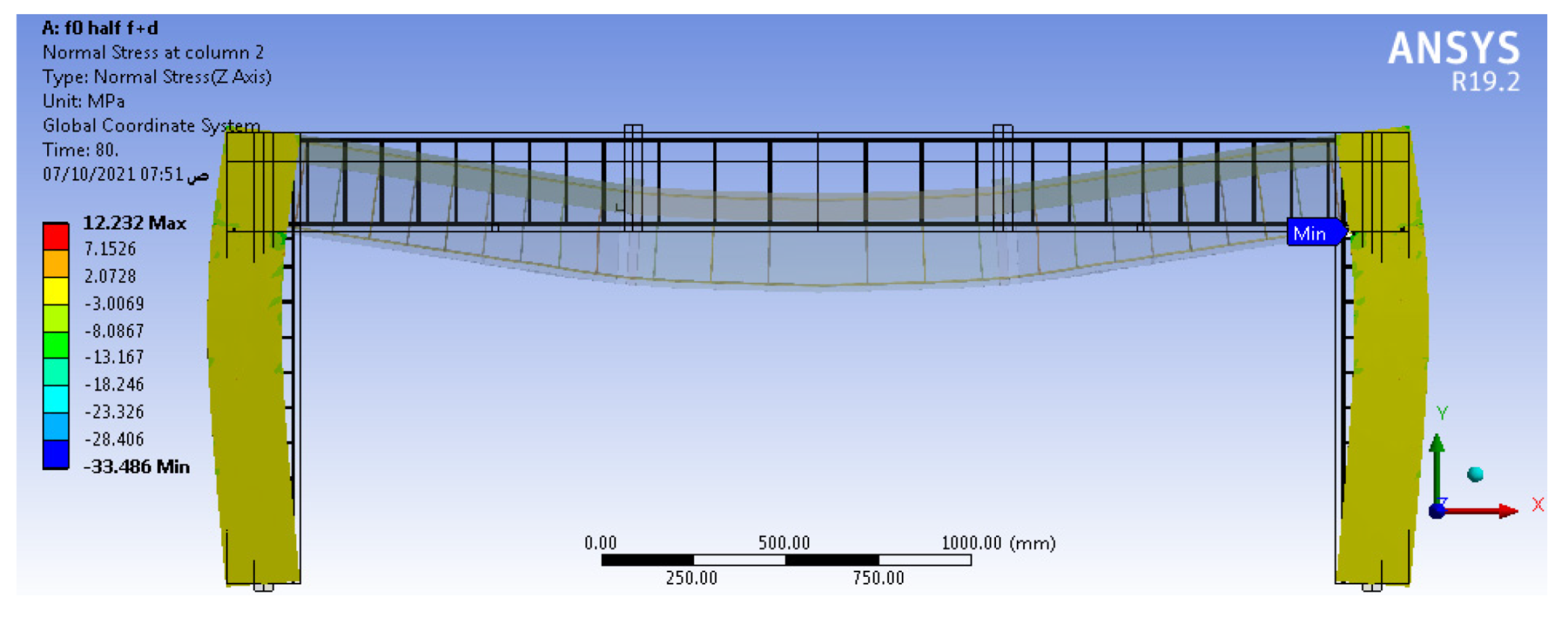
4.3. Stress of Columns
4.4. Load Capacity
4.5. Ductility Analysis
5. Conclusions and Recommendations
- Most of the FE results are roughly in agreement with those of the laboratory tests in the case of simple beams.
- The results show that strengthening with external pre-stressing tendons significantly improves the ultimate loading capacity and mechanical behavior of RC beams and frames.
- External strengthening frames with pre-stressing tendons can delay the initial cracking load by about 100–104% compared with the unstrengthening frame.
- External strengthening frames with pre-stressing tendons can increase the load-carrying by about 400–460% for yielding and 16–28% for failure compared to the unstrengthened sample.
- The tendon profile and the number of inner deviators exert a good effect on loading capacity and a light effect on ductility. All the samples that were strengthened with external tendons in the positive bending zone of the frame-beam (i.e., straight-line tendon F2 or U-shape tendons F6) increased loading capacity by about 11.5 and 19.1 %, respectively, compared to the samples that were strengthened without any tendons in the frame beam zone (i.e., straight-line tendon F3 or F4). Therefore, the technique of strengthening with external pre-stressing U-shaped tendons is recommended in the case of single-bay frames.
- Strengthening frames with external tendons in the beam-column connection zone is not an appropriate technique for single-bay frames because the tension in this region increases the stress on the columns and the effect of pre-stressing does not extend to the frame beam with adequate value.
- Further investigations need to be carried out to devise a convenient method of RC frames strengthening with external pre-stressing tendons based on the experimental study.
Author Contributions
Funding
Acknowledgments
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, J.; Huang, Y.; Feng, W.; Chen, Y.; Yue, H. Experimental study on flexural behavior of concrete T-beams strengthened with externally prestressed tendons. Math. Biosci. Eng. 2019, 16, 6962–6974. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-H.; Shin, K.-J.; Lee, H.-D. Post-Tensioning Steel Rod System for Flexural Strengthening in Damaged Reinforced Concrete (RC) Beams. Appl. Sci. 2018, 8, 1763. [Google Scholar] [CrossRef] [Green Version]
- Xin, Y.; Wu, J.; Wu, Q.; Cui, W.; Zhang, S.; Cheng, S. Study on the sickle anchoring joint in external prestressing strengthening of portal frame. Structures 2020, 28, 552–561. [Google Scholar] [CrossRef]
- Tan, K.-H.; Ng, C.-K. Effects of Deviators and Tendon Configuration on Behavior of Externally Prestressed Beams. ACI Struct. J. 1997, 94, 13–22. [Google Scholar] [CrossRef]
- Fan, Y.L. Collapse Behavior of RC Column-Beam Sub-Structure with External Prestressing Tendons. Appl. Mech. Mater. 2016, 847, 325–330. [Google Scholar] [CrossRef]
- Aslam, M.; Shafigh, P.; Jumaat, M.Z.; Shah, S.N.R. Strengthening of RC beams using prestressed fiber reinforced polymers—A review. Constr. Build. Mater. 2015, 82, 235–256. [Google Scholar] [CrossRef]
- Liu, T.; Xiao, Y.; Yang, J.; Chen, .S. CFRP Strip CableRetrofit of RC Frame for Collapse Resistance. J. Compos. Constr. 2017, 21, 04016067. [Google Scholar] [CrossRef]
- Mukherjee, A.; Rai, G. Performance of reinforced concrete beams externally prestressed with fiber composites. Constr. Build. Mater. 2009, 23, 822–828. [Google Scholar] [CrossRef]
- Nordin, H. Strengthening Structures with Externally Pre-Stressed Tendons Laboratory Tests; Technical Report; Department of Civil and Environmental Engineering, Division of Structural Engineering, Lulea University of Technology: Lulea, Sweden, 2005; ISRN LTU-TR--05/07—SE; Available online: http://www.diva-portal.org/smash/get/diva2:997963/FULLTEXT01.pdf (accessed on 20 November 2021).
- Nordin, H. Strengthening Structures with Externally Pre-Stressed Tendons Literature Review; Technical Report; Department of Civil and Environmental Engineering, Division of Structural Engineering, Lulea University of Technology: Lulea, Sweden, 2005; ISRN LTU-TR--05/06—SE; Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.620.5475&rep=rep1&type=pdf (accessed on 20 November 2021).
- Stoll, F.; Saliba, J.E.; Casper, L.E. Experimental study of CFRP-prestressed high-strength concrete bridge beams. Compos. Struct. 2000, 49, 191–200. [Google Scholar] [CrossRef]
- Picard, A.; Massicotte, B.; Bastien, J. Relative efficiency of external prestressing. J. Struct. Eng. 1995, 121, 1832–1841. [Google Scholar] [CrossRef]
- Abd-Elaty, I.; Eldeeb, H.; Vranayova, Z.; Zelenakova, M. Stability of Irrigation Canal Slopes Considering the Sea Level Rise and Dynamic Changes: Case Study El-Salam Canal, Egypt. Water 2019, 11, 1046. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Shin, W.-S. Retrofit of RC frames against progressive collapse using prestressing tendons. Struct. Des. Tall Spec. Build. 2013, 22, 349–361. [Google Scholar] [CrossRef]
- Mahmoud, N.S.; Badr, A.; Ssalem, F.A.; Ghannam, M. Strengthening steel frames by using post tensioned cable. Life Sci. J. 2014, 11, 111–116. Available online: https://www.researchgate.net/publication/289610723_Strengthing_steel_frames_by_using_post_tensioned_cable (accessed on 20 November 2021).
- Ghannam, M.; Mahmoud, N.S.; Badr, A.; Salem, F.A. Effect of post tensioning on strengthening different types of steel frames. J. King Saud Univ.-Eng. Sci. 2017, 29, 329–338. [Google Scholar] [CrossRef] [Green Version]
- Harajli, M.H. Strengthening of concrete beams by external prestressing. PCI J. 1993, 38, 76–88. Available online: https://www.pci.org/PCI_Docs/Publications/PCI%20Journal/1993/November/Strengthening%20of%20Concrete%20Beams%20by%20External%20Prestressing.pdfcable (accessed on 20 November 2021). [CrossRef]
- ANSYS WORKBENCH. Computer Software for Finite Element Analysis, Verification Manual, Release 19.2; ANSYS Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Harajli, M.; Khairallah, N.; Nassif, H. Externally prestressed members: Evaluation of second-order effects. J. Struct. Eng. 1999, 125, 1151–1161. [Google Scholar] [CrossRef]


| Beam Specimen | As (mm2) | fy (MPa) | Ape (mm2) | fpe (MPa) | fpu (MPa) | f ‘c (MPa) |
|---|---|---|---|---|---|---|
| For Steel | For Steel | For Tendon | For Tendon | For Tendon | for Concrete | |
| T2S | 340 | 612 | 39 | 935 | 1607 | 40.1 |
| T4S | 603 | 413.7 | 75 | 994 | 1986 | 41.8 |
| Sample No. | Cracking Stage | Yielding Stage | Ultimate Stage | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Load kN | Max. Deflection mm | Load kN | Max. Deflection mm | Max. Column Stress Mpa | Load kN | Max. Deflection mm | Max. Column Stress Mpa | Load kN | |
| F0 | 23 | 0.6 | 33 | 3.41 | 6.78 | 160 | 33.7 | 33.64 | 23 |
| F1 | 47 | 1.8 | 175.6 | 24.69 | 30.5 | 185.7 | 28.85 | 31.45 | 47 |
| F2 | 47 | 1.81 | 177.4 | 24.76 | 29.44 | 189.7 | 30.43 | 32 | 47 |
| F3 | 23 | 0.6 | 34 | 3.7 | 6.4 | 170.1 | 33.64 | 33.8 | 23 |
| F4 | 31 | 0.88 | 161 | 26 | 34.34 | 172.1 | 29.97 | 35 | 31 |
| F5 | 46 | 1.74 | 135.1 | 17.36 | 25.43 | 178.6 | 26.1 | 30 | 46 |
| F6 | 47 | 1.78 | 185.1 | 25.73 | 32.71 | 205 | 31.51 | 33.38 | 47 |
| Sample No. | Cracking Stage | Yielding Stage | Ultimate Stage | |||
|---|---|---|---|---|---|---|
| Load kN | % Increase | Load kN | % Increase | Load kN | % Increase | |
| F0 | 23 | - | 33 | - | 160 | - |
| F1 | 47 | 104.4 | 175.6 | 432.1 | 185.7 | 16.1 |
| F2 | 47 | 104.4 | 177.4 | 437.6 | 189.7 | 18.6 |
| F3 | 23 | 0 | 34 | 3 | 170.1 | 6.3 |
| F4 | 31 | 38.8 | 161 | 387.8 | 172.1 | 7.6 |
| F5 | 46 | 100 | 135.1 | 309.4 | 178.6 | 11.6 |
| F6 | 47 | 104.4 | 185.1 | 460.9 | 205 | 28.1 |
| Sample No. | ∆y mm | ∆u mm | µ = ∆u/∆y | % Decrease |
|---|---|---|---|---|
| F0 | 3.41 | 33.7 | 9.9 | - |
| F1 | 24.69 | 28.85 | 1.17 | 88.16 |
| F2 | 24.76 | 30.43 | 1.23 | 87.55 |
| F3 | 3.7 | 33.64 | 9.1 | 7.9 |
| F4 | 26 | 29.97 | 1.15 | 88.36 |
| F5 | 17.36 | 26.1 | 1.5 | 84.82 |
| F6 | 25.73 | 31.51 | 1.22 | 87.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, G.A.; Eisa, A.S.; Purcz, P.; El-Feky, M.H. Theoretical Study on the Flexural Behavior of Structural Elements Strengthened with External Pre-Stressing Methods. Appl. Sci. 2022, 12, 171. https://doi.org/10.3390/app12010171
Mohamed GA, Eisa AS, Purcz P, El-Feky MH. Theoretical Study on the Flexural Behavior of Structural Elements Strengthened with External Pre-Stressing Methods. Applied Sciences. 2022; 12(1):171. https://doi.org/10.3390/app12010171
Chicago/Turabian StyleMohamed, Gouda A., Ahmed S. Eisa, Pavol Purcz, and Mohamed H. El-Feky. 2022. "Theoretical Study on the Flexural Behavior of Structural Elements Strengthened with External Pre-Stressing Methods" Applied Sciences 12, no. 1: 171. https://doi.org/10.3390/app12010171
APA StyleMohamed, G. A., Eisa, A. S., Purcz, P., & El-Feky, M. H. (2022). Theoretical Study on the Flexural Behavior of Structural Elements Strengthened with External Pre-Stressing Methods. Applied Sciences, 12(1), 171. https://doi.org/10.3390/app12010171







