Calibration of Rotary Encoders Using a Shift-Angle Method
Abstract
:1. Introduction
2. Theory and Configuration
2.1. Shift-Angle Method for Polygon
2.2. Shift-Angle Method for Rotary Encoders
2.3. Self-Calibration
3. Experiments
3.1. Shift-Angle Method
3.2. Comparison of Calibration Results Obtained Using the Shift-Angle Method and Self-Calibration
3.3. Uncertainty Evaluation
- (1)
- Repeatability of angle error measurement.
- (2)
- Resolution of the autocollimator.
- (3)
- Traceability of the autocollimator.
- (4)
- Angle error of the autocollimator.
- (5)
- Resolution of SelfA rotary encoder.
- (6)
- Residual setup error calculation.
- (7)
- Repeatability of the pitch angle deviation measurement, β.
- (8)
- Setup error of the polygon, U.
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lu, X.D.; Trumper, D.L. Self-calibration of on-axis rotary encoders. CIRP Ann. 2007, 56, 499–504. [Google Scholar] [CrossRef]
- Masuda, T.; Kajitani, M. An Automatic Calibration System for Angular Encoders. Precis. Eng. 1989, 11, 95–100. [Google Scholar] [CrossRef]
- Probst, R.; Wittekopf, R.; Krause, M.; Dangschat, H.; Ernst, A. The new PTB angle comparator. Meas. Sci. Technol. 1998, 9, 1059–1066. [Google Scholar] [CrossRef]
- Probst, R. Self-calibration of divided circles on the basis of a prime factor algorithm. Meas. Sci. Technol. 2008, 19, 015101. [Google Scholar] [CrossRef]
- Geckeler, R.D.; Link, A.; Krause, M.; Elster, C. Capabilities and limitations of the self-calibration of angle encoders. Meas. Sci. Technol. 2014, 25, 055003. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Y.; Dong, Z.G.; Ding, Y.; Liu, P.K. Optimal arrangements of scanning heads for self-calibration of angle encoders. Meas. Sci. Technol. 2017, 28, 105013. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Y.; Ding, Y.; Dong, Z.G.; Huang, M.; Liu, P.K. Optimal-arrangement-based four-scanning-heads error separation technique for self-calibration of angle encoders. Meas. Sci. Technol. 2018, 29, 085005. [Google Scholar] [CrossRef]
- Watanabe, T.; Fujimoto, H.; Masuda, T. Self-calibratable rotary encoder. J. Phys. Conf. Ser. 2005, 13, 240. [Google Scholar] [CrossRef]
- Watanabe, T.; Hiroyuki, F. Application of a self-calibratable rotary encoder. Proc. ISMTII 2009, 3, 54–58. [Google Scholar]
- Watanabe, T.; Kon, M.; Nebeshima, N.; Taniguchi, K. An angle encoder for super-high resolution and super-high accuracy using SelfA. Meas. Sci. Technol. 2014, 25, 065002. [Google Scholar] [CrossRef]
- Ueyama, Y.; Furutani, R.; Watanabe, T. A super-high-accuracy angular index table. Meas. Sci. Technol. 2020, 31, 094006. [Google Scholar] [CrossRef]
- Pavlov, P.A. Aspects of the Cross-Calibration Method in Laser Gonimetry. Meas. Tech. 2015, 58, 970–974. [Google Scholar] [CrossRef]
- Pavlov, P.A. A Method for investigating the error of a laser dynamic goniometry. Meas. Tech. 2020, 63, 106–110. [Google Scholar] [CrossRef]
- Akgoz, S.-A.; Yangdayan, T. High precision calibration of polygons for emerging demands. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1065, 142005. [Google Scholar] [CrossRef]
- Jia, H.K.; Yu, L.D.; Zhao, H.N.; Jiang, Y.-Z. A new method of angle measurement error analysis of rotary encoders. Appl. Sci. 2019, 9, 3415. [Google Scholar] [CrossRef] [Green Version]
- Reeve, P.C. The calibration of indexing tables by subdivision. NBS Int. Rep. 1975, 1–37, 75–750. [Google Scholar]
- Estler, W.T.; Queen, Y.H.; Bryan, J. An advanced angle metrology system. CIRP Ann. 1993, 42, 573–576. [Google Scholar] [CrossRef]
- Kim, J.A.; Kim, J.W.; Kang, C.S.; Jin, J.H.; Eom, T.-B. Calibration of angle artifacts and instruments using a high precision angle generator. Int. J. Precis. Eng. Manuf. 2012, 14, 367–371. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, Z.; Huang, M.; Qiao, D. The NIM continuous full circle angel standard. Meas. Sci. Technol. 2018, 29, 074013. [Google Scholar] [CrossRef]
- Pisani, M.; Astrua, M. The new INRIM rotating encoder angle comparator (REAC). Meas. Sci. Technol. 2017, 28, 045008. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008. Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Estler, W.T. Uncertainty analysis for angle calibrations using circle closure. J. Res. NIST 1998, 103, 141–151. [Google Scholar] [CrossRef] [PubMed]

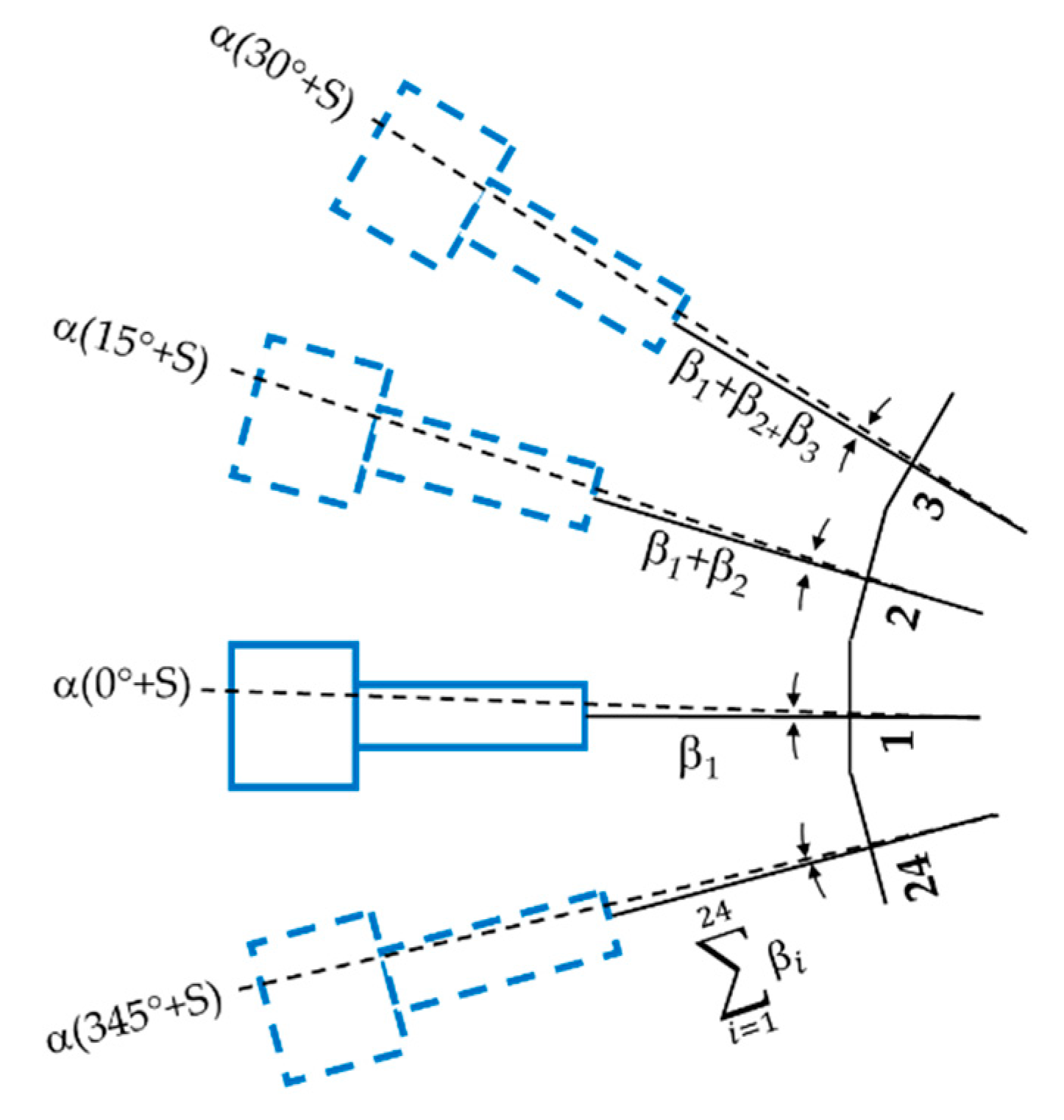
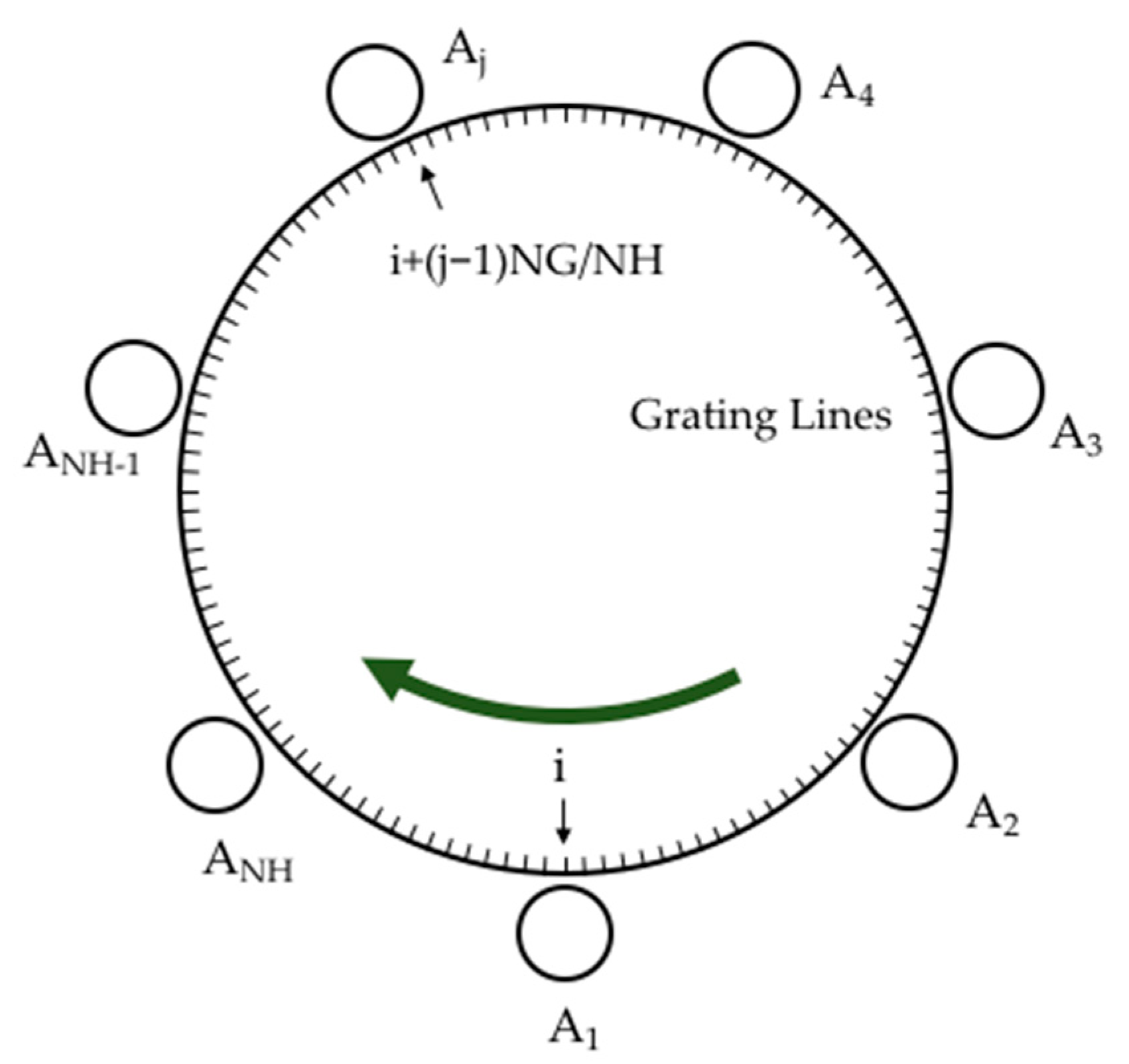

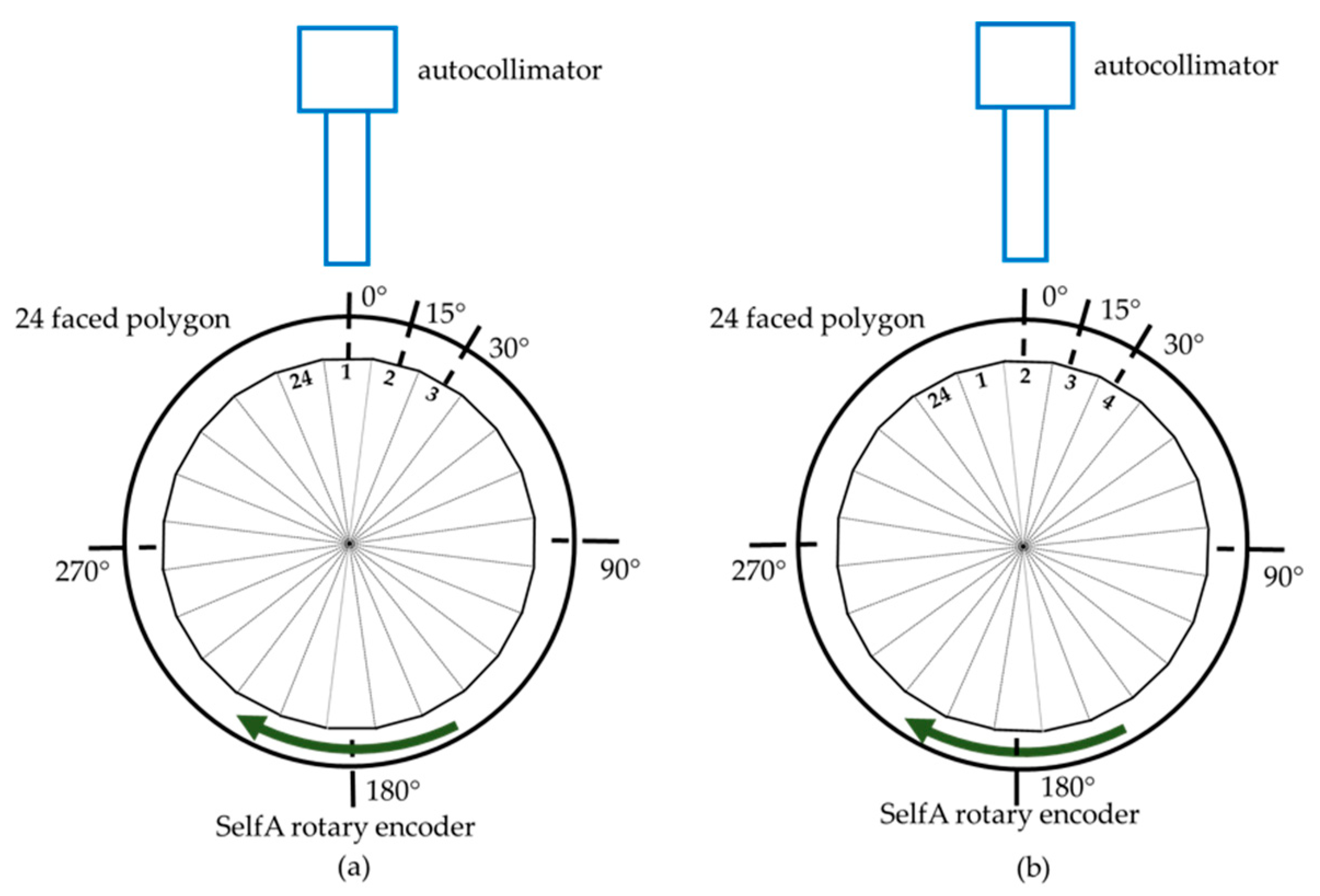


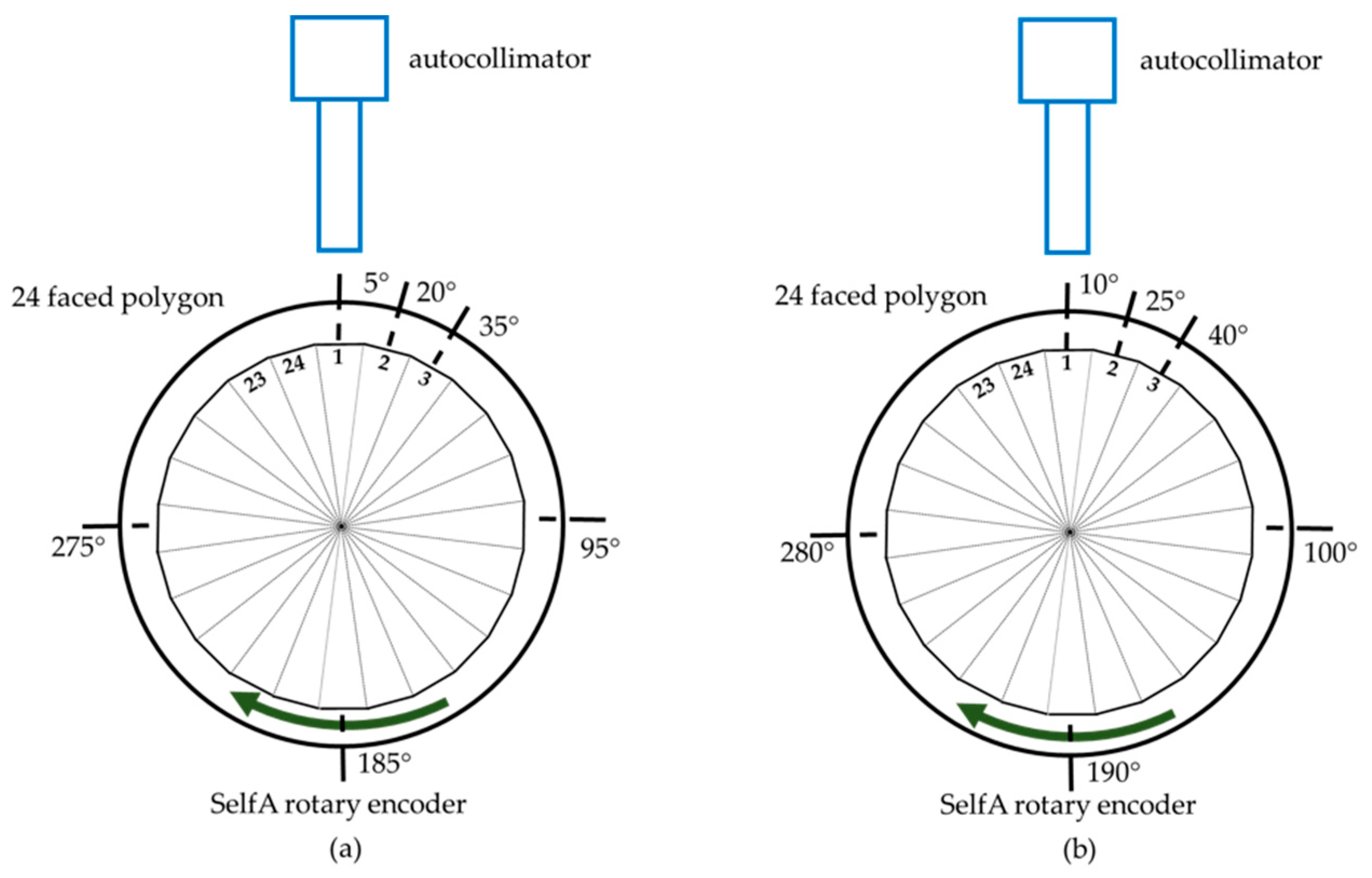




| i | 1 | 2 | … | 23 | 24 |
|---|---|---|---|---|---|
| j | |||||
| 1 | … | ||||
| 2 | … | ||||
| … | … | … | … | … | … |
| 23 | … | ||||
| 24 | … | ||||
| l,m n | 2,1 | l,m n | 3,2 | … | l,m n | 24,23 | l,m n | 25,24 | The Average of the Row |
|---|---|---|---|---|---|---|---|---|---|
| 24 | 23 | … | 2 | 1 | |||||
| 1 | 24 | … | 3 | 2 | |||||
| … | … | … | … | … | … | … | … | … | … |
| 22 | 21 | … | 24 | 23 | |||||
| 23 | 22 | … | 1 | 24 | |||||
| Standard Uncertainty | u | Degree of Freedom | ||
|---|---|---|---|---|
| measured value uncertainty, ε | 0.0676″ | 1 | 0.0676″ | 12 |
| Repeatability of angle error measurement | 0.0531″ | 1 | 0.0531″ | 5 |
| Resolution of the autocollimator | 0.0003″ | 1 | 0.0003″ | 50 |
| Traceability of the autocollimator | 0.0050″ | 1 | 0.0050″ | 50 |
| Angle error of autocollimator | 0.0404″ | 1 | 0.0404″ | 50 |
| Resolution of the rotary encoder | 0.0101″ | 1 | 0.0101″ | 50 |
| Residual setup error calculation | 0.0001″ | 1 | 0.0001″ | 50 |
| Repeatability of the pitch angle deviation measurement | 0.0490″ | 0.0401 | 0.0020″ | 5 |
| setup error uncertainty | 0.0144″ | 1 | 0.0144″ | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, T.-H.; Watanabe, T.; Hsu, P.-E. Calibration of Rotary Encoders Using a Shift-Angle Method. Appl. Sci. 2022, 12, 5008. https://doi.org/10.3390/app12105008
Hsieh T-H, Watanabe T, Hsu P-E. Calibration of Rotary Encoders Using a Shift-Angle Method. Applied Sciences. 2022; 12(10):5008. https://doi.org/10.3390/app12105008
Chicago/Turabian StyleHsieh, Tsung-Han, Tsukasa Watanabe, and Po-Er Hsu. 2022. "Calibration of Rotary Encoders Using a Shift-Angle Method" Applied Sciences 12, no. 10: 5008. https://doi.org/10.3390/app12105008
APA StyleHsieh, T.-H., Watanabe, T., & Hsu, P.-E. (2022). Calibration of Rotary Encoders Using a Shift-Angle Method. Applied Sciences, 12(10), 5008. https://doi.org/10.3390/app12105008







