Experimental and Numerical Study of Pressure Drop Characteristics of Soybean Grain under Vertical Pressure

Abstract

The vertical pressure lead to increased airflow resistance through the grain bulk, which affected the efficiency of ventilation and drying. The effects of vertical pressures at 50, 150, and 250 kPa on the pressure drop characteristics of soybeans were studied using experiment and numerical simulation. The random packing and different compression states for soybean packed beds were generated by the Discrete Element Method (DEM). The Discrete Element Method (DEM) and Computational Fluid Dynamics (CFD) were coupled to investigate the radial velocity and pressure drop of soybean bulk. The simulation results showed that the radial porosity had an oscillating distribution, and the radial average dimensionless velocity was consistent with the distribution trend of porosity. The increase in vertical pressure causes a decrease in porosity and an increase in local velocity. The PathFinder code was used as a supplementary method to calculate the pore path and pore characterization parameters, and the resistance coefficient term in the Forchheimer equation was determined. The compression of soybeans measured by the experiment mainly occurred within two hours after loading. The pressure drop of soybeans increased with the vertical pressure, with the average pressure drop at vertical pressures of 50, 150, and 250 kPa being 36%, 57%, and 92% higher than the uncompressed state (0 kPa). The pressure drop of soybeans calculated by the DEM-CFD method and the Forchheimer equation under different vertical pressures were in close agreement with the experimental results, and an average relative difference was found to be less than 10%. These results provide guidance for estimating the pressure drop of soybeans at different grain depths.

1. Introduction

Soybeans are mostly stored in bulk after harvesting, cleaning, and drying. Temperature and moisture in the grain storage ecosystem are principal factors affecting the security of grain storage. To ensure grain quality, grain bulk must be kept below a safe moisture level and temperature [1,2]. Effective aeration, temperature control, and humidity control measures are required promptly after monitoring abnormally high local grain temperatures. Aeration, the most commonly utilized method in grain storage technology, maintains the temperature in the grain bulk and avoids the temperature fluctuation caused by convection, grain metabolism, and insect and microbial growth [3,4]. In the grain bulk, the vertical pressure distribution is different due to the self-weight of grain. The grain is subjected to different levels of compression. The bulk density and porosity change with vertical pressure [5,6,7].

The process of aeration is to force external air into the grain bulk and thus reduce the grain temperature. However, airflow through the grain is hindered. Airflow resistance is the pressure drop per unit of grain depth due to friction and turbulence. Therefore, the fan power in the aeration system needs to overcome the airflow resistance through the grain bulk. Fans that are selected incorrectly lead to uneven cooling or increased aeration costs [8]. Specifying the airflow resistance through grain bulk is the basis of aeration system design.

Granular materials have creeping compression characteristics, which are more obvious under vertical pressure. As a typical porous medium, grain bulk has an irregular pore structure, making airflow characteristics more complex and variable [9]. Neethirajan et al. [10] found that the long axis of grain particles is more inclined in the horizontal direction after they enter the bin, which results in a higher porosity in the horizontal direction as compared to the vertical direction, leading to a difference in airflow resistance in the horizontal and vertical direction. Haque [11] showed that the bulk density and porosity change with the spatial position of the grain bulk, and the pressure drop considering the change in porosity will be higher than the value calculated by the Shedd equation. The pressure drop through grain bulk is greatly affected by the pore characteristics. For grain aeration technology, it is critical to determine the pressure drop through grain bulk under vertical pressure. Pressure drop in rice [12,13,14], wheat [15,16], soybeans [17], corn [18], rape [19], and other crops has been studied using a variety of variables such as airflow velocity, bed depth, moisture content, filling mode, and theoretical models of pressure drop calculation [20,21].

Khatchatourian et al. [22] found that since the grain is compacted with the increase in depth, the airflow velocity and pressure drop through the grain bulk change significantly with the heterogeneous pore structure. Kobus et al. [23] showed that the airflow resistance through oat grains increased with the external load and loading time. Haque et al. [24] and Cheng et al. [25] showed that the porosity decreased under vertical pressure, which increased the airflow resistance of the grain bulk and hindered the aeration operation. Yue et al. [26] verified that the pore structure in grain bulk is more complex and tortuous after compacting, resulting in higher airflow resistance.

Experimental and theoretical formula calculation methods are often used to study the pressure drop of the grain bulk, but there are few accurate and efficient numerical calculation models. Moses et al. [27] obtained a nonlinear model by the finite element method to study the airflow distribution in a three-dimensional grain-packed bed. Khatchatourian et al. [28] simulated the airflow distribution in the bin, after considering the inhomogeneity of porosity at different depths. But the above numerical calculation model cannot reflect the real pore structure distribution of packed grain particles. DEM, an efficient method to study the particle-packed structure in recent years, can construct the real-packed and compressed processes of particles [29]. The DEM-CFD coupling method, which has been widely used in biomass drying [30], chemical mass transfer [31], and nuclear reaction [32], can accurately simulate airflow and heat transfer processes in the packed bed.

In this research, an apparatus was designed to measure the airflow resistance through soybeans under vertical compression. Soybean pile units at different locations in grain silos were used as the research objects. The effects of the pressure drop characteristics of soybeans at 50, 150, and 250 kPa vertical pressures were studied through vertical compression and aeration tests. The DEM was used to simulate the random packing and compression process of soybeans, and the airflow velocity and pressure drop of soybeans at different vertical pressures were simulated and analyzed by the DEM-CFD method. The airflow path distribution and pressure drop equation coefficients were predicted based on the PathFinder code. The simulated and equation-calculated pressure drops were compared with experiments to verify their reliability.

2. Materials and Methods

2.1. Materials

The soybean used in this experiment was Zhonghuang 39, harvested in 2020. The soybean sample was filtered through a circular sieve to remove broken grains and foreign impurities. The initial moisture content of soybean samples was determined to be 12.8 ± 0.1% (w. b.) after drying at 103 °C for 72 h [33]. To determine the size characteristics of single soybean grains, 100 grains were randomly selected to measure their triaxial dimensions of length, width, and thickness. The geometric mean diameter was calculated using the procedure proposed by Aghbashlo [34]. The method of calculation is shown in Equation (1):

$$d_p=3L_p{W}_p{T}_p{(L_p{W}_p+L_p{T}_p+W_p{T}_p)}^{-1}$$

(1)

where d_p is the geometric mean diameter of the single soybean grain; L_p, W_p, and T_p are the length, width, and thickness of the soybean grain. The average diameter of soybean particles used in this experiment was d_p = 7.24 mm.

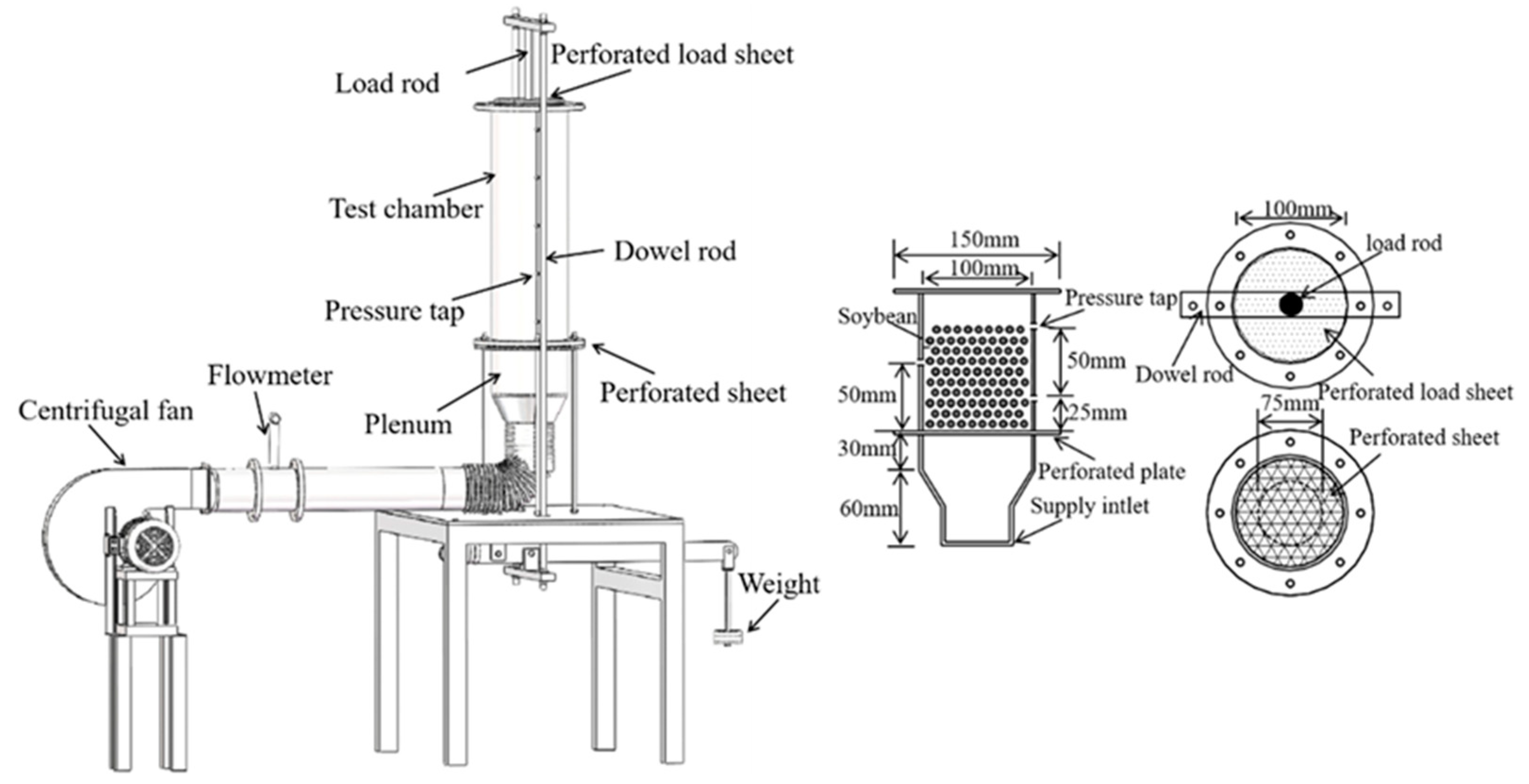
2.2. Experimental Apparatus

In Figure 1, the experimental apparatus with the aeration and the compaction system measures the pressure drop and compression characteristics. The aeration system includes a test chamber, a centrifugal fan, and a PVC pipeline. The test chamber is cylindrical, made of transparent acrylic sheet, with a diameter of 100 mm. The bottom is connected to the perforated sheet and installed on the support table. The centrifugal fan (Model RYP-025, Shanghai Junjie mechanical equipment Co., Ltd., Shanghai, China) is controlled by a frequency inverter (Model ZK880, Zhengkong New Energy Co., Ltd., Zhejiang, China) to obtain different inlet velocities. The PVC pipeline connects the centrifugal fan to the test chamber and uses a flowmeter (model 6443-DN80, Testo, Sparta Township, NJ, USA) installed on it to measure the airflow. Static pressure at the pressure taps was measured using a digital micromanometer (model DP-5815, TSI, Shoreview, MN, USA). To minimize the loss of air pressure, all pipeline connections were sealed. The vertical pressure was applied to the grain by a perforated load sheet. The weights were loaded on a tray, and the vertical pressure was transmitted to the perforated load sheet through a lever. During the experiment, air flowed upward and the grain was compressed downward.

2.3. Experimental Procedure

The soybean samples were dropped into the test chamber, and the grain surface was paved. The perforated loading sheet was placed on the grain surface. The loading rod was kept vertical, the lever was adjusted to horizontal, and the height of the packed grain section was recorded H = 75 mm. The pressure drop of the grain samples was measured without vertical pressure (0 kPa). The inlet velocity was set in a range of 0.02 to 0.6 m/s, and the static pressure at the pressure tap under different velocities was recorded. Tests were set up with three vertical pressures of 50, 150, and 250 kPa, and the displacement of the perforated loading sheet was obtained using a digital caliper every 5 min during the first hour after loading and every hour until the test was finished. Bulk grains show creep deformation under load, and grain compression reaches stability when the change in displacement is less than 0.2% of the total displacement [7,25]. The test measured the change in 12 h. After each set of compression tests was stabilized, the pressure drop under different vertical pressures was measured at the same inlet velocity as the uncompressed state (0 kPa).

3. Numerical Simulation Models and Methods

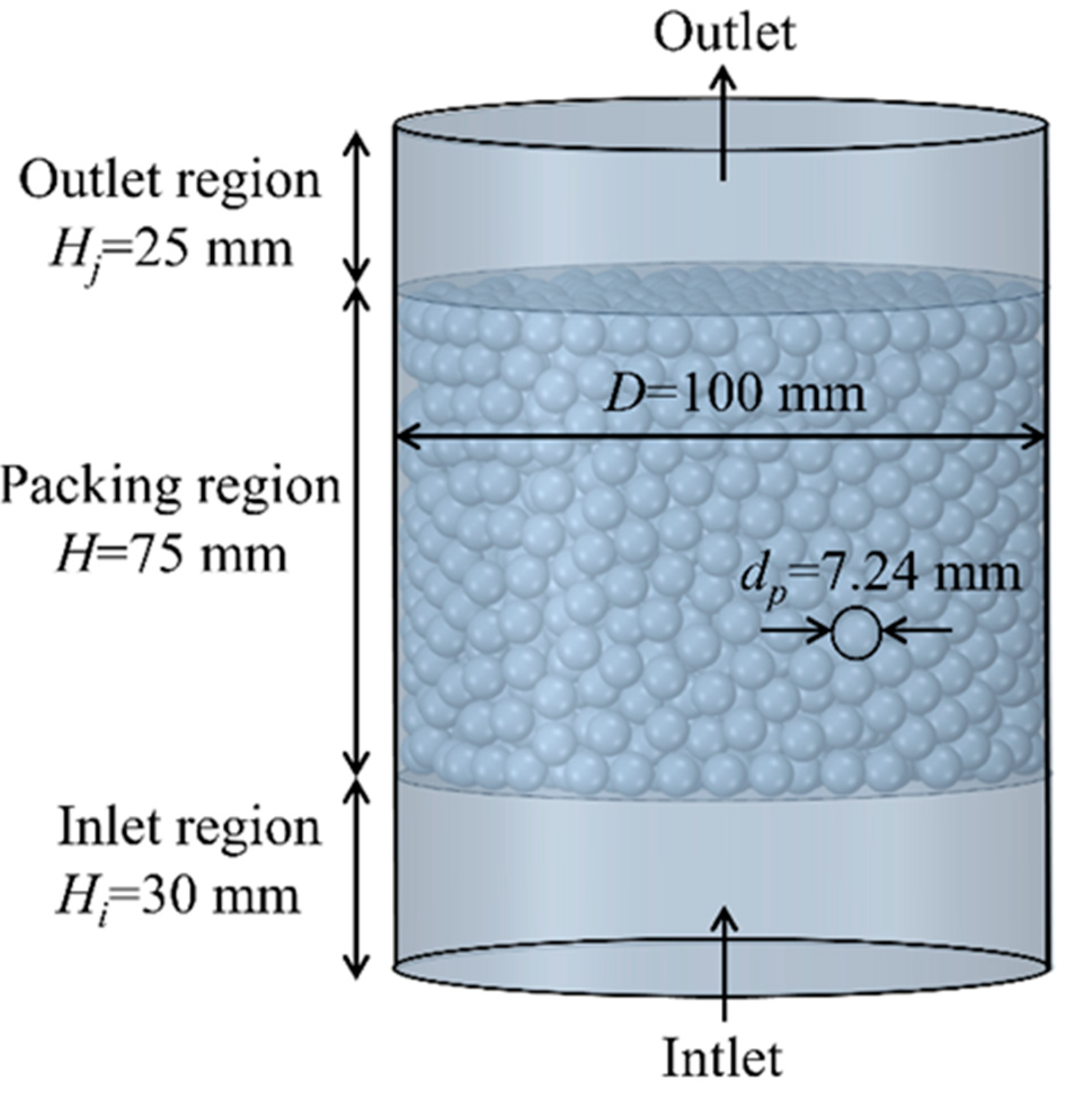
3.1. DEM Modeling

In this study, commercial software EDEM 2018 was used for particle stacking and vertical compression processes. During the DEM packing process, spherical particles with a diameter of 7.24 mm were generated at the top of the container and fell by gravity to form a cylindrical packed structure with a diameter of R = 100 mm and a height of H = 75 mm. The wall effect has less effect on the packing rate when the diameter ratio of packed bed to particle is more than 10 [35,36]. Based on the Hertz-Mindlin contact model, a total of 1815 particles were generated after considering the particle-particle and particle-wall interaction. The DEM packed structure modeling parameters are listed in

Table 1. Soybean particle parameters used in the DEM simulation.

Parameters	Symbol	Value
Packed bed dimension	D × H, m	0.1 × 0.075
Particle diameter	dp, m	0.00724
Particle density	ρp, kg/m3	1257
Poisson ratio	ν	0.4
Modulus of elasticity	E, Pa	7.6 × 108
static friction coefficient	μs	0.2
rolling friction Coefficient	μr	0.02
Coefficient of restitution	e	0.627

[37]. After the pack was constructed, a circular loading sheet was created on its upper surface and compressed downward at a constant speed, stopping when the downward movement of the loading sheet reaches the test displacement. The information of DEM gravity packing and compressed particles was exported, and then the Gambit software was used to reconstruct the geometric model of particles and the outer cylindrical wall of the packing section, setting the inlet region H_i = 30 mm and the outlet region H_j = 25 mm in the packing section to reduce the inlet and outlet effects. The geometric model of soybean particle packing is shown in Figure 2.

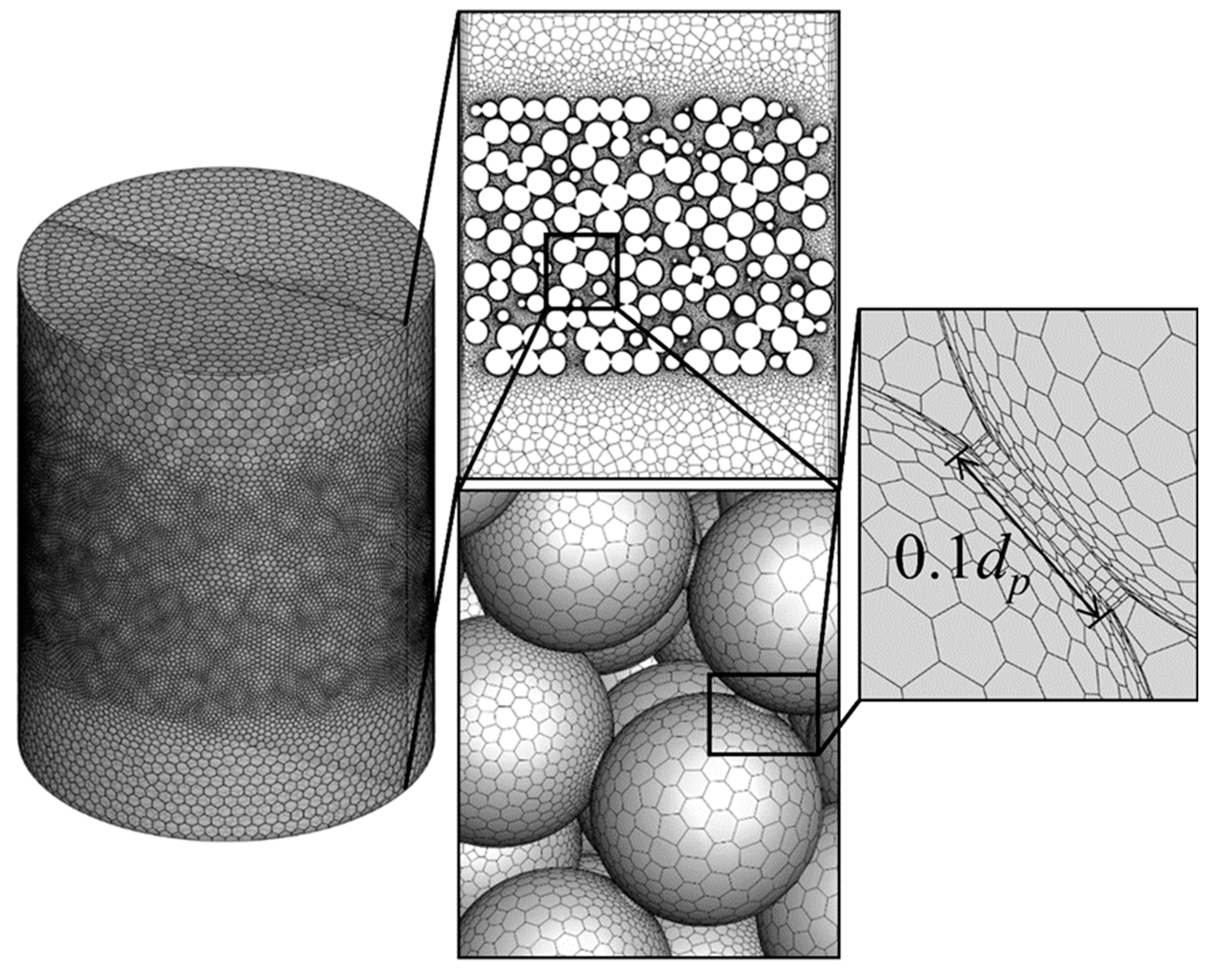
3.2. Mesh Generation

A self-developed scripting program was used to generate the constructed randomly packed particles and geometric models. The reconstructed spherical particles will have point contacts or narrow gaps between them, which is not suitable for mesh generation. When meshing directly, the grid cells near the contact points will have large skewness, making the simulation hard to converge and affecting the calculation accuracy, so the contact between the particles needs to be processed. The main existing treatment methods include decreased size, increased size, bridges, and caps [38]. The decreased size and increased size methods change the radius of the sphere, which changes the porosity of the packed bed. The bridges and caps methods only treat the contact points locally, ensuring the accuracy of the geometric model of the packed bed. In this study, we used the bridges method for contact treatments to simulate the airflow process more realistically, setting the diameter of the cylindrical bridge to 0.1 d_p and increasing the diameter of the geometric by 1% [39]. Due to the complexity of the packed bed, the model was meshed using polyhedral in ANSYS Fluent Meshing and the maximum mesh size was set to 1/15 d_p [40]. The particle surfaces and geometric cylindrical surfaces were set up with three boundary layers using the smooth transition method, and the boundary layer growth rate was 0.27. The mesh division and contact treatment are shown in Figure 3.

3.3. CFD Modeling

The commercial software ANSYS Fluent 18.2 was used to calculate and solve the pressure drop characteristics of the soybean packed bed. The inlet and outlet of the model were set as velocity inlet and pressure outlet boundaries, respectively, and the cylindrical wall surface and grain particle surface were set as nonslip velocity boundaries. Eisfeld et al. [41] provided an accurate definition of the flow in a fixed bed and showed that the flow in the bed is laminar when the particle Reynolds number Rep is less than 300. In this simulation, the inlet velocity was set to 0.02–0.6 m/s and the Rep was 10–297, so the laminar flow model was used for calculation. When solving the computational model, the energy equation is not considered, only the continuity equation (Equation (2)) and the momentum conservation equation (Equation (3)) of the fluid are solved.

$$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \overrightarrow{v}\right)=0$$

(2)

$$\frac{\rho \partial (\overrightarrow{v})}{\partial t}+\rho \overrightarrow{v}(\nabla \cdot \overrightarrow{v})=-\nabla p+\nabla \cdot (\overline{\tau })+\rho \overrightarrow{g}$$

(3)

where ρ is the density of the fluid, kg/m³; $\overrightarrow{v}$ is the velocity vector, m/s; p is the static pressure, Pa; $\overline{\tau }$ is the stress tensor; $\overrightarrow{g}$ is the gravitational acceleration, m/s². $\overline{\tau }$ is described as,

$$\overline{\overline{\tau }}=\mu \left[\left(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T\right)\right]-\frac{2}{3}\delta \nabla \cdot \overrightarrow{v}$$

(4)

where μ is the dynamic viscosity of the air, kg/(m∙s); $\delta$ is the unit tensor.

The flow process was solved by the steady-state method. The coupled pressure-velocity solver used the SIMPLE algorithm, and the pressure terms were discretized using the PRESTO! format. The other equations were discretized in the second-order windward format, and the convergence residuals of all variables were set to 10⁻⁶ to obtain more accurate results.

4. Results and Discussion

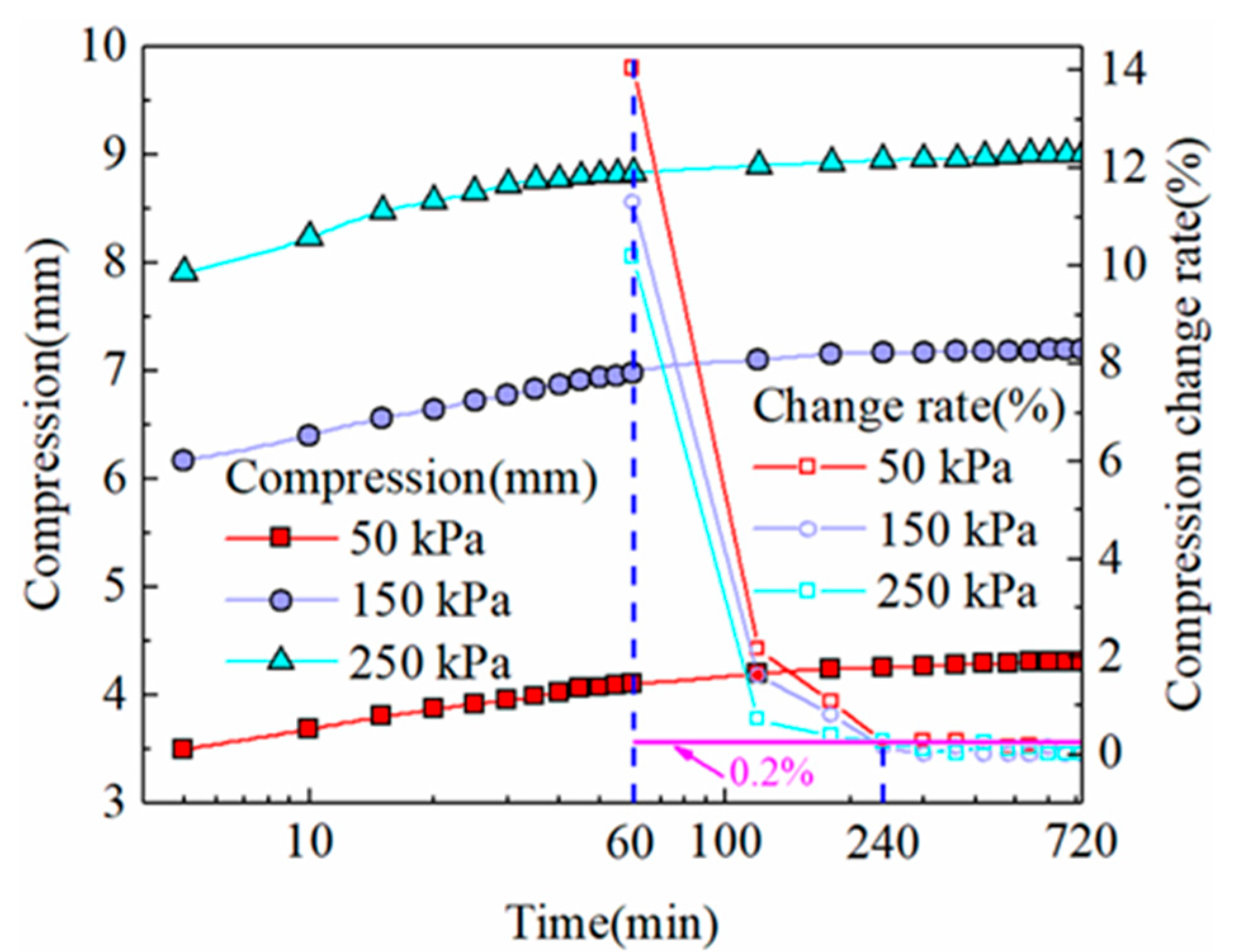
4.1. Compression Characteristics

Due to the self-weight of the grain load, the vertical pressure distribution in the grain bin is uneven and the degree of compression of the grain is different [24]. According to the mass-volume relationship, the experimentally calculated average porosity was 0.43. Compaction changes the pore structure distribution of the grain pile, which affects the pressure drop characteristics through the soybean packed bed. Vertical pressure causes the soybean packed bed to compact, increasing the resistance to airflow through the grain bulk. The compression and compression change rate of soybean bulk at 50, 150, and 250 kPa vertical pressures are shown in Figure 4. The vertical pressure had a significant effect on the deformation of the soybean bulk. After the application of vertical pressure, the grain had a notable transient deformation, and the change rate of deformation decreased with increasing time. The amount of transient deformation increased with the vertical pressure. The compression was 97.6%, 98.2%, and 98.8% of the total compression after two hours of loading at 50, 150, and 250 kPa, respectively, which indicates that the total compression of the grains occurred mainly within two hours after loading. After 4 h, the compression change rate was reduced to less than 0.2%. The compressions under 50, 150, and 250 kPa pressures were 4.29 mm, 7.18 mm, and 8.98 mm, respectively.

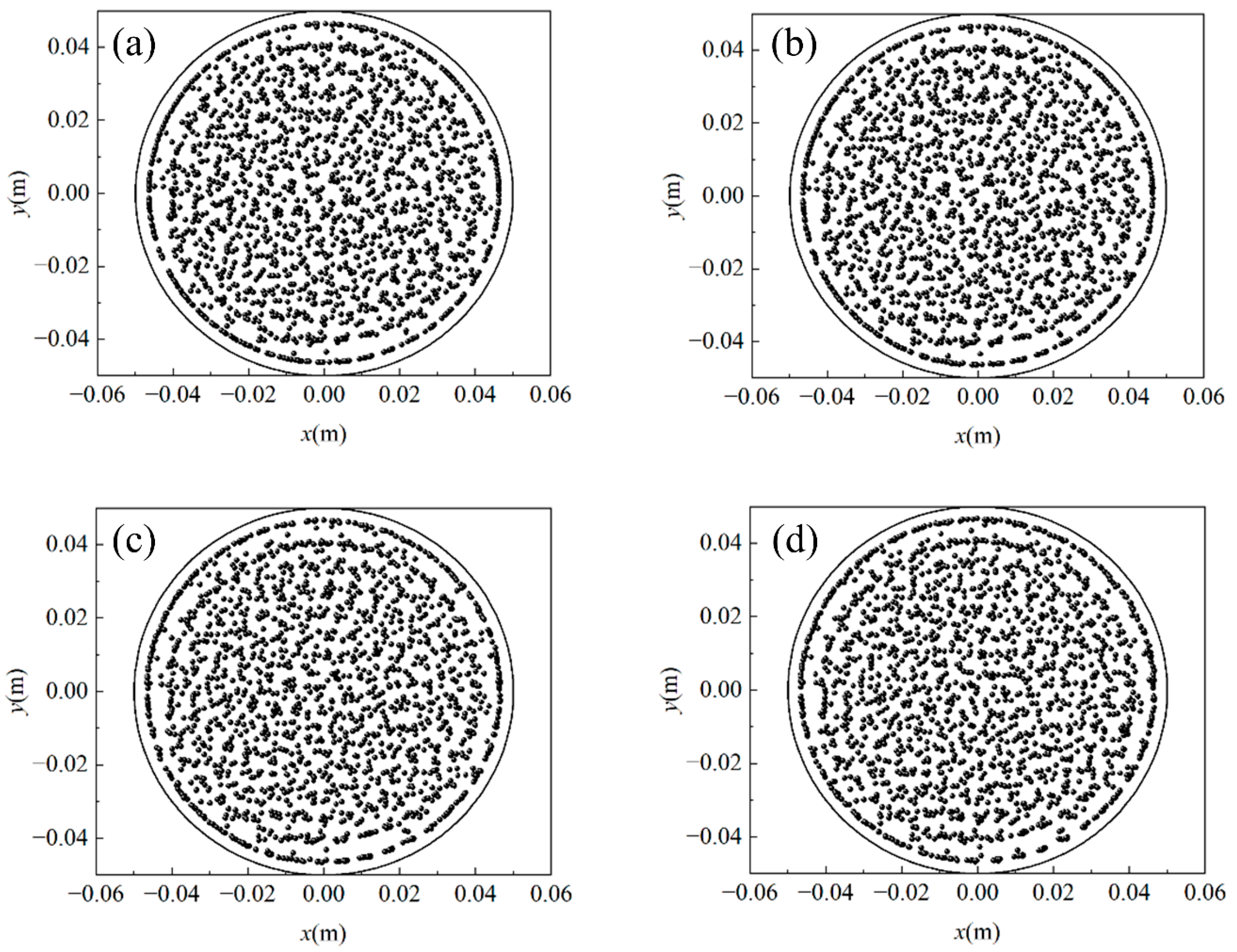
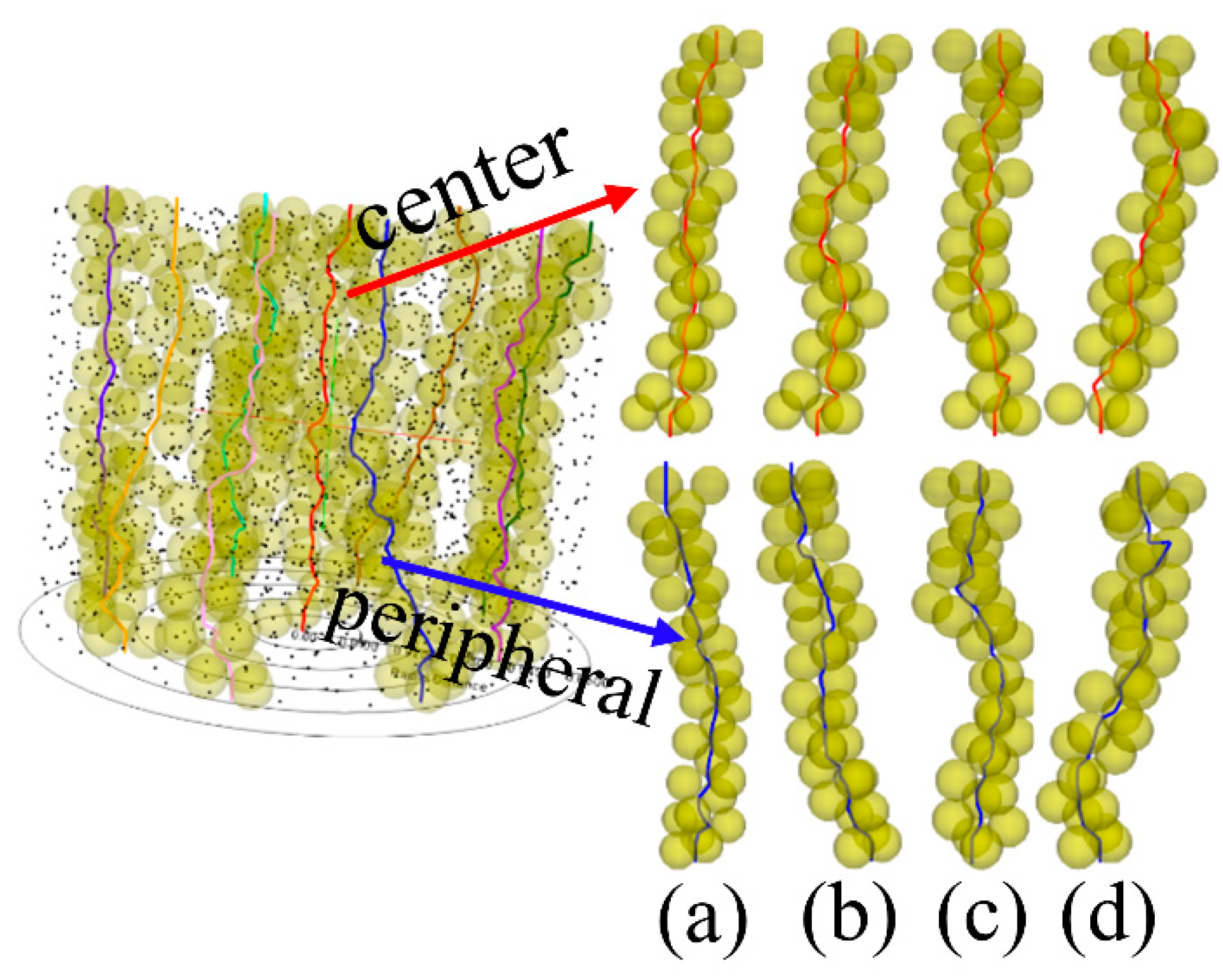
4.2. Radial Voidage

The distribution of the center coordinates of all particles in the X-Y plane is shown in Figure 5. It is found that the distribution of particle center coordinates is similar under different vertical pressures, and the center coordinates tend to be organized in circles in the vicinity of the cylindrical wall surface. The distance from the circle formed by the periphery particle coordinates to the cylindrical wall is approximately the same as the particle radius. The degree of random distribution of coordinates increased with distance from the cylindrical wall. The particle center coordinates are more dispersed in the X-Y plane as the vertical pressure increase.

The radial porosity distribution is an important indicator to verify the packing quality of the DEM. The pore distribution inside the packing structure links with the radial position under the constraint effect of the wall. The soybean packed bed is dense at the location of small radial porosity values. To verify the accuracy of the particle packing structure generated by DEM, the radial porosity distribution under different vertical pressures was compared with the results calculated by de Klerk. The empirical equation widely used to predict the radial porosity distribution in a cylindrical packed bed was derived by de Klery [42] experimentally, with the porosity being expressed as:

$$\epsilon (r)=\{\begin{array}{l}2.14n^2-2.53n+1,n\le 0.637\hfill \\ \overline{\epsilon }+0.29e^{-0.6n}\times \cos [2.3\pi (n-0.16)]+0.15e^{-0.9n},n>0.637\hfill \end{array}$$

(5)

where $\epsilon (r)$ is the radial porosity of the packed bed; n is the wall dimensionless distance; $n=(R-r)/d_p$; r is the distance from the radial position of the packed bed to the central axis; d_p is the particle radius; $\overline{\epsilon }$ is the central porosity of the packed bed.

The particle-packed region is divided into multiple coaxial cylindrical surfaces along the radial direction. The porosity is the ratio of the fluid area intercepted by the cylindrical surface to the cylindrical area, and the calculation formula can be expressed as [43]:

$$\epsilon (r)=\frac{A_{void}(r)}{2\pi rH}$$

(6)

where A_void(r) is the fluid area, m²; ε(r) is the radial porosity of the packed bed. Figure 6 shows that the radial porosity distribution of the packed bed calculated using DEM and de Klerk’s formula is in close agreement. The radial porosity distribution of the packed bed at different vertical pressures was similar, and the maximum radial porosity was about 1, near the cylindrical wall (n = 0), owning to the point contact between the cylindrical wall and the particle. The fluid area intercepted by the coaxial cylindrical surface was approximately the entire cylindrical area. With increasing dimensionless distance, the minimum radial porosity was 0.25 at about the distance of the particle radius from the cylindrical wall, which is the same location as the center coordinate distribution near the cylindrical wall. The radial porosity oscillates and decreases toward the center of the packed bed, with a smaller amplitude toward the center, eventually approaching the average porosity of the packed bed. From Figure 6, the porosity of the center of the packed bed in the uncompressed state (0 kPa) was $\overline{\epsilon }\approx 0.43$. The central porosity of the packed bed was 0.39, 0.36, and 0.35, respectively, in 50, 150, and 250 kPa compression states. The amplitude of radial porosity oscillation decreases with the increase in vertical pressure. The compression process increased the density of the packed bed and made the particle distribution continuous, which corresponds with the central coordinate distribution shown in Figure 5.

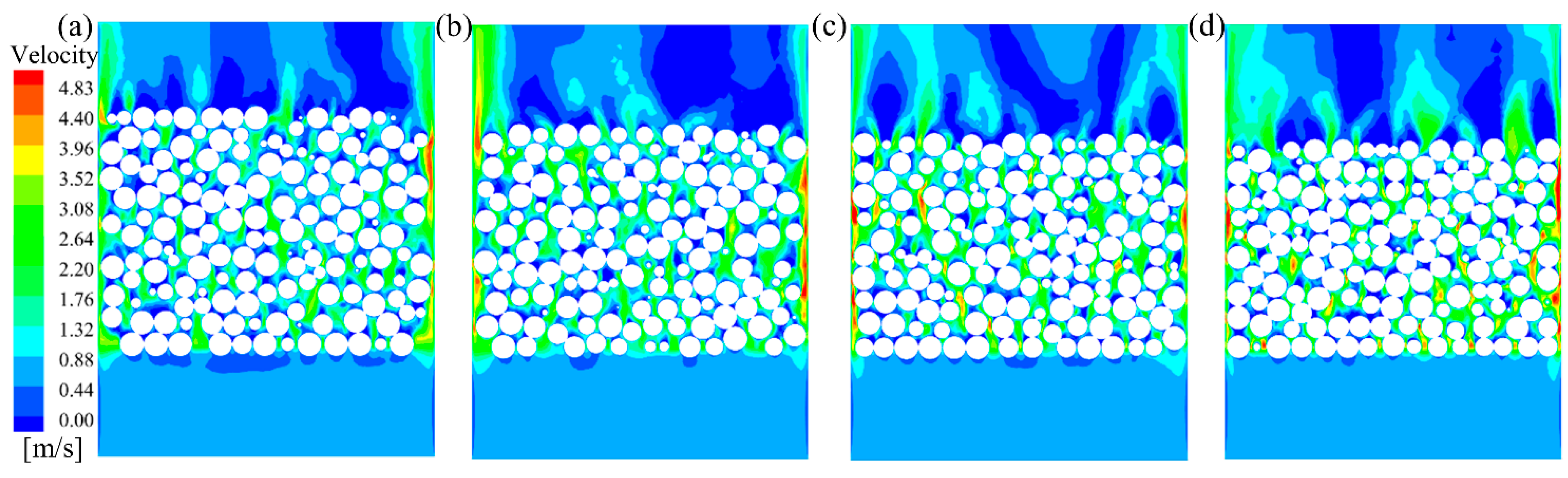
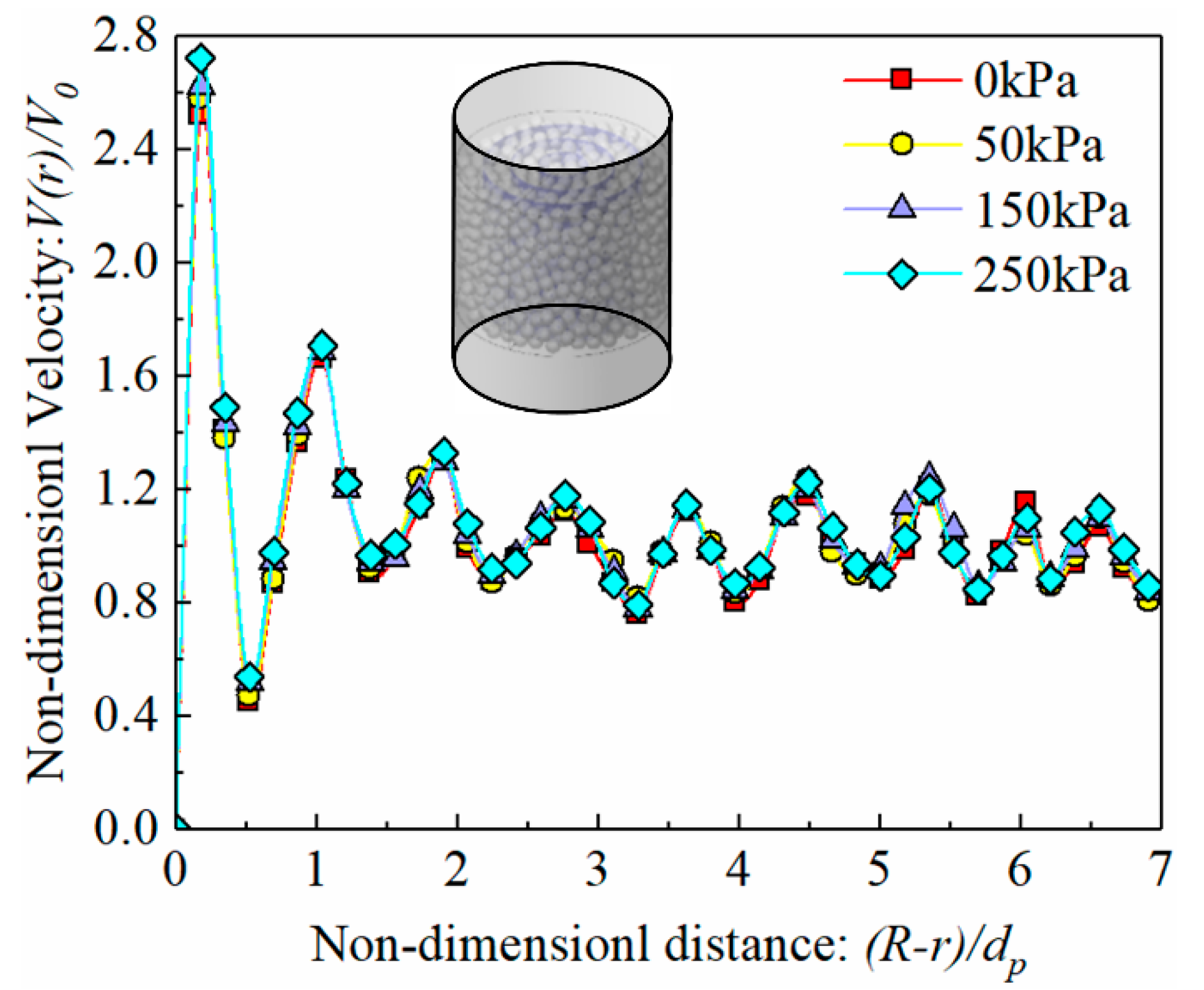
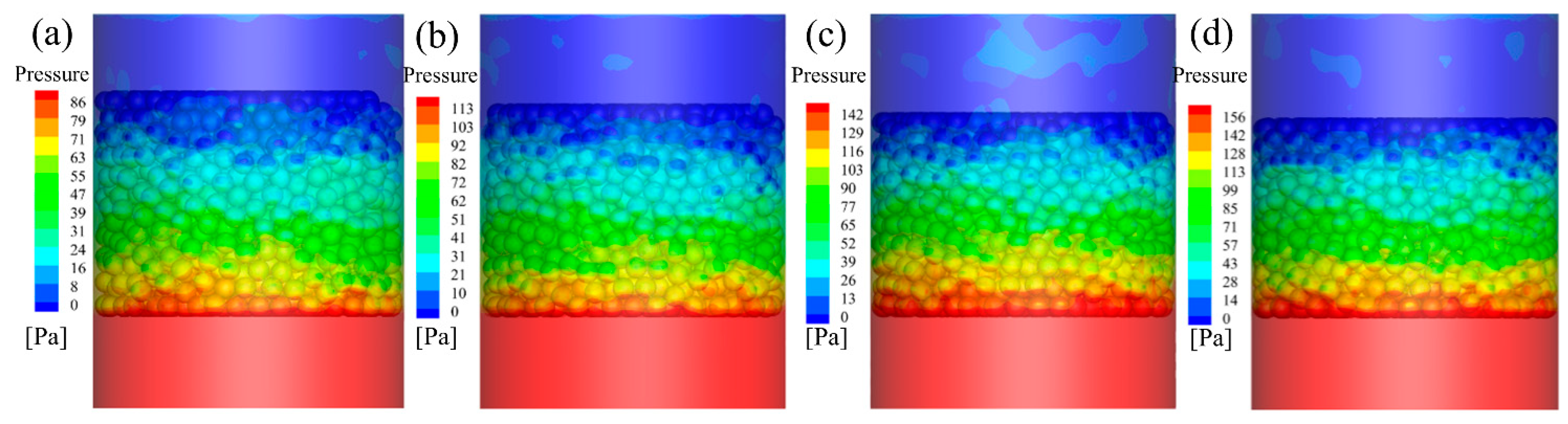
4.3. Velocity Distribution

The contours of velocity under different vertical pressures are shown in Figure 7. The airflow characteristics of packed beds are more noticeable at higher inlet velocities. The inlet velocity V₀ = 0.6 m/s was chosen for the study. The velocity field distribution was similar under different vertical pressures. In the axial direction of the packed bed, the inlet airflow is in contact with the particles in the front part of the packed region. The particles form a barrier to the airflow, and a zero-velocity region exists at the back of the particles. In the packed region, the local velocity distribution shows a clear difference. In the outlet region, the airflow stagnates and backflows. The velocity near the cylindrical wall is higher than in other regions, with the local maximum velocity near the wall about 9 times the inlet velocity under 250 kPa vertical pressure. The velocity in the packed bed is not just dependent on the porosity size but also on the connectivity of the pore paths [26]. The particle distribution is more dispersed with the increase in vertical pressure, which improves the internal pore connectivity and causes the velocity to increase.

Consistent with the radial porosity distribution measurement method, the same coaxial cylindrical surface measurement was used to obtain the radial mean dimensionless velocity (V_r/V₀) distribution of the packed bed as shown in Figure 8. The distribution of the radial mean dimensionless velocity at different vertical pressures was similar and consistent with the trend of the oscillatory distribution of porosity. The velocity was at maximum at about one-half particle radius from the cylindrical wall, with the local maximum velocity being 2.51, 2.58, 2.63, and 2.74 times the inlet velocity with increasing vertical pressure, respectively. The mean velocity inside the packed bed increases with the vertical pressure, with the mean velocities 0.75 m/s, 0.78 m/s, 0.81 m/s, and 0.86 m/s at vertical pressures of 0, 50, 150, and 250 kPa, respectively.

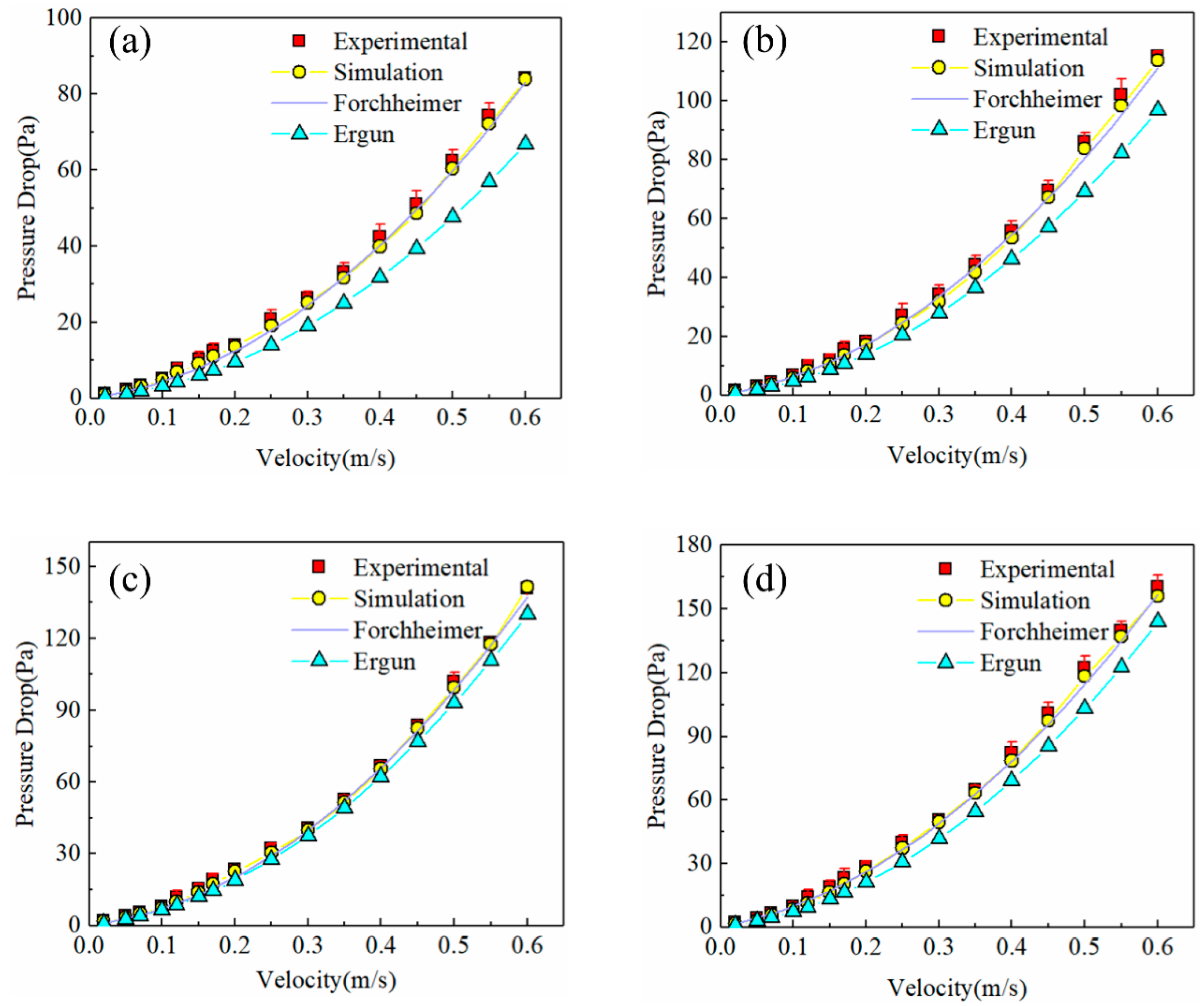
4.4. Pressure Drop

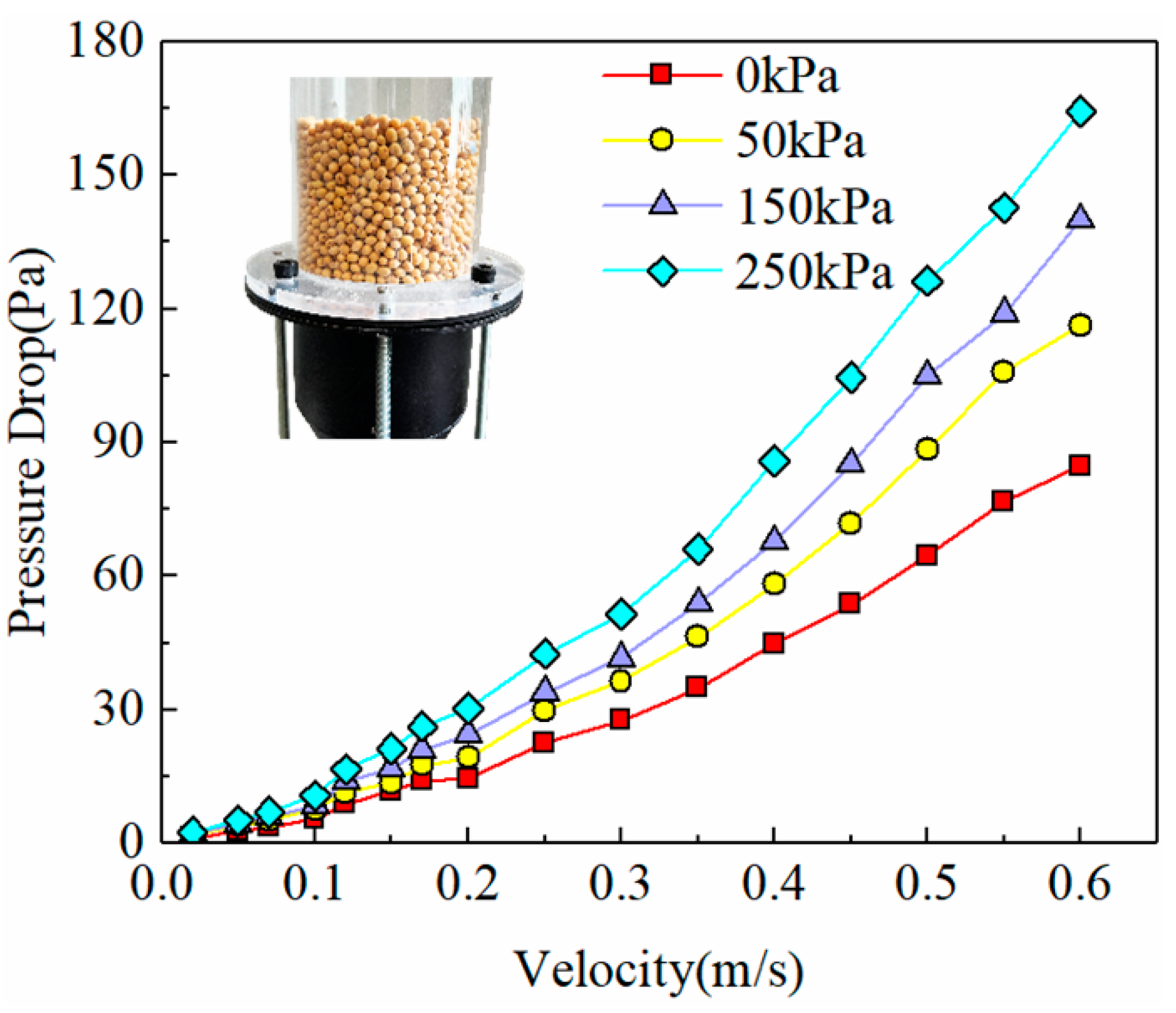
4.4.1. Experimental Pressure Drop

The test values of the pressure drop of soybeans at different vertical pressures are shown in Figure 9. The pressure drop increases with the increase in inlet velocity and vertical pressure. Pressure drop through soybean in the uncompressed state (0 kPa) was in the range of 1.24 to 84.68 Pa at inlet velocities ranging from 0.02 to 0.6 m/s. The pressure drop increases with vertical compression. Soybean pressure drop increases to a range of 2.05 to 116.35 Pa at a vertical pressure of 50 kPa. The pressure drop was in the range of 2.18 to 139.89 Pa at a vertical pressure of 150 kPa. The pressure drop ranges from 2.46 to 164.27 Pa at a vertical pressure of 250 kPa. When the vertical pressure increases, the pressure drop increases by 36%, 57%, and 92% on average, as the inlet velocity increases from 0.02 to 0.6 m/s.

4.4.2. Numerical Simulation of Pressure Drop

The Ergun [44] equations and Forchheimer [45] equations (as Equations (7) and (8), respectively), are the most widely used methods for calculating the flow resistance coefficient and pressure drop in porous media. A PathFinder code was developed by Sobieski [46] to calculate pore-scale features based on DEM simulations of particle-packed structures. The center coordinates of each particle were calculated by a C program with an accuracy of 10⁻⁷ and converted to a format readable by PathFinder code. In this study, the changes in airflow paths during soybean packing and compression were recreated using the PathFinder code. The flow resistance coefficient term in the Forchheimer equation was determined based on the DEM particle information at different vertical pressures. The pressure drop results from numerical simulations and equations were compared with the experimental results for verification to verify model accuracy. The results of the PathFinder code calculation are shown in

Table 2. Results of PathFinder code calculations.

Parameters	Symbol	Value
		0 kPa	50 kPa	150 kPa	250 kPa
Average number of path points	-	34	33	32	30
Tortuosity	τ	1.25	1.32	1.43	1.47
Porosity	ε	0.428	0.391	0.362	0.353
Inner surface	Sp, m2	0.275
Solid volume	Vb, m3	0.00033
Specific surface	S0, m2	824.73
pore shape factor	Ckc	5
Forchheimer coefficient	A	17,740,438.61	27,852,990.67	41,729,700.98	47,576,815.47
Forchheimer coefficient	B	191.24	246.34	320.98	329.47

.

Ergun Equation:

$$-\frac{\mathsf{\Delta }P}{L}=150\mu \frac{{(1-\epsilon )}^2}{{\epsilon }^3}\frac{u}{d_p{}^2}+1.75\rho \frac{(1-\epsilon )}{{\epsilon }^3}\frac{u^2}{d_p}$$

(7)

Forchheimer Equation:

$$-\frac{\Delta P}{L}=A\cdot \mu \cdot u+B\cdot \rho \cdot u^2$$

(8)

where μ is the dynamic viscosity of the air, μ = 1.79 × 10⁻⁵ kg/(m∙s); ρ is the density of the air, ρ = 1.025 kg/m³; u is the inlet velocity; A is the expression for the permeability coefficient in the Kozeny-Carman equation, $A=\frac{1}{k}=C_{kz}\cdot \tau \cdot S_0^2\cdot \frac{{(1-\epsilon )}^2}{{\epsilon }^3}$, C_kz is the Kozeny-Carman pore shape factor, C_kz = 5.0; τ is the tortuosity; S₀ is the the specific surface of the packed bed.

A total of nine inlet points in the center and periphery of the packed bed were selected for airflow path calculation. The airflow path distribution calculated by PathFinder software is shown in Figure 10. The shape and length of the airflow path change with the vertical pressure. The deviation from the bottom inlet point to the top outlet increases with the vertical pressure, and the airflow path becomes more tortuous, with continuous bends in the airflow path at 250 kPa. As the vertical pressure increases, the particles move toward the pore area, making the packed bed more compact and the pore connection path curved and narrow. Compared to the central and peripheral airflow paths, the curvature of the path near the peripheral region was more intense as the vertical pressure increased. The path curvature due to vertical compression can visually reflect the phenomenon of increased pressure drop in the packed bed.

The pressure drop results simulated by the DEM-CFD method for different inlet velocities and vertical pressure conditions are shown in Figure 11, and are being compared with the empirical equations and experimental results. The calculated results of the DEM-CFD simulation and the Forchheimer equation under different vertical pressures were in close agreement with the experimental results, and the average difference was less than 10%. The Ergun equation underestimates the pressure drop values clearly, with an average difference of more than 24% in the uncompressed state (0 kPa) and a reduced average difference of 15% at 150 kPa. The DEM-CFD method and Forchheimer equation coefficients calculated by the PathFinder code take into account not only the decrease in porosity of the packed bed under the difference in vertical pressure but also the increase in the tortuosity of the pore path, which means the calculations were more accurate. The Ergun equation can only consider the effect of porosity variation on pressure drop, and the results have a greater difference.

The contours of pressure drop under different vertical pressures are shown in Figure 12. The inlet velocity V₀ = 0.6 m/s was chosen for the study. The distribution of static pressure values at different vertical pressures was similar, and the static pressure decreases gradually. The static pressure decreased gradually and showed a clear layered phenomenon along the outlet direction, and the static pressure distribution was constant at the inlet and outlet regions. The static pressure at the inlet and the pressure drop through the soybean packed bed increase with the vertical pressure, which was consistent with the pressure drop test and empirical equation calculation.

The test and simulation results can be extrapolated at a larger scale. However, it is worth mentioning that the DEM-CFD method requires high computer computing power and requires reasonable simplification of operations. The pressure drop is relevant for the bed characteristics, which increase with the compression of the bed. As to an actual on-farm silo, the static pressure distribution is uneven under compaction by the self-weight of grain [47,48]. The temperature and moisture distributions will be quite different in a larger packed bed.

Summarizing the velocity distribution and pressure drop under vertical pressure, the DEM-CFD method is suitable to describe the airflow characteristics precisely. The vertical pressure reduces the porosity of the packed bed, reducing the voids occupied by air, resulting in a larger particle contact area and increased thermal conductivity. The temperature and moisture change in the soybean packed bed accelerated under vertical pressure. The temperature and moisture distributions should be considered in further investigations using the DEM-CFD method.

5. Conclusions

To clarify the effect of different vertical pressures on the pressure drop of soybean bulk, the DEM-CFD method was used to simulate the pressure drop characteristics of soybean packed beds under different compression states. The following conclusions were obtained by comparing the experimental and empirical equation results.

(1)

The deformation of the soybean bulk increases with vertical pressure. After applying vertical pressure, a large transient deformation of the grain bulk occurs, and then the deformation change rate decreases. The total compression of soybean bulk occurred mainly within two hours after loading and stabilized after about four hours. The compressions under 50, 150, and 250 kPa pressures were 4.29 mm, 7.18 mm, and 8.98 mm, respectively.

(2)

The distribution of particle center coordinates close to the cylindrical wall generated by DEM is approximately circular. With the increase in vertical pressure, the internal particles move towards the pore area and the central coordinates become more scattered. The amplitude of radial porosity oscillation decreases with increasing vertical pressure. The compression process leads to an increase in the compactness of the packed bed and a more continuous particle distribution. The central porosity of the packed bed was 0.39, 0.36, and 0.35, respectively, in 50, 150, and 250 kPa compression states. The porosity distribution simulated by DEM is consistent with the experimental results in the literature.

(3)

The radially mean dimensionless velocity is consistent with the trend of porosity oscillation distribution. The local maximum velocity increases with the vertical pressure. The mean velocities in the particle packed region were 0.75 m/s, 0.78 m/s, 0.81 m/s, and 0.86 m/s at vertical pressures of 0, 50, 150, and 250 kPa, respectively. The radially averaged dimensionless velocity distribution is not only determined by the porosity but also related to the pore channel connectivity.

(4)

The packed bed airflow path is more tortuous with the increase in vertical pressure, and the pressure drop of the soybean packed bed increases with the increase in inlet velocity and vertical pressure. Considering the variation in porosity and pore connectivity, the pressure drop results calculated by the DEM-CFD method and the Forchheimer equation were in close agreement with the experimental results.