Seismic Response of a Large LNG Storage Tank Based on a Shaking Table Test
Abstract
:1. Introduction
2. Shaking Table Test of Storage Tank Models
2.1. The Design of Storage Tank Models
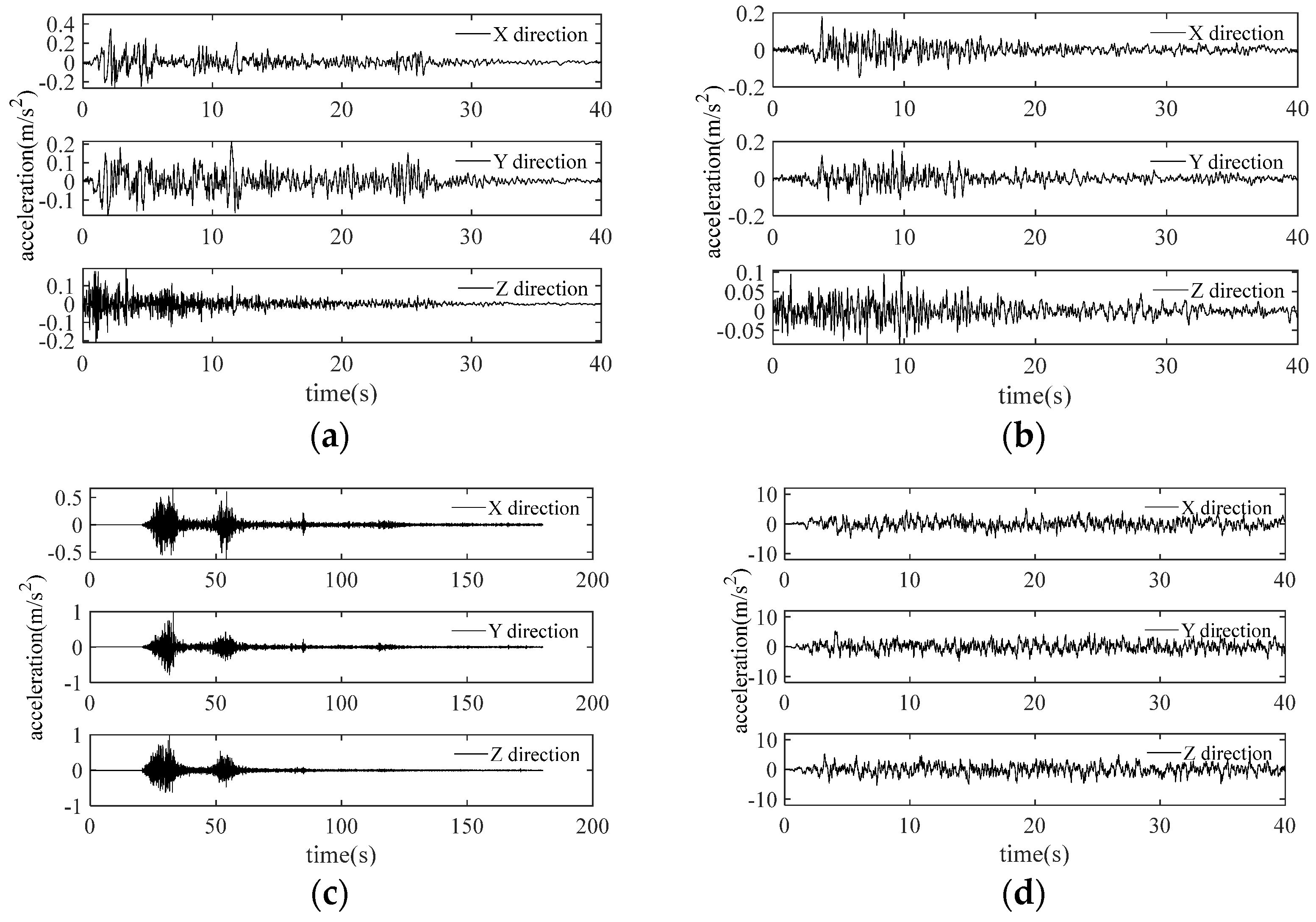
2.2. Seismic Wave Selection
2.3. Analysis of Test Results
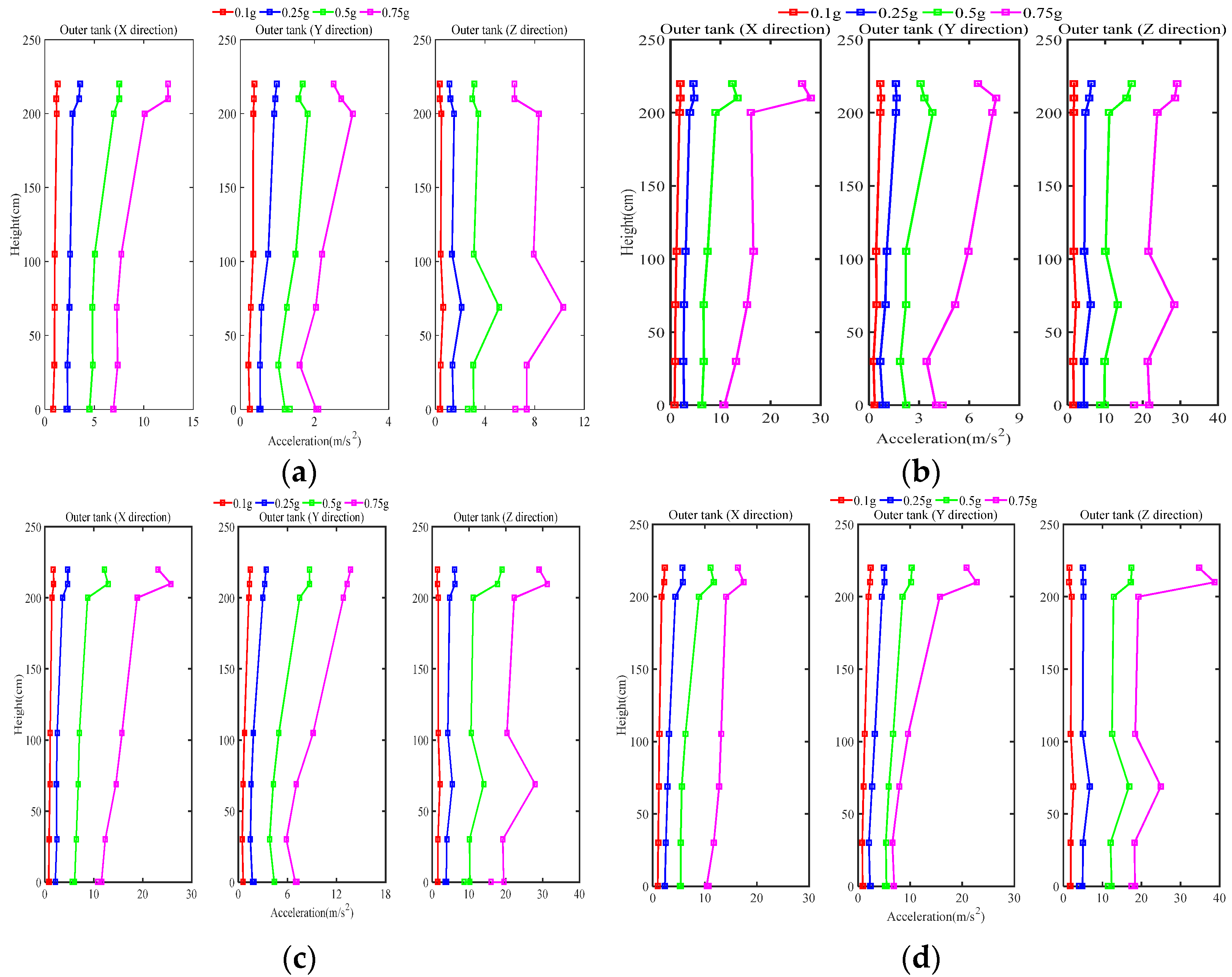
2.3.1. Non-Isolated Storage Tanks
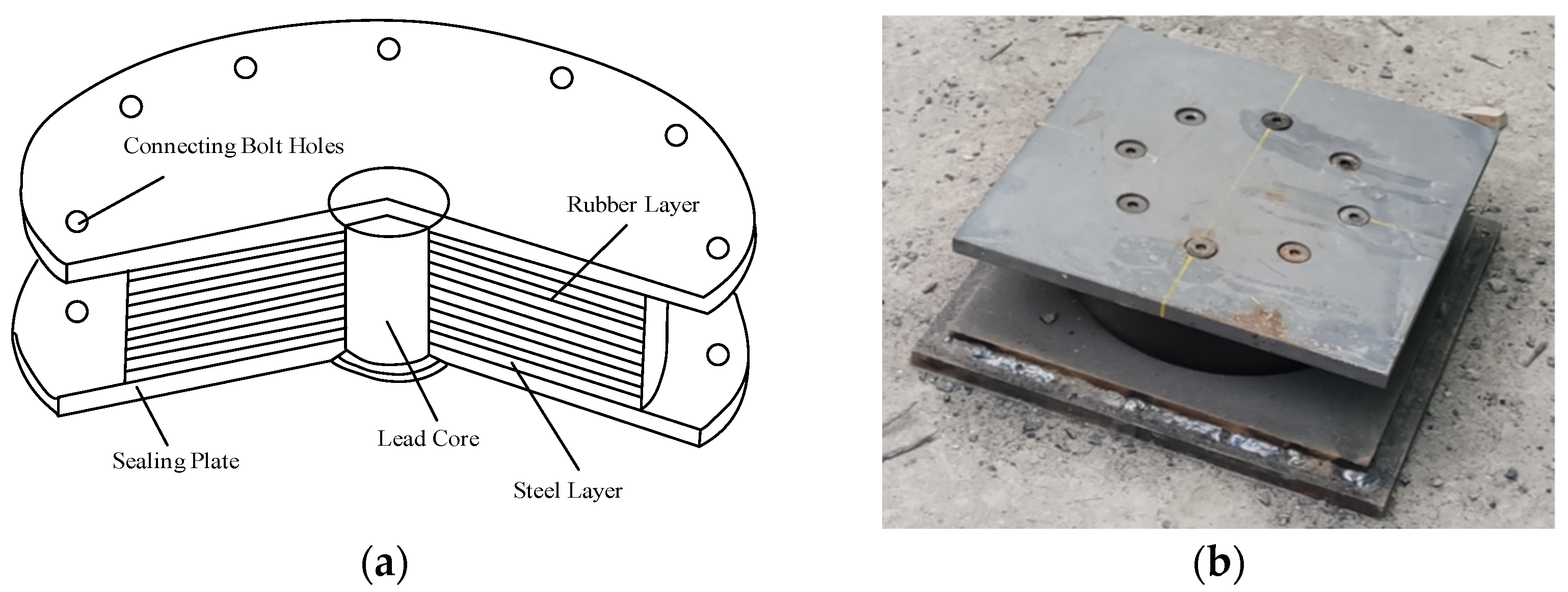
2.3.2. Isolated Storage Tank
3. Simplified Mechanical Model of the Storage Tank
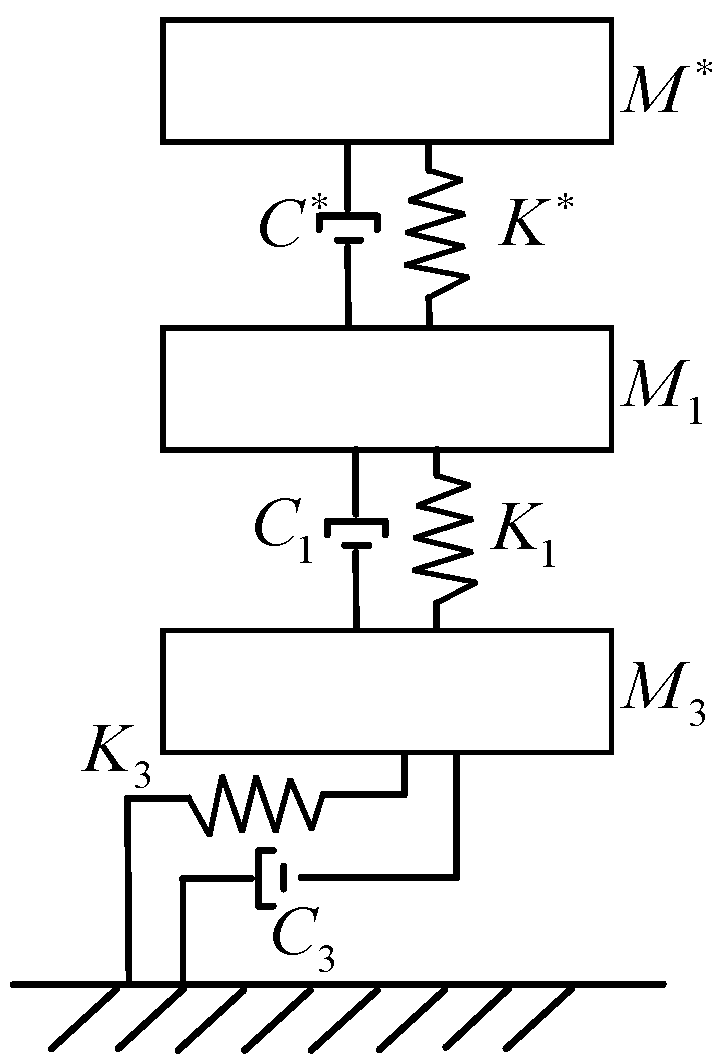
3.1. Comparison of Simplified Models with Different Degrees of Freedom
3.2. Equations of Motion for Non-Isolated Storage Tank
3.3. Equation of Motion of the Isolated Storage Tank
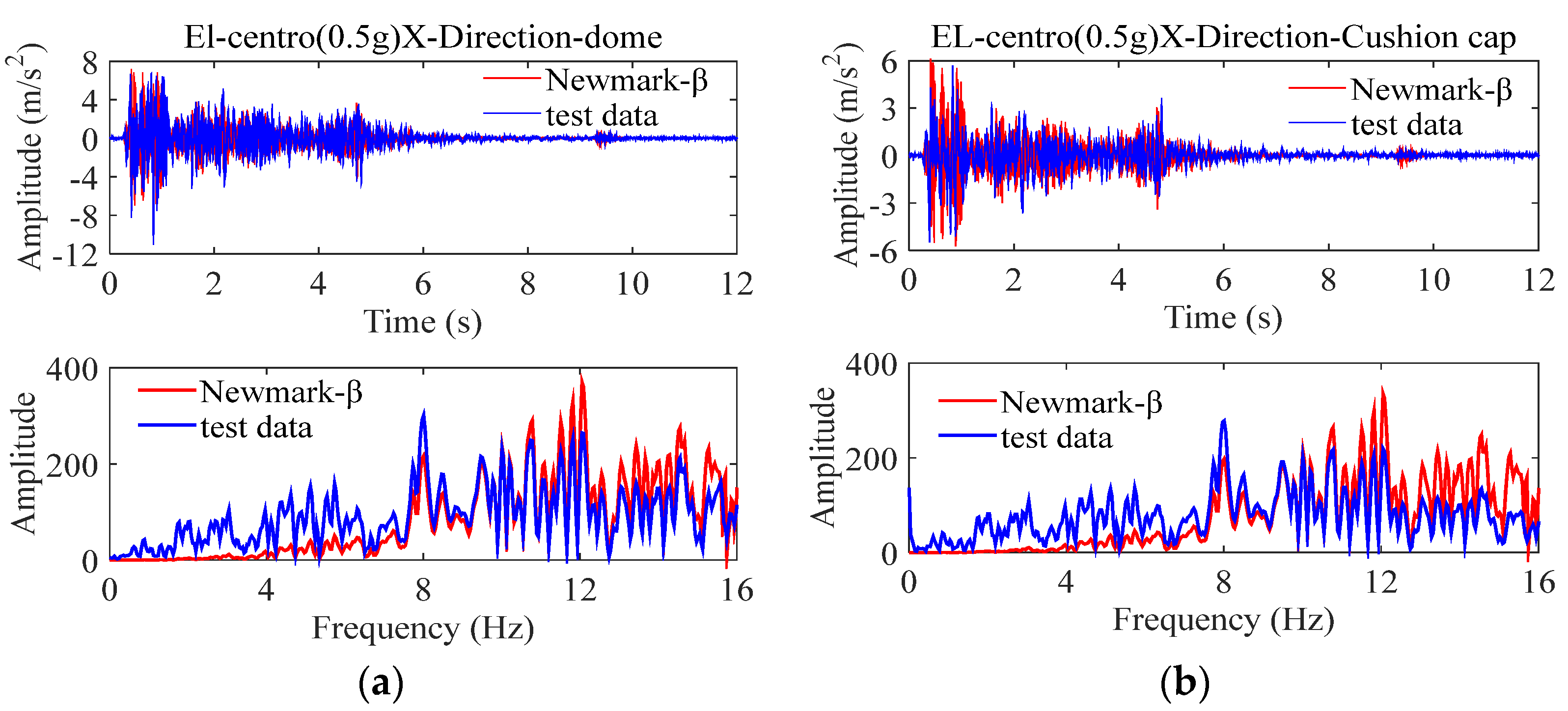
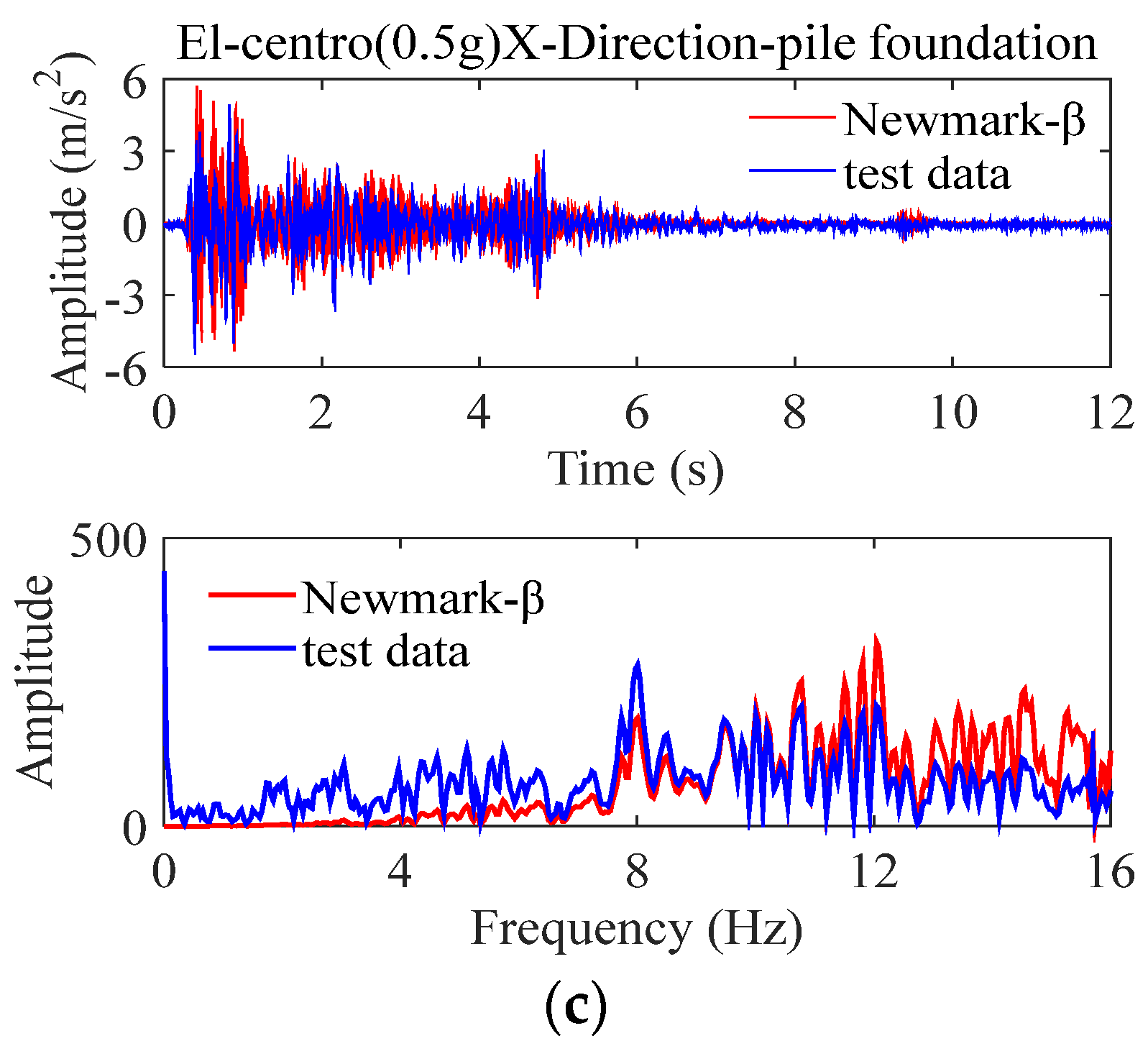
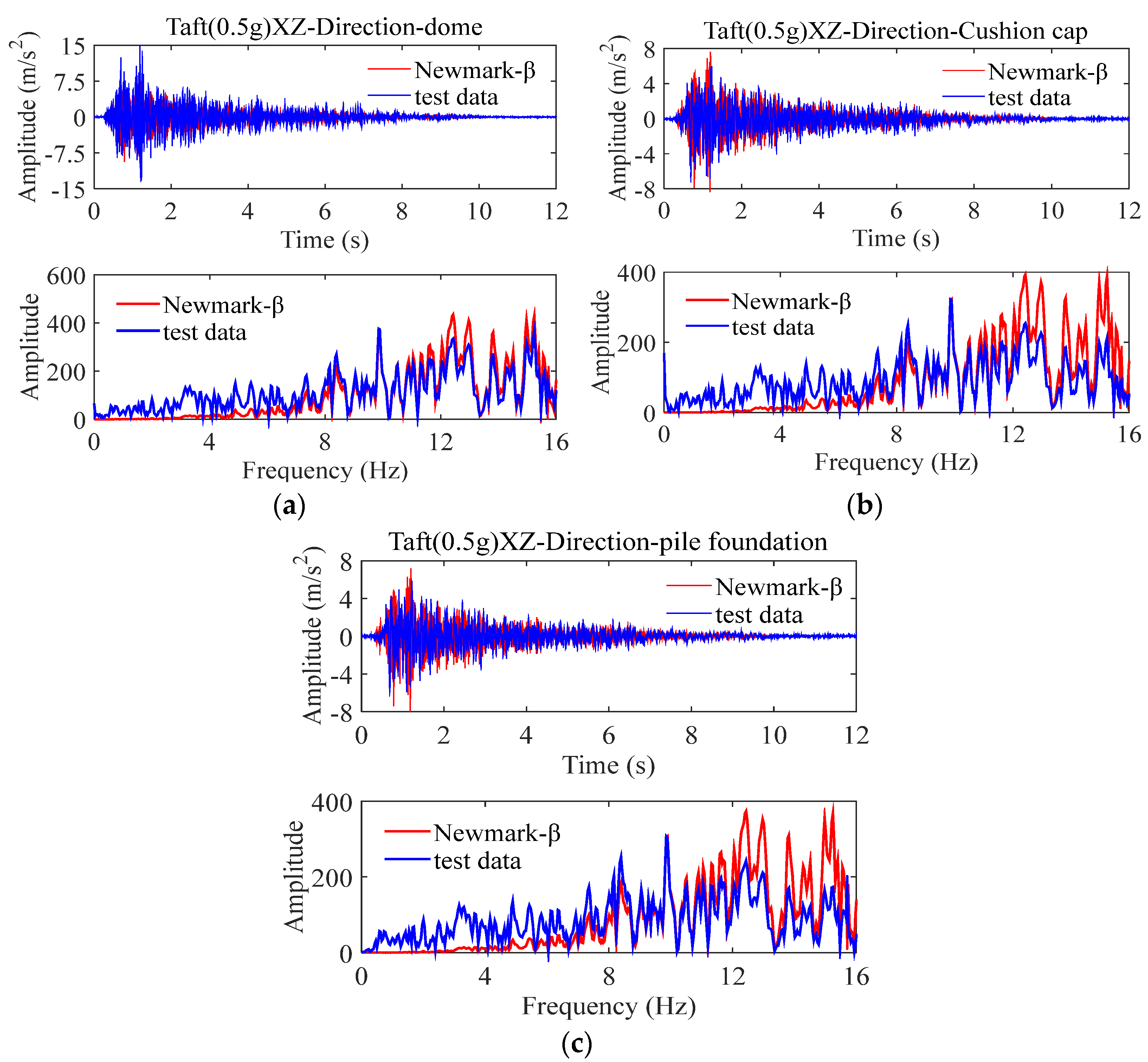
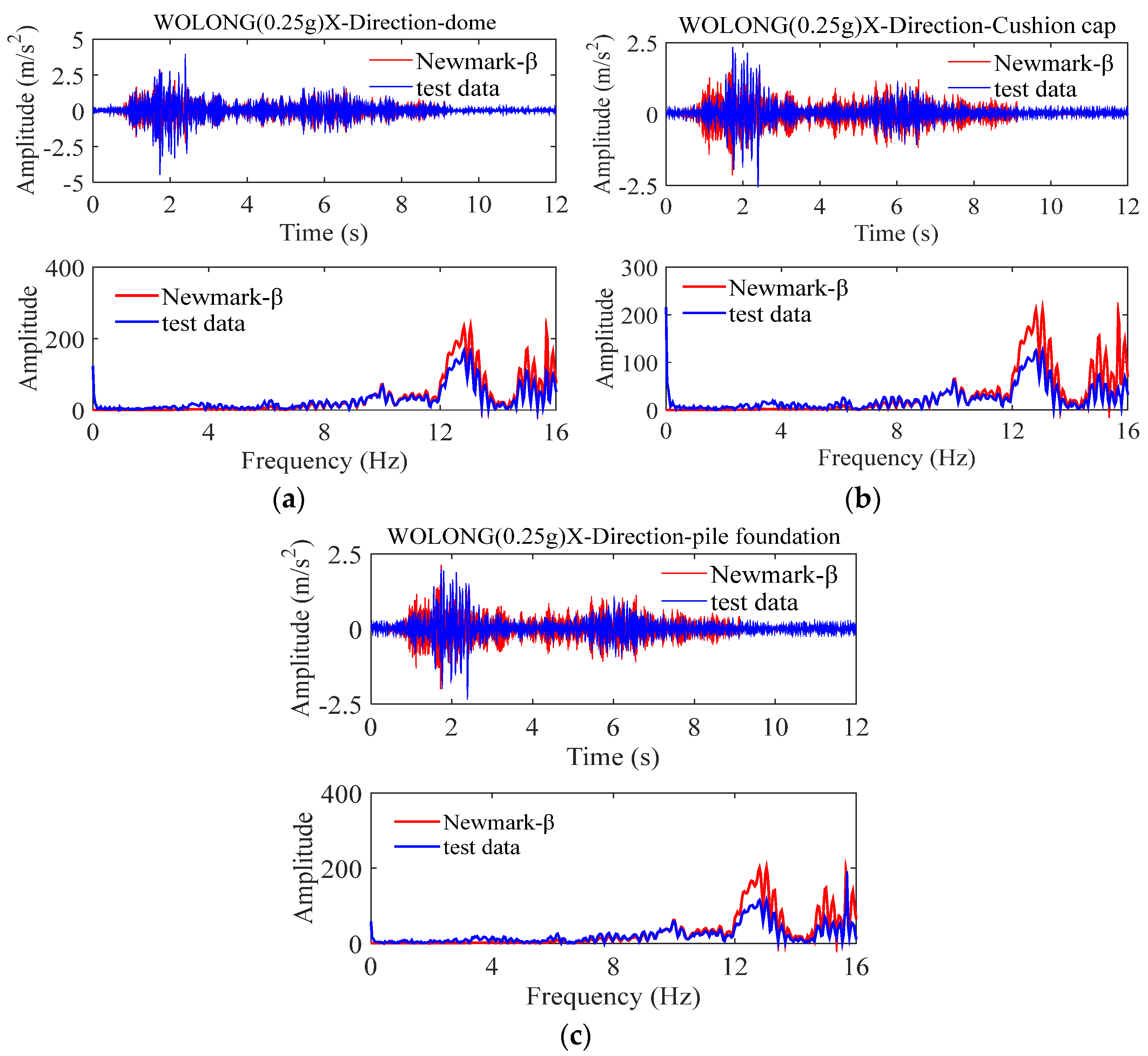
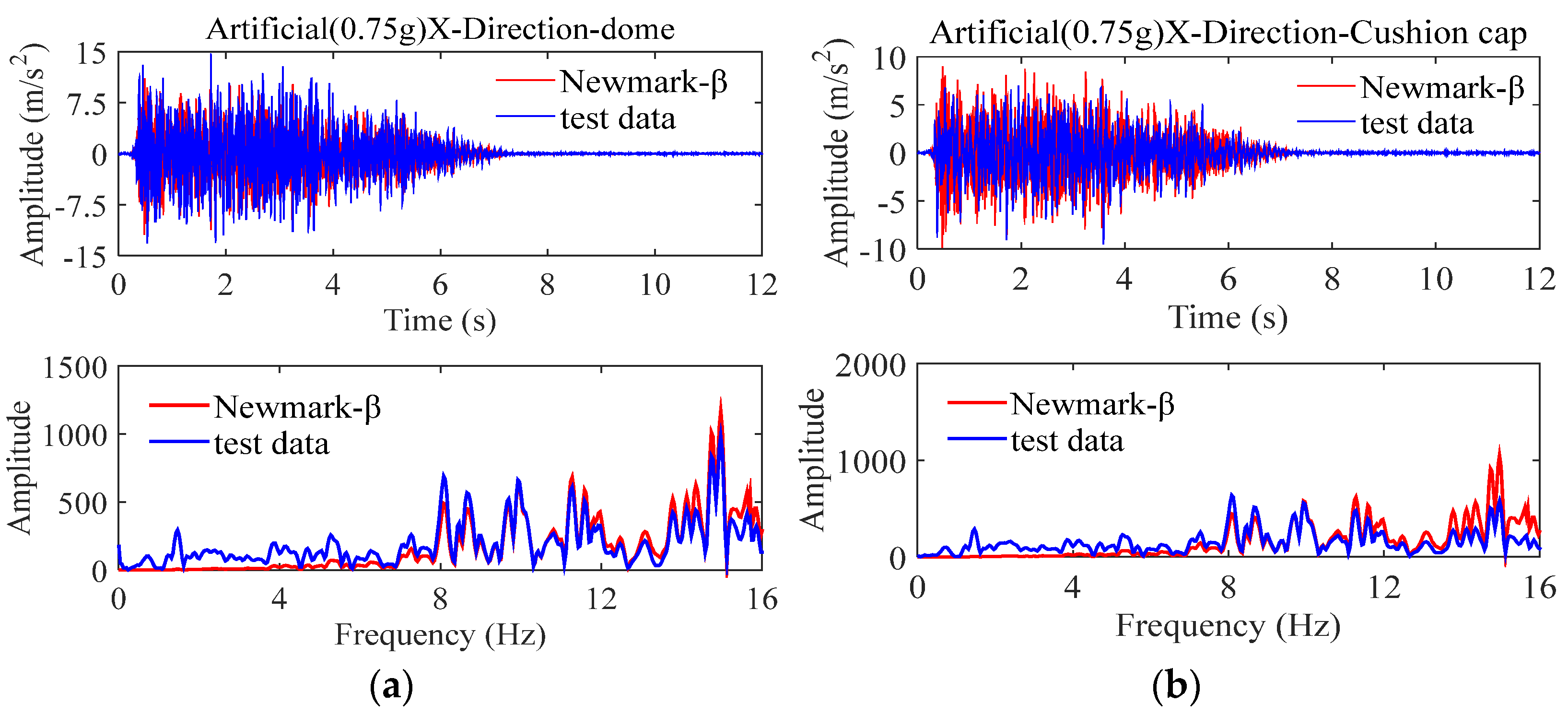
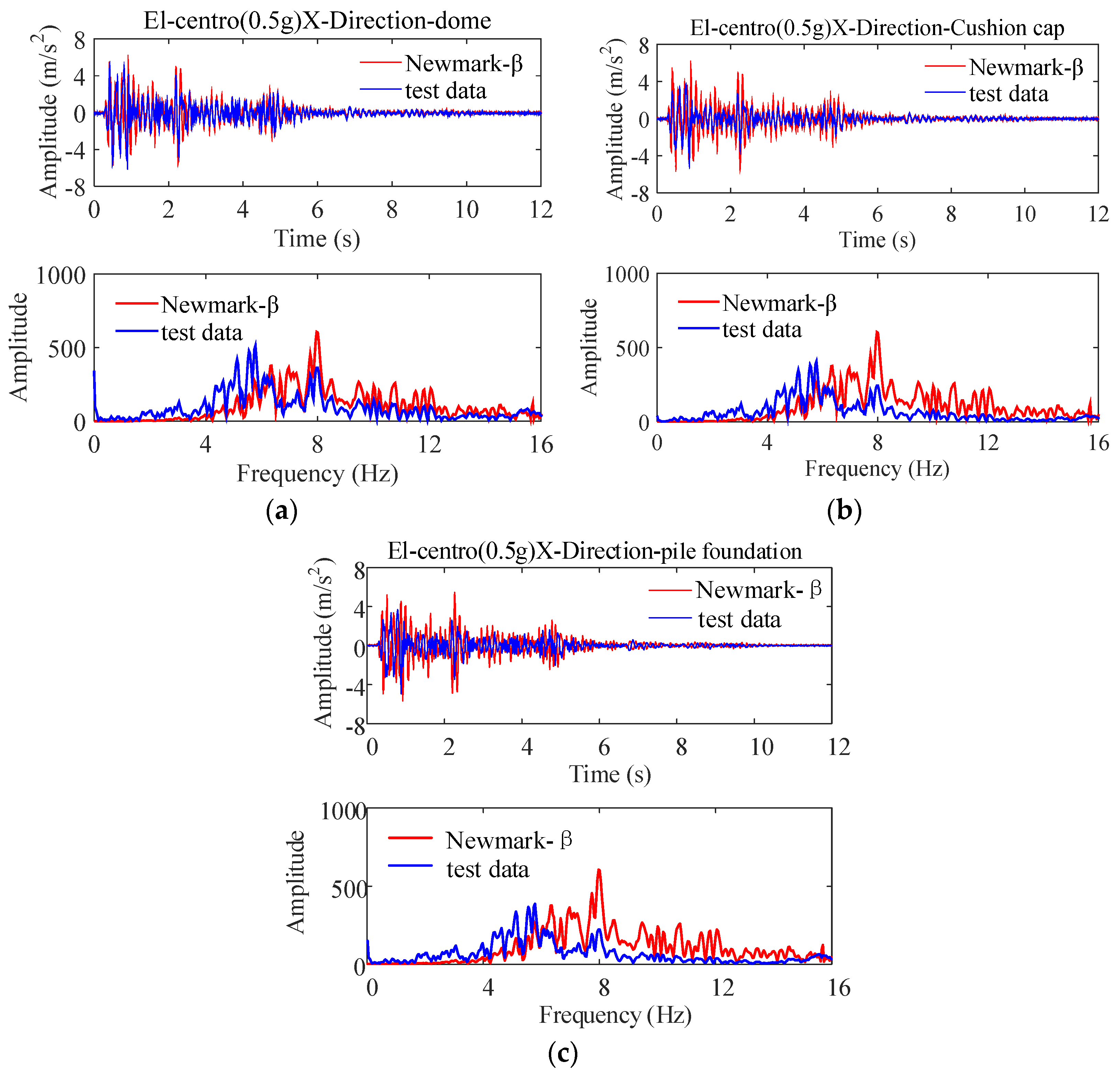
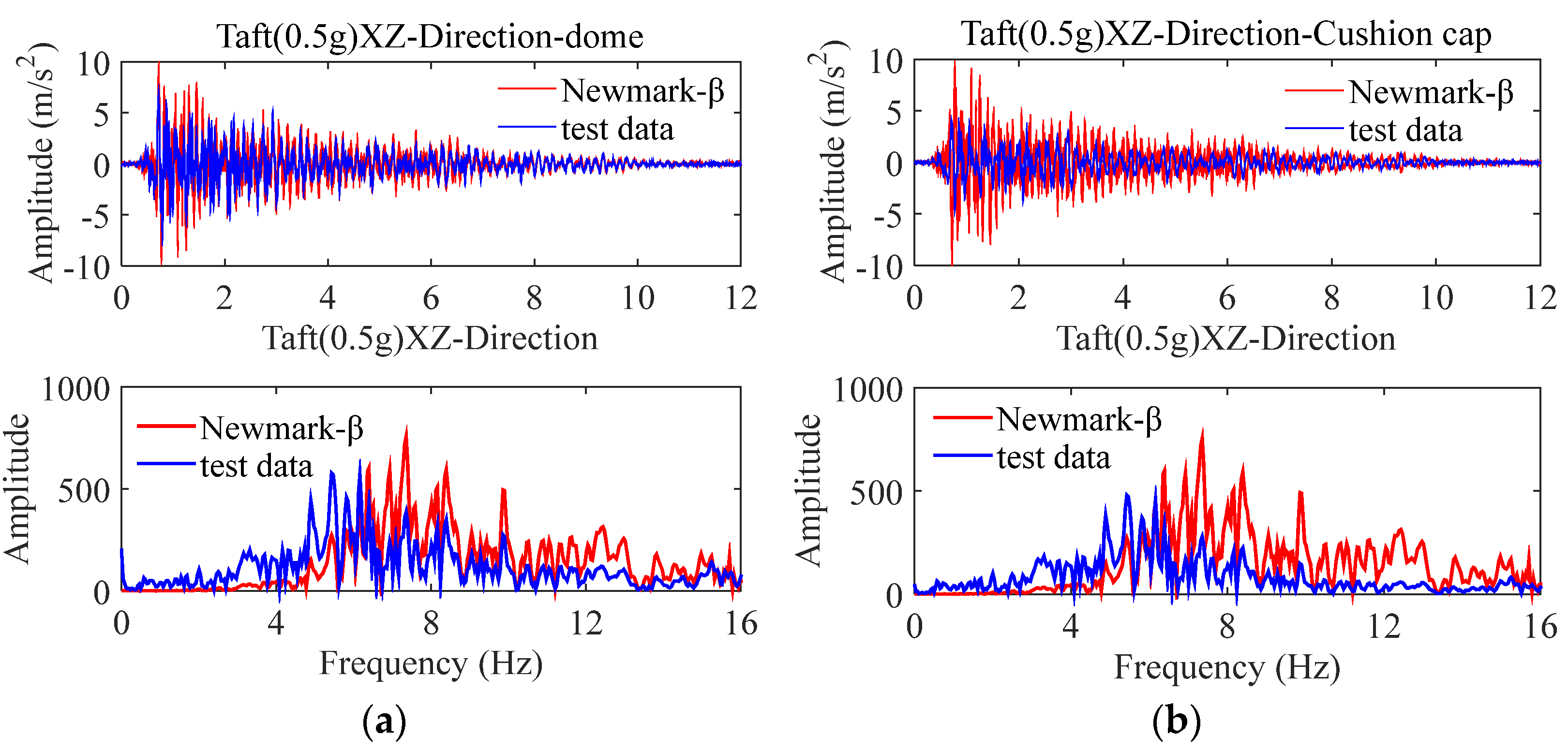
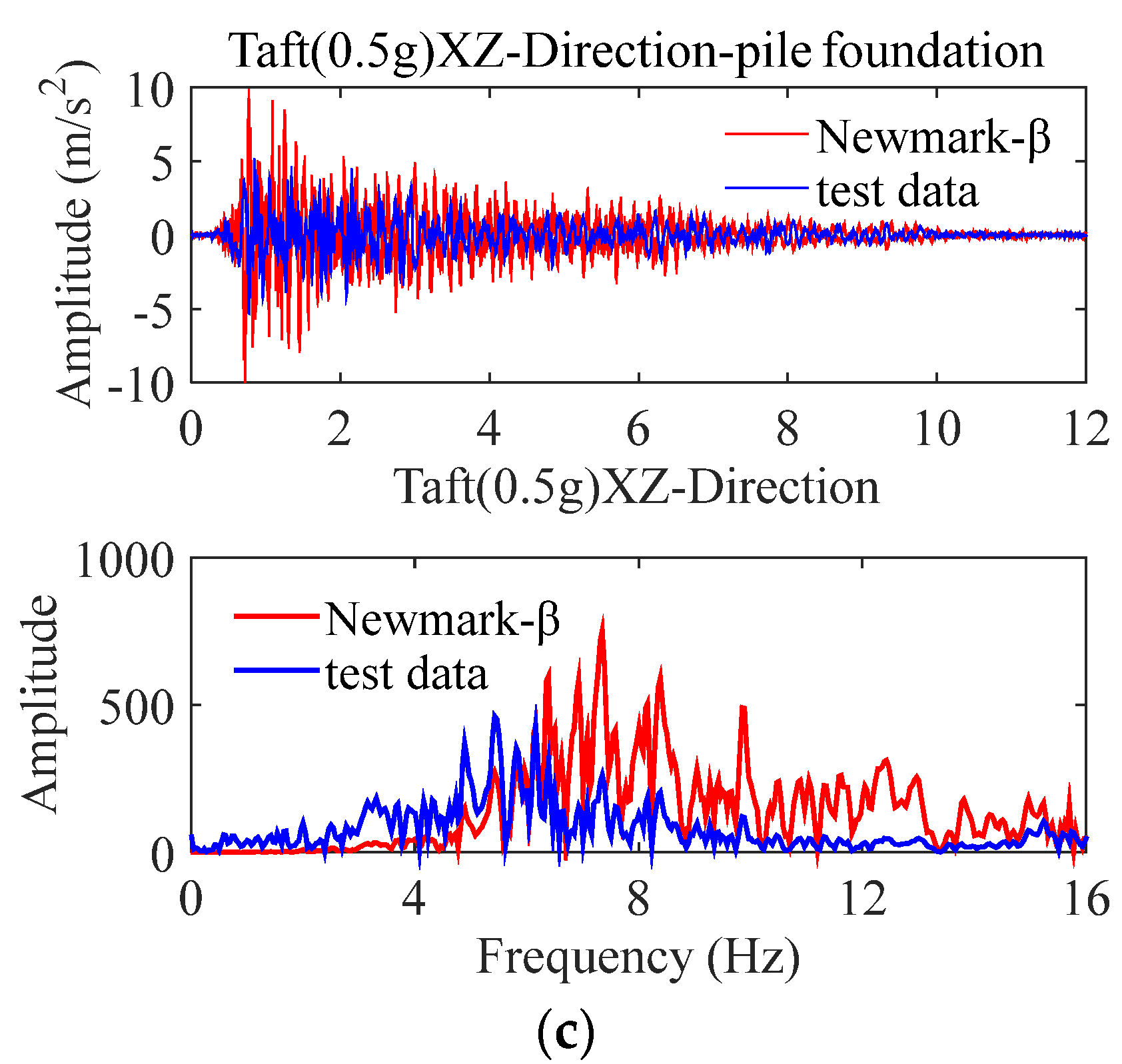
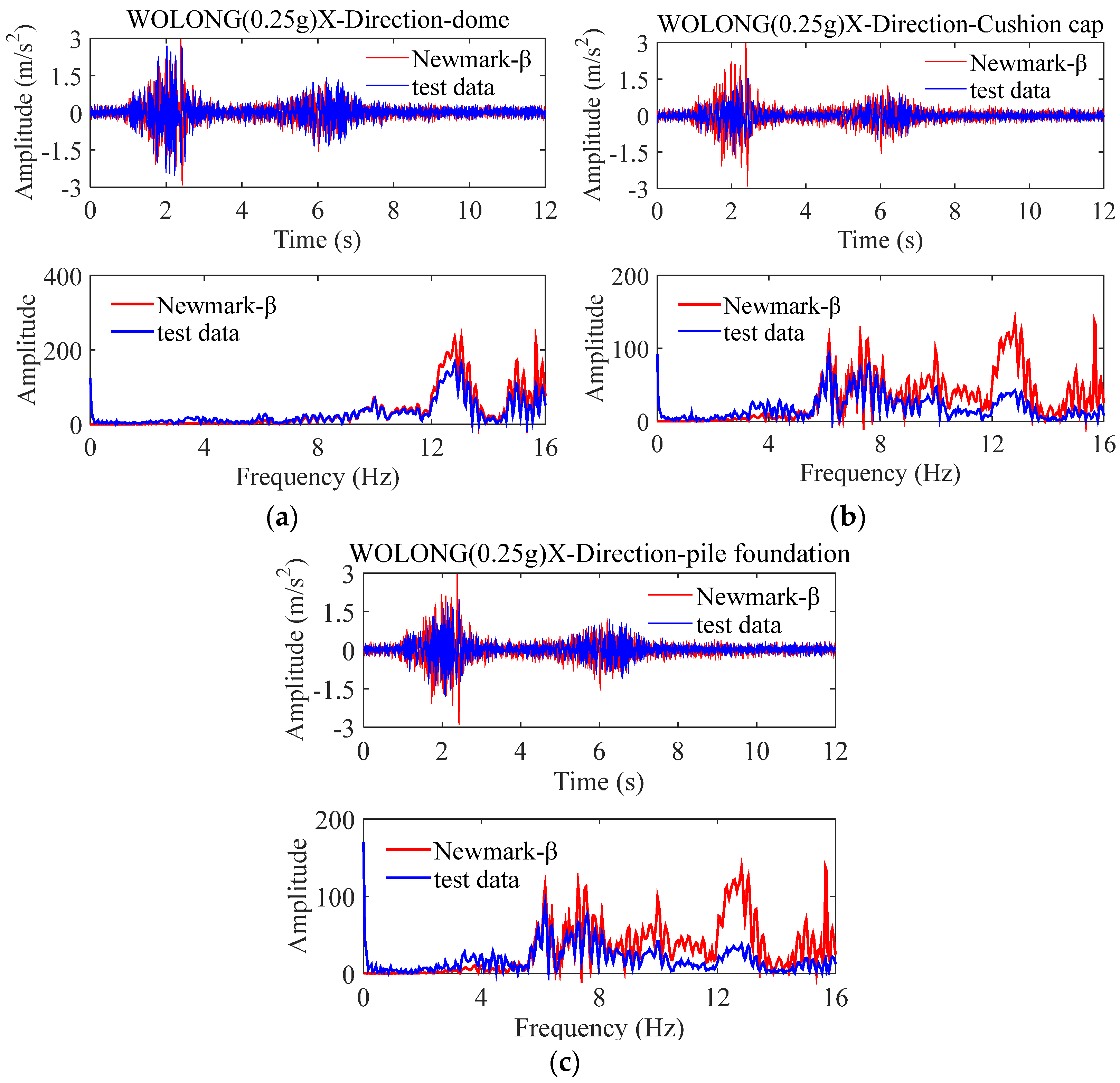
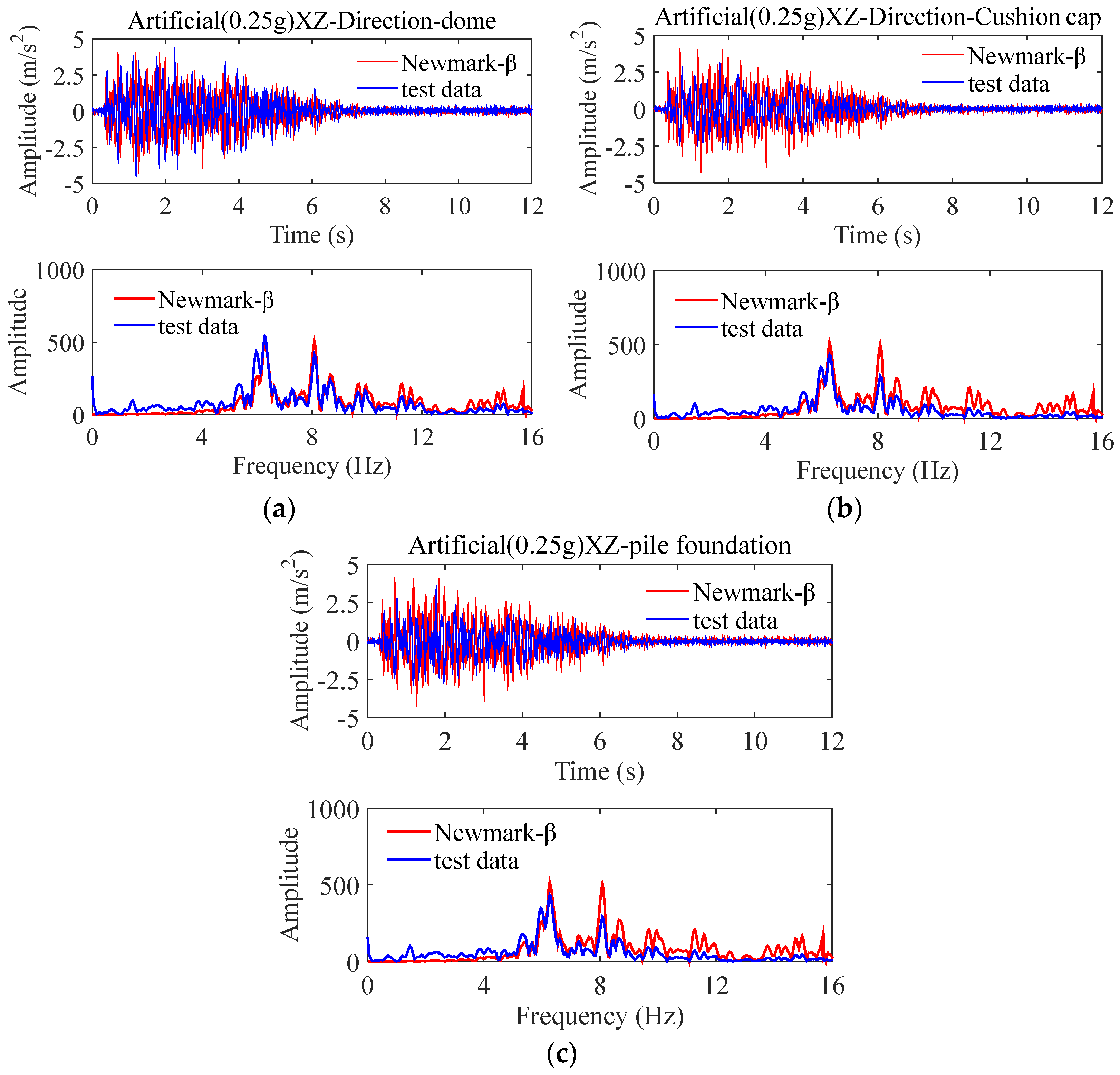
4. Comparative Analysis of Results
4.1. Non-Isolated Storage Tank
4.2. Isolated Storage Tank
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Housner, G.W. Dynamic pressures on accelerated fluid containers. Bull. Seismol. Soc. Am. 1957, 47, 15–35. [Google Scholar] [CrossRef]
- Haroun, M.A.; Housner, G.W. Earthquake Response of Deformable Liquid Storage Tanks. J. Appl. Mech. 1981, 48, 411–418. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Tang, Y.; Tang, H.T. Dynamic Response of Flexibly Supported Liquid-Storage Tanks. J. Struct. Eng. 1992, 118, 264–283. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Tang, Y. Dynamics of Vertically Excited Liquid Storage Tanks. J. Struct. Eng. 1986, 112, 1228–1246. [Google Scholar] [CrossRef]
- Malhotra, P.K.; Wenk, T.; Wieland, M. Simple Procedure for Seismic Analysis of Liquid-Storage Tanks. Struct. Eng. Int. 2000, 10, 197–201. [Google Scholar] [CrossRef] [Green Version]
- Shrimali, M.K.; Jangid, R.S. Seismic response of liquid storage tanks isolated by sliding bearings. Eng. Struct. 2002, 24, 909–921. [Google Scholar] [CrossRef]
- Shrimali, M.K.; Jangid, R.S. Seismic analysis of base-isolated liquid storage tanks. J. Sound Vib. 2004, 275, 59–75. [Google Scholar] [CrossRef]
- Zhang, R.; Weng, D.; Ren, X. Seismic analysis of a LNG storage tank isolated by a multiple friction pendulum system. Earthq. Eng. Eng. Vib. 2011, 10, 253–262. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, Z.; Pan, C. Influence of mechanical layout of inerter systems on seismic mitigation of storage tanks. Soil Dyn. Earthq. Eng. 2018, 114, 639–649. [Google Scholar] [CrossRef]
- Ruifu, Z.; Zhipeng, Z.; Xuchuan, L.; Lingxin, Z. Optimal design of inerter systems for the force-transmission suppression of oscillating structures. Earthq. Eng. Eng. Vib. 2022, 21, 441–454. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Q.; Zhang, R.; Pan, C.; Jiang, Y. Energy dissipation mechanism of inerter systems. Int. J. Mech. Sci. 2020, 184, 105845. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, Z.; Zhang, R.; De Domenico, D.; Pan, C. Optimal design based on analytical solution for storage tank with inerter isolation system. Soil Dyn. Earthq. Eng. 2020, 129, 105924. [Google Scholar] [CrossRef]
- Lin, S.; Wang, J.; Gao, S.; Zhao, H. Real-time hybrid test of a LNG storage tank with a variable curvature friction pendulum system. Arch. Civ. Mech. Eng. 2021, 21, 90. [Google Scholar] [CrossRef]
- Christovasilis, I.P.; Whittaker, A.S. Seismic Analysis of Conventional and Isolated LNG Tanks Using Mechanical Analogs. Earthq. Spectra 2008, 24, 599–616. [Google Scholar] [CrossRef]
- Rawat, A.; Matsagar, V.A.; Nagpal, A.K. Numerical study of base-isolated cylindrical liquid storage tanks using coupled acoustic-structural approach. Soil Dyn. Earthq. Eng. 2019, 119, 196–219. [Google Scholar] [CrossRef]
- Moslemi, M.; Kianoush, M.R. Parametric study on dynamic behavior of cylindrical ground-supported tanks. Eng. Struct. 2012, 42, 214–230. [Google Scholar] [CrossRef]
- Panchal, V.R.; Jangid, R.S. Seismic response of liquid storage steel tanks with variable frequency pendulum isolator. KSCE J. Civ. Eng. 2011, 15, 1041–1055. [Google Scholar] [CrossRef]
- Luo, D.; Liu, C.; Sun, J.; Cui, L.; Wang, Z. Liquefied natural gas storage tank simplified mechanical model and seismic response analysis. Soil Dyn. Earthq. Eng. 2021, 141, 106491. [Google Scholar] [CrossRef]
- Luo, D.; Sun, J.; Liu, C.; Cui, L.; Wang, Z. Damping Effect of Insulation on a Liquefied Natural Gas Tank Based on Shaking Table Tests. J. Earthq. Eng. 2022, 26, 2846–2866. [Google Scholar] [CrossRef]
- Cheng, X.; Luo, B.; Chen, J. Seismic Response considering LSI for Steel Rectangular Water Purification Structures. KSCE J. Civ. Eng. 2021, 25, 4261–4273. [Google Scholar] [CrossRef]
- Cheng, X.; Jing, W.; Gong, L. Simplified Model and Energy Dissipation Characteristics of a Rectangular Liquid-Storage Structure Controlled with Sliding Base Isolation and Displacement-Limiting Devices. J. Perform. Constr. Facil. 2017, 31, 04017071. [Google Scholar] [CrossRef]
- Scislo, L.; Guinchard, M. Non-invasive measurements of ultra-lightweight composite materials using Laser Doppler Vibrometry system. In Proceedings of the 26th International Congress on Sound and Vibration, Montreal, QC, Canada, 7–11 July 2019. [Google Scholar]





| - | Elastic Modulus | Poisson’s Ratio | Density |
|---|---|---|---|
| C50 concrete | 34.5 GPa | 0.167 | 2500 kg/m3 |
| HRB400 steel bar | 210 GPa | 0.3 | 7800 kg/m3 |
| Type | Design Load (KN) | Vertical Stiffness (KN/mm) | Second Shape Factor | Yield Force (KN) | Stiffness after Yield (KN/m) | Equivalent Horizontal Stiffness (KN/m) | Equivalent Damping Ratio (%) | Overall Height of the Bearing (mm) |
|---|---|---|---|---|---|---|---|---|
| LRB300 | 707 | 887 | 5.77 | 22.6 | 469 | 821 | 30.9 | 150 |
| Loading Case | Tank Dome Maximum Displacement Response (mm) | |
|---|---|---|
| X | Y | |
| Wolong wave (XYZ direction, 0.10 g) | 0.87 | 0.17 |
| Wolong wave (XYZ direction, 0.25 g) | 1.78 | 1.51 |
| Wolong wave (XYZ direction, 0.50 g) | 3.77 | 3.7 |
| Wolong wave (XZ direction, 0.75 g) | 6.16 | 0.17 |
| Wolong wave (X direction, 0.75 g) | 6.02 | 0.15 |
| Wolong wave (XYZ direction, 0.75 g) | 6.73 | 6.67 |
| Artificial wave (XYZ direction, 0.10 g) | 3.80 | 6.23 |
| Artificial wave (XYZ direction, 0.25 g) | 9.29 | 16.56 |
| Artificial wave (XYZ direction, 0.50 g) | 20.63 | 32.22 |
| Artificial wave (XZ direction, 0.75 g) | 28.85 | 1.18 |
| Artificial wave (XYZ direction, 0.75 g) | 31.04 | 48.07 |
| Loading Case | Isolated Storage Tank | Non-Isolated Storage Tank | Amplification Factor | |||
|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | |
| Wolong wave (X direction, 0.5 g) | 4.04 | 0.18 | 3.90 | 0.17 | 3.59% | 5.88% |
| Wolong wave (XZ direction, 0.5 g) | 4.14 | 0.14 | 3.77 | 0.13 | 9.81% | 7.69% |
| Wolong wave (XYZ direction, 0.5 g) | 3.97 | 3.95 | 3.77 | 3.70 | 5.31% | 6.76% |
| Wolong wave (XZ direction, 0.75 g) | 5.89 | 0.18 | 5.55 | 0.17 | 6.13% | 5.88% |
| Wolong wave (XYZ direction, 0.75 g) | 7.88 | 7.27 | 7.37 | 7.14 | 6.92% | 1.82% |
| Artificial wave (XYZ direction, 0.25 g) | 9.50 | 16.63 | 9.29 | 16.56 | 2.26% | 0.42% |
| Artificial wave (XZ direction, 0.5 g) | 19.03 | 0.21 | 19.02 | 0.20 | 0.05% | 5.00% |
| Artificial wave (XYZ direction, 0.5 g) | 20.68 | 32.26 | 20.63 | 32.22 | 0.24% | 0.12% |
| Artificial wave (X direction, 0.75 g) | 29.94 | 2.12 | 29.05 | 2.02 | 3.06% | 4.95% |
| Artificial wave (XZ direction, 0.75 g) | 29.13 | 1.19 | 28.85 | 1.18 | 0.97% | 0.85% |
| Artificial wave (XYZ direction, 0.75 g) | 31.25 | 48.72 | 31.04 | 48.07 | 0.68% | 1.35% |
| - | Experimental Data | 1-DOF | 2-DOF | 3-DOF | 4-DOF |
|---|---|---|---|---|---|
| Acceleration amplitude (m/s2) | 20.71 | 16.83 | 9.68 | 17.29 | 25.93 |
| Fitting degree (%) | - | 81.24% | 46.72% | 83.46% | 79.87% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, Z.; Liu, Y.; Fu, J.; Cheng, H.; Zhang, L.; Xue, X. Seismic Response of a Large LNG Storage Tank Based on a Shaking Table Test. Appl. Sci. 2022, 12, 7663. https://doi.org/10.3390/app12157663
Chen Z, Xu Z, Liu Y, Fu J, Cheng H, Zhang L, Xue X. Seismic Response of a Large LNG Storage Tank Based on a Shaking Table Test. Applied Sciences. 2022; 12(15):7663. https://doi.org/10.3390/app12157663
Chicago/Turabian StyleChen, Zengshun, Zhengang Xu, Yang Liu, Jun Fu, Huayan Cheng, Likai Zhang, and Xuanyi Xue. 2022. "Seismic Response of a Large LNG Storage Tank Based on a Shaking Table Test" Applied Sciences 12, no. 15: 7663. https://doi.org/10.3390/app12157663
APA StyleChen, Z., Xu, Z., Liu, Y., Fu, J., Cheng, H., Zhang, L., & Xue, X. (2022). Seismic Response of a Large LNG Storage Tank Based on a Shaking Table Test. Applied Sciences, 12(15), 7663. https://doi.org/10.3390/app12157663






