Analytical Investigation of Sound Radiation from Functionally Graded Thin Plates Based on Elemental Radiator Approach and Physical Neutral Surface

Abstract

This paper analyzes the sound radiation behavior of a clamped thin, functionally graded material plate using the classical plate theory and Rayleigh Integral with the elemental radiator approach. The material properties of the plate are assumed to vary according to the power-law distribution of the constituent materials in the transverse direction. The functionally graded material is modeled using a physical neutral surface instead of a geometric middle surface. The effects of the power-law index, elastic modulus ratio, different constituent materials, and damping loss factor on the sound radiation of functionally graded plate are analyzed. It was found that, for the considered plate, the power-law index significantly influences sound power level and radiation efficiency. There exists a critical value of the power-law index for which the corresponding peak of sound power level is minimum. In a wide operating frequency range, approximately 500–1500 Hz, this research suggests that the radiation efficiency is lower for the power-law index equal to 0 and 1. However, for very low frequencies (less than 250 Hz), the power-law index does not affect radiation efficiency significantly. Further, as the modulus ratio increases, the sound power peak decreases for a given power-law index. For the given material constituents of the functionally graded plate, the different values of damping loss factors do not significantly influence radiation efficiency. However, the selection of material constituents affects the radiation efficiency peak.

1. Introduction

Functionally graded materials (FGM) are ceramic–metal composites whose material properties continuously vary in the thickness direction [1,2,3]. This constant variation in the material characteristic guarantees that the stress field varies smoothly across the entire thickness range. The ceramic constituents in FGM plates are resistant to high temperatures due to their low thermal conductivity. A range of applications can be customized by gradually tweaking the characteristic. Ceramic metal FGM plates, for example, are a better choice for aeronautical applications in hot climates. Furthermore, because plate-like structures are less rigid in the transverse direction, they are more likely to vibrate, amplifying the acoustic radiation. As per the present scenario, control of noise in modern machine fabrication becomes important, for which FGM plates have played significant roles.

In this paper, the sound radiation of the P-FGM plate is computed by solving the Rayleigh Integral with the elemental radiator approach. Parametric effects of plate variables (such as power-law index, modulus ratio, and damping loss factor) on the vibroacoustic response of a clamped, thin power-law index, functionally graded plate under point forcing are discussed. Researchers estimated that the sound radiation response of isotropic [4,5,6,7,8,9,10,11], orthotropic [12,13,14,15], composite [16,17,18], sandwich plates [19,20,21], and FGM [22,23,24,25,26,27,28,29] plates using the Rayleigh integral method. The authors used the elemental radiator approach to estimate the sound power radiated by plate structures [13,29,30,31,32,33,34,35,36,37,38]. The literature is scarce on sound radiation from FGM plates, but here is a brief review.

Using the elemental radiator approach, Chandra et al. [22] analyzed the sound response of sandwich plates with FGM core along with the thickness. Using the Rayleigh Integral, they discussed the effect of core thickness on the overall sound power level. The authors [23] broadened their investigation to include the sound radiation and transmission loss of a vibrating functionally graded plate in terms of plate velocity and radiated sound power for point and uniformly distributed load cases. They investigated the sound transmission and reflection from unbounded panels of functionally graded materials. Zhou et al. [27] examined temperature-dependent porous functionally graded plate for vibration and sound radiation. They used first-order shear deformation theory with the temperature-dependent material properties to formulate the governing equation of porous FGM plates using Hamilton’s principle and demonstrated that structural stiffness and rigidity played a significant role in the dynamics and acoustics response of porous FGM plates. Yang et al. [28] expanded on their previous work to provide a semi-analytical solution to the sound radiation of functionally graded plates in a thermal environment. Chandra et al. [29] also presented analytical studies on sound radiation transmission loss from functionally graded plates using FSDT and elemental radiator approach. They calculated the sound radiation under variable excitation strategies. They considered the geometric mid-surface of the FGM plate as the physical neutral surface. Chukwuemeke et al. [39] used FSDT and the finite element method to investigate the vibroacoustic responses of P-FGM panels with various boundary conditions.

According to the above literature review, most researchers, while studying the acoustic response of P-FGM plates, used the geometric mid-surface as the physical neutral surface [24,28,29,37,40,41,42]. However, this is not true for FGM material plates because the property varies in the thickness direction [1,43,44] leading to stretching–bending coupling and making it difficult to maintain interlaminar material continuities. The physical neutral surface over the geometric mid-surface has an added advantage of avoiding stretching–bending coupling [1,41,43] and assisting in preserving interlaminar material continuities.

2. Theoretical Modeling

2.1. Geometry and Material Properties

Figure 1 depicts a thin solid rectangular FGM plate of size a × b × h made of ceramic and metal mixture constituents. As the material properties of the FGM plate vary along with the thickness as a function of the power-law function, the FGM plate is termed the P-FGM plate. The P-FGM plate’s top surface is made of ceramic, while the bottom surface is made of metal.

The volume fraction of the metal and ceramic constituents varies with the power-law index k. The volume fraction is expressed as

$$V_c={\left(z/h+1/2\right)}^k; V_C+V_m=1$$

(1)

where $V_c$ denotes the volume fraction of ceramic constituent in the FGM plate, while $V_{m } \mathrm{denotes} \mathrm{the}$ volume fraction of metallic constituent in the FGM. z represents the thickness variation of each layer, h represents the half-ply thickness from the middle surface, and k represents the power-law index ranging from $0 \le k \le \infty .$

The rule of the mixture does not appear to work with multi-layered models because it does not account for the interaction of the intermittent layered constituents [44]. Therefore, the Mori–Tanaka scheme [45,46,47,48,49] is used to compute the effective modulus of the P-FGM plate. Hence, the effective density and effective Young’s modulus of the FGM plate are respectively given by

$$\rho \left(z\right)={\rho }_c{V}_c+{\rho }_m{V}_m$$

(2)

and

$$E\left(z\right)=E_m+\left(E_c-E_m\right)\frac{V_c}{1+V_m\left(\frac{E_c}{E_m}-1\right)\left(1+\nu \right)3\left(1-\nu \right)}$$

(3)

where c and m denote ceramic and metal, respectively, rho denotes density, and E denotes the FGM plate’s Young’s modulus of elasticity. Because the plate is thin, the variation in Poisson’s ratio (v) along the thickness direction is considered negligible [50,51,52,53]. Material properties of different P-FGM plates can be deduced from [28,54,55,56].

Table 1. Material properties of different FGM plates [28,55].

Sr. No.	Materials	$\mathbf{Young}’\mathbf{s} \mathbf{Modulus} (\mathit{E}, \mathbf{P}\mathbf{a})$	$\mathbf{Poisson}’\mathbf{s} \mathbf{Ratio} (\mathit{\nu })$	$\mathbf{Density} (\mathit{\rho },\mathbf{kg}/{\mathbf{m}}^3)$
1	Aluminum (Al)	70 × 109	0.3	2700
2	$\mathrm{Aluminum} \mathrm{Oxide} ({\mathrm{Al}}_2{\mathrm{O}}_3$)	380 × 109	0.3	3800
3	$\mathrm{Zirconia} ({\mathrm{ZrO}}_2$)	151 × 109	0.3	3000
4	$\mathrm{Stainless} \mathrm{Steel} (\mathrm{SUS}304$)	208 × 109	0.32	8166
5	$\mathrm{Silicon} \mathrm{Nitride} ({\mathrm{Si}}_3{\mathrm{N}}_4)$	322 × 109	0.24	2370
6	Ti-6Al-4V	106 × 1011	0.298	4429

summarizes the different FGM material constituents.

2.2. Significance of Physical Neutral Surface and Classical Plate Theory (CPT)

As per the theory of rectangular thin plate’s bending [1] using classical plate theory, the displacement components along with all three directions $\left(x,y,z\right)$ are given by

$$\begin{gathered} u=u_0\left(x,y\right)-z\frac{\partial w}{\partial x}; \\ \upsilon ={\upsilon }_0\left(x,y\right)-z\frac{\partial w}{\partial y}; \\ w=w\left(x,y\right) \end{gathered}$$

(4)

where u, v, and w are the displacement components in each of the three directions, respectively, $\left(x,y,z\right)$. Because of variations in material properties in the thickness direction, there is an eccentric gap between the physical neutral surface and the geometric mid-surface of the P-FGM plate. Hence, by constructing a new reference coordinate $z_{ns}=z-z_0,$ the stretching–bending coupling can be neglected [1]. $\mathrm{Here} z_0$ denotes the distance between the physical neutral surface and the geometric mid-surface of the P-FGM plate. As a result, Equation (4) changes to

$$\begin{gathered} u=-z_{ns}\frac{\partial w}{\partial x}=-\left(z-z_0\right)\frac{\partial w}{\partial x}; \\ v=-z_{ns}\frac{\partial w}{\partial y}=-\left(z-z_0\right)\frac{\partial w}{\partial y}; \\ w=w\left(x,y\right) \end{gathered}$$

(5)

As a result, the strain caused by the displacements as mentioned earlier is of the form

$$\begin{gathered} {\mathrm{ϵ}}_{xx}=-z_{ns}\frac{{\partial }^{2}w}{\partial x^2}; \\ {\mathrm{ϵ}}_{yy}=-z_{ns}\frac{{\partial }^{2}w}{\partial y^2}; \\ { \mathsf{\gamma }}_{xy}=-2z_{ns}\frac{{\partial }^{2}w}{\partial x\partial y} \end{gathered}$$

(6)

where ${\mathrm{ϵ}}_{xx}, {\mathrm{ϵ}}_{yy}$ represent the normal strains in the x and y directions, respectively, and ${\mathsf{\gamma }}_{xy}$ represents the shear strain along the x, y plane. Assuming that the P-FGM plate obeys generalized Hooke’s law, the stress–strain relationship is

$$\left\{\begin{array}{c}{\mathsf{\sigma }}_{xx}\\ {\mathsf{\sigma }}_{yy}\\ {\mathsf{\tau }}_{xy}\end{array} \right\}=\left[\begin{array}{ccc}{Q}_{11}& Q_{12}& 0\\ Q_{21}& Q_{22}& 0\\ 0& 0& Q_{66}\end{array}\right]\left\{\begin{array}{c}{\mathrm{ϵ}}_{xx}\\ {ϵ}_{yy}\\ {\gamma }_{xy}\end{array}\right\}$$

(7)

where the normal stresses are ${\mathsf{\sigma }}_{xx} {\mathrm{and} \mathsf{\sigma }}_{yy}$ and the shear stress is ${\mathsf{\tau }}_{xy}$, and the reduced stiffness matrix ${\mathit{Q}}_{\mathit{i}\mathit{j}}$ is given by

$$\begin{gathered} Q_{11}=Q_{22}=\frac{E\left(z_{ns}\right)}{1-{\mathsf{\nu }}^2}; \\ {Q}_{12}=Q_{21}=\frac{\mathsf{\nu }E\left(z_{ns}\right)}{1-{\mathsf{\nu }}^2}; \\ {Q}_{66}=\frac{E\left(z_{ns}\right)}{2\left(1+\mathsf{\nu }\right)} \end{gathered}$$

(8)

The physical neutral surface $\left(z_0\right)$ $\mathrm{can} \mathrm{be} \mathrm{computed} \mathrm{by} \mathrm{setting} \mathrm{net} \mathrm{force} \mathrm{along} \mathrm{a} \mathrm{direction} \mathrm{to} \mathrm{zero}.$ Thus,

$$\sum F_x={{\displaystyle \int }}_{-h/2-z_0}^{h/2-z_0}{\mathsf{\sigma }}_{xx}dA$$

(9)

which simplifies [1] to

$$z_0=\frac{kh\left(E_{rat}-1\right)}{2\left(k+2\right)\left(E_{rat}+1\right)}$$

(10)

where $E_{rat}=\frac{E_c}{E_m}$ is the modulus ratio, and as observed, for $E_{rat} \mathrm{is} \mathrm{one}$, the P-FGM plate becomes an isotropic plate. Therefore, the volume fraction and material properties of the FGM plate is

$$\begin{gathered} \left(V_f\left(z_{ns}\right)={\left(\frac{1}{2}+\frac{Z_{ns}+Z_0}{h}\right)}^k\right) \\ \mathrm{and} P\left(z_{ns}\right)=V_f\left(Z_{ns}\right)P_c+\left(1-V_f\left(Z_{ns}\right)\right)P_m \end{gathered}$$

where $V_f$ is the volume fraction of P-FGM material constituents, while P represents the material properties of the P-FGM plate considering the physical neutral surface.

2.3. The FGM Plate’s Governing Differential Equation and Eigenvalues Computation Using CPT

Based on Hamilton’s principle, the governing equation for out of plane free vibration of a FGM plate yields the following equations [1].

$$D_{eff}{\nabla }^{4}w+I_0\frac{{\partial }^{2}w}{\partial t^2}=0$$

(11)

where $w\left(x,y\right)$ is the transverse displacement, and ${\nabla }^4=\frac{{\partial }^4}{x^4}+2\frac{{\partial }^4}{\partial x^2\partial y^2}+\frac{{\partial }^4}{y^4}$ and $I_0$ and $D_{eff}$ are the transverse inertia and effective dynamic stiffness of the P-FGM plate, respectively, and are given by

$$\begin{gathered} D_{eff}={{\displaystyle \int }}_{-h/2-z_0}^{h/2-z_0}{z}_{ns}^2{Q}_{11}\left(z_{ns}\right)d{z}_{ns}={{\displaystyle \int }}_{-h/2}^{h/2}{\left(z-z_0\right)}^2{Q}_{11}\left(z\right)dz \\ =\frac{12D_c}{E_{rat}}\left(\frac{3E_{rat}\left(k^2+k+2\right)+\left(k^3+3k^2+8k\right)}{12\left(k+1\right)\left(k^2+5k+6\right)}-\frac{z_0}{h}\frac{k\left(E_{rat}-1\right)}{\left(k+1\right)\left(k+2\right)}+{\left(\frac{z_0}{h}\right)}^2\frac{E_{rat}+k}{k+1}\right) \end{gathered}$$

(12)

$$I_0={{\displaystyle \int }}_{-h/2-z_0}^{h/2-z_0}\rho \left(z_{ns}\right)d{z}_{ns}=\frac{{\rho }_{c}h}{{\rho }_{rat}}\left(\frac{{\rho }_{rat}-1}{k+1}+1\right)$$

(13)

$D_{eff}$ is dependent upon $E_{rat}=\frac{E_c}{E_m}$ and the power-law index $‘k’$ and $D_c=\frac{E_c{h}^3}{12\left(1-{\mathsf{\nu }}^2\right)}$.

$I_0$ is dependent upon ${\rho }_{rat}=\frac{{\rho }_c}{{\rho }_m}$ and the power-law index is $‘k’$.

In the case of harmonic free vibration, $w\left(x,y\right)$ can be written as the superposition of the infinite number of the mode shape function $\varphi \left(x,y\right)$ and can be written as

$$w\left(x,y\right)={{\displaystyle \sum }}_{m=1}^{\infty }{{\displaystyle \sum }}_{n=1}^{\infty }{\varphi }_{mn}\left(x,y\right){\eta }_{mn}{e}^{i\omega t}$$

(14)

where ${\eta }_{mn}$ is the modal participation factor representing the contribution of each mode to harmonic response analysis. Because these mode shapes are orthogonal to each other [7,29,32,34,35], we get,

$${{\displaystyle \int }}_0^a{{\displaystyle \int }}_0^b{I}_0{\varphi }_{mn}\left(x,y\right){\varphi }_{jk}\left(x,y\right)dxdy \left\{\begin{array}{c}{M}_{mn}\\ 0\end{array}\right.\begin{array}{c}if m=j, n=k\\ \mathrm{other}\end{array}$$

(15)

where $M_{mn}$ is the modal mass.

Seeking a harmonic solution, Equation (11) is reduced in terms of mode shape function ${\varphi }_{mn}$ and is given by

$$D_{eff}{\nabla }^4{\varphi }_{mn}\left(x,y\right)-{\omega }_{mn}^2{I}_0{\varphi }_{mn}\left(x,y\right)=0$$

(16)

The mode shape function ${\varphi }_{mn}\left(x,y\right)$ is generally the product of the individual beam function [35].

$${\varphi }_{mn}\left(x,y\right)=X_m\left(x\right)Y_n\left(y\right)$$

(17)

The two beam functions $X_m\left(x\right) \mathrm{and} Y_n\left(y\right)$ are dependent upon boundary conditions used over the P-FGM plate’s edges. For clamped boundary conditions, these functions are given by

$$X_m\left(x\right)=cosh\left(\frac{{\lambda }_{m}x}{a}\right)-cos\left(\frac{{\lambda }_{m}x}{a}\right)-{\beta }_m\left[sinh\left(\frac{{\lambda }_{m}x}{a}\right)-sin\left(\frac{{\lambda }_{m}x}{a}\right)\right]$$

(18)

$$Y_n\left(y\right)=cosh\left(\frac{{\lambda }_{n}y}{b}\right)-cos\left(\frac{{\lambda }_{n}y}{b}\right)-{\beta }_n\left[sinh\left(\frac{{\lambda }_{n}y}{b}\right)-sin\left(\frac{{\lambda }_{n}y}{b}\right)\right]$$

(19)

where

$${\beta }_i=\frac{cosh\left({\lambda }_i\right)-cos\left({\lambda }_i\right)}{sinh\left({\lambda }_i\right)-sin\left({\lambda }_i\right)} \mathrm{for} i=m,n$$

(20)

and ${\mathsf{\lambda }}_{m }\& {\mathsf{\lambda }}_n$ are the roots of Equation (21).

$$cosh\left(\lambda \right)cos\left(\lambda \right)-1=0$$

(21)

The ${\left(m,n\right)}^{th} \mathrm{natural}$ frequency of the P-FGM plate, ${\omega }_{mn}$ is given by [35]

$${\omega }_{mn}=\sqrt{\frac{D_{eff}}{I_0}}\times \sqrt{\frac{I_1{I}_2+2I_3{I}_4+I_5{I}_6}{I_2{I}_6}}$$

(22)

Considering a combination of individual beam function and boundary condition along the edges of the plate, these “I” terms can be computed. For the present problem, $I_i$ is [32,35]

$$\begin{gathered} I_i=\frac{1}{4}{\left(1+{\beta }_i\right)}^{2}sinh\left(2{\lambda }_i\right)+sinh\left({\lambda }_i\right)[2{\beta }_{i}sin\left({\lambda }_i\right)- \\ \left(1-{\beta }_i^2\right))cos({\lambda }_i\left)\right] \\ -\left(1+{\beta }_i{}^2\right)sin\left({\lambda }_i\right)cos\left({\lambda }_i\right))+\frac{1}{2}\left(1-{\beta }_i{}^2\right)sin\left({\lambda }_i\right)cos\left({\lambda }_i\right)+{\lambda }_i-\frac{1}{2}{\beta }_i\left[1+cosh\left(2{\lambda }_i\right)\right]+{\beta }_{i}co{s}^2\left({\lambda }_i\right) \end{gathered}$$

(23)

where i = one to six.

Hence, Equation (22) can be rewritten as

$${\omega }_{mn}=\sqrt{\frac{D_{eff}}{I_0}}\times \sqrt{{\left(\frac{{\lambda }_m}{a}\right)}^4+{\left(\frac{{\lambda }_n}{b}\right)}^4+2{\left(\frac{{\lambda }_m{\lambda }_n}{ab}\right)}^2\frac{T_m{T}_n}{I_m{I}_n}}$$

(24)

where $T_i$ can be given by

$$T_i=\frac{1}{4}{\left(1+{\beta }_i\right)}^{2}sinh\left(2{\lambda }_i\right)-\frac{1}{2}{\beta }_{i}cosh\left(2{\lambda }_i\right)-\frac{1}{2}{\left(1+{\beta }_i\right)}^{2}sin\left({\lambda }_i\right)cos\left({\lambda }_i\right)-{\beta }_{i}co{s}^2\left({\lambda }_i\right)-{\beta }_i^2{\lambda }_i+\frac{3}{2}{\beta }_i$$

(25)

The eigenvalues and mode shape were obtained in MATLAB and used in the aforementioned equations.

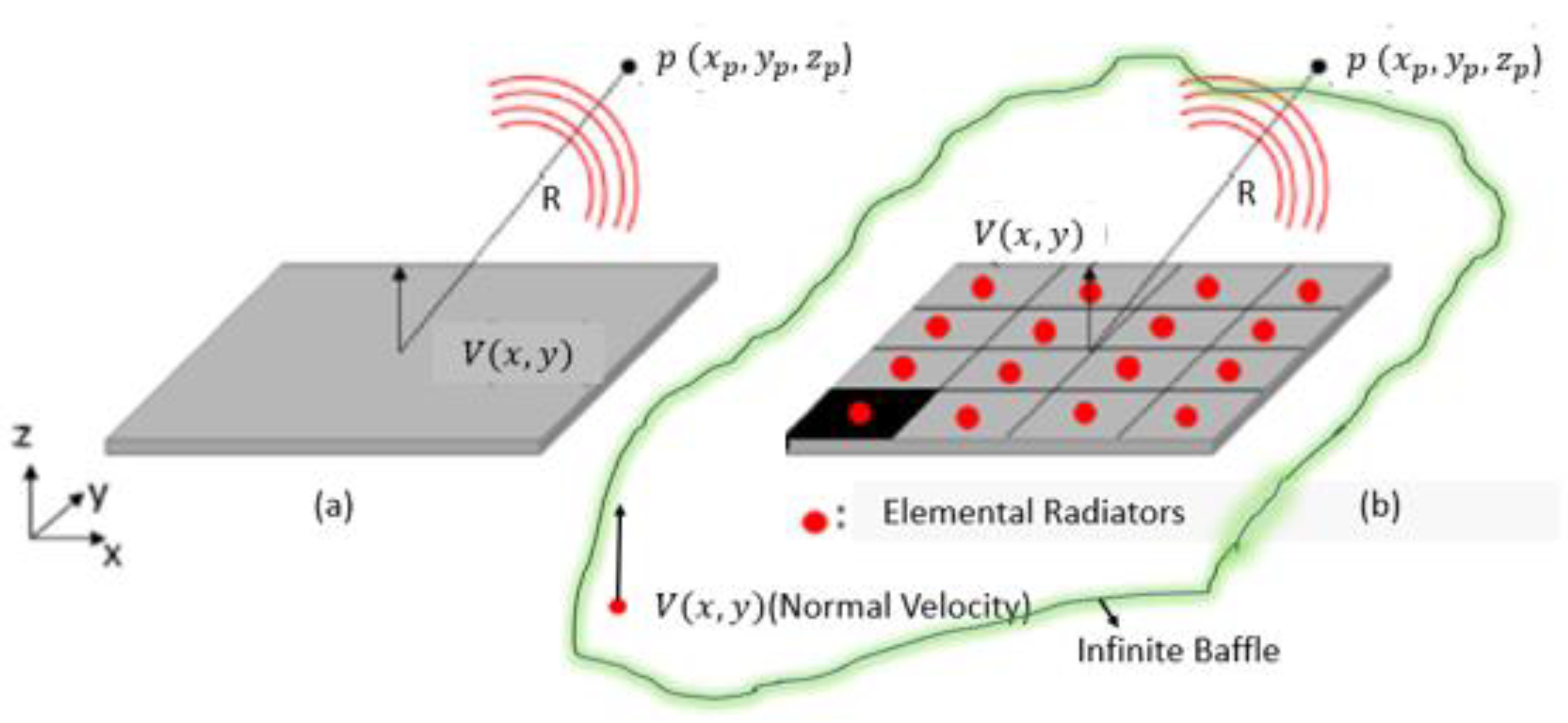
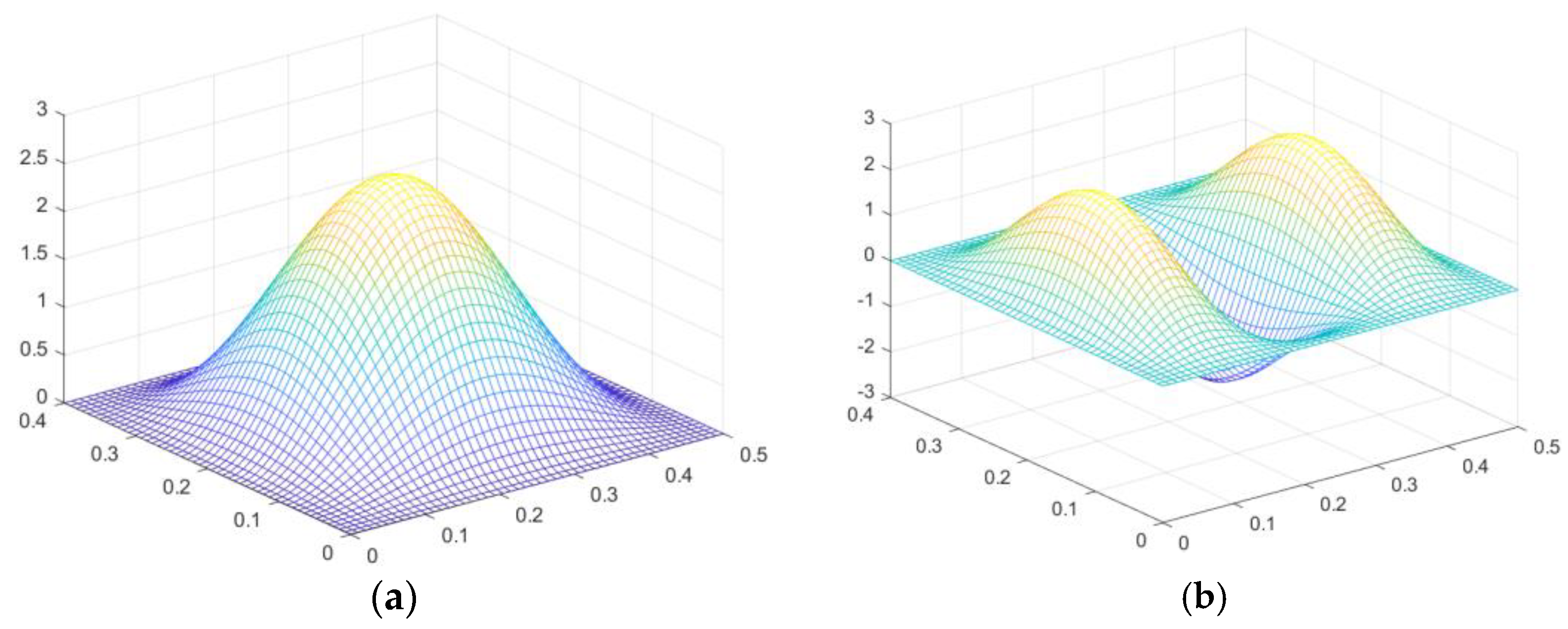
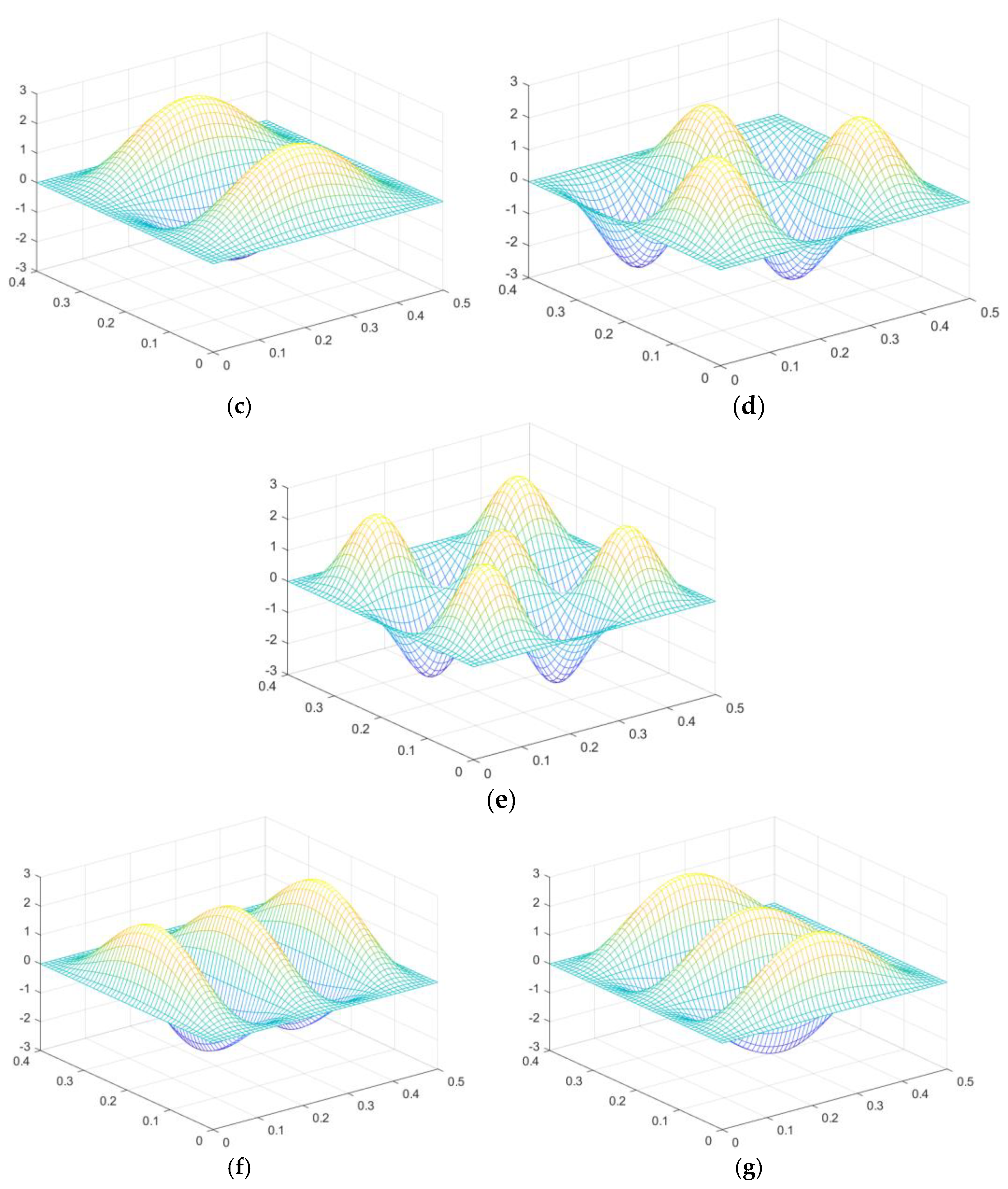
2.4. Surface Velocity Computation in Normal Direction

The out of plane displacement of the P-FGM plate excited by point load in the center is given by [32]

$$w\left(x,y\right)=\frac{1}{I_{0}ab}{\displaystyle \sum }_{i=1}^{ss}{\displaystyle \sum }_{m=1}^{M^{″}}{\displaystyle \sum }_{n=1}^{N^{″}}{F}_{i } \frac{{\varphi }_{mn}\left(x,y\right){\varphi }_{mn}\left(x^{\ast },y^{\ast }\right)}{\gamma \left({\omega }_{mn}^2\left(1+j\psi \right)-{\omega }^2\right)}$$

(26)

where,$m$ and $n \mathrm{are} \mathrm{the} \mathrm{modal}$ indices of the order $M^{″}$ and $N^{″}$, respectively. $\omega$ is the excitation frequency, $F_i$ is 1N point load applied at the center of the P-FGM plate, $\psi$ is the damping loss factor, and $\mathsf{\gamma }$ is given by

$$\gamma =\frac{1}{S}{{\displaystyle \int }}_0^a{{\displaystyle \int }}_0^b{\varphi }_{mn}^2\left(x,y\right)dxdy$$

(27)

The normal velocity of plate at any coordinate $\left(x,y\right)$ is [32,54,55,56]

$$V\left(x,y\right)=j\omega w\left(x,y\right)e^{\left\{j\omega t\right\}}$$

(28)

2.5. Computation of Sound Radiation Fields

The Rayleigh Integral gives the acoustic pressure for any point in the half-space $\left(x_p,y_p,z_p\right)$ as shown in Figure 2.

$$p\left(x_p,y_p,z_p\right)=\frac{j\omega {\rho }_0}{2\pi }{{\displaystyle \int }}_{S}V\left(x,y\right)\cdot \frac{e^{-j\kappa R}}{R}dS$$

(29)

where $R=\left|x-x_s\right|=\sqrt{{\left(x_p-x\right)}^2+{\left(y_p-y\right)}^2+z_p^2}$ is the distance between the source point $\left|x_s\right|$= $\left(x,y,0\right)$ on the plate surface to the observation point $\left|x\right|$ = $\left(x_p,y_p,z_p\right)$ with $z_p\ge 0$ The density of the acoustic medium, air is given by ${\rho }_0$, $\kappa$ is the acoustic wavenumber, $c_0$ is the speed of sound in acoustic medium air, and $S$ is the plate’s radiating surface. Each element can also be considered a compact acoustic source, resembling a monopole source. $S_e=dx\ast dy$, gives the elemental area, where dx and dy are the element sizes in the x and y directions, respectively.

Every elemental radiator has a constant velocity [32,52] because the characteristics length of each elemental radiator is smaller than acoustic and structural wavelengths.

Thus, Equation (29) can be expressed in discretized form as

$$p\left(x_p,y_p,z_p\right)=\frac{j\omega {\rho }_0}{2\pi }{\displaystyle \sum }_s{V}_{M,N}\frac{e^{-j\kappa R}}{R}dxdy$$

(30)

For a meshed P-FGM plate, Equation (30) can be expressed as an impedance matrix

$$\overrightarrow{p}\approx {\mathit{Z}}_{\mathit{v}}\overrightarrow{\mathit{V}}$$

(31)

Writing Equations (30) and (31) in terms of impedance matrix ${\mathit{Z}}_{\mathit{v}}$ as

$${\left({\mathit{Z}}_{\mathit{v}}\right)}_{il}=\frac{j\omega {\rho }_0{S}_e}{2\pi }\frac{e^{-j\kappa R_{il}}}{R_{il}}; \mathrm{for} i,l=M,N$$

(32)

where $S_e$ is the $i^{th}$ elemental radiator area located at source point $\left(x,y,0\right)$ and $R_{il}$ denotes the distance from $i^{th}$ to $l^{th}$ element located at observation point $\left(x_p,y_p,0\right)$. For Green’s function integrand [10,32], the reciprocity principle holds.

$$(\frac{e^{-j\kappa R_{il}}}{R_{il}}) i.e. G\left(x_s|x\right)=G(x|x_s)$$

The radiation resistance matrix ${\mathit{R}}_{\mathit{m}\mathit{a}\mathit{t}}$ is defined per relation ${\mathit{R}}_{\mathit{m}\mathit{a}\mathit{t}}=\frac{S_e}{2}Re\left({\mathit{Z}}_{\mathit{v}}\right)$ as given by [35], which converts to

$${\mathit{R}}_{\mathit{m}\mathit{a}\mathit{t}}=\frac{{\omega }_{mn}^2{\rho }_0{S}_e^2}{4\pi c}\left[\begin{array}{cccc}1& \frac{sin \kappa R_{12}}{k{R}_{12}}& \dots & \frac{sin \kappa R_{1N}}{k{R}_{1N}}\\ \frac{sin \kappa R_{21}}{k{R}_{21}}& 1& \dots & ⋮\\ ⋮& ⋮& \ddots & ⋮\\ \frac{sin \kappa R_{N1}}{k{R}_{N1}}& \dots & \dots & 1\end{array}\right]$$

(33)

Because of reciprocity, ${\mathit{R}}_{\mathit{m}\mathit{a}\mathit{t}}$ is symmetric, real, and positive definite. Equation (33)’s matrix elements are determined by the acoustic medium’s properties, the natural frequencies and geometry of the P-FGM plate. As a result, sound power from each of the elemental radiators $\overline{W_e}$ is given as

$$\overline{W_e}=\frac{S_e}{2}Re\left\{\right(\overrightarrow{V^{\ast }}\}{\mathit{Z}}_{\mathit{v}}\overrightarrow{\mathit{V}})=\overrightarrow{{\mathit{V}}^{\ast }}{\mathit{R}}_{\mathit{m}\mathit{a}\mathit{t}}\overrightarrow{\mathit{V}}$$

(34)

where $\overrightarrow{\mathit{V}}$ is the normal surface velocity vectors of each elemental radiator and * denotes the complex conjugate. Considering all the elemental radiators, the total approximate sound power can be rewritten as

$$W=\sum \overline{W_e}$$

(35)

The SPL in (dB) is computed by

$$W\left(\mathrm{dB}\right)=10lo{g}_{10}\left(W/W_{ref}\right);\mathrm{with} W_{ref}={10}^{-12}W$$

(36)

The radiation efficiency can be calculated by

$$\sigma =\frac{W}{\frac{1}{2}{\rho }_{0}cS<v^2>}$$

(37)

for $<v^2>$ is the mean square average normal velocity of the plate and is given by

$$<v^2>=\frac{1}{2S}{{\displaystyle \int }}_{S}V{\left(x,y\right)}^{\ast }V\left(x,y\right)dS\approx \frac{MN}{2{\left(ab\right)}^2}\overrightarrow{{\mathit{V}}^{\ast }}\overrightarrow{\mathit{V}}$$

(38)

The ${\mathrm{V}}_{rms}$ is given by

$$V_{rms}=\frac{\overrightarrow{{\mathit{V}}^{\ast }}\overrightarrow{\mathit{V}}}{\sqrt{2}}$$

(39)

3. Results and Discussion

The sound radiation fields are computed by solving Rayleigh Integral in MATLAB using the present approach mentioned in the aforementioned topic. This section discusses the validation studies and parametric effects of various parameters on the sound radiation fields.

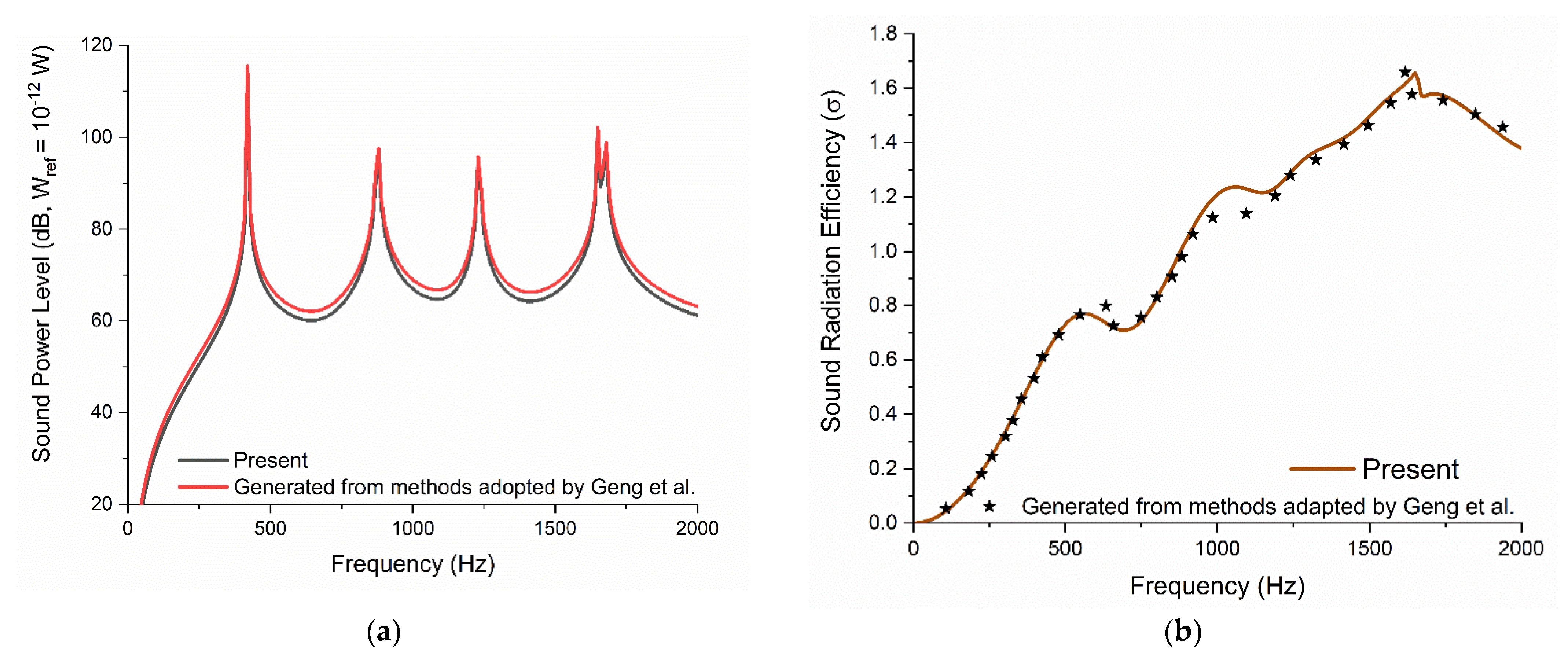
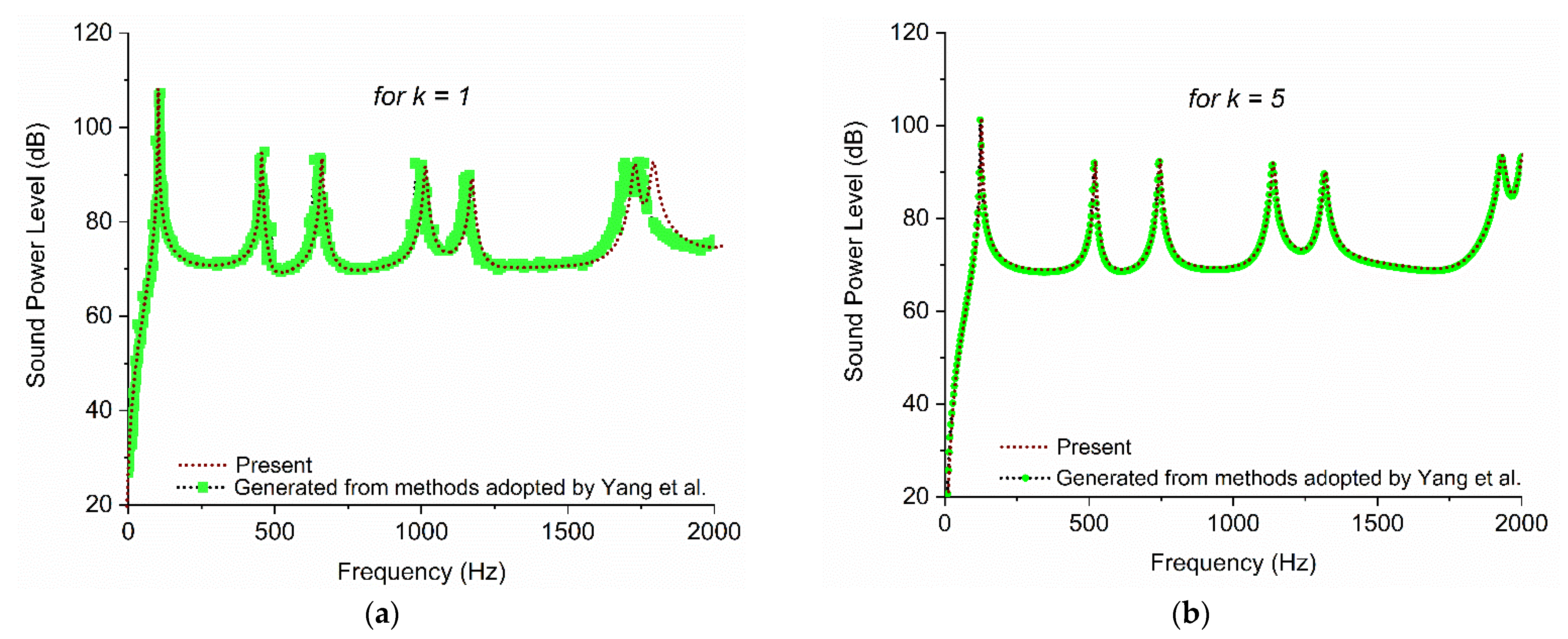
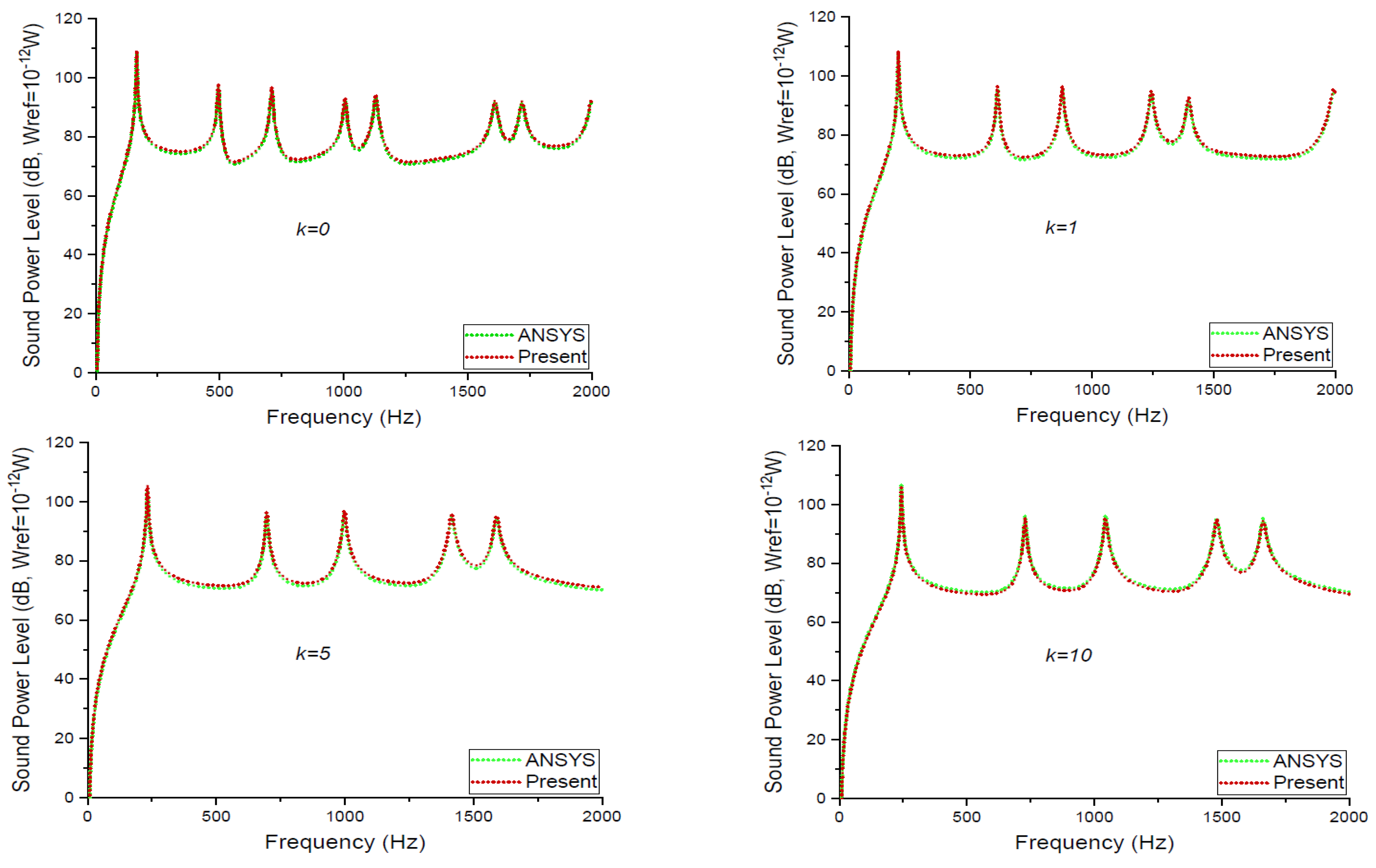
3.1. Comparative Study with the Available Published Results

The P-FGM is reduced to a homogeneous isotropic plate when k = 0. As a result, in Figure 3, the sound radiation fields computed by the aforementioned present approach are compared to those calculated by the method used by Geng et al. [7]. The assumption used in this study is that the size of the element is smaller than half of the structural and acoustic wavelength, leading to constant normal velocity over each elemental radiator. The constant velocity eases solving the Rayleigh integral by elemental radiator approach with radiation resistance matrix. Geng et al. [7] used the direct integration approach with the assumption that the plate is significantly thin (a/h = 40). An excellent agreement is observed in Figure 3.

For two values of the power-law index, k = 1 and 5, the sound power level is computed using the present approach and cross-compared against results in Yang et al. [28] and illustrated in Figure 4. In addition to above assumption mentioned in Section 3.1, the thermal effects are ignored. Furthermore, the plate is assumed to be placed in an infinite rigid baffle. In general, a good agreement is obtained in Figure 4. A small discrepancy is found at higher frequencies for k = 1 because Yang et al. [28] used first-order shear deformation theory with subspace method, while in the present paper, classical plate theory with elemental radiator approach is used. Yang et al. [28] used a frequency resolution of 1 Hz for a frequency range of 0 to 2000 Hz, while in the current paper, the frequency resolution is 3 Hz.

Figure 5 compares the sound power level radiated from the vibrating P-FGM plate computed using the present approach and finite element package, Ansys. Al\/Al_2 0_3 P-FGM is the material composition used for the clamped FGM plate. In Ansys, SOLID185 and Contact174 elements are used for structural modeling, while FLUID221 elements are used for acoustic medium modeling. The results show a high level of agreement.

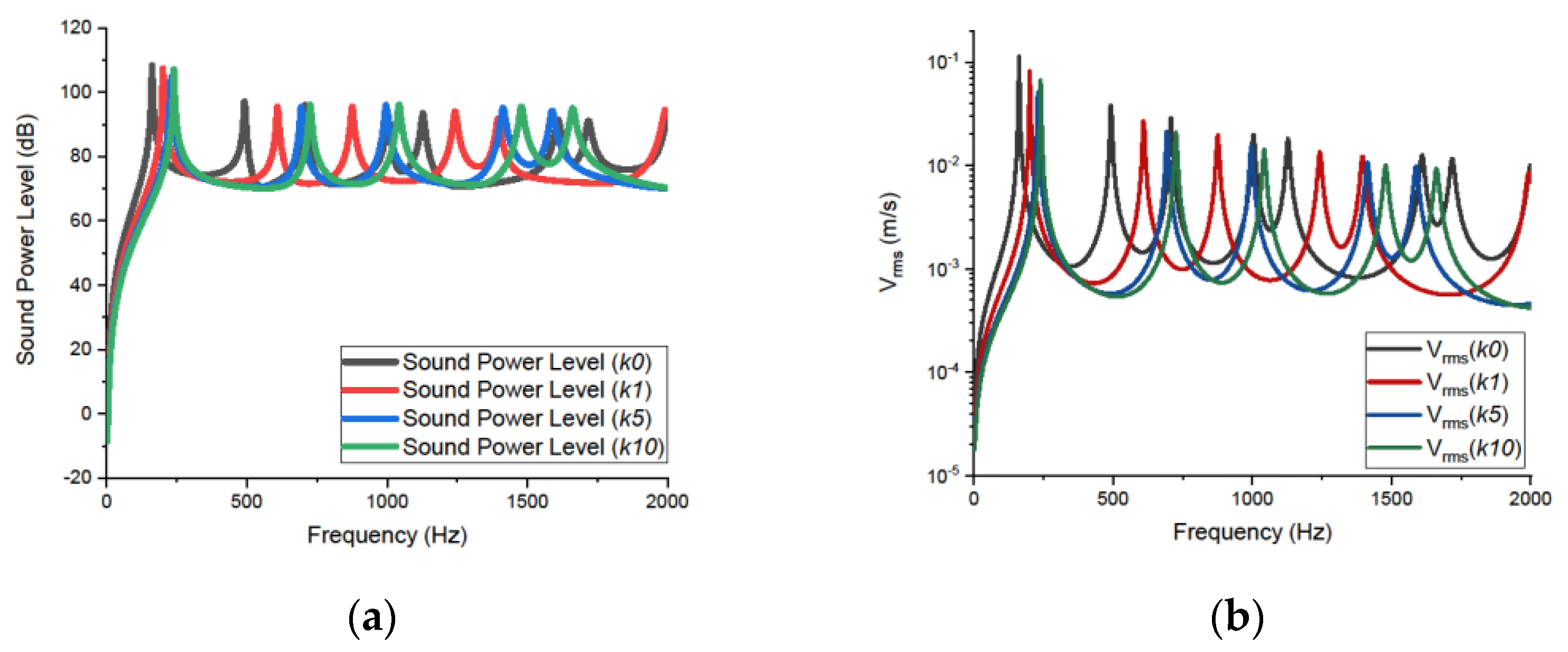
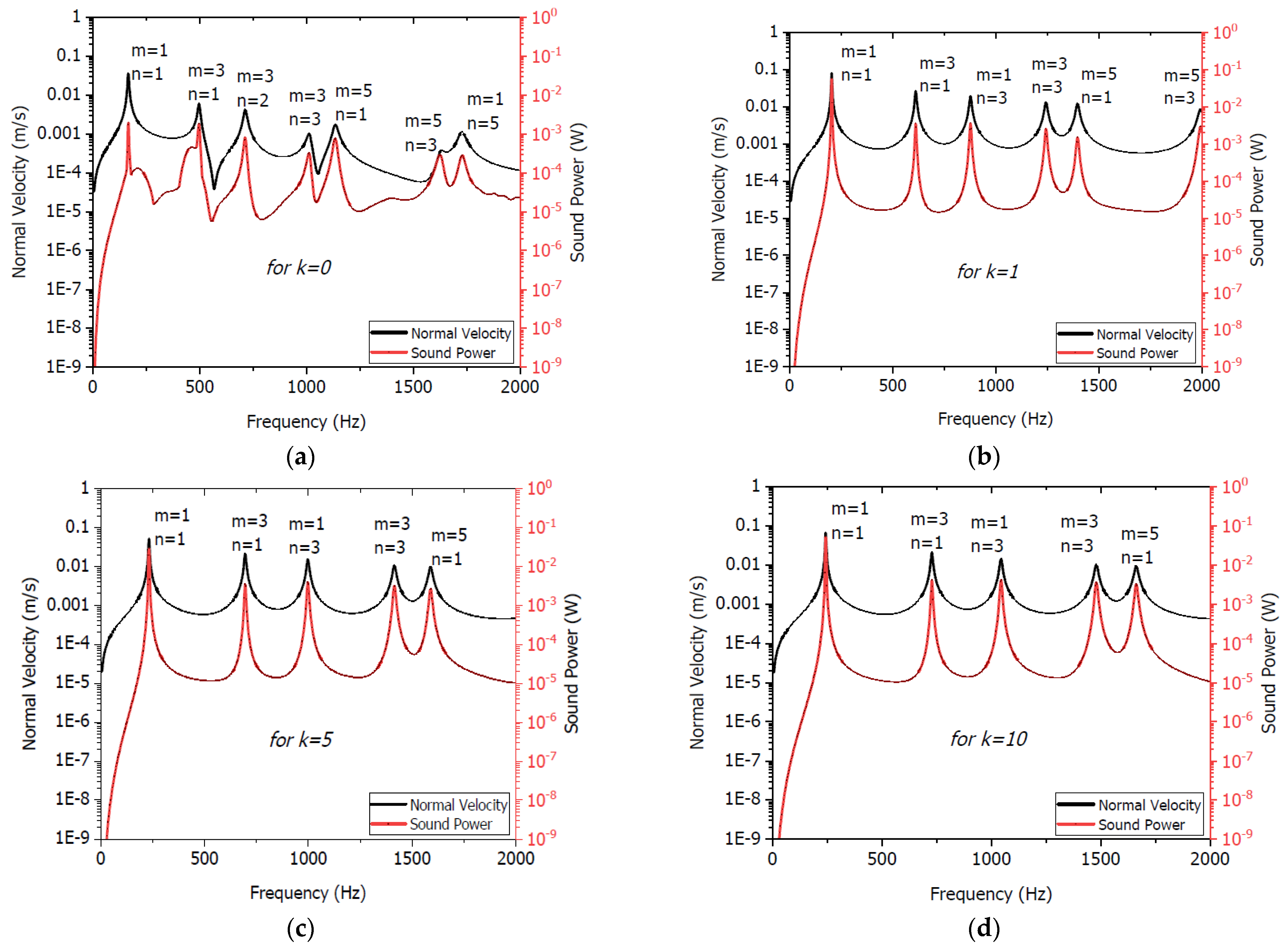
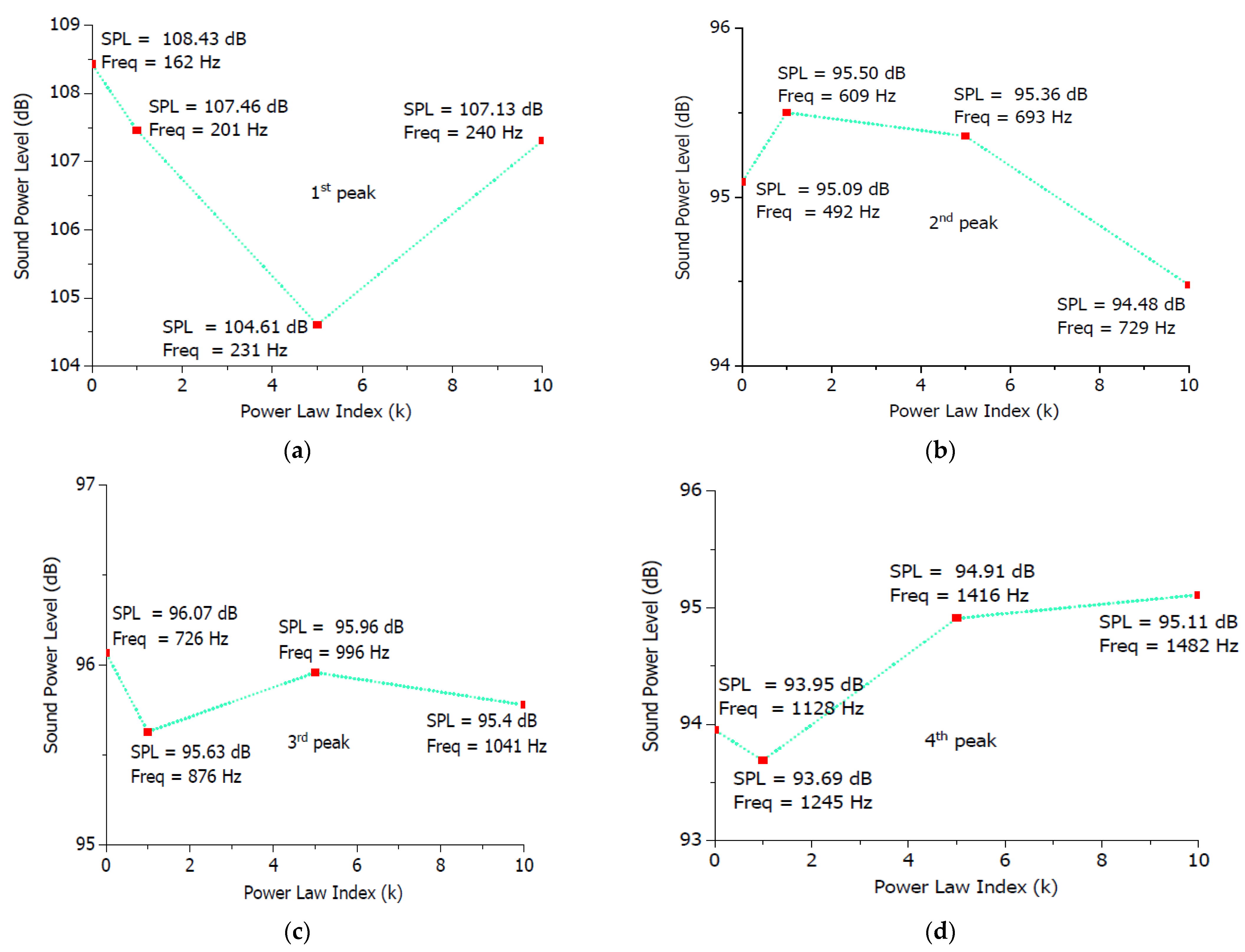
3.2. Effects of the Power-Law Index on the Sound Radiation Fields of P-FGM Plate

Figure 6 depicts the effect of the power-law index, k, on the sound power level and rms velocity of the FGM plate. For different values of the power-law index, the pattern variation in sound power level with frequency is similar. Furthermore, the peaks of the sound power level shift to higher frequencies.

The influence on the SPL peaks is further investigated for the plate’s normal V_rms peaks, different power-law indexes, k, and plate modal indices (m, n), as shown in Figure 7 and Figure 8. It was discovered that sound power level peaks at the same frequencies correlate well with normal velocity peaks. The velocity profiles, also known as mobility response curves, depict the relationship between how sound is emitted at the FGM plate’s surface. In Figure 7, the velocity profile peaks contribute significantly to the sound power level peaks. Furthermore, as illustrated in Figure 8, axisymmetric modes for various power-law indexes significantly contribute to sound power level. The modes shapes are only shown for k = 1 for brevity. As illustrated in Figure 7a, the modal density contribution to plate velocity is greatest for the investigated frequency range up to 2000 Hz for the power-law index k = 0. As the power-law index, k, increases, the modal density’s contribution to plate velocity decreases, as shown in Figure 7b,c.

Figure 9 illustrates sound power peaks variation with ‘k’ and rms velocity. It illustrates that peak sound power level does not monotonically increase with the increase in power-law indexes. As per Figure 9, a critical value of the power-law index exists, for which the corresponding sound power level peak is minimum [29]. Because each of these peaks corresponds to a different frequency, a proper combination of the power-law index, k, and frequency range will aid in proper material tailoring for the P-FGM plate’s sound radiation behavior. In the low-frequency band around 231 Hz, for example, a power-law index of around five will help lower the first sound power level peak, as shown in Figure 9a. This type of information is especially important for designing for sound radiation from the P-FGM plate. It is noteworthy that as the power-law index changes, the modal frequency changes that leads to change in the contributing modes. These contributing modes have significant effects on the sound radiation fields radiated by the P-FGM plates. Due to continuous variation in contributing modes, with the change in power-law indexes, the sound power level does not always increase with increase in power-law index.

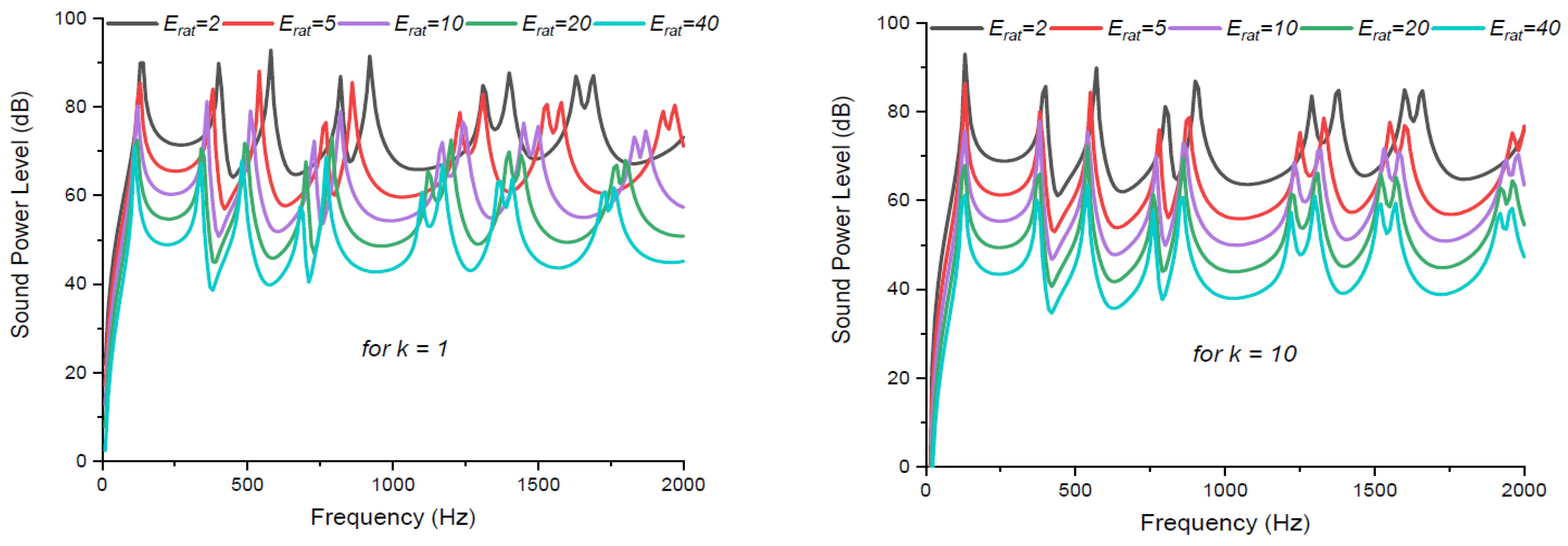
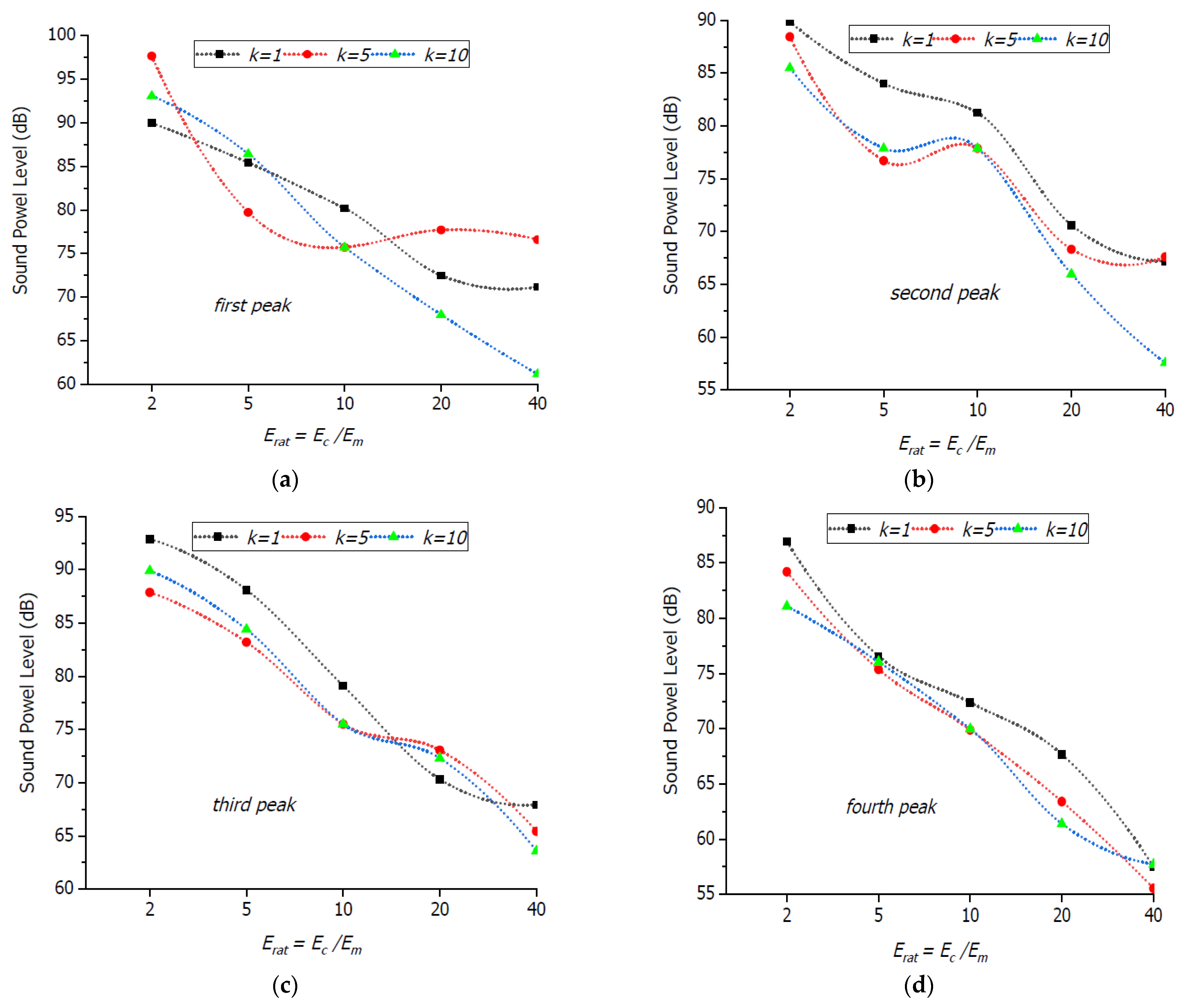
3.3. Influence of E_rat = E_c/E_m Ratio on Sound Radiation Fields

Figure 10 illustrates the influence of the parameter E_rat on sound power level for power-law indexes, k = 1, 5, and 10 similar to as reported by researchers [57]. The effects of modulus ratios on sound power level are documented in this research. A frequency shift is observed in the stiffness control region (first mode—the region of interest) with an increase in modulus ratios.

As $E_{rat}$ increases, a decrease in sound power level peaks is observed. $E_{rat}$ denotes the elasticity ratio of ceramic and metal constituents. To better understand the effect of $E_{rat}$ = $E_c/E_m$ on the peaks of sound power level, Figure 11 is presented. Obviously, the sound power level decreases with an increase in modulus ratios, and SPL peaks shift towards the right. When the power-law index, k increases, and the SPL radiated by the P-FGM plate increases. The findings suggest that the parameter $E_{rat}$ and the power-law index, k, could be used as design variables to reduce the sound radiation.

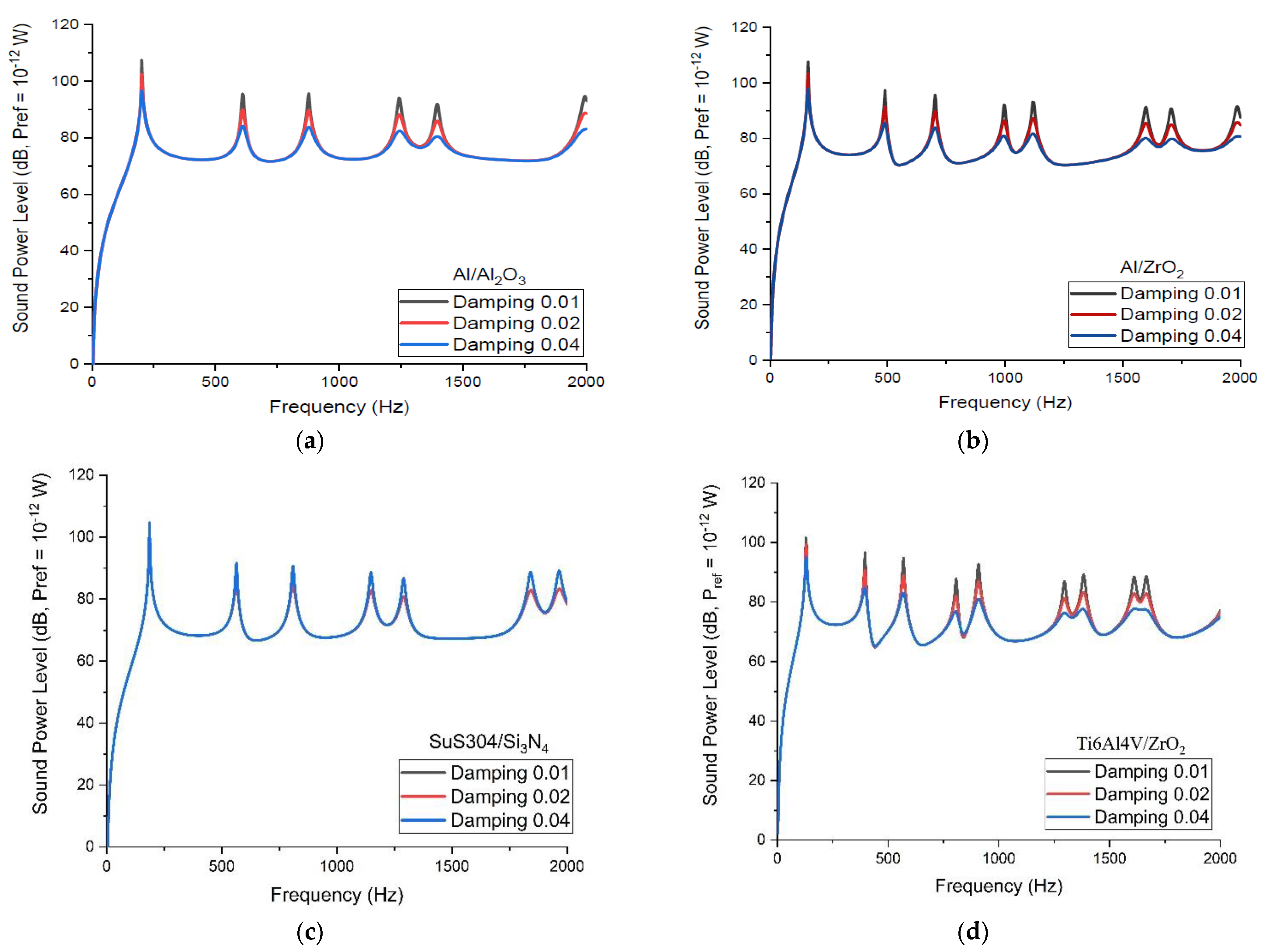
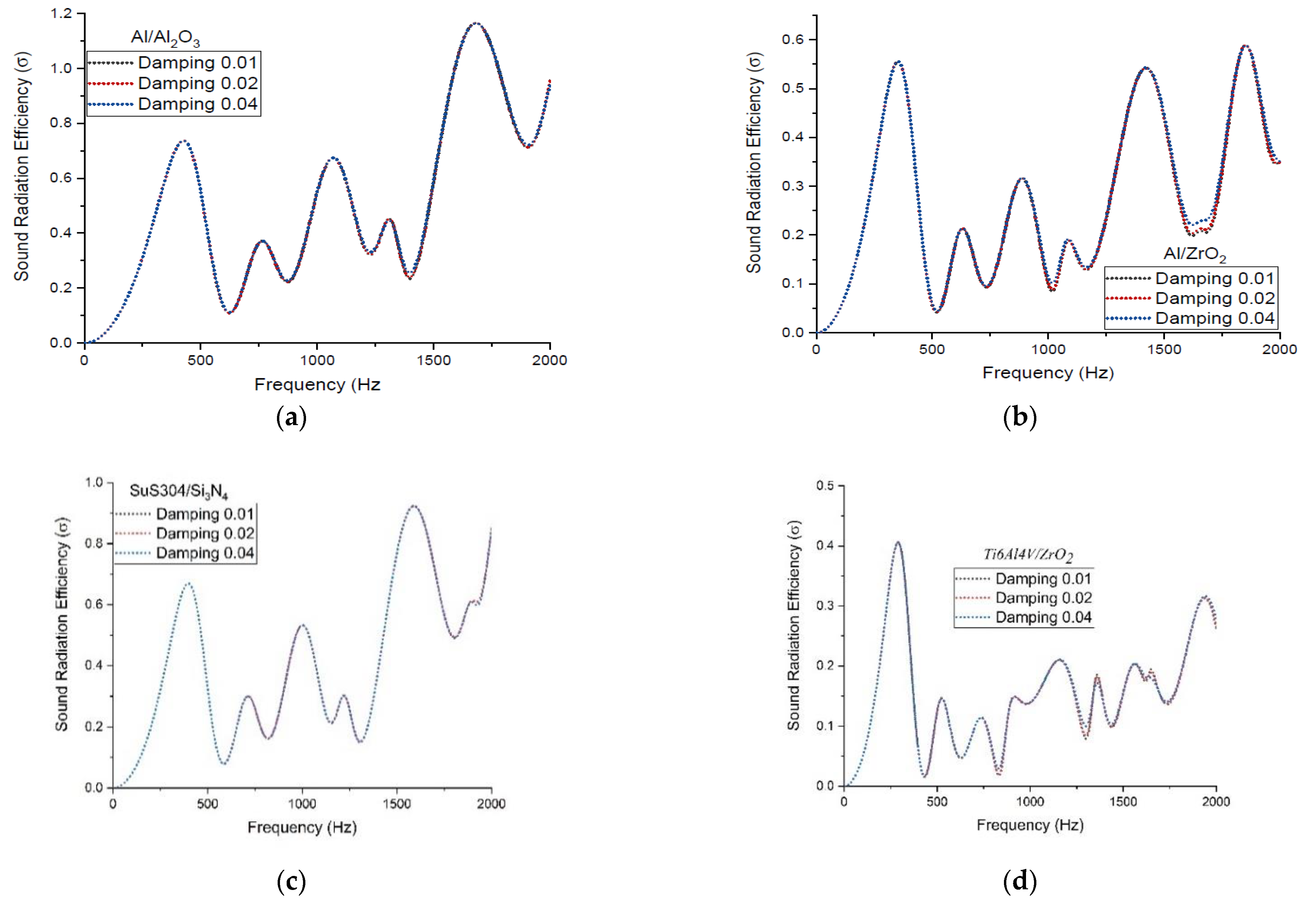
3.4. Influence of Damping Loss Factor on the Sound Power Level of the P-FGM Constituents

Figure 12 illustrates the SPL levels radiated by four distinct P-FGM plate constituents with varying damping loss factors for k = 1. It is found that with the P-FGM material Ti6Al4V/ZrO₂, the decrease in sound power peak is more pronounced. The material Ti6Al4V/ZrO₂ is less rigid than Al/Al₂O₃ SuS304/Si₃N₄, and Al/ZrO₂, which reduces sound power level. The sound power level peaks are also lowered when the damping loss factor increases. The variation is shown only for the power-law index, k = 1, for the sake of brevity.

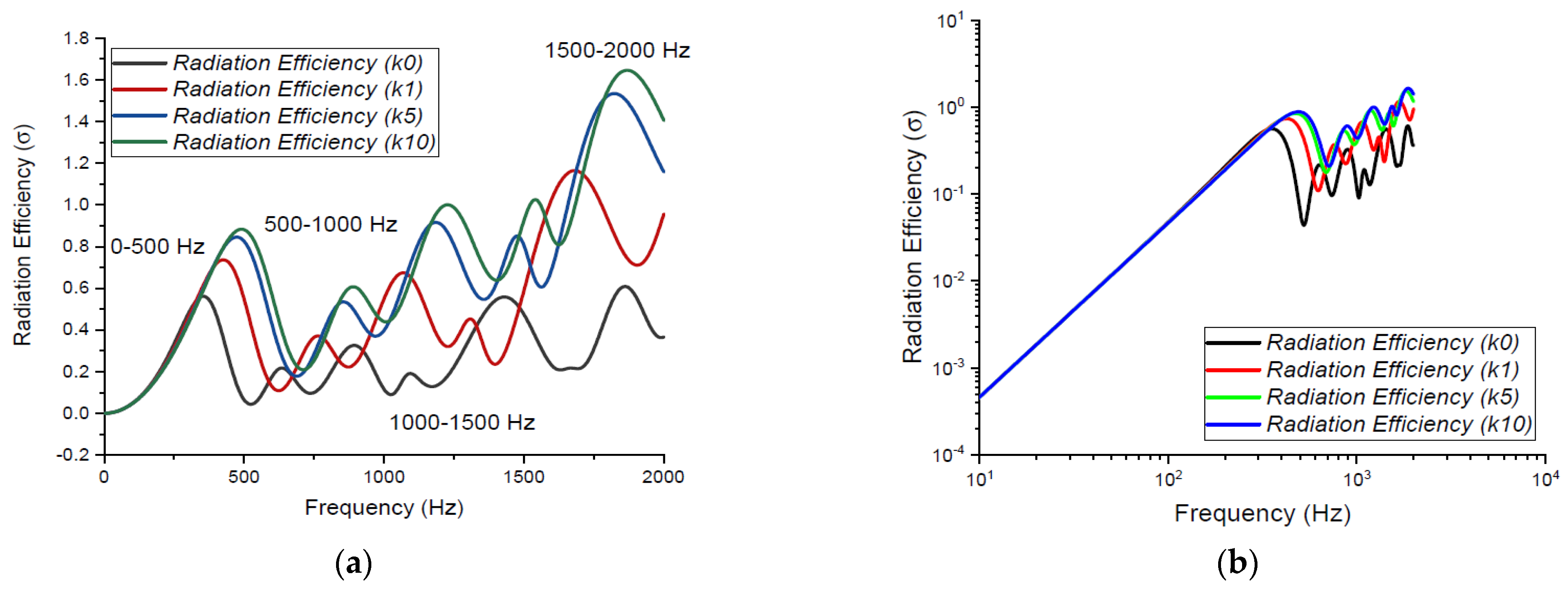
3.5. Radiation Efficiencies Variation with Power-Law Indexes, Varied P-FGM Constituents, and Effects of Damping Loss Factor

The radiation efficiency is a metric that measures how well a structure radiates sound in an acoustic medium. Figure 13 shows how the variable, k, affects the radiation efficiency of a P-FGM plate. With an increase in the power-law index, the first radiation efficiency peak rises. It is also worth noting that the radiation efficiency for a wide range of forcing frequencies (say, 500–1500 Hz) is lower for the power-law index, k = 1. This decrease in radiation efficiency suggests that choosing the right variable ‘k’ and the frequency range of excitation can be well utilized as a design variable to control the sound radiation of vibrating P-FGM plates. In this case, the radiation efficiency peak is highest for the power-law index, k = 10, near 1900–2000 Hz.

Figure 14 compares the radiation efficiencies of four P-FGM plates on a normal scale with different damping loss factors. It is clear that different damping loss factors have minute effects on the radiation efficiency, while P-FGM constituents affect radiation efficiency. It is also found that sound radiation efficiency increases with an increase in frequency until it approaches its maximum amplitude and then tries to approach towards unity. The lowest radiation efficiency is possessed by the $\mathrm{Ti}6\mathrm{Al}4\mathrm{V}$/${\mathrm{ZrO}}_2$ FGM plate signifying it to be a better sound radiator as it has lower stiffness than other FGM plates for k = 1. Thus, the order of sound radiation efficiency by P-FGM plates is $\mathrm{Ti}6\mathrm{Al}4\mathrm{V}$/${\mathrm{ZrO}}_2$ < $\mathrm{Al}$/${\mathrm{ZrO}}_2$ < $\mathrm{SuS}304/{\mathrm{Si}}_3{\mathrm{N}}_4$ < $\mathrm{Al}/{\mathrm{Al}}_2{\mathrm{O}}_3$.

4. Conclusions

In this paper, the analytical solution to the vibro-acoustic response of a vibrating clamped P-FGM plate is analyzed. Several validation studies and parametric effects are presented. Listed below are the conclusions of the present research:

(a)

The sound radiation fields validated with ANSYS and literature are in good agreement.

(b)

The sound power level monotonically increases with an increase in the power-law index because of a reduction in the stiffness of the FGM plate.

(c)

However, contrary to what other authors [29] have claimed, the acoustic response of P-FGM plates does not appear to always increase with an increase in the power-law index in the current study.

(d)

The current findings lead to conclude that there exists a key value of the power-law index for which the sound power level is at minimum in a specific frequency range.

(e)

Sound power level peak decreases and level shifts to higher frequencies with an increase in $E_{rat}$ = $E_c/E_m$ = 2, 5, 10, 20, and 40.

(f)

It can also be said that the P-FGM plates’ material distribution (due to variation in power-law index ‘k’) plays the major role in the computation of the sound radiation of the FGM plate because it characterizes the stiffness variation of the structure.

Hence, it is found that the power-law index does not appear to have a significant impact on radiation efficiency at low frequencies of less than 250 Hz. Overall, the mono-ceramic P-FGM plate can be considered as a better sound radiator because of higher stiffness.