Study of Crack Growth of Transparent Materials Subjected to Laser Irradiation by Digital Holography
Abstract
:1. Introduction
2. Fundamental Principle
3. Experimental Setup
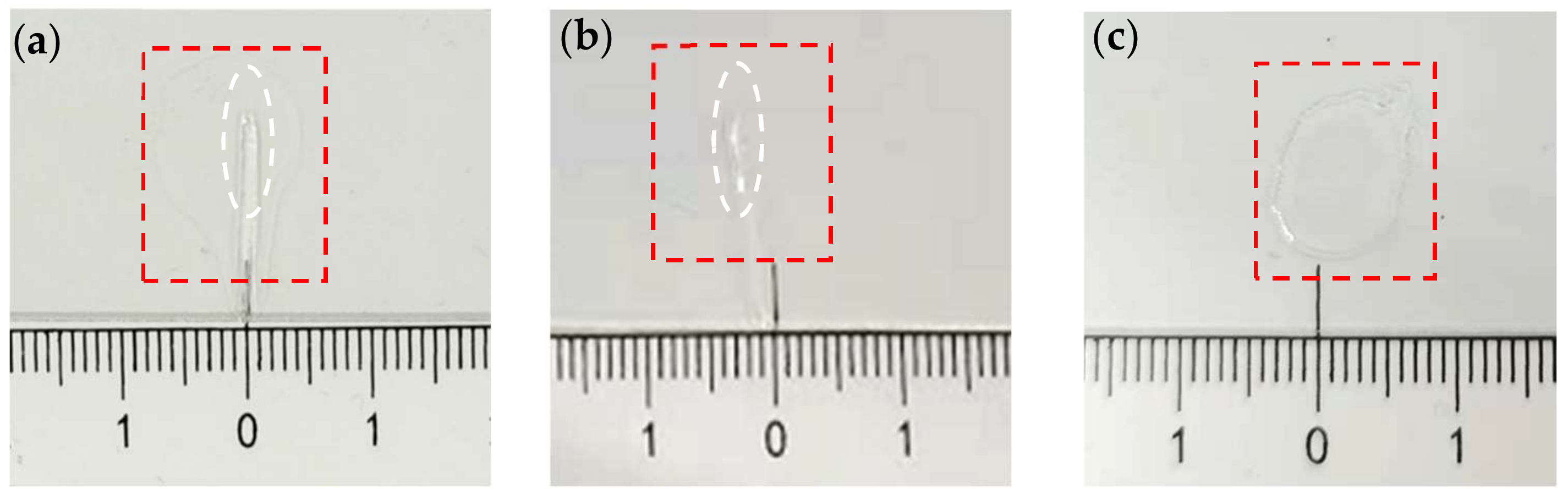
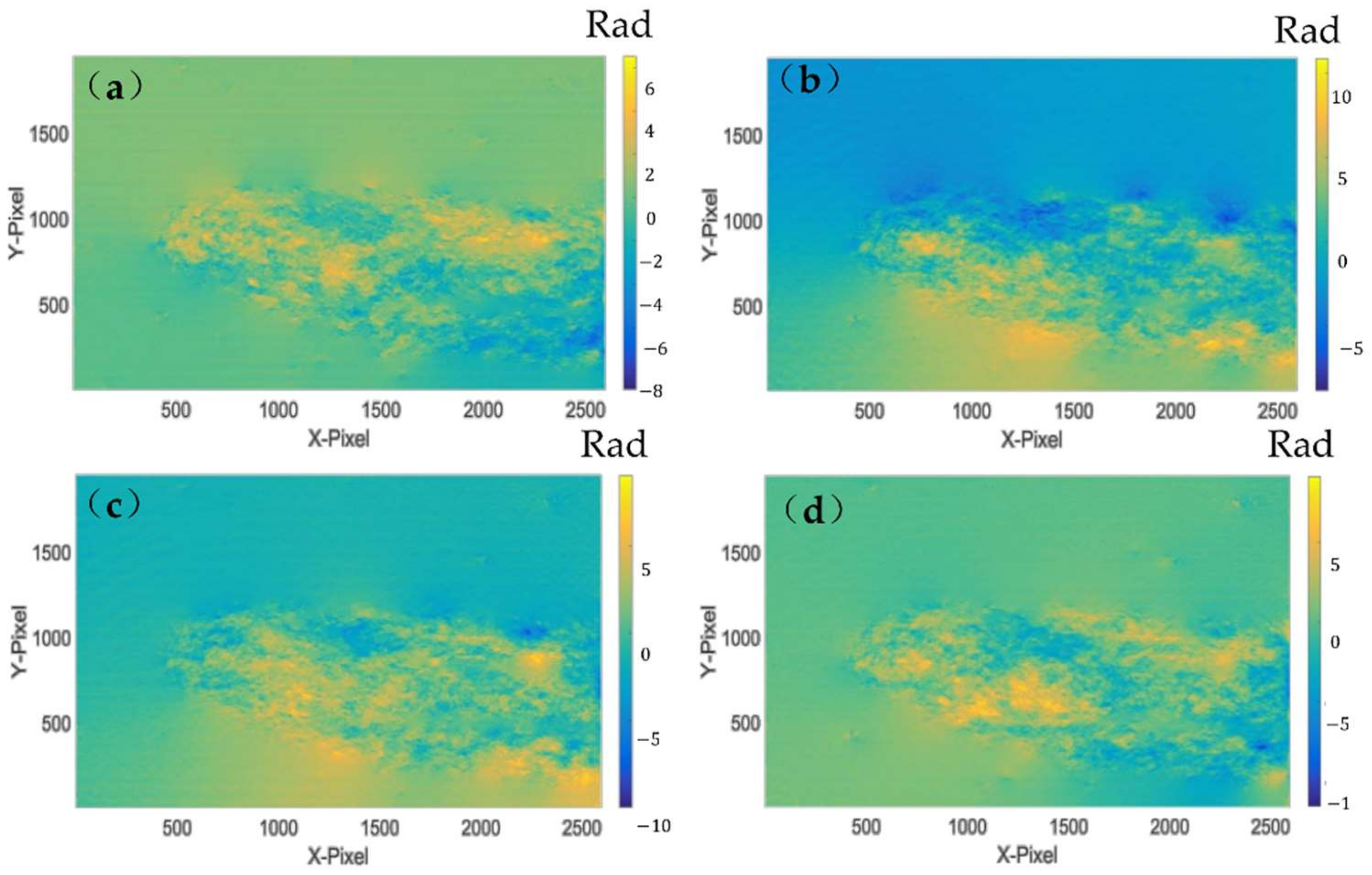
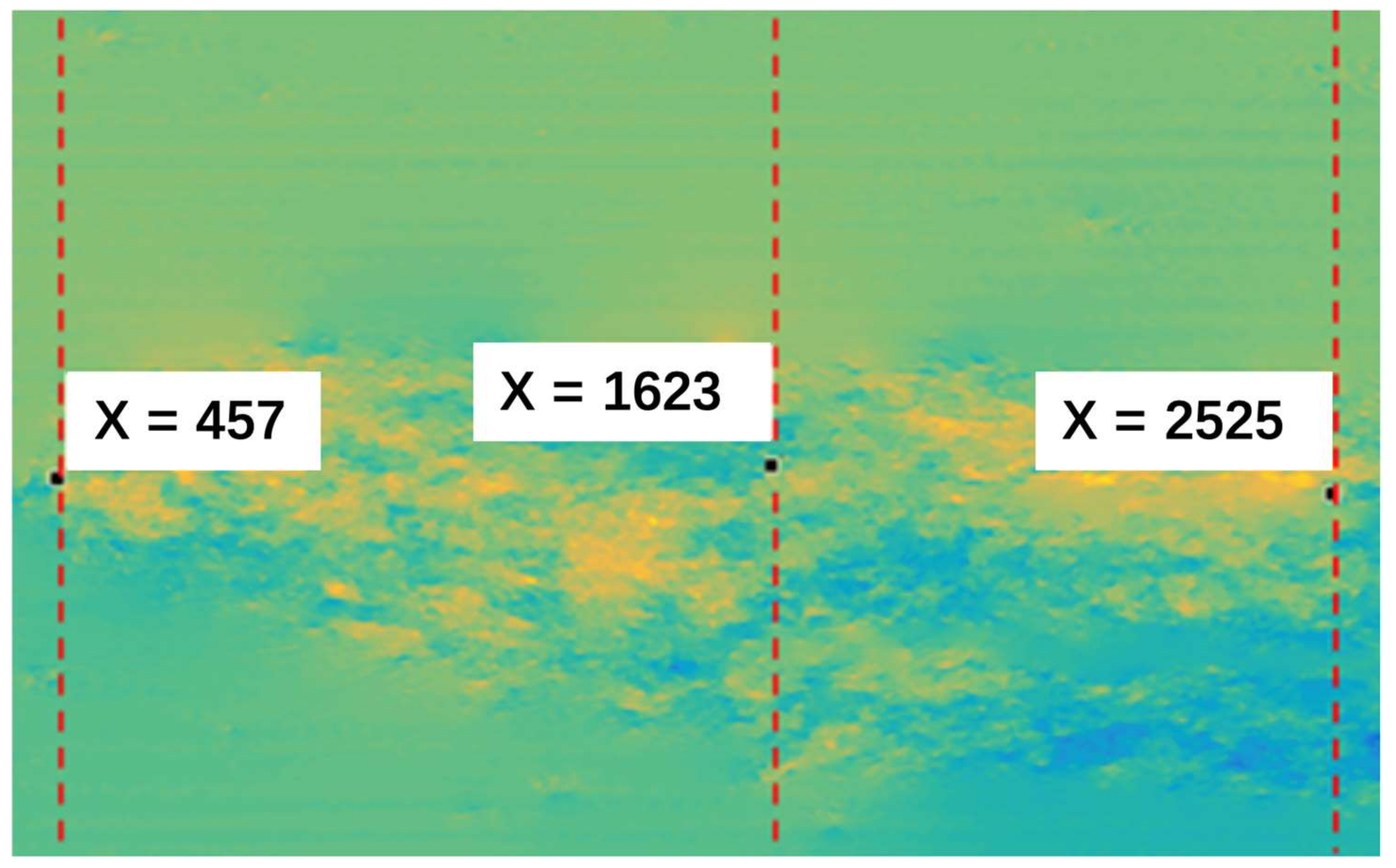
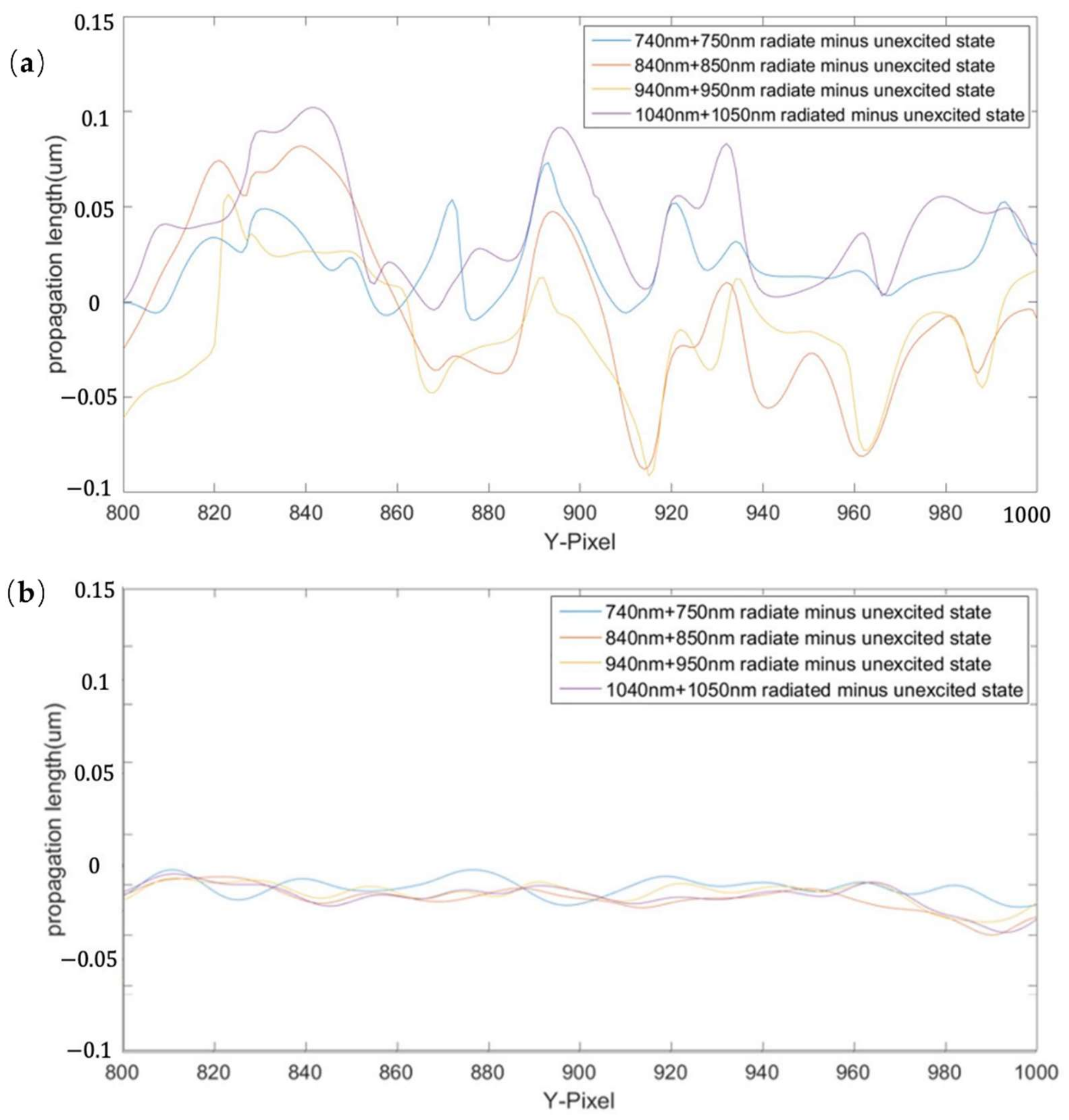
4. Experiment and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tomkins, B. Fatigue Crack Propagation—An Analysis. Philos. Mag. 1968, 18, 1041–1066. [Google Scholar] [CrossRef]
- Zweig, D.; Venugopalan, V.; Deutsch, T.F. Stress generated in polyimide by excimer-laser irradiation. J. Appl. Phys. 1993, 74, 4181. [Google Scholar] [CrossRef]
- Gerasimov, A.B.; Chiradze, G.D.; Kutivadze, N.G. On the physical nature of a photomechanical effect. Semiconductors 2001, 35, 72–76. [Google Scholar] [CrossRef]
- Paltauf, G.; Dyer, P.E. Photomechanical Processes and Effects in Ablation. Chem. Rev. 2003, 103, 487–518. [Google Scholar] [CrossRef]
- Perez-Gutierrez, F.G. Photomechanical, Photothermal and Photothermomechanical Mechanisms of Interaction of Nanosecond Laser Pulses with Artificial Tissue Models and Pigmented Melanoma Cells in Medical Applications. Ph.D. Thesis, UC Riverside, Riverside, CA, USA, 2010. [Google Scholar]
- White, T.J. Photomechanical Effects in Materials, Composites, and Systems: Outlook and Future Challenges. In Photomechanical Materials, Composites, and Systems: Wireless Transduction of Light into Work; Wiley: Hoboken, NJ, USA, 2017; pp. 393–403. [Google Scholar]
- Miguel, P.; Robert, M.; Mattheij, M. Crack Propagation Analysis; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2017. [Google Scholar]
- Bosco, E.; Suiker, A.S.J.; Fleck, N.A. Crack channelling mechanisms in brittle coating systems under moisture or temperature gradients. Int. J. Fract. 2020, 225, 1–30. [Google Scholar] [CrossRef]
- Menouillard, T.; Song, J.-H.; Duan, Q.; Belytschko, T. Time dependent crack tip enrichment for dynamic crack propagation. Int. J. Fract. 2010, 162, 33–49. [Google Scholar] [CrossRef]
- Tornari, V.; Tsiranidou, E.; Bernikola, E. Crack-Growth on Canvas Paintings during Transport Simulation Monitored with Digital Holographic Speckle Interferometry. Adv. Res. 2014, 2, 967–986. [Google Scholar] [CrossRef]
- Dias-da-Costa, D.; Valença, J.; Júlio, E.; Araújo, H. Crack propagation monitoring using an image deformation ap-proach: Crack Propagation Monitoring Using an Image Deformation Approach. Struct. Control. Health Monit. 2017, 24, e1973. [Google Scholar] [CrossRef]
- Réthoré, J. Automatic crack tip detection and stress intensity factors estimation of curved cracks from digital images: Automatic crack tip detection and SIF estimation of curved cracks. Int. J. Numer. Methods Eng. 2015, 103, 516–534. [Google Scholar] [CrossRef]
- Rezaie, A.; Achanta, R.; Godio, M.; Beyer, K. Comparison of crack segmentation using digital image correlation measurements and deep learning. Constr. Build. Mater. 2020, 261, 120474. [Google Scholar] [CrossRef]
- Elkhuizen, W.S.; Callewaert, T.W.J.; Leonhardt, E.; Vandivere, A.; Song, Y.; Pont, S.; Geraedts, J.M.P.; Dik, J. Comparison of three 3D scanning techniques for paintings, as applied to Vermeer’s ‘Girl with a Pearl Earring’. Heritage Sci. 2019, 7, 1–22. [Google Scholar] [CrossRef]
- Pouli, P.; Melessanaki, K.; Giakoumaki, A.; Argyropoulos, V.; Anglos, D. Measuring the thickness of protective coatings on historic metal objects using nanosecond and femtosecond laser induced breakdown spectroscopy depth profiling. Spectrochim. Acta Part B At. Spectrosc. 2005, 60, 1163–1171. [Google Scholar] [CrossRef]
- Malowany, K.; Tymińska-Widmer, L.; Malesa, M.; Kujawińska, M.; Targowski, P.; Rouba, B.J. Application of 3D digital image correlation to track displacements and strains of canvas paintings exposed to relative humidity changes. Appl. Opt. 2014, 53, 1739–1749. [Google Scholar] [CrossRef]
- Bacchin, P.; Brutin, D.; Davaille, A.; Di Giuseppe, E.; Chen, X.D.; Gergianakis, I.; Giorgiutti-Dauphiné, F.; Goehring, L.; Hallez, Y.; Heyd, R.; et al. Drying colloidal systems: Laboratory models for a wide range of applications. Eur. Phys. J. E 2018, 41, 94. [Google Scholar] [CrossRef]
- Georgiou, S.; Zafiropulos, V.; Anglos, D.; Balas, C.; Tornari, V.; Fotakis, C. Excimer laser restoration of painted artworks: Procedures, mechanisms and effects. Appl. Surf. Sci. 1998, 127–129, 738–745. [Google Scholar] [CrossRef]
- Bonarou, A.; Antonucci, L.; Tornari, V.; Georgiou, S.; Fotakis, C. Holographic interferometry for the structural diagnostics of UV laser ablation of polymer substrates. Appl. Phys. A 2001, 73, 647–651. [Google Scholar] [CrossRef]
- Tornari, V.; Bonarou, A.; Zafiropulos, V.; Antonucci, L.; Fotakis, C. Holographic interferometry sequential investi-gation of long-term photomechanical effects in the excimer laser restoration of artworks. In Proceedings of the ROMOPTO 2000: Sixth Conference on Optics, Bucharest, Romania, 4–7 September 2000; International Society for Optics and Photonics: Bellingham, WA, USA, 2000; Volume 4430, pp. 153–159. [Google Scholar]
- Athanassiou, A.; Andreou, E.; Bonarou, A.; Tornari, V.; Anglos, D.; Georgiou, S.; Fotakis, C. Examination of chemical and structural modifications in the UV ablation of polymers. Appl. Surf. Sci. 2002, 197–198, 757–763. [Google Scholar] [CrossRef]
- Esposito, E.; Scalise, L.; Tornari, V. Measurement of stress waves in polymers generated by UV laser ablation. Opt. Lasers Eng. 2002, 38, 207–215. [Google Scholar] [CrossRef]
- Tornari, V. Delocalized Photomechanical Effects of UV ns Laser Ablation on Polymer Substrates Captured by Optical Holography Workstation: An Overview on Experimental Result. Adv. Opt. 2014, 2014, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Tornari, V.; Andrianakis, M.; Chaban, A.; Kosma, K. Heat Transfer Effects on Defect Boundaries Captured by Digital Holographic Interferometry and Infrared Thermography Workstation: An Overview on Experimental Results. Exp. Tech. 2020, 44, 59–74. [Google Scholar] [CrossRef]
- Pan, A.; Wang, W.; Mei, X.; Zheng, B.; Yan, Z. Cracks growth behaviors of commercial pure titanium under nanosecond laser irradiation for formation of nanostructure-covered microstructures (with sub-5-μm). Appl. Surf. Sci. 2016, 387, 1046–1053. [Google Scholar] [CrossRef]
- Eto, S.; Miura, Y.; Tani, J.; Fujii, T. Effect of residual stress induced by pulsed-laser irradiation on initiation of chloride stress corrosion cracking in stainless steel. Mater. Sci. Eng. A 2014, 590, 433–439. [Google Scholar] [CrossRef]
- Huang, H.; Noguchi, J.; Yan, J. Shield gas induced cracks during nanosecond-pulsed laser irradiation of Zr-based metallic glass. Appl. Phys. A 2016, 122, 881. [Google Scholar] [CrossRef]
- Pouli, P.; Oujja, M.; Castillejo, M. Practical issues in laser cleaning of stone and painted artefacts: Optimisation procedures and side effects. Appl. Phys. A 2012, 106, 447–464. [Google Scholar] [CrossRef]
- Tam, A.C.; Leung, W.P.; Zapka, W.; Ziemlich, W. Laser-cleaning techniques for removal of surface particulates. J. Appl. Phys. 1992, 71, 3515–3523. [Google Scholar] [CrossRef]
- Myridis, N.E. Lasers in the Preservation of Cultural Heritage: Principles and Applications, by C. Fotakis, D. Anglos, V. Zafiropulos, S. Georgiou, and V. Tornari. Contemp. Phys. 2012, 53, 288–289. [Google Scholar] [CrossRef]
- Tornari, V.; Fantidou, D.; Zafiropulos, V.; Vainos, N.A.; Fotakis, C. Photomechanical effects of laser cleaning: A long-term non-destructive holographic interferometric investigation on painted artworks. SPIE 1998, 3411, 420–430. [Google Scholar]
- Tornari, V.; Zafiropulos, V.; Vainos, N.A.; Fantidou, D.; Fotakis, C. Discrimination of photomechanical effects in the laser cleaning of artworks by means of holographic interferometry. In Optics and Lasers in Biomedicine and Culture; Springer: Berlin/Heidelberg, Germany, 2000; pp. 208–212. [Google Scholar]
- Tiennot, M.; Paardekam, E.; Iannuzzi, D.; Hermens, E. Mapping the mechanical properties of paintings via nanoindentation: A new approach for cultural heritage studies. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef]
- Schuh, C.A. Nanoindentation studies of materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Gautham, S.; Sasmal, S. Recent Advances in Evaluation of intrinsic mechanical properties of cementitious composites using nanoindentation technique. Constr. Build. Mater. 2019, 223, 883–897. [Google Scholar] [CrossRef]
- Gai, S.; Da, F.; Dai, X. A novel dual-camera calibration method for 3D optical measurement. Opt. Lasers Eng. 2018, 104, 126–134. [Google Scholar] [CrossRef]
- Trivedi, V.; Joglekar, M.; Mahajan, S.; Patel, N.; Chhaniwal, V.; Javidi, B.; Anand, A. Digital holographic imaging of refractive index distributions for defect detection. Opt. Laser Technol. 2019, 111, 439–446. [Google Scholar] [CrossRef]
- Deng, Y.; Hong, W.; He, J.; Guo, Z.; Chen, Y.; Huang, Z. Micro-cracks on crosslinked Poly(dimethylsiloxane) (PDMS) surface treated by nanosecond laser irradiation. Appl. Surf. Sci. 2018, 445, 488–495. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, W.; Hu, Z.; Zhou, Q.; Zhang, W. Surface roughness measurement based on digital holography. J. Appl. Opt. 2014, 35, 1040–1047. [Google Scholar] [CrossRef]
- Zhou, W.-J.; Li, B.-Y.; Shen, H.-X.; He, D.-K.; Zhang, H.-B.; Yu, Y.-J.; Tornari, V. Tip Crack Imaging on Transparent Materials by Digital Holographic Microscopy. J. Imaging 2019, 5, 80. [Google Scholar] [CrossRef] [Green Version]
- Masayuki, A.; Kenji, I.; Tomoki, M.; Kiyohiro, I.; Hiroki, Y.; Tatsuo, S. Delaying Effect of Fatigue Crack Propagation by Single-Pulse Laser Irradiation. Proceedings 2018, 2, 478. [Google Scholar]
- Zhou, W.; Peng, K.; Yu, Y. Surface roughness measurement and analysis of mechanical parts based on digital ho-lography. Adv. Manuf. 2016, 4, 217–224. [Google Scholar] [CrossRef]


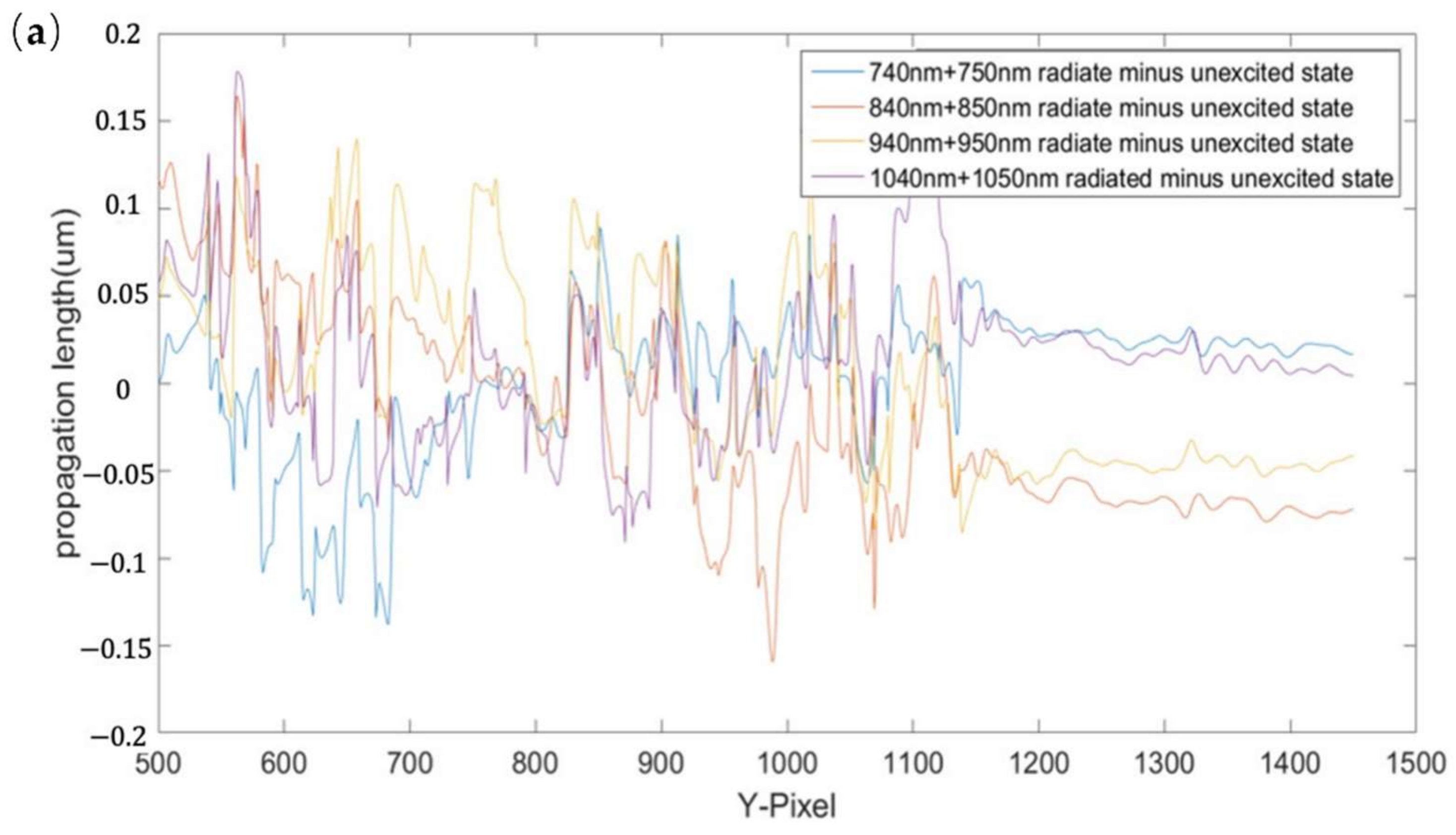
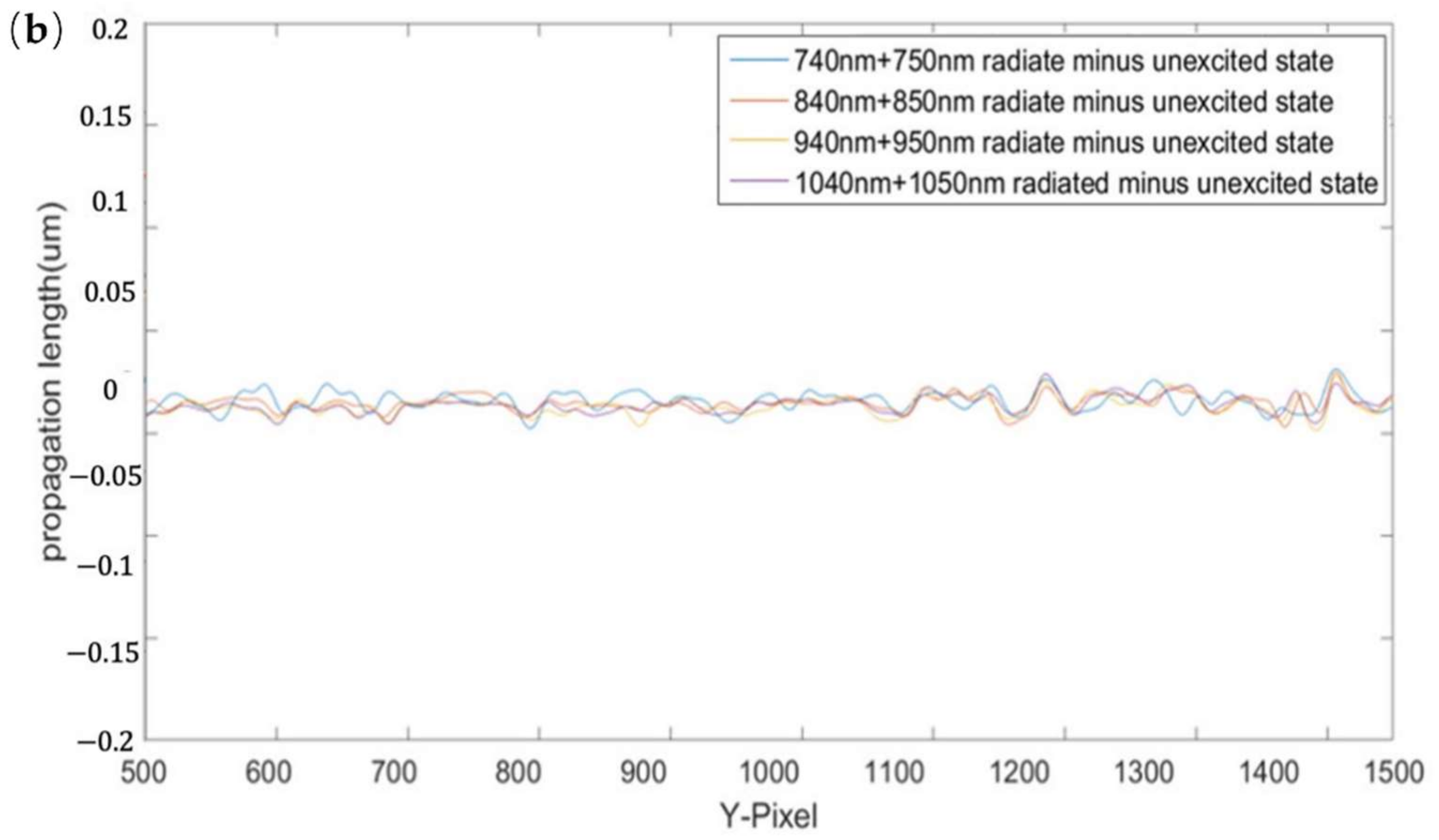
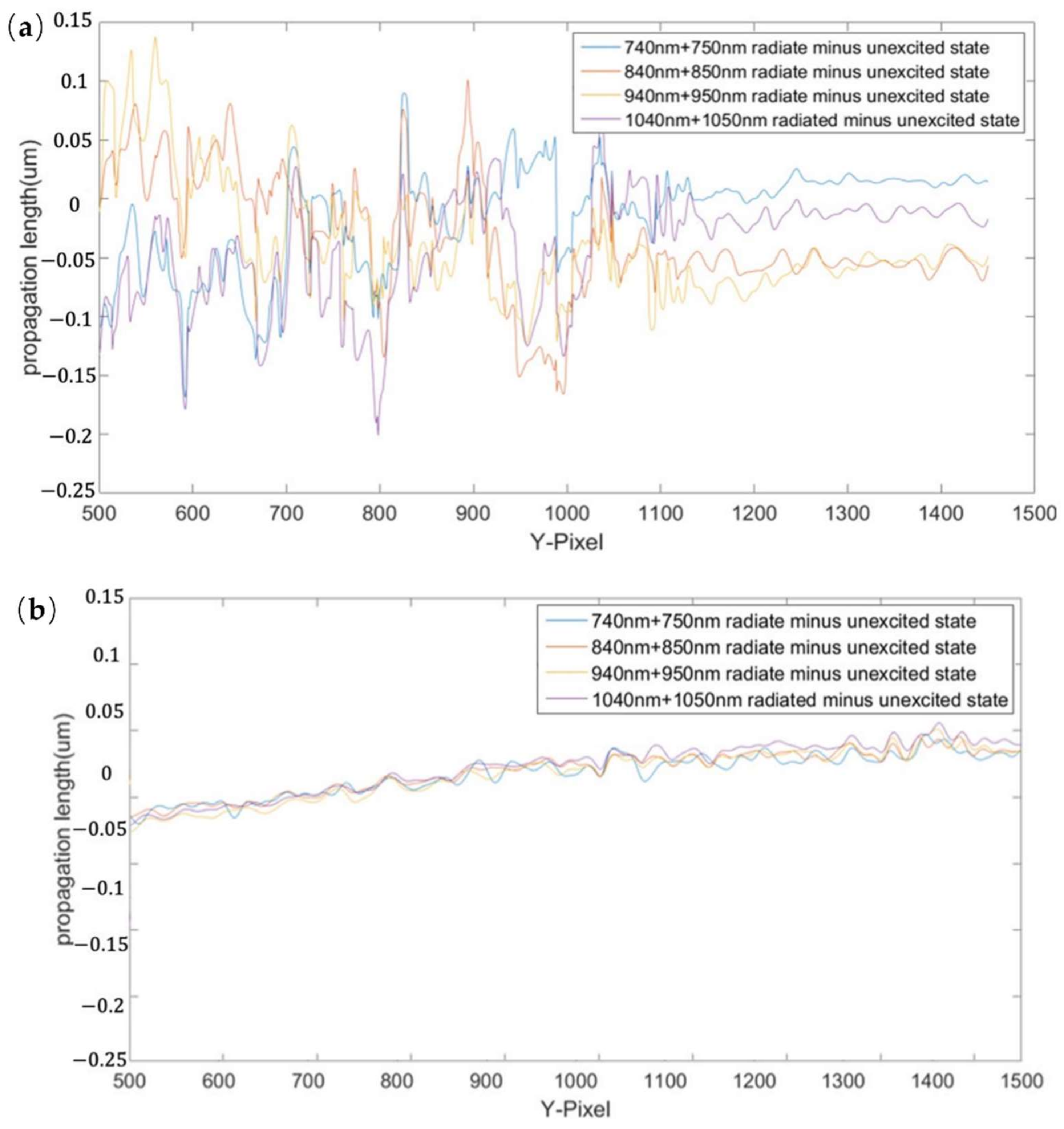
| Irradiation Wavelength (nm) | 740 + 750 | 840 + 850 | 940 + 950 | 1040 + 1050 |
|---|---|---|---|---|
| Experimental group X = 457 | 0.072 | 0.087 | 0.090 | 0.101 |
| Control group X = 457 | 0.001 | 0.001 | 0.005 | 0.004 |
| Experimental group X = 1625 | 0.136 | 0.138 | 0.134 | 0.176 |
| Control group X = 1625 | 0.016 | 0.016 | 0.023 | 0.018 |
| Experimental group X = 2525 | 0.168 | 0.166 | 0.163 | 0.198 |
| Control group X = 2525 | 0.008 | 0.013 | 0.006 | 0.014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Liu, Y.; Chen, Z.; Chen, Y.; Zhang, H.; Yu, Y.; Tornari, V. Study of Crack Growth of Transparent Materials Subjected to Laser Irradiation by Digital Holography. Appl. Sci. 2022, 12, 7799. https://doi.org/10.3390/app12157799
Zhou W, Liu Y, Chen Z, Chen Y, Zhang H, Yu Y, Tornari V. Study of Crack Growth of Transparent Materials Subjected to Laser Irradiation by Digital Holography. Applied Sciences. 2022; 12(15):7799. https://doi.org/10.3390/app12157799
Chicago/Turabian StyleZhou, Wenjing, Yuhang Liu, Zhenkai Chen, Yao Chen, Hongbo Zhang, Yingjie Yu, and Vivi Tornari. 2022. "Study of Crack Growth of Transparent Materials Subjected to Laser Irradiation by Digital Holography" Applied Sciences 12, no. 15: 7799. https://doi.org/10.3390/app12157799
APA StyleZhou, W., Liu, Y., Chen, Z., Chen, Y., Zhang, H., Yu, Y., & Tornari, V. (2022). Study of Crack Growth of Transparent Materials Subjected to Laser Irradiation by Digital Holography. Applied Sciences, 12(15), 7799. https://doi.org/10.3390/app12157799








