The Role of a DirectDensity® CT Reconstruction in a Radiotherapy Workflow: A Phantom Study
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. DirectDensity® Reconstruction Algorithm
2.2. Calibration Curve Building
2.3. Metal Artifact Influence on Non-Metal ROIs
2.4. Dose Distributions
3. Results
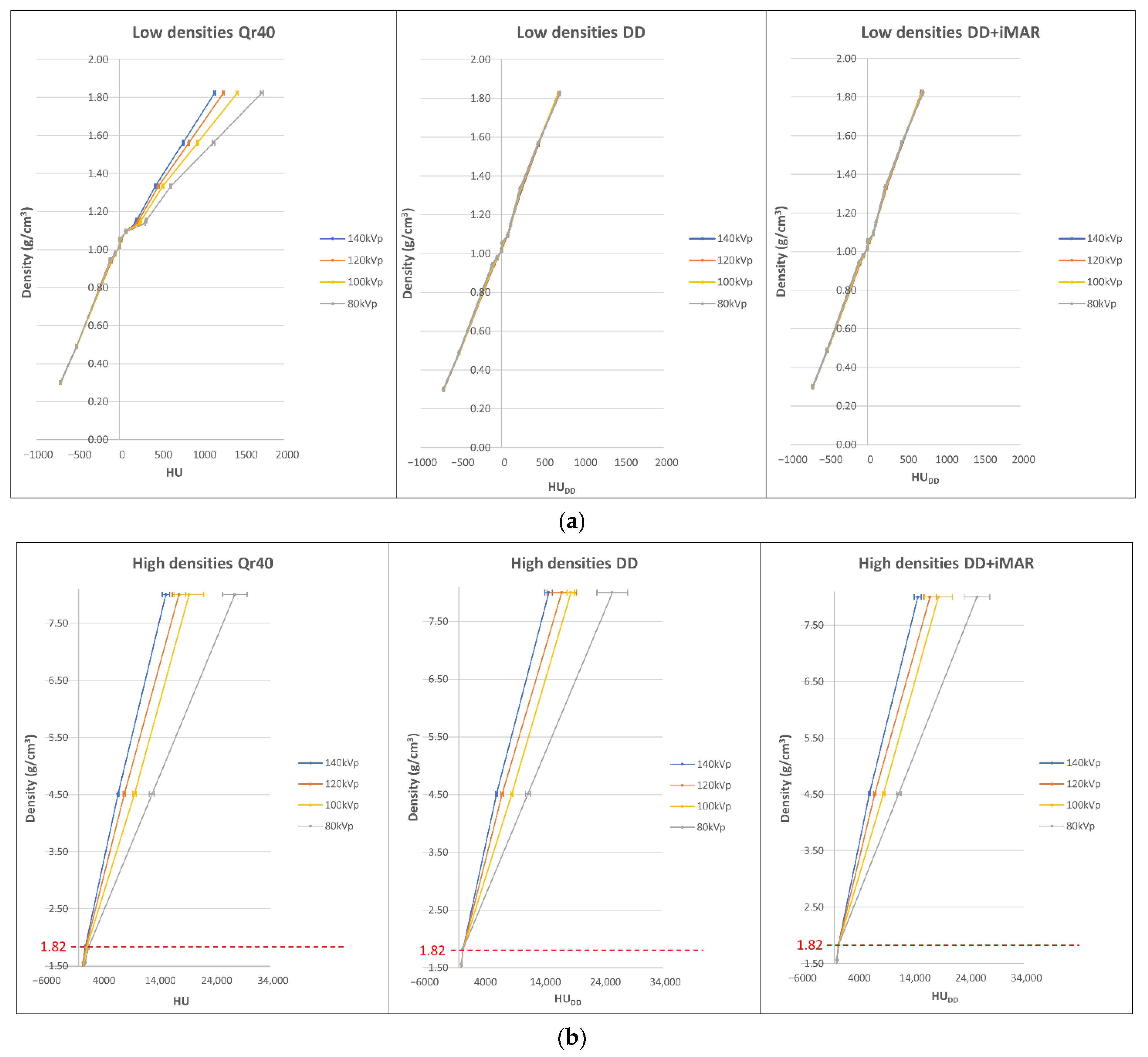
3.1. Curve Building and Metal Artifact Influence on Non-Metal ROIs
3.2. Mean Calibration Curves
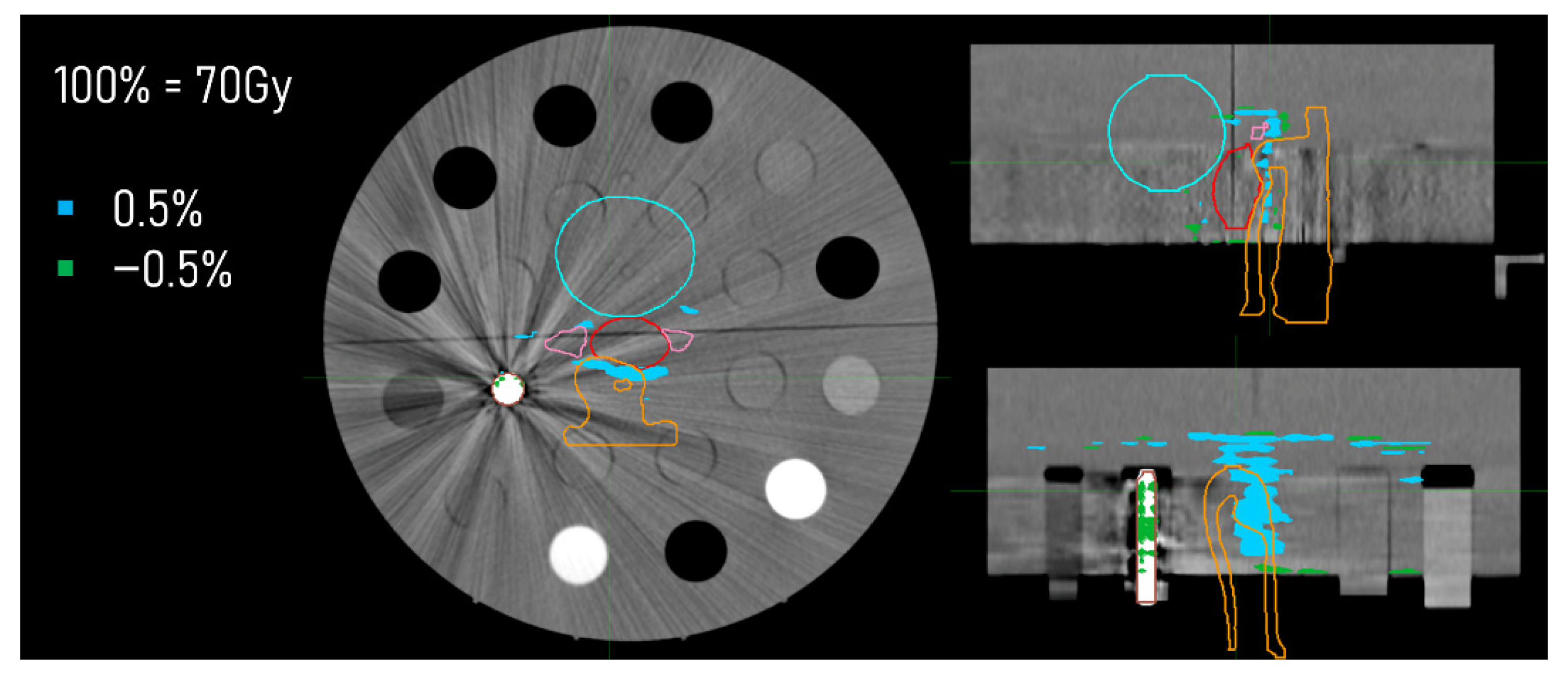
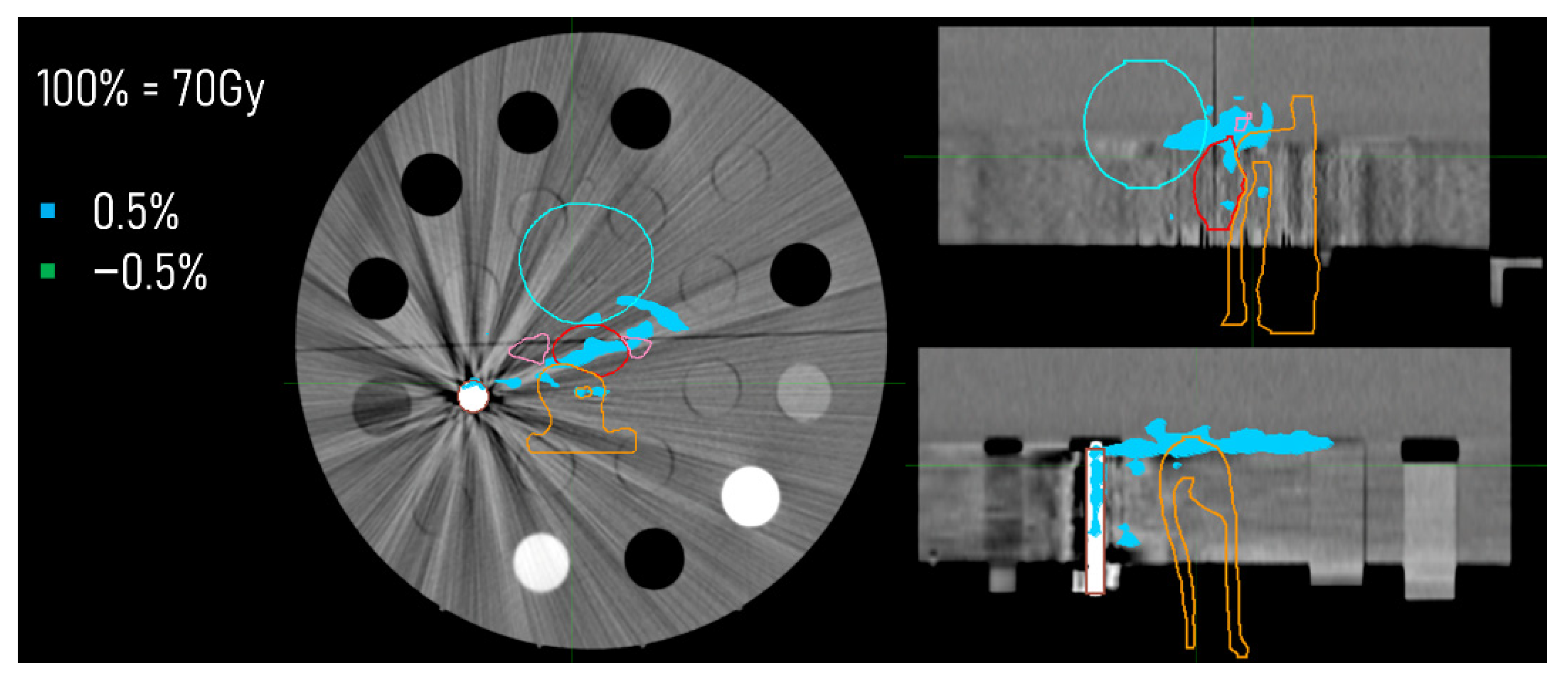
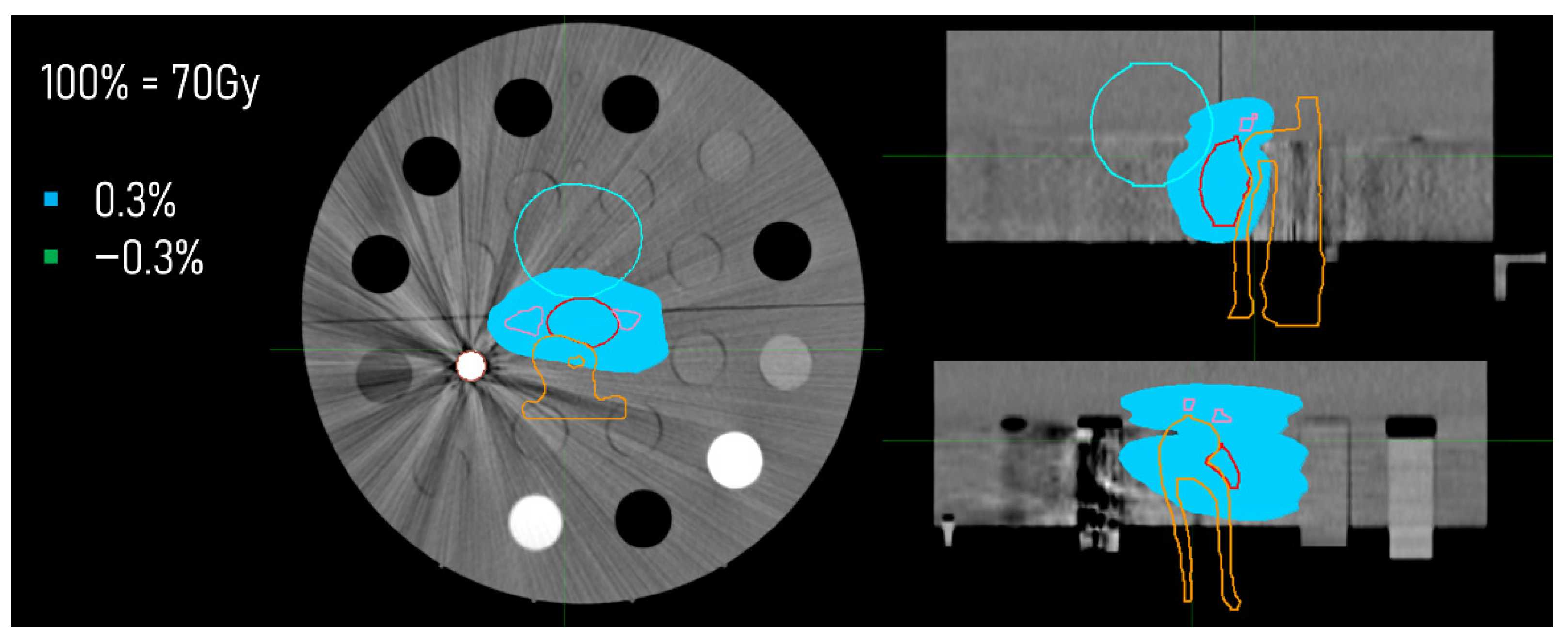
3.3. Dose Distributions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Davis, A.T.; Palmer, A.L.; Nisbet, A. Can CT Scan Protocols Used for Radiotherapy Treatment Planning Be Adjusted to Optimize Image Quality and Patient Dose? A Systematic Review. Br. J. Radiol. 2017, 90, 20160406. [Google Scholar] [CrossRef] [PubMed]
- Schneider, U.; Pedroni, E.; Lomax, A. The Calibration of CT Hounsfield Units for Radiotherapy Treatment Planning. Phys. Med. Biol. 1996, 41, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Kolarević, G.; Jaroš, D.; Pavičar, B.; Ignjić, T.; Kostovski, A.; Marošević, G.; Predojević, B.; Mirjanić, D. Computed Tomography Simulator Conversion Curve Dependence on Scan Parameters and Phantom Dimension. J. Health Sci. 2020, 10, 226–233. [Google Scholar] [CrossRef]
- Brevitt, B.A.; Suarez, E.G.; Clemente, R.A.M.; Voutchkov, M. Evaluating the Impact of CT Scanning Parameters on Dose Calculations by the Treatment Planning System in External Beam Radiation Therapy. J. Can. Res. 2021, 2, 8. [Google Scholar]
- Constantinou, C.; Harrington, J.C.; DeWerd, L.A. An Electron Density Calibration for Ct-based Treatment Planning Computers. Med. Phys. 1992, 19, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Reid, J.; Gamberoni, J.; Dong, F.; Davros, W. Optimization of KVp and MAs for Pediatric Low-Dose Simulated Abdominal CT: Is It Best to Base Parameter Selection on Object Circumference? Am. J. Roentgenol. 2010, 195, 1015–1020. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.P.; Noid, G.; Tai, A.; Liu, F.; Lawton, C.; Erickson, B.; Li, X.A. Improving CT Quality with Optimized Image Parameters for Radiation Treatment Planning and Delivery Guidance. Phys. Imaging Radiat. Oncol. 2017, 4, 6–11. [Google Scholar] [CrossRef]
- Seyal, A.R.; Arslanoglu, A.; Abboud, S.F.; Sahin, A.; Horowitz, J.M.; Yaghmai, V. CT of the Abdomen with Reduced Tube Voltage in Adults: A Practical Approach. Radiographics 2015, 35, 1922–1939. [Google Scholar] [CrossRef] [PubMed]
- Kalender, W.A. Dose in X-Ray Computed Tomography. Phys. Med. Biol. 2014, 59, R129–R150. [Google Scholar] [CrossRef] [PubMed]
- Ritter, A.; Mistry, N. DirectDensity®: Technical Principles and Implications for Radiotherapy; White paper; Technical Report; Siemens Healthineers: Erlangen, Germany, 2016. [Google Scholar]
- Van der Heyden, B.; Öllers, M.; Ritter, A.; Verhaegen, F.; van Elmpt, W. Clinical Evaluation of a Novel CT Image Reconstruction Algorithm for Direct Dose Calculations. Phys. Imaging Radiat. Oncol. 2017, 2, 11–16. [Google Scholar] [CrossRef]
- Flatten, V.; Friedrich, A.; Engenhart-Cabillic, R.; Zink, K. A Phantom Based Evaluation of the Dose Prediction and Effects in Treatment Plans, When Calculating on a Direct Density CT Reconstruction. J. Appl. Clin. Med. Phys. 2020, 21, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Kachelrieß, M.; Krauss, A.; Healthcare, S. Iterative Metal Artifact Reduction (IMAR): Technical Principles and Clinical Results in Radiation Therapy; White paper; Siemens Healthcare: Erlangen, Germany, 2016. [Google Scholar]
- Trabzonlu, T.A.; Terrazas, M.; Mozaffary, A.; Velichko, Y.S.; Yaghmai, V. Application of Iterative Metal Artifact Reduction Algorithm to CT Urography for Patients with Hip Prostheses. Am. J. Roentgenol. 2020, 214, 137–143. [Google Scholar] [CrossRef] [PubMed]
- Piper, J.; Nelson, A.; Harper, J. Deformable Image Registration in MIM Maestro® Evaluation and Description; White paper; MIM Software Inc.: Cleveland, OH, USA, 2018. [Google Scholar]
- MIM Software Inc. Available online: https://www.mimsoftware.com/ (accessed on 17 July 2022).
- Boas, F.E.; Fleischmann, D. CT Artifacts: Causes and Reduction Techniques. Imaging Med. 2012, 4, 229–240. [Google Scholar] [CrossRef]
- Katsura, M.; Sato, J.; Akahane, M.; Kunimatsu, A.; Abe, O. Current and Novel Techniques for Metal Artifact Reduction at CT: Practical Guide for Radiologists. Radiographics 2018, 38, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Moudi, E.; Haghanifar, S.; Madani, Z.; Bijani, A.; Nabavi, Z.S. The Effect of Metal Artifacts on the Identification of Vertical Root Fractures Using Different Fields of View in Cone-Beam Computed Tomography. Imaging Sci. Dent. 2015, 45, 147–151. [Google Scholar] [CrossRef] [PubMed][Green Version]
- IAEA. Quality Assurance Programme for Computed Tomography: Diagnostic and Therapy Applications; IAEA: Vienna, Austria, 2012. [Google Scholar]
- D’Alessio, A.; D’Ippolito, E.; Tenconi, C.; Cavallo, A.; Stucchi, C.; Pignoli, E. Potentials and Limits of a Novel CT Reconstruction Algorithm (DirectDensityTM) Developed for Radiotherapy Treatment Planning. Biomed. Phys. Eng. Express 2019, 5, 065014. [Google Scholar] [CrossRef]

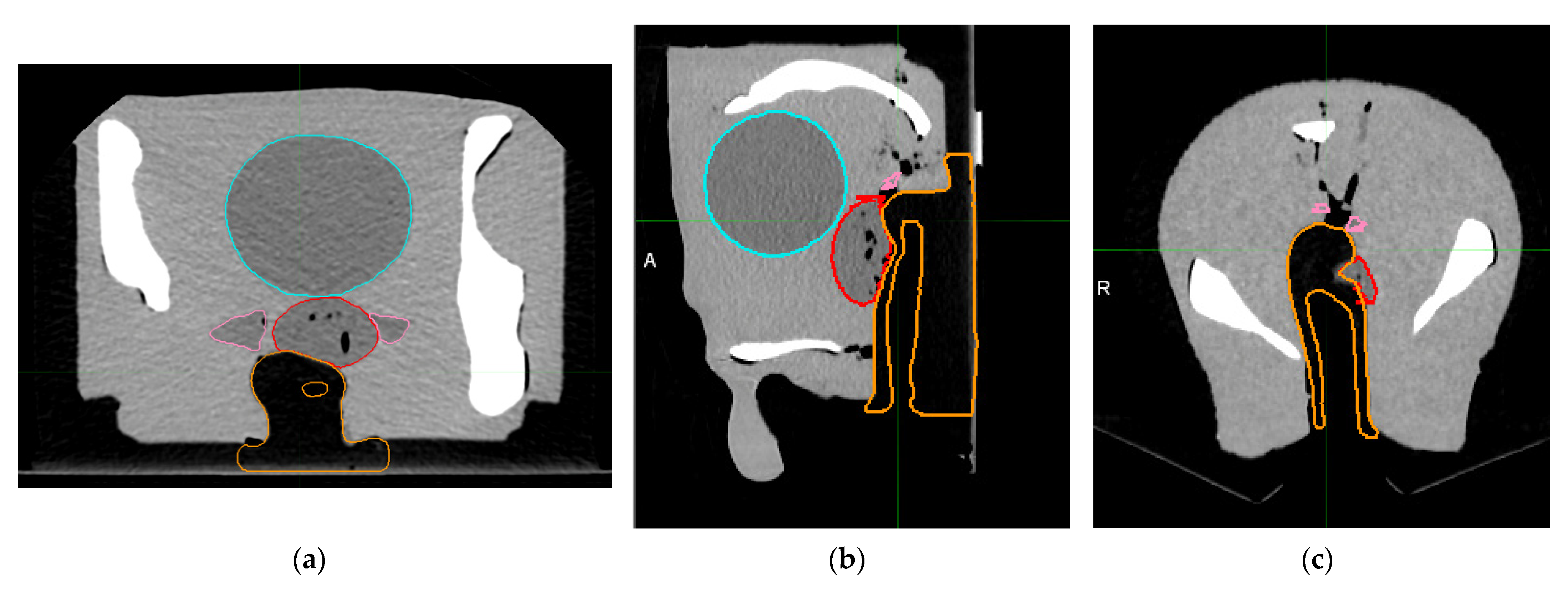
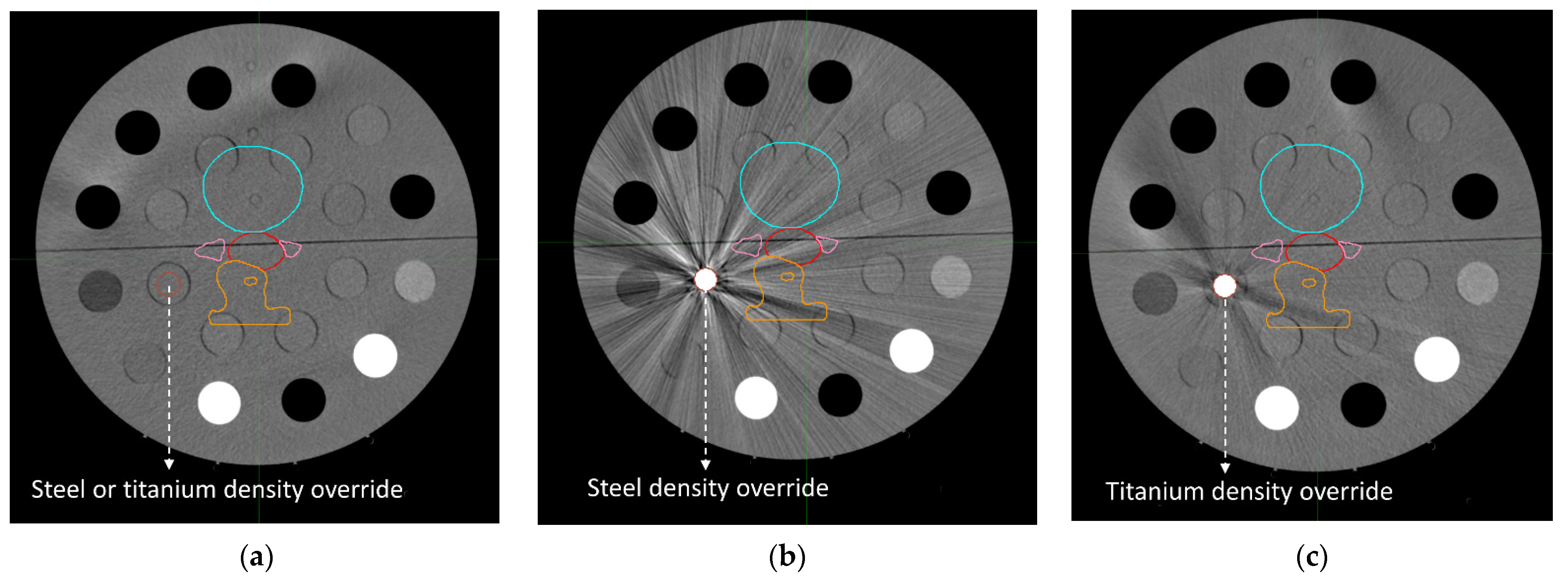
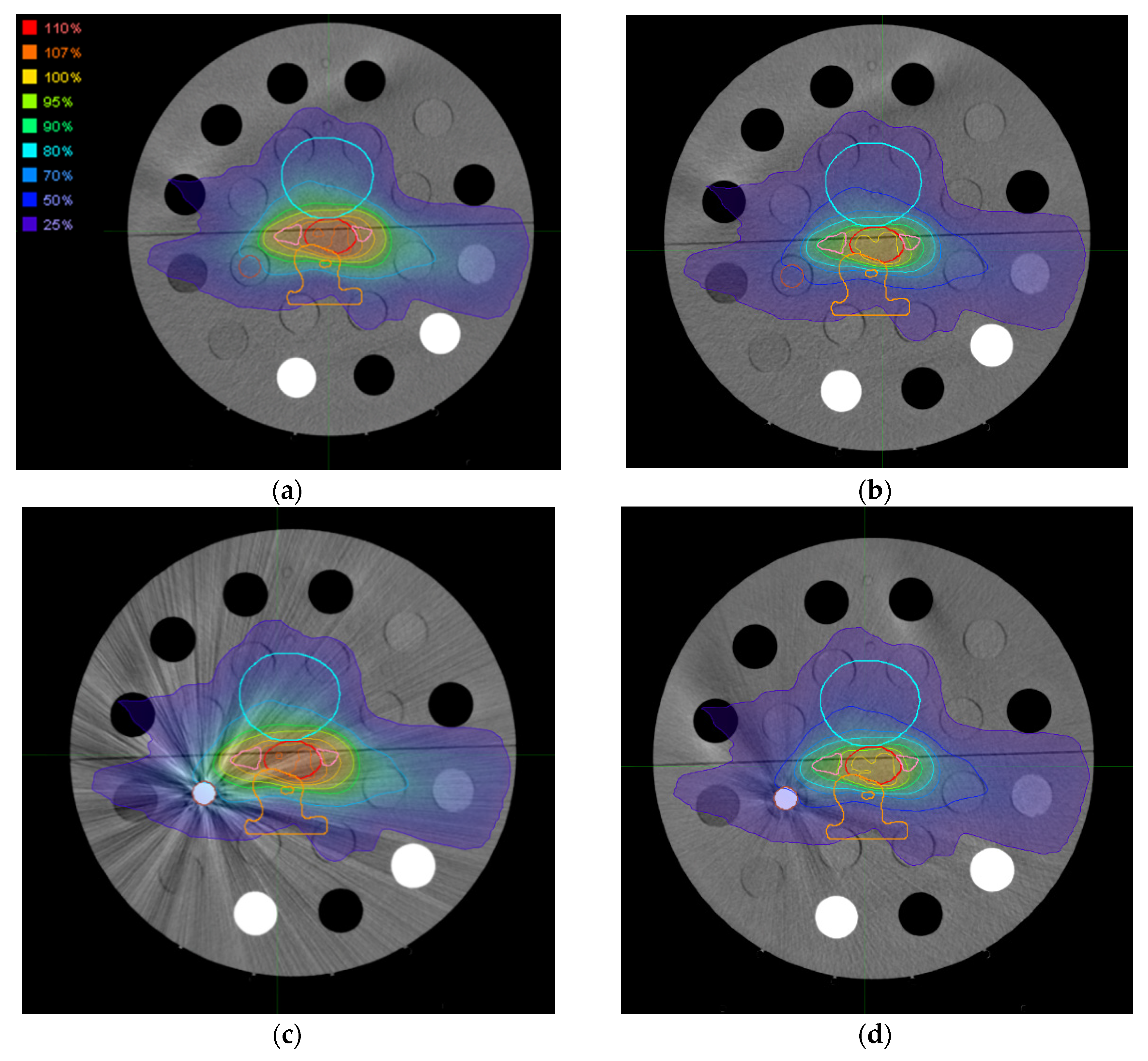
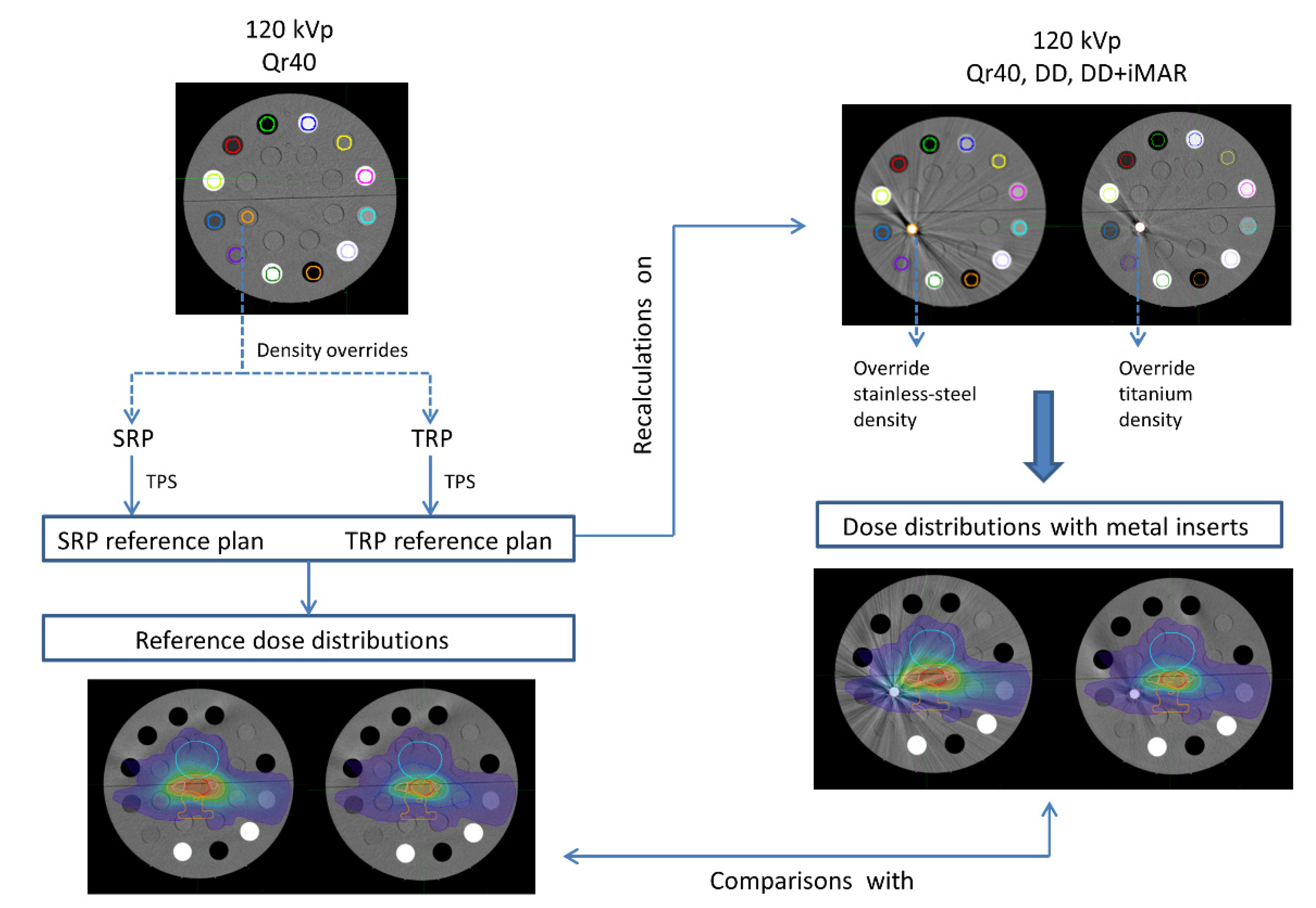

| Equivalent Material | Density (g/cm3) |
|---|---|
| LN-300 Lung | 0.300 |
| LN-450 Lung | 0.490 |
| Adipose | 0.942 |
| Breast | 0.979 |
| Solid Water | 1.018 |
| Brain | 1.053 |
| Liver | 1.095 |
| Inner Bone | 1.139 |
| B-200 Bone | 1.152 |
| CB2-30% | 1.334 |
| CB2-50% | 1.562 |
| Cortical Bone | 1.824 |
| Titanium | 4.510 |
| Stainless-steel | 8.000 |
| Convolution Kernel | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Qr40 | DD | DD + iMAR | ||||||||||||
| 80 kVp | 100 kVp | 120 kVp | 140 kVp | 80 kVp | 100 kVp | 120 kVp | 140 kVp | 80 kVp | 100 kVp | 120 kVp | 140 kVp | |||
| Metal Insert | Insert Name | Density (g/cm3) | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean | HU Mean |
| None | LN-300 Lung | 0.30 | −710 ± 15 | −713 ± 15 | −712 ± 14 | −711 ± 15 | −714 ± 11 | −717 ± 11 | −715 ± 10 | −714 ± 11 | - | - | - | - |
| LN-450 Lung | 0.49 | −511 ± 18 | −512 ± 15 | −513 ± 15 | −516 ± 17 | −520 ± 14 | −519 ± 12 | −520 ± 12 | −522 ± 14 | - | - | - | - | |
| Adipose | 0.94 | −115 ± 11 | −102 ± 10 | −95 ± 8 | −90 ± 10 | −118 ± 7 | −105 ± 7 | −97 ± 5 | −92 ± 7 | - | - | - | - | |
| Breast | 0.98 | −57 ± 11 | −52 ± 9 | −48 ± 8 | −46 ± 12 | −61 ± 7 | −55 ± 6 | −51 ± 5 | −48 ± 7 | - | - | - | - | |
| Solid Water | 1.02 | 9 ± 12 | 4 ± 9 | 3 ± 9 | 1 ± 13 | 7 ± 7 | 3 ± 6 | 2 ± 5 | 0 ± 9 | - | - | - | - | |
| Brain | 1.05 | 4 ± 14 | 16 ± 9 | 23 ± 11 | 28 ± 10 | 2 ± 9 | 15 ± 6 | 22 ± 7 | 27 ± 6 | - | - | - | - | |
| Liver | 1.10 | 84 ± 15 | 80 ± 9 | 78 ± 12 | 77 ± 11 | 80 ± 77 | 77 ± 6 | 76 ± 7 | 74 ± 6 | - | - | - | - | |
| Inner Bone | 1.14 | 314 ± 15 | 253 ± 12 | 220 ± 11 | 196 ± 10 | 106 ± 5 | 107 ± 4 | 108 ± 4 | 107 ± 4 | - | - | - | - | |
| B-200 Bone | 1.15 | 328 ± 15 | 263 ± 10 | 233 ± 13 | 209 ± 11 | 112 ± 4 | 113 ± 3 | 116 ± 4 | 114 ± 4 | - | - | - | - | |
| CB2-30% | 1.33 | 621 ± 15 | 525 ± 11 | 471 ± 11 | 438 ± 16 | 226 ± 7 | 235 ± 6 | 243 ± 6 | 250 ± 7 | - | - | - | - | |
| CB2-50% | 1.56 | 1151 ± 23 | 952 ± 13 | 847 ± 13 | 776 ± 15 | 448 ± 13 | 447 ± 9 | 453 ± 9 | 455 ± 9 | - | - | - | - | |
| Cortical Bone | 1.82 | 1734 ± 28 | 1449 ± 22 | 1269 ± 1163 | 1163 ± 18 | 719 ± 14 | 712 ± 13 | 703 ± 10 | 703 ± 10 | - | - | - | - | |
| Titanium | LN-300 Lung | 0.30 | −708 ± 16 | −710 ± 14 | −712 ± 15 | −710 ± 14 | −713 ± 12 | −714 ± 11 | −716 ± 11 | −713 ± 11 | −716 ± 11 | −716 ± 11 | −717 ± 11 | −715 ± 11 |
| LN-450 Lung | 0.49 | −513 ± 20 | −515 ± 16 | −516 ± 16 | −58 ± 16 | −521 ± 16 | −521 ± 13 | −521 ± 13 | −522 ± 13 | −522 ± 19 | −521 ± 13 | −521 ± 14 | −522 ± 13 | |
| Adipose | 0.94 | −114 ± 12 | −101 ± 9 | −94 ± 11 | −89 ± 8 | −118 ± 8 | −104 ± 6 | −97 ± 8 | −92 ± 6 | −118 ± 7 | −104 ± 6 | −97 ± 8 | −92 ± 6 | |
| Breast | 0.98 | −51 ± 18 | −48 ± 9 | −44 ± 11 | −42 ± 11 | −58 ± 12 | −53 ± 6 | −48 ± 7 | −46 ± 7 | −61 ± 10 | −54 ± 6 | −49 ± 7 | −46 ± 7 | |
| Solid Water | 1.02 | 14 ±18 | 7 ± 10 | 4 ± 9 | 4 ± 13 | 10 ± 12 | 4 ± 6 | 2 ± 6 | 3 ± 9 | 7 ± 10 | 2 ± 6 | 0 ± 6 | 1 ± 9 | |
| Brain | 1.05 | 5 ± 12 | 17 ± 9 | 24 ± 8 | 28 ± 8 | 3 ± 8 | 16 ± 6 | 23 ± 5 | 27 ± 6 | 2 ± 8 | 15 ± 6 | 23 ± 5 | 28 ± 6 | |
| Liver | 1.10 | 85 ± 13 | 79 ± 9 | 77 ± 9 | 77 ± 10 | 80 ± 9 | 77 ± 6 | 75 ± 6 | 75 ± 6 | 80 ± 8 | 77 ± 6 | 75 ± 6 | 75 ± 6 | |
| Inner Bone | 1.14 | 310 ± 16 | 251 ± 11 | 217 ± 10 | 195 ± 9 | 106 ± 5 | 107 ± 4 | 107 ± 4 | 107 ± 4 | 106 ± 5 | 107 ± 4 | 108 ± 4 | 107 ± 4 | |
| B-200 Bone | 1.15 | 323 ± 15 | 263 ± 9 | 228 ± 9 | 208 ± 9 | 111 ± 5 | 113 ± 3 | 113 ± 3 | 114 ± 4 | 111 ± 4 | 113 ± 3 | 112 ± 3 | 115 ± 4 | |
| CB2-30% | 1.33 | 623 ± 18 | 525 ± 11 | 470 ± 10 | 438 ± 14 | 228 ± 8 | 236 ± 6 | 243 ± 6 | 250 ± 6 | 228 ± 8 | 237 ± 6 | 243 ± 6 | 250 ± 7 | |
| CB2-50% | 1.56 | 1136 ± 21 | 949 ± 12 | 839 ± 11 | 775 ± 14 | 445 ± 12 | 448 ± 9 | 450 ± 8 | 456 ± 9 | 448 ± 12 | 449 ± 9 | 451 ± 8 | 456 ± 9 | |
| Cortical Bone | 1.82 | 1718 ± 30 | 1430 ± 21 | 1269 ± 19 | 1150 ± 16 | 719 ± 16 | 708 ± 12 | 708 ± 11 | 699 ± 9 | 728 ± 16 | 712 ± 13 | 711 ± 12 | 701 ± 10 | |
| Titanium | 4.51 | 13,021 ± 468 | 9891 ± 282 | 8059 ± 213 | 6953 ± 172 | 11,539 ± 429 | 8826 ± 245 | 7249 ± 186 | 6306 ± 149 | 11,541 ± 433 | 8828 ± 249 | 7251 ± 188 | 6308 ± 152 | |
| St. steel | LN-300 Lung | 0.30 | −700 ± 15 | −701 ± 15 | −705 ± 15 | −712 ± 17 | −706 ± 11 | −705 ± 12 | −709 ± 12 | −716 ± 13 | −708 ± 12 | −717 ± 11 | −716 ± 11 | −719 ± 12 |
| LN-450 Lung | 0.49 | −525 ± 18 | −513 ± 20 | −516 ± 27 | −516 ± 17 | −531 ± 11 | −518 ± 16 | −522 ± 21 | −520 ± 14 | −533 ± 11 | −524 ± 23 | −525 ± 27 | −523 ± 22 | |
| Adipose | 0.94 | −111 ± 11 | −97 ± 15 | −91 ± 12 | −87 ± 15 | −115 ± 10 | −100 ± 10 | −94 ± 8 | −90 ± 10 | −115 ± 9 | −105 ± 6 | −98 ± 6 | −91 ± 7 | |
| Breast | 0.98 | −52 ± 11 | −42 ± 33 | −42 ± 19 | −42 ± 15 | −58 ± 10 | −48 ± 22 | −47 ± 12 | −46 ± 10 | −61 ± 9 | −55 ± 14 | −50 ± 9 | −48 ± 7 | |
| Solid Water | 1.02 | 13 ± 12 | 18 ± 38 | 16 ± 28 | 5 ± 15 | 10 ± 9 | 15 ± 30 | 13 ± 22 | 3 ± 11 | 7 ± 9 | 4 ± 13 | 3 ± 9 | 0 ± 7 | |
| Brain | 1.05 | 5 ± 14 | 15 ± 16 | 25 ± 10 | 28 ± 13 | 3 ± 9 | 14 ± 11 | 24 ± 6 | 28 ± 8 | 2 ± 9 | 12 ± 8 | 22 ± 6 | 26 ± 7 | |
| Liver | 1.10 | 85 ± 15 | 78 ± 13 | 78 ± 13 | 77 ± 12 | 80 ± 9 | 74 ± 8 | 74 ± 8 | 73 ± 7 | 80 ± 9 | 76 ± 6 | 76 ± 6 | 75 ± 6 | |
| Inner Bone | 1.14 | 310 ± 15 | 247 ± 15 | 215 ± 11 | 196 ± 14 | 106 ± 9 | 106 ± 5 | 107 ± 4 | 108 ± 5 | 106 ± 8 | 107 ± 4 | 107 ± 4 | 109 ± 5 | |
| B-200 Bone | 1.15 | 322 ± 15 | 261 ± 14 | 229 ± 12 | 208 ± 12 | 111 ± 9 | 112 ± 5 | 112 ± 5 | 115 ± 5 | 111 ± 8 | 113 ± 4 | 114 ± 4 | 115 ± 4 | |
| CB2-30% | 1.33 | 623 ± 15 | 529 ± 23 | 481 ± 25 | 436 ± 15 | 228 ± 9 | 239 ± 9 | 249 ± 11 | 249 ± 7 | 228 ± 8 | 238 ± 10 | 247 ± 12 | 250 ± 8 | |
| CB2-50% | 1.56 | 1137 ± 23 | 944 ± 18 | 847 ± 18 | 770 ± 12 | 445 ± 8 | 446 ± 11 | 454 ± 11 | 454 ± 8 | 447 ± 7 | 451 ± 10 | 457 ± 10 | 457 ± 8 | |
| Cortical Bone | 1.82 | 1718 ± 28 | 1405 ± 25 | 1242 ± 23 | 1150 ± 22 | 719 ± 7 | 698 ± 13 | 693 ± 11 | 701 ± 13 | 728 ± 6 | 718 ± 14 | 713 ± 14 | 711 ± 12 | |
| St. steel | 8.00 | 27,708 ± 2217 | 19,552 ± 2640 | 17,790 ± 1188 | 15,464 ± 670 | 25,596 ± 2560 | 18,691 ± 2472 | 17,175 ± 1107 | 14,988 ± 625 | 25,591 ± 2303 | 18,682 ± 2488 | 17,170 ± 1116 | 14,989 ± 631 | |
| Convolution Kernel | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Qr40 | DD | DD + iMAR | ||||||||||||||||||||||||
| 80 kVp | 100 kVp | 120 kVp | 140 kVp | 80 kVp | 100 kVp | 120 kVp | 140 kVp | 80 kVp | 100 kVp | 120 kVp | 140 kVp | |||||||||||||||
| Metal Insert | Insert Name | Density (g/cm3) | dHU | % | dHU | % | dHU | % | dHU | % | dHUDD | % | dHUDD | % | dHUDD | % | dHUDD | % | dHUDD | % | dHUDD | % | dHUDD | % | dHUDD | % |
| Titanium | LN-300 Lung | 0.30 | 2 | 0 | 3 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 2 | 1 | 1 | 0 | 0 | 0 | 2 | 1 | 1 | 0 | 2 | 1 | 1 | 0 |
| LN-450 Lung | 0.49 | 2 | 0 | 3 | 1 | 2 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | |
| Adipose | 0.94 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Breast | 0.98 | 6 | 1 | 5 | 0 | 4 | 0 | 4 | 0 | 3 | 0 | 3 | 0 | 2 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 0 | |
| Solid Water | 1.02 | 4 | 0 | 3 | 0 | 1 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| Brain | 1.05 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| Liver | 1.10 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| Inner Bone | 1.14 | 3 | 0 | 2 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| B-200 Bone | 1.15 | 6 | 0 | 0 | 0 | 5 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | |
| CB2-30% | 1.33 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| CB2-50% | 1.56 | 15 | 1 | 3 | 0 | 8 | 0 | 1 | 0 | 3 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | |
| Cortical Bone | 1.82 | 16 | 1 | 19 | 1 | 0 | 0 | 13 | 0 | 1 | 0 | 4 | 0 | 5 | 0 | 4 | 0 | 10 | 0 | 0 | 0 | 8 | 0 | 2 | 0 | |
| St.steel | LN-300 Lung | 0.30 | 10 | 3 | 12 | 4 | 6 | 2 | 1 | 0 | 8 | 3 | 11 | 4 | 6 | 2 | 2 | 1 | 6 | 2 | 0 | 0 | 1 | 0 | 5 | 2 |
| LN-450 Lung | 0.49 | 14 | 3 | 1 | 0 | 2 | 0 | 0 | 0 | 11 | 2 | 1 | 0 | 2 | 0 | 2 | 0 | 12 | 3 | 5 | 1 | 6 | 1 | 1 | 0 | |
| Adipose | 0.94 | 4 | 0 | 5 | 1 | 3 | 0 | 3 | 0 | 2 | 0 | 4 | 0 | 2 | 0 | 2 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |
| Breast | 0.98 | 6 | 1 | 10 | 1 | 6 | 1 | 4 | 0 | 3 | 0 | 7 | 1 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| Solid Water | 1.02 | 4 | 0 | 14 | 1 | 13 | 1 | 4 | 0 | 2 | 0 | 12 | 1 | 11 | 1 | 3 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |
| Brain | 1.05 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | |
| Liver | 1.10 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Inner Bone | 1.14 | 3 | 0 | 5 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| B-200 Bone | 1.15 | 6 | 0 | 2 | 0 | 4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |
| CB2-30% | 1.33 | 2 | 0 | 4 | 0 | 10 | 1 | 2 | 0 | 2 | 0 | 4 | 0 | 6 | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 4 | 0 | 0 | 0 | |
| CB2-50% | 1.56 | 15 | 1 | 8 | 0 | 0 | 0 | 6 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 4 | 0 | 4 | 0 | 2 | 0 | |
| Cortical Bone | 1.82 | 16 | 1 | 44 | 2 | 27 | 1 | 12 | 1 | 1 | 0 | 14 | 1 | 9 | 0 | 2 | 0 | 10 | 0 | 6 | 0 | 10 | 1 | 8 | 0 | |
| Insert Name | Density (g/cm3) | Convolution Kernel | ||
|---|---|---|---|---|
| Qr40 | DD | DD + iMAR | ||
| Abs dHU (dHU%) | Abs dHU (dHU%) | Abs dHU (dHU%) | ||
| LN-300 Lung | 0.30 | 5 (2) | 3 (1) | 5 (2) |
| LN-450 Lung | 0.49 | 0 (0) | 3 (1) | 5 (1) |
| Adipose | 0.94 | 24 (3) | 26 (3) | 25 (3) |
| Breast | 0.98 | 10 (1) | 12 (1) | 14 (1) |
| Solid Water | 1.02 | 9 (1) | 7 (1) | 7 (1) |
| Brain | 1.05 | 23 (2) | 24 (2) | 25 (2) |
| Liver | 1.10 | 7 (1) | 6 (0) | 6 (0) |
| Inner Bone | 1.14 | 116 (10) | 1 (0) | 2 (0) |
| B-200 Bone | 1.15 | 116 (10) | 3 (0) | 3 (0) |
| CB2-30% | 1.33 | 185 (23) | 22 (2) | 22 (2) |
| CB2-50% | 1.56 | 368 (21) | 9 (0) | 9 (1) |
| Cortical Bone | 1.82 | 569 (26) | 18 (1) | 22 (1) |
| Titanium | 4.51 | 6068 (76) | 5233 (72) | 5234 (72) |
| Stainless-steel | 8.00 | 12,243 (74) | 10,608 (66) | 10,602 (66) |
| Qr40 | ||||
|---|---|---|---|---|
| SRP/TRP | Steel | Titanium | ||
| Qr40 | Steel | 100% | - | - |
| Titanium | 100% | - | - | |
| DD | Steel | 100% | 100% | - |
| Titanium | 100% | - | 100% | |
| DD + iMAR | Steel | 100% | 100% | - |
| Titanium | 100% | - | 100% | |
| Qr40 | ||||
|---|---|---|---|---|
| SRP/TRP | Steel | Titanium | ||
| Qr40 | Steel | 2.6% | - | - |
| Titanium | 1.6% | - | - | |
| DD | Steel | 0.5% | 1.6% | - |
| Titanium | 0.5% | - | 0.5% | |
| DD + iMAR | Steel | 0.5% | 1.6% | - |
| Titanium | 0.5% | - | 0.5% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feliciani, G.; Guidi, C.; Belli, M.L.; D’Errico, V.; Loi, E.; Mezzenga, E.; Sarnelli, A. The Role of a DirectDensity® CT Reconstruction in a Radiotherapy Workflow: A Phantom Study. Appl. Sci. 2022, 12, 7845. https://doi.org/10.3390/app12157845
Feliciani G, Guidi C, Belli ML, D’Errico V, Loi E, Mezzenga E, Sarnelli A. The Role of a DirectDensity® CT Reconstruction in a Radiotherapy Workflow: A Phantom Study. Applied Sciences. 2022; 12(15):7845. https://doi.org/10.3390/app12157845
Chicago/Turabian StyleFeliciani, Giacomo, Claretta Guidi, Maria Luisa Belli, Vincenzo D’Errico, Emiliano Loi, Emilio Mezzenga, and Anna Sarnelli. 2022. "The Role of a DirectDensity® CT Reconstruction in a Radiotherapy Workflow: A Phantom Study" Applied Sciences 12, no. 15: 7845. https://doi.org/10.3390/app12157845
APA StyleFeliciani, G., Guidi, C., Belli, M. L., D’Errico, V., Loi, E., Mezzenga, E., & Sarnelli, A. (2022). The Role of a DirectDensity® CT Reconstruction in a Radiotherapy Workflow: A Phantom Study. Applied Sciences, 12(15), 7845. https://doi.org/10.3390/app12157845






