High-Efficiency Characterization of Optical Vortices with Arbitrary State of Polarization Using Straight-Line and Parabolic-Line Polarization Gratings
Abstract
:Featured Application
Abstract
1. Introduction
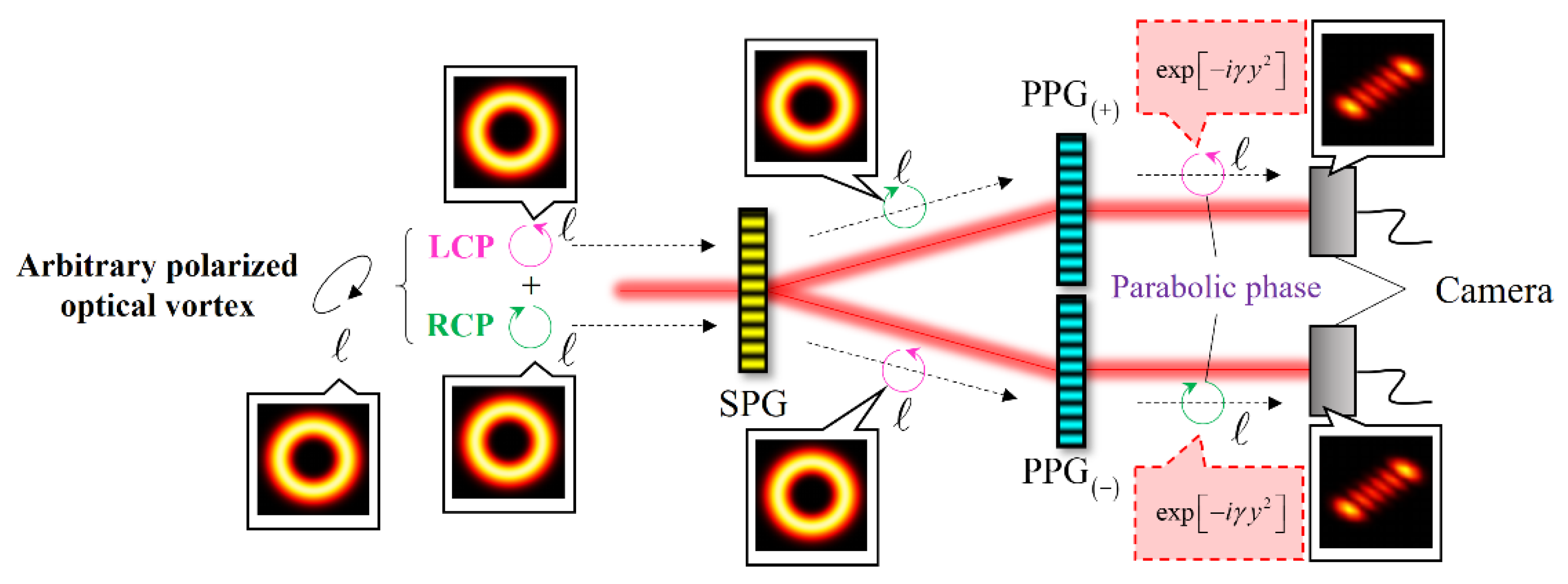
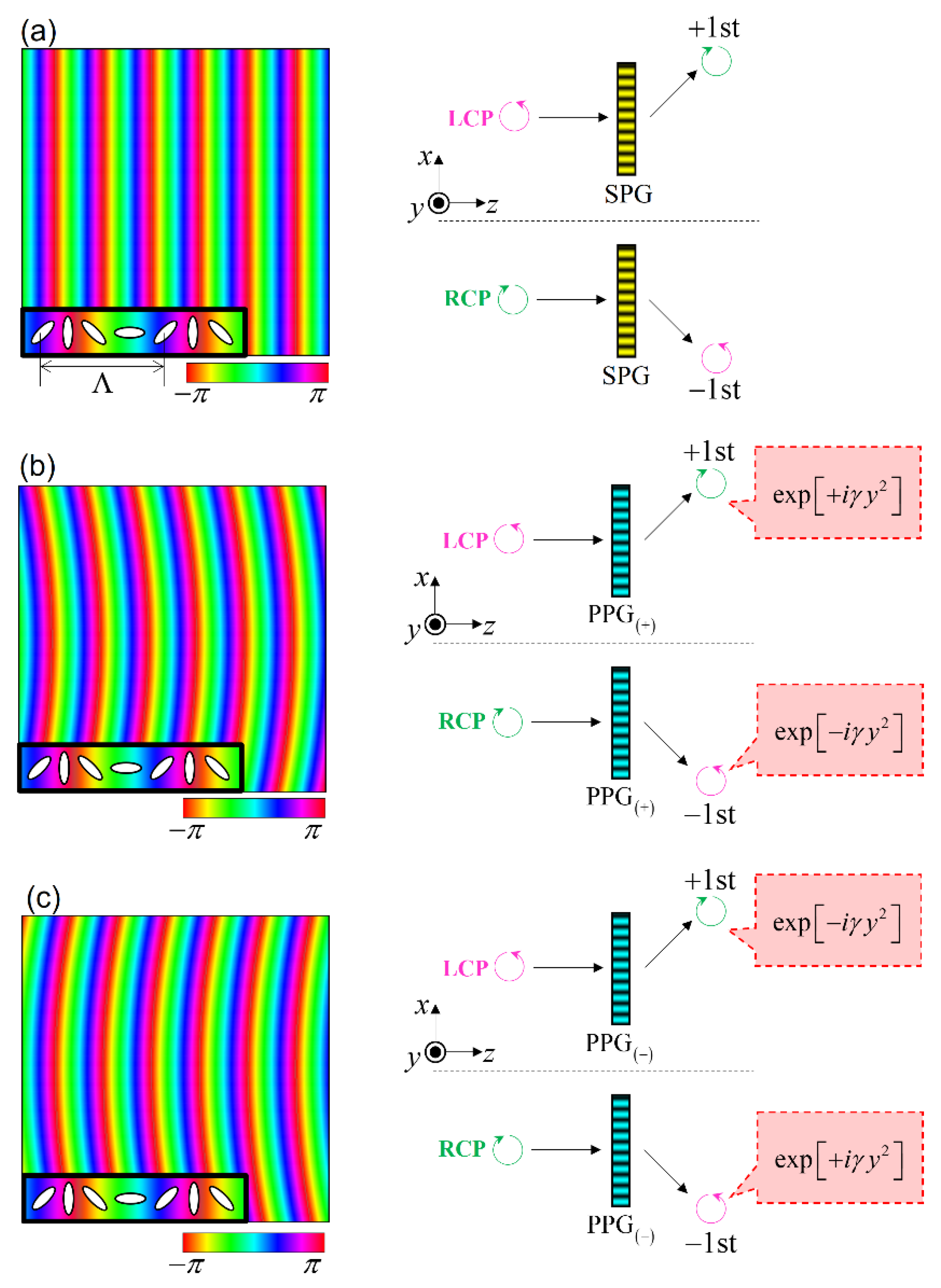
2. Operating Principle of Our OV Characterizer
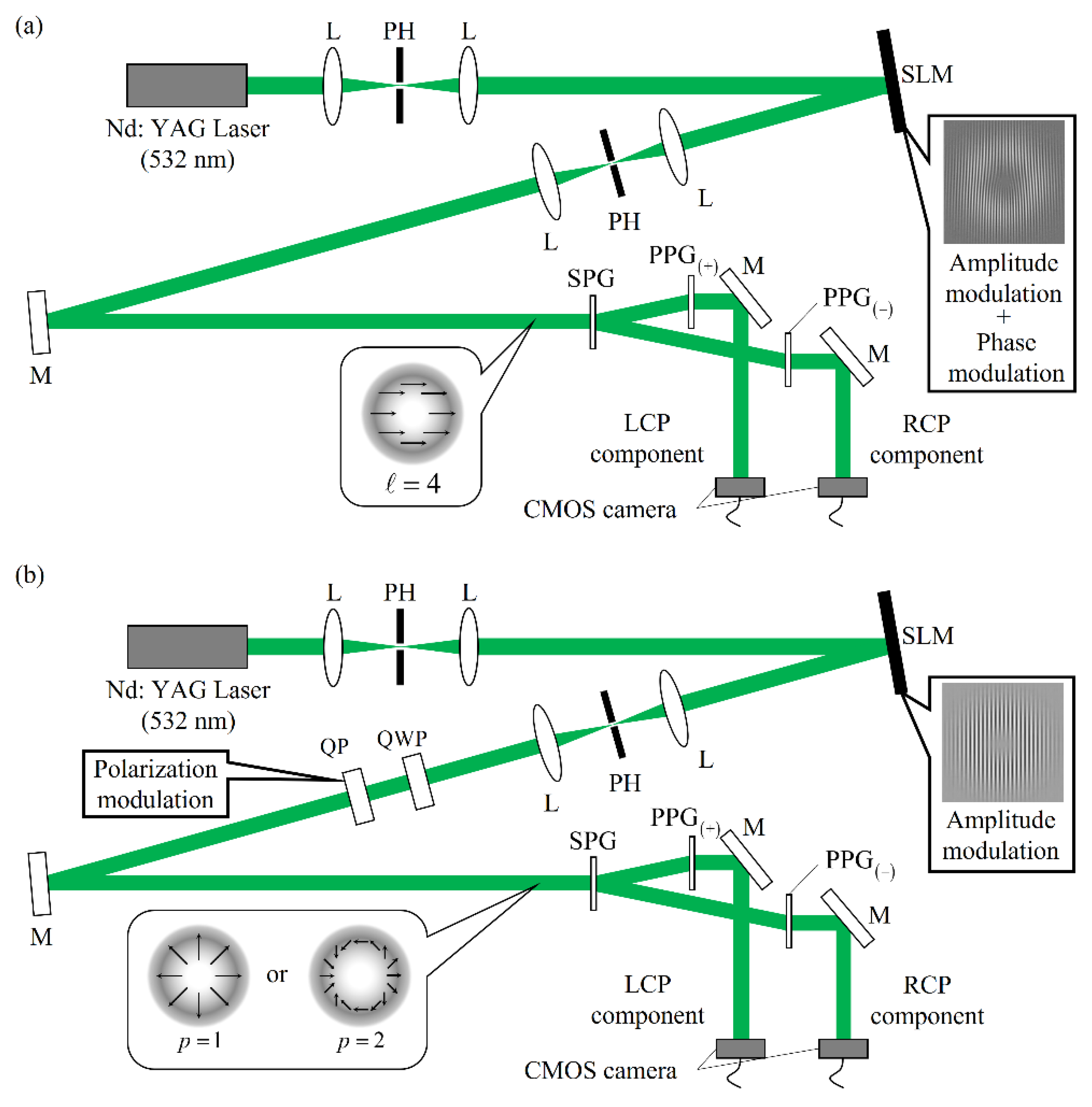
3. Experimental Methods
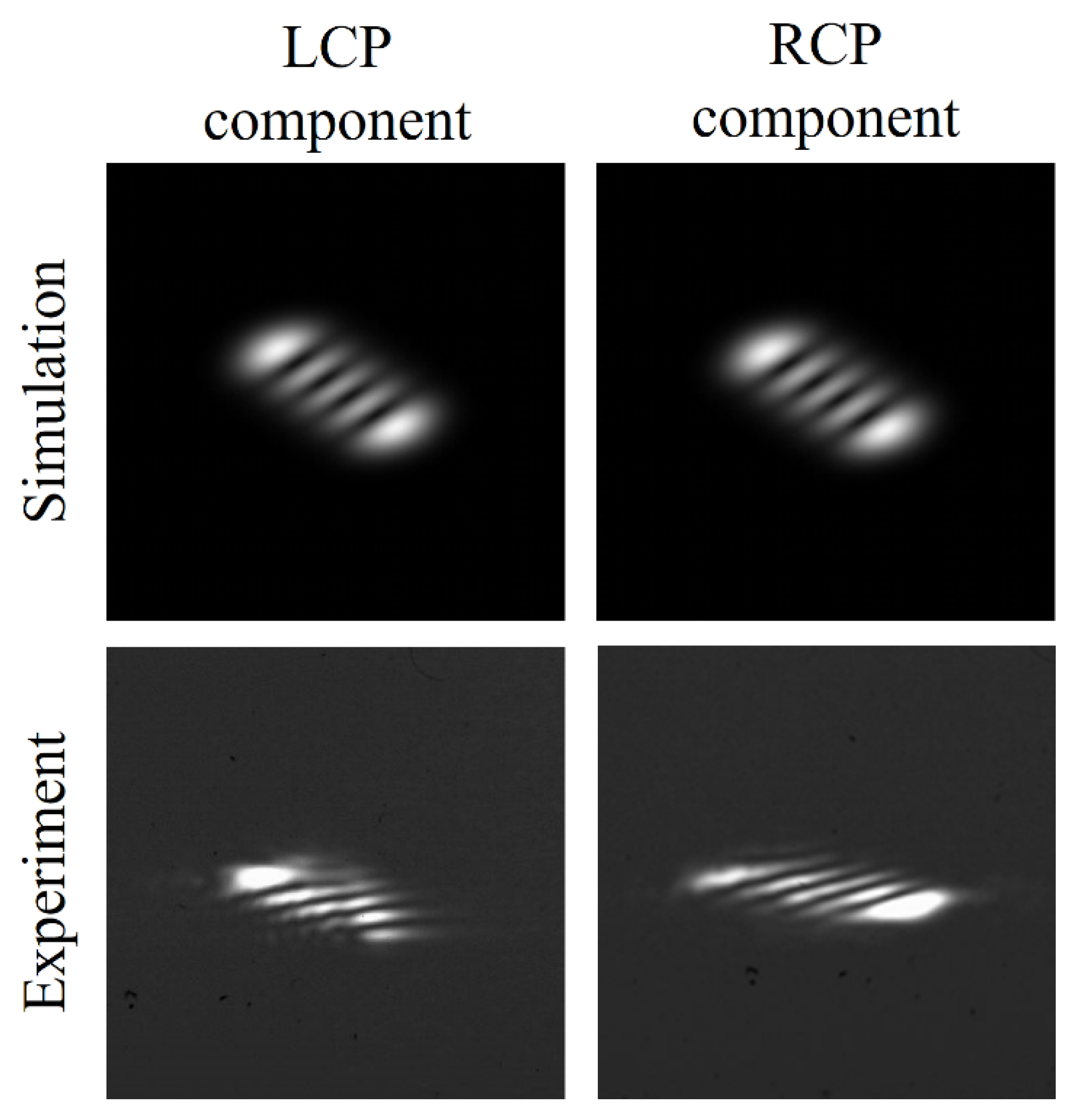
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photon. Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.J. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, K.; Takahashi, F.; Takizawa, S.; Tokizane, Y.; Miyamoto, K.; Morita, R.; Omatsu, T. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 2013, 110, 143603. [Google Scholar] [CrossRef] [PubMed]
- Gahagan, K.T.; Swartzlander, G.A., Jr. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Harris, M.; Hill, C.A.; Tapster, P.R.; Vaughan, J.M. Laser modes with helical wave fronts. Phys. Rev. A 1994, 49, 3119–3122. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.S.; Lu, L.L.; Wang, H.T. Characterizing topological charge of optical vortices by using an annular aperture. Opt. Lett. 2009, 34, 3686–3688. [Google Scholar] [CrossRef] [PubMed]
- Hickmann, J.M.; Fonseca, E.J.S.; Soares, W.C.; Chavez-Cerda, S. Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 2010, 105, 053904. [Google Scholar] [CrossRef] [PubMed]
- De Araujo, L.E.; Anderson, M.E. Measuring vortex charge with a triangular aperture. Opt. Lett. 2011, 36, 787–789. [Google Scholar] [CrossRef]
- Hebri, D.; Rasouli, S.; Dezfouli, A.M. Theory of diffraction of vortex beams from structured apertures and generation of elegant elliptical vortex Hermite-Gaussian beams. J. Opt. Soc. Am. A 2019, 36, 839–852. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, W.; Chen, L. Experimental detection of high-order or fractional orbital angular momentum of light based on a robust mode converter. Appl. Phys. Lett. 2016, 108, 111108. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Pascoguin, B.M.; Mitry, M.J.; Cottrell, D.M. Vortex sensing diffraction gratings. Opt. Lett. 2009, 34, 2927–2929. [Google Scholar] [CrossRef]
- Berkhout, G.C.; Lavery, M.P.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef]
- Amiri, P.; Dezfouli, A.M.; Rasouli, S. Efficient characterization of optical vortices via diffraction from parabolic-line linear gratings. J. Opt. Soc. Am. B 2020, 37, 2668–2677. [Google Scholar] [CrossRef]
- Bekshaev, A.Y.; Soskin, M.S.; Vasnetsov, M.V. Transformation of higher-order optical vortices upon focusing by an astigmatic lens. Opt. Commun. 2004, 241, 237–247. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Influence of astigmatism and defocusing on the focusing of a singular beam. Opt. Commun. 2006, 270, 128–138. [Google Scholar] [CrossRef]
- Denisenko, V.; Shvedov, V.; Desyatnikov, A.S.; Neshev, D.N.; Krolikowski, W.; Volyar, A.; Soskin, M.; Kivshar, Y.S. Determination of topological charge of polychromatic optical vortices. Opt. Express 2009, 23374–23379. [Google Scholar] [CrossRef]
- Todorov, T.; Nikolova, L.; Tomova, N. Polarization holography. 2: Polarization holographic gratings in photoanisotropic materials with and without intrinsic birefringence. Appl. Opt. 1984, 23, 4588–4591. [Google Scholar] [CrossRef]
- Davis, J.A.; Adachi, J.; Fernandez-Pousa, C.R.; Moreno, I. Polarization beam splitters using polarization diffraction gratings. Opt. Lett. 2001, 26, 587–589. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam-Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 27, 1141–1143. [Google Scholar] [CrossRef]
- Ono, H.; Emoto, A.; Kawatsuki, N.; Takahashi, F.; Hasegawa, T. Highly stable polarization gratings in photocrosslinkable polymer liquid crystals. J. Appl. Phys. 2003, 94, 1298–1303. [Google Scholar] [CrossRef]
- Escuti, M.J.; Oh, C.; Sanchez, C.; Bastiaansen, C.; Broer, D.J. Simplified spectropolarimetry using reactive mesogen polarization gratings. Proc. SPIE 2006, 6302, 630207. [Google Scholar]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Kawatsuki, N.; Goto, K.; Kawakami, T.; Yamamoto, T. Reversion of alignment direction in the thermally enhanced photo orientation of photo-cross-linkable polymer liquid crystal films. Macromolecules 2002, 35, 706–713. [Google Scholar] [CrossRef]
- Momosaki, R.; Ashikawa, K.; Sakamoto, M.; Noda, K.; Sasaki, T.; Kawatsuki, N.; Ono, H. Incident angle dependence-reduced polarization grating performed by using optically biaxial polymer liquid crystal. Opt. Lett. 2019, 44, 5929–5932. [Google Scholar] [CrossRef] [PubMed]
- Bomzon, Z.; Kleiner, V.; Hasman, E. Formation of radially and azimuthally polarized light using space-variant subwavelength metal stripe gratings. Appl. Phys. Lett. 2001, 79, 1587–1589. [Google Scholar] [CrossRef]
- Niv, A.; Beiner, G.; Kleiner, V.; Hasman, E. Manipulation of the Pancharatnam phase in vectorial vortices. Opt. Express 2006, 14, 4208–4220. [Google Scholar] [CrossRef] [PubMed]
- Cardano, F.; Karimi, E.; Slussarenko, S.; Marrucci, L.; de Lisio, C.; Santamato, E. Polarization pattern of vector vortex beams generated by q-plates with different topological charge. Appl. Opt. 2012, 51, C1–C6. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakamoto, M.; Yayama, T.; Noda, K.; Sasaki, T.; Kawatsuki, N.; Ono, H. High-Efficiency Characterization of Optical Vortices with Arbitrary State of Polarization Using Straight-Line and Parabolic-Line Polarization Gratings. Appl. Sci. 2022, 12, 8768. https://doi.org/10.3390/app12178768
Sakamoto M, Yayama T, Noda K, Sasaki T, Kawatsuki N, Ono H. High-Efficiency Characterization of Optical Vortices with Arbitrary State of Polarization Using Straight-Line and Parabolic-Line Polarization Gratings. Applied Sciences. 2022; 12(17):8768. https://doi.org/10.3390/app12178768
Chicago/Turabian StyleSakamoto, Moritsugu, Tomoki Yayama, Kohei Noda, Tomoyuki Sasaki, Nobuhiro Kawatsuki, and Hiroshi Ono. 2022. "High-Efficiency Characterization of Optical Vortices with Arbitrary State of Polarization Using Straight-Line and Parabolic-Line Polarization Gratings" Applied Sciences 12, no. 17: 8768. https://doi.org/10.3390/app12178768
APA StyleSakamoto, M., Yayama, T., Noda, K., Sasaki, T., Kawatsuki, N., & Ono, H. (2022). High-Efficiency Characterization of Optical Vortices with Arbitrary State of Polarization Using Straight-Line and Parabolic-Line Polarization Gratings. Applied Sciences, 12(17), 8768. https://doi.org/10.3390/app12178768







