Abstract
The objective of this research is to solve the problem of the lack of prediction methods and basis for the long-term road performance of oil shale residue-modified soil in seasonally frozen regions. This paper summarizes and expands the resilient modulus prediction methods in the related literature. Based on the measured soil–water characteristic curve (SWCC) of the compacted modified soil and the trend characteristics of dynamic resilient modulus under freeze–thaw cycles, a semi-empirical prediction model is proposed. This model was used to quantitatively forecast the resilient modulus of unsaturated modified subgrade soil after the freeze–thaw cycle in a seasonal permafrost region. The applicability and accuracy of the method were verified by dynamic resilient modulus tests of the oil shale residue-modified soil under various freeze–thaw cycles and moisture content. The results show that the model has a high degree of fit to the experimental data and is more suitable for predicting the dynamic resilient modulus of modified soil under the change of moisture and the freeze–thaw cycle compared to the existing models.
1. Introduction
To estimate the service performance of subgrade materials under vehicle loads and provide a reference for the design of road and railway subgrades, increasingly more researchers in recent years have focused on the study of the dynamic characteristics of compacted subgrades. The same is true for the research on various new modified subgrade materials. The dynamic modulus of resilience (MR) of the subgrade is an important parameter reflecting the deformation characteristics and impact strength of the subgrade, and it is often used as a criterion for evaluating the compaction quality of the subgrade. The modulus is affected by many factors, such as the self-consolidation state, soil particle characteristics, water content, and stress level. When subgrade is considered as a whole in a layered-resilience system, researchers often express the MR of the subgrade under dynamic load as mathematical models related to stress, including the K-θ model [1], composite prediction model [2], etc. These models express the nonlinear stress–strain properties of the subgrade by combining the soil physical properties (such as water content and dry density) and stress state variables (such as deviatoric, confining, volumetric, and shear stresses). The AASHTO Pavement Design Guide (NCHRP1-37A) [3] proposes a prediction model to improve the characteristics of model uncertainty and dimensional disagreement:
where k1, k2, and k3 are regression parameters dependent on the material types and soil physical properties; is the bulk stress, i.e., σ1+ σ2+ σ3 (σ1, σ2, and σ3 are the three principal stresses); is the octahedral shear stress, i.e., ; is the atmospheric pressure. In the method of determining the modulus of resilience by the triaxial test under dynamic load, represents the applied vertical stress, = = confining compressive stress.
The subgrade surface clay in arid or semi-arid areas is always unsaturated, and its mechanical properties are very different from those in the saturated state. The subgrade strength and deformation will be affected obviously when climate change or groundwater migration causes the subgrade moisture fluctuation [4,5].
It relates to the problems in the field of unsaturated soil mechanics. With the development of unsaturated soil research, it is widely believed that matric suction is an important variable affecting the structural mechanical behavior of unsaturated soil. Matric suction is related to the capillary effect [6,7,8], which is different from the external stress effect caused by an external load. Its response in soil mechanics can be seen as the surface tension at the water–air interface strengthens the links and bonds between soil particles, which in turn reduces the possibility of sliding between particles and hinders the plastic deformation of the soil [9,10]. Matric suction depends on many factors, such as the soil saturation state, initial dry density, particle composition, etc., [11,12], and many studies have shown a strong correlation between the MR and suction. Abd, I. A. et al. demonstrated using a modified triaxial test device that matric suction can increase the soil elasticity and that all stress variables also increased the angle of internal friction between the soil particles [13]. The MR has shown a nonlinear increasing trend with a decrease in matric suction in the referenced review literature [14,15]. Ng et al. found that when the acyclic stress was 30 kPa, the increase in the suction from 0 to 250 kPa increased the MR by up to one order of magnitude [16].
Some models for predicting the MR considering the influence of matric suction have been proposed successively. Such a prediction model was proposed by Yao et al. [17], considering matric suction, minimum bulk stress, and octahedral shear stress.
where ψm is the total suction, and θm is the minimum bulk stress.
This model avoids the problem of equal body stress values under different combinations of deviatoric stress and confining pressure. However, the regression coefficients of the model are obtained based on the physical parameters of the fully weathered granite. Therefore, its applicability to other types of soil remains to be further verified. Azam et al. [18] proposed a model for the modulus of resilience of recycled unbonded materials that uses the density ratio to characterize the effect of soil density on soil resilience.
where σm is the mean normal stress (i.e.,), is the reference shear stress (i.e.,), qf is the peak shear strength, DDR is the dry density ratio (%), RCM is the percentage of recycled clay masonry (%), and k4 and k5 are regression parameters (factors and exponents).
Bishop [19] proposed an expression for the effective stress of unsaturated soils, which extended the Terzaghi effective stress principle in traditional soil mechanics to the study of unsaturated soils. This principle has been widely used as a theoretical basis in the study of the strength and deformation of unsaturated soils, and as one of its applications, it is often introduced to improve existing elastic modulus models. This expression describes the effective stress in the soil as
where is matric suction, ua is pore air pressure, and uw is pore water pressure. Subsequent researchers have proved that the parameter is related to saturation. Many researchers have successively put forward some expressions similar to the formula, but the measured soil parameters have different values for different problems (volume deformation or shear strength), different stress paths, and different soil types. Although the effective stress parameters of unsaturated soils are not easy to measure accurately, the approximate expression of can be obtained through experiments, and then the theoretical estimation of the stress–strain problem of unsaturated soils has practical value [20,21].
In addition to the influence of suction, the subgrade in the seasonal frozen soil area also undergoes long-term freezing and thawing. The weathering effect caused by freezing and thawing will not only change the soil structure, which will affect the strength of the subgrade, but also lead to water migration, resulting in the softening and deformation of the subgrade. Cui Honghuan’s research [22] shows that the strength of unsaturated soil decreases first and then tends to be stable with the increase in the freeze–thaw cycles. Liu Yueqing et al. [23] found, from a microscopic point of view, that a decrease in the freeze–thaw temperature and an increase in the freeze–thaw cycles led to the gradual decomposition of large loess particles into small particles, and the arrangement of the particles changed. Therefore, when testing the service performance of the improved subgrade filler in seasonally frozen areas, it is necessary to simulate complex environmental loads. When investigating the empirical prediction method of the elastic modulus under dynamic stress, researchers must also carefully take into account the engineering characteristics of their material as well as the effects of climate change.
In this paper, by analyzing the contribution of matric suction to the effective stress of subgrade and the loss law of the MR after the freeze–thaw cycle, a semi-empirical prediction model of the MR suitable for oil shale waste subgrade filling under the unsaturated conditions of seasonally frozen soil is proposed. This model fits the change trend of the MR of oil shale residue subgrade filler under humidity changes and large cyclic loading, which provides help for the long-term deformation evaluation of oil shale residue-modified soil in actual road use.
2. Methodology
Based on the theory of multinomial continuum mechanics, the overall stress state of unsaturated soil can be represented by two independent tensors under the condition that soil pores and pore water are incompressible.
where corresponds to suction, which is a common key variable in unsaturated soil analysis. Since the suction does not directly act on the soil skeleton element, the normal action area of the soil element is not equal to the external load and cannot be directly added to . Due to the complexity of the elasto-plastic problem of unsaturated soils, this study was guided by the Bishop effective stress principle [19]. When constructing the elastic modulus model, the suction force was simplified as a three-dimensional isobaric external force. Under this premise, discuss the parameter so that it can modify and make it addable to .
In order to find a suitable construction method for the modified soil, the soil–water characteristic curve of the compacted modified soil was measured in advance. The soil–water characteristic curve (SWCC) is often used to express the relationship between the water content and suction in unsaturated soil research, which can provide a reference for the research of other characteristics. In this study, the SWCC of oil shale waste residue-modified soil was measured using the filter paper method [24]. The test sample was made out of oil shale waste residue powder, fly ash, and silty clay with the same particle size, and the mass ratio of the three materials was 2:1:2. This ratio was obtained according to the research group’s previous experimental research on the improvement of subgrade soil by oil shale waste residue [25]. Under this ratio, the road performance indexes (such as unconfined compressive strength and shear strength, etc.) of the improved soil reach the best. The basic physical properties of modified soil are shown in Table 1.

Table 1.
Basic physical properties of modified soil [25].
The compacted modified soil samples with the initial volumetric moisture contents of 20%, 25%, 30%, 35%, and 40% were prepared, and the sample was a cylinder of a standard ring cutter size (diameter 61.6 mm, height 20 mm, volume 60 mm³). The experimental process was according to the American Society for Testing and Materials (ASTM) standard [24]. Since data measured by the filter paper method are discontinuous, in order to better observe the law between matric suction and water content, this study used the classic Fredlund model [10] to fit them.
where θs is the saturated moisture content coefficient (unless otherwise specified below, the moisture content mentioned is the volumetric moisture content), which represents the starting position of the Fredlund fitting curve, and m, n, and are soil parameters that affect the soil–water characteristic curve.
The fitted SWCCs were then plotted on a semi-logarithmic coordinate system (Figure 1). Auxiliary lines and feature points are also shown according to the morphological features of the SWCC.
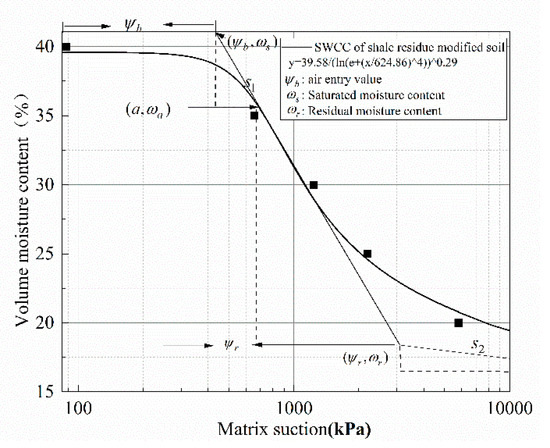
Figure 1.
Soil–water characteristic curve of compacted modified soil.
In Figure 1, the transitions from the boundary effect section to the transition section and from the transition section to the residual section occur at points and , respectively. In the semi-logarithmic coordinates, the slope of the transition segment between these two locations is significantly different from the other two sections.
is the point on the right side of the air-entry value and is close to it. In the image located in the semi-log coordinate system, the slope of SWCC at a certain interval from point tends to be constant, and the Fredlund model can be used to fit the value of directly.
Since the feature points found by the traditional graphical method are relatively fuzzy, the SWCC graphic analytical calculation method proposed by Qian Zhai [26] was used to calculate the SWCC eigenvalues. This method provides a mathematical relationship between the SWCC eigenvalues and the fitting parameters of the Fredlund model (5), which replaces the traditional graphical method of finding the SWCC eigenvalues and gives consistent results. The eigenvalue calculation results are shown in Table 2.

Table 2.
Soil–water characteristic curve eigenvalues of modified soil.
In previous studies, has been considered to be an indefinite coefficient between 0 and 1 related to saturation, which can be constructed as a function by the ratio of water content or matric suction variable to a certain eigenvalue or an exponential function of that ratio [21,22]. The parameter construction in this study takes into account the following factors.
Due to the influence of rainfall infiltration and groundwater migration, the optimal water content (OMC) of subgrade soil will gradually increase to the equilibrium water content during the whole life of the subgrade. In order to improve the pertinence of the prediction model and reduce errors, this study focused on the saturation range between 0.5 and 0.75, referring to studies related to the range of equilibrium humidity [27,28]. Combined with Table 2, it can be judged that the humidity profile concerned in this study is located between and . In this interval, the SWCC does not contain special turns, and its slope is close to constant. This means that the liquid phase in the soil is continuous at this stage, and the water content in the soil will continue to dissipate rapidly with the increase in suction.
In addition, the calculation method of the value is relatively simple, while the calculations of other eigenvalues require the use of traditional graphical methods with low accuracy or the accumulation of large systematic errors through multiple calculations. Another factor that needs attention is that, in the subgrade experiments, it is difficult to achieve the experimental conditions of too-low moisture content, so the characteristic values of the residual water content obtained may have large errors. So, in this study, the parameter was used to construct the effective stress parameter after a series of tests.
where is obtained by fitting the Fredlund model (5). k is a regression parameter depending on the material type and soil physical properties. By introducing it into the octahedral shear stress correction model (1) [7], the MR can be expressed as
where k1, k2, and k3 are regression parameters dependent on the material types and soil physical properties; is the bulk stress; is the octahedral shear stress; is the atmospheric pressure.
Considering the empirical prediction of the MR in seasonally frozen areas, it is also necessary to adapt and describe the changing trend of the MR after freeze–thaw cycles. Jilin University’s research group [25,29] conducted a series of tests under dynamic loads on oil shale residue-modified soil after freeze–thaw cycles, the relationship between the MR obtained from the experiments and the freeze-thaw cycles was shown in Figure 2.
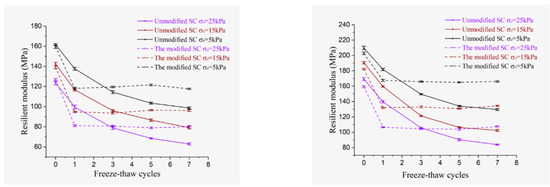
Figure 2.
Variation curves of resilient modulus for test soils after F–T cycles of loading process [25].
The research shows that after the oil shale-modified soil sample underwent freeze–thaw cycles, both the dynamic strength and the MR decreased significantly. However, it was found that the MR of the modified soil did not gradually decrease with the increase in the number of freeze–thaw cycles, and the MR always showed a small rebound between freeze–thaw cycles 1–3, while the dynamic MR tended to be stable after freeze–thaw cycles 5–7. The freeze–thaw cycle causes the internal structure of the material to be destroyed and reorganized, and a new stable structure is formed after the reorganization. These experimental laws cannot be ignored. The concept of the freeze–thaw damage degree has often been introduced in previous studies on the strength characteristics of subgrade under freeze–thaw cycles, which can analyze the damage degree of the subgrade dynamic performance between each freeze–thaw cycle and the overall attenuation of the subgrade performance under large cycles.
However, the purpose of this paper was to build a prediction model to predict the dynamic elastic modulus after the freeze–thaw cycle rather than to analyze the change law and cause. Therefore, it was necessary to establish a coefficient, which can be expressed as a continuous functional form and can fit the special change trend of the MR of modified soils after freeze–thaw cycles. In addition to this, it can preferably be coupled to the model (7) in a simple form. After observation and several attempts, the coefficient was used in this study to represent the ratio of the MR after n freeze–thaw cycles to the MR without freeze–thaw cycles. The modified normal function is used to describe the variation law of the MR under freeze–thaw cycles. Its functional form is expressed as follows
where n represents the number of freeze–thaw cycles, and A, B, C, and D are regression parameters.
3. Model Validation
- (1)
- Data sources for method validation
This research group completed an orthogonal test of oil shale-modified soil under different water content and freeze–thaw cycles. This study used the test data to verify the accuracy and error distribution of the above empirical method. For the test, a cylindrical compacted sample with a diameter of 5 cm and a height of 10cm (dry density is 1.52 g/cm³) was used, with the same proportion and batch of the modified soil in Section ii. A half-sine pulse load was applied to the sample by the GDS dynamic triaxial tester, the load frequency was 1 Hz, and the loading duration and intermittent time of the load were 0.2 and 0.8 s, respectively. Before the formal test, the specimen was preloaded with a half-sine cyclic longitudinal load with a peak value of 66 kPa 1000 times, and a confining pressure of 30 kPa was applied. When the load was formally applied, the confining pressures of 30, 40, and 50 kPa, and the cyclic deviatoric stresses of 5, 15, and 25 kPa were used for each group of specimens as the target confining pressure and deviatoric stress amplitude of this MR. The number of cyclic loads under the condition was 100. After the test, the stress and the axial recoverable deformation of the sample during the test were recorded according to the last 5 waveform curves collected under each group of stress conditions. The MR was calculated according to the following formula:
where MR is the modulus of resilience, is the average axial stress amplitude (MPa) under each group of stress, and is the average strain amplitude (mm/mm) under each group of stress states.
- (2)
- Error distribution under different moisture contents
The MR at different moisture contents tested in the experiment are shown in Table 3.

Table 3.
Resilient modulus(kPa) of modified soil at different moisture contents.
In this section, the experimental data are substituted into the model (7) proposed in this study for fitting calculation, and the fitting effect and error distribution are observed. The error distribution is shown in Figure 3.
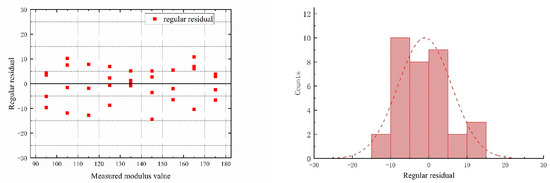
Figure 3.
Residual distribution diagram.
At the same time, two reference models are introduced to fit the experimental data for comparison. The first is model (1) without considering the suction contribution. The second includes the effective stress parameter proposed by Khalili [17] in model (1) in the same way as the model proposed in this study, which is referred to as the Khalili&K-θ model in the following. Khalili [17] defines as follows
where represents the air entry value.
In the fitting result, model (1) cannot fit the same set of modulus coefficients for convergence under different water contents, and the fitted coefficients for different water contents are different. The fitting statistics of model (7) and the Khalili&τ-θ model to the MR of the modified soil are compared in Table 4.

Table 4.
Statistical parameter.
As can be seen in Figure 3, the prediction residuals of model (7) are mainly distributed between −10 and 10, accounting for 85.2% of the sample size, and the residual distribution is close to the normal distribution. There is no obvious distribution relationship between the prediction error and the modulus. In Table 4, the fitting parameter R2 is greater than 0.95, which represents the proportion of the sum of squares of total errors that can be explained by the sum of squares of regression in linear regression analysis, indicating a good degree of fit.
In contrast, model (1) cannot fit a set of modulus coefficients for convergence under different moisture content, and the fitting coefficients of different water contents are different. Therefore, model (1) is not suitable for the prediction of moisture change conditions, which also confirms the importance of considering the matric suction contribution to the effective stress in the study of the resilient modulus of unsaturated soils. After the introduction of (10), the fitting coefficient R2 is still less than 0.5, which indicates that the fitting effect of model (10) on the resilient modulus data set of modified soil is not good and cannot be used for the MR prediction of modified soil. It also precisely illustrates the importance of constructing a specific resilient modulus prediction model for modified soil.
- (3)
- Error analysis under freeze–thaw cycles
As proposed in the above section, the test data after 1, 3, 5, and 7 times of freezing and thawing were used for fitting, as shown in Figure 4. The fitting parameters are shown in Table 5
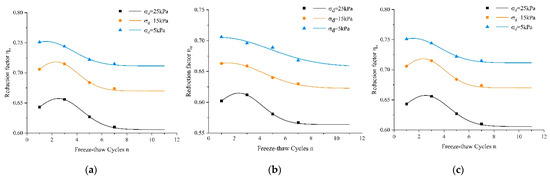
Figure 4.
Fitting curves of freeze–thaw reduction coefficients. (a) σ3 = 50 kPa; (b) σ3 = 40 kPa; (c) σ3 = 30 kPa.

Table 5.
Fitting parameters of freeze–thaw reduction coefficients.
It can be seen in Figure 4 that can well fit the decreasing law of the MR of oil shale- and fly ash-modified soil after freeze–thaw cycles. It was introduced into model (7) for fitting and prediction calculations, and the predicted values were compared with the experimental observations. In addition, the errors of the predicted values of modulus under 1, 3, 5, and 7 freeze–thaw cycles were counted and discussed in conjunction with statistical parameters and images. The distribution of prediction errors is shown in Figure 5, and the error analysis results are shown in Table 6.
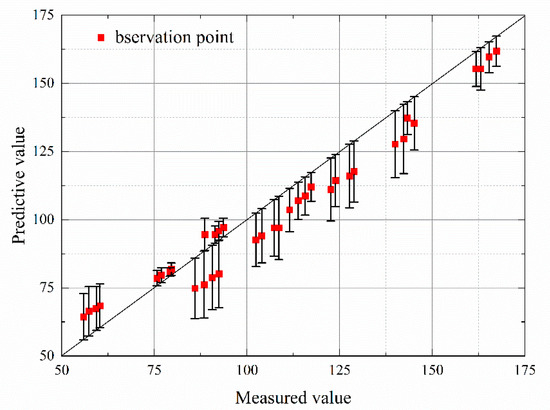
Figure 5.
Error distribution diagram.

Table 6.
Regression parameters of predicted and measured values.
As shown in the figure, the predicted value of the model has good regression performance with the measured value. In the observation interval, when the modulus is greater than 100, the prediction error is relatively small, and the predicted value is mostly smaller than the actual value. The statistics in Table 6 show that the prediction results of the model for the MR of 1, 3, 5, and 7 freeze–thaw cycles are close. Their maximum residuals are all around 10, and the maximum error of the predicted values within the survey range is 12.21. The RMSE of the model is between 6.54 and 7.15, with a slight increase in the number of freeze–thaw cycles. Under four cycles, the R2 distribution range is 0.95 to 0.96, indicating that the predicted value of the model fits well with the measured value and that the combination of (7) and (9) can reliably predict the dynamic elastic modulus after freeze–thaw cycles.
4. Conclusions
This paper proposes a semi-empirical prediction model to predict the long-term dynamic resilient modulus of oil shale residue-modified subgrade soil under unsaturated and seasonal permafrost complex conditions. To verify the prediction model, the dynamic load triaxial experiment, with different moisture contents, freeze–thaw cycles, and stress combinations, was conducted for the modified subgrade soil of oil shale waste residue. The following results can be drawn.
- (1)
- Based on the analysis of the soil–water characteristic relation curve of modified soil and the principle of effective stress, this paper constructed a suitable parameter for modified soil to express the contribution ratio of suction to soil element stress. Through observation and discussion of the relationship between the MR of oil shale residue-modified soil and the freeze–thaw cycles, the coefficient function describing the ratio of roadbed after a freeze–thaw cycle to the original state was established. These two were incorporated into the MR prediction model proposed by AASHTO [3] so that the new prediction model could comprehensively respond to the influence of stress, water content, and matric suction changes.
- (2)
- When the freeze–thaw cycle was 0, the fitting coefficient R2 of the model reached 0.971. Under the conditions of different moisture contents, 89.2% of the statistical samples had a prediction error ≤10, which shows that the model fitted the test data well and the prediction results were accurate, while the maximum R2 of the model used as a comparison for the experimental data of the modified soil was 0.404, so it cannot be used for the MR prediction of the modified soil. This shows the importance of constructing a specific modified soil resilient modulus prediction model.
- (3)
- It was proved by multiple freeze–thaw experiments that the coefficient can well fit the decreasing law of the MR of oil shale residue-modified soil after freeze–thaw cycles. After applying freeze–thaw cycles, the maximum prediction error of the prediction model increased to 12.21, the R2 distribution range of different freeze–thaw cycles was 0.95–0.96, and the RMSE of the model was between 6.54 and 7.15. This shows that the coefficient can well simulate the change in the MR with the increase in the freeze–thaw cycles. The introduction of the coefficient had high accuracy for the MR prediction after freeze–thaw cycles.
In summary, the prediction model proposed in this paper has good applicability to the MR prediction of unsaturated oil shale waste-modified soil in seasonally frozen areas. It can provide a reference for the prediction of the long-term resilience modulus of oil shale slag subgrade filling during a road life cycle.
Author Contributions
Conceptualization, L.H. and X.L.; methodology, L.H. and X.L.; software, L.H.; validation, X.L.; formal analysis, L.H.; resources, L.H.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, L.H. and X.L.; project administration, L.H.; funding acquisition, L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of the Jilin Province Transportation Department, grant number 2017ZDGC6.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their appreciation for the financial support of the Science and Technology Project of Jilin Province Transportation Department, grant number 2017ZDGC6. Our thanks go to the editors and reviewers for their efficient work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Monismith, C.; Seed, H.B.; Mitry, F.; Chan, C. Prediction of flexible pavement deflections from laboratory repeatedload tests. NCHRP Rep. 1967, 35, 117. [Google Scholar]
- Uzan, J. Characterization of granular material. Transp. Res. Rec. 1985, 1022, 52–59. [Google Scholar]
- AASHTO. Resilient Modulus as Function of Soil. Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2000. [Google Scholar]
- Khoury, N.; Brooks, R.; Khoury, C.; Yada, D. Modeling resilient modulus hysteretic behavior with moisture variation. Int. J. Geomech. 2012, 12, 519–527. [Google Scholar] [CrossRef]
- Khoury, N.; Brooks, R.; Boeni, S.Y.; Yada, D. Variation of resilient modulus, strength, and modulus of elasticity of stabilized soils with postcompaction moisture contents. J. Mater. Civ. Eng. 2012, 25, 160–166. [Google Scholar] [CrossRef]
- Leong, E.C.; Abuel-Naga, H. Contribution of osmotic suction to shear strength of unsaturated high plasticity silty soil. Geomech. Energy Environ. 2018, 15, 65–73. [Google Scholar] [CrossRef]
- Yang, S.R.; Huang, W.H.; Tai, Y.T. Variation of resilient modulus with soil suction for compacted subgrade soils. Transp. Res. Rec. 2005, 1913, 99–106. [Google Scholar] [CrossRef]
- Taibi, S.; Duperret, A.; Fleureau, J.M. The effect of suction on the hydro-mechanical behaviour of chalk rocks. Eng. Geol. 2009, 106, 40–50. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Abd, I.A.; Fattah, M.Y.; Mekkiyah, H. Relationship between the Matric Suction and the Shear Strength in Unsaturated Soil. Case Stud. Constr. Mater. 2020, 13, e00441. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Salim, N.M.; Irshayyid, E.J. Determination of the soil–water characteristic curve of unsaturated bentonite–sand mixtures. Environ. Earth Sci. 2017, 76, 1–12. [Google Scholar] [CrossRef]
- Al-Obaidi, A.H.; Fattah, M.Y.; Al-Dorry, M.K. Variation of suction during wetting of unsaturated collapsible gypseous soils. Int. J. Eng. Technol. 2018, 7, 79–85. [Google Scholar] [CrossRef]
- Chu, X. A review on the resilient response of unsaturated subgrade soils. Adv. Civ. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Zaman, M.; Khoury, N. Effect of Soil Suction and Moisture on Resilient Modulus of Subgrade Soils in Oklahoma; No. ORA 125-6662; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2007. [Google Scholar]
- Ng, K.; Henrichs, Z.R.; Ksaibati, K.; Wulff, S.S. Resilient modulus of subgrade materials for mechanistic-empirical pavement design guide. Road Mater. Pavement Des. 2018, 19, 1523–1545. [Google Scholar] [CrossRef]
- Yao, Y.; Zheng, J.; Zhang, J.; Peng, J.; Li, J. Model for predicting resilient modulus of unsaturated subgrade soils in south China. KSCE J. Civ. Eng. 2018, 22, 2089–2098. [Google Scholar] [CrossRef]
- Azam, A.M.; Cameron, D.A.; Rahman, M.M. Permanent strain of unsaturated unbound granular materials from construction and demolition waste. J. Mater. Civ. Eng. 2015, 27, 04014125. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Géotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Khalili, N.; Khabbaz, M.H. A unique relationship for χ for the determination of the shear strength of unsaturated soils. Geotechnique 1998, 48, 681–687. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Honghuan, C.U.I.; Xiaopeng, Q.I.N.; Wentao, W. Study on the strength and microscopic characteristics of unsaturated subgrade soil under freezing-thawing conditions. J. Glaciol. Geocryol. 2019, 41, 1115–1121. [Google Scholar]
- Liu, L.; Zhang, W.; Zhang, B.; Gu, Y.; Xie, B. Effect of freezing-thawing cycles on mechanical properties and microscopic mechanisms of loess. Hydrogeol. Eng. Geol. 2021, 48, 109–115. [Google Scholar]
- ASTM. Standard Test Method for Measurement of Soil Potential (Suction) Using Filter Paper; ASTM International: West Conshohocken, PA, USA, 2010; pp. 1–5. [Google Scholar]
- Wei, H.; Zhang, Y.; Wang, F.; Che, G.; Li, Q. Experimental research on resilient modulus of silty clay modified by oil shale ash and fly ash after freeze-thaw cycles. Appl. Sci. 2018, 8, 1298. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Determination of soil–water characteristic curve variables. Comput. Geotech. 2012, 42, 37–43. [Google Scholar] [CrossRef]
- Uzan, J. Characterization of clayey subgrade materials for mechanistic design of flexible pavements. Transp. Res. Rec. 1998, 1629, 189–196. [Google Scholar] [CrossRef]
- Thadkamalla, G.B.; George, K.P. Characterization of subgrade soils at simulated field moisture. Transp. Res. Rec. 1995, 1481. [Google Scholar]
- Wei, H.; Li, Q.; Han, L.; Han, S.; Wang, F.; Zhang, Y.; Chen, Z. Experimental research on deformation characteristics of using silty clay modified by oil shale ash and fly ash as the subgrade material after freeze-thaw cycles. Sustainability 2019, 11, 5141. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).