A Symmetry Evaluation Method, Using Elevation Angle, for Lower Limb Movement Patterns during Sitting-to-Standing †
Abstract
:1. Introduction
2. Methods
2.1. Participants
2.2. Experiment
- Each participant sat in a chair and maintained their posture to initiate the STS movement.
- When we judged that the participant’s sitting posture was stationary, we signaled the start of STS.
- On hearing the cue, the participant initiated the STS movement.
- When the participant stood up and we judged that the standing posture was stationary, we signaled the end of the STS movement.
- The video images from the cue for the start of the movement to the cue for the end of the movement were included in the analysis.
2.3. Analysis
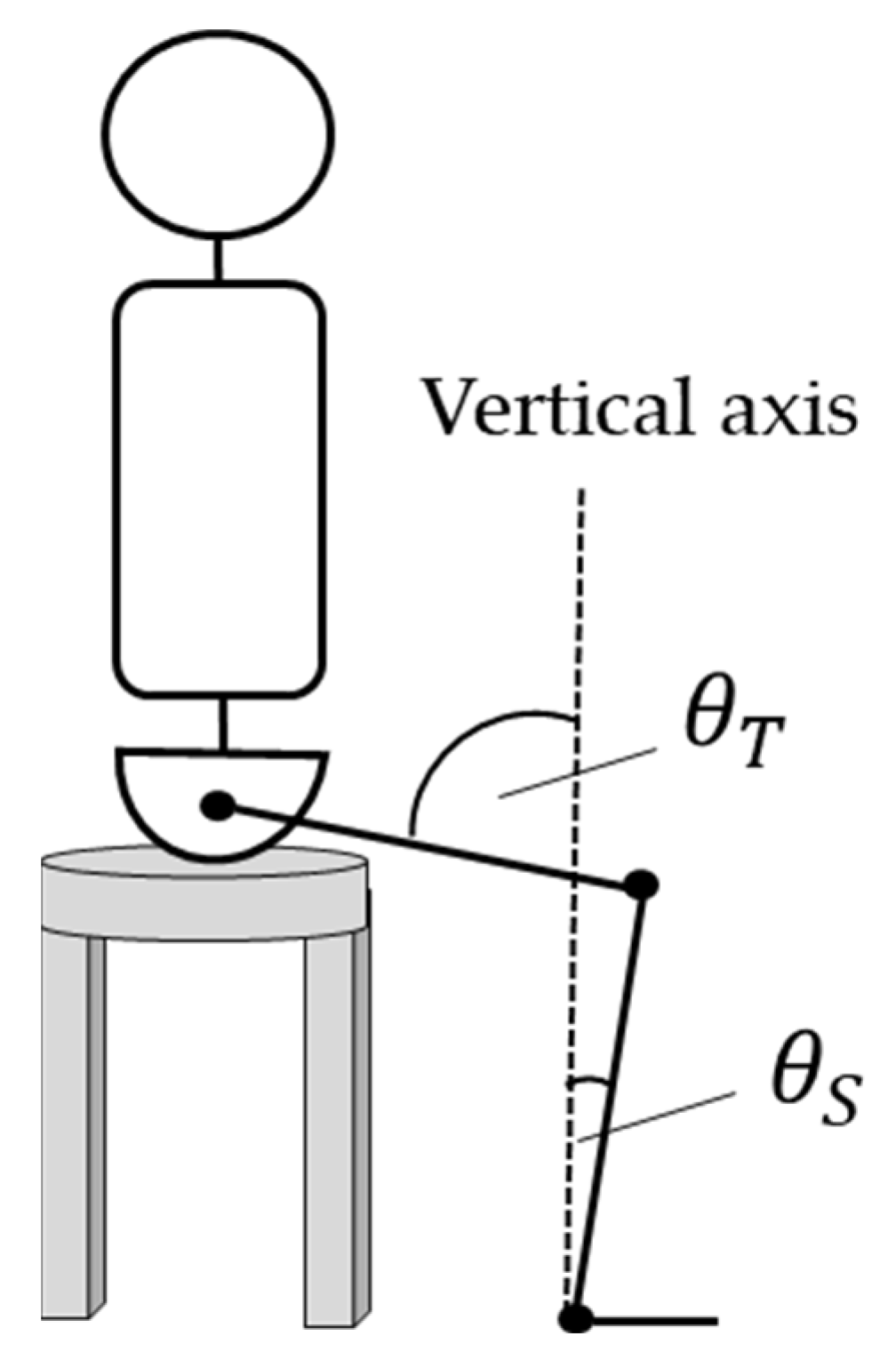
2.3.1. Definition of the EA error
2.3.2. Analysis of Measured EA changes
3. Results
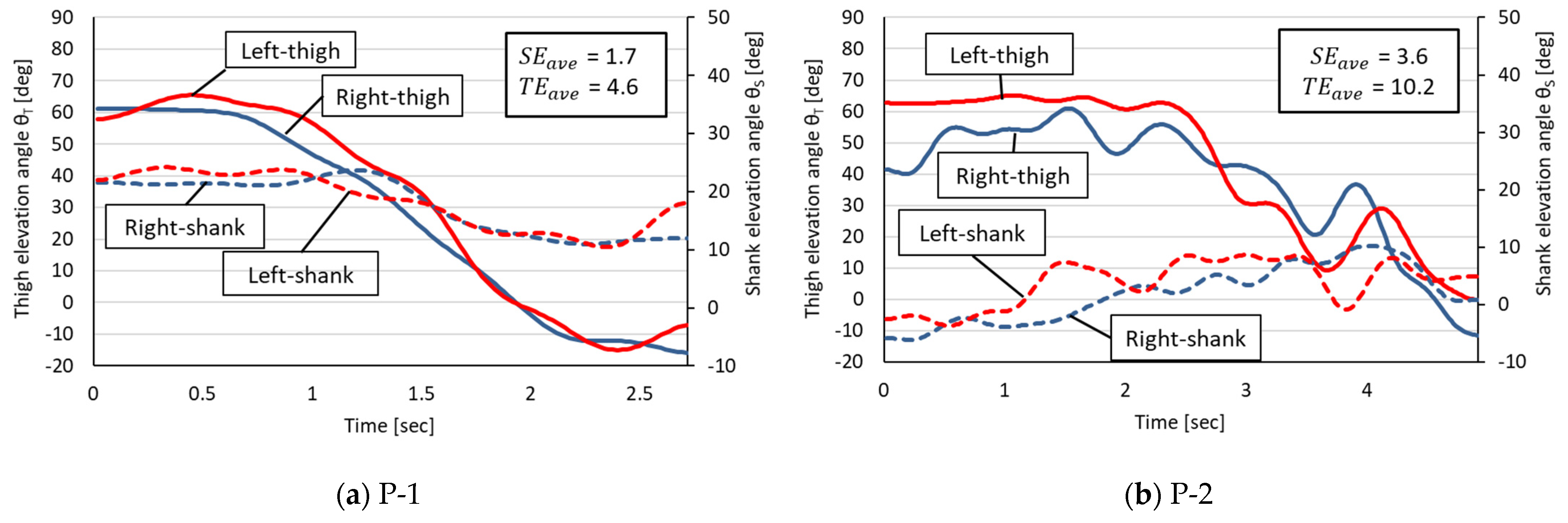
3.1. Symmetrical Comparison Using Measured EAs
- -
- Phase 1: The STS start angle;
- -
- Phase 2: A decrease in the thigh EA and an increase in the shank EA;
- -
- Phase 3: A decrease in the thigh EA and a decrease in the shank EA;
- -
- Phase 4: The STS end angle.
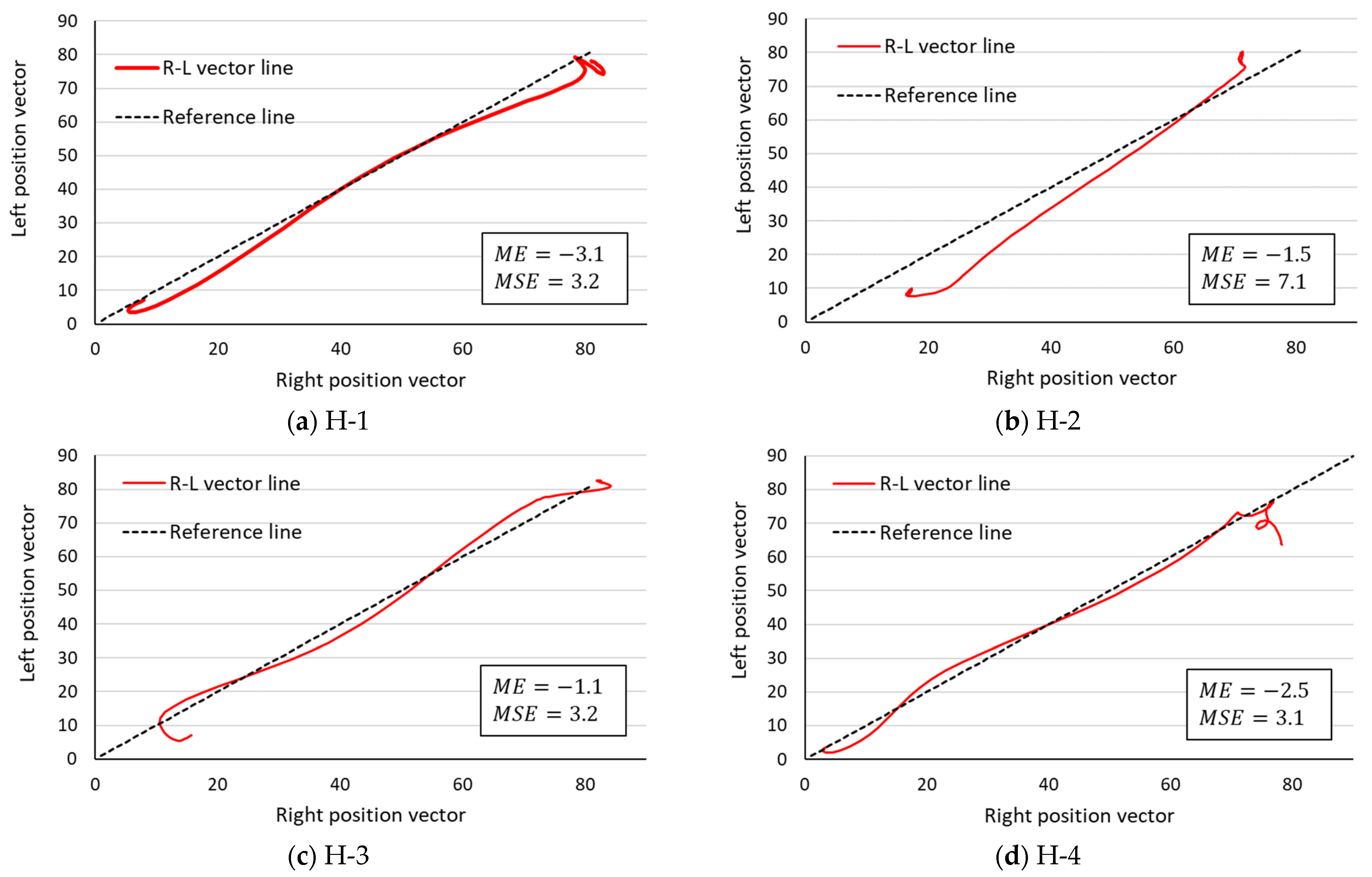
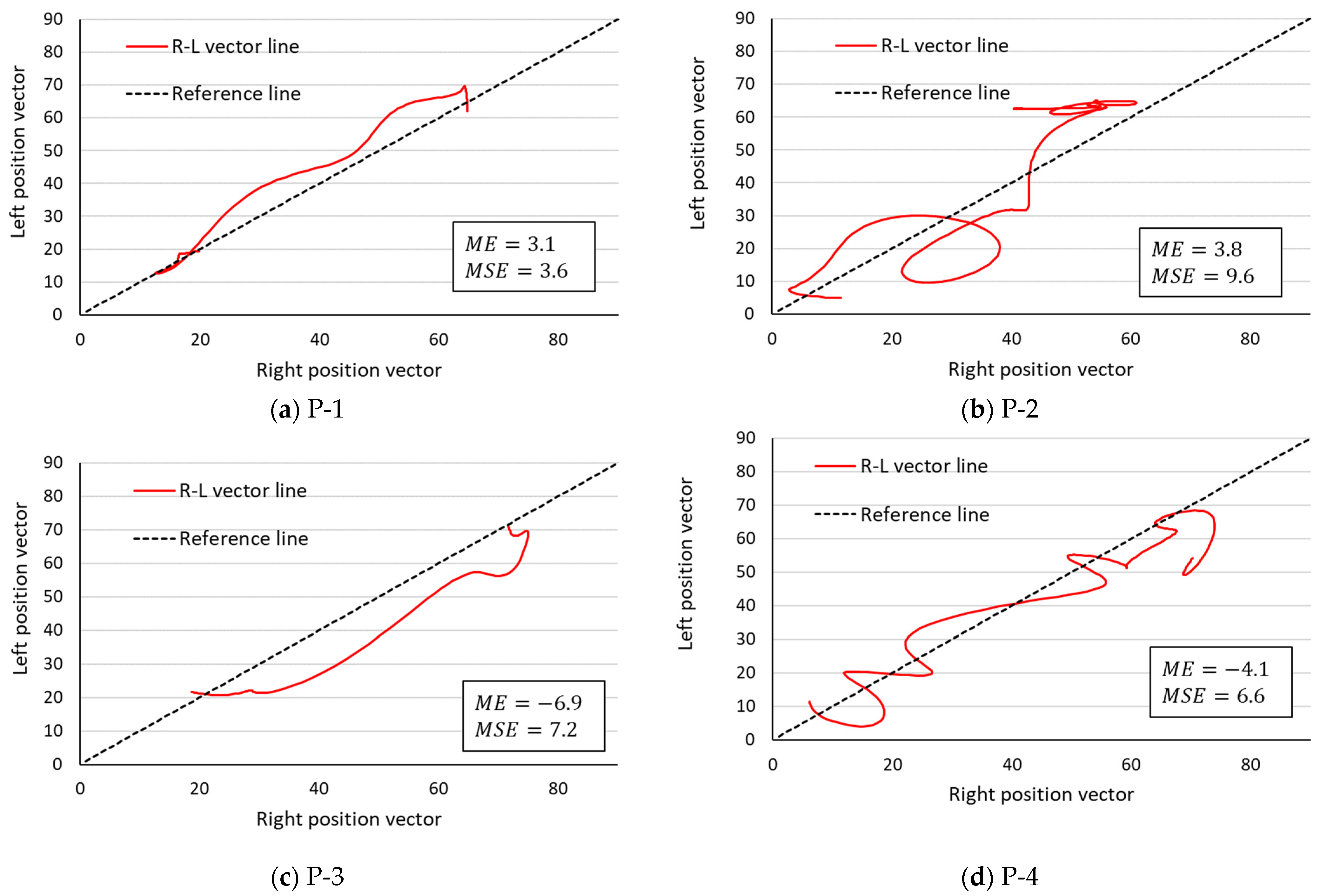
3.2. Comparison of R–L Symmetry by the R–L Vector Line
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Susan, S. The long-term impact of wheelchair delivery on the lives of people with disabilities in three countries of the world. Afr. J. Disabil. 2017, 6, a344. [Google Scholar] [CrossRef]
- Sui, F.H.; Avril, T.; Tricia, M.; Julie, M.; Andrew, K. Automated Movement Feedback for Recovering Independence in the Sit-to-Stand Movement in an Older Population: A Pilot Randomised. OBM Geriatr. 2019, 3, 1904089. [Google Scholar] [CrossRef]
- Janet, A.K.; Tiffany, N.H.; Josh, T.; Jeff, R.H. Weight-Bearing Asymmetry in Individuals PostHip Fracture During the Sit to Stand Task. Clin. Biomech. 2015, 30, 14–21. [Google Scholar]
- Bivalkar, A.; Varadharajulu, G. Establishment and Analysis of Ideal Lifting Technique Based on Kinesiological Principles for Outpatient Stroke Patients: An Experimental Study. Int. J. Curr. Res. Rev. 2020, 12, 14–18. [Google Scholar]
- Cheng, P.-T.; Liaw, M.-Y.; Wong, M.-K.; Tang, F.-T.; Lee, M.-Y.; Lin, P.-S. The sit-to-stand movement in stroke patients and its correlation with falling. Arch. Phys. Med. Rehabil. 1998, 79, 1043–1046. [Google Scholar] [CrossRef]
- Pai, Y.-C.; Rogers, M.W.; Hedman, L.D.; Hanke, T.A. Alterations in Weight-Transfer Capabilities in Adults With Hemiparesis. Phys. Ther. 1994, 74, 647–657. [Google Scholar] [CrossRef]
- Ryan, L.M.; Lynn, S.-M. Altered loading during walking and sit-to-stand is affected by quadriceps weakness after total knee arthroplasty. J. Orthop. Res. 2005, 23, 1083–1090. [Google Scholar] [CrossRef]
- Ryoichiro, S.; Hiroaki, K.; Yoshiyuki, S. Development of sit-to-stand and stand-to-sit training system for hemiplegie patients. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
- Wendy, G.; Jack, C.; Richard, S. Rising to stand from a chair: Symmetry, and frontal and transverse plane kinematics and kinetics. Gait Posture 2008, 27, 8–15. [Google Scholar]
- Helga, H.; Maria, T.; Elisabeth, O. Coordinated Ground Forces Exerted by Buttocks and Feet are Adequately Programmed for Weight Transfer During Sit-to-Stand. J. Neurophysiol. 1999, 82, 3021–3029. [Google Scholar]
- Michalina, B.; Ida, W.; Andrzej, W. A new method of determination of phases and symmetry in stand-to-sit-to-stand movement. Int. J. Occup. Med. Environ. Health 2014, 27, 660–671. [Google Scholar]
- Cabinet Office. White Paper on Aging Society. 2018. Available online: https://www8.cao.go.jp/kourei/whitepaper/w-2021/zenbun/03pdf_index.html (accessed on 5 September 2021).
- Yosra, C.; Maryam, H.; Michael, B.; Nicolas, T. Muscle coordination during robotic assisted walking using Lokomat. Comput. Methods Biomech. Biomed. Eng. 2020, 22, S216–S218. [Google Scholar]
- Ningjia, Y.; Qi, A.; Hiroki, K.; Hiroshi, Y.; Yusuke, T.; Kouji, T.; Kinomoto, M.; Yamasaki, H.; Itkonen, M.; Shibata-Alnajjar, M.; et al. Temporal Features of Muscle Synergies in Sit-to-Stand Motion Reflect the Motor Impairment of Post-Stroke Patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2118–2127. [Google Scholar]
- Lacquaniti, F.; Grasso, R.; Zago, M. Motor Patterns in Walking. Physiology 1999, 14, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Francesco, L.; Yury, I.; Mattia, Z. Kinematic control of walking. Arch. Ital. Biol. 2002, 140, 263–272. [Google Scholar]
- Gianluca, U.S.; Philippe, S.A.; Joyce, F. The Effects of a Virtual Environment and Robot-Generated Haptic Forces on the Coordination of the Lower Limb During Gait in Chronic Stroke Using Planar and 3D Phase Diagrams. In Proceedings of the International Conference on Virtual Rehabilitation (ICVR), Tel Aviv, Israel, 21–24 July 2019. [Google Scholar]
- Plug-in-Gait Maker Placement. Available online: http://www.idmil.org/mocap/Plug-in-Gait+Marker+Placement.pdf (accessed on 14 August 2022).
- Talos, V.L.; Grishin, A.A.; Solopova, I.A.; Oslanyan, T.L.; Blenky, V.E.; Ivanenko, Y.P. Asymmetric leg loading during sit-to-stand, walking and quiet standing in patients after unilateral total hip replacement surgery. Clin. Biomech. 2008, 23, 424–433. [Google Scholar] [CrossRef]
- Cyril, D.; Sylvia, N.; Julie, L. Lateral Trunk Displacement and Stability During Sit-to-Stand Transfer in Relation to Foot Placement in Patients With Hemiparesis. Neurorehabilit. Neural Repair 2008, 22, 715–722. [Google Scholar]
- Kogami, H.; An, Q.; Yang, N.; Wang, R.; Yoshida, K.; Hamada, H.; Yamakawa, H.; Tamura, Y.; Shimoda, S.; Yamasaki, H.; et al. Analysis of muscle synergy and kinematics in sit-to-stand motion of hemiplegic patients in subacute period. Adv. Robot. 2021, 35, 867–877. [Google Scholar] [CrossRef]
- Jinsook, R.; William, Z.R.; Eric, J.P.; Seng, B.Y.; Randall, F.B. Alterations in upper limb muscle synergy structure in chronic stroke survivors. J. Neurophysiol. 2013, 109, 768–781. [Google Scholar]
- van Criekinge, T.; Vermeulen, J.; Wagemans, K.; Schröder, J.; Embrechts, E.; Truijen, S.; Hallemans, A.; Saeys, W. Lower limb muscle synergies during walking after stroke: A systematic review. Disabil. Rehabil. 2020, 42, 2836–2845. [Google Scholar] [CrossRef]
- Damholt, V.; Termansen, N.B. Asymmetry of Plantar Flexion Strength in the Foot. Acta Orthop. Scand. 1977, 49, 215–219. [Google Scholar] [CrossRef] [Green Version]
- Yoshihiro, K.; Shin, M.; Shinichi, T. Comparision of Foot Gripping Strength and Quadriceps Femoris Muscle Strength of the Dominat Foot and Non-Dominant Foot. Phys. Ther. 2007, 22, 365–368. [Google Scholar]
- Tomote, Y.; Fuyuko, I.; Yoshihiro, I.; Tositaka, T.; Masahiko, Y.; Mitsuya, S. The dominant foot affects the postural control mechanism: Examination by body tracking test. Acta Oto-Laryngol. 2014, 134, 1146–1150. [Google Scholar]
- Jason, C.G.; Catherine, A.S. The effects of symmetric and asymmetric foot placements on sit-to-stand joint moments. Gait Posture 2012, 35, 78–82. [Google Scholar]
- Ningjia, Y.; Qi, A.; Hiroshi, Y.; Yusuke, T.; Atsushi, Y.; Hajime, A. Muscle synergy structure using different strategies in human standing-up motion. Adv. Robot. 2017, 31, 40–54. [Google Scholar]
- Qi, A.; Hiroshi, Y.; Atsushi, Y.; Hajime, A. Different Temporal Structure of Muscle Synergy Between Sit-to-Walk and Sit-to-Stand Motions in Human Standing Leg. In Converging Clinical and Engineering Research on Neurorehabilitation II; Springer: Cham, Switzerland, 2016; pp. 933–937. [Google Scholar]
- Takahiro, U.; Kouji, T.; Takuya, Z.; Eiji, S.; Kazuhiko, H. Kinetic and Electromyographic Analysesof Sit-to-StandMotion in Patients with Proximal Femoral Fracture: Comparison of Patients with Pain and without Pain. Phys. Ther. 2015, 42, 228–236. [Google Scholar]
- Chun, K.T.; Hideki, K.; Hiroki, W.; Aiki, M.; Masashi, Y.; Yoshiyuki, S.; Kenji, S. Lateral Symmetry of Synergies in Lower Limb Muscles of Acute Post-stroke Patients After Robotic Intervention. Front. Neurosci. 2018, 12, 276. [Google Scholar] [CrossRef]
- Katherine, M.S.; Matthew, C.T.; Eric, J.P. The number and choice of muscles impact the results of muscle synergy analyses. Front. Comput. Neurosci. 2013, 7, 105. [Google Scholar] [CrossRef] [Green Version]
- Silvia, M.; Deborah, F.; Dario, F. Reorganization of muscle synergies during multidirectional reaching in the horizontal plane with experimental muscle pain. Neurophysiology 2014, 111, 1615–1630. [Google Scholar]
- Michael, R.P.; Peter, M.T.; Victoria, G. Women with fibromyalgia walk with an altered muscle synergy. Gait Posture 2005, 22, 210–218. [Google Scholar]
- Takamitsu, H. Sample size determination given data of preliminary experiment for Student’s t-test, ANOVA and Tukey’s multiple comparison. Jpn. J. Psychol. 2004, 75, 213–219. (In Japanese) [Google Scholar]
- Anabèle, B.; Séléna, L.; Denis, G.; Sylvie, N. Perception of Weight-Bearing Distribution During Sit-to-Stand Tasks in Hemiparetic and Healthy Individuals. Stroke 2010, 41, 1704–1708. [Google Scholar]




| Group | Code | Gender | Age | Height | Weight | BMI | Muscle Mass | Body Fat |
|---|---|---|---|---|---|---|---|---|
| (cm) | (kg) | (kg) | (%) | |||||
| Health (N 1 = 4) | H-1 | Male | 22 | 169.0 | 54.0 | 18.9 | 42.3 | 17.3 |
| H-2 | Male | 22 | 176.0 | 81.8 | 26.4 | 59.7 | 23.1 | |
| H-3 | Male | 22 | 172.0 | 68.4 | 23.1 | 49.8 | 23.3 | |
| H-4 | Male | 22 | 177.0 | 67.6 | 21.6 | 49.2 | 23.2 | |
| Mean ± SD 2 | 22.3±0.5 | 173.5±3.7 | 67.9±11.4 | 22.5±3.1 | 50.2±7.2 | 21.7±3.0 | ||
| Patient (N = 4) | P-1 | Male | 86 | 139.0 | 48.8 | 25.2 | 27.7 | 40.3 |
| P-2 | Female | 78 | 165.5 | 40.3 | 14.7 | 35.6 | 6.5 | |
| P-3 | Female | 81 | 156.0 | 56.0 | 23.0 | 33.9 | 36.0 | |
| P-4 | Female | 86 | 134.5 | 33.0 | 18.2 | 23.1 | 27.2 | |
| Mean ± SD | 82.8 ± 3.1 | 148.8 ± 11.2 | 44.5 ± 7.8 | 20.3 ± 3.7 | 30.1 ± 4.5 | 27.5 ± 11.6 | ||
| Group | Code | Sample | SEave | TEave | Esum |
|---|---|---|---|---|---|
| (n 2) | (deg/n) | (deg/n) | (deg/n) | ||
| Health (N 1=4) | H-1 | 81 | 2.1 | 3.1 | 5.2 |
| H-2 | 101 | 3.2 | 8.7 | 11.9 | |
| H-3 | 81 | 1.7 | 4.6 | 6.3 | |
| H-4 | 101 | 4.1 | 3.3 | 7.4 | |
| Mean ± SD | 91.0 ± 11.5 | 2.8 ± 1.1 | 4.9 ± 2.6 | 7.7 ± 3.0 | |
| Patient (N = 4) | P-1 | 136 | 1.7 | 4.6 | 6.4 |
| P-2 | 246 | 3.6 | 10.2 | 13.9 | |
| P-3 | 111 | 7.5 | 5.5 | 13.0 | |
| P-4 | 195 | 12.6 | 8.5 | 21.2 | |
| Mean ± SD 3 | 172.0 ± 60.6 | 6.4 ± 4.8 | 7.2 ± 2.6 | 13.6 ± 6.1 | |
| Sample | ME | MSE | ||
|---|---|---|---|---|
| Health (N = 4) | H-1 | 81 | −3.1 | 3.2 |
| H-2 | 101 | −1.5 | 7.1 | |
| H-3 | 81 | −1.1 | 3.2 | |
| H-4 | 101 | −2.5 | 3.1 | |
| Mean ± SD | 91.0 ± 11.5 | −2.0 ± 0.9 | 4.2 ± 2.0 | |
| Patient (N = 4) | P-1 | 136 | 3.1 | 3.6 |
| P-2 | 246 | 3.8 | 9.6 | |
| P-3 | 111 | −6.9 | 7.2 | |
| P-4 | 195 | −4.1 | 6.6 | |
| Mean ± SD | 172.0 ± 60.6 | −1.0 ± 5.3 | 6.8 ± 2.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K.; Saga, N. A Symmetry Evaluation Method, Using Elevation Angle, for Lower Limb Movement Patterns during Sitting-to-Standing. Appl. Sci. 2022, 12, 9454. https://doi.org/10.3390/app12199454
Nakamura K, Saga N. A Symmetry Evaluation Method, Using Elevation Angle, for Lower Limb Movement Patterns during Sitting-to-Standing. Applied Sciences. 2022; 12(19):9454. https://doi.org/10.3390/app12199454
Chicago/Turabian StyleNakamura, Kensuke, and Norihiko Saga. 2022. "A Symmetry Evaluation Method, Using Elevation Angle, for Lower Limb Movement Patterns during Sitting-to-Standing" Applied Sciences 12, no. 19: 9454. https://doi.org/10.3390/app12199454
APA StyleNakamura, K., & Saga, N. (2022). A Symmetry Evaluation Method, Using Elevation Angle, for Lower Limb Movement Patterns during Sitting-to-Standing. Applied Sciences, 12(19), 9454. https://doi.org/10.3390/app12199454







