Elastic Analysis of Three-Layer Concrete Slab Based on Numerical Homogenization with an Analytical Shear Correction Factor
Abstract
:1. Introduction
2. Materials and Methods
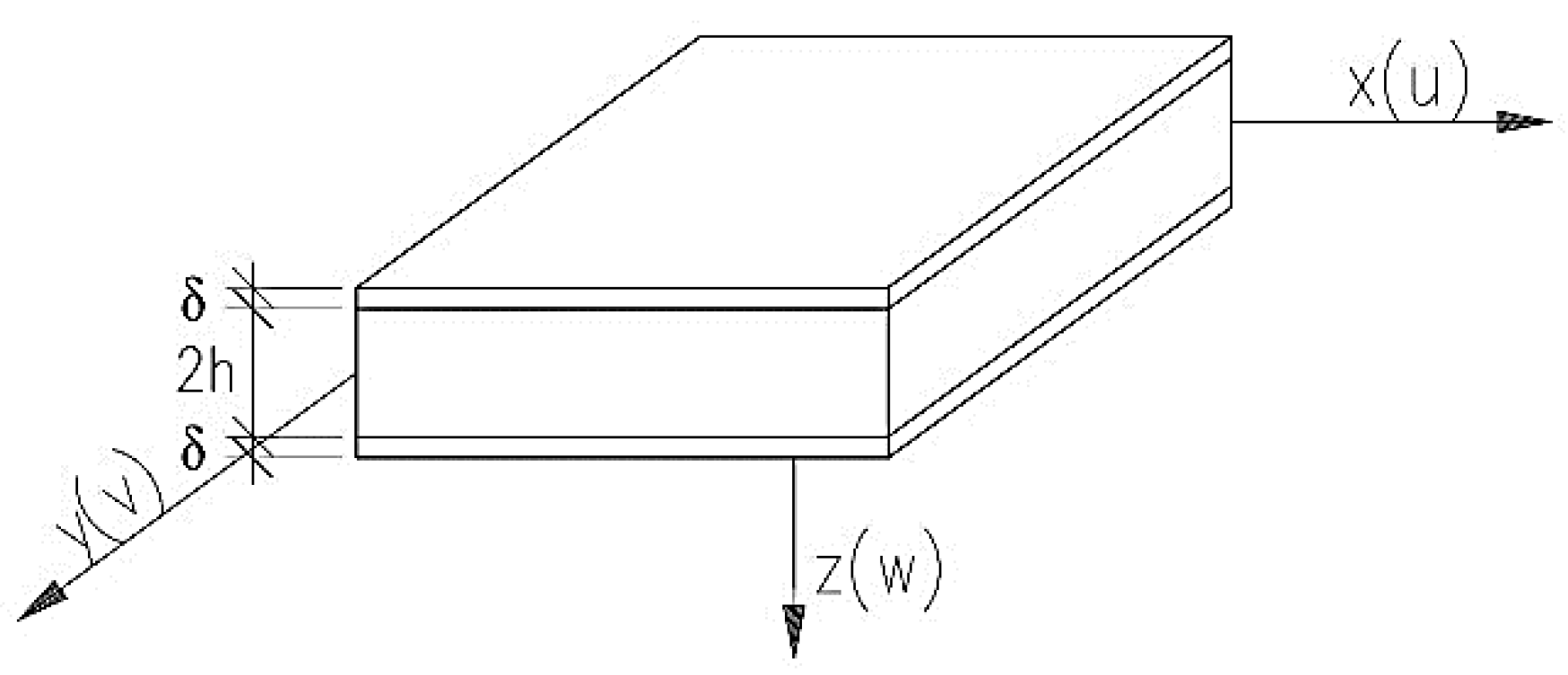
2.1. Basic Assumptions
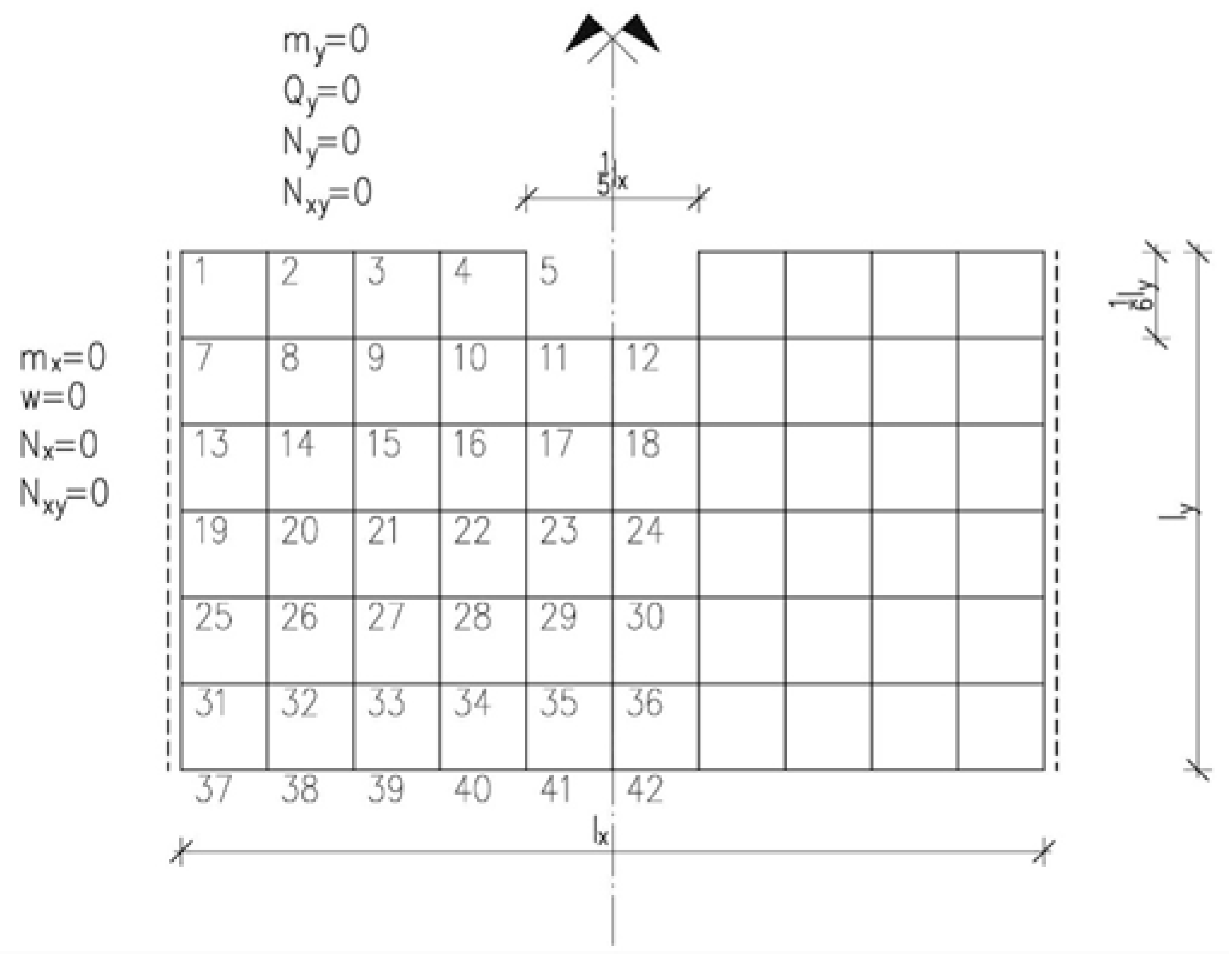
2.2. Finite Difference in Variational Form
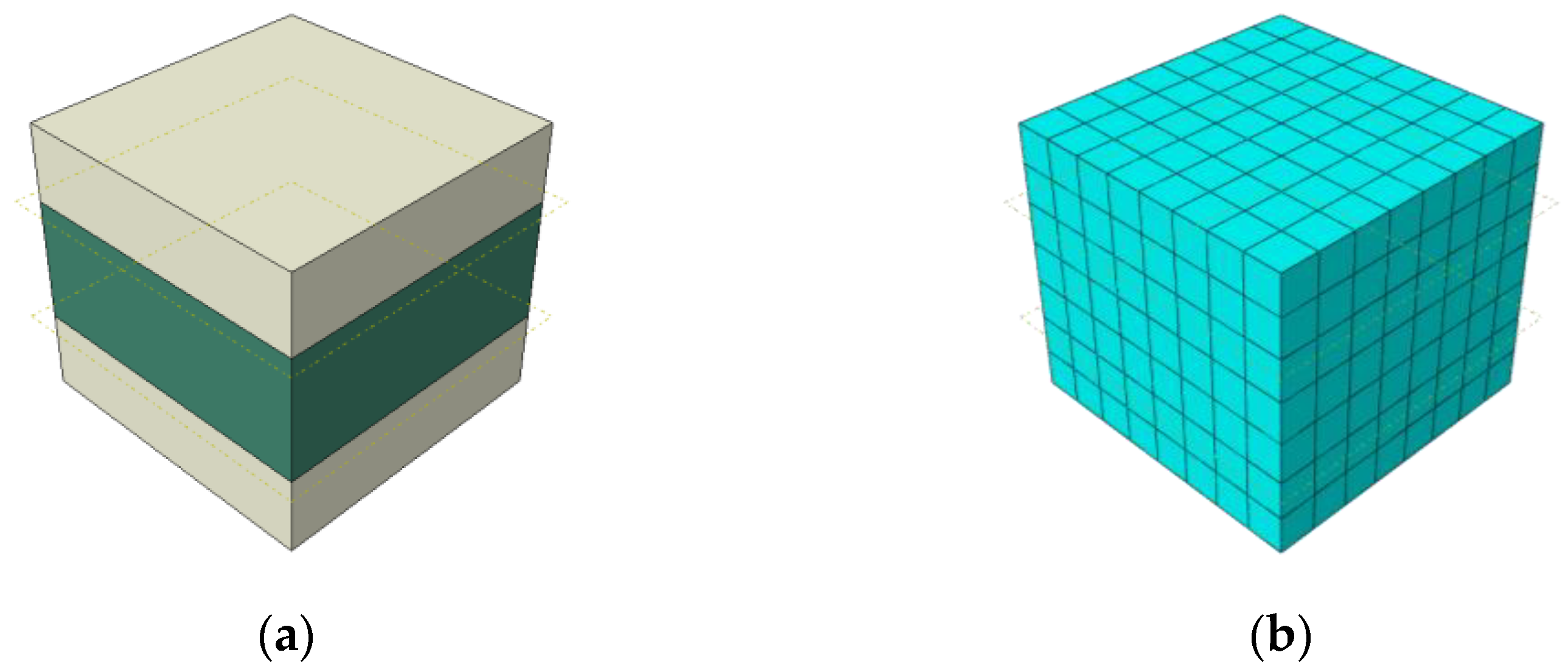
2.3. Numerical Homogenization
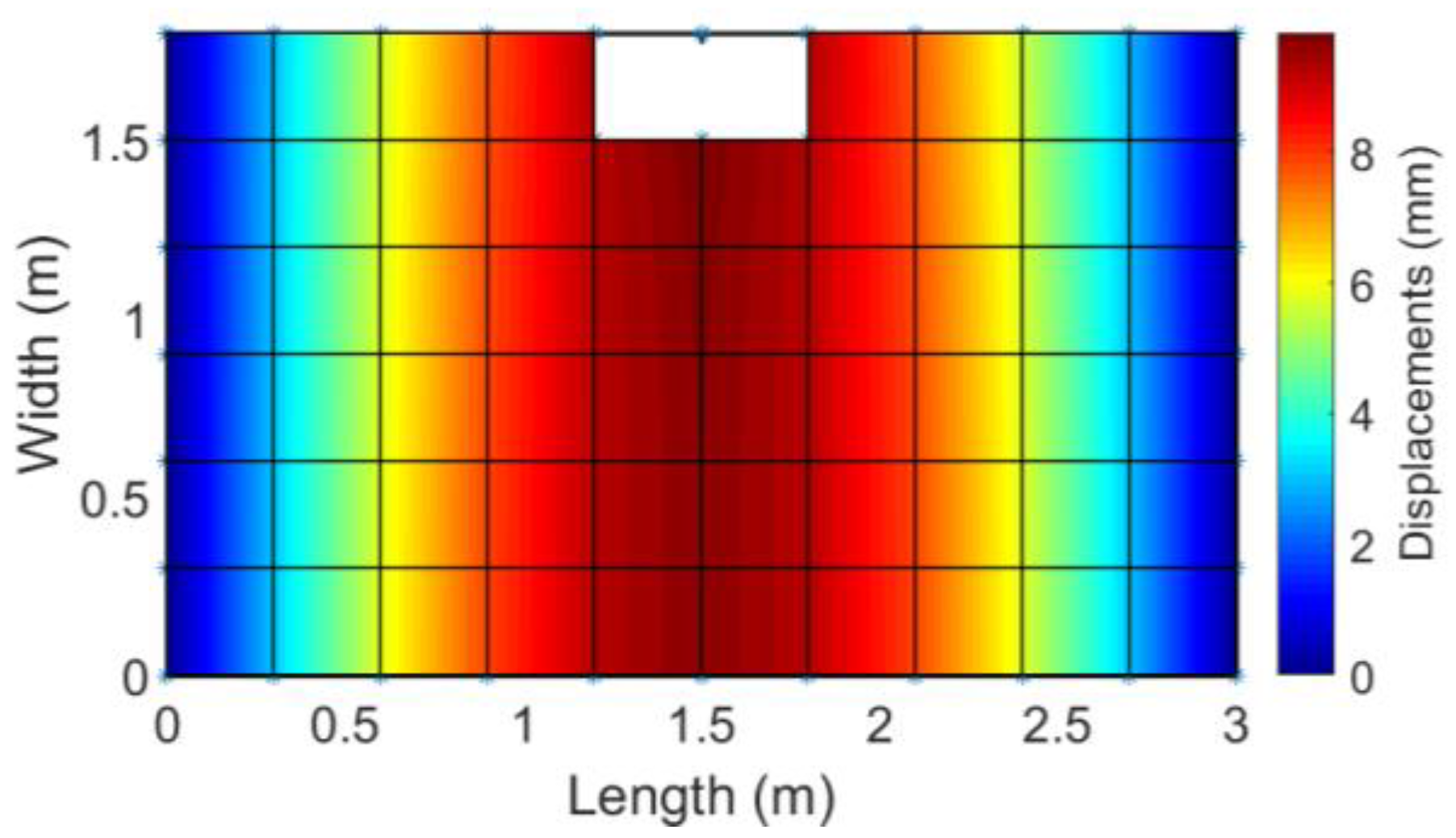
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buczkowski, W. Numerical analysis of sandwich panels (in polish). Arch. Civ. Eng. 1981, 27, 51–61. [Google Scholar]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B: Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Hause, T.J. Sandwich Structures: Theory and Responses; Springer: Cham, Switzerland, 2021; pp. 1–3. [Google Scholar]
- Altenbach, H.; Altenbach, J.; Kissing, W. Mechanics of Composite Structural Elements, 2nd ed.; Springer Nature: Singapore, 2018; p. 503. [Google Scholar]
- Zhang, J.; Yan, Z.; Xia, L. Vibration and Flutter of a Honeycomb Sandwich Plate with Zero Poisson’s Ratio. Mathematics 2021, 9, 2528. [Google Scholar] [CrossRef]
- Lu, C.; Zhao, M.; Jie, L.; Wang, J.; Gao, Y.; Cui, X.; Chen, P. Stress Distribution on Composite Honeycomb Sandwich Structure Suffered from Bending Load. Procedia Eng. 2015, 99, 405–412. [Google Scholar] [CrossRef] [Green Version]
- Szekrényes, A. Analytical solution of some delamination scenarios in thick structural sandwich plates. J. Sandw. Struct. Mater. 2017, 21, 1271–1315. [Google Scholar] [CrossRef] [Green Version]
- Burlayenko, V.N.; Sadowski, T.; Dimitrova, S. Three-Dimensional Free Vibration Analysis of Thermally Loaded FGM Sandwich Plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef] [Green Version]
- Garg, A.; Belarbi, M.-O.; Chalak, H.; Chakrabarti, A. A review of the analysis of sandwich FGM structures. Compos. Struct. 2020, 258, 113427. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Daniel, I.M. Composite Materials, Chapter 19 in Handbook on Experimental Mechanics; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Katouzian, M.; Vlase, S.; Calin, M.R. Experimental procedures to determine the viscoelastic parameters of laminated composites. J. Optoelectron. Adv. Mater. 2011, 13, 1185–1188. [Google Scholar]
- Motoc, D.L.; Vlase, S. Micromechanical based simulation and experimental approaches in the thermal conductivities assessment of hybrid polymeric composite materials. In Proceedings of the ASME 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; pp. 21–26. [Google Scholar]
- Suemasu, H. Effects of Multiple Delaminations on Compressive Buckling Behaviors of Composite Panels. J. Compos. Mater. 1993, 27, 1172–1192. [Google Scholar] [CrossRef]
- Li, D.; Zhu, H.; Gong, X. Buckling Analysis of Functionally Graded Sandwich Plates under Both Mechanical and Thermal Loads. Materials 2021, 14, 7194. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, B.; Dash, P.; Singh, B. Buckling analysis of porous FGM sandwich plates under various types nonuniform edge compression based on higher order shear deformation theory. Compos. Struct. 2020, 251, 112597. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Arabi, E.; Masoodi, A.R. Nonlinear analysis of FG-sandwich plates and shells. Aerosp. Sci. Technol. 2019, 87, 178–189. [Google Scholar] [CrossRef]
- Szymczak-Graczyk, A. Rectangular Plates of a Trapezoidal Cross-Section Subjected to Thermal Load. IOP Conf. Ser. Mater. Sci. Eng. 2019, 603, 032095. [Google Scholar] [CrossRef]
- Jalali, S.; Naei, M.; Poorsolhjouy, A. Thermal stability analysis of circular functionally graded sandwich plates of variable thickness using pseudo-spectral method. Mater. Des. 2010, 31, 4755–4763. [Google Scholar] [CrossRef]
- Kiani, Y.; Bagherizadeh, E.; Eslami, M.R. Thermal and mechanical buckling of sandwich plates with FGM face sheets resting on the Pasternak elastic foundation. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2011, 226, 32–41. [Google Scholar] [CrossRef]
- Van Do, V.N.; Lee, C.-H. Thermal buckling analyses of FGM sandwich plates using the improved radial point interpolation mesh-free method. Compos. Struct. 2017, 177, 171–186. [Google Scholar] [CrossRef]
- Swaminathan, K.; Sangeetha, D. Thermal analysis of FGM plates—A critical review of various modeling techniques and solution methods. Compos. Struct. 2017, 160, 43–60. [Google Scholar] [CrossRef]
- Burlayenko, V.N. Modelling Thermal Shock in Functionally Graded Plates with Finite Element Method. Adv. Mater. Sci. Eng. 2016, 2016, 7514638. [Google Scholar] [CrossRef] [Green Version]
- Do, T.; Bui, T.; Yu, T.; Pham, D.; Nguyen, C. Role of material combination and new results of mechanical behavior for FG sandwich plates in thermal environment. J. Comput. Sci. 2017, 21, 164–181. [Google Scholar] [CrossRef]
- Itu, C.; Öchsner, A.; Vlase, S.; Marin, M.I. Improved rigidity of composite circular plates through radial ribs. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 233, 1585–1593. [Google Scholar] [CrossRef]
- Pendleton, R.L.; Tutle, M.E. Manual of Experimental Methods for Mechanical Testing of Composites; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Itu, C.; Vlase, S.; Scutaru, M.L.; Modrea, A. Bending behavior of a high rigidity plate made by a composite panel. Procedia Manuf. 2019, 32, 144–150. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Itu, C.; Marin, M.; Grif, H. Bending Tests Used to Determine the Mechanical Properties of the Components of a Composite Sandwich Used in Civil Engineering. Procedia Manuf. 2019, 32, 259–267. [Google Scholar] [CrossRef]
- Hoff, N.J. Bending and Buckling of Rectangular Sandwich Plates; NACA: Washington, DC, USA, 1950. [Google Scholar]
- Wachowiak, J.; Wilde, P. Wolnopodparte prostokątne płyty trójwarstwowe. Arch. Inżynierii Lądowej 1966, 22, 71–90. [Google Scholar]
- Mikołajczak, H. Zagadnienia Nieciągłych Warunków Brzegowych dla Prostokątnych Płyt Trójwymiarowych; Roczniki WSR: Poznań, Poland, 1965. [Google Scholar]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Grillo, A. Effective properties of hierarchical fiber-reinforced composites via a three-scale asymptotic homogenization approach. Math. Mech. Solids 2019, 24, 3554–3574. [Google Scholar] [CrossRef]
- Garbowski, T.; Marek, A. Homogenization of corrugated boards through inverse analysis. In Proceedings of the 1st International Conference on Engineering and Applied Sciences Optimization, Kos Island, Greece, 4–6 June 2014; pp. 1751–1766. [Google Scholar]
- Hohe, J. A direct homogenisation approach for determination of the stiffness matrix for microheterogeneous plates with application to sandwich panels. Compos. Part B Eng. 2003, 34, 615–626. [Google Scholar] [CrossRef]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Comp. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T. Determination of Transverse Shear Stiffness of Sandwich Panels with a Corrugated Core by Numerical Homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Knitter-Piątkowska, A.; Mrówczyński, D. Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation. Materials 2021, 14, 3786. [Google Scholar] [CrossRef] [PubMed]
- Staszak, N.; Gajewski, T.; Garbowski, T. Shell-to-Beam Numerical Homogenization of 3D Thin-Walled Perforated Beams. Materials 2022, 15, 1827. [Google Scholar] [CrossRef]
- Kączkowski, Z. Plates. Static Calculations; Arkady: Warsaw, Poland, 2000. [Google Scholar]
- Gołaś, J. Pewne rozwiązania dla kołowych płyt trójwarstwowych obciążonych na krawędzi. Rozpr. Inżynierskie 1971, 19, 275–286. [Google Scholar]
- Donnell, L.H. Beams, Plates and Shells; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Naghdi, P.M. The Theory of Shells and Plates; Handbuch der Physick: Berlin, Germany, 1972. [Google Scholar]
- Panc, V. Theories of Elastic Plates; Academia: Prague, Czech Republic, 1975. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Coatings; Arkady: Warsaw, Poland, 1962. [Google Scholar]
- Szlilard, R. Theory and Analysis of Plates. Classical and Numerical Methods; Prentice Hall, Englewood Cliffs: Bergen, NJ, USA; Prentice-Hall: Upper Saddle River, NJ, USA, 1974. [Google Scholar]
- Ugural, A.C. Stresses in Plates and Shells; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Wilde, P. Variational approach of finite differences in the theory of plate. In Proceedings of the Materials of XII Scientific Conference of the Committee of Science PZiTB and the Committee of Civil Engineering of Polish Academy of Sciences, Krynica, Poland, 12–17 September 1966. [Google Scholar]
- Tribiłło, R. Application of the generalized finite difference method for plate calculations. Arch. Inżynierii Lądowej 1975, 2, 579–586. [Google Scholar]
- Son, M.; Jung, H.S.; Yoon, H.H.; Sung, D.; Kim, J.S. Numerical Study on Scale Effect of Repetitive Plate-Loading Test. Appl. Sci. 2019, 9, 4442. [Google Scholar] [CrossRef] [Green Version]
- Nowacki, W. From the application of the calculus of finite differences in structure mechanics. Arch. Mech. Stos. 1951, 3, 419–435. (In Polish) [Google Scholar]
- Rapp, B.E. Finite Difference Method, Chapter 30 in Microfluidics: Modelling, Mechanics and Mathematics, Micro and Nano Technologies; Rapp, B.E., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 623–631. [Google Scholar] [CrossRef]
- Blazek, J. Principles of Solution of the Governing Equations, Chapter 3 in Computational Fluid Dynamics: Principles and Applications; Blazek, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 29–72. [Google Scholar] [CrossRef]
- Sadd, M.H. Formulation and Solution Strategies, Chapter 5 in Elasticity, Theory, Applications, and Numerics; Sadd, M.H., Ed.; Academic Press; Elsevier: Cambridge, MA, USA, 2005; pp. 83–102. [Google Scholar] [CrossRef]
- Szymczak-Graczyk, A. Numerical Analysis of the Impact of Thermal Spray Insulation Solutions on Floor Loading. Appl. Sci. 2020, 10, 1016. [Google Scholar] [CrossRef] [Green Version]
- Numayr, K.S.; Haddad, R.H.; Haddad, M.A. Free vibration of composite plates using the finite difference method. Thin-Walled Struct. 2004, 42, 399–414. [Google Scholar] [CrossRef]
- Buczkowski, W.; Szymczak-Graczyk, A.; Walczak, Z. Experimental validation of numerical static calculations for a monolithic rectangular tank with walls of trapezoidal cross-section. Bull. Pol. Acad. Sci. Technol. Sci. 2017, 65, 799–804. [Google Scholar] [CrossRef] [Green Version]
- Szymczak-Graczyk, A. Floating platforms made of monolithic closed rectangular tanks. Bull. Pol. Acad. Sci. Technol. Sci. 2018, 66, 209–216. [Google Scholar] [CrossRef]
- Szymczak-Graczyk, A. Numerical Analysis of the Bottom Thickness of Closed Rectangular Tanks Used as Pontoons. Appl. Sci. 2020, 10, 8082. [Google Scholar] [CrossRef]
- Szymczak-Graczyk, A. The Effect of Subgrade Coefficient on Static Work of a Pontoon Made as a Monolithic Closed Tank. Appl. Sci. 2021, 11, 4259. [Google Scholar] [CrossRef]
- Buczkowski, W. Numerical Calculation of Three-Layer Panels Used in Agricultural Construction. Ph.D. Thesis, Institute of Water and Melioration Construction. Agricultural University in Poznań, Poznań, Poland, 1977. (In Polish). [Google Scholar]
- Mikołajczak, H.; Buczkowski, W.; Łęcki, W.; Wosiewicz, B. Three-layer ceiling slabs for livestock buildings. Ann. Agric. Univ. 1975, 77, 43–52. (In Polish) [Google Scholar]
- Mikołajczak, H. Asymptotic solution for a three-layer plate strand (in polish). Sci. Pap. Gdańsk Univ. Technol. 1977, 31, 169–175. [Google Scholar]
- Romanow, F.; Stricker, L.; Teisseyre, J. Stability of Sandwich Structures (In Poilsh); Publishing House of the Wrocław University of Technology: Wrocław, Poland, 1972. [Google Scholar]
- Catania, G.; Strozzi, M. Damping Oriented Design of Thin-Walled Mechanical Components by Means of Multi-Layer Coating Technology. Coatings 2018, 8, 73. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Ma, Y.; Zhou, C.; Xu, H. Damping efficiency of the coating structure. Int. J. Solids Struct. 2005, 42, 3045–3058. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, R.; Li, X.; Guo, Z.X. Damping behaviors of metal matrix composites with interface layer. Sci. China Ser. E-Technol. Sci. 2001, 44, 640–646. [Google Scholar] [CrossRef]

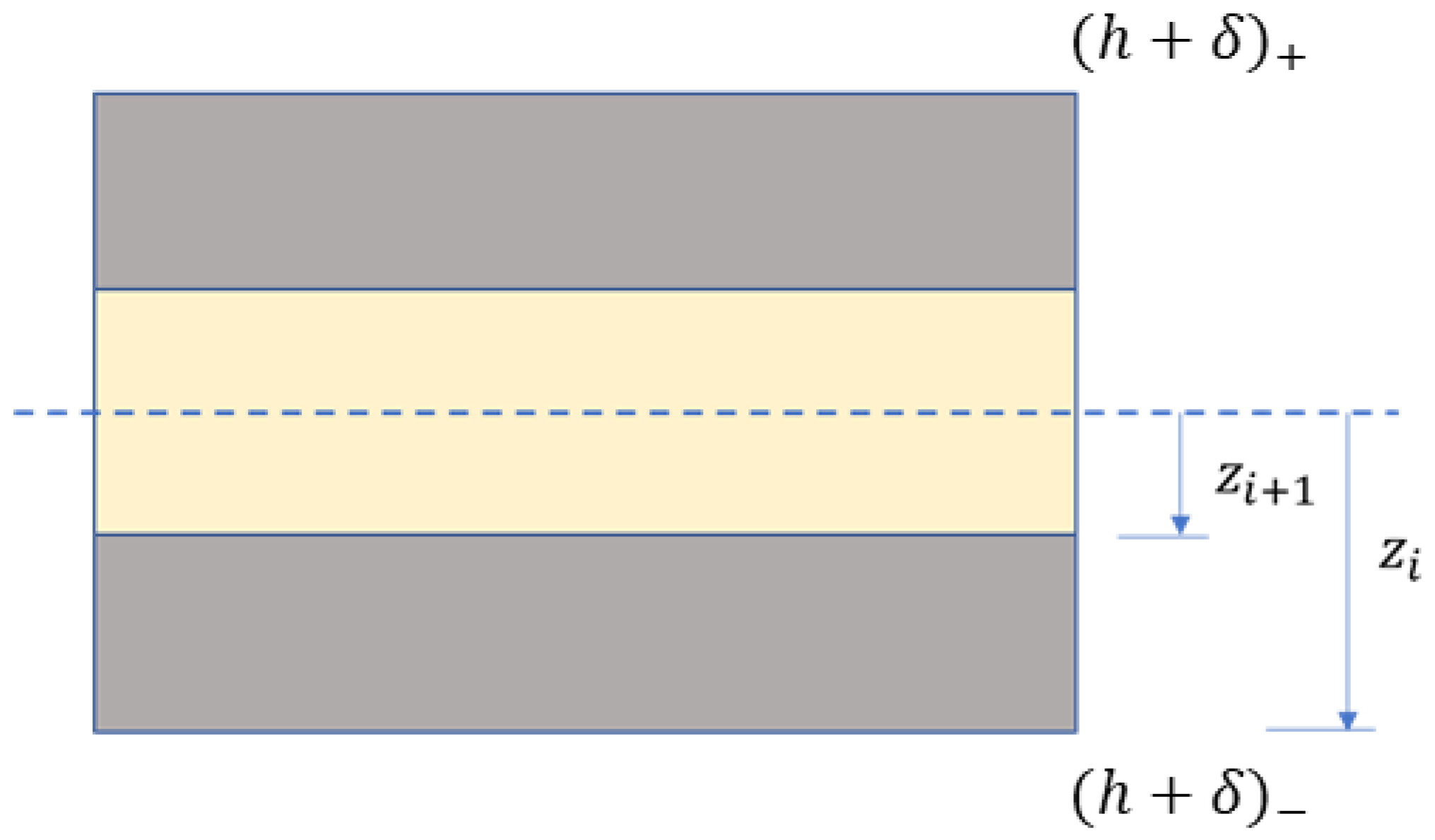
( | ( | ( | ||
|---|---|---|---|---|
| 300 | 180 | 5 | 8 | 10 |
| External layers | 0.2 | ||
| Middle core | 6 | 3 | 0 |
| Stiffness | Homogenization Method | CLPT Method |
|---|---|---|
| MPa mm) | 2.7359 | 2.7088 |
| MPa mm) | 0.5688 | 0.5417 |
| MPa mm) | 2.7359 | 2.7088 |
| MPa mm) | 1.0836 | 1.0835 |
| MPa mm) | 1.2125 | 1.2007 |
| MPa mm) | 0.2519 | 0.2401 |
| MPa mm) | 1.2125 | 1.2007 |
| MPa mm) | 0.4803 | 0.4803 |
| MPa mm) | 1.3203 | 1.2833 |
| MPa mm) | 1.3203 | 1.2833 |
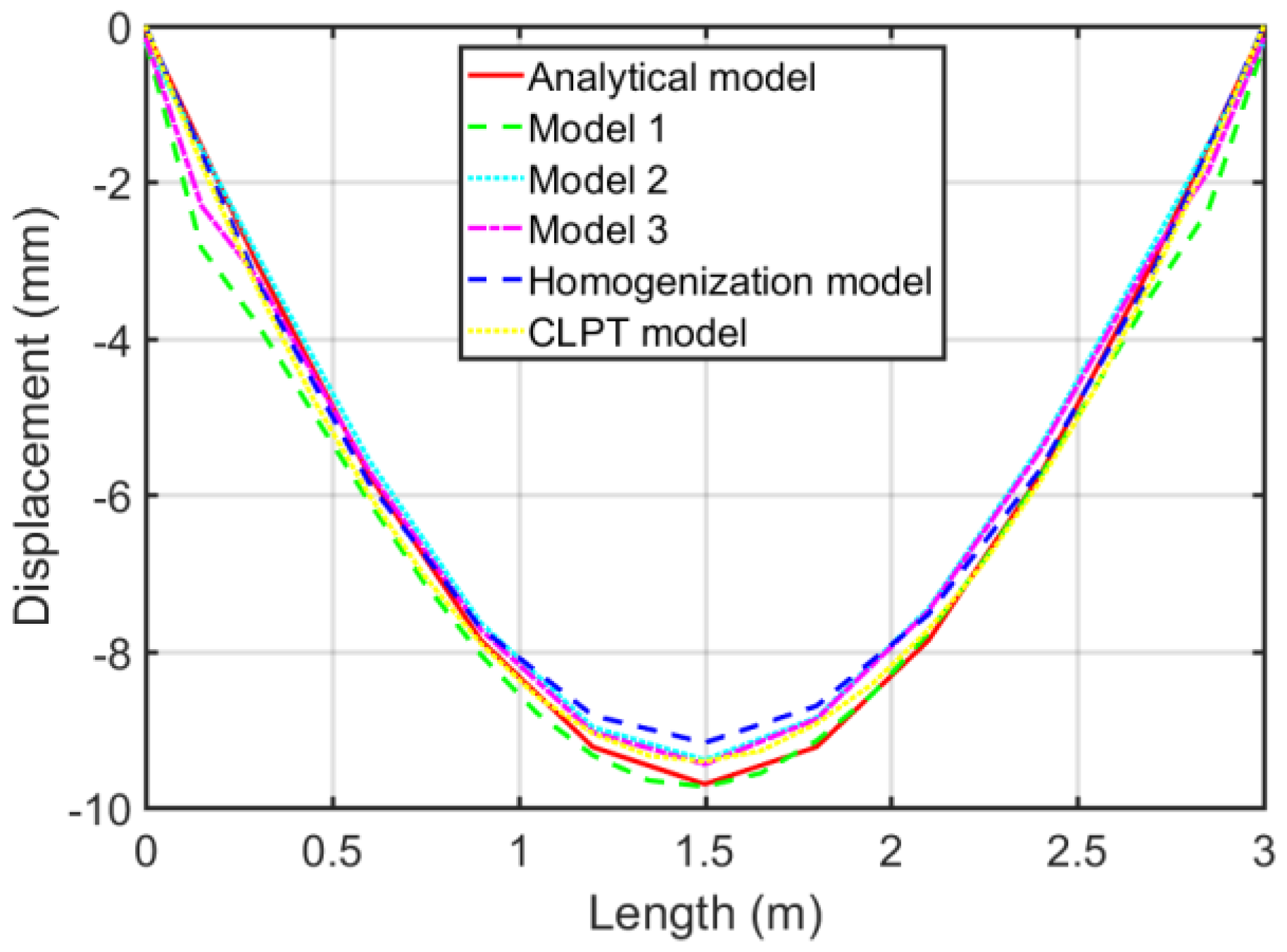
| Name of Model | Value of Displacements (mm) |
|---|---|
| Analytical model | 9.82 |
| Model 1 | 10.18 |
| Model 2 | 9.93 |
| Model 3 | 9.94 |
| Model 4 | 17.43 |
| Homogenization model | 9.71 |
| CLPT model | 9.89 |
| Grid Point No | Finite Difference Method in the Variational Approach [63] | Numerical Homogenization | ||
|---|---|---|---|---|
| mx (Nm/m) | Mx (Nm/m) | mx (Nm/m) | Mx (Nm/m) | |
| 12 | 3381 | 19,550 | 3214 | 18,753 |
| 18 | 3036 | 14,016 | 2963 | 13,507 |
| 24 | 2856 | 12,134 | 2731 | 11,834 |
| 30 | 2777 | 11,244 | 2663 | 10,868 |
| 36 | 2746 | 10,619 | 2615 | 10,054 |
| 42 | 2735 | 9865 | 2597 | 9352 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staszak, N.; Szymczak-Graczyk, A.; Garbowski, T. Elastic Analysis of Three-Layer Concrete Slab Based on Numerical Homogenization with an Analytical Shear Correction Factor. Appl. Sci. 2022, 12, 9918. https://doi.org/10.3390/app12199918
Staszak N, Szymczak-Graczyk A, Garbowski T. Elastic Analysis of Three-Layer Concrete Slab Based on Numerical Homogenization with an Analytical Shear Correction Factor. Applied Sciences. 2022; 12(19):9918. https://doi.org/10.3390/app12199918
Chicago/Turabian StyleStaszak, Natalia, Anna Szymczak-Graczyk, and Tomasz Garbowski. 2022. "Elastic Analysis of Three-Layer Concrete Slab Based on Numerical Homogenization with an Analytical Shear Correction Factor" Applied Sciences 12, no. 19: 9918. https://doi.org/10.3390/app12199918






