Determination of Polypropylene Fiber-Reinforced Concrete Compressive Strength and Elasticity Modulus via Ultrasonic Pulse Tests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Design
2.2. Materials and Mixture
2.3. Specimens
2.4. Test Procedure
2.4.1. Non-Destructive Ultrasonic Pulse Testing
2.4.2. Destructive Testing of The Static Elasticity Modulus and the Poisson Ratio
3. Results
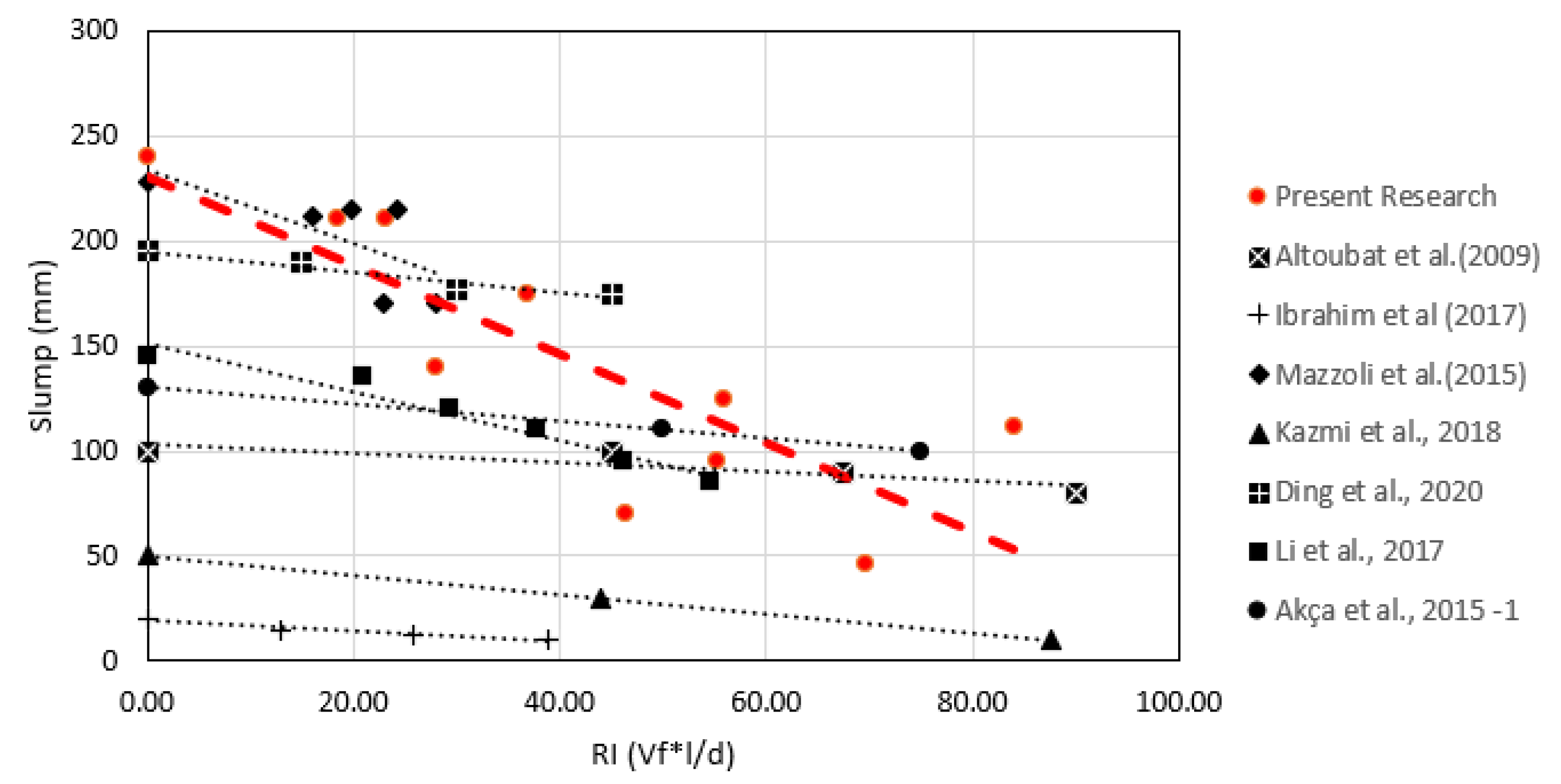
3.1. Fresh State Properties
3.2. Mechanical Properties of Concrete
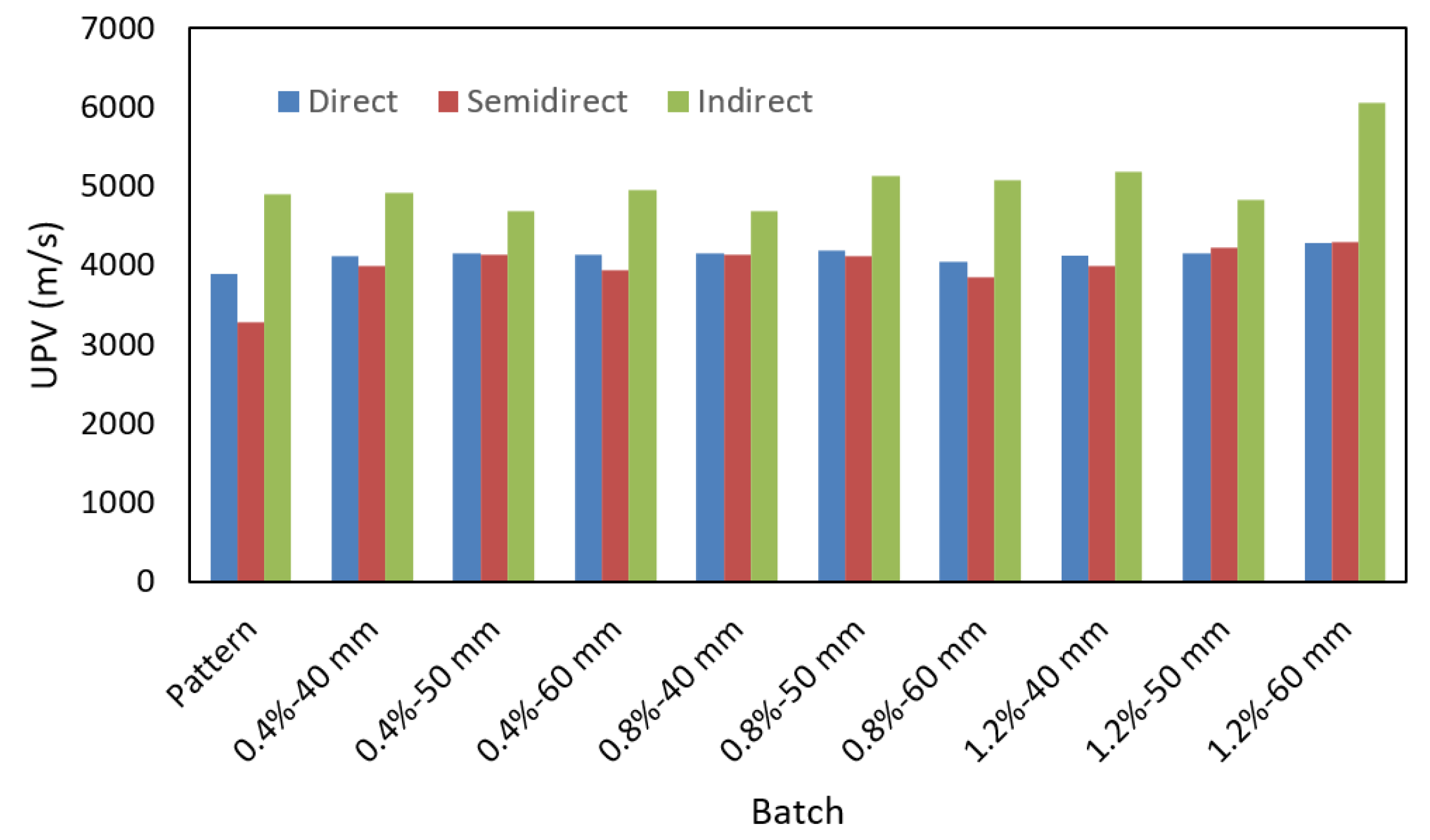
3.3. Ultrasonic Pulse Velocity and the Dynamic Elasticity Modulus of Concrete
4. Discussion
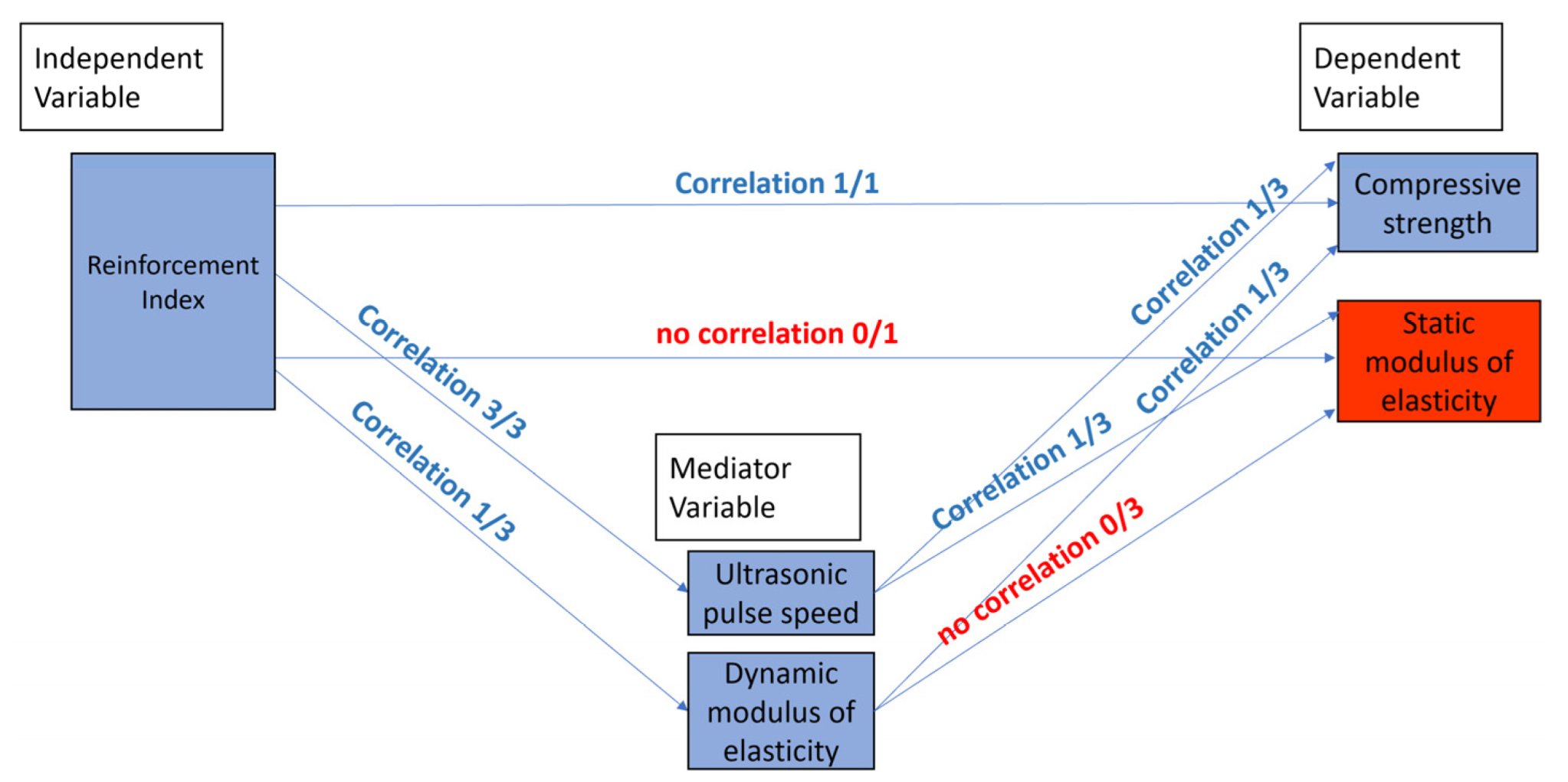
4.1. Correlation between the Reinforcement Index and the Mechanical Properties of Concrete
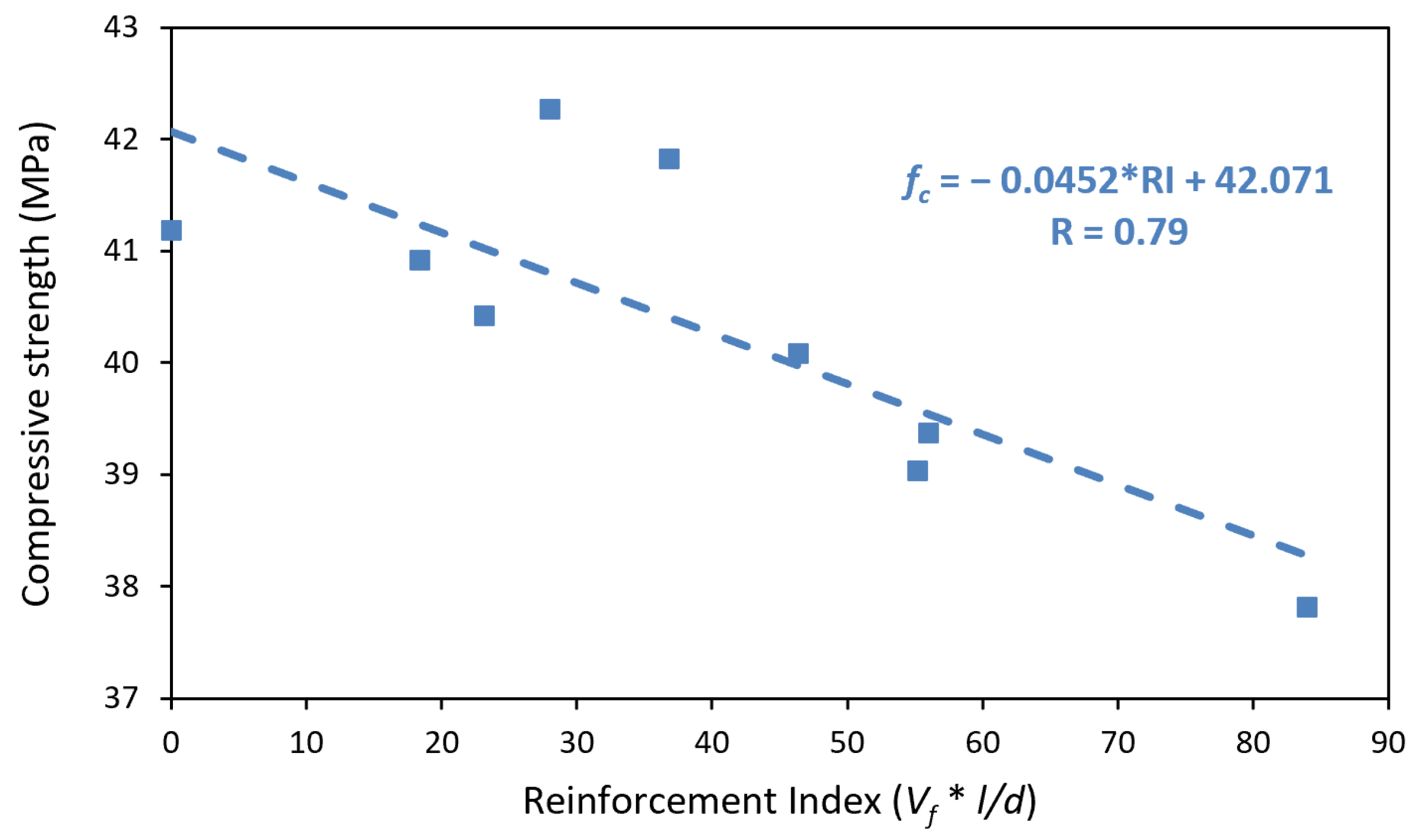
4.1.1. Correlation of the Reinforcement Index and the Compressive Strength of Concrete
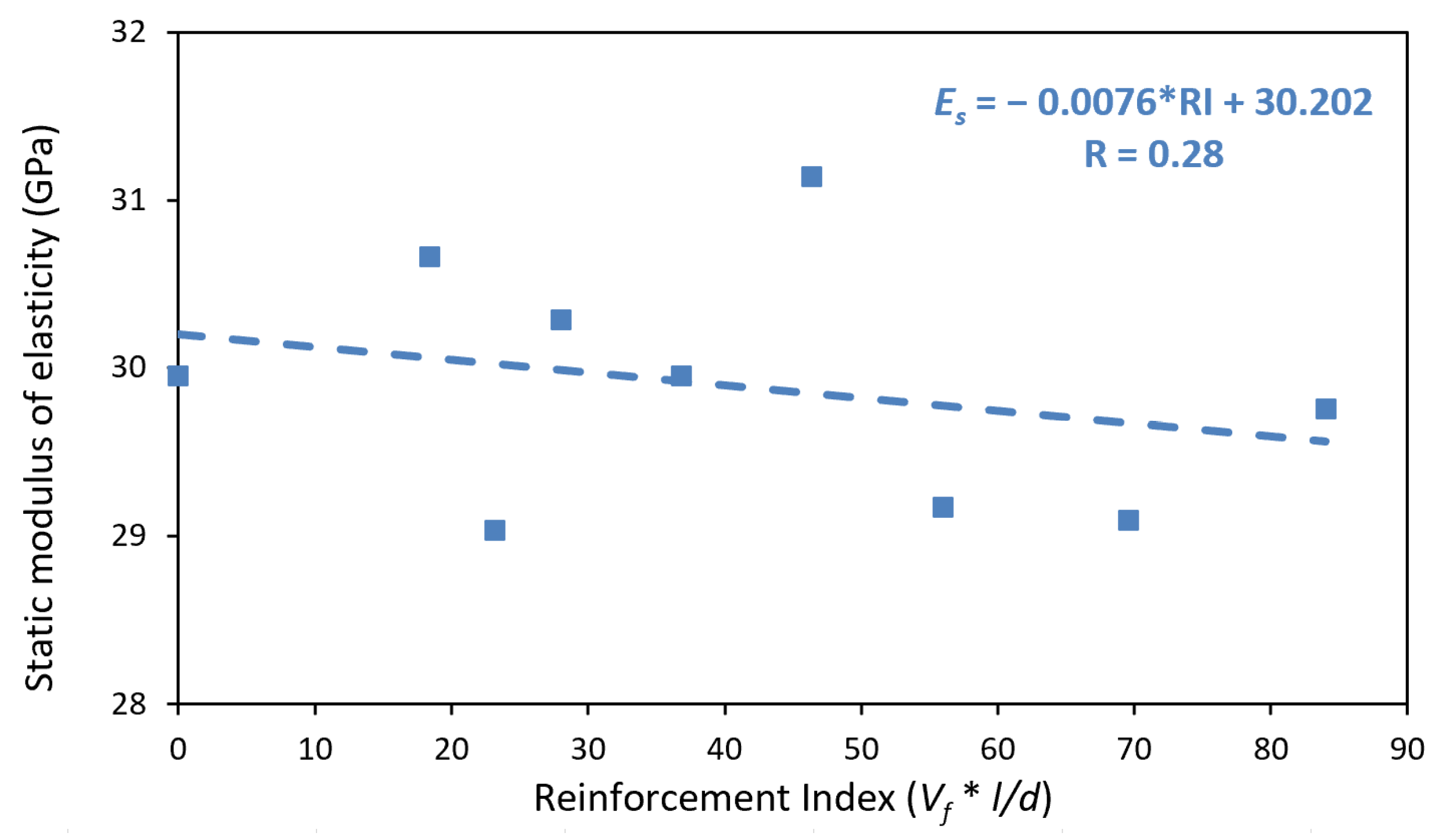
4.1.2. Correlation of the Reinforcement Index and the Static Elasticity Modulus of Concrete
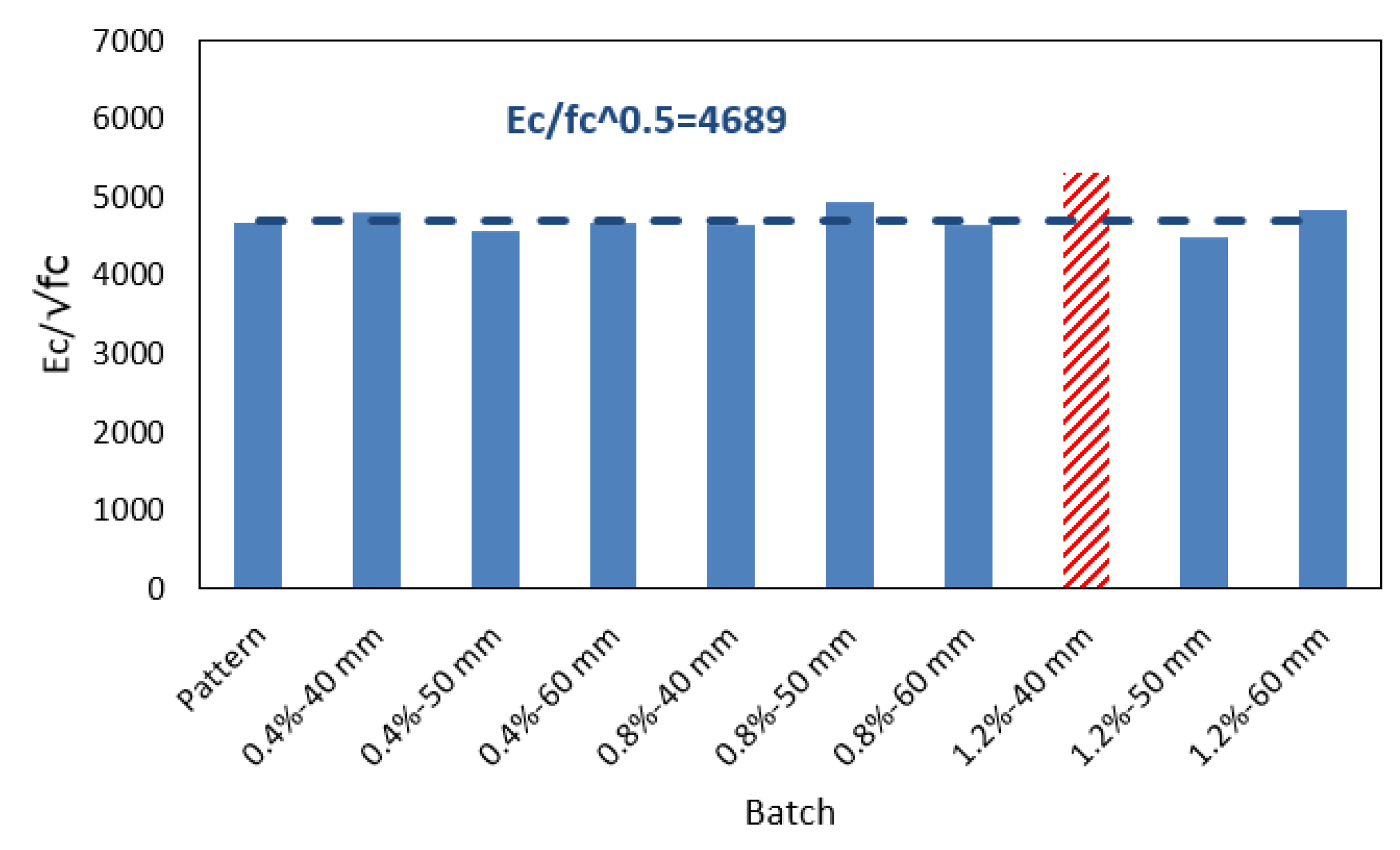
4.1.3. Correlation between Compressive Strength and the Static Elasticity Modulus of Concrete
4.2. Correlation between the Reinforcement Index and the Mechanical Properties of Concrete
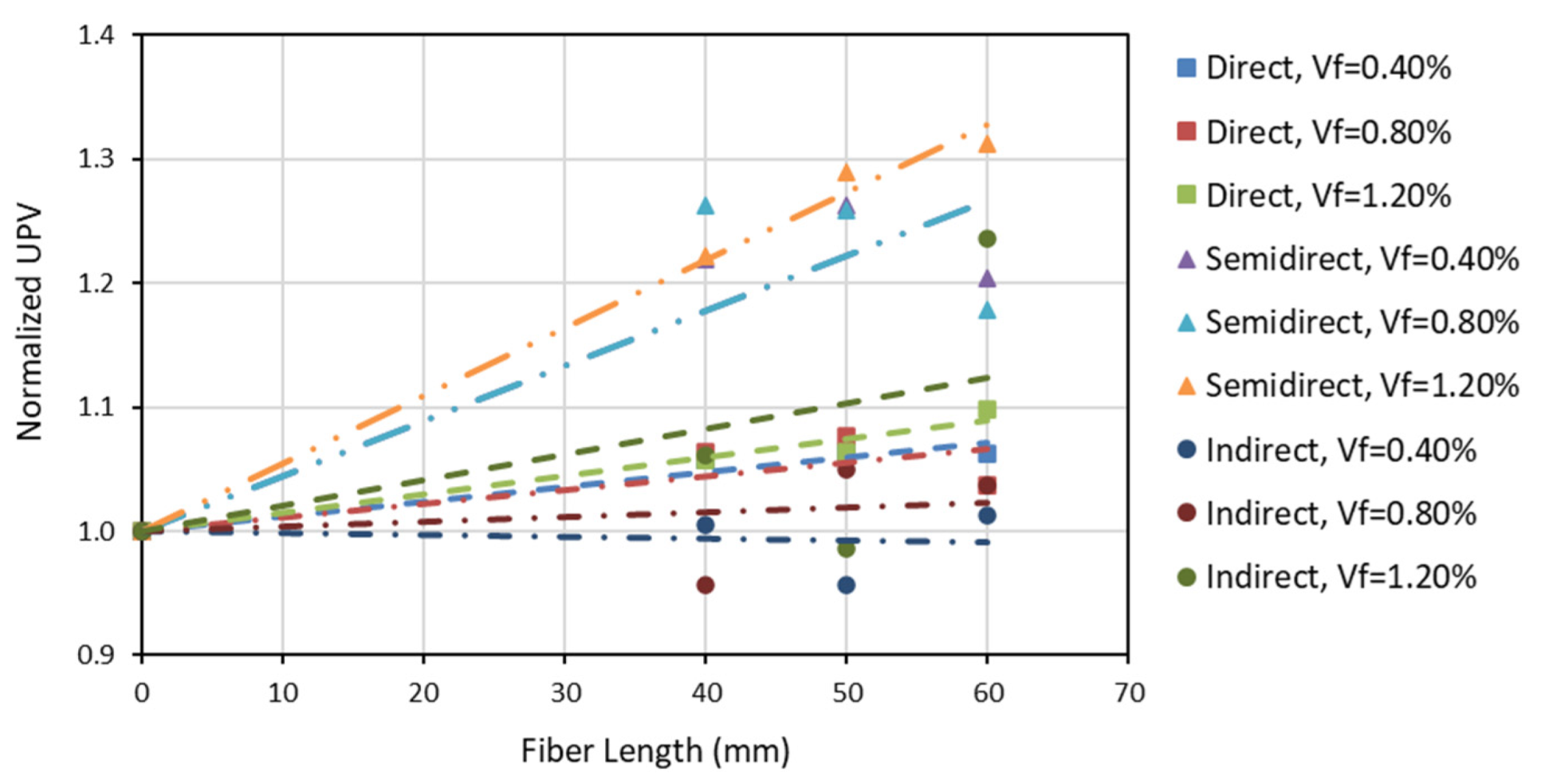
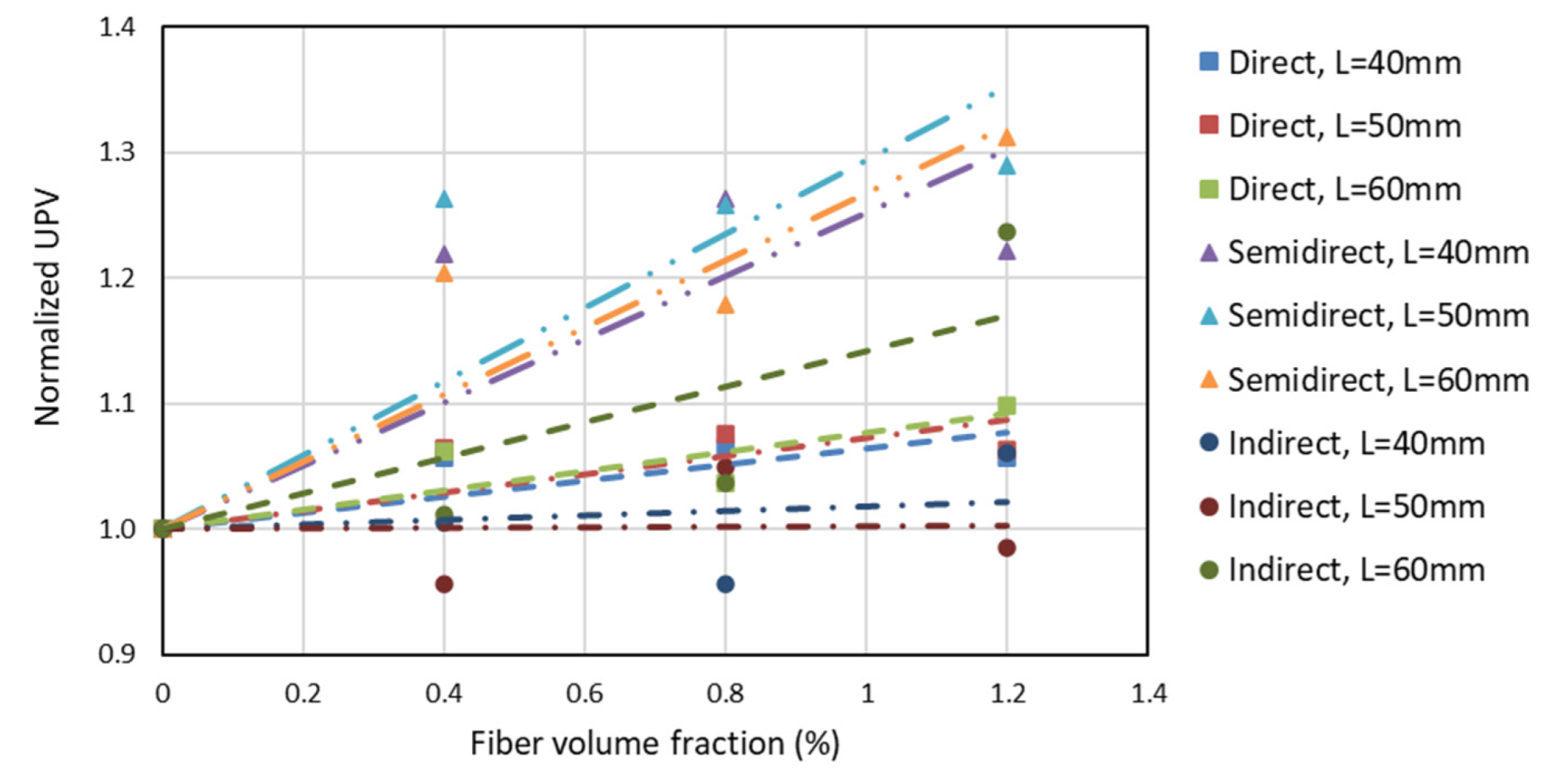
4.2.1. Correlation between the Reinforcement Index and the Ultrasonic Pulse Velocity of Concrete
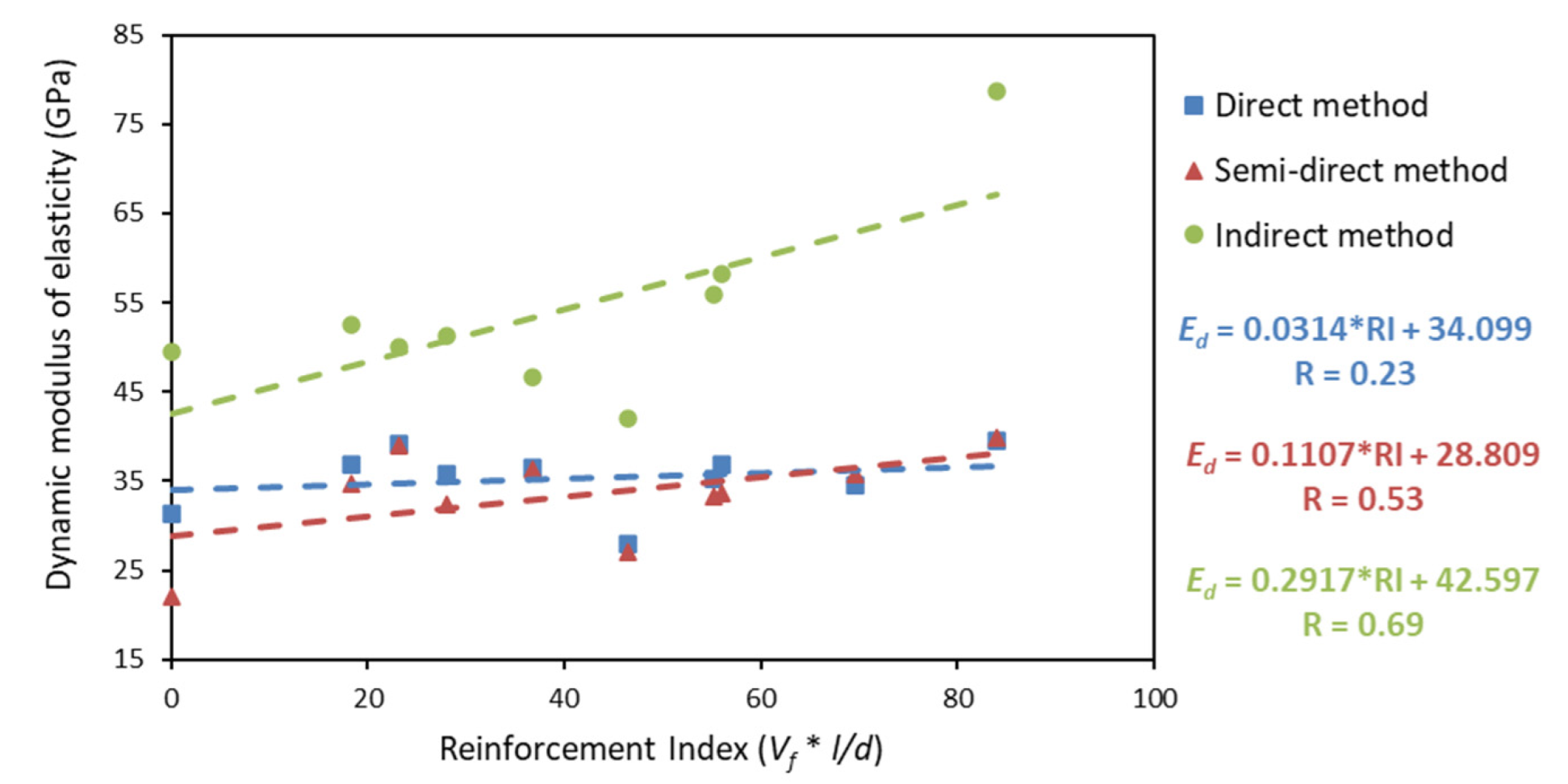
4.2.2. Correlation of the Reinforcement Index in the Dynamic Elasticity Modulus of Concrete
4.3. Correlation between the Dynamic and Mechanical Properties of Concrete
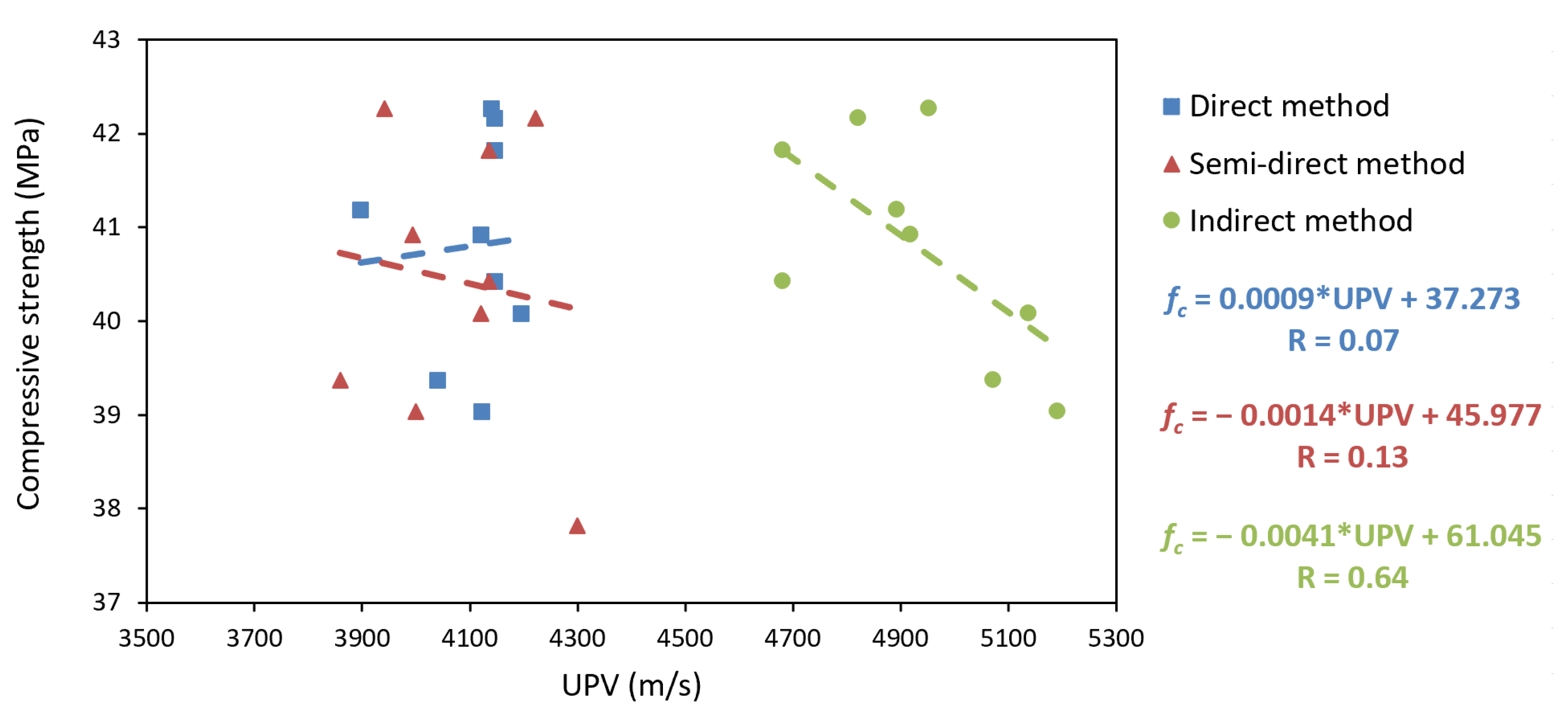
4.3.1. Correlation between Ultrasonic Pulse Velocity and the Compressive Strength of Concrete
4.3.2. Correlation between Ultrasonic Pulse Velocity and the Static Modulus of Elasticity of Concrete
4.3.3. Correlation between the Dynamic Modulus of Elasticity and the Compressive Strength of Concrete
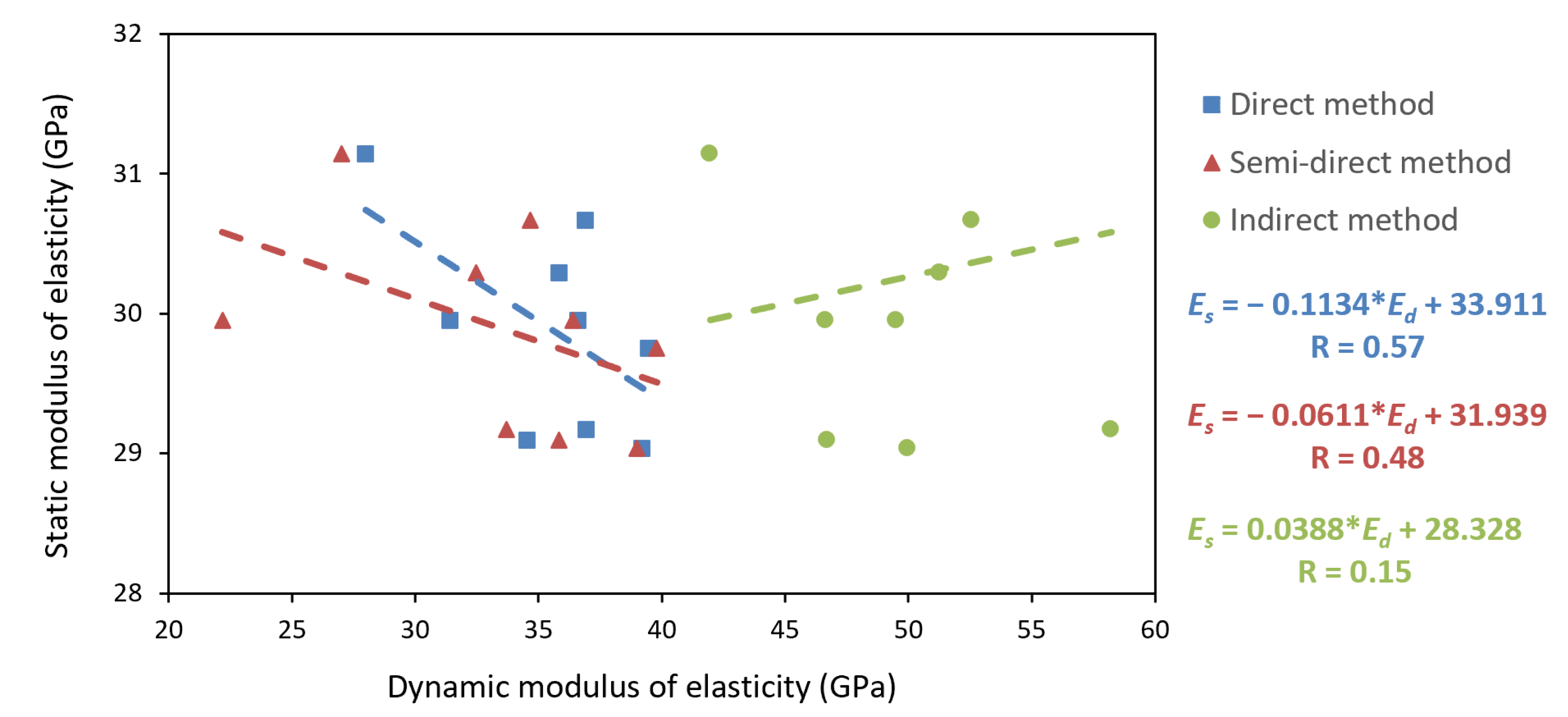
4.3.4. Correlation between the Dynamic and the Static Modulus of Elasticity of Concrete
4.4. Relation between Variables
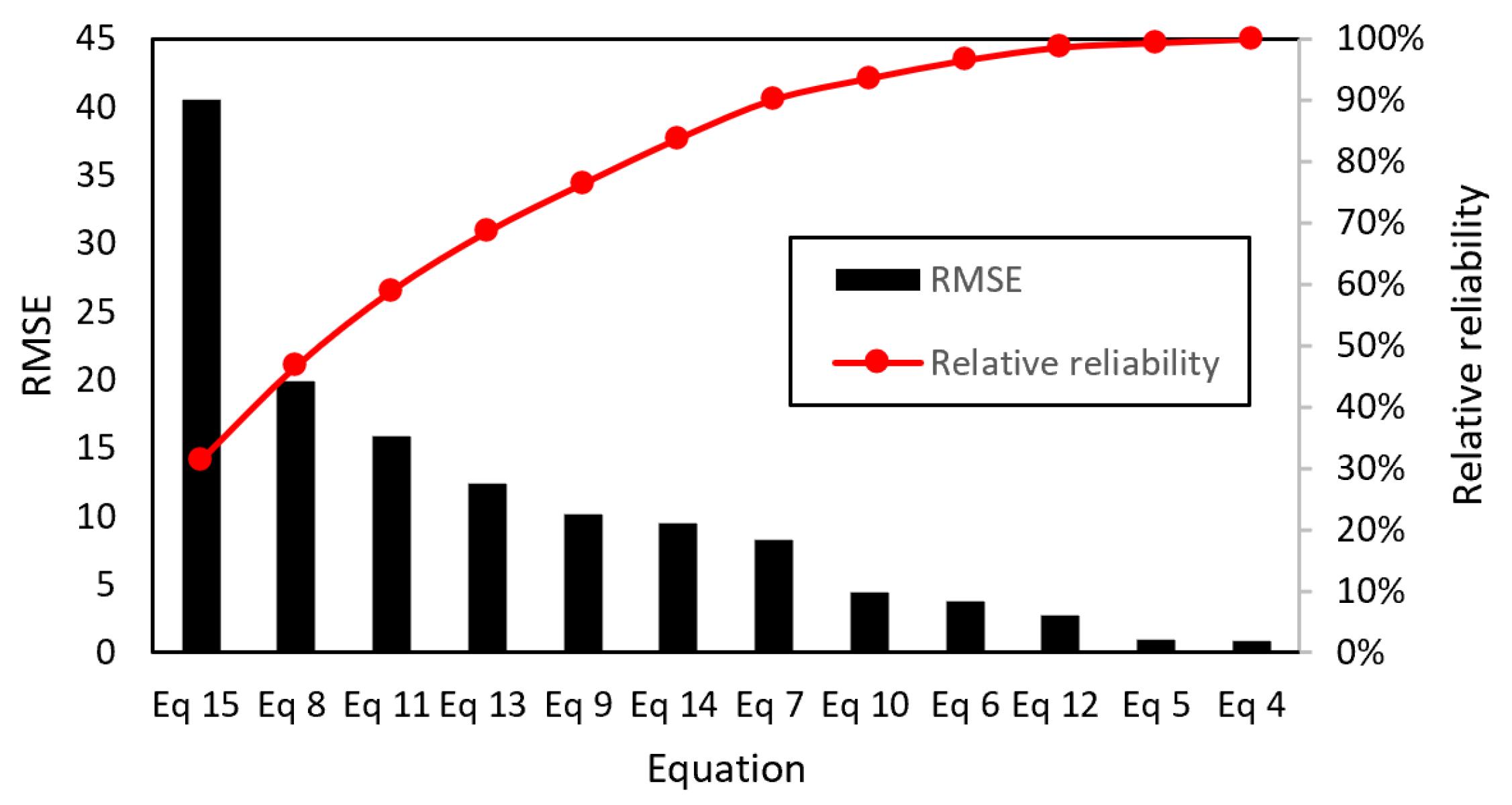
5. Predictive Statistical Analysis
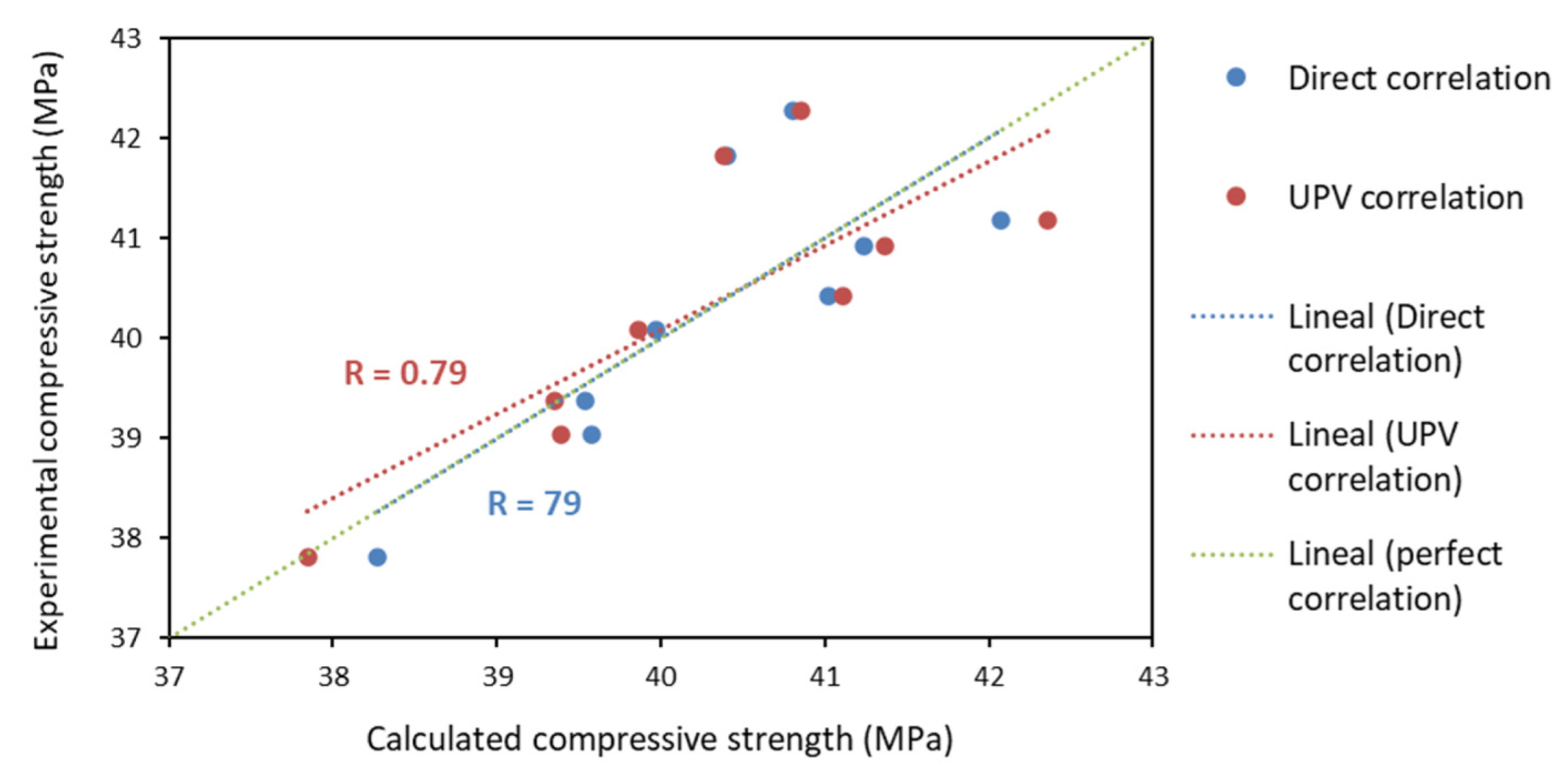
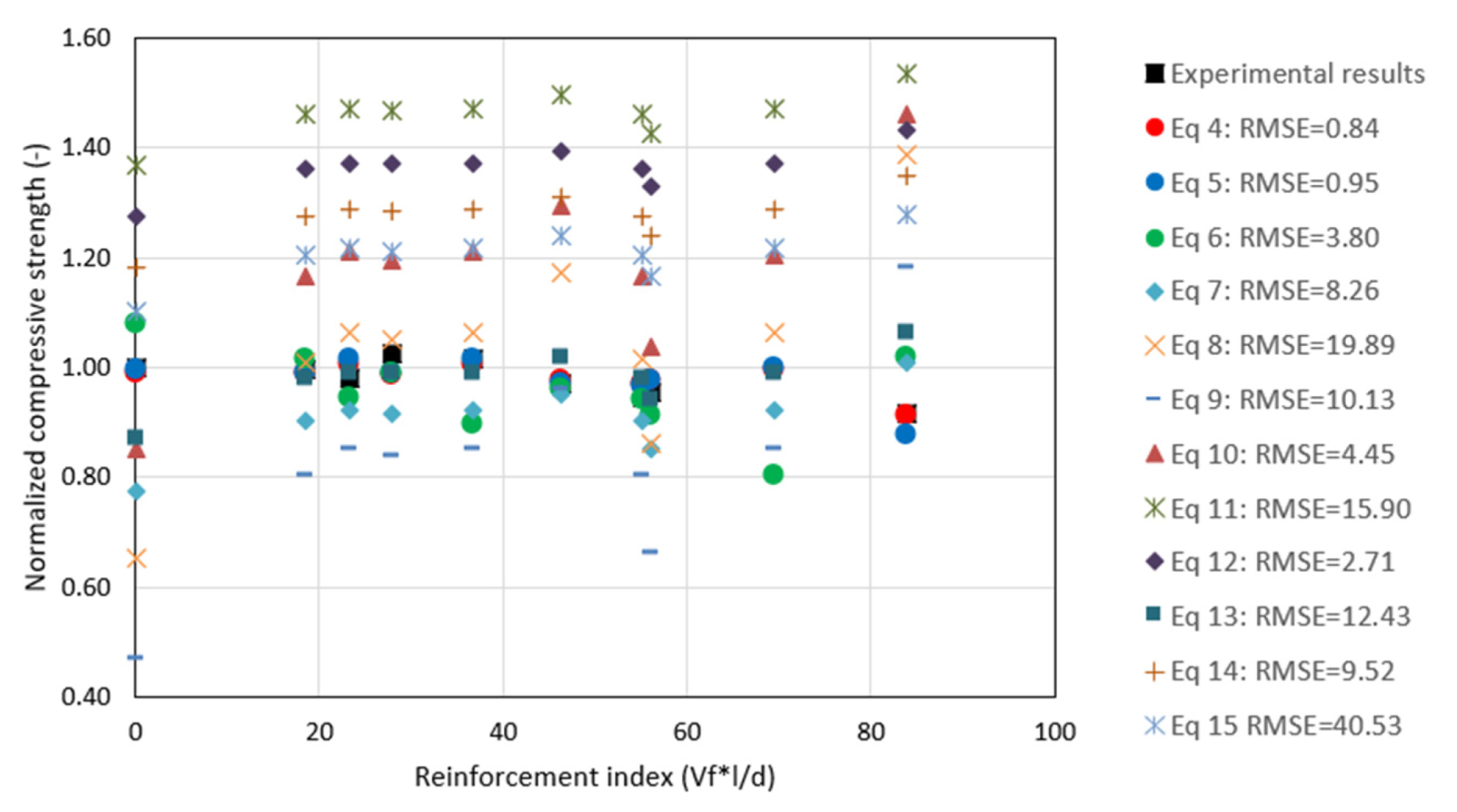
5.1. Prediction of Compressive Strength as a function of Ultrasonic Pulse Velocity
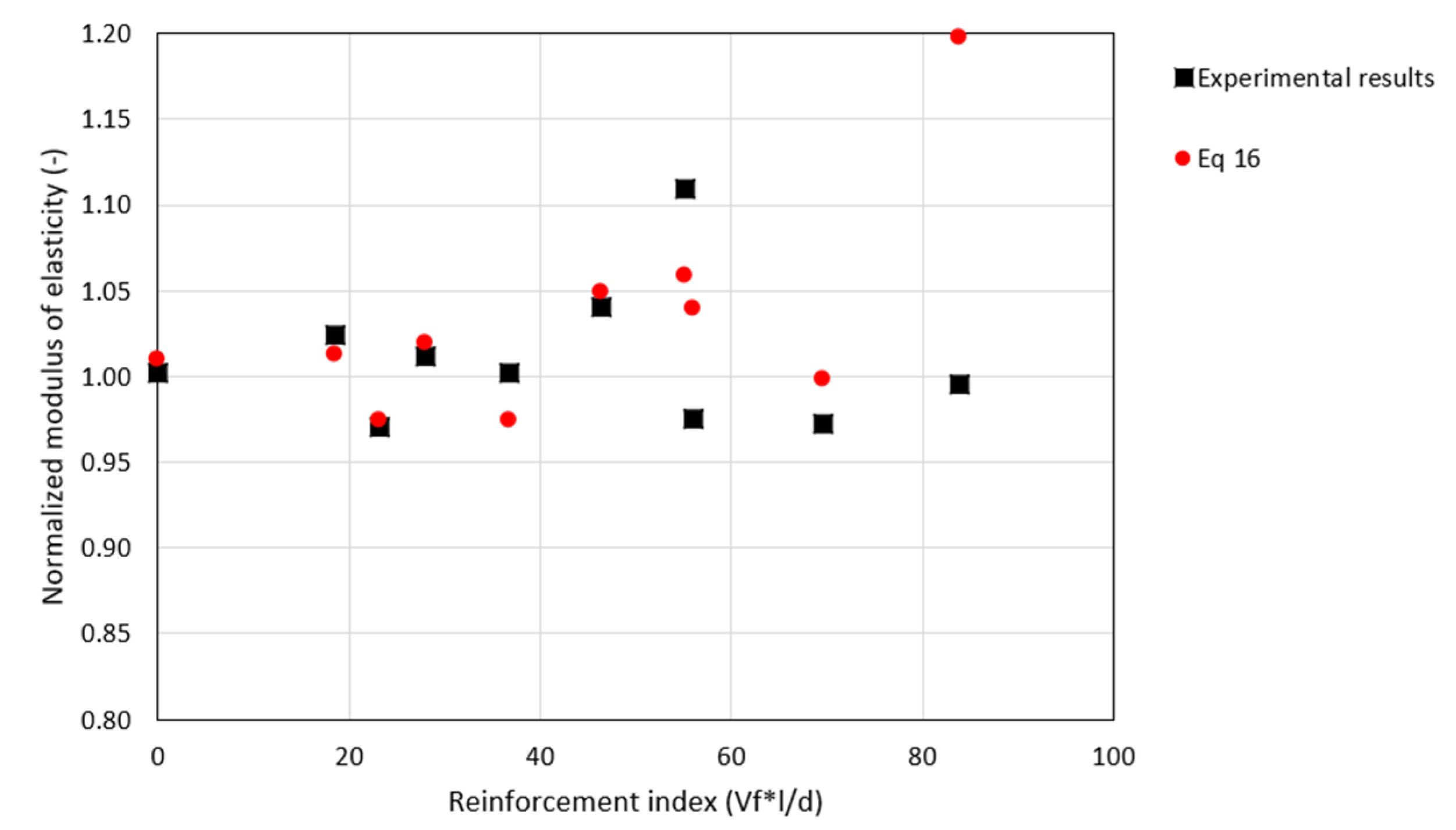
5.2. Prediction of the Static Modulus of Elasticity as a function of Ultrasonic Pulse Velocity
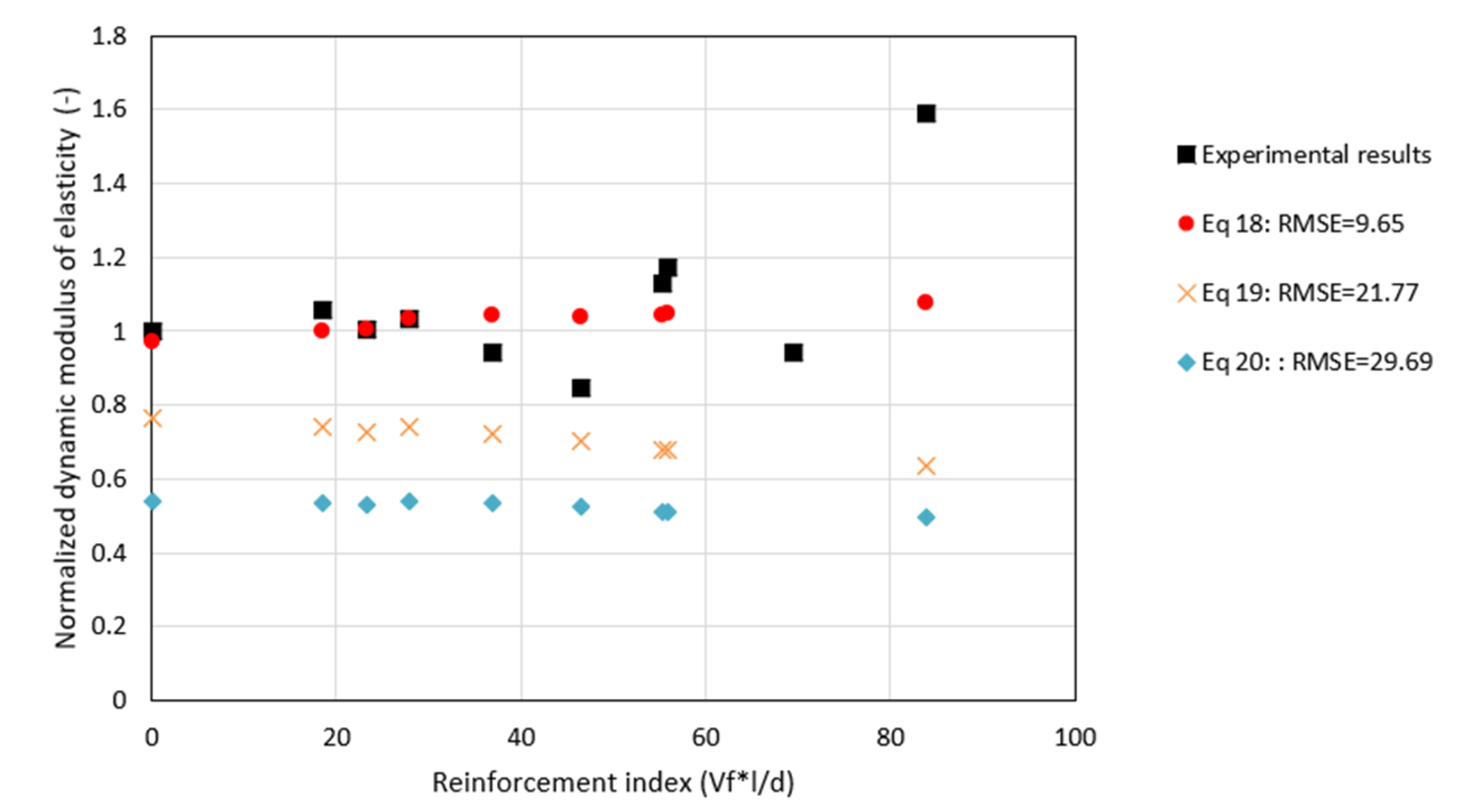
5.3. Prediction of the Dynamic Modulus of Elasticity as a function of Ultrasonic Pulse Velocity
6. Conclusions
- From the relation between the Reinforcement Index and the mechanical properties, it is concluded that there is a linear correlation between RI and compressive strength with a correlation coefficient of 0.79. The higher the RI, the lower the compressive strength. On the other hand, from the results, the non-existent correlation between IR and the Static Modulus of Elasticity cannot be ruled out, even when the correlation coefficient is 0.47. The average ratio for the modulus of elasticity between the root of compressive strength is 4690, a value that is very close to that of 4700 given by the ACI Committee 318; therefore, it can be concluded that the Static Modulus of Elasticity is not significantly affected by PP fibers, and its value can be calculated with the traditional concrete formulas without reinforcing fibers for PP fiber volume fractions of 0, 0.4, 0.8 and 1.2%.
- From the relation between the Reinforcement Index and Ultrasonic Pulse Velocity, it is concluded that there is a correlation using the three prospecting methods. The higher the RI, the higher the UPV. However, a significant correlation was found only through the indirect method regarding the relationship between the Dynamic Modulus of Elasticity and RI.
- The relation between dynamic and mechanical properties shows a significant correlation between UPV and compressive strength and between UPV and the Static Modulus of Elasticity. In both cases, the indirect prospecting method was the only method that had significant correlations. Therefore, empirical equations of these relations have been developed. In the first case, the higher the UPV, the lower the compressive strength, with a correlation coefficient of 0.64. In the second case, the higher the UPV, the greater the Static Modulus of Elasticity, with a correlation coefficient of 0.68. On the other hand, it was shown that there is a correlation between the Dynamic Modulus of Elasticity and compressive strength. Still, the relation is not repeated with the Static Modulus of Elasticity. Therefore, a correlation Equation of the Dynamic Modulus of Elasticity with compressive strength and RI has been developed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Washer, G.; Fuchs, P.; Rezai, A.; Ghasemi, H. Ultrasonic measurement of the elastic properties of ultra-high performance concrete (UHPC). Proc. SPIE 2005, 5767. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 3rd ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Hussain, I.; Ali, B.; Akhtar, T.; Jameel, M.S.; Raza, S.S. Comparison of mechanical properties of concrete and design thickness of pavement with different types of fiber-reinforcements (steel, glass, and polypropylene). Case Stud. Constr. Mater. 2020, 13, e00429. [Google Scholar] [CrossRef]
- Das, C.S.; Dey, T.; Dandapat, R.; Mukharjee, B.B.; Kumar, J. Performance evaluation of polypropylene fibre reinforced recycled aggregate concrete. Constr. Build. Mater. 2018, 189, 649–659. [Google Scholar] [CrossRef]
- Afroughsabet, V.; Ozbakkaloglu, T. Mechanical and durability properties of high-strength concrete containing steel and polypropylene fibers. Constr. Build. Mater. 2015, 94, 73–82. [Google Scholar] [CrossRef]
- Nehdi, M.; Duquette, J. Fiber Synergy in Fiber-Reinforced Self-Consolidating Concrete. ACI Mater. J. 2004, 101, 508–517. [Google Scholar] [CrossRef]
- Corinaldesi, V.; Moriconi, G. Use of synthetic fibers in self-compacting lightweight aggregate concretes. J. Build. Eng. 2015, 4, 247–254. [Google Scholar] [CrossRef]
- Del Savio, A.A.; La Torre, D.; Cedrón, J.P. Experimental Volume Incidence Study and the Relationship of 2 Polypropylene Macrofiber Slenderness to the Mechanical 3 Strengths of Fiber-Reinforced Concretes. Appl. Sci. 2022, 12, 9126. [Google Scholar] [CrossRef]
- Boulekbache, B.; Hamrat, M.; Chemrouk, M.; Amziane, S. Failure mechanism of fibre reinforced concrete under splitting test using digital image correlation. Mater. Struct. 2015, 48, 2713–2726. [Google Scholar] [CrossRef]
- Washer, G.; Fuchs, P.; Rezai, A.; Ghasemi, H. Ultrasonic Testing for Quality Control of Ultra-High Performance Concrete. In Proceedings of the Structures Congress 2006, St. Louis, MO, USA, 18–21 May 2006; pp. 1–8. [Google Scholar] [CrossRef]
- Qixian, L.; Bungey, J.H. Using compression wave ultrasonic transducers to measure the velocity of surface waves and hence determine dynamic modulus of elasticity for concrete. Constr. Build. Mater. 1996, 10, 237–242. [Google Scholar] [CrossRef]
- Jones, R. The non-destructive testing of concrete. Mag. Concr. Res. 1949, 1, 67–78. [Google Scholar] [CrossRef]
- Tsioulou, O.; Lampropoulos, A.; Paschalis, S. Combined Non-Destructive Testing (NDT) method for the evaluation of the mechanical characteristics of Ultra High Performance Fibre Reinforced Concrete (UHPFRC). Constr. Build. Mater. 2017, 131, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Lim, Y.Y.; Kwong, K.Z.; Liew, W.Y.H.; Soh, C.K. Non-destructive concrete strength evaluation using smart piezoelectric transducer—a comparative study. Smart Mater. Struct. 2016, 25, 085021. [Google Scholar] [CrossRef] [Green Version]
- Bungey, J.H.; Millard, S.G.; Grantham, M.G. Testing of Concrete in Structures, 4th ed.; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Malhotra, V.M.; Carino, N.J. Nondestructive Testing of Concrete, 2nd ed.; ASTM Interntional: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Hassan, M.T.; Jones, S.W. Non-destructive testing of ultra high performance fibre reinforced concrete (UHPFRC): A feasibility study for using ultrasonic and resonant frequency testing techniques. Constr. Build. Mater. 2012, 35, 361–367. [Google Scholar] [CrossRef]
- Petro, J.T.; Kim, J. Detection of delamination in concrete using ultrasonic pulse velocity test. Constr. Build. Mater. 2011, 26, 574–582. [Google Scholar] [CrossRef]
- Benaicha, M.; Jalbaud, O.; Alaoui, A.H.; Burtschell, Y. Correlation between the mechanical behavior and the ultrasonic velocity of fiber-reinforced concrete. Constr. Build. Mater. 2015, 101, 702–709. [Google Scholar] [CrossRef]
- Mahapatra, C.K.; Barai, S.V. Sustainable self compacting hybrid fiber reinforced concrete using waste materials. Struct. Concr. 2019, 20, 756–765. [Google Scholar] [CrossRef]
- Reufi, E.; Marku, J.; Bier, T. Ultrasonic Pulse Velocity Investigation of Polypropylene and Steel Fiber Reinforced Concrete. Int. J. Civ. Environ. Eng. 2016. [Google Scholar] [CrossRef]
- Rucka, M.; Wojtczak, E.; Knak, M.; Kurpińska, M. Characterization of fracture process in polyolefin fibre-reinforced concrete using ultrasonic waves and digital image correlation. Constr. Build. Mater. 2021, 280, 122522. [Google Scholar] [CrossRef]
- Noushini, A.; Samali, B.; Vessalas, K. Effect of polyvinyl alcohol (PVA) fibre on dynamic and material properties of fibre reinforced concrete. Constr. Build. Mater. 2013, 49, 374–383. [Google Scholar] [CrossRef]
- Carrillo, J.; Ramirez, J.; Lizarazo-Marriaga, J. Modulus of elasticity and Poisson’s ratio of fiber-reinforced concrete in Colombia from ultrasonic pulse velocities. J. Build. Eng. 2019, 23, 18–26. [Google Scholar] [CrossRef]
- Chakrawarthi, V.; Dharmar, B.; Avudaiappan, S.; Amran, M.; Flores, E.S.; Alam, M.A.; Fediuk, R.; Vatin, N.I.; Rashid, R.S.M. Destructive and Non-Destructive Testing of the Performance of Copper Slag Fiber-Reinforced Concrete. Materials 2022, 15, 4536. [Google Scholar] [CrossRef] [PubMed]
- ACI Committee 211; Standard Practice for Selecting Proportions for Normal, Heavyweight, and Mass Concrete. American Concrete Institute: Detroit, MI, USA, 1991.
- ASTM Standard C192/C192M-19; Standard Practice for Making and Curing Concrete Test Specimens in the Laboratory. ASTM Special Technical Publication; ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM International. Standard Test Method for Pulse Velocity through Concrete. 2016. Available online: https://www.astm.org/c0597-16.html (accessed on 21 March 2022).
- British Standards Institution. Specification for Testing Concrete. Part 203. Recommendations for Measurement of Velocity of Ultrasonic Pulses in Concrete; BSI: London, UK, 1986; p. 16. [Google Scholar]
- ASTM Standard C469/C469M−14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014; pp. 1–5. Available online: www.astm.org (accessed on 21 March 2022).
- Altoubat, S.; Yazdanbakhsh, A.; Rieder, K.A. Shear behavior of macro-synthetic fiber-reinforced concrete beams without stirrups. ACI Mater. J. 2009, 106, 381–389. [Google Scholar] [CrossRef]
- Ibrahim, M.H.W.; Mangi, S.A.; Burhanudin, M.K.; Ridzuan, M.B.; Jamaluddin, N.; Shahidan, S.; Wong, Y.; Faisal, S.; Fadzil, M.A.; Ramadhansyah, P.J.; et al. Compressive and flexural strength of concrete containing palm oil biomass clinker and polypropylene fibres. IOP Conf. Ser. Mater. Sci. Eng. 2017, 271, 012011. [Google Scholar] [CrossRef] [Green Version]
- Kazmi, S.M.S.; Munir, M.J.; Wu, Y.F.; Patnaikuni, I. Effect of macro-synthetic fibers on the fracture energy and mechanical behavior of recycled aggregate concrete. Constr. Build. Mater. 2018, 189, 857–868. [Google Scholar] [CrossRef]
- Song, H.; Ding, Y. Investigation on the spatial distribution of steel fiber in concrete matrix using barcelona test. Jianzhu Cailiao Xuebao/J. Build. Mater. 2016, 19, 381–389. [Google Scholar] [CrossRef]
- Ding, Y.; Li, D.; Zhang, Y.; Azevedo, C. Experimental investigation on the composite effect of steel rebars and macro fibers on the impact behavior of high performance self-compacting concrete. Constr. Build. Mater. 2017, 136, 495–505. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Niu, J.; Wan, C.; Liu, X.; Jin, Z. Comparison of flexural property between high performance polypropylene fiber reinforced lightweight aggregate concrete and steel fiber reinforced lightweight aggregate concrete. Constr. Build. Mater. 2017, 157, 729–736. [Google Scholar] [CrossRef]
- Akça, K.I.R.; Çakir, Ö.; Ipek, M. Properties of polypropylene fiber reinforced concrete using recycled aggregates. Constr. Build. Mater. 2015, 98, 620–630. [Google Scholar] [CrossRef]
- Mazzoli, A.; Monosi, S.; Plescia, E.S. Evaluation of the early-age-shrinkage of Fiber Reinforced Concrete (FRC) using image analysis methods. Constr. Build. Mater. 2015, 101, 596–601. [Google Scholar] [CrossRef]
- Wang, W.; Shen, A.; Lyu, Z.; He, Z.; Nguyen, K.T.Q. Fresh and rheological characteristics of fiber reinforced concrete—A review. Constr. Build. Mater. 2021, 296, 123734. [Google Scholar] [CrossRef]
- Ding, Y.; Zeng, W.; Wang, Q.; Zhang, Y. Topographical analysis of fractured surface roughness of macro fiber reinforced concrete and its correlation with flexural toughness. Constr. Build. Mater. 2020, 235, 117466. [Google Scholar] [CrossRef]
- Zhu, J.; Kee, S.-H.; Han, D.; Tsai, Y.-T. Effects of air voids on ultrasonic wave propagation in early age cement pastes. Cem. Concr. Res. 2011, 41, 872–881. [Google Scholar] [CrossRef]
- Noushini, A.; Hastings, M.; Castel, A.; Aslani, F. Mechanical and flexural performance of synthetic fibre reinforced geopolymer concrete. Constr. Build. Mater. 2018, 186, 454–475. [Google Scholar] [CrossRef]
- Nik, A.S.; Omran, O.L. Estimation of compressive strength of self-compacted concrete with fibers consisting nano-SiO2 using ultrasonic pulse velocity. Constr. Build. Mater. 2013, 44, 654–662. [Google Scholar] [CrossRef]
- Meddah, M.S.; Bencheikh, M. Properties of concrete reinforced with different kinds of industrial waste fibre materials. Constr. Build. Mater. 2009, 23, 3196–3205. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Poorhosein, R. Estimating properties of reactive powder concrete containing hybrid fibers using UPV. Comput. Concr. 2017, 20, 491–502. [Google Scholar] [CrossRef]
- Nematzadeh, M.; Dashti, J.; Ganjavi, B. Optimizing compressive behavior of concrete containing fine recycled refractory brick aggregate together with calcium aluminate cement and polyvinyl alcohol fibers exposed to acidic environment. Constr. Build. Mater. 2018, 164, 837–849. [Google Scholar] [CrossRef]
- Belaribi, H.; Mellas, M.; Rahmani, F. The relationship between the compressive strength and ultrasonic pulse velocity concrete with fibers exposed to high temperatures. Appl. Energet. Pollut. 2016, 3, 31–36. [Google Scholar]








| Batch | Cement (kg) | Water (kg) | Sand (kg) | Gravel (kg) | SP (kg) | Fibers | |||
|---|---|---|---|---|---|---|---|---|---|
| Vf (%) | Diameter (mm) | Length, l (mm) | RI * (Vf ∗ l/d) | ||||||
| B-Pattern | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.0 | - | - | 0.0 |
| B-0.4%-40 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.4 | 0.86 | 40 | 18.4 |
| B-0.4%-50 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.4 | 0.86 | 50 | 23.2 |
| B-0.4%-60 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.4 | 0.86 | 60 | 28.0 |
| B-0.8%-40 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.8 | 0.86 | 40 | 36.8 |
| B-0.8%-50 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.8 | 0.86 | 50 | 46.4 |
| B-0.8%-60 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 0.8 | 0.86 | 60 | 56.0 |
| B-1.2%-40 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 1.2 | 0.86 | 40 | 55.2 |
| B-1.2%-50 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 1.2 | 0.86 | 50 | 69.6 |
| B-1.2%-60 | 502.8 | 226.6 | 721.1 | 891.2 | 7.1 | 1.2 | 0.86 | 60 | 84.0 |
| Batch | RI (Vf ∗ l/d) | Density (kg/m3) | Slump (mm) | Air Content (%) |
|---|---|---|---|---|
| B-Pattern | 0.0 | 2254.7 | 240 | 6.2 * |
| B-0.4%-40 | 18.4 | 2229.2 | 210 | 6.0 * |
| B-0.4%-50 | 23.2 | 2322.8 | 210 | 4.0 |
| B-0.4%-60 | 28.0 | 2283.1 | 140 | 3.9 |
| B-0.8%-40 | 36.8 | 2268.9 | 175 | 4.0 |
| B-0.8%-50 | 46.4 | 2331.3 | 70 | 2.8 |
| B-0.8%-60 | 56.0 | 2296.3 | 125 | 3.5 |
| B-1.2%-40 | 55.2 | 2268.9 | 95 | 2.8 |
| B-1.2%-50 | 69.6 | 2243.4 | 46 | 3.0 |
| B-1.2%-60 | 84.0 | 2263.2 | 111 | 3.0 |
| Batch | RI (Vf ∗ l/d) | µ | fc | Ec | |||
|---|---|---|---|---|---|---|---|
| (-) | CV | (MPa) | CV | (GPa) | CV | ||
| B-Pattern | 0.0 | 0.18 | 15.6% | 41.18 | 3.6% | 29.95 | 4.8% |
| B-0.4%-40 | 18.4 | 0.11 | 0.4% | 40.92 | 4.0% | 30.67 | 0.3% |
| B-0.4%-50 | 23.2 | 0.09 | 15.9% | 40.42 | 3.1% | 29.03 | 7.7% |
| B-0.4%-60 | 28.0 | 0.19 | 16.4% | 42.27 | 0.3% | 30.29 | 0.1% |
| B-0.8%-40 | 36.8 | 0.16 | 3.4% | 41.82 | 0.2% | 29.95 | 3.1% |
| B-0.8%-50 | 46.4 | 0.33 | 0.3% | 40.08 | 8.6% | 31.14 | 5.4% |
| B-0.8%-60 | 56.0 | 0.08 | 4.8% | 39.37 | 6.1% | 29.17 | 0.5% |
| B-1.2%-40 | 55.2 | 0.19 | 4.9% | 39.03 | 1.5% | 33.20 | 1.1% |
| B-1.2%-50 | 69.6 | 0.20 | 17.1% | 42.16 | 1.7% | 29.09 | 0.7% |
| B-1.2%-60 | 84.0 | 0.14 | 6.8% | 37.82 | * | 29.75 | 8.7% |
| Batch | UPV (m/s) | Ed (GPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Direct | Semidirect | Indirect | Direct | Semidirect | Indirect | ||||
| CV | CV | CV | |||||||
| B-Pattern | 3897 | 5.0% | 3275 | 5.0% | 4893 | 5.8% | 31.41 | 22.17 | 49.50 |
| B-0.4%-40 | 4120 | 0.2% | 3994 | 0.7% | 4918 | 0.9% | 36.91 | 34.67 | 52.57 |
| B-0.4%-50 | 4146 | 0.1% | 4136 | 2.8% | 4681 | 1.1% | 39.20 | 39.00 | 49.97 |
| B-0.4%-60 | 4139 | 0.1% | 3942 | 0.7% | 4952 | 0.6% | 35.81 | 32.48 | 51.27 |
| B-0.8%-40 | 4146 | 0.1% | 4136 | 2.8% | 4681 | 1.1% | 36.59 | 36.41 | 46.64 |
| B-0.8%-50 | 4195 | 0.1% | 4121 | 0.8% | 5137 | 0.8% | 27.98 | 27.00 | 41.95 |
| B-0.8%-60 | 4040 | 0.2% | 3859 | 1.3% | 5073 | 3.0% | 36.93 | 33.70 | 58.22 |
| B-1.2%-40 | 4121 | 1.4% | 4000 | 1.3% | 5192 | 0.3% | 35.28 | 33.23 | 56.00 |
| B-1.2%-50 | 4145 | 0.2% | 4222 | 3.7% | 4822 | 0.9% | 34.54 | 35.83 | 46.72 |
| B-1.2%-60 | 4281 | 0.4% | 4299 | 1.3% | 6049 | 3.9% | 39.46 | 39.80 | 78.78 |
| Author | Equation | Type of Concrete | ID |
|---|---|---|---|
| Current Research Study | PPFRC | Equation (2) | |
| ACI Committee 318 | Normal Concrete | Equation (3) |
| Author | Equation | Method | Type of Fibers | Vf (%) | Id |
|---|---|---|---|---|---|
| ** | fc = 57.5079 × Exp(−0.00007 × UPV) | Indirect | Polypropylene | 0, 0.4, 0.8, 1.2% | Equation (4) |
| ** | fc = 61.045 − 0.0041 × UPV | Indirect | Polypropylene | 0, 0.4, 0.8, 1.2% | Equation (5) |
| ** | fc = 0.0091 × UPV − 0.155 × RI | Indirect | Polypropylene | 0, 0.4, 0.8, 1.2% | Equation (6) |
| [19] | fc = 2.080 × Exp(0.0007 × UPV) | Direct | Steel | 0, 0.5, 1.3, 1.5, 2, 2.5% | Equation (7) |
| [45] [45] | fc = 0.013 × Exp(1.959/1000 × UPV) fc = 0.0016 × Exp(2.411/1000 × UPV) | Direct Direct | Steel PVA | 1, 2, 3% 0.25, 0.50, 0.75% | Equation (8) Equation (9) |
| [46] | fc = 0.15 ∗ Exp(1.40/1000 × UPV) | Direct | Polyvinyl | 0.5% | Equation (10) |
| [47] [47] | fc = 17.476 × Exp(0.0003 × UPV) fc = 16.312 × Exp(0.0003 × UPV) | * * | Steel Polypropylene | 0.19, 0.25, 0.50% 0.055, 0.11, 0.16% | Equation (11) Equation (12) |
| [43] [43] [43] | fc = 4.9428 × Exp(0.5096/1000 × UPV) fc = 12.916 × Exp(0.3408/1000 × UPV) fc = 10.265 × Exp(0.3822/1000 × UPV) | Direct Direct Direct | Polypropylene Polypropylene Polypropylene | 2% 4% 6% | Equation (13) Equation (14) Equation (15) |
| Author | Equation | Method | Fibers | Vf (%) | Id |
|---|---|---|---|---|---|
| * | Ec = 0.0049 × UPV + 6.2271 | Indirect | Polypropylene | 0, 0.4, 0.8, 1.2% | Equation (16) |
| [19] ** | Ec = (1.06 × 10^(−4) × UPV^2) − 1.156 × UPV + 3210 | Direct | Steel | 0, 0.5, 1.3, 1.5, 2, 2.5% | Equation (17) |
| Author | Equation | Method | Fibers | Vf (%) | Id |
|---|---|---|---|---|---|
| * | Ed_ind = (7.5084 + 0.0137 × RI) × (fc)^0.5 | Indirect | Polypropylene | 0, 0.4, 0.8, 1.2% | Equation (18) |
| [24] [24] | Ed_dir = (5920 − 9.4 × RI) × (fc)^0.5 Ed_sem = (4170 − 1.7 × RI) × (fc)^0.5 | Direct Semi-direct | Steel/PP Steel/PP | Various Various | Equation (19) Equation (20) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Savio, A.A.; La Torre Esquivel, D.; Carrillo, J.; Chi Yep, E. Determination of Polypropylene Fiber-Reinforced Concrete Compressive Strength and Elasticity Modulus via Ultrasonic Pulse Tests. Appl. Sci. 2022, 12, 10375. https://doi.org/10.3390/app122010375
Del Savio AA, La Torre Esquivel D, Carrillo J, Chi Yep E. Determination of Polypropylene Fiber-Reinforced Concrete Compressive Strength and Elasticity Modulus via Ultrasonic Pulse Tests. Applied Sciences. 2022; 12(20):10375. https://doi.org/10.3390/app122010375
Chicago/Turabian StyleDel Savio, Alexandre Almeida, Darwin La Torre Esquivel, Julian Carrillo, and Emilio Chi Yep. 2022. "Determination of Polypropylene Fiber-Reinforced Concrete Compressive Strength and Elasticity Modulus via Ultrasonic Pulse Tests" Applied Sciences 12, no. 20: 10375. https://doi.org/10.3390/app122010375
APA StyleDel Savio, A. A., La Torre Esquivel, D., Carrillo, J., & Chi Yep, E. (2022). Determination of Polypropylene Fiber-Reinforced Concrete Compressive Strength and Elasticity Modulus via Ultrasonic Pulse Tests. Applied Sciences, 12(20), 10375. https://doi.org/10.3390/app122010375







