Risk Coupling Analysis of Deep Foundation Pits Adjacent to Existing Underpass Tunnels Based on Dynamic Bayesian Network and N–K Model
Abstract
:1. Introduction
2. Methodology
2.1. Risk Association Analysis and Apriori Algorithm
2.1.1. Relevant Concepts of Association Rules
- 1.
- Minimum support: the minimum support that the association rule must statistically satisfy.
- 2.
- Minimum confidence: the minimum confidence level that the association rule must statistically satisfy.
2.1.2. Apriori Algorithm and Association Rule Mining
2.2. Theory of Dynamic Bayesian Networks
2.2.1. Dynamic Bayesian Network (DBN)
- (1)
- Smoothness assumption: Assuming that the network topology does not change over time, the probability change process of the variables is uniformly smooth over a finite time t (i.e., the conditional probability remains constant for all t).
- (2)
- Markov assumption: Given the state at the current moment t, the state at the future moment t + 1 is only related to the state at moment t and not to the state at the moment t + 1, as expressed by the following equation:
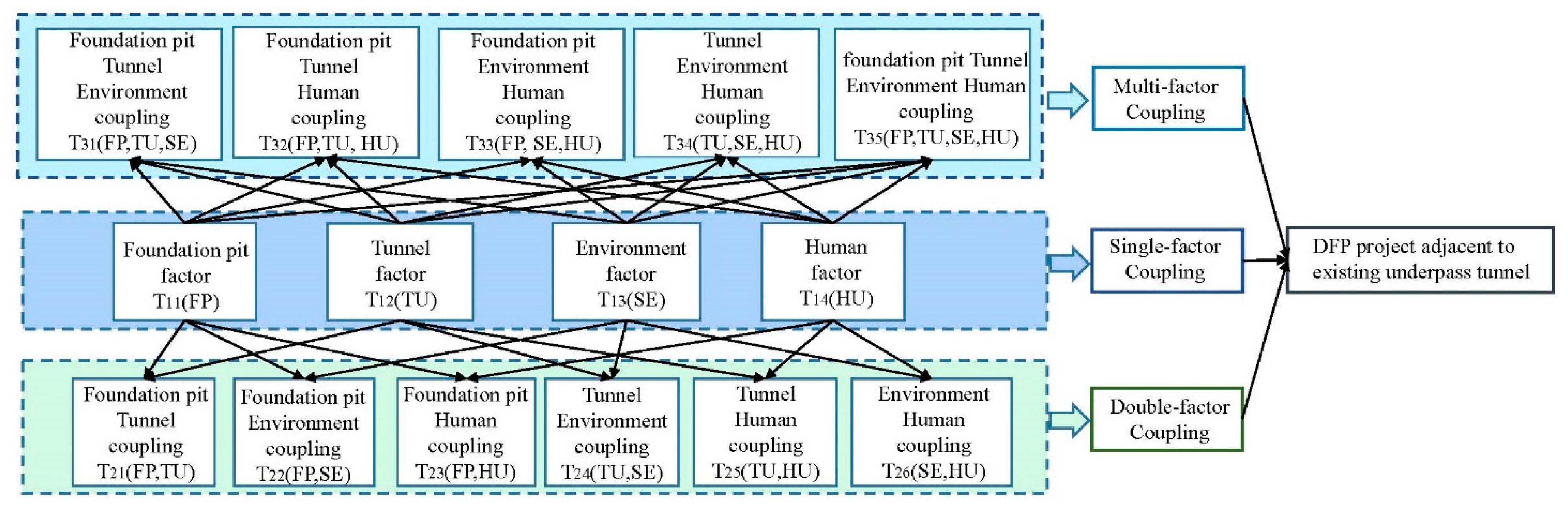
2.3. N–K Model
3. Establishment of a Dynamic Analysis Model for Coupled Risk Analysis of DFPs Adjacent to Existing Underpass Tunnels Based on DBN and N–K Models
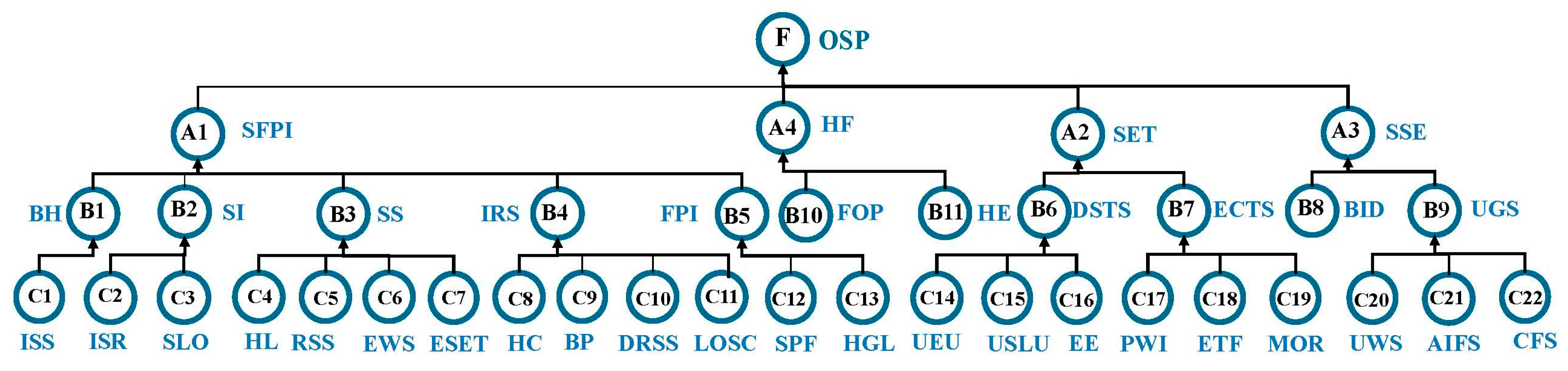
3.1. Identification of Risk Factors and Bayesian Network Nodes
3.2. Construction of a Coupled Risk Bayesian Network Model Structure
3.3. Determine the Conditional Probabilities
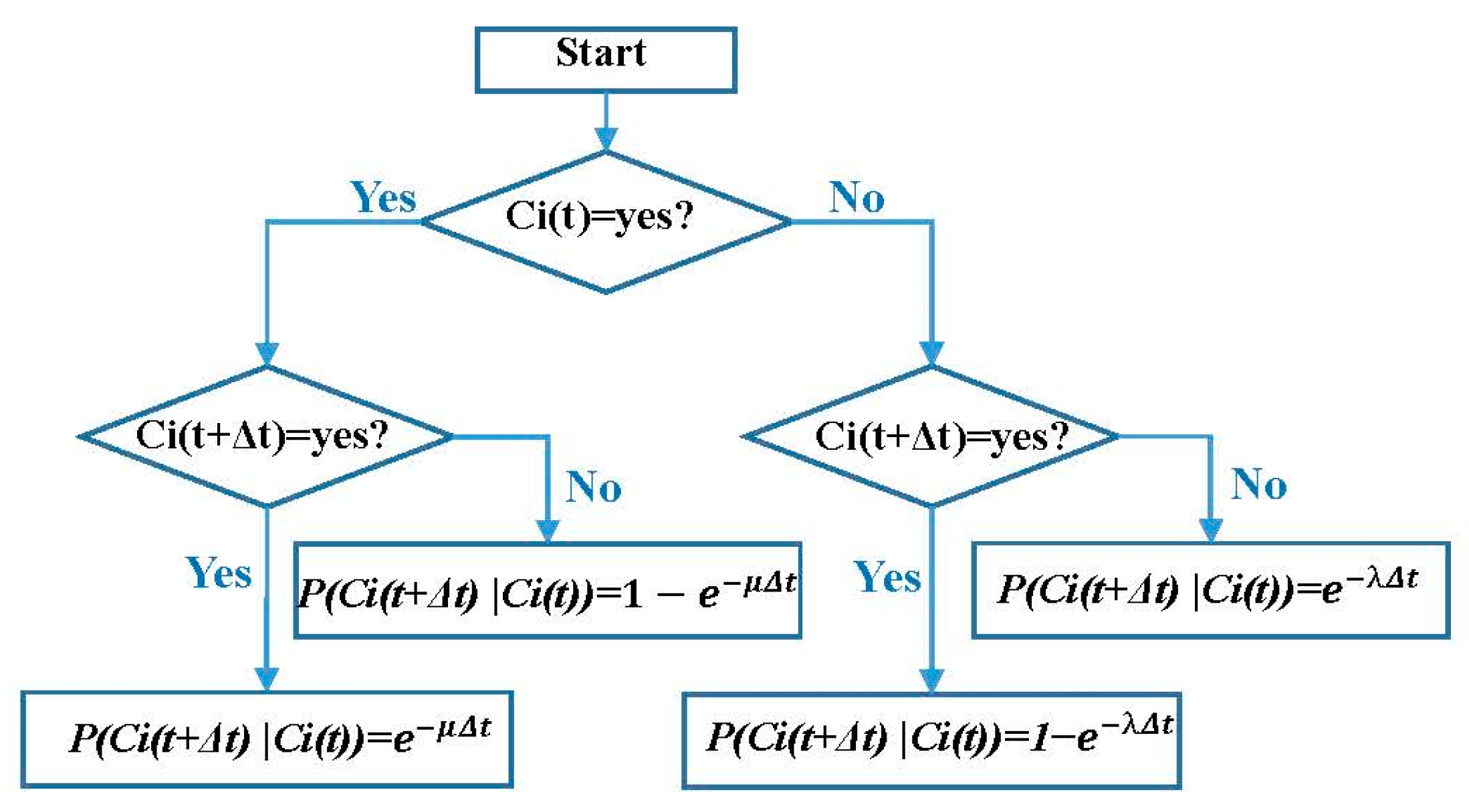
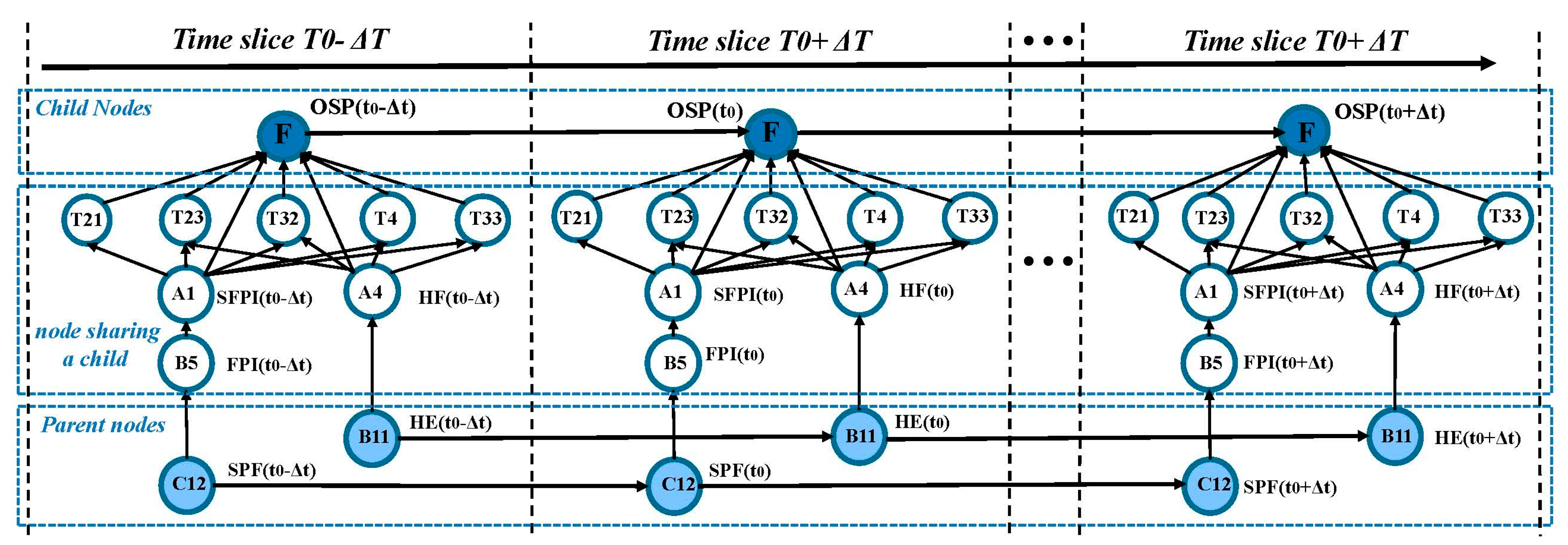
3.4. Determine the Transfer Probability of the Nodes of a Dynamic Bayesian Network
- (i)
- Transfer the probability of sump pump failure
- (ii)
- Human error transfer probability
3.5. Dynamic Analysis of Coupled Risk Dynamics Based on Dynamic Bayesian Networks
- 1.
- A priori analysis (causal inference):
- 2.
- Sensitivity analysis
- 3.
- A posteriori analysis (causative analysis):
3.6. Model Validation
4. Case Study
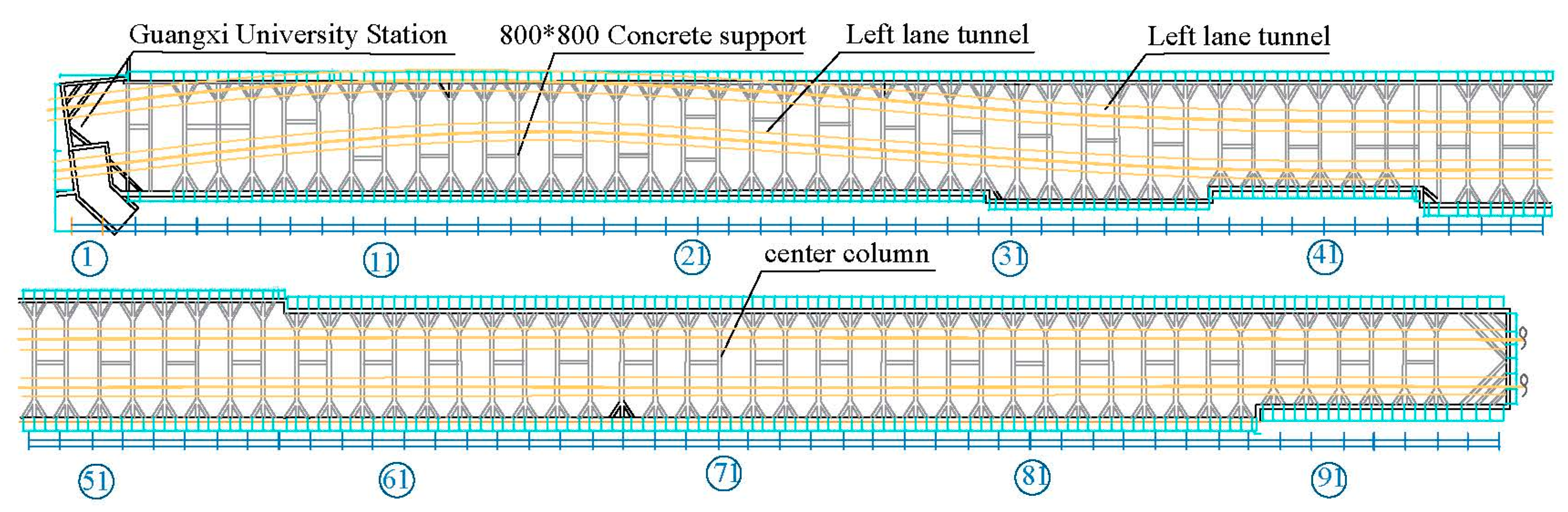
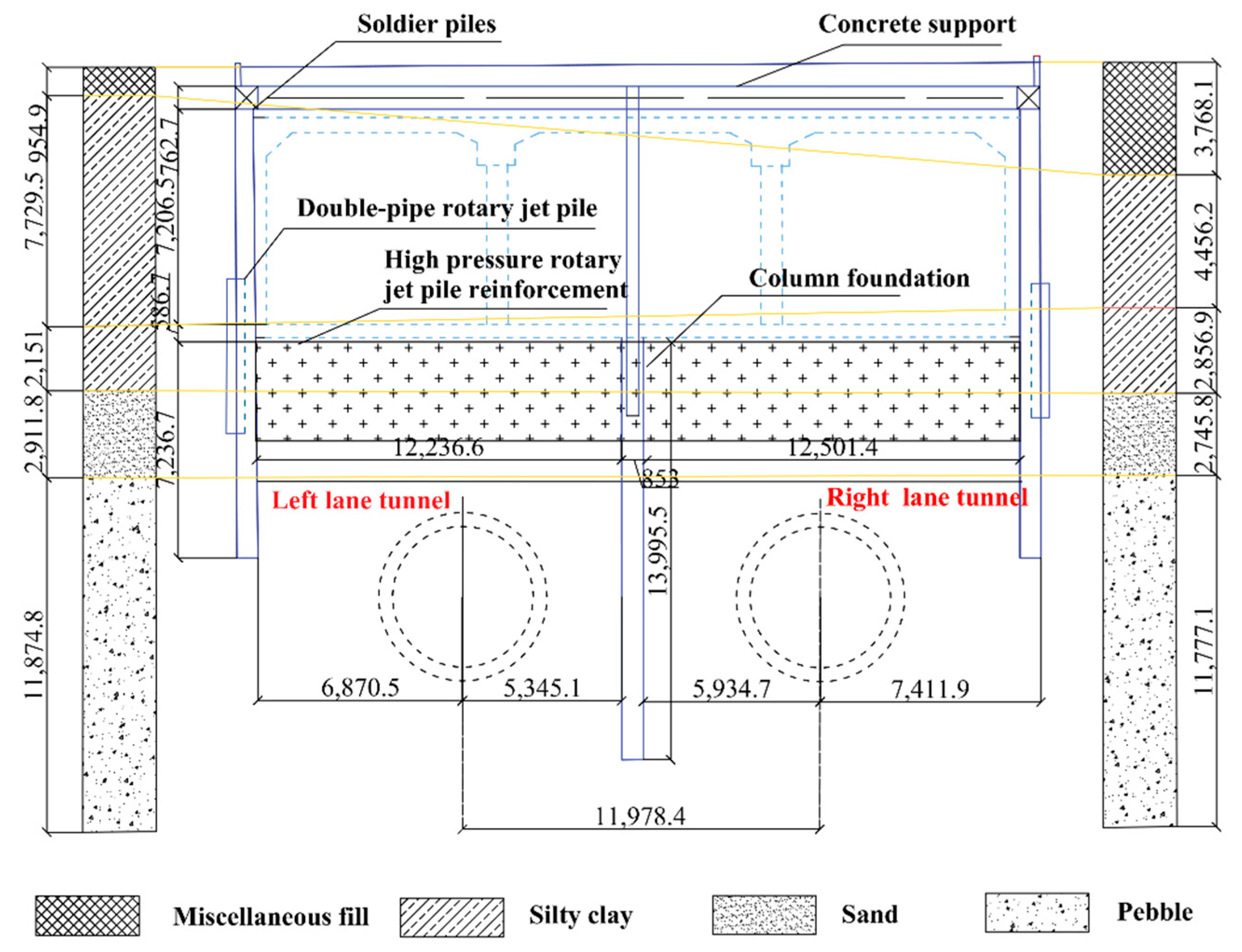
4.1. Project Overview
4.2. Monitoring Data Collection and Processing
4.3. Association Rule Mining
4.4. Risk Coupling of DFP Construction in Adjacent Existing Underpass Tunnels
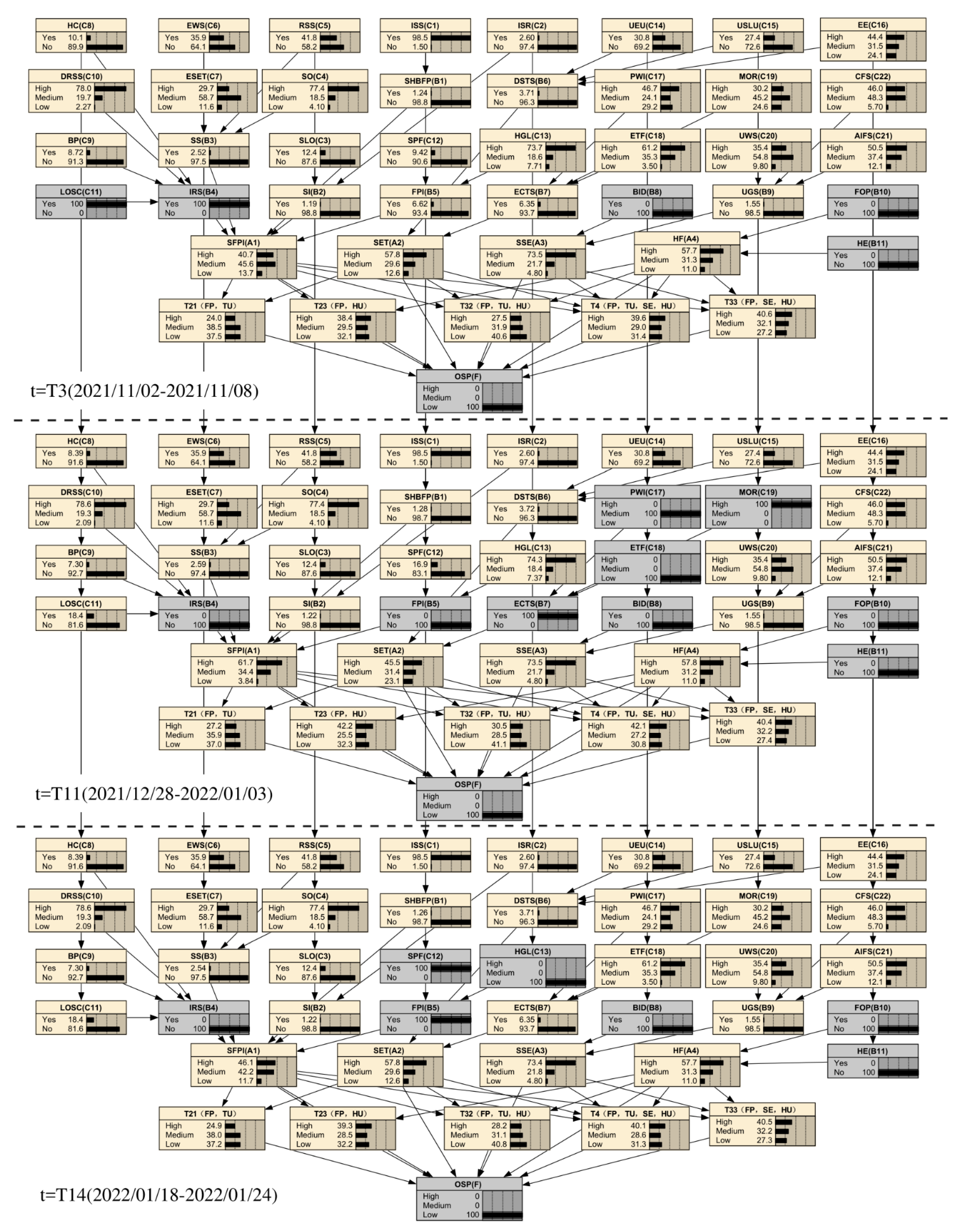
4.5. Establishment of Dynamic Bayesian Network for Construction Risk of DFPs Adjacent to Existing Underpass Tunnels
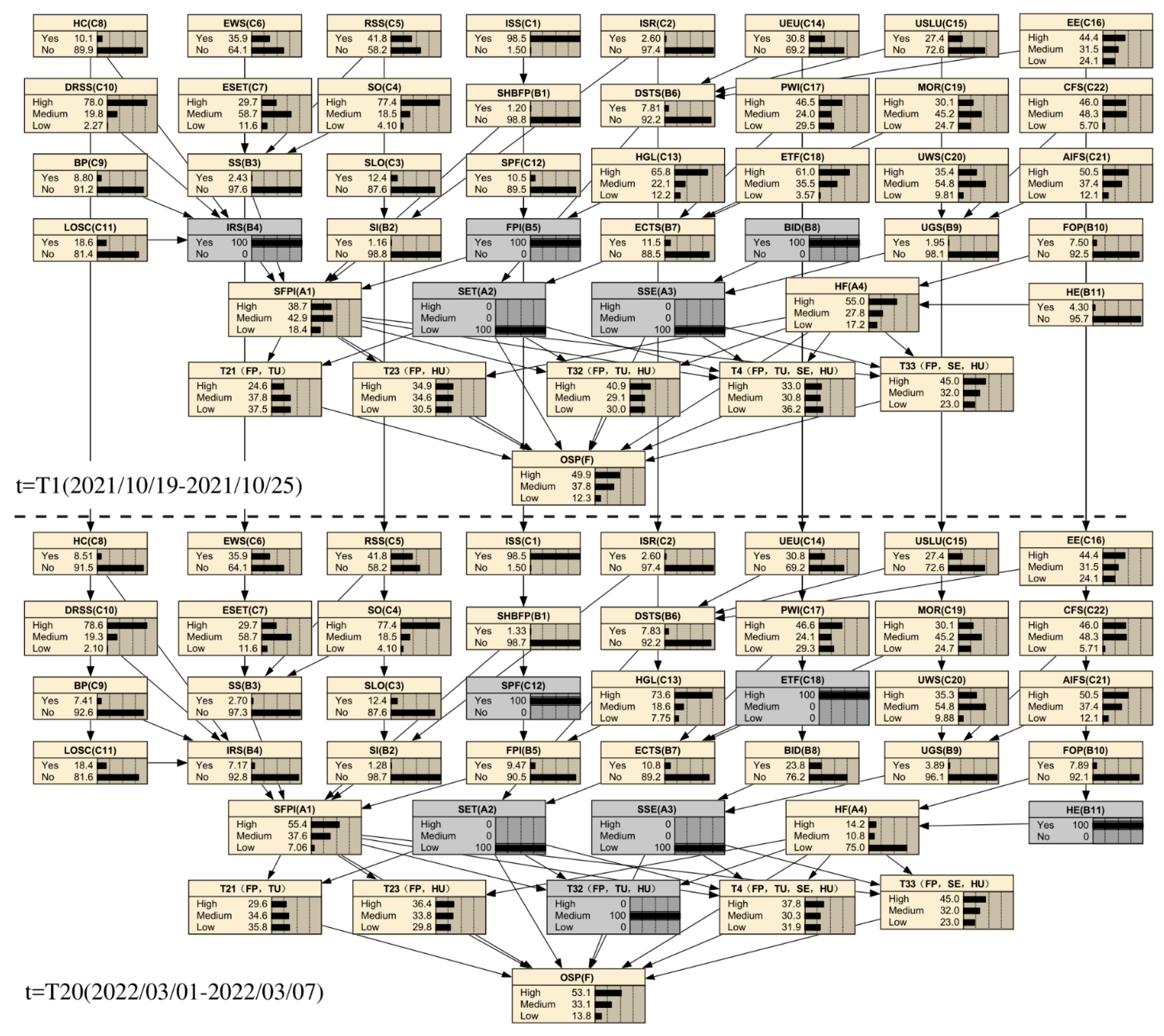
4.6. Model Validation Stage
5. Results and Discussion
5.1. Risk Prediction Based on Dynamic Bayesian Networks for Foundation Pits Adjacent to Existing Underpass Tunnels
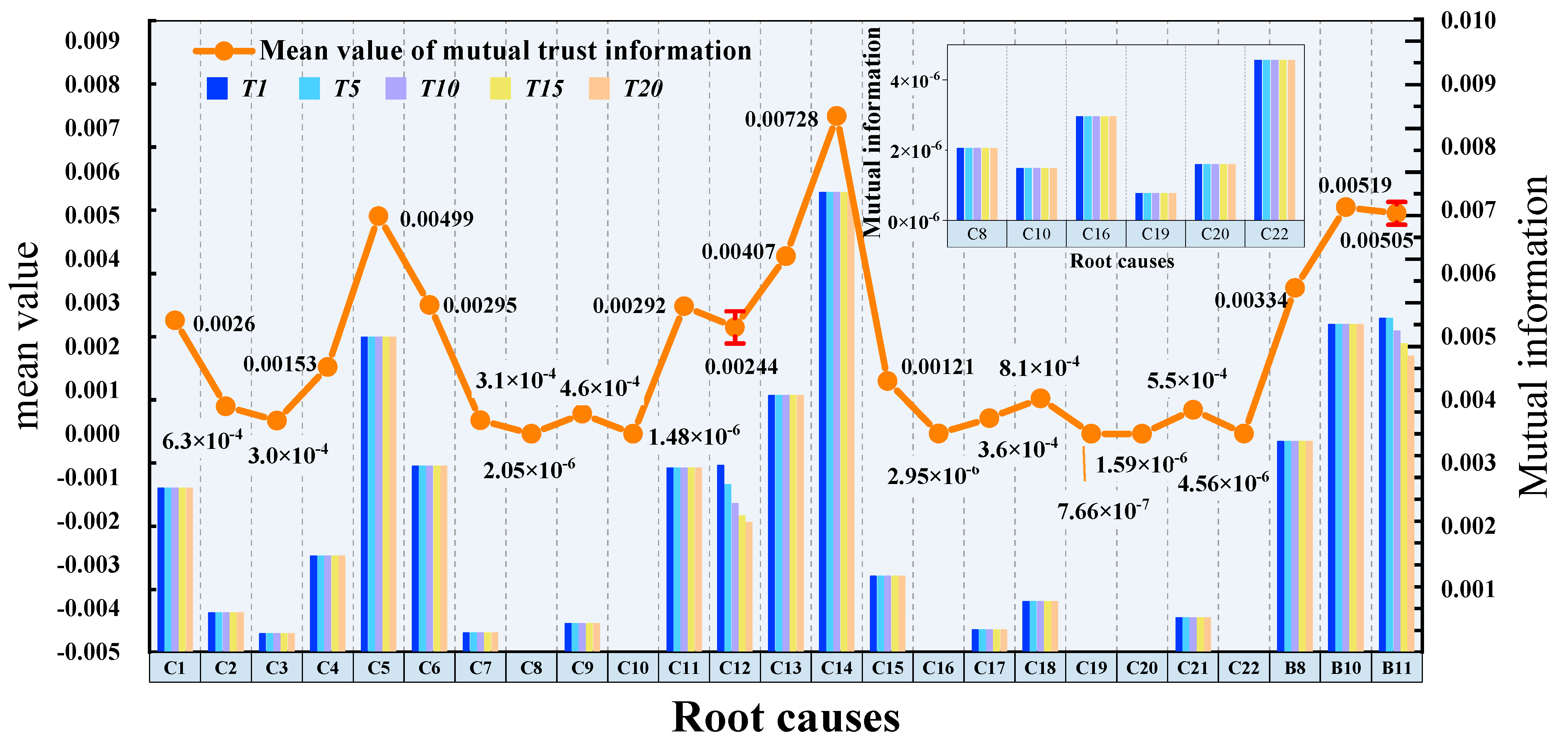
5.2. Mutual Information-Based Sensitivity Analysis
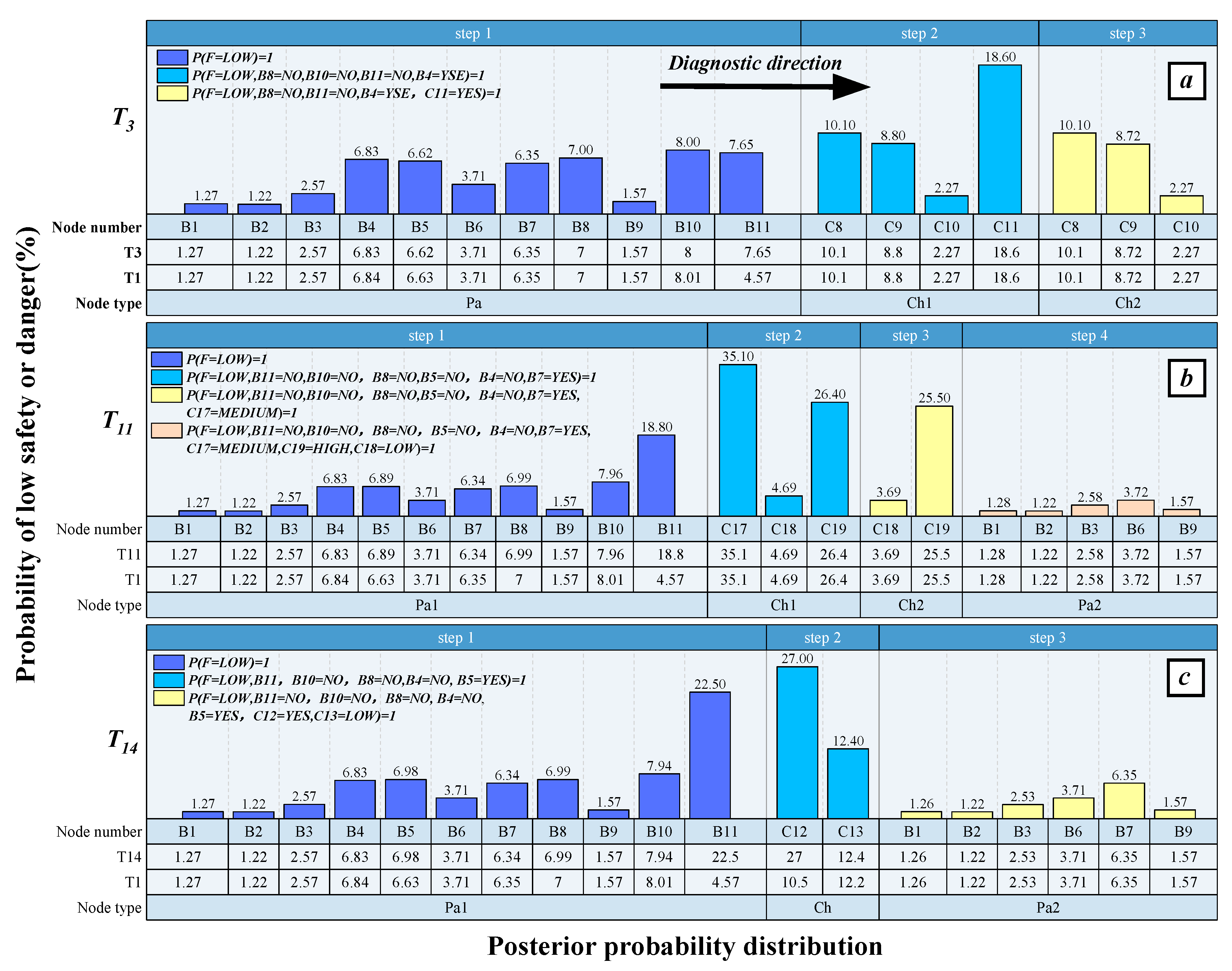
5.3. Practical Application (Backward Inference)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, Q. Present state, problems and development trends of urban underground space in China. Tunn. Undergr. Space Technol. 2016, 55, 280–289. [Google Scholar] [CrossRef]
- Castaldo, P.; Jalayer, F.; Palazzo, B. Probabilistic assessment of groundwater leakage in diaphragm wall joints for deep excavations. Tunn. Undergr. Space Technol. 2018, 71, 531–543. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Ding, L.; Sekula, P.; Love, P.E.; Zhou, C. Combining association rules mining with complex networks to monitor coupled risks. Reliab. Eng. Syst. Saf. 2019, 186, 194–208. [Google Scholar] [CrossRef]
- Wei, M.; Meng, W.; Dai, F.; Wu, W. Application of machine learning to prediction of rate-dependent compressive strength of rocks. J. Rock Mech. Geotech. Eng. 2022, 14, 1356–1365. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, G.; Li, Y.; Wei, M.; Liu, B. Displacement Back-Analysis of Rock Mass Parameters for Underground Caverns Using a Novel Intelligent Optimization Method. Int. J. Geomech. 2020, 20, 04020035. [Google Scholar] [CrossRef]
- Dong, L. Research on the Safety Risk of Existing Tunnel Adjacent to Deep Excavation. Master’s Thesis, Hunan University, Changsha, China, 2018. [Google Scholar]
- Nezarat, H.; Sereshki, F.; Ataei, M. Ranking of geological risks in mechanized tunneling by using Fuzzy Analytical Hierarchy Process (FAHP). Tunn. Undergr. Space Technol. 2015, 50, 358–364. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.; Zhang, L.; Skibniewski, M.J.; Deng, Q.; Teng, J. A dynamic Bayesian network based approach to safety decision support in tunnel construction. Reliab. Eng. Syst. Saf. 2015, 134, 157–168. [Google Scholar] [CrossRef]
- Sihombing, F.; Torbol, M. Parallel fault tree analysis for accurate reliability of complex systems. Struct. Saf. 2018, 72, 41–53. [Google Scholar] [CrossRef]
- Kabir, S. An overview of fault tree analysis and its application in model based dependability analysis. Expert Syst. Appl. 2017, 77, 114–135. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wei, M.; Su, G.; Li, Y.; Zeng, J.; Deng, X. A Novel Intelligent Method for Predicting the Penetration Rate of the Tunnel Boring Machine in Rocks. Math. Probl. Eng. 2020, 2020, 3268694. [Google Scholar] [CrossRef]
- Ding, L.; Fang, W.; Luo, H.; Love, P.E.D.; Zhong, B.; Ouyang, X. A deep hybrid learning model to detect unsafe behavior: Integrating convolution neural networks and long short-term memory. Autom. Constr. 2018, 86, 118–124. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Skibniewski, M.J.; Zhong, J.; Lu, Y. Bayesian-network-based safety risk analysis in construction projects. Reliab. Eng. Syst. Saf. 2014, 131, 29–39. [Google Scholar] [CrossRef]
- Wang, H.; Yajima, A.; Liang, R.Y.; Castaneda, H. Bayesian Modeling of External Corrosion in Underground Pipelines Based on the Integration of Markov Chain Monte Carlo Techniques and Clustered Inspection Data. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 300–316. [Google Scholar] [CrossRef]
- Yang, K. Multi-Factor Coupling Disaster-Causing Mechanism and Disaster Control Study of City Gas Pipeline Leakage. Ph.D. Thesis, Capital University of Economics and Business, Beijing, China, 2016. [Google Scholar]
- Qiao, W. Analysis and measurement of multifactor risk in underground coal mine accidents based on coupling theory. Reliab. Eng. Syst. Saf. 2021, 208, 107433. [Google Scholar] [CrossRef]
- Telikani, A.; Shahbahrami, A. Data sanitization in association rule mining: An analytical review. Expert Syst. Appl. 2018, 96, 406–426. [Google Scholar] [CrossRef]
- Song, K.; Lee, K. Predictability-based collective class association rule mining. Expert Syst. Appl. 2017, 79, 1–7. [Google Scholar] [CrossRef]
- Luna, J.M.; Cano, A.; Sakalauskas, V.; Ventura, S. Discovering useful useful patterns from multiple instance data. Inf. Sci. 2016, 357, 23–38. [Google Scholar] [CrossRef]
- Sowan, B.; Dahal, K.; Hossain, M.A.; Zhang, L.; Spencer, L. Fuzzy association rule mining approaches for enhancing prediction performance. Expert Syst. Appl. 2013, 40, 6928–6937. [Google Scholar] [CrossRef]
- Li, N.; Zeng, L.; He, Q.; Shi, Z. Parallel implementation of apriori algorithm based on mapreduce. In Proceedings of the 2012 13th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing: IEEE, Kyoto, Japan, 8–10 August 2012; pp. 236–241. [Google Scholar]
- Pearl, J. Fusion, propagation, and structuring in belief networks. Artif. Intell. 1986, 29, 241–288. [Google Scholar] [CrossRef] [Green Version]
- Liu, S. A Study on Oil Company Risk of ProductionSafety Based on Employee Behavior Reliability. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2014. [Google Scholar]
- Kauffman, S.A.; Weinberger, E.D. The NK model of rugged fitness landscapes and its application to maturation of the immune response. J. Theor. Biol. 1989, 141, 211–245. [Google Scholar] [CrossRef]
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Ganco, M. NK model as a representation of innovative search. Res. Policy 2017, 46, 1783–1800. [Google Scholar] [CrossRef]
- Kohda, T.; Cui, W. Risk-based reconfiguration of safety monitoring system using dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2007, 92, 1716–1723. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Ding, L.; Skibniewski, M.J.; Yan, Y. Decision support analysis for safety control in complex project environments based on Bayesian Networks. Expert Syst. Appl. 2013, 40, 4273–4282. [Google Scholar] [CrossRef]
- Lee, E.; Park, Y.; Shin, J.G. Large engineering project risk management using a Bayesian belief network. Expert Syst. Appl. 2009, 36, 5880–5887. [Google Scholar] [CrossRef]
- Jones, B.; Jenkinson, I.; Yang, Z.; Wang, J. The use of Bayesian network modelling for maintenance planning in a manufacturing industry. Reliab. Eng. Syst. Saf. 2010, 95, 267–277. [Google Scholar] [CrossRef]







| Risk Factors | Overall Project Risk Indicators | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Heaped Load q (KPa) | Storm Water Volume Q (mm) | Soil Exposure Time T (h) | … | Unit Weight of Soil γ (KN/m3) | The Angle of Internal Friction φ (°) | Cohesive Forces of Soil c (KPa) | Surrounding Surface Sedimentation (mm) | Bottom Heave (mm) | … | Lateral Displacement of Enclosure (mm) |
| 1 | 4.58 | 12.4 | 9 | … | 18.7 | 7 | 13 | −3.8724 | 5.4341 | … | −4.5328 |
| 2 | 4.49 | 64.2 | 8 | … | 18.7 | 7 | 13 | −3.3455 | 11.6254 | … | −5.3243 |
| 3 | 4.98 | 0.0 | 7 | … | 19.6 | 12 | 50 | −4.5126 | 9.5108 | … | −6.5427 |
| 4 | 5.34 | 5.8 | 12 | … | 19.6 | 12 | 50 | −2.1458 | 8.1652 | … | −4.2258 |
| 5 | 3.98 | 0.0 | 10 | … | 19.6 | 12 | 50 | −2.5219 | 12.8014 | … | −5.1078 |
| 6 | 4.17 | 0.0 | 8 | … | 19.2 | 11 | 30 | −2.9757 | 11.5201 | … | −4.0549 |
| 7 | 4.95 | 0.0 | 9 | … | 19.6 | 12 | 50 | −4.5542 | 7.0734 | … | −5.5245 |
| 8 | 6.24 | 0.0 | 10 | … | 19.6 | 12 | 50 | −9.8245 | 15.9219 | … | −5.4378 |
| 9 | 5.83 | 205.9 | 13 | … | 19.2 | 11 | 30 | −8.4597 | 18.4524 | … | −4.3218 |
| 10 | 7.84 | 72.5 | 9 | … | 19.2 | 11 | 3 | −11.3248 | 19.5203 | … | −2.4245 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 136 | 5.39 | 9.0 | 15 | … | 18.1 | 3 | 5 | −5.5256 | 10.3251 | … | −3.4324 |
| 137 | 9.51 | 0.0 | 18 | … | 18.1 | 3 | 5 | −3.4457 | 11.4983 | … | −4.5267 |
| 138 | 8.37 | 14.3 | 14 | … | 22.0 | 33 | 0 | −9.2864 | 9.7247 | … | 5.6271 |
| 139 | 12.84 | 11.8 | 15 | … | 22.0 | 33 | 0 | −2.7458 | 14.6214 | … | 3.8245 |
| 140 | 11.92 | 0.0 | 10 | … | 19.2 | 11 | 30 | −11.8124 | 8.6328 | … | 9.7794 |
| 141 | 16.07 | 0.0 | 8 | … | 19.6 | 12 | 50 | −14.1579 | 12.8047 | … | −3.5124 |
| 142 | 8.64 | 8.5 | 19 | … | 19.6 | 12 | 50 | −4.2781 | 12.4125 | … | −2.4469 |
| 143 | 9.75 | 0.0 | 14 | … | 19.6 | 12 | 50 | −7.6413 | 13.2934 | … | 9.7728 |
| Risk Events | Levels | Description | Prior p | Risk Events | Levels | Description | Prior p |
|---|---|---|---|---|---|---|---|
| C1 Insufficient soil strength (ISS) | Yes | Soil reinforced | 0.015 | C18 Excavation is too fast (ETF) | Low | L > 0.7 H | 0.035 |
| No | Soil reinforcement | 0.985 | Medium | 0.3 H < L ≤ 0.7 H | 0.353 | ||
| C2 Insufficient support resistance (ISR) | Yes | Whether the resistance reaches the design value | 0.026 | High | L ≤ 0.3H | 0.612 | |
| No | 0.974 | C19 Mechanical operation regularity (MOR) | Low | The degree of regulation of operation | 0.246 | ||
| C3 Support load overload (SLO) | Yes | Whether the actual axial force exceeds the design value | 0.124 | Medium | 0.452 | ||
| No | 0.876 | High | 0.302 | ||||
| C4 Heaped load (HL) | Low | q > 20 KPa | 0.041 | C20 unit weight of soil (UWS) | Low | γ > 19% | 0.098 |
| Medium | 15 KPa < q ≤ 20 KPa | 0.185 | Medium | 17% < γ ≤ 19% | 0.548 | ||
| High | q ≤ 15 KPa | 0.774 | High | γ ≤ 17% | 0.354 | ||
| C5 Release slope too steep (RSS) | Yes | The sloping coefficient k > 0.7 | 0.418 | C21 The angle of internal friction of soil (AIFS) | Low | ψ ≤ 9 | 0.121 |
| No | The sloping coefficient k ≤ 0.7 | 0.582 | Medium | 9 < ψ ≤ 18 | 0.374 | ||
| C6 Excessive amount of water in the storm (EWS) | Yes | Q > 200 mm | 0.359 | High | ψ > 18 | 0.505 | |
| No | Q < 200 mm | 0.641 | C22 The cohesive forces of soil (CFS) | Low | c ≤ 10 | 0.057 | |
| C7 Excessive soil exposure time (ESET) | Low | T > 24 h | 0.116 | Medium | 10 < c ≤ 20 | 0.483 | |
| Medium | 18 < T ≤ 24 h | 0.587 | High | c > 20 | 0.460 | ||
| High | T ≤ 18 h | 0.297 | B1 bottom heave (BH) | Yes | Whether the bottom is heaving | 0.012 | |
| No | 0.099 | ||||||
| C8 Hole collapse (HC) | Yes | Hole collapse occurs | 0.085 | ||||
| No | No hole collapse | 0.915 | B2 Support instability (SI) | Yes | Whether the support deformation instability | 0.012 | |
| C9 Broken Pile (BP) | Yes | Jet grouting pile deformation | 0.074 | No | 0.988 | ||
| No | No deformation | 0.926 | B3 Slope slip (SS) | Yes | Whether slope instability occurs | 0.243 | |
| C10 Depth of retaining structure into soil (DRSS) | Low | W ≤ 0.7 H | 0.021 | No | 0.976 | ||
| Medium | 0.7 H < W ≤ 0.9 H | 0.193 | B4 Instability of retaining structure (IRS) | Yes | Whether the retaining structure is destabilized | 0.065 | |
| High | W > 0.9 H | 0.786 | No | 0.935 | |||
| C11 Leakage occurred in the sealing curtain (LOSC) | Yes | Whether the curtain has water seepage | 0.184 | B5 Foundation pit inrush (FPI) | Yes | Whether a sudden water-inrush accident occurs | 0.064 |
| No | 0.816 | No | 0.936 | ||||
| C12 Sewage pump failure (SPF) | Yes | Whether the sewage pump is faulty | 0.076 | B6 Differential settlement of tunnel structure (DSTS) | Yes | Whether uneven settlement occurs | 0.037 |
| No | 0.924 | No | 0.964 | ||||
| C13 High groundwater level (HGL) | Low | D > −8 m | 0.047 | B7 Excessive convergence of tunnel section (ECTS) | Yes | Whether the tunnel section is excessive convergence | 0.063 |
| Medium | −10 m < D ≤ −8 m | 0.216 | No | 0.937 | |||
| High | D ≤ −10 m | 0.737 | B8 Building inclination and damage (BID) | Yes | Whether damage occurs to the surrounding buildings | 0.068 | |
| C14 Uneven excavation and unloading (UEU) | Yes | Does the excavation meet the specifications | 0.308 | No | 0.932 | ||
| No | 0.692 | B9 Uneven ground settlement (UGS) | Yes | Whether the surface is unevenly settled | 0.015 | ||
| C15 Uneven soil layer underneath (USLU) | Yes | Uneven stratigraphic conditions | 0.274 | No | 00985 | ||
| No | 0.726 | B10 Failure to follow operating procedures (FOP) | Yes | Whether there are irregular operations | 0.075 | ||
| C16 Excess Excavation (EE) | Low | Over-excavation ≤ 10% | 0.241 | No | 0.925 | ||
| Medium | 10% < Over-excavation ≤ 30% | 0.315 | B11 Human error (HE) | Yes | Whether fatigue and distraction | 0.043 | |
| High | Over-excavation > 30% | 0.444 | No | 0.957 | |||
| C17 Presence of weak interlayer (PWI) | Low | P > 30% | 0.292 | A1 Stability of foundation pit itself (SFPI) | Low | Comprehensive evaluation by experts | 0.038 |
| Medium | 10 < P ≤ 30% | 0.241 | Medium | 0.310 | |||
| High | P ≤ 10% | 0.467 | High | 0.652 | |||
| A2 Stability of existing tunnel (SET) | Low | Comprehensive evaluation by experts | 0.117 | A3 Stability of surrounding environment (SSE) | Low | Comprehensive evaluation by experts | 0.056 |
| Medium | 0.284 | Medium | 0.226 | ||||
| High | 0.600 | High | 0.718 | ||||
| A4 Human factors (HF) | Low | Comprehensive evaluation by experts | 0.265 | F Overall safety of the project (OSP) | Low | Comprehensive evaluation by experts | 0.105 |
| Medium | 0.250 | Medium | 0.235 | ||||
| High | 0.484 | High | 0.659 |
| Two Frequent Item Sets | Support | Three Frequent Item Sets | Support | Four Frequent Item Sets | Support |
|---|---|---|---|---|---|
| {SLO-Y, SI-Y} | 0.511 | {ISR-Y, SLO-Y, SI-Y} | 0.452 | {SS-Y, HL-M, RSS-Y, SFPI-M} | 0.405 |
| {RSS-Y, SS-Y} | 0.498 | {RSS-Y, EWS-M, SS-Y} | 0.471 | {HL-M, RSS-Y, SS-Y, EWS-L} | 0.409 |
| {UGS-Y, CFS-L} | 0.492 | {BP-Y, DRSS-L, IRS-Y} | 0.422 | {SET-M, UEU-Y, USLU-Y, DSTS-M} | 0.401 |
| {HF-Y, FOP-Y} | 0.507 | {DRSS-M, HC-Y, IRS-Y} | 0.455 | {SSE-M, BID-Y, UGS-Y, UWS-M} | 0.411 |
| {BH-Y, ISS-N} | 0.514 | {UEU-Y, DSTS-Y, EE-Y} | 0.436 | {SS-Y, SI-Y, BH-Y, SFPI-M} | 0.413 |
| {HF-Y, HE-Y} | 0.489 | {PWI-M, ETF-L, ECTS-Y} | 0.408 | {IRS-Y, HC-Y, BP-Y, SFPI-Y} | 0.414 |
| {IRS-Y, DRSS-L} … | 0.496 … | {UWS-M, CFS-M, UGS-Y} … | 0.434 … | {FPI-Y, SFPI-M, SPF-Y, HGL-Y} … | 0.408 … |
| Left Side of Association Rules | Right Side of Association Rules | Lift | Support | Confidence |
|---|---|---|---|---|
{UEU-Y, DSTS-Y, EE-Y}  | {SET-M} | 1.3327 | 0.581 | 0.983 |
{PWI-M, ETF-L, ECTS-Y}  | {OSP-M, SET-M} | 1.3319 | 0.560 | 0.982 |
{SS-Y, HL-M, RSS-Y, SFPI-M}  | {OSP-M} | 1.3218 | 0.552 | 0.982 |
{IRS-Y, HC-Y, BP-Y, LOSC-Y}  | {SFPI-M} | 1.3201 | 0.561 | 0.966 |
{PWI-M, ETF-L, ECTS-Y}  | {OSP-M, SET-M} | 1.3105 | 0.540 | 0.931 |
{HL-M, RSS-Y, SS-Y, EWS-L}  | {OSP-M, SFPI-M} | 1.3098 | 0.551 | 0.932 |
{DRSS-M, HC-Y, IRS-Y}  … | {SFPI-M} … | 1.3051 … | 0.511 … | 0.879 … |
| Types of Risk Coupling | Involving Risk Factors | Times | Probability |
|---|---|---|---|
| Single-factor risk coupling | Foundation pit | 6 | P1000 = 0.070 |
| Existing tunnel | 1 | P0100 = 0.012 | |
| Surrounding environment | 24 | P0010 = 0.279 | |
| Human factors | 12 | P0001 = 0.140 | |
| Double-factor risk coupling | Foundation pit–existing tunnel | 4 | P1100 = 0.047 |
| Foundation pit–surrounding environment | 16 | P1010 = 0.186 | |
| Foundation pit–human factors | 3 | P1001 = 0.035 | |
| Existing tunnel–surrounding environment | 2 | P0110 = 0.023 | |
| Existing tunnel–human factors | 0 | P0101 = 0.000 | |
| Surrounding environment–human factors | 8 | P0011 = 0.093 | |
| Multifactor risk coupling | Foundation pit–existing tunnel–surrounding environment | 6 | P1110 = 0.070 |
| Foundation pit–existing tunnel–human factors | 0 | P1101 = 0.000 | |
| Foundation pit–surrounding environment–human factors | 2 | P1011 = 0.023 | |
| Existing tunnel–surrounding environment–human factors | 1 | P0111 = 0.012 | |
| Foundation pit–existing tunnel–surrounding environment–human factors | 1 | P1111 = 0.012 |
| P0... | P1... | P.0.. | P.1.. | P..0. | P..1. | P…0 | P…1 | P00.. | P01.. | P10.. | P11.. | P0.0. | P1.0. | P0.1. | P1.1. |
| 0.558 | 0.372 | 0.826 | 0.174 | 0.302 | 0.698 | 0.686 | 0.314 | 0.512 | 0.047 | 0.314 | 0.128 | 0.151 | 0.151 | 0.407 | 0.291 |
| P0..0 | P1..0 | P0..1 | P1..1 | P.00. | P.10. | P.01. | P.11. | P.0.0 | P.1.0 | P.0.1 | P.1.1 | P..00 | P..10 | P..01 | P..11 |
| 0.314 | 0.372 | 0.244 | 0.070 | 0.244 | 0.058 | 0.581 | 0.116 | 0.535 | 0.105 | 0.291 | 0.023 | 0.128 | 0.558 | 0.174 | 0.140 |
| P000. | P100. | P010. | P001. | P110. | P101. | P011. | P111. | P00.0 | P10.0 | P01.0 | P00.1 | P11.0 | P10.1 | P01.1 | P11.1 |
| 0.140 | 0.105 | 0.012 | 0.372 | 0.047 | 0.209 | 0.035 | 0.081 | 0.279 | 0.256 | 0.035 | 0.233 | 0.116 | 0.058 | 0.012 | 0.012 |
| P0.00 | P1.00 | P0.10 | P0.01 | P1.10 | P1.01 | P0.11 | P1.11 | P.000 | P.100 | P.010 | P.001 | P.110 | P.101 | P.011 | P.111 |
| 0.012 | 0.116 | 0.302 | 0.140 | 0.256 | 0.035 | 0.105 | 0.035 | 0.070 | 0.058 | 0.465 | 0.174 | 0.093 | 0.000 | 0.116 | 0.023 |
| T21 | T22 | T23 | T24 | T25 | T26 | T31 | T32 | T33 | T34 | T4 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.183 | 0.115 | 0.178 | 4 × 10−4 | 2 × 10−4 | 0.091 | 0.174 | 0.238 | 0.343 | 0.176 | 0.463 |
| No. | Test Samples | Safety of DFPs Adjacent to Existing Underpass Tunnels | Expectation | Actuality | ||
|---|---|---|---|---|---|---|
| High | Medium | Low | ||||
| 1 | C1 = No; C3 = Yes; C13 = Low; C14 = No; B5 = Yes | 64.8% | 24.8% | 10.5% | High | High |
| 2 | A1 = Medium; A2 = Low; B7 = No; B7, B11 = Yes | 43.3% | 43.6% | 13.1% | Medium | Medium |
| 3 | A2 = Medium; B5, C11, C3 = Yes; B6 = No; C18 = High | 60.5% | 28.6% | 10.9% | High | High |
| 4 | C1, C3 = Yes; B2, C12 = No; C13, C22 = High | 67.0% | 23.0% | 10.0% | High | High |
| 5 | A4, A1 = Low, B6, B7, B8, B9 = Yes | 42.3% | 42.4% | 15.2% | Medium | High |
| 6 | B5 = No; C2 = Yes; C18 = High; A1 = Medium | 49.8% | 38.0% | 12.2% | High | High |
| 7 | A4 = Medium, B2, B7 = Yes, B5, C2 = No, C20 = Low | 62.0 | 26.9% | 11.1% | High | High |
| … | … | … | … | … | … | … |
| 19 | B8, B6, C11, C12 = No; B2 = Yes; C17 = High | 64.3% | 25.1% | 10.6% | High | High |
| 20 | B2, B3, B8, B9,C11, C12 = No; C13, C21, C16 = High | 59.6% | 29% | 11.4% | High | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Liu, G.; Ou, X. Risk Coupling Analysis of Deep Foundation Pits Adjacent to Existing Underpass Tunnels Based on Dynamic Bayesian Network and N–K Model. Appl. Sci. 2022, 12, 10467. https://doi.org/10.3390/app122010467
Jiang J, Liu G, Ou X. Risk Coupling Analysis of Deep Foundation Pits Adjacent to Existing Underpass Tunnels Based on Dynamic Bayesian Network and N–K Model. Applied Sciences. 2022; 12(20):10467. https://doi.org/10.3390/app122010467
Chicago/Turabian StyleJiang, Jie, Guangyang Liu, and Xiaoduo Ou. 2022. "Risk Coupling Analysis of Deep Foundation Pits Adjacent to Existing Underpass Tunnels Based on Dynamic Bayesian Network and N–K Model" Applied Sciences 12, no. 20: 10467. https://doi.org/10.3390/app122010467
APA StyleJiang, J., Liu, G., & Ou, X. (2022). Risk Coupling Analysis of Deep Foundation Pits Adjacent to Existing Underpass Tunnels Based on Dynamic Bayesian Network and N–K Model. Applied Sciences, 12(20), 10467. https://doi.org/10.3390/app122010467





