Model for Estimating the Modulus of Elasticity of Asphalt Layers Using Machine Learning
Abstract
:1. Introduction
2. Theory and Calculation
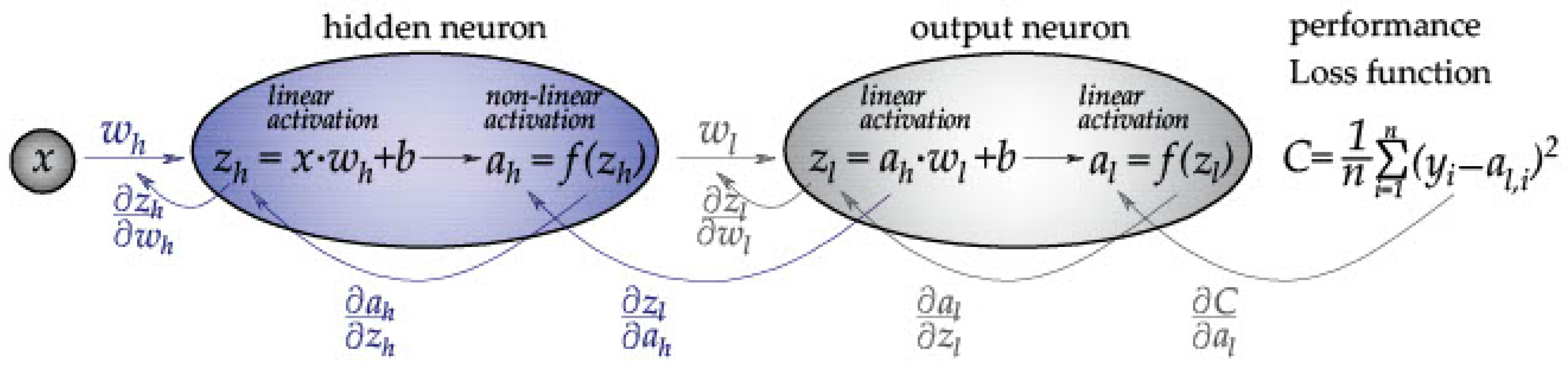
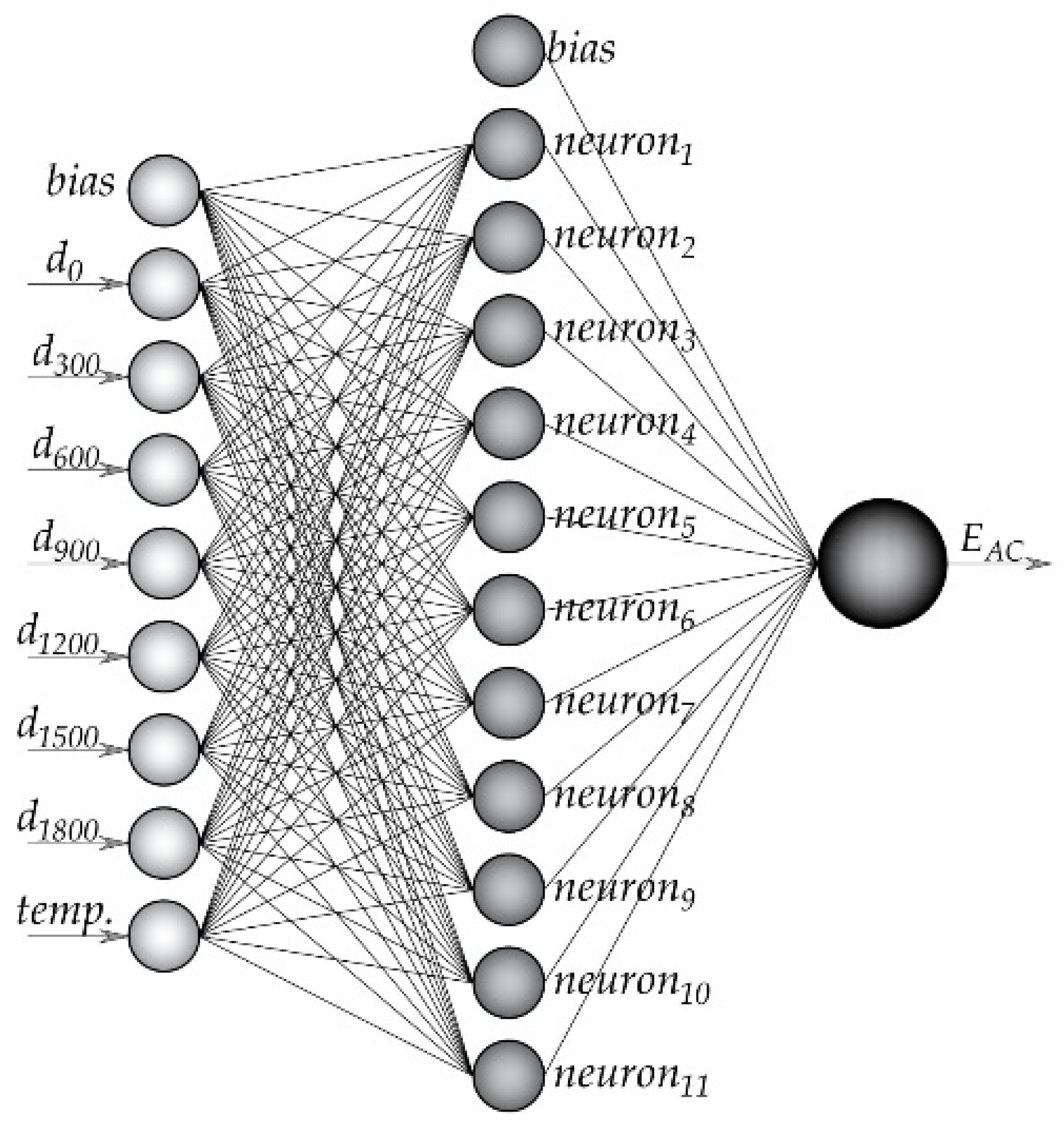
2.1. Artificial Neural Networks (ANN)
- number of input parameters;
- number of layers and neurons in them;
- number of output data;
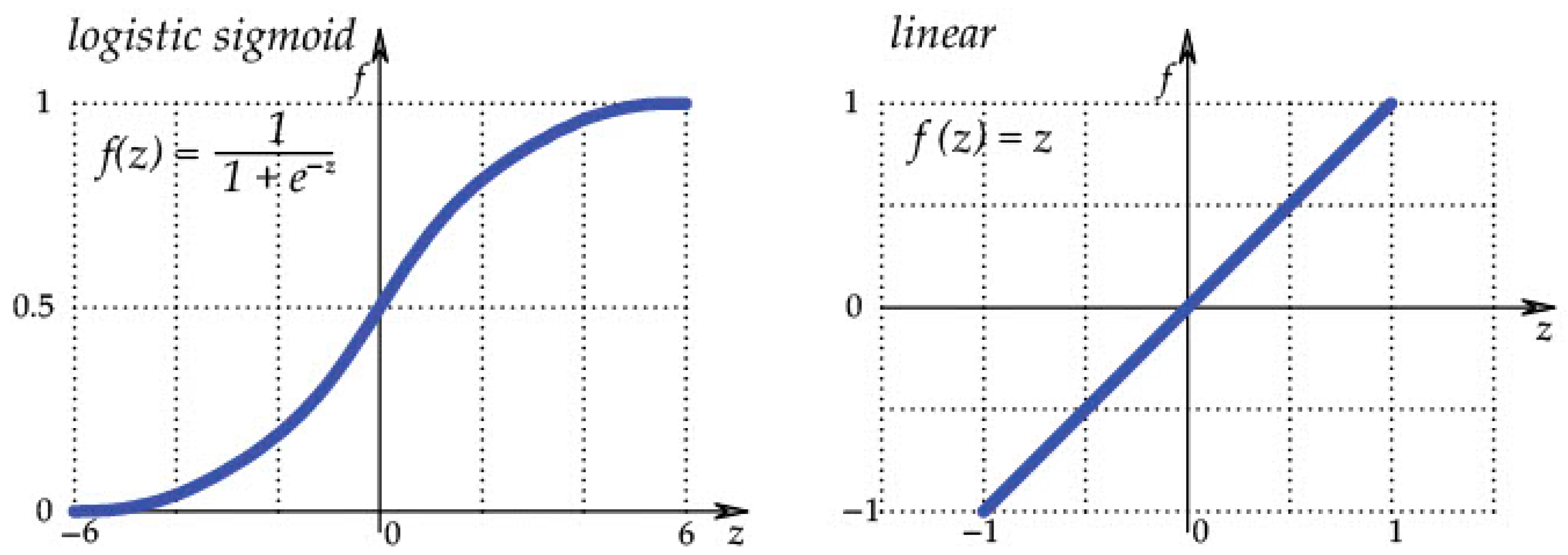
- selection of activation functions of hidden and output neurons;
- type of training function, whether the network is forward- or backward-oriented.
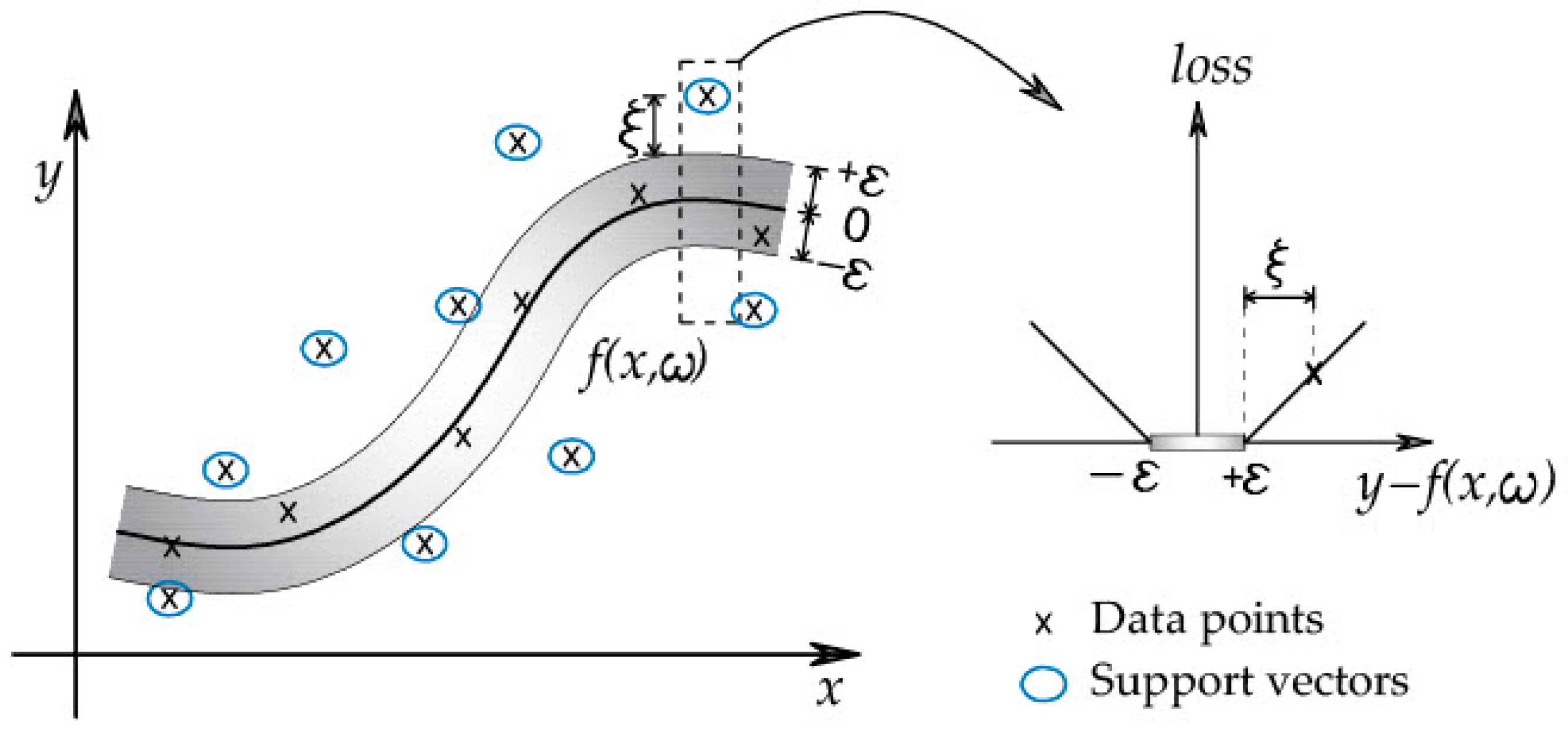
2.2. Support Vector Machine (SVM)
- optimal weight vector:
- optimal bias:
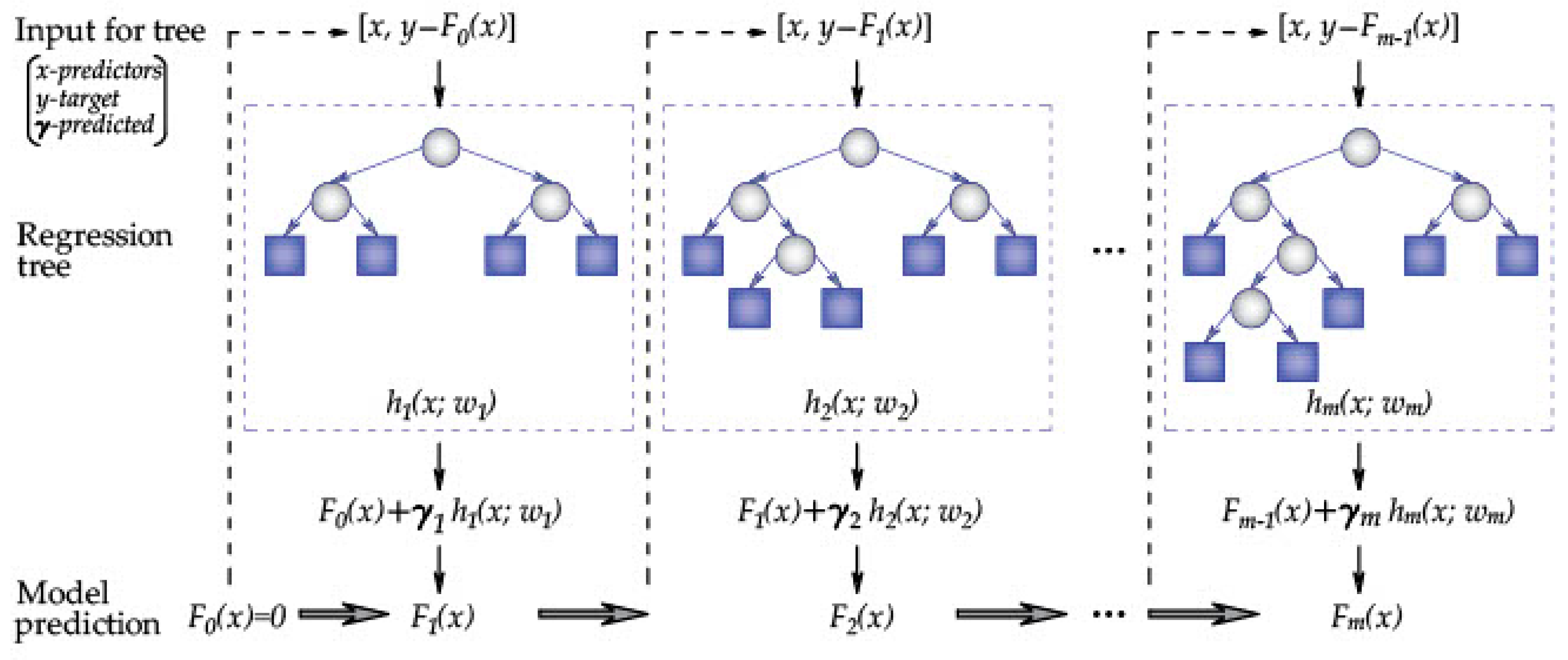
2.3. Boosted Regression Tree (BRT)
- (1)
- The negative value of the gradient of the loss function is calculated, and then it is used as the estimate of the residual, as given in Equation (12):
- (2)
- A regression tree is optimized for the residual obtained in the previous iteration. The step size of the gradient drop is calculated, as represented in Equation (13):
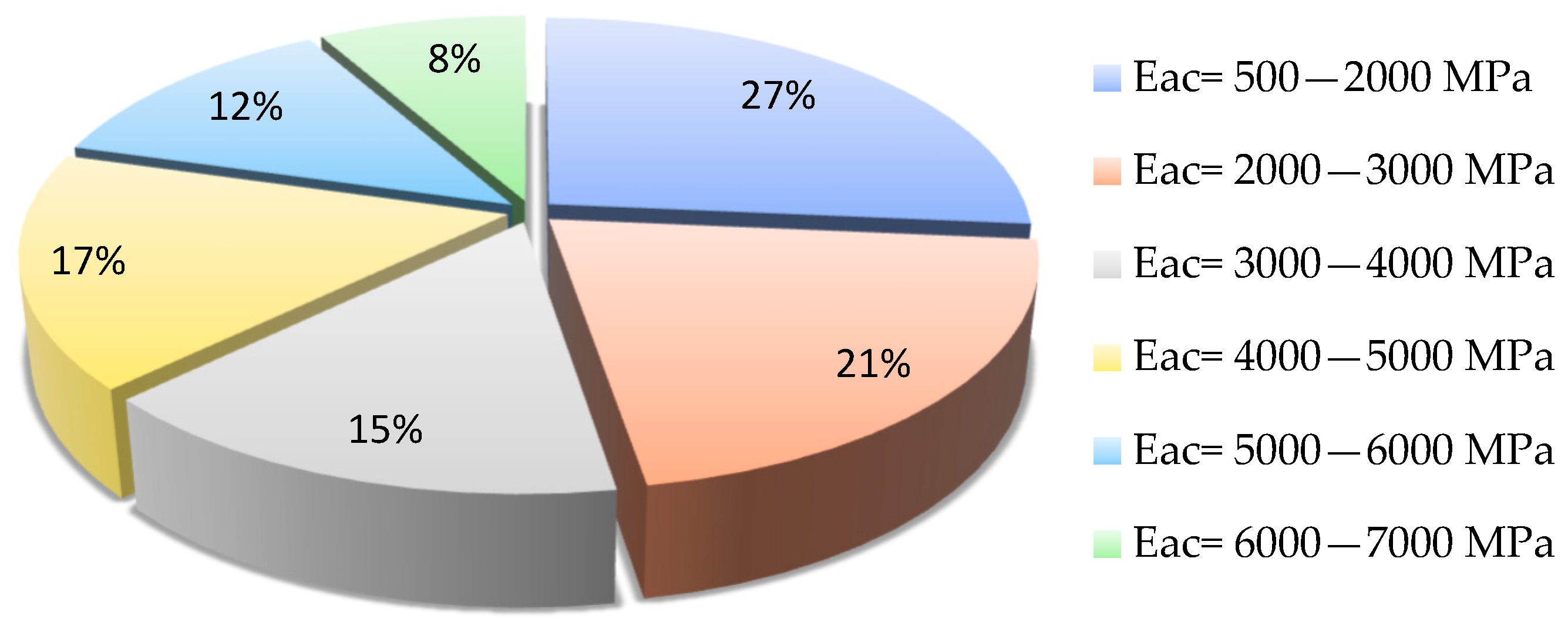
3. Dataset
- modules up to 3000 MPa—poor bearing capacity overall;
- modules from 3000 MPa to 7000 MPa—there are damages in some places;
- modules above 7000 MPa—good bearing capacity overall.
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Talvik, O.; Aavik, A. Use of FWD Deflection Basin Parameters (SCI, BDI, BCI) for Pavement Condition Assessment. Balt. J. Road Bridge Eng. 2009, 4, 196–202. [Google Scholar] [CrossRef]
- Bianchini, A.; Bandini, P. Prediction of pavement performance through Neuro-Fuzzy reasoning. Comput.-Aided Civ. Infrastruct. Eng. 2010, 25, 39–54. [Google Scholar] [CrossRef]
- Karasahin, M.; Terzi, S. Performance model for asphalt concrete pavement based on the fuzzy logic approach. Transport 2014, 29, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Nabipour, N.; Karballaeezadeh, N.; Dineva, A.; Mosavi, A.; Mohammadzadeh, S.D.; Shamshirband, S. Comparative Analysis of Machine Learning Models for Prediction of Remaining Service Life of Flexible Pavement. Mathematics 2019, 7, 1198. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; He, D.; Li, J. Research on the Fatigue Life Prediction for a New Modified Asphalt Mixture of a Support Vector Machine Based on Particle Swarm Optimization. Appl. Sci. 2021, 11, 11867. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Zaremotekhases, F.; Shamshirband, S.; Mosavi, A.; Nabipour, N.; Csiba, P.; Várkonyi-Kóczy, A. Intelligent Road Inspection with Advanced Machine Learning; Hybrid Prediction Models for Smart Mobility and Transportation Maintenance Systems. Energies 2020, 13, 1718. [Google Scholar] [CrossRef] [Green Version]
- Pandelea, A.; Budescu, M.; Covatariu, G. Applications of artificial neural networks in civil engineering. In Proceedings of the 2nd International Conference for Ph.D. Students in Civil Engineering and Architecture CE-PhD 2014, Cluj-Napoca, Romania, 10–13 December 2014. [Google Scholar]
- Abioye, S.; Oyedele, L.; Akanbi, L.; Ajayi, A.; Delgado, J.; Bilal, M.; Akinade, O.; Ahmed, A. Artificial intelligence in the construction industry: A review of present status, opportunities and future challenges. J. Build. Eng. 2021, 44, 103299. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness Modulus and Marshall Parameters of Hot Mix Asphalts: Laboratory Data Modeling by Artificial Neural Networks Characterized by Cross-Validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef] [Green Version]
- Peško, I.; Mučenski, V.; Šešlija, M.; Radović, N.; Vujkov, A.; Bibić, D.; Krklješ, M. Estimation of Costs and Durations of Construction of Urban Roads Using ANN and SVM. Complexity 2017, 2017, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gopalakrishnan, K. Neural Networks Analysis of Airfield Pavement Heavy Weight Deflectometer Data. Open Civ. Eng. J. 2008, 2, 15–23. [Google Scholar] [CrossRef]
- Saltan, M.; Terzi, S. Modeling deflection basin using artificial neural networks with cross-validation technique in backcalculating flexible pavement layer moduli. Adv. Eng. Softw. 2008, 39, 588–592. [Google Scholar] [CrossRef]
- Tutka, P.; Nagórski, R.; Złotowska, M.; Rudnicki, M. Sensitivity Analysis of Determining the Material Parameters of an Asphalt Pavement to Measurement Errors in Backcalculations. Materials 2021, 14, 873. [Google Scholar] [CrossRef]
- Alkasawneh, W. Backcalculation of Pavement Moduli Using Genetic Algorithms. Ph.D. Thesis, The University of Akron, Akron, OH, USA, 2007. [Google Scholar]
- Zang, X.; Otto, F.; Oeser, M. Pavement moduli back-calculation using artificial neural network and genetic algorithms. Construct. Build. Mater. 2021, 287, 123026. [Google Scholar] [CrossRef]
- Meier, R.W.; Rix, G.J. Backcalculation of Flexible Pavement Moduli Using Artificial Neural Networks. Transp. Res. Rec. 1994, 1448, 75–82. [Google Scholar]
- Meier, R.W. Backcalculation of Flexible Pavement Moduli from Falling Weight Deflectometer Data Using Artificial Neural Networks. Ph.D. Thesis, School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA, USA, 1995. [Google Scholar]
- Bredenhann, S.; Ven, M. Application of artificial neural networks in the back-calculation of flexible pavement layer moduli from deflection measurements. In Proceedings of the 8th Conference on Asphalt Pavements for Southern Africa, Roads, The Arteries of Africa, South Africa, 12–16 September 2004; pp. 651–667. [Google Scholar]
- Gopalakrishnan, K.; Thompson, M.R. Backcalculation of airport flexible pavement non-linear moduli using artificial neural networks. In Proceedings of the 17th International FLAIRS Conference, Miami Beach, FL, USA, 2004. [Google Scholar]
- Gopalakrishnan, K. Effect of training algorithms on neural networks aided pavement diagnosis. Int. J. Eng. Sci. Technol. 2010, 2, 83–92. [Google Scholar] [CrossRef]
- Baldo, N.; Miani, M.; Rondinella, F.; Celauro, C. A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data. Sustainability 2021, 13, 8831. [Google Scholar] [CrossRef]
- Baldo, N.; Miani, M.; Rondinella, F.; Celauro, C. Artificial Neural Network Prediction of Airport Pavement Moduli Using Interpolated Surface Deflection Data. Mater. Sci. Eng. 1203, 2021, 022112. [Google Scholar] [CrossRef]
- Saltan, M.; Terzi, S. Backcalculation of pavement layer parameters using Artificial Neural Networks. Indian J. Eng. Mater. Sci. 2004, 11, 38–42. [Google Scholar]
- Gopalakrishnan, K.; Kim, S. Support vector machines for nonlinear pavement backanalysis. J. Civ. Eng. (IEB) 2010, 38, 173–190. [Google Scholar]
- Saltan, M.; Terzi, S.; Küçüksille, E.U. Backcalculation of pavement layer moduli and Poisson’s ratio using data mining. Expert Syst. Appl. 2011, 38, 2600–2608. [Google Scholar] [CrossRef]
- Fauset, L. Fundamentals of Neural Networks: Architectures, Algoritms, and Applications; Prentice Hall: Enlewood Cliffs, NJ, USA, 1994; pp. 289–300. [Google Scholar]
- Goktepe, A.B.; Agar, E.; Lav, A.H. Comparison of multilayer perceptron and adaptive neuro-fuzzy system on backcalculating the mechanical properties of flexible pavements. ARI Bull. Istanb. Tech. Univers. 2004, 54, 1–13. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Manufactured in The Netherlands. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth & Brooks/Cole Advanced Books & Software: Monterey, CA, USA, 1984. [Google Scholar]
- MATLAB Neural Network ToolboxTM. User’s Guide. Available online: https://ww2.mathworks.cn/help/deeplearning/index.html (accessed on 3 March 2010).
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; Jes’us, O.D. Neuron model and network architectures. In Neural Network Design, 2nd ed.; Hagan, M.T., Ed.; PWS Publishing: Boston, MA, USA, 2014; pp. 1–23. [Google Scholar]
- Math Works. MATLAB: The Language of Technical Computing from Math Works; Math Works: Natick, MA, USA, 2018. [Google Scholar]
- Smola, A.; Scholkopf, B. A tutorial on support vector regression. Manufactured in The Netherlands. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Moudiki, T. LSBoost, Gradient Boosted Penalized Nonlinear Least Squares. Available online: https://www.researchgate.net/publication/346059361 (accessed on 21 November 2020).
- Nega, A.; Nikraz, H.; Al-Qadi, I. Dynamic analysis of falling weight deflectometer. J. Traffic Transp. Eng. 2016, 3, 427–437. [Google Scholar] [CrossRef]
- Lytton, R. Backcalculation of pavement layer properties. In Nondestructive Testing of Pavements and Backcalculation of Moduli ASTM STP 1026; American Society for Testing and Materials: Philadelphia, PA, USA, 1989. [Google Scholar]
- Chou, Y.J.; Lytton, R.L. Accuracy and Consistency of Backcalculated Pavement Layer Moduli. Transp. Res. Rec. 1991, 1293, 72–85. [Google Scholar]
- Harichandran, R.; Mahmood, T.; Raab, A.; Baladi, G. Modified Newton Algorithm for Backcalculation of Pavement Layer Properties. Transp. Res. Rec. 1993, 1384, 15–22. [Google Scholar]
- Design Manual for Roads and Bridges. HD 30/08. Volume 7, Section 3, Part 3, p. 24. Available online: https://www.standardsforhighways.co.uk/prod/attachments/97a0477a-49c3-4969-9d15-57ca13d709c9 (accessed on May 2008).
| SVM Parameters | Values |
|---|---|
| precision parameter | 0.9 |
| tolerance parameter | 1600 |
| kernel scale factor | 72 |
| BRT Parameters | Values |
|---|---|
| Learning rate, | 0.03 |
| Boosting stages | 190 |
| Leaf size | 12 |
| Input and Output Variables for All Data | ||||||
|---|---|---|---|---|---|---|
| Variables | Min. | Max. | Mean | Median | St.Dev | Count |
| d0 (mm) | 164.90 | 1383.80 | 445.25 | 397.25 | 171.95 | 462.00 |
| d300 (mm) | 86.20 | 860.30 | 310.03 | 288.00 | 105.29 | 462.00 |
| d600 (mm) | 75.60 | 370.40 | 189.20 | 184.40 | 49.59 | 462.00 |
| d900 (mm) | 56.40 | 222.10 | 119.48 | 118.95 | 28.68 | 462.00 |
| d1200 (mm) | 41.50 | 148.20 | 83.25 | 82.20 | 19.47 | 462.00 |
| d1500 (mm) | 34.30 | 102.80 | 61.92 | 61.85 | 13.65 | 462.00 |
| d1800 (mm) | 27.10 | 83.20 | 49.39 | 48.85 | 10.59 | 462.00 |
| temperature (°C) | 10.35 | 40.53 | 23.15 | 28.46 | 10.82 | 462.00 |
| EAC (MPa) | 589.00 | 6963.90 | 3394.70 | 3167.55 | 1672.38 | 462.00 |
| Input and Output Variables for Training Set | ||||||
| Variables | Min. | Max. | Mean | Median | St.Dev | Count |
| d0 (mm) | 164.90 | 1383.80 | 445.56 | 397.85 | 171.01 | 438.00 |
| d300 (mm) | 86.20 | 860.30 | 310.15 | 288.60 | 104.64 | 438.00 |
| d600 (mm) | 75.60 | 370.40 | 189.32 | 184.70 | 49.32 | 438.00 |
| d900 (mm) | 56.40 | 222.10 | 119.55 | 119.15 | 28.60 | 438.00 |
| d1200 (mm) | 41.50 | 148.20 | 83.34 | 82.50 | 19.41 | 438.00 |
| d1500 (mm) | 34.30 | 102.80 | 61.96 | 62.00 | 13.59 | 438.00 |
| d1800 (mm) | 27.10 | 83.20 | 49.41 | 49.15 | 10.54 | 438.00 |
| temperature (°C) | 10.35 | 40.53 | 23.05 | 27.24 | 10.84 | 439.00 |
| EAC (MPa) | 589.00 | 6963.90 | 3395.42 | 3165.70 | 1673.77 | 439.00 |
| Input and Output Variables for Test Set | ||||||
| Variables | Min. | Max. | Mean | Median | St.Dev | Count |
| d0 (mm) | 227.30 | 998.50 | 450.08 | 394.50 | 189.52 | 23.00 |
| d300(mm) | 170.30 | 644.10 | 314.71 | 287.50 | 116.74 | 23.00 |
| d600 (mm) | 117.30 | 309.30 | 190.71 | 182.00 | 53.66 | 23.00 |
| d900 (mm) | 77.20 | 175.80 | 120.13 | 113.30 | 29.66 | 23.00 |
| d1200 (mm) | 55.20 | 126.50 | 83.08 | 81.00 | 20.32 | 23.00 |
| d1500 (mm) | 43.70 | 94.60 | 62.24 | 56.00 | 14.63 | 23.00 |
| d1800 (mm) | 35.90 | 76.30 | 49.72 | 44.90 | 11.53 | 23.00 |
| temperature (°C) | 10.51 | 39.89 | 24.77 | 29.24 | 10.85 | 23.00 |
| EAC (MPa) | 1049.30 | 6921.60 | 3380.95 | 3257.60 | 1682.66 | 23.00 |
| Evaluation Criteria | Definition |
|---|---|
| Coefficient of correlation | |
| Coefficient of determination | |
| Mean absolute percentage error | |
| Root mean squared error |
| Model | Data Set | Performance Index | |||
|---|---|---|---|---|---|
| R | R2 | MAPE | RMSE | ||
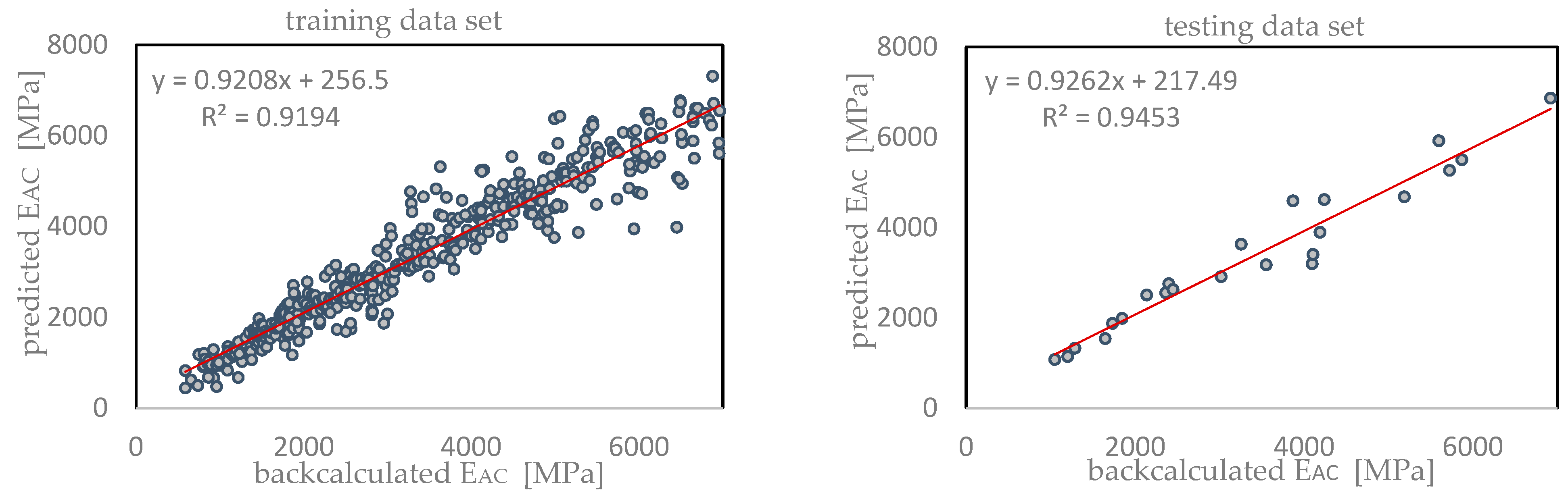
| ANN | training | 0.959 | 0.919 | 10.75% | 0.074 |
| testing | 0.972 | 0.945 | 9.13% | 0.066 | |
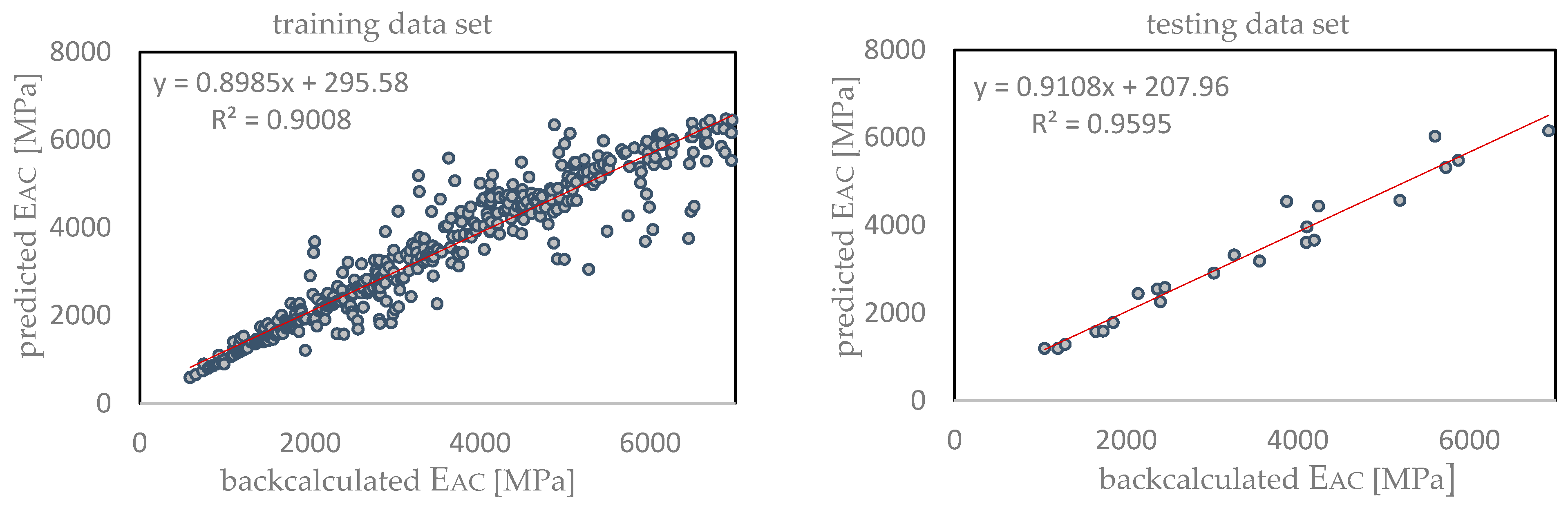
| SVM | training | 0.949 | 0.901 | 8.63% | 0.083 |
| testing | 0.980 | 0.960 | 7.64% | 0.059 | |
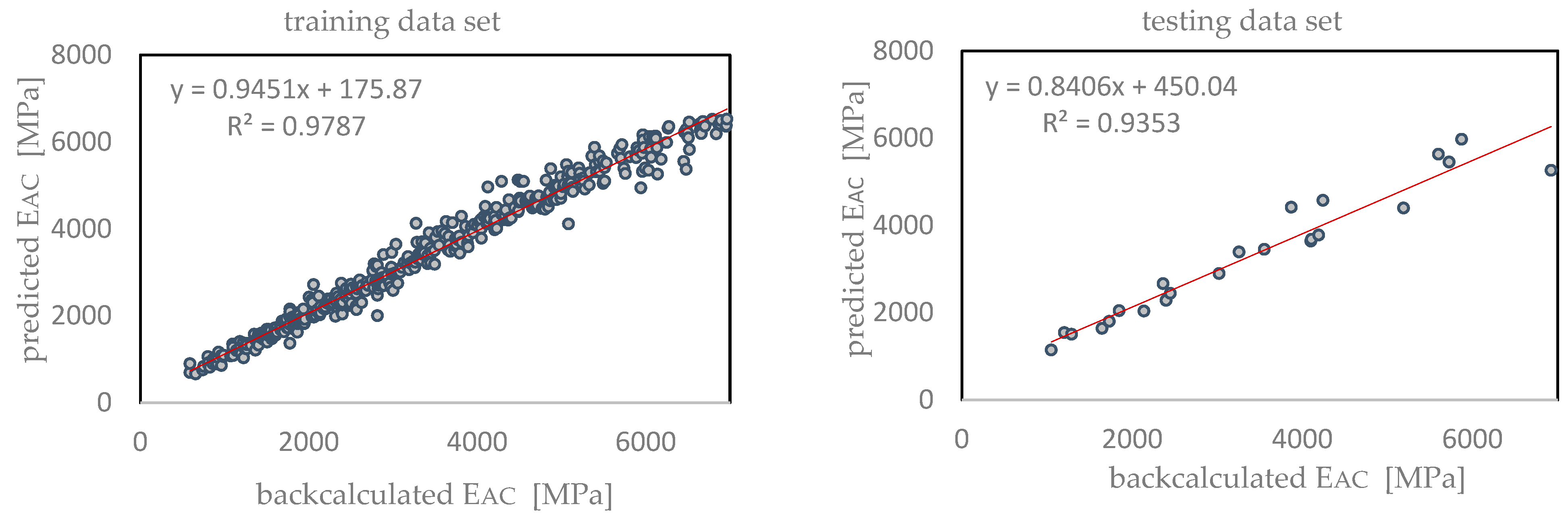
| BRT | training | 0.989 | 0.979 | 5.67% | 0.039 |
| testing | 0.967 | 0.935 | 8.84% | 0.078 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svilar, M.; Peško, I.; Šešlija, M. Model for Estimating the Modulus of Elasticity of Asphalt Layers Using Machine Learning. Appl. Sci. 2022, 12, 10536. https://doi.org/10.3390/app122010536
Svilar M, Peško I, Šešlija M. Model for Estimating the Modulus of Elasticity of Asphalt Layers Using Machine Learning. Applied Sciences. 2022; 12(20):10536. https://doi.org/10.3390/app122010536
Chicago/Turabian StyleSvilar, Mila, Igor Peško, and Miloš Šešlija. 2022. "Model for Estimating the Modulus of Elasticity of Asphalt Layers Using Machine Learning" Applied Sciences 12, no. 20: 10536. https://doi.org/10.3390/app122010536
APA StyleSvilar, M., Peško, I., & Šešlija, M. (2022). Model for Estimating the Modulus of Elasticity of Asphalt Layers Using Machine Learning. Applied Sciences, 12(20), 10536. https://doi.org/10.3390/app122010536






