Experimental Investigation on Flow-Induced Rotation of Two Mechanically Tandem-Coupled Cylinders
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Principle of Flow-Induced Rotation
2.2. Dynamic Model of Flow-Induced Rotation (FIR) System
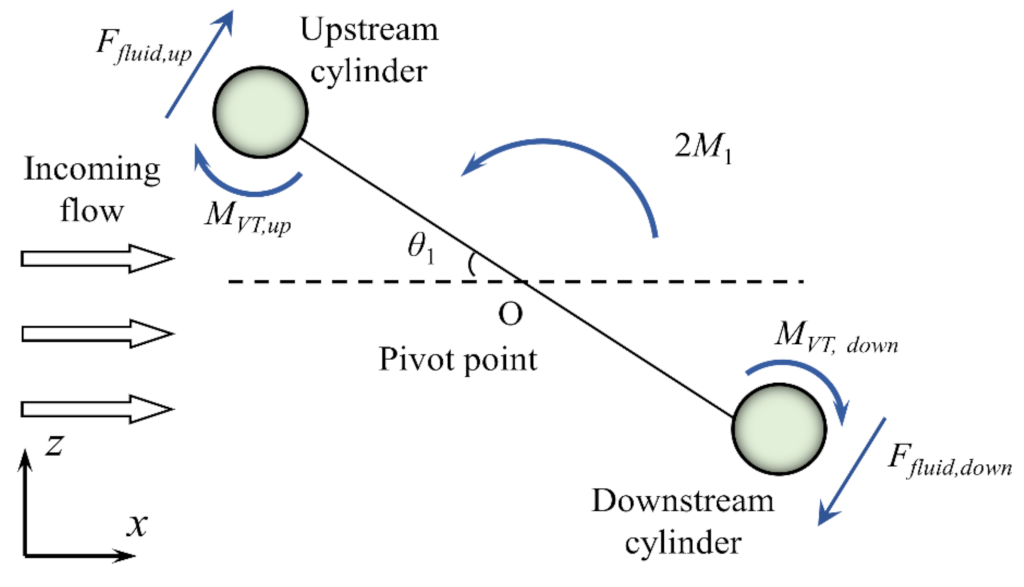
2.2.1. Pendulum System
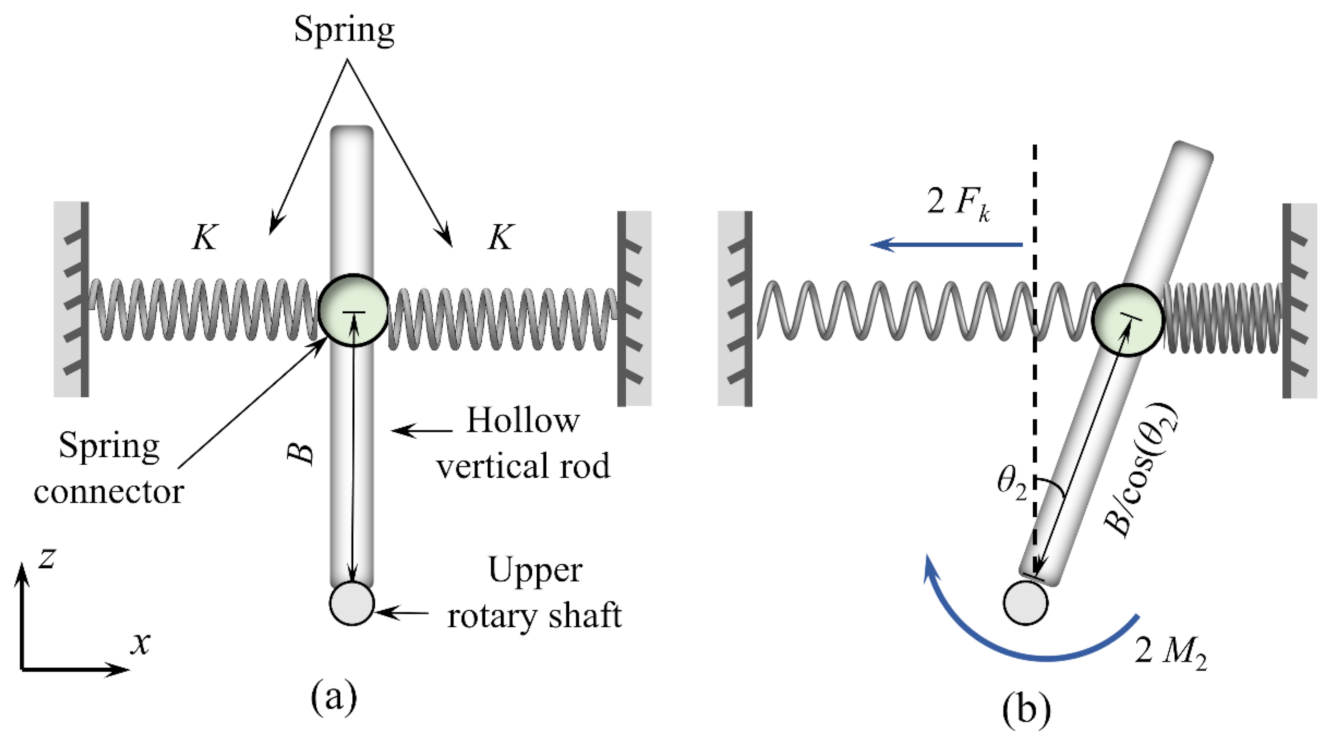
2.2.2. Restoration System
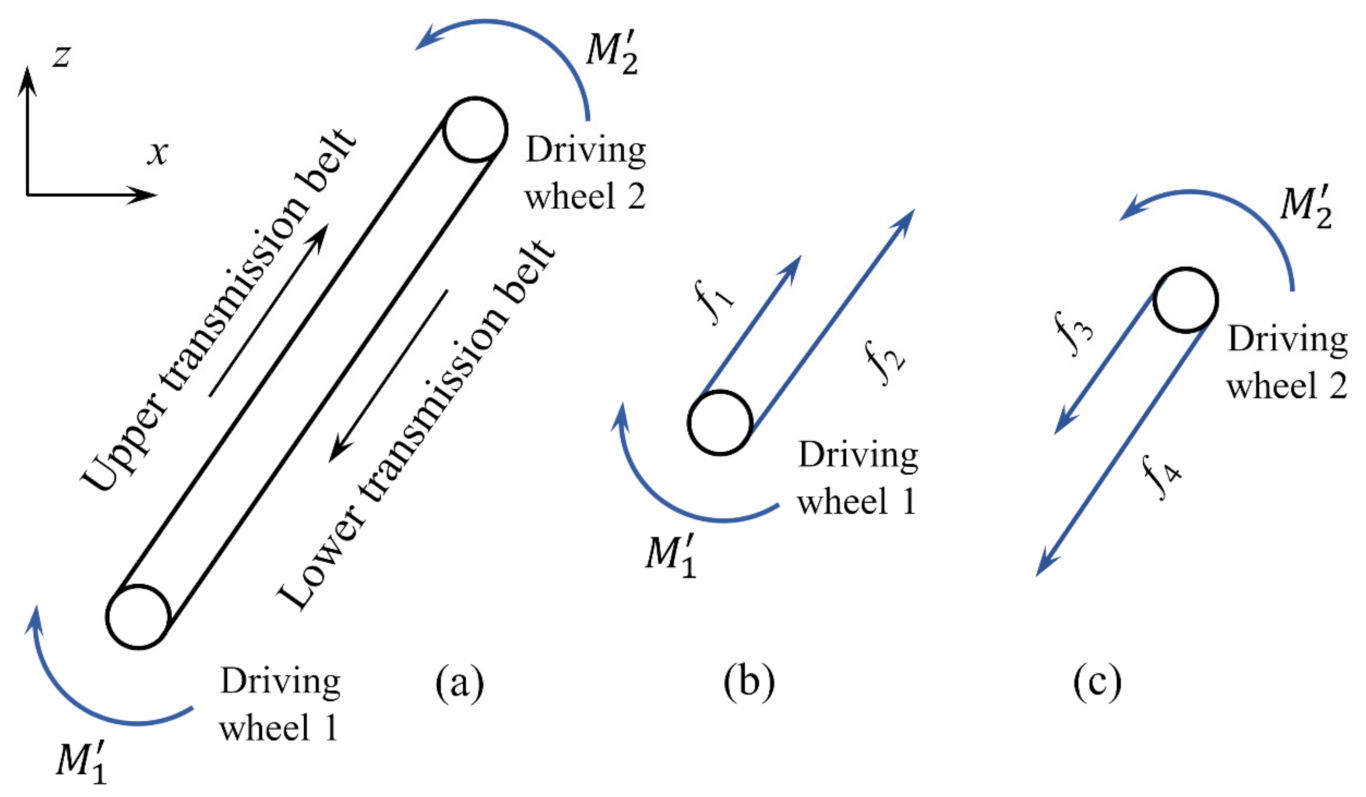
2.2.3. Transmission System
2.2.4. Total Kinetic Equation of FIR System
3. Experimental Methods
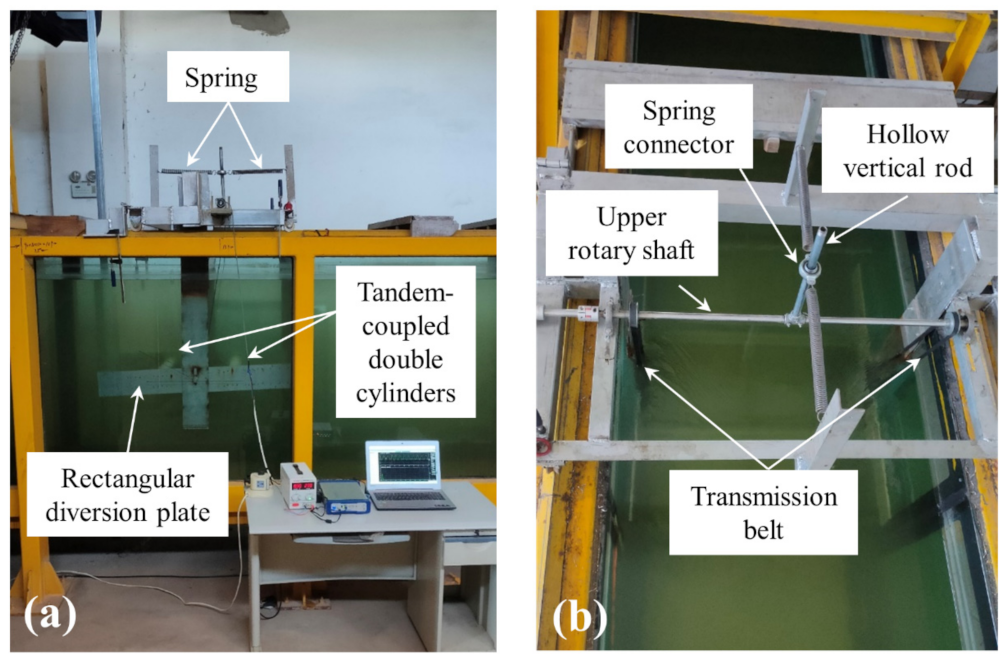
3.1. Physical Model
3.1.1. Recirculating Water Tunnel
3.1.2. Flow-Induced Rotation Device
3.1.3. Test Circular Cylinder
3.2. Data Acquisition and Processing System
3.3. Free Decay Tests
3.4. Validation of Mathematical Model
4. Results and Discussion
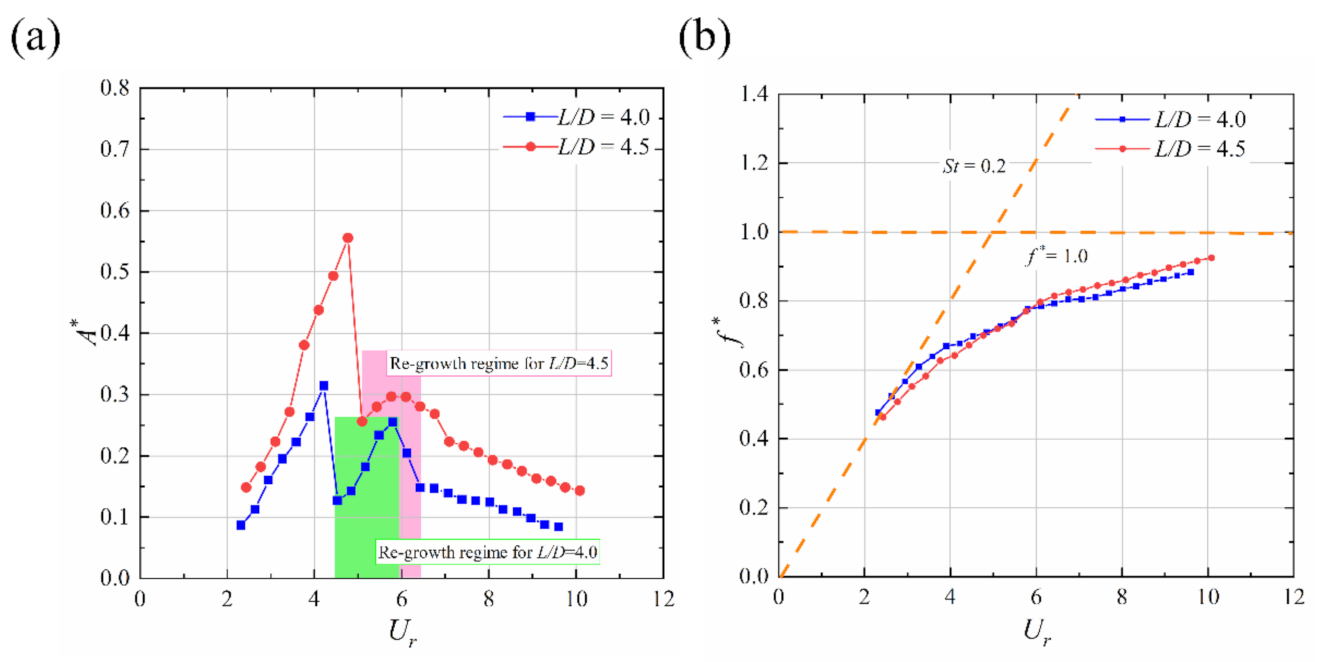
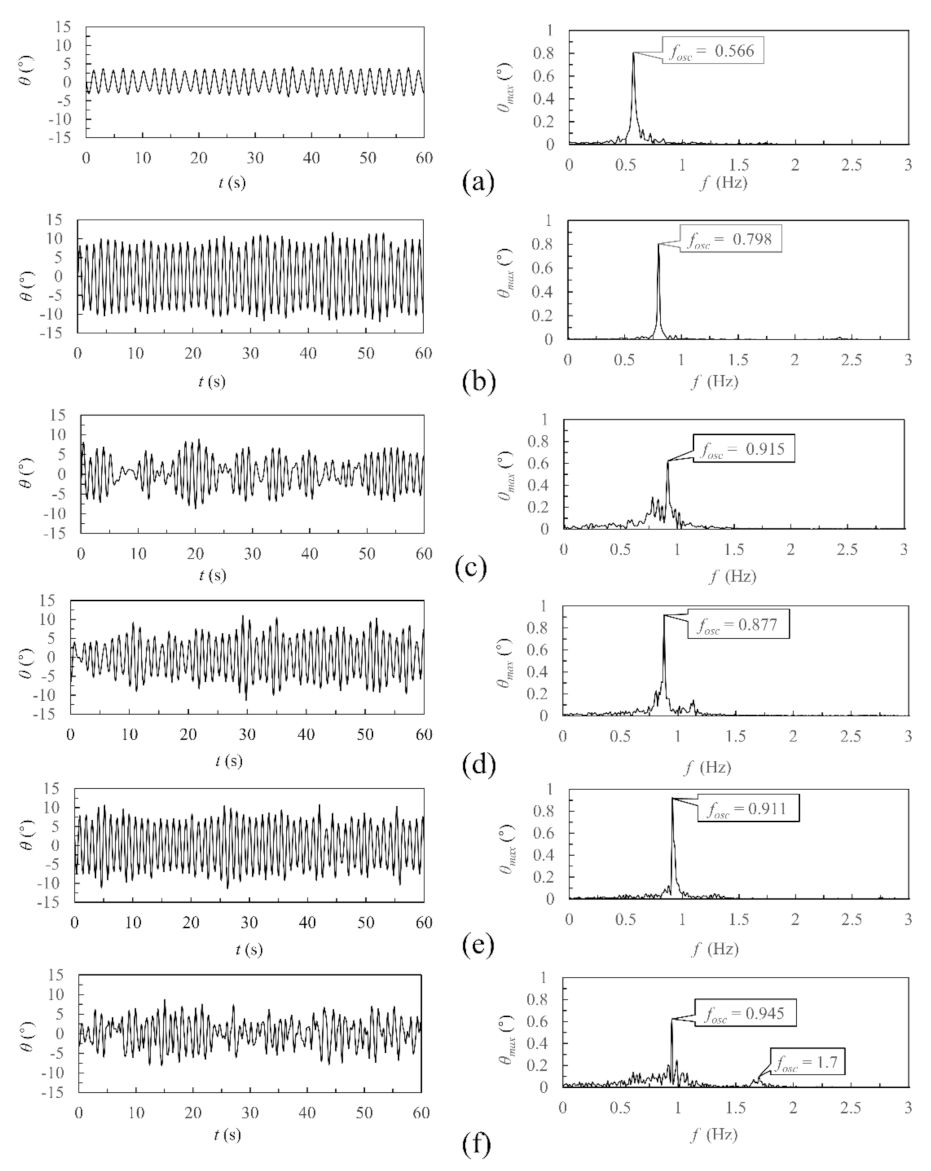
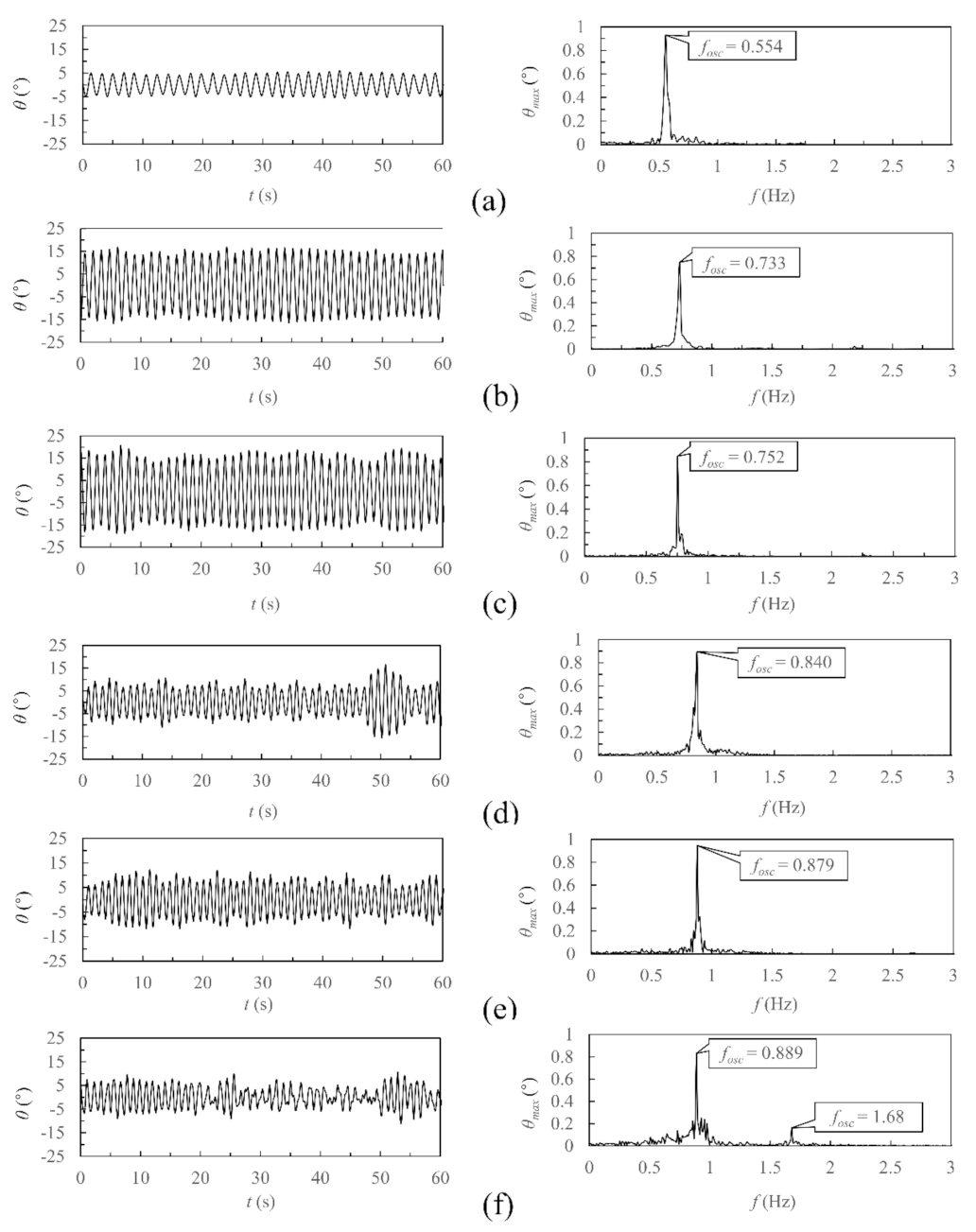
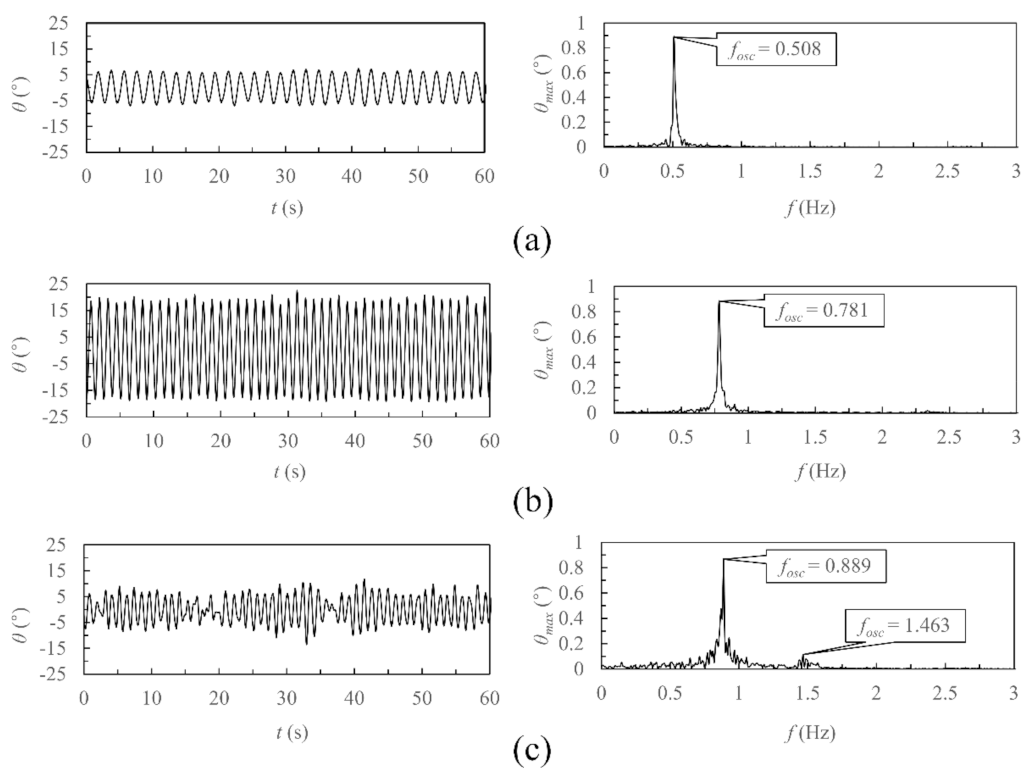
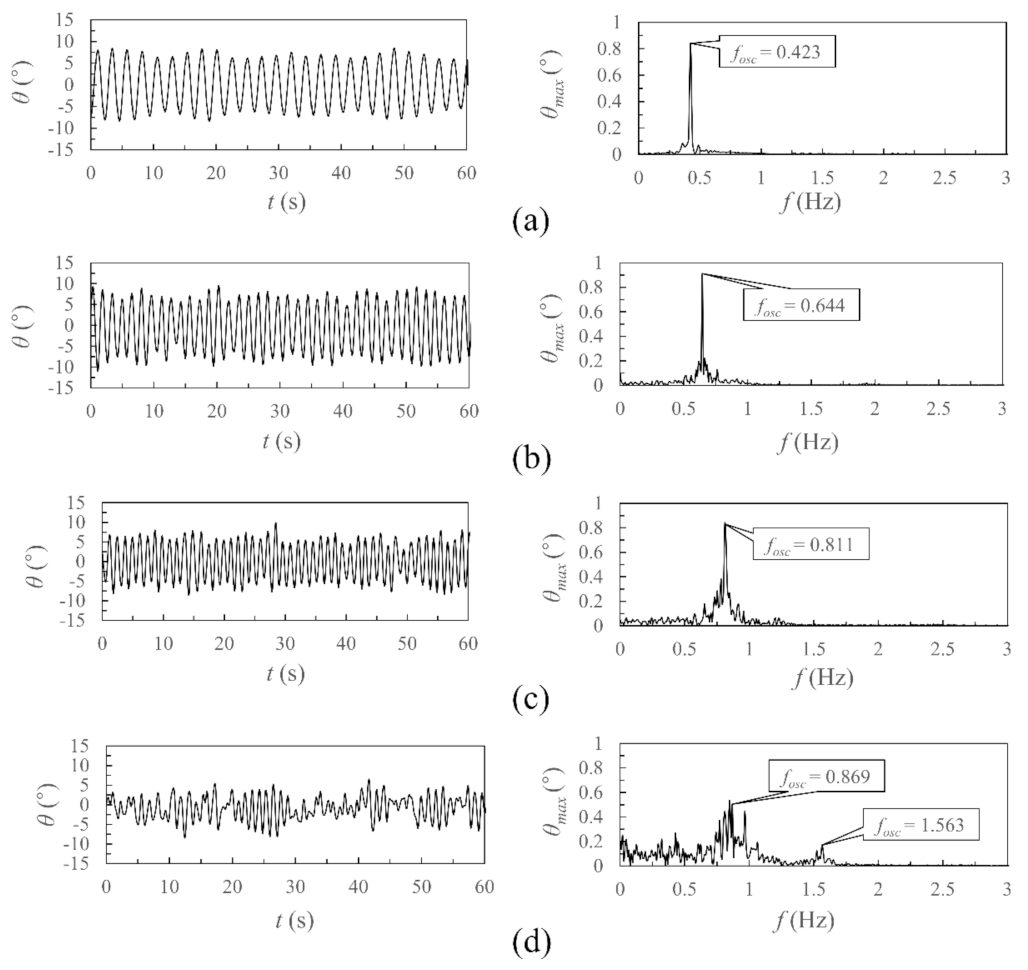
4.1. L/D = 4.0 and 4.5
4.1.1. Rotation Response
4.1.2. Oscillation Time History and Spectral Characteristics
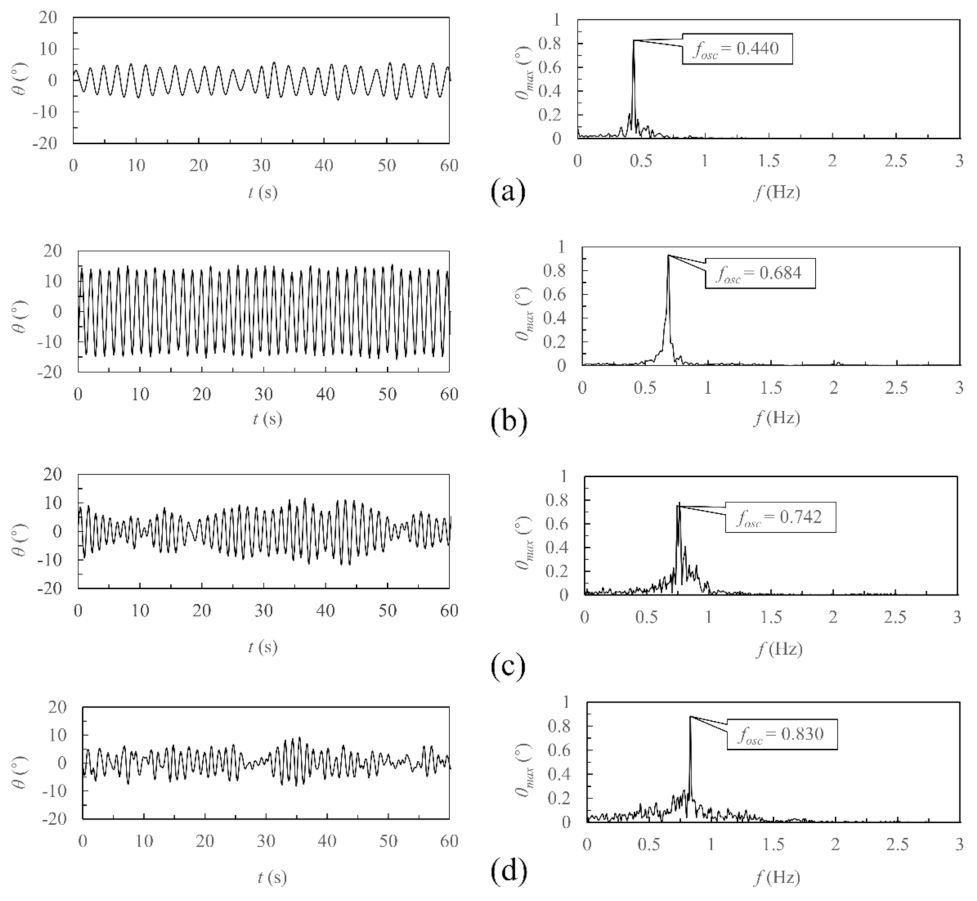
4.2. L/D = 5.0, 5.5 and 6.0
4.2.1. Rotation Response
4.2.2. Oscillation Time History and Spectral Characteristics
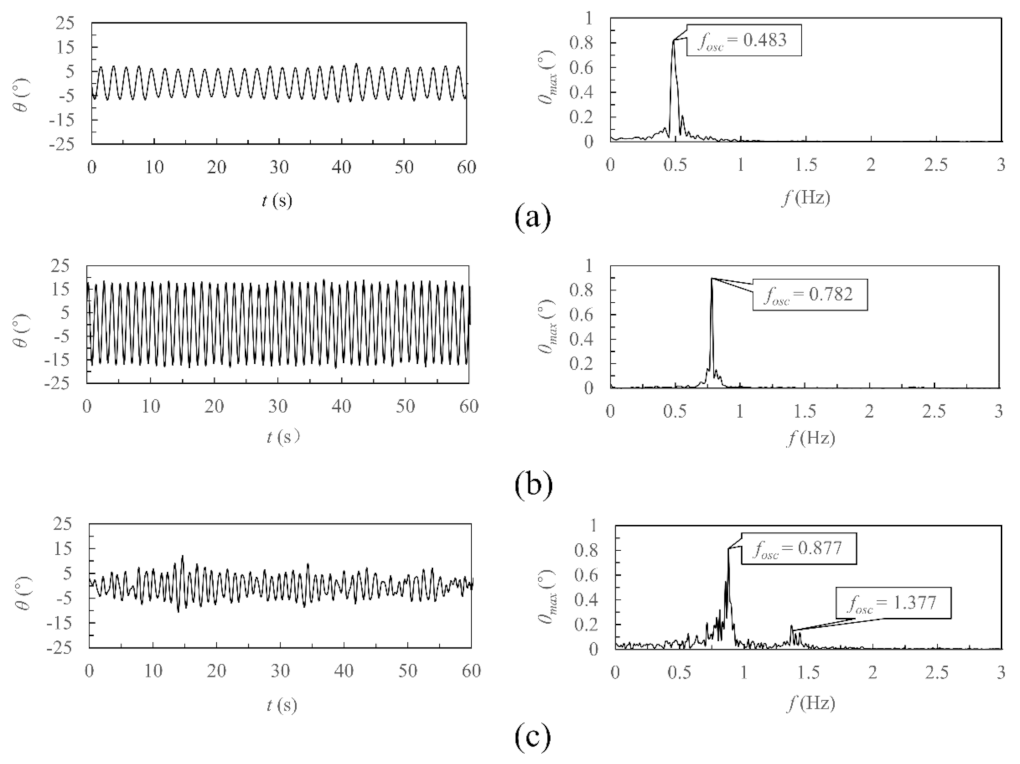
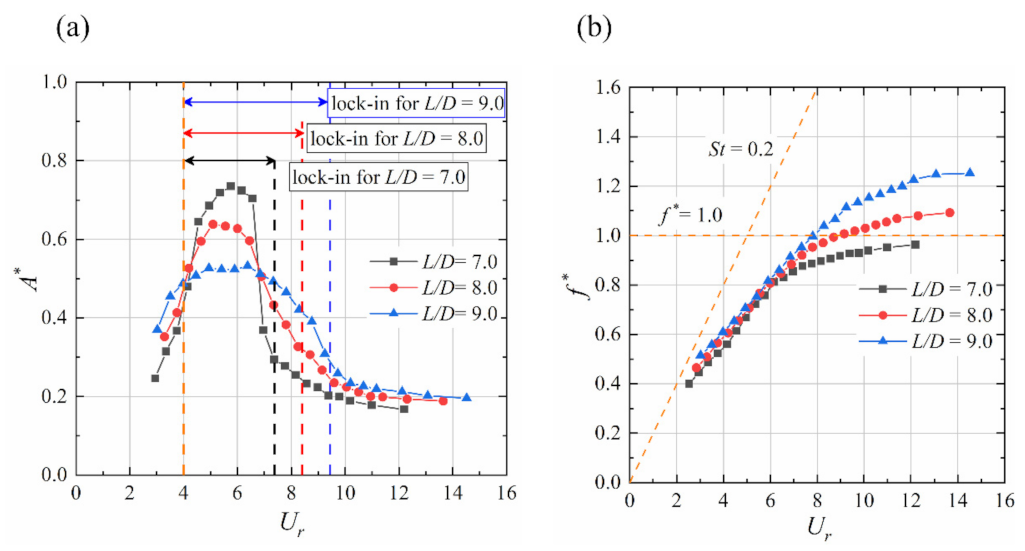
4.3. L/D = 7.0, 8.0 and 9.0
4.3.1. Rotation Response
4.3.2. Oscillation Time History and Spectral Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohamed, A.; Zaki, S.A.; Shirakashi, M.; Ali, M.S.; Samsudin, M.Z. Experimental investigation on vortex-induced vibration and galloping of rectangular cylinders of varying side ratios with a downstream square plate. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104563. [Google Scholar] [CrossRef]
- Hong, K.S.; Shah, U.H. Vortex-induced vibrations and control of marine risers: A review. Ocean Eng. 2018, 152, 300–315. [Google Scholar] [CrossRef]
- Xu, W.; Ji, C.; Sun, H.; Ding, W.; Bernitsas, M.M. Flow-induced vibration of two elastically mounted tandem cylinders in cross-flow at subcritical Reynolds numbers. Ocean Eng. 2019, 173, 375–387. [Google Scholar] [CrossRef]
- Liu, G.; Li, H.; Qiu, Z.; Leng, D.; Li, Z.; Li, W. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 106704. [Google Scholar] [CrossRef]
- Leng, D.; Liu, D.; Li, H.; Jin, B.; Liu, G. Internal flow effect on the cross-flow vortex-induced vibration of marine risers with different support methods. Ocean Eng. 2022, 257, 111487. [Google Scholar] [CrossRef]
- Hwang, Y.C.; Kim, S.; Kim, H.K. Cause investigation of high-mode vortex-induced vibration in a long-span suspension bridge. Struct. Infrastruct. Eng. 2020, 16, 84–93. [Google Scholar] [CrossRef]
- Khan, H.H.; Islam, M.D.; Fatt, Y.Y.; Janajreh, I.; Alam, M.M. Flow-induced vibration on two tandem cylinders of different diameters and spacing ratios. Ocean Eng. 2022, 258, 111747. [Google Scholar] [CrossRef]
- Yan, B.; Ren, H.; Li, D.; Yuan, Y.; Li, K.; Yang, Q.; Deng, X. Numerical Simulation for Vortex-Induced Vibration (VIV) of a High-Rise Building Based on Two-Way Coupled Fluid-Structure Interaction Method. Int. J. Struct. Stab. Dyn. 2022, 22, 2240010. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar]
- Allen, J.J.; Smits, A.J. Energy harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Taylor, G.W.; Burns, J.R.; Kammann, S.A.; Powers, W.B.; Welsh, T.R. The energy harvesting eel: A small subsurface ocean/river power generator. IEEE J. Ocean. Eng. 2001, 26, 539–547. [Google Scholar] [CrossRef] [Green Version]
- Pobering, S.; Schwesinger, N. A novel hydropower harvesting device. In Proceedings of the International Conference on MEMS, NANO and Smart System, Banff, AB, Canada, 25–27 August 2004. [Google Scholar]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A new concept in generation of clean and renewable energy from fluid flow. J. Offshore Mech. Arct. Eng. 2008, 130, 041101. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Ben-Simon, Y.; Raghavan, K.; Garcia, E.M.H. The VIVACE converter: Model tests at high damping and Reynolds number around 105. J. Offshore Mech. Arct. Eng. 2009, 131, 011102. [Google Scholar] [CrossRef]
- Raghavan, K.; Bernitsas, M.M. Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Eng. 2011, 38, 719–731. [Google Scholar] [CrossRef]
- Lee, J.H.; Bernitsas, M.M. High-damping, high-Reynolds VIV tests for energy harnessing using the VIVACE converte. Ocean Eng. 2011, 38, 1697–1712. [Google Scholar] [CrossRef]
- Shao, N.; Xu, G.; Liu, F.; Yan, X.; Wang, X.; Deng, H.; Zheng, Z. Experimental Study on the Flow-Induced Motion and Hydrokinetic Energy of Two T-section Prisms in Tandem Arrangement. Appl. Sci. 2020, 10, 1136. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Wang, H.; Shao, F.; Jin, X.; Tang, G.; Yang, F. Numerical investigation on vortex-induced vibration of an elastically mounted circular cylinder with multiple control rods at low Reynolds number. Appl. Ocean Res. 2022, 118, 102987. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Xu, D.; Alam, M.M. Three-dimensional direct numerical simulations of two interfering side-by-side circular cylinders at intermediate spacing ratios. Appl. Ocean Res. 2022, 123, 103162. [Google Scholar] [CrossRef]
- King, R.; Johns, D.J. Wake interaction experiments with two flexible circular cylinders in flowing water. J. Sound Vib. 1976, 45, 259–283. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Review of flow interference between two circular cylinders in various arrangements. J. Fluids Eng. 1977, 99, 618–633. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 1985, 101, 511–521. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull. JSME 1981, 24, 323–331. [Google Scholar] [CrossRef]
- Bokaian, A.; Geoola, F. Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 1984, 146, 383–415. [Google Scholar] [CrossRef]
- Bokaian, A.; Geoola, F. Wake displacement as cause of lift force on cylinder pair. J. Eng. Mech. 1985, 111, 92–99. [Google Scholar] [CrossRef]
- Yao, X.; Chen, Q.; Xu, W. Experimental research on two circular cylinders in tandem arrangements at critical Reynolds numbers. J. Vib. Eng. 1994, 7, 17–22. [Google Scholar]
- Mahir, N.; Rockwell, D. Vortex formation from a forced system of two cylinders. Part I: Tandem arrangement. J. Fluids Struct. 1996, 10, 473–489. [Google Scholar] [CrossRef]
- Mahir, N.; Rockwell, D. Vortex formation from a forced system of two cylinders. Part II: Side-by-side arrangement. J. Fluids Struct. 1996, 10, 491–500. [Google Scholar] [CrossRef]
- Brika, D.; Laneville, A. Wake interference between two circular cylinders. J. Wind Eng. Ind. Aerodyn. 1997, 72, 61–70. [Google Scholar] [CrossRef]
- Meneghini, J.R.; Saltara, F.; Siqueira, C.L.R.; Ferrarijr, J.A. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 2001, 15, 327–350. [Google Scholar] [CrossRef]
- Lin, J.C.; Yang, Y.; Rockwell, D. Flow past two cylinders in tandem: Instantaneous and averaged flow structure. J. Fluids Struct. 2002, 16, 1059–1071. [Google Scholar] [CrossRef]
- Zhou, Y.; Yiu, M.W. Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 2006, 548, 17–48. [Google Scholar] [CrossRef] [Green Version]
- Prasanth, T.K.; Mittal, S. Flow-induced oscillation of two circular cylinders in tandem arrangement at low Re. J. Fluids Struct. 2009, 25, 1029–1048. [Google Scholar] [CrossRef]
- Prasanth, T.K.; Mittal, S. Vortex-induced vibration of two circular cylinders at low Reynolds number. J. Fluids Struct. 2009, 25, 731–741. [Google Scholar] [CrossRef]
- Assi, G.R.S.; Meneghini, J.R.; Aranha, J.A.P.; Bearman, P.W.; Casaprima, E. Experimental investigation of flow-induced vi-bration interference between two circular cylinders. J. Fluids Struct. 2006, 22, 819–827. [Google Scholar] [CrossRef]
- Assi, G.R.S.; Bearman, P.W.; Meneghini, J.R. On the wake-induced vibration of tandem circular cylinders: The vortex interaction excitation mechanism. J. Fluid Mech. 2010, 661, 365–401. [Google Scholar] [CrossRef]
- Bao, Y.; Huang, C.; Zhou, D.; Tu, J.; Han, Z. Two-degree-of-freedom flow-induced vibrations on isolated and tandem cylinders with varying natural frequency ratios. J. Fluids Struct. 2012, 35, 50–75. [Google Scholar] [CrossRef]
- Ji, C.; Chen, W.; Huang, J.; Xu, W. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms. Acta Mech. Sin. 2014, 46, 862–870. [Google Scholar]
- Chen, W.; Ji, C.; Williams, J.; Xu, D.; Yang, L.; Cui, Y. Vortex-induced vibrations of three tandem cylinders in laminar crossflow: Vibration response and galloping mechanism. J. Fluids Struct. 2018, 78, 215–238. [Google Scholar] [CrossRef]
- Qin, B.; Alam, M.M.; Ji, C.; Liu, Y.; Xu, S. Flow-induced vibrations of two cylinders of different natural frequencies. Ocean Eng. 2018, 155, 189–200. [Google Scholar] [CrossRef]
- Arionfard, H.; Nishi, Y. Flow-induced vibrations of two mechanically coupled pivoted circular cylinders: Characteristics of vibration. J. Fluids Struct. 2018, 80, 165–178. [Google Scholar] [CrossRef]
- Arionfard, H.; Nishi, Y. Flow-induced vibration of two mechanically coupled pivoted circular cylinders: Vorticity dynamics. J. Fluids Struct. 2018, 82, 505–519. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, T.; Alam, M.M.; Song, J.; Zhou, T. Flow-induced rotation of a circular cylinder with a detached splitter plate and its bifurcation behavior. Appl. Ocean Res. 2022, 122, 103150. [Google Scholar] [CrossRef]
- Chen, L.; Wu, G. Vortex-induced three-degree-of-freedom vibration of a piggyback circular cylinder system. Appl. Ocean Res. 2022, 123, 103145. [Google Scholar] [CrossRef]
- Ding, L.; Bernitsas, M.M.; Kim, E.S. 2-D URANS vs. experiments of flow induced motions of two circular cylinders in tandem with passive turbulence control for 30,000 <Re <105,000. Ocean Eng. 2013, 72, 429–440. [Google Scholar]
- Kim, E.S.; Bernitsas, M.M. Performance prediction of horizontal hydrokinetic energy converter using multiple-cylinder synergy in flow induced motion. Appl. Energy 2016, 170, 92–100. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Ma, C.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Hydrokinetic energy conversion by two rough tandem-cylinders in flow induced motions: Effect of spacing and stiffness. Renew. Energy 2017, 107, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef] [Green Version]
- Shao, N.; Lian, J.; Xu, G.; Liu, F.; Deng, H.; Ren, Q.; Yan, X. Experimental investigation of flow-induced motion and energy conversion of a T-section prism. Energies 2018, 11, 2035. [Google Scholar] [CrossRef] [Green Version]
- Khalak, A.; Williaamson, C.H.K. Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 1997, 11, 973–982. [Google Scholar] [CrossRef]
- Raghavan, K. Energy Extraction from a Steady Flow Using Vortex Induced Vibration. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2007. [Google Scholar]









| Parameters | Symbol | Value |
|---|---|---|
| Full incoming velocity range | Y [m/s] | 0.0 ≤ Y ≤ 1.8 |
| Water depth | h [m] | 1.34 |
| Reynolds numbers | Re (UD/ν) | 20,105 ≤ Re ≤ 96,575 |
| Test velocity range | U [m/s] | 0.229 ≤ U ≤ 1.1 |
| Reduced velocity | Ur (U/fn D) | 2.314 ≤ Ur ≤ 14.513 |
| Kinematic viscosity | ν [m2/s] | 1.139 × 10−6 |
| Water density | ρ [kg/m3] | 1000 |
| Total stiffness of system | K [N/m] | 1960 |
| Distance between the upper shaft P and the spring connector when θ2 = 0 | B [m] | 0.21 |
| Spacing ratio | L/D | 4.0, 4.5, 5.0, 5.5, 6.0, 7.0, 8.0, 9.0 |
| L/D | Josc (kg·m2) | Jd (kg·m2) | J* |
|---|---|---|---|
| 4.0 | 1.443 | 0.583 | 2.475 |
| 4.5 | 1.602 | 0.733 | 2.186 |
| 5.0 | 1.779 | 0.901 | 1.974 |
| 5.5 | 1.974 | 1.087 | 1.816 |
| 6.0 | 2.188 | 1.290 | 1.696 |
| 7.0 | 2.673 | 1.750 | 1.527 |
| 8.0 | 3.231 | 2.280 | 1.417 |
| 9.0 | 3.865 | 2.881 | 1.342 |
| Item | Symbol | Upstream Cylinder | Downstream Cylinder |
|---|---|---|---|
| Diameter | D [m] | 0.1 | 0.1 |
| Height | H [m] | 0.9 | 0.9 |
| Thickness | d [m] | 0.01 | 0.01 |
| L/D | Test 1 fn,air,1 (Hz) | Test 2 fn,air,2 (Hz) | Test 3 fn,air,3 (Hz) | Test 4 fn,air,4 (Hz) | Average fn,air,ave (Hz) | Relative Error δ |
|---|---|---|---|---|---|---|
| 4.0 | 1.146 | 1.147 | 1.147 | 1.146 | 1.1465 | — |
| 4.5 | 1.102 | 1.092 | 1.090 | 1.085 | 1.0923 | 0.0496 |
| 5.0 | 1.048 | 1.049 | 1.000 | 1.048 | 1.0363 | 0.0540 |
| 5.5 | 1.020 | 1.013 | 1.011 | 1.013 | 1.0142 | 0.0218 |
| 6.0 | 0.953 | 0.953 | 0.953 | 0.953 | 0.9530 | 0.0642 |
| 7.0 | 0.903 | 0.855 | 0.856 | 0.902 | 0.8790 | 0.0842 |
| 8.0 | 0.806 | 0.807 | 0.805 | 0.806 | 0.8060 | 0.0906 |
| 9.0 | 0.758 | 0.756 | 0.756 | 0.758 | 0.7570 | 0.0647 |
| L/D | Test 1 ζtotal,1 | Test 2 ζtotal,2 | Test 3 ζtotal,3 | Test 4 ζtotal,4 | Average ζtotal,ave | Relative Error ε |
|---|---|---|---|---|---|---|
| 4.0 | 0.060 | 0.055 | 0.052 | 0.052 | 0.0548 | — |
| 4.5 | 0.054 | 0.051 | 0.050 | 0.048 | 0.0508 | 0.0788 |
| 5.0 | 0.056 | 0.044 | 0.051 | 0.045 | 0.0490 | 0.0357 |
| 5.5 | 0.050 | 0.045 | 0.040 | 0.045 | 0.0450 | 0.0889 |
| 6.0 | 0.043 | 0.052 | 0.042 | 0.040 | 0.0443 | 0.0169 |
| 7.0 | 0.046 | 0.042 | 0.034 | 0.037 | 0.0398 | 0.1132 |
| 8.0 | 0.042 | 0.044 | 0.035 | 0.035 | 0.0390 | 0.0192 |
| 9.0 | 0.044 | 0.038 | 0.034 | 0.040 | 0.0390 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Feng, W.; Yan, X.; Ran, D.; Shao, N.; Wang, X.; Yang, D. Experimental Investigation on Flow-Induced Rotation of Two Mechanically Tandem-Coupled Cylinders. Appl. Sci. 2022, 12, 10604. https://doi.org/10.3390/app122010604
Liu F, Feng W, Yan X, Ran D, Shao N, Wang X, Yang D. Experimental Investigation on Flow-Induced Rotation of Two Mechanically Tandem-Coupled Cylinders. Applied Sciences. 2022; 12(20):10604. https://doi.org/10.3390/app122010604
Chicago/Turabian StyleLiu, Fang, Weipeng Feng, Xiang Yan, Danjie Ran, Nan Shao, Xiaoqun Wang, and Defeng Yang. 2022. "Experimental Investigation on Flow-Induced Rotation of Two Mechanically Tandem-Coupled Cylinders" Applied Sciences 12, no. 20: 10604. https://doi.org/10.3390/app122010604
APA StyleLiu, F., Feng, W., Yan, X., Ran, D., Shao, N., Wang, X., & Yang, D. (2022). Experimental Investigation on Flow-Induced Rotation of Two Mechanically Tandem-Coupled Cylinders. Applied Sciences, 12(20), 10604. https://doi.org/10.3390/app122010604








