High Bandwidth-Utilization Digital Holographic Reconstruction Using an Untrained Neural Network
Abstract
1. Introduction
2. Principle
3. Method
4. Simulation
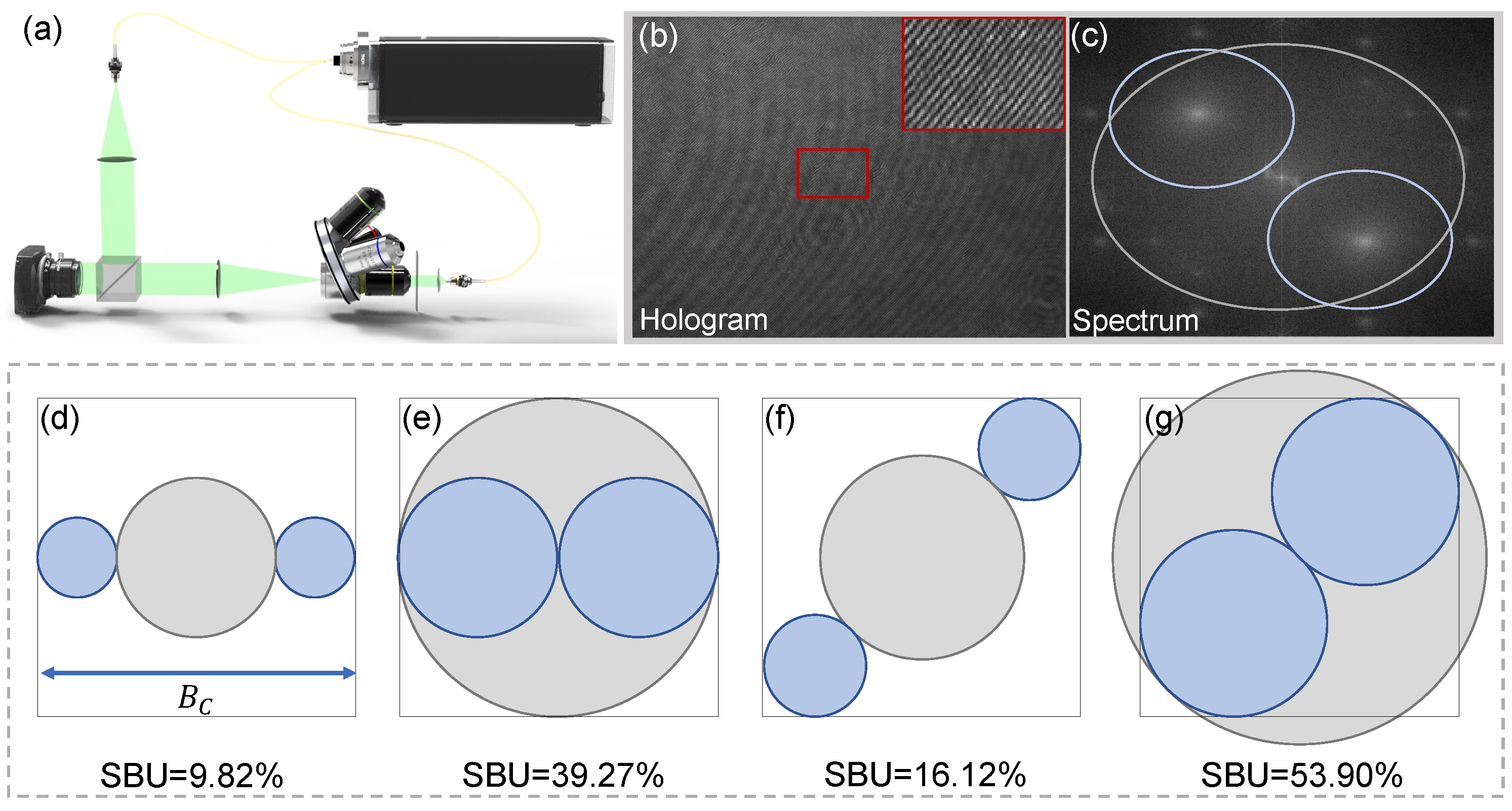
5. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, K.; Kim, K.; Jung, J.; Heo, J.; Cho, S.; Lee, S.; Chang, G.; Jo, Y.; Park, H.; Park, Y. Quantitative phase imaging techniques for the study of cell pathophysiology: From principles to applications. Sensors 2013, 13, 4170–4191. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Fan, Y.; Li, J.; Lu, L.; Sun, J.; Hu, Y.; Zhang, J.; Li, Z.; Shen, Q.; Wang, B.; Zhang, R.; et al. Smart computational light microscopes (SCLMs) of smart computational imaging laboratory (SCILab). PhotoniX 2021, 2, 1–64. [Google Scholar] [CrossRef]
- Vicar, T.; Balvan, J.; Jaros, J.; Jug, F.; Kolar, R.; Masarik, M.; Gumulec, J. Cell segmentation methods for label-free contrast microscopy: Review and comprehensive comparison. BMC Bioinform. 2019, 20, 1–25. [Google Scholar] [CrossRef]
- Gao, P.; Wirth, R.; Lackner, J.; Sunbul, M.; Jaeschke, A.; Nienhaus, G.U. Superresolution Imaging of Live Cells with Genetically Encoded Silicon Rhodamine-Binding RNA Aptamers. Biophys. J. 2020, 118, 145a. [Google Scholar] [CrossRef]
- Li, Z.; Fan, Y.; Sun, J.; Zuo, C.; Chen, Q. A commercialized digital holographic microscope with complete software supporting. In Proceedings of the Optics Frontier Online 2020: Optics Imaging and Display, SPIE, Shanghai, China, 19–20 June 2020; Volume 11571, pp. 341–347. [Google Scholar]
- Kim, M.K. Principles and techniques of digital holographic microscopy. SPIE Rev. 2010, 1, 018005. [Google Scholar] [CrossRef]
- Kemper, B.; Von Bally, G. Digital holographic microscopy for live cell applications and technical inspection. Appl. Opt. 2008, 47, A52–A61. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Yuan, C. Resolution enhancement of digital holographic microscopy via synthetic aperture: A review. Light. Adv. Manuf. 2022, 3, 105–120. [Google Scholar] [CrossRef]
- Gao, P.; Zheng, J.; Yao, B.; Pedrini, G.; Osten, W. Autofocusing and resolution enhancement in speckle-illuminated digital holographic microscopy. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Optica Publishing Group, Shanghai, China, 24–28 May 2015; p. DT3A–2. [Google Scholar]
- Carl, D.; Kemper, B.; Wernicke, G.; von Bally, G. Parameter-optimized digital holographic microscope for high-resolution living-cell analysis. Appl. Opt. 2004, 43, 6536–6544. [Google Scholar] [CrossRef]
- Gabai, H.; Baranes-Zeevi, M.; Zilberman, M.; Shaked, N.T. Continuous wide-field characterization of drug release from skin substitute using off-axis interferometry. Opt. Lett. 2013, 38, 3017–3020. [Google Scholar] [CrossRef][Green Version]
- Coppola, G.; Ferraro, P.; Iodice, M.; De Nicola, S.; Finizio, A.; Grilli, S. A digital holographic microscope for complete characterization of microelectromechanical systems. Meas. Sci. Technol. 2004, 15, 529. [Google Scholar] [CrossRef]
- Huang, Z.; Memmolo, P.; Ferraro, P.; Cao, L. Dual-plane coupled phase retrieval for non-prior holographic imaging. PhotoniX 2022, 3, 1–16. [Google Scholar] [CrossRef]
- Wu, X.; Sun, J.; Zhang, J.; Lu, L.; Chen, R.; Chen, Q.; Zuo, C. Wavelength-scanning lensfree on-chip microscopy for wide-field pixel-super-resolved quantitative phase imaging. Opt. Lett. 2021, 46, 2023–2026. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.C. Digital Holography and Three-Dimensional Display: Principles and Applications; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Poon, T.C.; Liu, J.P. Introduction to Modern Digital Holography: With MATLAB; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zhong, Z.; Bai, H.; Shan, M.; Zhang, Y.; Guo, L. Fast phase retrieval in slightly off-axis digital holography. Opt. Lasers Eng. 2017, 97, 9–18. [Google Scholar] [CrossRef]
- Xue, L.; Lai, J.; Wang, S.; Li, Z. Single-shot slightly-off-axis interferometry based Hilbert phase microscopy of red blood cells. Biomed. Opt. Express 2011, 2, 987–995. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, L. High Bandwidth-Utilization Digital Holographic Multiplexing: An Approach Using Kramers–Kronig Relations. Adv. Photonics Res. 2022, 3, 2100273. [Google Scholar] [CrossRef]
- Pavillon, N.; Seelamantula, C.S.; Kühn, J.; Unser, M.; Depeursinge, C. Suppression of the zero-order term in off-axis digital holography through nonlinear filtering. Appl. Opt. 2009, 48, H186–H195. [Google Scholar] [CrossRef]
- Baek, Y.; Lee, K.; Shin, S.; Park, Y. Kramers–Kronig holographic imaging for high-space-bandwidth product. Optica 2019, 6, 45–51. [Google Scholar] [CrossRef]
- Baek, Y.; Park, Y. Intensity-based holographic imaging via space-domain Kramers–Kronig relations. Nat. Photonics 2021, 15, 354–360. [Google Scholar] [CrossRef]
- Trusiak, M.; Cywińska, M.; Micó, V.; Picazo-Bueno, J.Á.; Zuo, C.; Zdańkowski, P.; Patorski, K. Variational Hilbert quantitative phase imaging. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Shen, Q.; Sun, J.; Fan, Y.; Li, Z.; Gao, P.; Chen, Q.; Zuo, C. High-throughput artifact-free slightly off-axis holographic imaging based on Fourier ptychographic reconstruction. Front. Photonics 2022, 3, 936561. [Google Scholar] [CrossRef]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light. Sci. Appl. 2022, 11, 1–54. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.; Tian, L. Machine learning for 3D microscopy. Nature 2015, 523, 416–417. [Google Scholar] [CrossRef]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep learning in holography and coherent imaging. Light. Sci. Appl. 2019, 8, 1–8. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Q.; Gu, G.; Tao, T.; Zhang, L.; Hu, Y.; Zuo, C. Fringe pattern analysis using deep learning. Adv. Photonics 2019, 1, 025001. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Günaydın, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light. Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Wang, F.; Bian, Y.; Wang, H.; Lyu, M.; Pedrini, G.; Osten, W.; Barbastathis, G.; Situ, G. Phase imaging with an untrained neural network. Light. Sci. Appl. 2020, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Chen, X.; Chi, Z.; Mann, C.; Razi, A. Deep DIH: Single-shot digital in-line holography reconstruction by deep learning. IEEE Access 2020, 8, 202648–202659. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, J.; Li, J.; Si, C.; Li, Y.; Li, X. An improve convolutional auto-encode denoising method. In Proceedings of the 82nd EAGE Annual Conference & Exhibition. European Association of Geoscientists & Engineers, Online, 18–21 October 2021; Volume 2021, pp. 1–5. [Google Scholar]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. Phase aberration compensation in digital holographic microscopy based on principal component analysis. Opt. Lett. 2013, 38, 1724–1726. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Q.; Zhang, Y.; Zuo, C. Optimal principal component analysis-based numerical phase aberration compensation method for digital holography. Opt. Lett. 2016, 41, 1293–1296. [Google Scholar] [CrossRef]
- Herráez, M.A.; Burton, D.R.; Lalor, M.J.; Gdeisat, M.A. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Appl. Opt. 2002, 41, 7437–7444. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the Icml, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Rivenson, Y.; Wu, Y.; Wang, H.; Zhang, Y.; Feizi, A.; Ozcan, A. Sparsity-based multi-height phase recovery in holographic microscopy. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cywińska, M.; Trusiak, M.; Patorski, K. Automatized fringe pattern preprocessing using unsupervised variational image decomposition. Opt. Express 2019, 27, 22542–22562. [Google Scholar] [CrossRef]
- León-Rodríguez, M.; Rayas, J.A.; Cordero, R.R.; Martínez-García, A.; Martínez-Gonzalez, A.; Téllez-Quiñones, A.; Yañez-Contreras, P.; Medina-Cázares, O. Dual-plane slightly off-axis digital holography based on a single cube beam splitter. Appl. Opt. 2018, 57, 2727–2735. [Google Scholar] [CrossRef]
- Han, J.; Gao, P.; Yao, B.; Gu, Y.; Huang, M. Slightly off-axis interferometry for microscopy with second wavelength assistance. Appl. Opt. 2011, 50, 2793–2798. [Google Scholar] [CrossRef]
- Trusiak, M.; Picazo-Bueno, J.A.; Patorski, K.; Zdankowski, P.; Mico, V. Single-shot two-frame π-shifted spatially multiplexed interference phase microscopy. J. Biomed. Opt. 2019, 24, 096004. [Google Scholar] [CrossRef]
- Choi, W.; Fang-Yen, C.; Badizadegan, K.; Oh, S.; Lue, N.; Dasari, R.R.; Feld, M.S. Tomographic phase microscopy. Nat. Methods 2007, 4, 717–719. [Google Scholar] [CrossRef]
- Sung, Y.; Choi, W.; Fang-Yen, C.; Badizadegan, K.; Dasari, R.R.; Feld, M.S. Optical diffraction tomography for high resolution live cell imaging. Opt. Express 2009, 17, 266–277. [Google Scholar] [CrossRef]
- Li, J.; Matlock, A.C.; Li, Y.; Chen, Q.; Zuo, C.; Tian, L. High-speed in vitro intensity diffraction tomography. Adv. Photonics 2019, 1, 066004. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, S.; Ma, C.; Xi, T.; Di, J.; Zhao, J. A review of common-path off-axis digital holography: Towards high stable optical instrument manufacturing. Light. Adv. Manuf. 2021, 2, 333–349. [Google Scholar] [CrossRef]
- Mico, V.; Zalevsky, Z.; Garcia, J. Superresolution optical system by common-path interferometry. Opt. Express 2006, 14, 5168–5177. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Y.; Sun, J.; Jin, Y.; Shen, Q.; Gao, P.; Chen, Q.; Zuo, C. High Bandwidth-Utilization Digital Holographic Reconstruction Using an Untrained Neural Network. Appl. Sci. 2022, 12, 10656. https://doi.org/10.3390/app122010656
Li Z, Chen Y, Sun J, Jin Y, Shen Q, Gao P, Chen Q, Zuo C. High Bandwidth-Utilization Digital Holographic Reconstruction Using an Untrained Neural Network. Applied Sciences. 2022; 12(20):10656. https://doi.org/10.3390/app122010656
Chicago/Turabian StyleLi, Zhuoshi, Yuanyuan Chen, Jiasong Sun, Yanbo Jin, Qian Shen, Peng Gao, Qian Chen, and Chao Zuo. 2022. "High Bandwidth-Utilization Digital Holographic Reconstruction Using an Untrained Neural Network" Applied Sciences 12, no. 20: 10656. https://doi.org/10.3390/app122010656
APA StyleLi, Z., Chen, Y., Sun, J., Jin, Y., Shen, Q., Gao, P., Chen, Q., & Zuo, C. (2022). High Bandwidth-Utilization Digital Holographic Reconstruction Using an Untrained Neural Network. Applied Sciences, 12(20), 10656. https://doi.org/10.3390/app122010656










