Numerical Investigation of Air Entrapment Dynamics for High-Speed Thermal Spraying
Abstract
:1. Introduction
2. Numerical Model
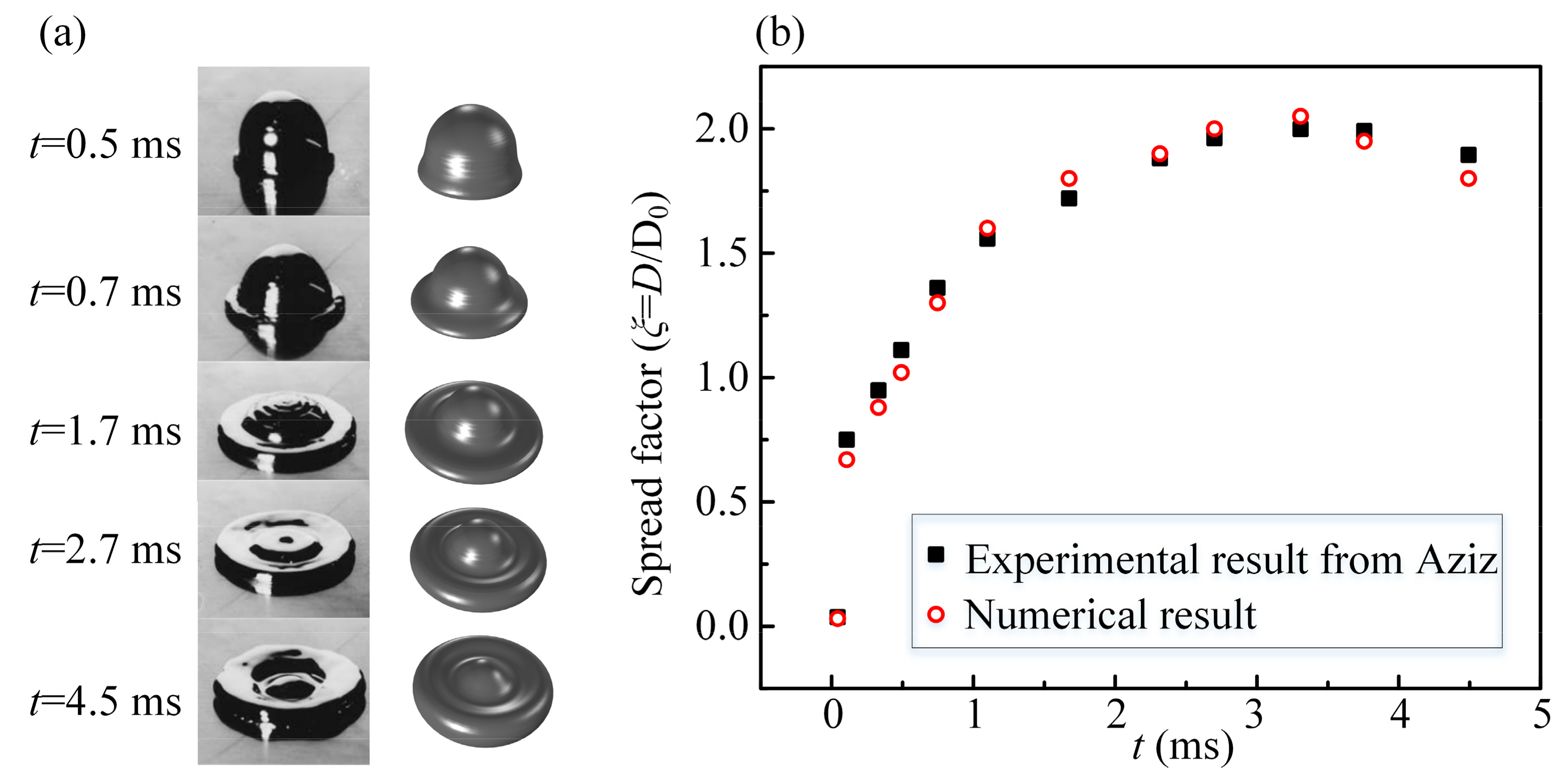
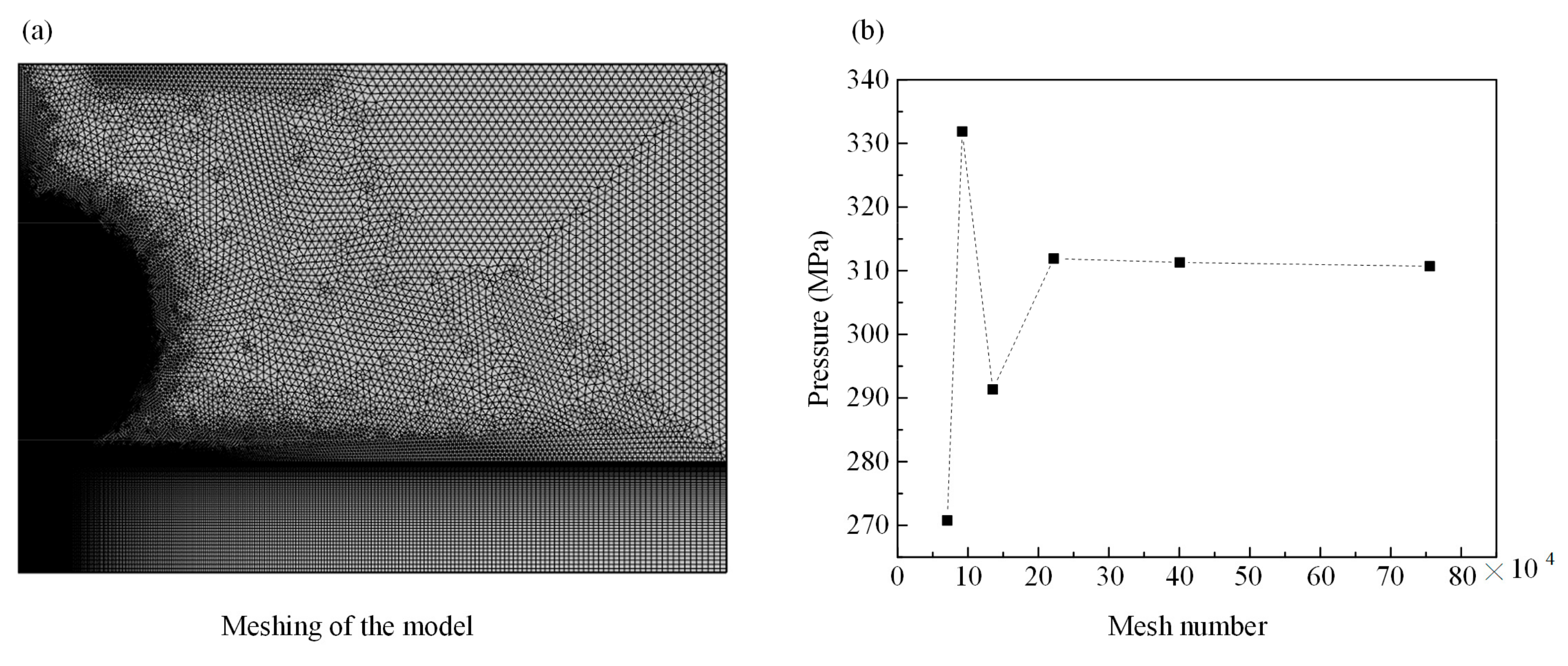
3. Model Validation
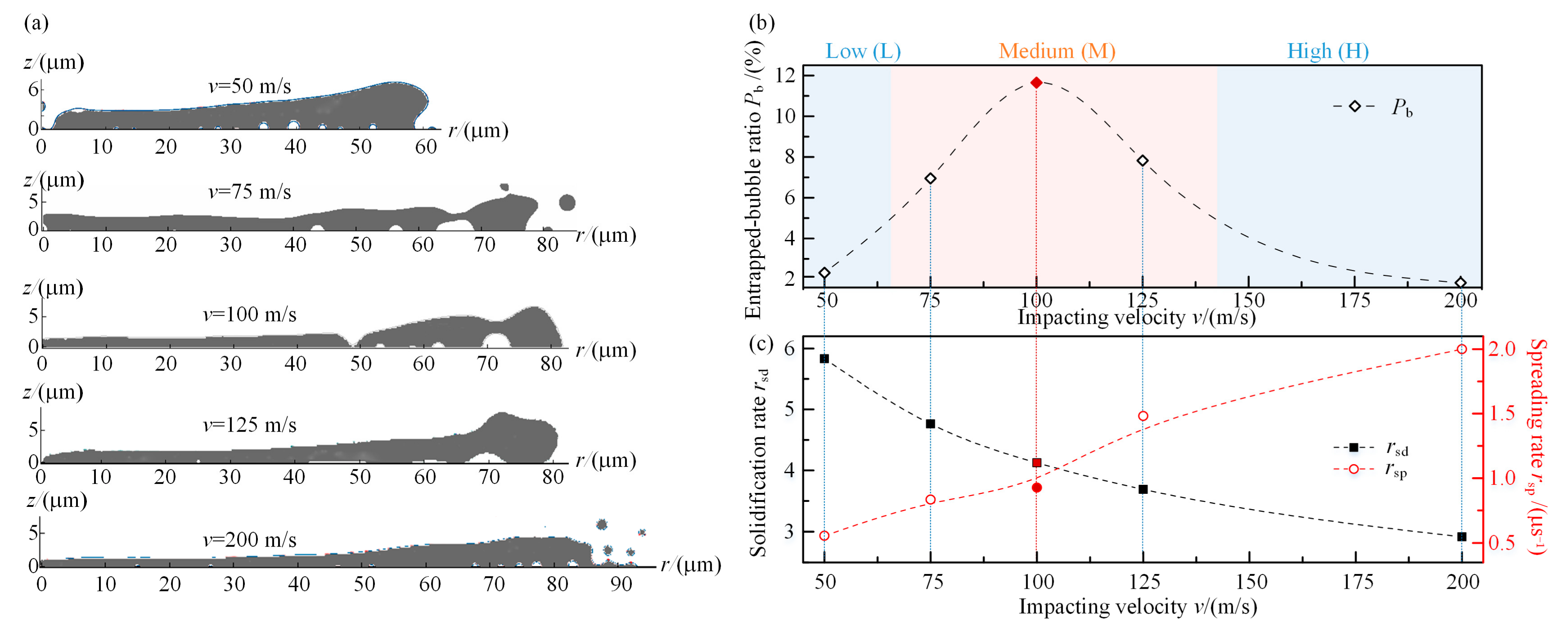
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qin, Y.Z.; Guo, Q.Y.; Chen, R.X.; Zhuang, Y.; Wang, Y.L. Numerical investigation of water droplet impact on PEM fuel cell flow channel surface. Renew Energy 2021, 168, 750–763. [Google Scholar] [CrossRef]
- Almohammadi, H.; Amirfazli, A. Droplet impact: Viscosity and wettability effects on splashing. J. Colloid Interface Sci. 2019, 553, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Andrzej, L.; Ariana, S.P.; Michelle, M.D.; Cacey, S.S.; Nagel, S.R. Creation of Prompt and Thin-Sheet Splashing by Varying Surface Roughness or Increasing Air Pressure. Phys. Rev. Lett. 2012, 109, 054501. [Google Scholar]
- Kenneth, R.L.; Alfonso, A.C.P.; Sigurdur, T.T. Droplet impacts onto soft solids entrap more air. Soft Matter 2020, 16, 5702–5710. [Google Scholar]
- Lee, J.S.; Weon, B.M.; Je, J.H.; Fezzaa, K. How does an air film evolve into a bubble during drop impact? Phys. Rev. Lett. 2012, 109, 204501. [Google Scholar] [CrossRef] [Green Version]
- Zhan, X.H.; Liu, Y.C.; Yi, P.; Feng, W.L.; Feng, Z.H.; Jin, Y.C. Effect of Substrate Surface Texture Shapes on the Adhesion of Plasma-Sprayed Ni-Based Coatings. J. Therm. Spray Technol 2020, 30, 270–284. [Google Scholar] [CrossRef]
- Chandra, S.; Avedisian, C.T. On the collision of a Droplet with a Solid Surface. Proc. R. Soc. Lond. A 1991, 432, 13–41. [Google Scholar] [CrossRef]
- Ruiter, J.D.; Oh, J.M.; Ende, D.V.D.; Mugele, F. Dynamics of Collapse of Air Films in Drop Impact. Phys. Rev. Lett. 2012, 108, 074505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruiter, J.D.; Ende, D.V.D.; Mugele, F. Air cushioning in droplet impact. II. Experimental characterization of the air film evolution, Phys. Fluids 2015, 27, 12105. [Google Scholar]
- Thoroddsen, S.T.; Etoh, T.G.; Takehara, K.; Ootsuka, N.; Hatsuki, Y. The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 2005, 545, 203–212. [Google Scholar] [CrossRef]
- Hicks, P.D.; Purvis, R. Air cushioning and bubble entrapment in three-dimensional droplet impacts. J. Fluid Mech. 2010, 649, 135–163. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Zhang, D.; Zheng, Z.W.; Tian, X.S. Numerical analysis on air entrapment during a droplet impacts on a dry flat surface. Int. J. Heat Mass Transf. 2017, 115, 186–193. [Google Scholar] [CrossRef]
- Yeganehdoust, F.; Attarzadeh, R.; Karimfazli, I.; Dolatabadi, A. A numerical analysis of air entrapment during droplet impact on an immiscible liquid film. Int. J. Multiph. Flow 2020, 124, 103175. [Google Scholar] [CrossRef]
- Qu, M.; Wu, Y.; Srinivasan, V.; Gouldstone, A. Observations of nanoporous foam arising from impact and rapid solidification of molten Ni droplets. Appl. Phys. Lett. 2007, 90, 254101. [Google Scholar] [CrossRef]
- Shukla, R.K.; Kumar, A. Substrate melting and re-solidification during impact of high-melting point droplet material. J. Therm. Spray Technol. 2015, 24, 1368–1376. [Google Scholar] [CrossRef]
- Mehdi-Nejad, V.; Mostaghimi, J.; Chandra, S. Air bubble entrapment under an impacting droplet. Phys. Fluids 2003, 15, 173–183. [Google Scholar] [CrossRef]
- Xiong, W.; Cheng, P. Numerical investigation of air entrapment in a molten droplet impacting and solidifying on a cold smooth substrate by 3D lattice Boltzmann method. Int. J. Heat Mass Transf. 2018, 124, 1262–1274. [Google Scholar] [CrossRef]
- Shukla, R.K.; Kumar, A.; Kumar, R.; Singh, D.; Kumar, A. Numerical study of pore formation in thermal spray coating process by investigating dynamics of air entrapment. Surf. Coat. Technol. 2019, 378, 124972. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Goland, A.; Herman, H.; Allen, A.J.; IIavsky, J.; Long, G.G.; Carlo, F.D. Advanced Microstructural Characterization of Plasma-Sprayed Zirconia Coating Over extended Length Scales. J. Therm. Spray Technol. 2005, 14, 239–250. [Google Scholar] [CrossRef]
- Tabbara, H.; Gu, S. Modelling of impingement phenomena for molten metallic droplets with low to high velocities. Int. J. Heat Mass Transf. 2012, 55, 2081–2086. [Google Scholar] [CrossRef]
- Zhang, Y.; Matthews, S.; Hyland, M. Role of solidification in the formation of plasma sprayed nickel splats through simulation and experimental observation. Int. J. Heat Mass Transf. 2017, 115, 488–501. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.D.M. Inertial effects in droplet spreading: A comparison between diffuse-interface and level-set simulations. J. Fluid Mech. 2007, 576, 287–296. [Google Scholar] [CrossRef]
- Zheng, Y.Z.; Li, Q.; Zheng, Z.H.; Zhu, J.F.; Cao, P.L. Modeling the impact, flattening and solidification of a molten droplet on a solid substrate during plasma spraying. Appl. Surf. Sci. 2014, 317, 526–533. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Aziz, S.D.; Chandra, S. Impact, recoil and splashing of molten metal droplets. Int. J. Heat Mass Transf. 2000, 43, 2841–2857. [Google Scholar] [CrossRef]
- Schiaffno, S.; Sonin, A.A. Molten droplet deposition and solidification at low Weber numbers. Phys. Fluids 1997, 9, 3172–3187. [Google Scholar] [CrossRef]
- Tran, A.T.T.; Brossard, S.; Hyland, M.M.; James, B.J.; Munroe, P. Evidence of substrate melting of NiCr particles on stainless steel substrate by experimental observation and simulations. Plasma Chem. Plasma Process 2009, 29, 475–495. [Google Scholar] [CrossRef]
- Shukla, R.K.; Yadav, S.K.; Shete, M.H.; Kumar, A. Numerical modelling of impact and solidification of a molten alloy droplet on a substrate. In 5th International and 26th All India Manufacturing Technology, Design and Research Conference, Advances in Material Forming and Joining; Narayanan, R., Dixit, U., Eds.; Springer: New Delhi, India, 2014; pp. 307–322. [Google Scholar]
- Bi, Z.M. Finite Element Analysis Applications; Academic Press: Cambridge, MA, USA, 2019; pp. 341–377. [Google Scholar]
- Panwar, V.; Shweta, S.; Chawla, V.; Grover, N.K. A comprehensive review of thermal spray coating for coal fired power plants. Int. J. Mech. Eng. Technol. 2017, 8, 1208–1217. [Google Scholar]
- Zhang, H. Theoretical Analysis of Spreading and Solidification of Molten Droplet During Thermal Spray Deposition. Int. J. Heat Mass Transf. 1999, 42, 2499–2508. [Google Scholar] [CrossRef]
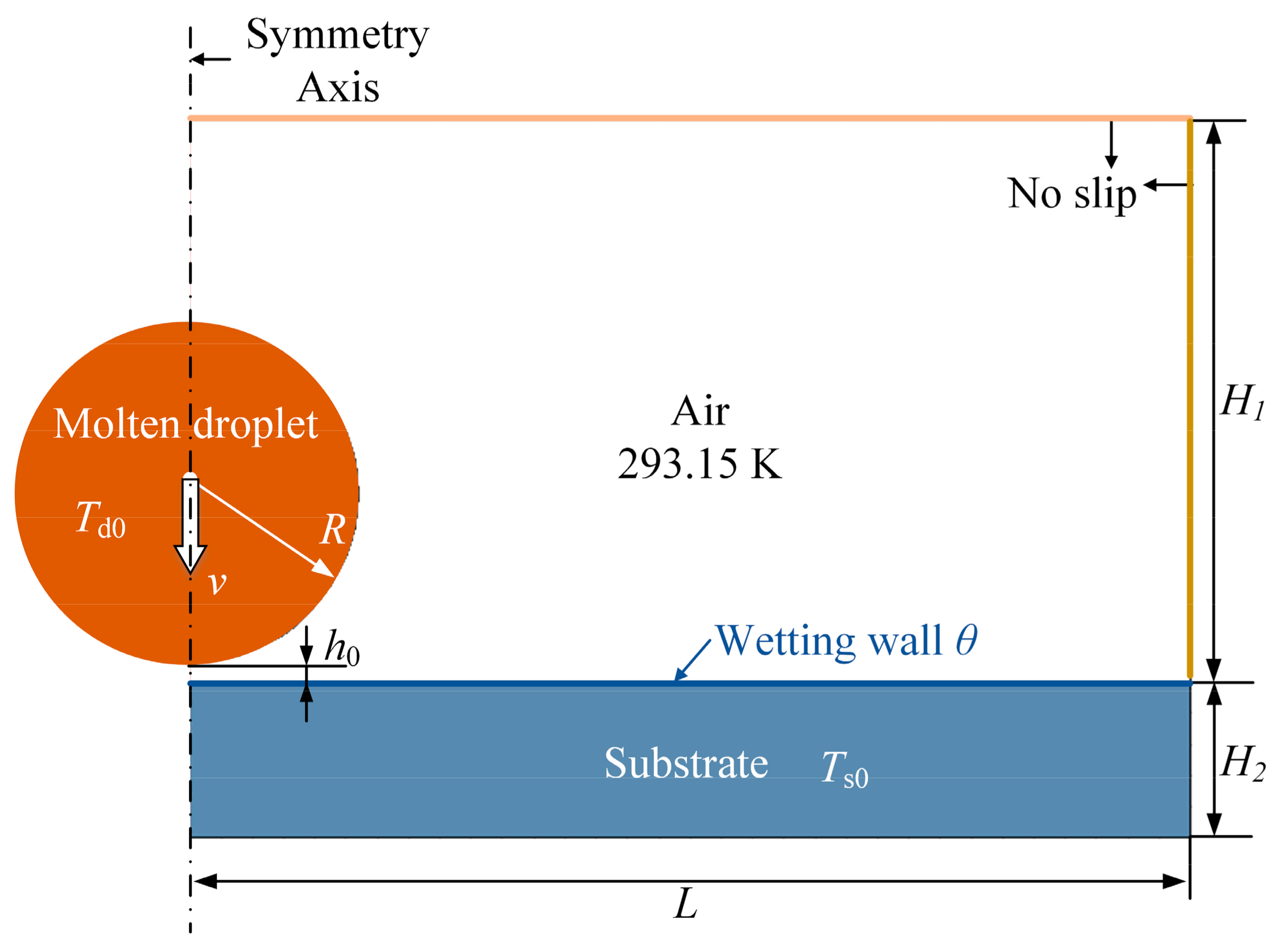
 represents the mushy zone of the molten droplet.
represents the mushy zone of the molten droplet.
 represents the mushy zone of the molten droplet.
represents the mushy zone of the molten droplet.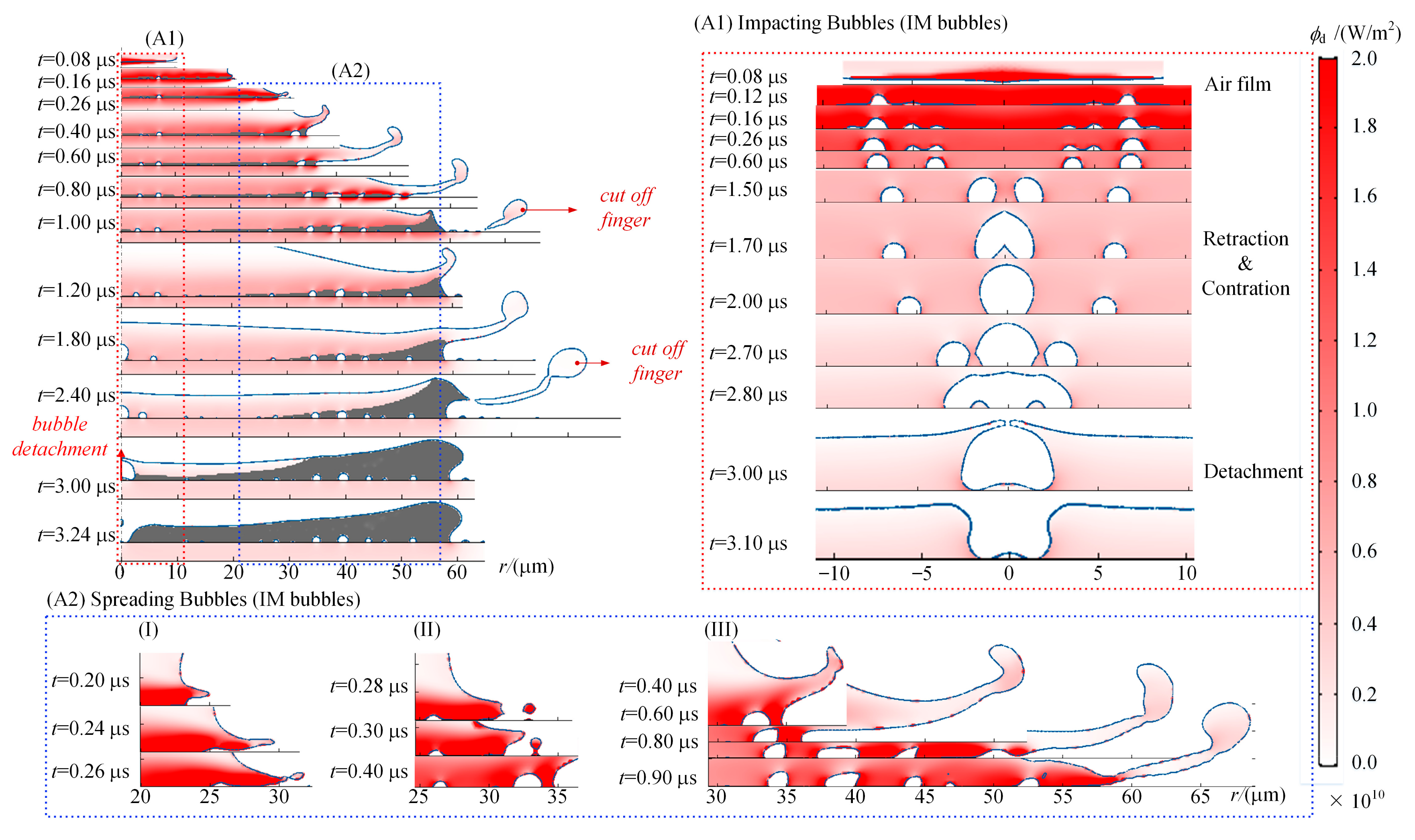
 represents the mushy zone.
represents the mushy zone.
 represents the mushy zone.
represents the mushy zone.
| Material | Melt Point (K) | Density (kg/m3) | Thermal Conductivity (W/m∙K) | Specific Heat (J/kg∙K) | Latent Heat (kJ/kg) | Viscosity (Pa∙s) | Surface Tension (N/m) |
|---|---|---|---|---|---|---|---|
| Nickel | 1728 | 7850 (L) | 69.2 (L) | 735 (L) | 292 | 0.006 (L) | 1.6 (L) |
| 8450 (S) | 80 (S) | 595 (S) | |||||
| Stainless-Steel | 1723 | 7854 | 15 | 480 | — | — | — |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, H.; Wang, K.; Chen, J.; Zhu, R.; Lazarus, M.; Yan, D. Numerical Investigation of Air Entrapment Dynamics for High-Speed Thermal Spraying. Appl. Sci. 2022, 12, 12039. https://doi.org/10.3390/app122312039
Ge H, Wang K, Chen J, Zhu R, Lazarus M, Yan D. Numerical Investigation of Air Entrapment Dynamics for High-Speed Thermal Spraying. Applied Sciences. 2022; 12(23):12039. https://doi.org/10.3390/app122312039
Chicago/Turabian StyleGe, Han, Kaichuang Wang, Jiawang Chen, Ronghua Zhu, Marisa Lazarus, and Dayun Yan. 2022. "Numerical Investigation of Air Entrapment Dynamics for High-Speed Thermal Spraying" Applied Sciences 12, no. 23: 12039. https://doi.org/10.3390/app122312039
APA StyleGe, H., Wang, K., Chen, J., Zhu, R., Lazarus, M., & Yan, D. (2022). Numerical Investigation of Air Entrapment Dynamics for High-Speed Thermal Spraying. Applied Sciences, 12(23), 12039. https://doi.org/10.3390/app122312039





_Zhu.png)


